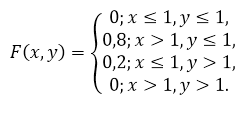Как найти функцию распределения двумерной случайной величины - Avtoru.top

113

Системы
случайных величин. Функция
распределения двумерной случайной
величины. Числовые характеристики
двумерной случайной величины. Коэффициент
корреляции.

9. Системы случайных величин

9.1. Функция распределения двумерной случайной величины

До сих пор мы
рассматривали случайные величины,
возможные значения которых определялись
одним числом. Такие величины называются
одномерными.
Например, число очков, которое может
выпасть при бросании игральной кости,
является случайной величиной; расстояние
от орудия до места падения снаряда –
непрерывной одномерной случайной
величиной. Кроме таких одномерных
величин, часто приходится рассматривать
одновременно системы из двух, трех и
большего числа случайных величин.
Например, координаты точки попадания
при стрельбе характеризуются двумя
случайными величинами: абсциссой и
ординатой; осколок, образовавшийся при
разрыве снаряда, характеризуется рядом
случайных величин: весом, размерами,
начальной скоростью, направлением
полета и т.д.

При рассмотрении
вопросов, связанных с системами случайных
величин, удобно пользоваться геометрической
интерпретацией системы. Например,
систему двух случайных величин {X₁,
X₂}
можно изобразить случайной
точкой
на плоскости с координатами X₁
и X₂.
Часто вместо образа случайной точки
для геометрической интерпретации
пользуются образом случайного
вектора

В дальнейшем мы
будем в зависимости от удобства
пользоваться как одной, так и другой
интерпретацией. Изложение мы проводить
в основном для случая двумерных величин.
Общий n-мерный
случай рассматривается совершенно
аналогично.

Функцией
распределения
F(x,
y)
двумерной
случайной
величины
{X,
Y}
называется
вероятность совместного выполнения
двух неравенств:
X<x,
Y<y:

.
(9.1)

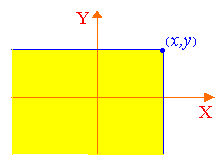
Рис.
9.1

Двумерная функция распределения,
по определению, представляет собой не
что иное, как вероятность попадания
точки с координатами {X,
Y}
в бесконечный квадрант с вершиной в
точке (x,y),
лежащий левее и ниже ее (см. рис. 9.1).

Рассмотрим свойства
двумерной функции распределения, которые
аналогичны свойствам функции распределения
одномерной случайной величины.

Так как F(x,y)
– вероятность, то очевидно следующее
свойство:

Свойство
1.
Функция
распределения – величина неотрицательная,
не превышающая единицы:

Свойство
2.
Функция
распределения есть неубывающая функция
по каждому аргументу:

Эти неравенства
следуют из свойств одномерных функций
распределения, которые получаются из
F(x,y)
при фиксировании y
и x
соответственно.

Свойство
3. Если
хотя бы один из аргументов стремится к
–,
то функция распределения стремится к
нулю:

Эти равенства
следуют из того, что события {X₁<–}
и {X₂<–}
есть события невозможные.

Свойство
4. Если
оба аргумента стремятся к +,
то функция распределения стремится к
единице:

Это равенство
следуют из того, что события {X₁<+}
и {X₂<+}
есть события достоверные.

Свойство
5. Если
один из аргументов обращается в +,
то функция распределения F(x,y)
становится функцией распределения,
соответствующей другому аргументу:

Первое равенство
следуют из того, что события {Y<+}
есть событие достоверное, тогда F(x,+)
определяет вероятность события {X<x},
т.е. представляет собой функцию
распределения составляющей X.
Аналогично обосновывается второе
равенство.

Зная функцию
распределения F(x,y)
можно найти вероятность попадания
случайной величины {X,
Y}
в прямоугольник со сторонами R=(x₁X<x₂,
y₁Y<y₂):

.
(9.2)

Рис.
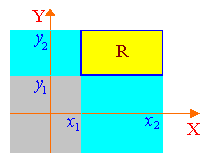
9.2

Действительно, вероятность попадания
в прямоугольникR
равна вероятности попадания в квадрант
(x₂,y₂)
минус вероятность попадания в квадрант
(x₁,y₂)
минус вероятность попадания в квадрант
(x₂,y₁)
плюс вероятность попадания в квадрант
(x₁,y₁)
(так как мы дважды вычли вероятность
попадания в этот квадрант).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Двумерная непрерывная случайная величина

Краткая теория
Примеры решения задач

Краткая теория

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

на плоскости

либо как случайный вектор

Непрерывной называют двумерную величину, составляющие которой непрерывны.

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Функция распределения двумерной случайной величины и ее свойства

Функцией распределения двумерной случайной величины

называют функцию

, определяющую для каждой
пары чисел

вероятность того, что

примет значение, меньшее

, и при этом

примет значение, меньшее

Свойство 1.

Значения
функции распределения удовлетворяют двойному неравенству:

Свойство 2.

есть неубывающая функция по каждому аргументу,
то есть:

если

Свойство 3.

Имеют место предельные соотношения:

Свойство 4.

При

функция распределения системы становится
функцией распределения составляющей

При

функция распределения системы становится
функцией распределения составляющей

Плотность распределения двумерной случайной величины и ее свойства

Плотностью совместного распределения вероятностей

двумерной непрерывной случайной величины

называют вторую смешанную частную производную
от функции распределения:

Зная
плотность совместного распределения

можно найти функцию распределения

по формуле:

Свойство 1.

Двумерная
плотность вероятности неотрицательна:

Свойство 2.

Двойной
несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Безусловные и условные законы распределения составляющих

Пусть
известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из составляющих.

Аналогично
находится плотность распределения составляющей

Итак,
плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения системы, причем
переменная интегрирования соответствует другой составляющей.

Пусть

— непрерывная двумерная случайная величина.

Условной
вероятностью

распределения составляющих

при данном значении

называют отношение плотности совместного
распределения

системы

к плотности распределения

составляющей

Аналогично
определяется условная плотность составляющей

при данном значении

Если
известна плотность совместного распределения

, то условные плотности
составляющих могут быть найдены по формулам:

Эти
формулы можно записать в виде:

Аналогично
определяется условная плотность составляющей

при данном значении

То есть
умножая закон распределения одной из составляющих на условный закон
распределения другой составляющей, найдем закон распределения системы случайных
величин.

Смежные темы решебника:

Двумерная дискретная случайная величина
Линейный выборочный коэффициент корреляции
Парная линейная регрессия и метод наименьших квадратов

Примеры решения задач

Пример 1

Найти
плотность совместного распределения f(x,y) системы случайных величин (X,Y) по
известной функции распределения:

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

По определению плотности совместно
распределения:

Искомая плотность совместного распределения:

Пример 2

Найти
функцию распределения системы случайных величин F(x,y) по известной плотности
совместного распределения f(x,y):

Решение

Воспользуемся
формулой:

В нашем
случае:

Ответ:

Пример 3

Двумерная
случайная величина (X,Y) имеет равномерное распределение вероятностей в
треугольнике ABC. Определить функции плотности распределения
компонент этой случайной величины f(x), f(y), их математические
ожидания M(X), M(Y), дисперсии D(X), D(Y),
коэффициент корреляции r_xy. Выяснить, являются ли
случайные величины X и Y независимыми?

A(0;0),B(-1;1),C(1;1)

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

где

– площадь треугольника

Разделим
область

на две равные части вдоль оси

, тогда из условия:

или

Тогда
плотность двумерной случайной величины

Вычислим
плотность составляющей

при

Откуда
плотность составляющей

Вычислим
плотность составляющей

при

Плотность
составляющей

Найдем
условную плотность составляющей

при

Следовательно,
случайные величины

зависимы

Найдем
математическое ожидание случайной величины

Найдем
дисперсию случайной величины

Найдем
математическое ожидание случайной величины

Найдем
дисперсию случайной величины

Найдем
математическое ожидание двумерной случайной величины

Тогда
ковариация:

Значит
коэффициент корреляции:

Следовательно,
случайные величины

– зависимые, но некоррелированные

Пример 4

Двумерная
случайная величина (X,Y) имеет плотность
распределения:

Найти
вероятность попадания значения (X,Y) в область x₁≤x≤x₂,
y₁≤y≤y₂, вероятность попадания значения X в
интервал x₁≤x≤x₂, математическое ожидание M[X] и
условное математическое ожидание M[Y⁄X=x].

a=8, b=2, x₁=6, x₂=9, y₁=0, y₂=4

Решение

Найдем
вероятность попадания в область

по формуле:

При
вычислении интеграла учитывается та часть области

, где

, т.е.

Плотность
вероятности для составляющей

имеет вид:

Если

или

, то

. При

находим:

Таким
образом, плотность имеет вид:

Тогда:

Условное математическое ожидание

определяется с
помощью условной плотности распределения

составляющей

Получаем:

Искомое
математическое ожидание:

Краткая теория
Примеры решения задач

Источник

Елена Борисовна Калюжная

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Для начала напомним следующие определения:

Определение 1

Случайная величина называется двумерной, если она определяется двумя числами и обозначается $(X,Y)$.

Определение 2

Для одномерной случайной величины $X$ функцией распределения называется функция, удовлетворяющая равенству

[Fleft(xright)=P(X

Введем теперь аналогичное определение для функции распределения двумерной случайной величины $(X,Y)$.

Определение 3

Для двумерной случайной величины $(X,Y)$ интегральной функцией распределения называется функция, удовлетворяющая равенству

[Fleft(x,yright)=P(X

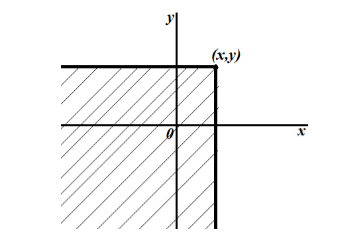
Геометрически данное определение можно истолковать следующим образом: интегральная функция распределения геометрически определяет вероятность попадания случайной величины $(X,Y)$ в бесконечный квадрат, правая верхняя вершина которого лежит в точке $(x,y)$ (рис. 1).

Рисунок 1. Геометрическое изображение функции $F(x)$.

Отметим несколько свойств функции распределения двумерной случайной величины:

Свойство 1: Все значения функции распределения лежат в промежутке $[0,1]$:

[0le F(x,y)le 1]

Свойство 2: Функция распределения не убывает по каждой из своих компонент:

[Fleft(x_2,yright)ge Fleft(x_1,yright), если x_2Это свойство непосредственно следует из случая с одномерной случайной величиной.

Свойство 3: Если хотя бы одна из переменных $x$ или $y$ стремится к $-infty $, то сама функция распределения стремится к нулю:

[Fleft(-infty ,yright)=Fleft(x,-infty right)=Fleft(-infty ,-infty right)=0]

Это следует из того, что события $(X

Свойство 4: Если обе переменные $x$ и $y$ стремятся к $+infty $, то сама функция распределения стремится к единице:

[Fleft(+infty ,+infty right)=1]

Это следует из того, что события $(X

Свойство 5: Если одна из переменных функции распределения стремится к $+infty $, то функция распределения двумерной величины становится функцией распределения одномерной случайной величины, которая не стремится к $+infty $.

[Fleft(+infty ,yright)=Fleft(yright)=P(YЭто свойство также следует из того, что события $(X

Плотность распределения двумерной случайной величины.

С понятием функции распределения двумерной случайной величины тесно связано понятие плотности двумерной случайной величины. Придадим значениям $x и y$ двумерной случайной величины приращения $triangle x$ и $triangle y$.

Определение 4

Определение 4: Функция $varphi (x,y)$ называется плотностью распределения двумерной случайной величины $(X,Y)$, если, с точностью до бесконечно малых высшего порядка относительно $triangle p=sqrt{{triangle x}^2+{triangle y}^2}$, выполняется равенство:

[P(x

Геометрически выражение $P(x

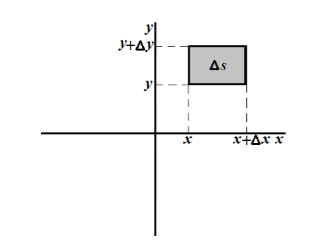
Обозначим этот прямоугольник через $triangle s$. Тогда равенство в определении плотности распределения можно записать следующим образом:

[P((X,Y)in triangle )approx varphi (x,y)triangle s]

Отметим, что функция распределения и функция плотности распределения двумерной случайной величины, аналогично одномерному случаю, связаны по формуле:

[Fleft(x,yright)=intlimits^x_{-infty }{intlimits^y_{-infty }{varphi left(t,zright)dtdz}}]

Функция распределения дискретной двумерной случайной величины

Пусть случайная величина $(X,Y)$ является дискретной. И пусть для нее дан закон её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:

[Fleft(x,yright)=Pleft(XФункция распределения непрерывной случайной величины

Пусть случайная величина $(X,Y)$ теперь является непрерывной. И пусть для нее дана плотность её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:

[Fleft(x,yright)=intlimits^x_{-infty }{intlimits^y_{-infty }{varphi left(t,zright)dtdz}}]

где $varphi left(x,yright)$ — плотность непрерывной случайной величины $(X,Y)$.

Пример задачи на нахождение функции распределения двумерной случайной величины

Пример 1

Вероятность попадания футбольным игроком по воротам при одном ударе равна $0,8$. Найти интегральную функцию распределения числа попаданий и промахов при этом ударе.

Решение.

Составим сначала закон распределения данной случайной величины. Пусть $X$ число попаданий по воротам, а $Y$ — число промахов по воротам. Вероятность промаха равна $1-0,8=0,2$. Из этого всего получаем следующий закон распределения случайной величины $(X,Y)$:

Рисунок 3.

Замечание: по главной диагонали нули, так как нельзя одновременно и попасть и промахнуться.

Из полученного закона, очевидно, что функция распределения имеет вид:

Рисунок 4.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

9. Системы случайных величин

9.1. Функция распределения двумерной случайной величины

Двумерная непрерывная случайная величина

Краткая теория

Функция распределения двумерной случайной величины и ее свойства

Плотность распределения двумерной случайной величины и ее свойства

Безусловные и условные законы распределения составляющих

Примеры решения задач

Пример 1

Пример 2

Пример 3

Пример 4

Функция распределения дискретной двумерной случайной величины

Пример задачи на нахождение функции распределения двумерной случайной величины

Не пропустите также: