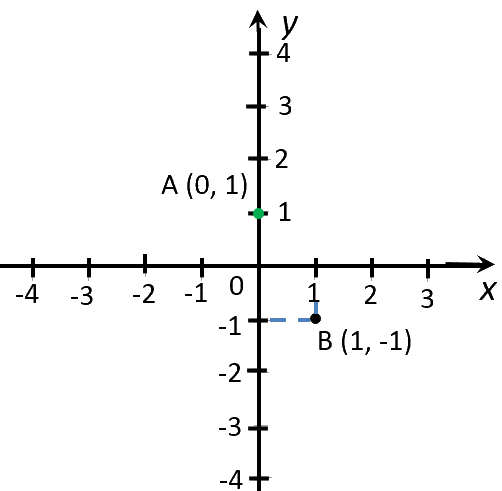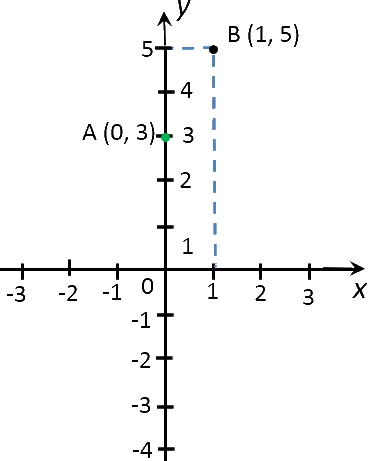построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Инфоурок
›
Алгебра
›Конспекты›Алгоритм определения формулы линейной функции по графику
Алгоритм определения формулы линейной функции по графику
Скачать материал
Скачать материал


- Сейчас обучается 971 человек из 80 регионов


- Сейчас обучается 98 человек из 37 регионов


- Сейчас обучается 105 человек из 36 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 743 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема
16. Линейная функция и её график
Больше материалов по этой теме
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Скачать материал
-
30.09.2020
54984
-
DOCX
549.2 кбайт -
253
скачивания -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 104353
-
Всего материалов:
37
Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Важно!
Функцию вида «y = kx + b» называют линейной функцией.
Буквенные множители «k» и «b»
называют
числовыми коэффициентами.
Вместо «k» и «b»
могут стоять любые числа (положительные, отрицательные или дроби).
Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.
Примеры функций типа «y = kx + b».
- y = 5x + 3
- y = −x + 1
- y = x − 2
- y = 0,5x
Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».
| Функция | Коэффициент «k» | Коэффициент «b» | ||||
|---|---|---|---|---|---|---|
| y = 5x + 3 | k = 5 | b = 3 | ||||
| y = −x + 1 | k = −1 | b = 1 | ||||
y =
x − 2 |
k =
|
b = −2 | ||||
| y = 0,5x | k = 0,5 | b = 0 |
Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».
Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.
Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.
Как построить график линейной функции
«y = kx + b»
Запомните!
Графиком линейной функции «y = kx + b» является прямая.
Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.
Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.
Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.
Для примера построим график функции «y = −2x + 1».
Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».
Важно!
Выбирая произвольные числовые значения вместо «x», лучше брать числа
«0» и «1».
С этими числами легко выполнять расчеты.
| x | Расчет «y = −2x + 1» |
|---|---|
| 0 | y(0) = −2 · 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Полученные значения «x» и «y» — это координаты точек графика функции.
Запишем полученные координаты точек «y = −2x + 1» в таблицу.
| Точка |
Координата по оси «Оx» (абсцисса) |
Координата по оси «Оy» (ордината) |
|---|---|---|
| (·)A | 0 | 1 |
| (·)B | 1 | −1 |
Отметим полученные точки на системе координат.
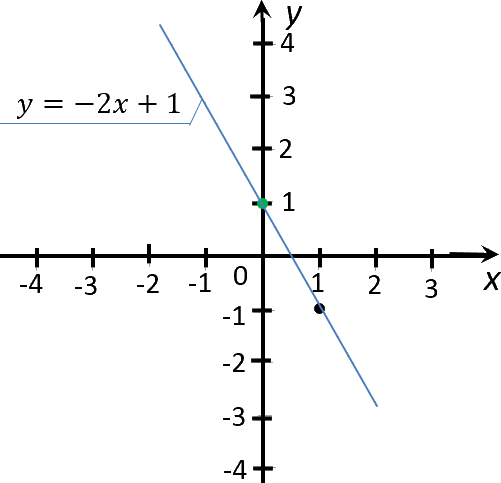
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».
Как решать задачи на
линейную функцию «y = kx + b»
Рассмотрим задачу.
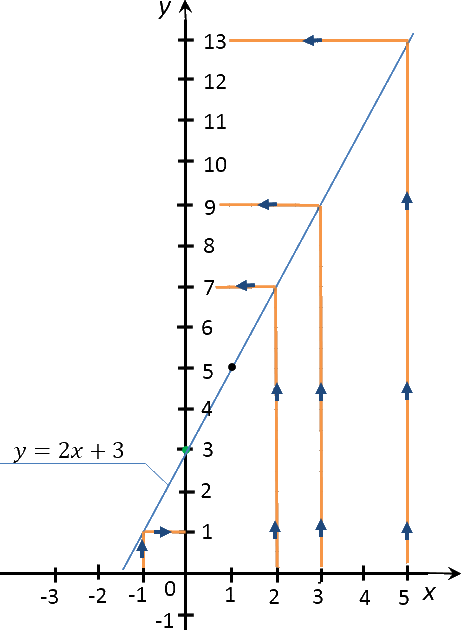
Построить график функции «y = 2x + 3». Найти по графику:
- значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
- значение «x», если значение «y» равно
1; 4; 0; −1.
Вначале построим график функции «y = 2x + 3».
Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.
Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».
Выполним расчеты и запишем их результаты в таблицу.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = 2 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = 2 ·1 + 3 = 5 |
Отметим полученные точки на прямоугольной системе координат.
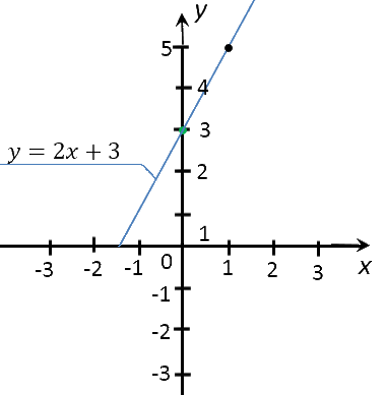
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».
Теперь работаем с построенным графиком функции «y = 2x + 3».
Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.
Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Запомните!
Чтобы найти значение «y» по известному значению «x» на графике
функции необходимо:
- провести перпендикуляр от оси «Ox»
(ось абсцисс)
из заданного числового значения «x»
до пересечения
с графиком функции; - из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«Oy»
(ось ординат); - полученное числовое значение на оси «Oy» и будет искомым значением.
По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.
Запишем полученные результаты в таблицу.
| Заданное значение «x» | Полученное с графика значение «y» |
|---|---|
| −1 | 1 |
| 2 | 7 |
| 3 | 9 |
| 5 | 13 |
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.
Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».
Запишем полученные результаты в таблицу.
| Заданное значение «y» | Полученное с графика значение «x» |
|---|---|
| −1 | −2 |
| 0 | −1,5 |
| 1 | −1 |
| 4 | 0,5 |
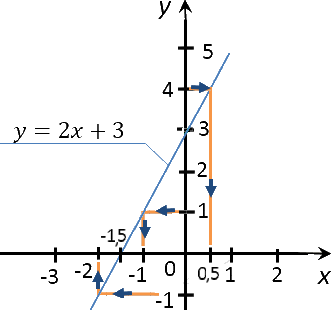
Как проверить, проходит ли график через точку
Рассмотрим другое задание.
Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).
Запомните!
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Подставим в функцию
«y = 2x −
»
координаты точки (0;
− ).
− = 2 · 0
−
− =
−
(верно)
Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).
Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».
−2 = 2 · 1 −
−2 = 2 −
−2 = 1 −
−2 = 1 (неверно)
Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).
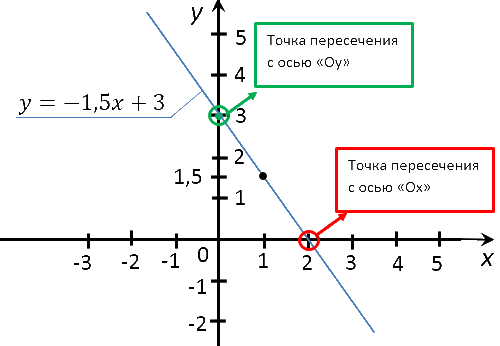
Как найти точки пересечения графика с осями
Рассмотрим задачу.
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.
Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.
Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».
Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = −1,5 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = −1,5 · 1 + 3 = 1,5 |
Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.
Запомните!
Чтобы найти координаты точки пересечения графика функции
с осью
«Oy»
(осью ординат)
нужно:
- приравнять координату точки по оси
«Ox» к нулю
(x = 0); - подставить вместо «x» в формулу функции ноль и найти значение
«y»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.
y(0) = −1,5 · 0 + 3 = 3
(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».
Запомните!
Чтобы найти координаты точки пересечения графика функции
с осью
«Ox»
(осью абсцисс)
нужно:
- приравнять координату точки по оси
«Oy» к нулю
(y = 0); - подставить вместо «y» в формулу функции ноль и найти значение
«x»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.
0 = −1,5x + 3
1,5x = 3 | :(1,5)
x = 3 : 1,5
x = 2
(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».
Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».
Важно!
Если нужно найти координаты точки пересечения графика с осью
«Ox», то приравниваем
«y» к нулю.
И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«Oy»,
то приравниваем «x» к нулю.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
19 мая 2023 в 9:06
Михаил Лысенко
Профиль
Благодарили: 0
Сообщений: 1
Михаил Лысенко
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
19 мая 2023 в 13:04
Ответ для Михаил Лысенко
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Добрый день!
Это квадратичная функция. Они разобраны в другом уроке
0
Спасибо
Ответить
Линейные функции
Движение с постоянной скоростью (или равномерное движение) по определению – это движение, при котором с изменением времени на одну и ту же величину, пройденный путь также изменяется одинаково (Рис. 1).
Рис. 1. График изменения пути при равномерном движении
Такие функции, как , у которых одинаковые изменения аргумента приводят к одинаковым изменениям значения функции (Рис. 2), называются линейными функциями.
Рис. 2. Одинаковые изменения аргумента приводят к одинаковым изменениям значениям функции
Правильнее было бы называть их прямолинейными (потому что их графиками являются прямые, о чём мы поговорим чуть позже), но прижилось именно такое сокращенное название.
Примеры линейных функций в жизни
Линейную функцию (или линейную зависимость) мы часто используем в жизни. Например, если из книги, в которой 50 страниц, мы за день прочитали 10 страниц, то можно сделать предположение, что всю книгу мы прочитаем за 5 дней (Рис. 3).
Рис. 3. Пример линейной зависимости в жизни
Или если мы идем в школу и прошли третью часть пути за 5 минут, то предполагаем, что на оставшийся путь потратим 10 минут.
Конечно, вряд ли мы будем успевать читать каждый день одно и то же количество страниц или будем идти в школу, не меняя свою среднюю скорость движения. Но для оценки значения некоторых величин, как видим, линейная функция является удобным инструментом.
Различные классы функций
Чтобы изучать какие-то объекты, их часто разбивают на группы, которые чем-то похожи. Например, разных живых организмов очень много, поэтому, чтобы их изучать, их делят на царства (животные, растения и т.д.), которые в свою очередь также делятся на более мелкие группы.
Различных функций очень много, поэтому для изучения их разбивают на разные классы. Как в жизни, мы объединяем объекты в одну группу по некоторым общим признакам (например, в супермаркете – хлебобулочные изделия, бакалея, соки-воды и т.д.), так и классы функций объединяют функции одного вида.
Линейные функции – один из этих классов (Рис. 4). Все остальные функции – нелинейные и их гораздо больше: реальные процессы описываются, в основном нелинейными функциями (Рис. 5).
Рис. 4. Линейные функции
Рис. 5. Нелинейные функции
Но, во-первых, линейные функции мы умеем изучать и описывать, а во-вторых, многие нелинейные функции в малых областях можно рассматривать как линейные (Рис. 6).
Рис. 6. Приближение нелинейных функций линейными
Значит, линейные функции можно использовать как удобный инструмент для изучения других функций.
Конечно, линейные функции – не единственный класс функций, который мы умеем и будем изучать. Ещё будут квадратичные функции, показательные, обратная пропорциональность и т.д. Но о них поговорим позже.
Аналитическое задание линейной функции и ее характеристическое свойство
Итак, линейные функции часто встречаются и их можно изучать. Поэтому на этом уроке мы и займемся этим классом функций.
Аналитически линейная функция задается формулой , где
и
– произвольные заданные числа,
– угловой коэффициент,
– свободный коэффициент (свободен от
).
Ее характеристическое свойство (т.е. свойство, которым обладают только линейные функции, ее эквивалентное определение) состоит в том, что при изменении аргумента на одну и ту же величину значение функции так же изменяется на одну и ту же величину.
Только для линейных функций совершенно неважно, изменился на
от
до
или от
до
и т.д. –
тоже изменится одинаково (Рис. 7).
Рис. 7. Эквивалентное определение линейной функции
Например, растём мы нелинейно (с до
лет и с
до
изменение роста сильно отличается), бегаем – тоже (бежать первый километр значительно легче, чем, например, пятый) и т.д.
Линейное уравнение с двумя переменными
Рассмотрим линейное уравнение .
Мы уже умеем его решать – для этого перенесем число из левой части в правую, затем разделим на коэффициент при переменной:
Рассмотрим похожее уравнение . Его решение будет практически таким же:
Аналогично:
Обобщим рассмотренные уравнения и напишем в правой части число , решение от этого не изменится:
Когда меняется значение , меняется и значение
. Если мы не знаем значение
, то тогда в уравнении
две неизвестных:
и
.
Уравнение вида называют линейным уравнением с двумя переменными, где
– переменные,
– произвольные числа.
Перепишем уравнение следующим образом:
.
Если , то на него мы можем разделить обе части уравнения:
.
Перепишем так, чтобы один член был с переменной , а второй – без:
Переобозначим коэффициенты:
Тогда .
Т.е. линейное уравнение с двумя переменными задает линейную функцию.
Рассмотрим отдельно случай, когда :
При мы получим
. Или просто
.
Такое уравнение тоже задает прямую (только вертикальную), но линейной функцией не является, т.к. одному значению
(
) соответствует бесконечное множество значений
(Рис. 1).
Рис. 1. Одному значению соответствует бесконечное множество значений
Построение графика линейной функции
Чтобы охарактеризовать поведение функции, обычно строят ее график.
Пример 1. Построить график функции .
Решение:
Найдем несколько значений при различных значениях
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь возьмем пары и отметим их в декартовой системе координат (Рис. 8).
Рис. 8. Построение графика линейной функции
Соединим отмеченные точки линией (Рис. 9).
Рис. 9. Построение графика линейной функции
Похоже, что все точки лежат на одной прямой. И на самом деле графиком любой линейной функции является прямая.
Полученная прямая и есть график линейной функции .
На уроках геометрии мы уже обсуждали, что через две точки можно провести только однупрямую. Поэтому, если мы найдем две точки, которые принадлежат графику линейной функции (т.е. прямой), мы сможем его построить. Вывод: для построения графика линейной функции достаточно найти координаты двух точек, которые ей принадлежат (найти значения
при любых двух значениях
).
Интерполяция и аппроксимация
При проведении различных исследований возникает такая задача: по некоторым известным значениям функции попытаться восстановить саму функцию (график или формулу) (Рис. 1). Если мы знаем, что функция линейная, то достаточно двух значений (прямая однозначно задаётся двумя точками).
Рис. 1. Восстановление функции по некоторым известным значениям функции
Например, сила растяжения пружины зависит от растяжения пружины по закону Гука (Рис. 2).
Достаточно измерить силу для двух различных значений растяжения пружины, чтобы найти жёсткость пружины (коэффициент ) и восстановить функцию (Рис. 3).
Рис. 2. Закон Гука
Рис. 3. Нахождение жёсткости пружины при помощи закона Гука
Но можно ли попытаться восстановить функцию, не зная, какой вид она имеет? (Рис. 4).
Рис. 4. Восстановление функции, вид которой заранее неизвестен
Такая задача называется аппроксимацией – на основании экспериментального набора значений функции в нескольких точках построить функцию, на которую с высокой точностью попадут получаемые в ходе эксперимента значения (как те, что у нас уже есть, так и остальные, которые можно получить).
Если мы хотим, чтобы построенной функции точно принадлежали все имеющиеся значения функции, то этот частный случай аппроксимации называется интерполяцией.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации (т.е. приближении) какой-либо сложной функции другой, более простой функцией. (Рис. 5).
Рис. 5. Приближение сложной функции к более простой
Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но для некоторых задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Подробнее почитать об интерполяции и аппроксимации можно в Интернете.
Пример 2. Построить график функции .
Решение:
Возьмем два произвольных значения переменной , например, 0 и 4.
Двух точек нам достаточно, чтобы построить прямую. Поэтому возьмем полученные пары , отметим их в декартовой системе координат и соединим их линией (Рис. 10).
Рис. 10. Иллюстрация к примеру 2
Частные случаи линейных функций
Отдельно рассматривают два частных случая линейной функции :
,
.
Если , то функцию
называют прямой пропорциональностью. Ее график всегда проходит через начало координат. Например,
(Рис. 11).
Рис. 11. Графики прямой пропорциональности
О втором типе линейных функций мы поговорим чуть позже.
Угловой коэффициент 
Название углового коэффициента неслучайно: в зависимости от его значений будет изменяться угол наклона прямой по отношению к положительному направлению оси абсцисс.
1. – угол наклона острый.
Рассмотрим на примере функции (Рис. 12).
Рис. 12. Угловой коэффициент
2. – угол наклона тупой.
Рассмотрим на примере функции (Рис. 13).
Рис. 13. Угловой коэффициент
3. – прямая параллельная оси абсцисс.
Рассмотрим на примере функции (Рис. 14).
Рис. 14. Угловой коэффициент
Теперь посмотрим, какое значение будет принимать функция , когда
:
Мы получили, что графику прямой принадлежит точка , это его точка пересечения с осью ординат (Рис. 15).
Рис. 15. Значение линейной функции при
Параллельность и пересечение прямых
Мы знаем, что на плоскости две прямые могут или пересекаться, или быть параллельными. Зададим условия, при которых графики двух линейных функций будут параллельны.
Прямые и
будут параллельными тогда, когда у них совпадают угловые коэффициенты:
. Например,
;
;
(Рис. 16).
Рис. 16. Параллельные прямые
Доказательство
Пусть у нас есть две различных прямых, у которых равны угловые коэффициенты (Рис. 1).
Рис. 1. Прямые с одинаковыми угловыми коэффициентами
Докажем, что эти прямые параллельны, методом от противного.
Пусть они непараллельны, т.е. пересекаются, тогда существует точка с абсциссой , в которой их значение совпадает (Рис. 2).
Рис. 2. Предположение, что прямые пересекаются в точке
Перепишем в эквивалентном виде: .
Тогда , т.е. прямые совпадают. Получили противоречие, т.к. заданы разные прямые. Значит, наше предположение неверно, прямые не пересекаются, т.е. они параллельны.
Прямые и
пересекаются тогда, когда их угловые коэффициенты не равны:
. Например,
,
(Рис. 17).
Рис. 17. Пересекающиеся прямые
Перпендикулярность
Для пересекающихся прямых можно выделить особый случай, когда при пересечении получаются равные углы (прямые), т.е. прямые перпендикулярны (Рис. 1).
Рис. 1. Перпендикулярные прямые
Прямые и
перпендикулярны, когда выполнено
.
Пример 1
Графики этих функций действительно перпендикулярны (Рис. 2).
Рис. 2. Пример перпендикулярных прямых
Заключение
На этом уроке мы познакомились с линейной функцией (функцией, у которой при одинаковом изменении аргумента одинаково меняется значение самой функции).
Аналитически такие функции задаются уравнением , где
– произвольные числа,
– угловой коэффициент,
– свободный коэффициент.
Ее график – прямая. Чтобы его построить, достаточно найти две точки, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент – за точку пересечения графика функции с осью ординат.
Прямые параллельны, если их угловые коэффициенты равны () и пересекаются, если
.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, издательство «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал youclever.org (Источник)
- Интернет-портал tofmal.ru (Источник)
Домашнее задание
- Линейная функция задана формулой
. Найти значение
, соответствующее
. При каком значении
значение
равно
?
- Построить график функции, заданной уравнением:
.
- У ученика было
рублей. На эти деньги он купил
марок по
рублей. После покупки у него осталось
рублей. Задать формулой зависимость
от
. Является ли эта зависимость линейной?
Материал используется на уроке алгебры в 7 классе при изучении линейной функции.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
2 урок . По графику научить определять заданную функцию. Тема «Линейная функция и её график».
Слайд 2
На рисунке представлен график функции у = kx + b. Записать формулу линейной функции, соответствующей данному графику. Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1. у = kx + 1 Выбираем на графике произвольную точку и определяем её координаты: если x = 2, то у = 2 . Подставим в нашу формулу и получим уравнение относительно k. 2 = 2k+1 2k=1 k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.
По теме: методические разработки, презентации и конспекты
- Мне нравится