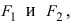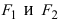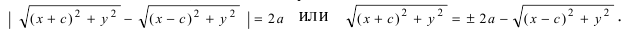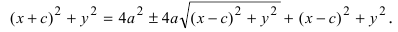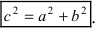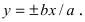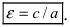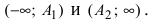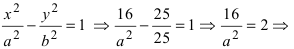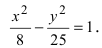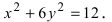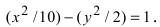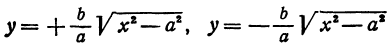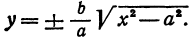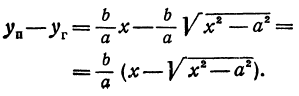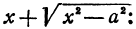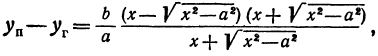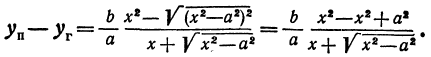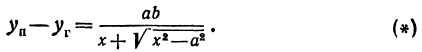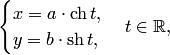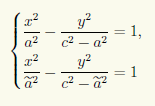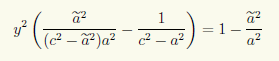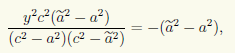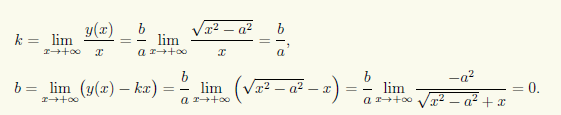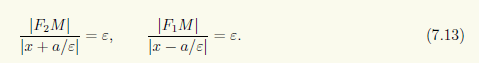Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Способы построения гиперболы самостоятельно
Содержание:
- Гипербола в математике — что это такое
- Как построить гиперболу самостоятельно
- Построение гиперболы по фокусам
- Как построить гиперболу по точкам
- Как построить график гиперболы по уравнению
Гипербола в математике — что это такое
определение 1
Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:
(frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9})
Согласно записанному правилу, все точки гиперболы (|x| geq a). Таким образом, данные точки расположены за пределами вертикальной полосы ширины (2a), как показано на рисунке. Ось абсцисс канонической системы координат имеет точки пересечения с гиперболой. Координаты этих точек соответствуют: ((a, 0)) и ((-a, 0)). Такие точки называют вершинами гиперболы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.
Определение 2
Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.
Определение 3
Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.
Определение 4
Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.
Определение 5
Центр гиперболы — это середина ее большой оси.
Определение 6
Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».
Определение 7
Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».
Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.
Определение 8
Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.
Определение 9
Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.
Определение 10
Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.
Определение 11
Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».
Определение 12
Перицентрическое расстояние — расстояние, на которое фокус удален от ближайшей вершины гиперболы, обозначается ({displaystyle r_{p}}r_{p}).
Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:
- ({displaystyle c^{2}=a^{2}+b^{2}}{displaystyle c^{2}=a^{2}+b^{2}})
- ({displaystyle varepsilon =c/a}{displaystyle varepsilon =c/a})
- ({displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}{displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)})
- ({displaystyle r_{p}=aleft(varepsilon -1right)}{displaystyle r_{p}=aleft(varepsilon -1right)})
- ({displaystyle a={frac {p}{varepsilon ^{2}-1}}}{displaystyle a={frac {p}{varepsilon ^{2}-1}}})
- ({displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}{displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}})
- ({displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}{displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}})
- ({displaystyle p={frac {b^{2}}{a}}}p={frac {b^{2}}{a}})
Определение 13
Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.
Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:
(y=kx)
Такой выбор связан с тем, что прямая (x=0 ) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:
(frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1)
Таким образом, при (b^{2}-a^{2}k^{2} > 0) получим:
(x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}})
Полученное равенство позволит рассчитать координаты точек пересечения:
((ab/v, abk/v))
((-ab/v, -abk/v))
В данном случае:
(v=(b^{2}-a^{2}k^{2})^{1/2})
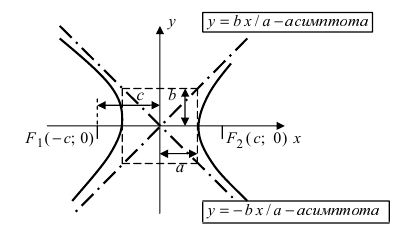
Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.
Числитель дроби (ab/v) является постоянной величиной, а знаменатель характеризуется максимальным значением, если (k=0). Таким образом, самую маленькую абсциссу имеет вершина ((a, 0)). При увеличении (k ) знаменатель убывает, и x растет, стремясь к бесконечности, когда k приближается к числу (b/a).
Прямая (y=bx/a) с угловым коэффициентом (b/a) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.
При сдвиге прямой от горизонтального положения по часовой стрелке, k будет уменьшаться, (k^{2}) — увеличиваться, и прямая будет иметь удаляющиеся точки пересечения с гиперболой до тех пор, пока не займет положения с угловым коэффициентом (-b/a).
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.
Определение 14
Асимптоты гиперболы являются прямыми, описываемыми уравнениями (y=bx/a) и (y=-bx/a ) в канонической системе координат.
Предположим, что уравнения асимптот имеют вид:
(bx-ay=0)
(bx+ay=0)
Расстояния от точки (M(x, y)) до асимптот составят
(h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}},)( h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}})
В том случае, когда точка M расположена на гиперболе:
(b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2})
(h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}})
Определение 15
Произведение расстояний от точки гиперболы до асимптот является постоянным и соответствует (a^{2}b^{2}/(a^{2}+b^{2})).
Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.
Определение 16
В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.
В действительности получим, что хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.
Введем такое число с, что:
(c^{2}=a^{2}+b^{2})
и (c > 0)
Определение 17
Фокусы гиперболы — точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.
Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).
Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов определяются абсциссой (x):
(r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|)
Следует отметить, что равенства eqref{ref11} можно представить в более подробной форме:
- для правой ветви гиперболы ((x geq a): r_{1}=varepsilon x-a), ( r_{2}=varepsilon x+a);
- для левой ветви гиперболы ((x leq -a): r_{1}= a-varepsilon x), ( r_{2}=-varepsilon x-a).
Таким образом, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях:
(|r_{2}-r_{1}|=2a)
Определение 18
Директрисы гиперболы — прямые, заданные в канонической системе координат уравнениями: (x=frac{a}{varepsilon}), ( x=-frac{a}{varepsilon}).
Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.
Определение 19
Для того чтобы точка (M) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.
С целью доказательства достаточности данного условия его следует записать в виде:
(sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}})
Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:
(c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2})
Определение 20
Для того чтобы точка была расположена на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon).
Можно доказать, к примеру, необходимость условия для фокуса (F_{2}(-c, 0).) Предположим, что (M'(x, y)) является точкой гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) равно:
(d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|)
Таким образом:
(r’/d’=varepsilon).
Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), которая принадлежит данной гиперболе, можно записать так же, как подобное уравнение в случае эллипса. Уравнение касательной к гиперболе:
(frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1)
Определение 21
Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.
Как построить гиперболу самостоятельно
Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:
- На листе бумаги нарисовать горизонтальную прямую. Выполнить действие следует таким образом, чтобы конец прямой с правой стороны был обозначен с помощью стрелки. Данная прямая является осью (X) и носит название абсциссы.
- На середине оси ( Х) необходимо опустить перпендикуляр. Конец полученной прямой в верхней части нужно обозначить стрелкой. В результате получена ось (Y), которую называют ординатой.
- На следующем шаге необходимо пронумеровать шкалу. С правой стороны на оси (Х) расположены положительные значения (Х) в порядке возрастания — от 1 и выше. С левой стороны — отрицательные. В верхней части на оси (Y) расположены положительные значения (Y) в порядке возрастания. В нижней части — отрицательные.
Примечание
Точка, в которой пересекаются абсцисса и ордината является началом координат, то есть числом 0. От данной точки следует откладывать все значения (Х) и (Y).
С помощью прямоугольной системы координат плоскость поделена на четыре части, которые называют четвертями и нумеруют против часовой стрелки. Для того чтобы построить график, требуется определить точки. Каждая точка координатной плоскости определяется парой чисел ((x;y)). Данные числа представляют собой координаты точки, где:
- (х) — абсцисса точки;
- (y) — ордината.
Гипербола представляет собой график функции, которая задана формулой:
(y=k/x)
где (k) — является каким-то коэффициентом, не равным нулю;
(x) — представляет собой независимую переменную.
Гипербола включает в себя две части, расположенные симметрично в разных четвертях. Данные части носят название ветвей гиперболы. При (k>0), ветви расположены в 1 и 3 четвертях. При (k<0), ветви гиперболы размещены во 2 и 4 четвертях.
Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:
(y=3/х)
Так как коэффициент 3 обладает положительным значением, гипербола, соответственно, будет находиться в 1 и 3 четвертях. Можно взять произвольно значения (Х) и найти значения (Y). Таким образом, получатся координаты точек, с помощью которых можно изобразить гиперболу. Важно отметить, что (Х) не должно иметь нулевое значение, так как на 0 делить нельзя.
Поскольку мы знаем, что гипербола располагается в двух четвертях, то берем как положительные значения, так и отрицательные. Предположим, что (Х) равен: -6, -3, -1, 1, 3, 6. Далее можно рассчитать ординаты путем подстановки каждого значение (Х) в начальную формулу:
(y=3/-6)
(у=3/-3)
(у=3/-1)
(у=3/1)
(у=3/3)
(у=3/6)
В результате, значения ( Y) равны: -0.5, -1, -3, 3, 1, 0.5.
Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.
Построение гиперболы по фокусам
Гиперболу можно построить, зная заданные вершины (А) и (В) и фокусное расстояние (FF1). Алгоритм построения следующий:
- В первую очередь фокусное расстояние следует разделить пополам, чтобы получить точку 0.
- Далее с левой стороны от фокуса (F) можно отметить ряд произвольных точек 1, 2, 3, 4 и так далее, расстояние между которыми постепенно увеличивается.
- Затем нужно начертить вспомогательные окружности с центром в фокусе (F), имеющие радиусы (R1=1B), (R2=2B), (R3=3B), (R4=4B) и так далее.
- На следующем этапе можно изобразить вспомогательные окружности с центром в фокусе (F1) и радиусами (r1=1A), (r2=2A), (r3=3A), (r4=4A) и так далее.
- При пересечении вспомогательных окружностей определяется положение точек гиперболы. (С), (С1 )представляют собой точки, которые образованы в результате пересечения окружностей радиусов (R1) и (r1). Точки (D,D1) являются точками, в которых пересекаются окружности (R2) и (r2).
- Полученные точки остается соединить с помощью плавной кривой линии, чтобы получить правую ветвь гиперболы.
- Аналогичным способом следует выполнить построение левой ветви гиперболы.
Как построить гиперболу по точкам
Исходя из определения гиперболы, разница между расстояниями (r1) и (r2) для всех ее точек является постоянной величиной. Таким образом, переход от одной точки гиперболы к другой осуществляется путем увеличения или уменьшения данных характеристик. Алгоритм действий:
- В первую очередь следует отложить точки (А1) и (А2). Точка ( А2) является точкой касания двух окружностей, центр одной из которых расположен в фокусе ( F1), а радиус составляет F1A2. Другая окружность обладает центром в фокусе (F2) и радиусом (F2A2).
- Следующие точки гиперболы можно определить при пересечении пар окружностей с радиусами, которые равны:
Таким образом, новые значения радиусов превышают предыдущие на одинаковую величину. Чем ближе расположены точки, тем точнее будет построен график гиперболы.
Как построить график гиперболы по уравнению
Каноническое уравнение гиперболы записывают таким образом:
где («a») и («b») являются положительными действительными числами, причем, («а») может быть больше или меньше, чем («b»).
Важно отметить, что гипербола обладает двумя симметричными ветвями и двумя асимптотами.
Построение гиперболы можно рассмотреть на примере. Предположим, что она задана следующим уравнением:
Рассматриваемое уравнение необходимо привести к каноническому виду:
Так как в правой части требуется получить единицу, необходимо обе части начального уравнения поделить на 20:
Далее следует сократить обе дроби:
Затем нужно выделить квадраты в знаменателях:
В результате получено каноническое уравнение:
Существует два подхода к построению гиперболы:
- геометрический;
- алгебраический.
С практической точки зрения, эффективнее воспользоваться расчетами. В первую очередь следует определить асимптоты:
Асимптоты равны:
На втором этапе можно определить вершины гиперболы, которые соответствуют точкам на оси абсцисс с координатами:
При у=0, каноническое уравнение гиперболы примет вид:
Таким образом:
Вершины гиперболы:
Затем необходимо определить дополнительные точки. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Согласно каноническому уравнению, можно выразить:
В результате получим две функции. Первая функция определяет верхние дуги гиперболы:
Вторая функция выражает нижние дуги гиперболы:
Напрашивается нахождение точек с абсциссами:
На последнем этапе следует изобразить асимптоты, вершины, дополнительные точки, симметричные точки в других координатных четвертях:
После того, как все точки соединены, будет изображена гипербола.
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 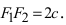
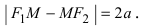
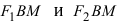
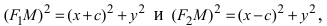
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим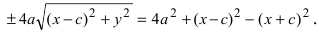
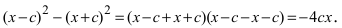
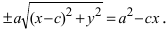
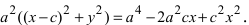
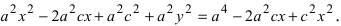
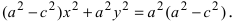
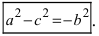
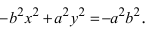
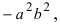
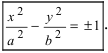
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 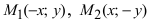
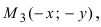
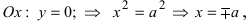
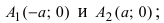
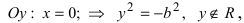
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 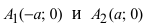
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 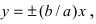
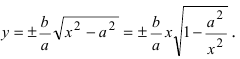
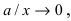
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 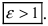
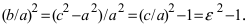
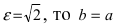
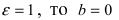
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
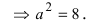
Пример:
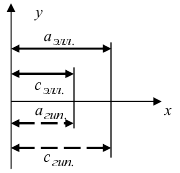
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 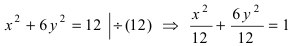
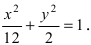
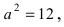
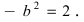
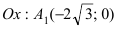
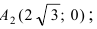
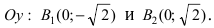
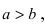
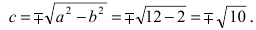
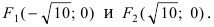
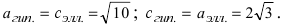
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 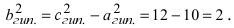
Гипербола в высшей математике
Рассмотрим уравнение
Решая его относительно 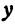
или одну двузначную функцию
Функция 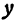

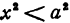
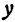
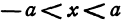
При 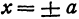
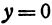
При 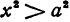
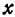
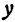
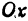
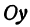
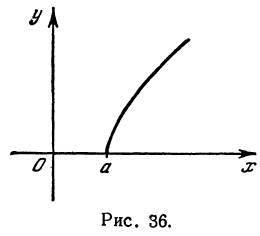
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 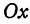
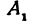
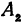
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 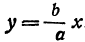
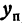
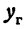
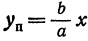
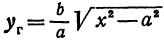
Умножим и разделим правую часть на
или
Окончательно
Будем придавать 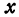
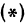

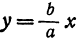
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 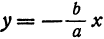
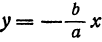
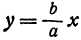
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
Гипербола: определение, свойства, построение
Гиперболой
называется геометрическое место точек
плоскости, модуль разности расстояний
от каждой из которых до двух заданных
точек и
есть
величина постоянная,
меньшая расстояниямежду
этими заданными точками (рис.3.40,а). Это
геометрическое определение
выражаетфокальное
свойство гиперболы.
Фокальное
свойство гиперболы
Точки и
называются
фокусами гиперболы, расстояниемежду
ними — фокусным расстоянием,
серединаотрезка
—
центром гиперболы, число—
длиной действительной оси гиперболы
(соответственно,—
действительной полуосью гиперболы).
Отрезкии
,
соединяющие произвольную точкугиперболы
с ее фокусами, называются фокальными
радиусами точки.
Отрезок, соединяющий две точки гиперболы,
называется хордой гиперболы.
Отношение ,
где,
называетсяэксцентриситетом
гиперболы.
Из определения следует,
что.
Геометрическое
определение гиперболы,
выражающее ее фокальное свойство,
эквивалентно ее аналитическому
определению — линии, задаваемой
каноническим уравнением гиперболы:
|
(3.50) |
Действительно,
введем прямоугольную систему координат
(рис.3.40,б). Центр гиперболы
примем за начало системы координат;
прямую, проходящую через фокусы (фокальную
ось), примем за ось абсцисс (положительное
направление на ней от точкик
точке);
прямую, перпендикулярную оси абсцисс
и проходящую через центр гиперболы,
примем за ось ординат (направление на
оси ординат выбирается так, чтобы
прямоугольная система координатоказалась
правой).
Составим
уравнение гиперболы, используя
геометрическое определение, выражающее
фокальное свойство. В выбранной системе
координат определяем координаты
фокусов и
.
Для произвольной точки,
принадлежащей гиперболе, имеем:
Записывая
это уравнение в координатной форме,
получаем:
Выполняя
преобразования, аналогичные преобразованиям,
используемым при выводе уравнения
эллипса (т.е. избавляясь от иррациональности),
приходим к каноническому уравнению
гиперболы:
где ,
т.е. выбранная система координат является
канонической.
Проводя
рассуждения в обратном порядке, можно
показать, что все точки, координаты
которых удовлетворяют уравнению (3.50),
и только они, принадлежат геометрическому
месту точек, называемому гиперболой.
Таким образом, аналитическое определение
гиперболы эквивалентно его геометрическому
определению.
Директориальное
свойство гиперболы
Директрисами
гиперболы называются две прямые,
проходящие параллельно оси ординат
канонической системы координат на
одинаковом расстоянии от
нее (рис.3.41,а). При,
когда гипербола вырождается в пару
пересекающихся прямых, директрисы
совпадают.
Гиперболу
с эксцентриситетом можно
определить, как геометрическое место
точек плоскости, для каждой из которых
отношение расстояния до заданной
точки(фокуса)
к расстоянию до заданной прямой(директрисы),
не проходящей через заданную точку,
постоянно и равно эксцентриситету(директориальное
свойство гиперболы).
Здесь и
—
один из фокусов гиперболы и одна из ее
директрис, расположенные по одну сторону
от оси ординат канонической системы
координат.
В
самом деле, например, для фокуса и
директрисы(рис.3.41,а)
условиеможно
записать в координатной форме:
Избавляясь
от иррациональности и заменяя ,
приходим к каноническому уравнению
гиперболы (3.50). Аналогичные рассуждения
можно провести для фокусаи
директрисы:
Уравнение
гиперболы в полярной системе координат
Уравнение
правой ветви гиперболы в полярной
системе координат (рис.3.41,б)
имеет вид
,
где —фокальный
параметр гиперболы.
В
самом деле, выберем в качестве полюса
полярной системы координат правый
фокус гиперболы,
а в качестве полярной оси — луч с началом
в точке,
принадлежащий прямой,
но не содержащий точки(рис.3.41,б).
Тогда для произвольной точки,
принадлежащей правой ветви гиперболы,
согласно геометрическому определению
(фокальному свойству) гиперболы, имеем.
Выражаем расстояние между точкамии
(см.
пункт 2 замечаний 2.8):
Следовательно,
в координатной форме уравнение гиперболы
имеет в
Уединяем
радикал, возводим обе части уравнения
в квадрат, делим на 4 и приводим подобные
члены:
Выражаем
полярный радиус и
делаем замены:
что
и требовалось доказать. Заметим, что в
полярных координатах уравнения гиперболы
и эллипса совпадают, но описывают разные
линии, поскольку отличаются эксцентриситетами
(для
гиперболы,для
эллипса).
Геометрический
смысл коэффициентов в уравнении гиперболы
Найдем
точки пересечения гиперболы (рис.3.42,а)
с осью абсцисс (вершины гиперболы).
Подставляя в уравнение ,
находим абсциссы точек пересечения:.
Следовательно, вершины имеют координаты.
Длина отрезка, соединяющего вершины,
равна.
Этот отрезок называется действительной
осью гиперболы, а число—
действительной полуосью гиперболы.
Подставляя,
получаем.
Длина отрезка оси ординат, соединяющего
точки,
равна.
Этот отрезок называется мнимой осью
гиперболы, а число—
мнимой полуосью гиперболы. Гипербола
пересекает прямую, содержащую
действительную ось, и не пересекает
прямую, содержащую мнимую ось.
Замечания
3.10.
1. Прямые ограничивают
на координатной плоскости основной
прямоугольник, вне которого находится
гипербола (рис.3.42,а).
2. Прямые ,
содержащие диагонали основного
прямоугольника, называются асимптотами
гиперболы (рис.3.42,а).
Для равносторонней
гиперболы,
описываемой уравнением (т.е.
при),
основной прямоугольник является
квадратом, диагонали которого
перпендикулярны. Поэтому асимптоты
равносторонней гиперболы также
перпендикулярны, и их можно взять в
качестве координатных осей прямоугольной
системы координат(рис.3.42,б).
В этой системе координат уравнение
гиперболы имеет вид(гипербола
совпадает с графиком элементарной
функции, выражающей обратно-пропорциональную
зависимость).
В
самом деле, повернем каноническую
систему координат на угол (рис.3.42,б).
При этом координаты точки в старой и
новой системах координат связаны
равенствами
Подставляя
эти выражения в уравнение равносторонней
гиперболы и приводя подобные члены,
получаем
3. Координатные
оси (канонической системы координат)
являются осями симметрии гиперболы
(называются главными осями гиперболы),
а ее центр — центром симметрии.
Действительно,
если точка принадлежит
гиперболе.
то и точкии
,
симметричные точкеотносительно
координатных осей, также принадлежат
той же гиперболе.
Ось
симметрии, на которой располагаются
фокусы гиперболы, является фокальной
осью.
4. Из
уравнения гиперболы в полярных
координатах (см.
рис.3.41,б) выясняется геометрический
смысл фокального параметра — это
половина длины хорды гиперболы, проходящей
через ее фокус перпендикулярно фокальной
оси (при
).
5. Эксцентриситет характеризует
форму гиперболы. Чем больше,
тем шире ветви гиперболы, а чем ближек
единице, тем ветви гиперболы уже
(рис.3.43,а).
Действительно,
величина угла
между асимптотами гиперболы, содержащего
ее ветвь, определяется отношением сторон
основного прямоугольника:.
Учитывая,чтои
,
получаем
Чем
больше ,
тем больше угол.
Для равносторонней гиперболыимеем
и
.
Дляугол
тупой,
а дляугол
острый
(рис.3.43,а).
6.
Две гиперболы, определяемые в одной и
той же системе координат
уравнениями и
называютсясопряженными
друг с другом.
Сопряженные гиперболы имеют одни и те
же асимптоты (рис.3.43,б). Уравнение
сопряженной гиперболы приводится
к каноническому при помощи переименования
координатных осей (3.38).7. Уравнение определяет
гиперболу с центром в точке,
оси которой параллельны координатным
осям (рис.3.43,в). Это уравнение сводится
к каноническому при помощи параллельного
переноса (3.36). Уравнениеопределяет
сопряженную гиперболу с центром в
точке.
Параметрическое
уравнение гиперболы
Параметрическое
уравнение гиперболы в канонической
системе координат имеет вид
где —
гиперболический косинус, aгиперболический
синус.
Действительно,
подставляя выражения координат в
уравнение (3.50), приходим к основному
гиперболическому тождеству .
Пример
3.21. Изобразить
гиперболу в
канонической системе координат.
Найти полуоси, фокусное расстояние,
эксцентриситет, фокальный параметр,
уравнения асимптот и директрис.
Решение. Сравнивая
заданное уравнение с каноническим,
определяем полуоси: —
действительная полуось,—
мнимая полуось гиперболы. Строим основной
прямоугольник со сторонамис
центром в начале координат (рис.3.44).
Проводим асимптоты, продлевая диагонали
основного прямоугольника. Строим
гиперболу, учитывая ее симметричность
относительно координатных осей. При
необходимости определяем координаты
некоторых точек гиперболы. Например,
подставляяв
уравнение гиперболы, получаем
Следовательно,
точки с координатами и
принадлежат
гиперболе. Вычисляем фокусное расстояние
эксцентриситет ;
фокальныи параметр.
Составляем уравнения асимптот,
то есть,
и уравнения директрис:.
Парабола
и её каноническое уравнение
Определение. Параболой
называется геометрическое место точек,
для каждой из которых расстояние до
некоторой фиксированной точки плоскости,
называемой фокусом, равно расстоянию
до некоторой фиксированной прямой, не
проходящей через фокус и называемой
директрисой.
Определение. Расстояние
от фокуса параболы до её директрисы
называется параметром параболы.
Эксцентриситет параболы принимается
равным единице.
Опустим
из фокуса перпендикуляр
на директрисуи
точку пересечения этого перпендикуляра
с директрисой параболы обозначим
буквой.
Введём на плоскости ДПСК, поместив
начало координатв
центре отрезка,
принимая за осьпрямую
,
с положительным направлением отк
(См.
рис.176).
Рис.
176
|
|
Расстояние от
фокусадо
директрисыобозначим
буквой(это
параметр параболы). В выбранной системе
координат фокусимеет
координаты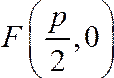
Уравнение директрисы
Пусть —
произвольная точка плоскости. Обозначим
черезрасстояние
от
точкидо
фокусапараболы,
а через—
расстояниеот
точкидо
директрисы этой параболы.
Точка лежит
на данной параболе тогда и
только
тогда, когда .
Так как
а 
то уравнение параболы имеет вид:

Это уравнение эквивалентно следующему
уравнению: 
Или: (1)
Определение. Уравнение
(1) называется каноническим уравнением
параболы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение 7.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.
Замечание 7.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса. Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
Фиксированные точки в определении гиперболы (обозначим их F1 и F2) называют фокусами гиперболы. Расстояние между ними (обозначим его 2с) называют фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на гиперболе с ее фокусами, — фокальными радиусами.
Вид гиперболы полностью определяется фокальным расстоянием |F1F2| = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов F1 и F2.
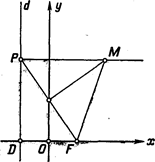
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.7). Первую из этих осей симметрии называют действительной осью гиперболы, а вторую — ее мнимой осью. Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы.
Середина отрезка F1F2, соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы.
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F1MF2 (см. рис. 7.7) справедливо неравенство ||F1M| — |F2M| | ≤ |F1F2|. Равенство а = с выполнено только для тех точек M, которые лежат на действительной оси симметрии гиперболы вне интервала F1F2. Отбрасывая этот вырожденный случай, далее будем предполагать, что а < с. Отметим также, что случай а = 0 соответствует геометрическому месту точек, равноудаленных от фиксированных точек F1 и F2. Как известно из курса школьной геометрии, это геометрическое место представляет собой прямую, перпендикулярную отрезку F1F2 и проходящую через его середину. Этот случай мы также не будем рассматривать.
Уравнение гиперболы. Рассмотрим на плоскости некоторую гиперболу с фокусами в точках F1 и F2 и действительной осью 2а. Пусть 2с — фокальное расстояние, 2c = |F1F2| > 2а.
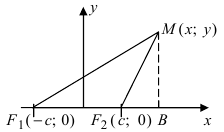
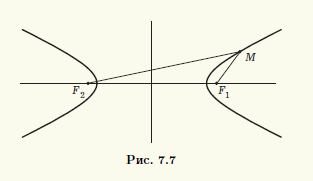
Согласно замечанию 7.2, гипербола состоит из тех точек M(х; у), для которых | |F1M| — — |F2M| | = 2а. Выберем прямоугольную систему координат Oxy так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс (рис. 7.8). Такую систему координат для рассматриваемой гиперболы называют канонической, а соответствующие переменные — каноническими.
В канонической системе координат фокусы гиперболы имеют координаты F1(c; 0) и F2(—с; 0). Используя формулу расстояния между двумя точками, запишем условие ||F1M| — |F2M|| = 2а в координатах |√((х — с)2 + у2) — √((х + с)2 + у2)| = 2а, где (x; у) — координаты точки M. Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с)2 + у2) — √((х + с)2 + у2) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с)2 + у2 = (х + с)2 + у2 ± 4а √((х + с)2 + у2) + 4а2. После упрощения получим —εх — а = ±√((х + с)2 + у2), или
√((х + с)2 + у2) = |εх + а| (7.7)
где ε = с/а. Возведем в квадрат вторично и снова приведем подобные члены: (ε2 — 1)х2 — у2 = с2 — а2, или, учитывая равенство ε = с/а и полагая b2 = c2 — a2,
x2/a2 — y2/b2 = 1 (7.8)
Величину b > 0 называют мнимой полуосью гиперболы.
Итак, мы установили, что любая точка на гиперболе с фокусами F1(с;0) и F2(—с; 0) и действительной полуосью а удовлетворяет уравнению (7.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовлетворяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами F1 и F2. У этого семейства гипербол оси симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих на действительной оси симметрии вне интервала F1F2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов F1 и F2 меняется от гиперболы к гиперболе. Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению 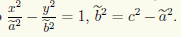
двух уравнений с двумя неизвестными
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при ã ≠ а это невозможно. Действительно, исключив, например, x из первого уравнения:
после преобразований получаем уравнение
которое при ã ≠ а не имеет решений, так как 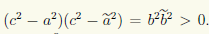
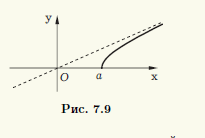
Вид гиперболы. По своему виду гипербола (7.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при x ≥ 0, у ≥ 0, каноническое уравнение гиперболы однозначно разрешается относительно у:
у = b/a √(x2 — а2). (7.9)
Исследование этой функции y(x) дает следующие результаты.
Область определения функции — {x: x ≥ а} ив этой области определения она непрерывна как сложная функция, причем в точке x = а она непрерывна справа. Единственным нулем функции является точка x = а.
Найдем производную функции y(x): y'(x) = bx/a√(x2 — а2). Отсюда заключаем, что при x > а функция монотонно возрастает. Кроме того, 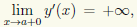
Указанная функция имеет наклонную асимптоту, это вытекает из существования двух пределов:
Наклонная асимптота описывается уравнением y = (b/a)x.
Проведенное исследование функции (7.9) позволяет построить ее график (рис. 7.9), который совпадает с частью гиперболы (7.8), содержащейся в первой четверти.
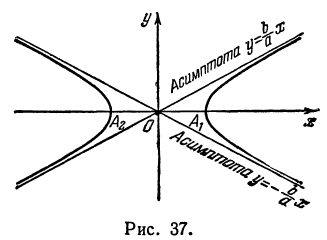
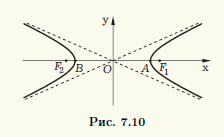
Так как гипербола симметрична относительно своих осей, вся кривая имеет вид, изображенный на рис. 7.10. Гипербола состоит из двух симметричных ветвей, расположенных по разные
стороны от ее мнимой оси симметрии. Эти ветви не ограничены с обеих сторон, причем прямые у = ±(b/a)x являются одновременно асимптотами и правой и левой ветвей гиперболы.
Оси симметрии гиперболы различаются тем, что действительная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересекает (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют вершинами гиперболы (точки A(a; 0) и B(—a; 0) на рис. 7.10).
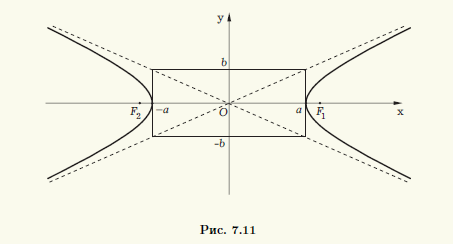
Построение гиперболы по ее действительной (2a) и мнимой (2b) осям следует начинать с прямоугольника с центром в начале координат и сторонами 2a и 2b, параллельными, соответ-ственно, действительной и мнимой осям симметрии гиперболы (рис. 7.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной осью симметрии. Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если эксцентриситет эллипса может принимать значения из полуинтервала [0,1) (значение 0 соответствует предельному варианту эллипса — окружности), то эксцентриситет гиперболы всегда попадает в интервал (1, + ∞).
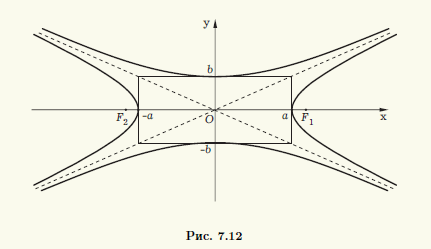
Построим прямоугольник с центром в начале системы координат Oxy и сторонами 2a, 2b, параллельными осям абсцисс и ординат соответственно. Проведем прямые y = (b/a)x и y = — (b/a)x, на которых лежат диагонали прямоугольника. Существует две гиперболы, соответствующие построенному прямоугольнику (рис. 7.12). Первая из них описывается каноническим уравнением (7.8), а вторая — уравнением
x2/a2 — y2/b2 = -1. (7.10)
Вторую гиперболу называют сопряженной по отношению к первой, а уравнение (7.10) — каноническим уравнением сопряженной гиперболы. Действительная и мнимая оси первой гиперболы являются соответственно мнимой и действительной осями сопряженной гиперболы, а асимптоты у них общие.
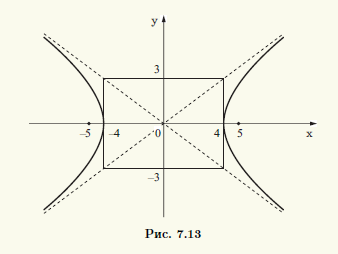
Пример 7.2. Найдем каноническое уравнение гиперболы по ее действительной полуоси a = 4 и фокальному расстоянию 2с = 10. Построим гиперболу и определим координаты ее вершин, фокусов и уравнения асимптот.
Так как действительная полуось a гиперболы известна, то, чтобы найти каноническое уравнение гиперболы, достаточно определить мнимую полуось b. Поскольку с = 5, b = √(с2 — а2), то
b = √(52 — 42) = 3. Итак, искомое уравнение имеет вид x2/42 — y2/32 = 1. Построим прямоугольник,соответствующий заданной гиперболе (рис. 7.13). Продолжим его диагонали до асимптот ги-перболы и построим саму гиперболу. Уравнениями асимптот являются у = ±3x/4, вершины находятся в точках (±4; 0), а фокусы совпадают с точками (±5; 0).
Геометрические свойства. Геометрические свойства гиперболы во многом повторяют свойства эллипса. Вернемся к формуле (7.7). Она эквивалентна каноническому уравнению гиперболы и дает выражение для длины фокального радиуса F2M ее точки M(х; у):
|F2M| = √((х + с)2 + у2) = ±(εх + a) (7.11)
где знак плюс соответствует правой ветви гиперболы, а знак минус — левой.
Аналогично можно получить формулу для длины другого фокального радиуса, если при выводе канонического уравнения гиперболы перед первым возведением в квадрат в правую часть равенства перенести не второй, а первый квадратный радикал. При этом вместо (7.7) получим εх — a = ±√((х — с)2 + у2) , откуда
|F1M| = √((х — с)2 + у2) = ±(εх — a) (7.12)
где, как и в (7.11), знак плюс соответствует правой ветви гиперболы, а знак минус — левой. Каждое из уравнений (7.11), (7.12) является уравнением гиперболы.
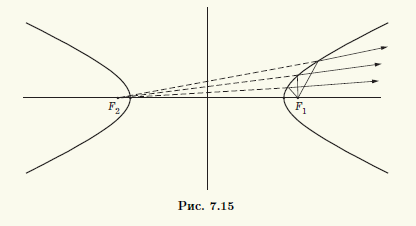
Гипербола не проходит через свои фокусы (при 0 < a < c). Поэтому фокальные радиусы любой ее точки M имеют ненулевую длину, т.е. |F1M| ≠ 0 и |F2M| ≠ 0. Но тогда в (7.11) и (7.12) правые части тоже отличны от нуля, и эти уравнения гиперболы можно переписать в следующем виде:
Рассмотрим прямую d’: x = —a/ε (рис. 7.14). Выражение |x + a/ε| представляет собой расстояние от точки M(x; у) до прямой d’. Аналогично выражение ±(x — a/ε) равно расстоянию |x — a/ε| от точки M гиперболы до прямой d: x = a/ε. Поэтому из уравнений (7.13) следует, что гипербола состоит из таких точек, для которых отношение расстояния до фокуса F2 (фокуса F1) к расстоянию до прямой d’ (прямой d) есть величина постоянная, равная ее эксцентриситету ε. Эти две прямые d и d’ называют директрисами гиперболы.
Геометрически директрисы определяются как прямые, перпендикулярные действительной оси симметрии гиперболы и удаленные от ее центра на расстояние, равное отношению действительной полуоси к эксцентриситету.
Расстояние p от директрисы гиперболы до ближайшего к директрисе фокуса, как и у эллипса, называют
фокальным параметром гиперболы. Отметим, что
p = c = a/ε = c — a2/c = (c2 — a2)/c = b2/c
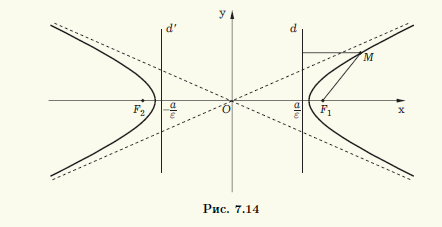
Гипербола также имеет и оптическое свойство, аналогичное оптическому свойству эллипса. Оно состоит в том, что лучи, вышедшие из одного фокуса, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса (рис. 7.15).