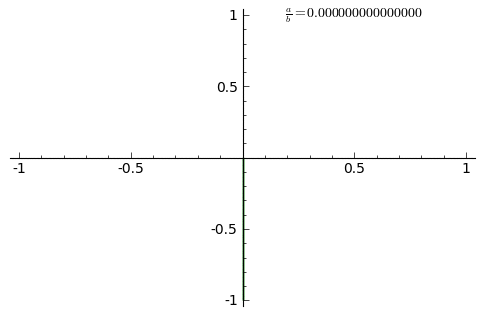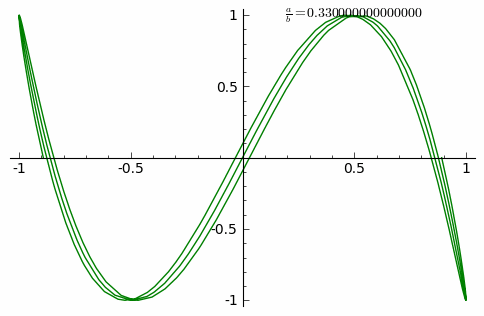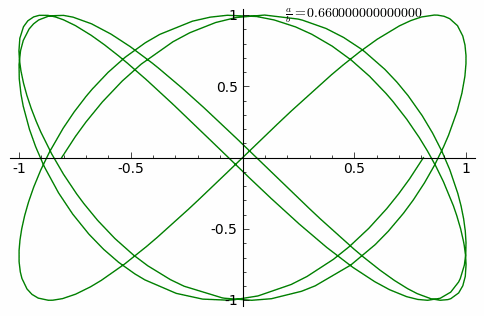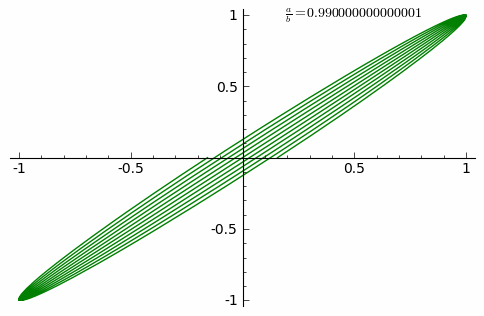Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.
Чтобы было более понятно, давайте представим девочку на качели из покрышки:
И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:
где
1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
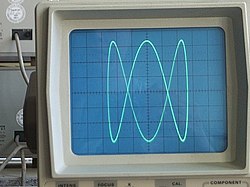
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.
Генератор №1
Генератор №2
и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON
Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.
А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:
На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:
Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display
Ну а потом с помощью дисплейных клавиш выбираем режим XY
И получается примерно вот такая хаотическая картинка:
Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:
Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:
В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:
Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:
Вот такие фигуры вы будете видеть на экране своего осциллографа:
А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов
А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:
В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение — это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 
From Wikipedia, the free encyclopedia
Not to be confused with spirographs, which are generally enclosed by a circular boundary, whereas Lissajous curves are enclosed by rectangular boundaries.
A Lissajous figure, made by releasing sand from a container at the end of a Blackburn pendulum
A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of parametric equations
which describe the superposition of two perpendicular oscillations in x and y directions of different angular frequency (a and b). The resulting family of curves was investigated by Nathaniel Bowditch in 1815, and later in more detail in 1857 by Jules Antoine Lissajous (for whom it has been named). Such motions may be considered as a particular of kind of complex harmonic motion.
The appearance of the figure is sensitive to the ratio a/b. For a ratio of 1, when the frequencies match a=b, the figure is an ellipse, with special cases including circles (A = B, δ = π/2 radians) and lines (δ = 0). A small change to one of the frequencies will mean the x oscillation after one cycle will be slightly out of synchronization with the y motion and so the ellipse will fail to close and trace a curve slightly adjacent during the next orbit showing as a precession of the ellipse. The pattern closes if the frequencies are whole number ratios i.e. a/b is rational.
Another simple Lissajous figure is the parabola (b/a = 2, δ = π/4). Again a small shift of one frequency from the ratio 2 will result in the trace not closing but performing multiple loops successively shifted only closing if the ratio is rational as before. A complex dense pattern may form see below.
The visual form of such curves is often suggestive of a three-dimensional knot, and indeed many kinds of knots, including those known as Lissajous knots, project to the plane as Lissajous figures.
Visually, the ratio a/b determines the number of «lobes» of the figure. For example, a ratio of 3/1 or 1/3 produces a figure with three major lobes (see image). Similarly, a ratio of 5/4 produces a figure with five horizontal lobes and four vertical lobes. Rational ratios produce closed (connected) or «still» figures, while irrational ratios produce figures that appear to rotate. The ratio A/B determines the relative width-to-height ratio of the curve. For example, a ratio of 2/1 produces a figure that is twice as wide as it is high. Finally, the value of δ determines the apparent «rotation» angle of the figure, viewed as if it were actually a three-dimensional curve. For example, δ = 0 produces x and y components that are exactly in phase, so the resulting figure appears as an apparent three-dimensional figure viewed from straight on (0°). In contrast, any non-zero δ produces a figure that appears to be rotated, either as a left–right or an up–down rotation (depending on the ratio a/b).
Lissajous figure on an oscilloscope, displaying a 1:3 relationship between the frequencies of the vertical and horizontal sinusoidal inputs, respectively. This particular Lissajous figure was adapted into the logo for the Australian Broadcasting Corporation
A circle is a simple Lissajous curve
Lissajous figures where a = 1, b = N (N is a natural number) and
are Chebyshev polynomials of the first kind of degree N. This property is exploited to produce a set of points, called Padua points, at which a function may be sampled in order to compute either a bivariate interpolation or quadrature of the function over the domain [−1,1] × [−1,1].
The relation of some Lissajous curves to Chebyshev polynomials is clearer to understand if the Lissajous curve which generates each of them is expressed using cosine functions rather than sine functions.
Examples[edit]
Animation showing curve adaptation as the ratio a/b increases from 0 to 1
The animation shows the curve adaptation with continuously increasing a/b fraction from 0 to 1 in steps of 0.01 (δ = 0).
Below are examples of Lissajous figures with an odd natural number a, an even natural number b, and |a − b| = 1.
-
δ = π/2, a = 1, b = 2 (1:2)
-
δ = π/2, a = 3, b = 2 (3:2)
-
δ = π/2, a = 3, b = 4 (3:4)
-
δ = π/2, a = 5, b = 4 (5:4)
-
Lissajous figures: various frequency relations and phase differences
Generation[edit]
Prior to modern electronic equipment, Lissajous curves could be generated mechanically by means of a harmonograph.
Practical application[edit]
Lissajous curves can also be generated using an oscilloscope (as illustrated). An octopus circuit can be used to demonstrate the waveform images on an oscilloscope. Two phase-shifted sinusoid inputs are applied to the oscilloscope in X-Y mode and the phase relationship between the signals is presented as a Lissajous figure.
In the professional audio world, this method is used for realtime analysis of the phase relationship between the left and right channels of a stereo audio signal. On larger, more sophisticated audio mixing consoles an oscilloscope may be built-in for this purpose.
On an oscilloscope, we suppose x is CH1 and y is CH2, A is the amplitude of CH1 and B is the amplitude of CH2, a is the frequency of CH1 and b is the frequency of CH2, so a/b is the ratio of frequencies of the two channels, and δ is the phase shift of CH1.
A purely mechanical application of a Lissajous curve with a = 1, b = 2 is in the driving mechanism of the Mars Light type of oscillating beam lamps popular with railroads in the mid-1900s. The beam in some versions traces out a lopsided figure-8 pattern on its side.
Application for the case of a = b[edit]
In this figure both input frequencies are identical, but the phase difference between them creates the shape of an ellipse.
Top: Output signal as a function of time.
Middle: Input signal as a function of time.
Bottom: Resulting Lissajous curve when output is plotted as a function of the input.
In this particular example, because the output is 90 degrees out of phase from the input, the Lissajous curve is a circle, and is rotating counterclockwise.
When the input to an LTI system is sinusoidal, the output is sinusoidal with the same frequency, but it may have a different amplitude and some phase shift. Using an oscilloscope that can plot one signal against another (as opposed to one signal against time) to plot the output of an LTI system against the input to the LTI system produces an ellipse that is a Lissajous figure for the special case of a = b. The aspect ratio of the resulting ellipse is a function of the phase shift between the input and output, with an aspect ratio of 1 (perfect circle) corresponding to a phase shift of ±90° and an aspect ratio of ∞ (a line) corresponding to a phase shift of 0° or 180°.[citation needed]
The figure below summarizes how the Lissajous figure changes over different phase shifts. The phase shifts are all negative so that delay semantics can be used with a causal LTI system (note that −270° is equivalent to +90°). The arrows show the direction of rotation of the Lissajous figure.[citation needed]
A pure phase shift affects the eccentricity of the Lissajous oval. Analysis of the oval allows phase shift from an LTI system to be measured.
In engineering[edit]
A Lissajous curve is used in experimental tests to determine if a device may be properly categorized as a memristor.[citation needed] It is also used to compare two different electrical signals: a known reference signal and a signal to be tested.[1][2]
In popular culture[edit]
In motion pictures[edit]
- Lissajous figures were sometimes displayed on oscilloscopes meant to simulate high-tech equipment in science-fiction TV shows and movies in the 1960s and 1970s.[3]
- The title sequence by John Whitney for Alfred Hitchcock’s 1958 feature film Vertigo is based on Lissajous figures.[4]
Company logos[edit]
Lissajous figures are sometimes used in graphic design as logos. Examples include:
- The Australian Broadcasting Corporation (a = 1, b = 3, δ = π/2)[5]
- The Lincoln Laboratory at MIT (a = 3, b = 4, δ = π/2)[6]
- The University of Electro-Communications, Japan (a = 5, b = 6, δ = π/2).[citation needed]
- Disney’s Movies Anywhere streaming video application uses a stylized version of the curve
- Facebook’s rebrand into Meta Platforms is also a Lissajous Curve, echoing the shape of a capital letter M (a = 1, b = -2, δ = π/20).
In modern art[edit]
- The Dadaist artist Max Ernst painted Lissajous figures directly by swinging a punctured bucket of paint over a canvas.[7]
See also[edit]
- Lissajous orbit
- Blackburn pendulum
- Lemniscate of Gerono
- Spirograph
Notes[edit]
- ^ Palmer, Kenneth; Ridgway, Tim; Al-Rawi, Omar; et al. (September 2011). «Lissajous Figures: An Engineering Tool for Root Cause Analysis of Individual Cases—A Preliminary Concept». The Journal of Extra-corporeal Technology. 43 (3): 153–156. ISSN 0022-1058. PMC 4679975. PMID 22164454.
- ^ «Lissajou Curves». datagenetics.com. Retrieved 2020-07-10.
- ^ «A long way from Lissajous figures». New Scientist. Reed Business Information: 77. 24 September 1987. ISSN 0262-4079.
- ^ McCormack, Tom (9 May 2013). «Did ‘Vertigo’ Introduce Computer Graphics to Cinema?». rhizome.org. Retrieved 18 December 2020.
- ^ «The ABC’s of Lissajous figures». abc.net.au. Australian Broadcasting Corporation.
- ^ «Lincoln Laboratory Logo». ll.mit.edu. Lincoln Laboratory, Massachusetts Institute of Technology. 2008. Retrieved 2008-04-12.
- ^ King, M. (2002). «From Max Ernst to Ernst Mach: epistemology in art and science» (PDF). Retrieved 17 September 2015.
External links[edit]
- Lissajous Curve at Mathworld
Interactive demos[edit]
- 3D Java applets depicting the construction of Lissajous curves in an oscilloscope:
- Tutorial from the NHMFL
- Physics applet by Chiu-king Ng
- Detailed Lissajous figures simulation Drawing Lissajous figures with interactive sliders in Javascript
- Lissajous Curves: Interactive simulation of graphical representations of musical intervals and vibrating strings
- Interactive Lissajous curve generator – Javascript applet using JSXGraph
- Animated Lissajous figures
- [1] Wolfram Mathematica — Lissajous figures with interactive sliders in Wolfram mathematica
Измерение частоты и сдвига фаз синусоидальных сигналов. Фигуры Лиссажу.
Осциллограф позволяет определить
значение частоты и сдвиг фаз синусоидальных
сигналов относительно друг друга.
Измерение частоты и сдвига фаз производится
сигнальным методом, называемым методом
фигур Лиссажу.
Измерение неизвестной частоты
синусоидального сигнала при помощи
фигур Лиссажу производится следующим
образом. Внутренняя развертка в данном
методе не применяется; при этом
переключатель осциллографов “Диапазоны
частот” устанавливается в положение
“0” — внутренняя развертка отключается.
Сигнал, частота fx которого
неизвестна, подается на один из входов
осциллографа, например на “вход Х”.
Сигнал известной частоты f0 от
эталонного генератора подается на
другой вход осциллографа — “вход У”.
Следовательно, электронный луч
осциллографа под действием двух сигналов
передвигается по сложной кривой, описывая
на экране определенную фигуру — фигуру
Лиссажу. Форма этой фигуры зависит от
отношения амплитуд, частот и начальных
фаз сравниваемых сигналов.
Рис.3а
Рис.3б
Рис.3в
Рис.4г Рис.4д
Образование фигуры Лиссажу на экране
осциллографа рассмотрим на примере
ряда синусоидальных сигналов, подаваемых
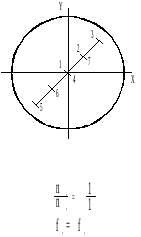
на входы Х и У (рис.3). Мы будем последовательно
рассматривать положение луча на экране
осциллографа в различные моменты времени
(рис. 3а); различные моменты времени
обозначены цифрами 1-9. В данном случае
сигналы имеют одинаковую фазу: начальный
момент времени t1 напряжение
Vx=Vy=0. Следовательно, в момент
времени t1 электронный луч попадает
в центр экрана (точка 1, рис.3а). Смещение
луча вправо или влево осуществляется
под действием переменного напряжения
Vx(t), изменяющегося с частотой fx;
смещение луча вверх или вниз осуществляется
под действием переменного напряжения
Vy изменяющегося с частотой fy;
в данном случае частоты fx и fy
равны друг другу (рис.3а). Предполагается,
что если напряжение Vx положительно,
то луч смещается к правой пластине, если
напряжение Vx отрицательно (например
в моменты времени 5,6), то луч смещается
влево, если напряжение Vy положительно
(например в моменты 2,3), то электронный
луч смещается вверх, если напряжение
Vy отрицательно (например в моменты
времени 5,6), то луч смещается вниз.
В момент времени t2 за счет напряжения
Vx луч смещается вправо, за счет
Vy — вверх, поэтому в целом луч
перемещается на экране по прямой в
первой координатной четверти. В момент
времени t3 луч отклоняется по
прямой 1-2-3 на максимальное расстояние.
К моменту времени t4 за счет
уменьшения напряжения Vx, Vy
луч смещается одновременно влево и
вниз, наконец, в момент времени t4
луч опять находится в центре экрана. В
дальнейшем, в момент времени t5
напряжение Vx и Vy имеют
отрицательный знак, поэтому луч сильно
смещен одновременно влево и вниз. В
момент времени t7 луч опять находится
в центре экрана.
Таким образом, при одинаковой частоте
сигналов и одинаковых фазах, фигура
Лиссажу представляет собой прямую
линию, наклон которой зависит только
от соотношения амплитуд сигналов,
подаваемых на входы Х и У. В частности,
увеличение амплитуда сигнала, подаваемого
на вход Х (напряжение Vx), приведет
к уменьшению угла
между осью Х и прямой линией фигуры
Лиссажу (рис.4,а, пунктирная линия).
Подадим на вход осциллографа (“вход
Х”) сигнал частотой fx; напряжение
Vx (t)
изображено на рис.3б; на “вход У” подадим
сигнал, частота fy которого в два
раза больше, чем fx, то есть fy=2fx.
Начальные фазы сигналов в данном случае
совпадают и равны 0: при начальном моменте
времени t=0 напряжения Vx=Vy=0.Построение
фигуры Лиссажу, получаемой на экране
осциллографа, можно произвести с учетом
напряжений Vx (t) и Vy(t) в моменты
времени t1, t2 и т.д. В данном
случае на экране получается устойчивая
фигура Лиссажу в форме “восьмерки”
(рис.3б); стрелками указано движение
электронного луча по экрану в различные
моменты времени.
Изменение фазы сравниваемых сигналов
приводит к изменению формы фигуры
Лиссажу. Например, на входы Х и У подаются
сигналы Vx(t) и Vy(t) с разными
начальными фазами: в момент времени t1
напряжение Vx=0, а напряжение Vy>0.
Частоты сигналов fx и fy
одинаковы. Построение фигуры Лиссажу
по принципу, описанному выше, показывает,
что на экране виден наклонный эллипс
(рис.3а).
Сравнивая рис.3а и 3в, получаем, что при
одинаковых частотах fx =fy фигура
Лиссажу может быть как прямой линией,
так и эллипсом.
Форма фигуры Лиссажу может быть описана
аналитически. Пусть на входы Х и У
подается синусоидальное напряжение,
для простоты одинаковой частоты f0.
Тогда координаты точки отклонения луча
на экране (с учетом выражения (1)) будет
описываться формулами:
;
(2)
;;
,
где х(t) и у(t) — отклонение луча по
горизонтали и вертикали в момент времени
t; а и b — амплитудные
значения отклонений; 0
— сдвиг фаз между исследуемыми сигналами.
Траектория луча на экране осциллографа
описывается зависимостью у(х), то есть
для получения зависимости у(х) необходимо
из уравнений (2) исключить время t. Для
этого делаем следующие преобразования:
;
(3)
или . (4)
Возведем выражение (3) в квадрат и умножим
на величину sin20,
выражение (4) возведем в квадрат. В
результате преобразований получим:
;
.
Сложим, получим выражения:
. (5)
Выражение (5) описывает геометрическую
фигуру — эллипс. Ориентировка эллипса
относительно осей Х и У зависит от
значения 0.
Для 0 = 0 или
0 = 180 уравнение
приобретает вид:
,
;
,
.
В этом случае на экране появляется
прямая линия, аналогичная рассмотренной
выше (см. рис. 3а).
В случае неравенства частот и фаз на
экране осциллографа возникают более
сложные фигуры Лиссажу. Фигуры на экране
будут неподвижными, если сравниваемые
частоты относятся как целые числа и
фаза не изменяется.
Для определения отношения частот
придерживаются следующего правила.
При измерении частоты неизвестного
сигнала частоту эталонного генератора
изменяют до тех пор, пока на экране не
возникнет одна из фигур Лиссажу, возможно,
более простой формы. Ее мысленно
пересекают линиями ХХ и УУ, параллельными
условным осям Х и У, и подсчитывают число
пересечений каждой из линий ХХ и УУ с
фигурой Лиссажу, видимой на экране
осциллографа. Математический анализ
показывает, что для соотношения частот
справедливо следующее выражение:
или
,
где fy, fx — частоты сигналов,
подаваемых на пластины Х и У соответственно;
nx, ny — число пересечений
линий ХХ и УУ с фигурой Лиссажу.
В частности, для случая (рис.3б) отношение
,
т. е.
;
справедливость расчета подтверждается
построением рис. 3б. Аналогично можно
доказать, что для фигур, изображенных
на рис. 4. г, д отличаются значениями
разности фаз между напряжениями сигналов,
подаваемых на входы Х и У. Таким образом,
подавая на пластины У сигналы эталонной
f0 (известной) частоты, а на пластины
Х — сигнал неизвестной частоты fx,
можно, определив отношение
,
найти значение неизвестной частоты
по формуле (6).
При помощи фигур Лиссажу можно измерять
разность фаз между двумя периодическими
сигналами. Рассмотрим метод измерения
разности фаз на примере двух сигналов
одинаковой частоты, подаваемых на входы
Х и У.
Видно, что сигналы, подаваемые на входы
Х и У, представляют собой гармонические
колебания и, следовательно, описываются
известным уравнением:
,
где U0
— максимальное значение напряжения
— амплитуда колебания; w
— круговая (циклическая) частота, равная
w=2f;
0
— начальная фаза колебаний в момент
времени t=0; (wt+0)
— фаза колебаний в момент времени
t. Поскольку значение синуса может
изменяться от -1 до +1, то напряжение
сигнала изменяется со временем от -U0
до +U0.
Для нашего конкретного случая имеем:
;
.
Обратим внимание на то, что в любой
момент времени фазы сигналов Ux
и Uy
одинаковы; в связи с этим говорят, что
разность между сигналами равна нулю,
сигналы изменяются с одинаковой фазой.
Для другого случая имеем
Ux(t)
= U0*sin
(wt+0) = U0*sin
(wt);
Uy(t)
= U0*sin
(wt+/2),
то есть разность фаз между сигналами,
очевидно, равна /2.
Для третьегос лучая, имеем
Ux(t)
= U0*sin
(wt+0) = U0*sin
(wt);
Uy(t)
= U0*sin
(wt+/4),
то есть для данного случая разность фаз
между сигналами равна /4.
Фигуры Лиссажу, получаемые на экранах
осциллографов для различных случаев,
представлены на рис. 5. Если сигналы
одинаковой частоты изменяются в фазе
(разность фаз равна нулю), то на экране
будет наклонная линия (рис. 5, а); если
сдвиг фаз равен /2,
на экране будет круг (при одинаковых
амплитудах сигналов); если разность фаз
находится в пределах 0<0</2,
то на экране осциллографа будет фигура
Лиссажу в виде наклонных эллипсов (рис.
5, в).
Исследование фигуры Лиссажу позволяет
определить разность фаз между сигналами.
Считаем, что на входы Х и У поданы сигналы
Ux
= U0*sin
wt, Uy
= U0*sin(wt+0);
разность фаз между ними равна 0.
Данные напряжения вызовут смещение
луча по горизонтали и вертикали экрана
с учетом соотношения (1)
по оси У: x(t) = Hx
= hx*U0*sin
wt;
по оси Х: y(t) = Hy
= hy*U0*sin
(wt+0). (7)
В зависимости от разности фаз фигура
Лиссажу пересекает ось Х в одной или
нескольких точках. Определим точку
пересечения фигуры Лиссажу с осью
абсцисс (точка М); из рис. 6.5, в видно, что
координаты точки М: У=0, Х=Х1. Значения
Х1 может быть определено на экране
экспериментально.
Из уравнения (7) следует: y = 0
= hy*U*sin
(wt+0),
то есть координата У = 0 при значении
аргумента wt = -0.
При данном значении аргумента
x = x1(0)
= hx*U0*sin
(-0)
= hx*U0*sin
0.
С другой стороны, максимальное значение
Х0 (см. рис.5,в), которое также может
быть определено экспериментально, равно
(из уравнения (7)): x0
= hx*U0.
Следовательно, отношение х1 / х0
= sin 0
определяет значение 0,
то есть
x1
/ x0 =
(hx*U0*sin
0)
/ (hx*U0)
= sin 0,
или разность фаз между сигналами равна
0 = arcsin (x1
/ x0) (8)
Таким образом, определяя в ходе
эксперимента значения Х1 и Х2,
вычисляя отношение Х1 / Х0,
можно с учетом уравнения (8) определить
разность фаз между сигналами, подаваемыми
на входы Х и У. Именно это осуществляется
на практике.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Время на прочтение
8 мин
Количество просмотров 9.4K
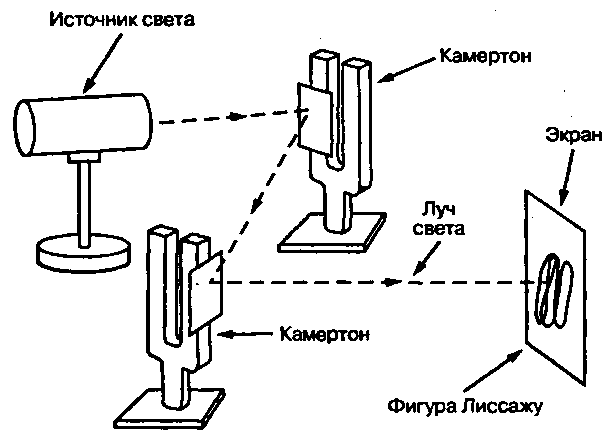
Картинки из сети, качество желает лучшего, но они достаточно точно отражают суть опыта по визуализации фигур. Зри в корень – основа мудрости поколений.
Немного истории
Ещё в школе на уроках физики я вглядывался в осциллограф, на экране которого, сменяя друг друга, появлялись разные фигуры: сначала простые – линия, парабола, круг, эллипс, потом фигуры становились всё более насыщенные непрерывными волнообразными линиями, напоминающие мне кружева. Автором этого кружевного дива был Жюль Антуан Лиссажу французский физик, член — корреспондент Парижской АН (1879) [1]. Сами фигуры — это замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях [2]. Думаю, что в те далёкие от современности годы основной заслугой Жюля, кроме конечно накопленных опытом знаний математики и физики, была простая механическая визуализация этих фигур подручными средствами. Захотелось конструировать подобно Жулю максимально просто и наглядно, реализовать его идеи применительно к современной задаче линейных измерений. Но сделать это путём математического моделирования с графической визуализацией его результатов на Python. Но сначала рассмотрим классический вариант [3] построения фигур.
Какими должны быть фигуры Лиссажу
Для этого воспользуемся системой уравнений, описывающих фигуры:
x(t), y(t) в общем случае зависящие от времени гармонические колебания вдоль взаимно перпендикулярных плоскостей, частоты b, a и начальная фаза d. Для анализа фигур в вычислениях принимают постоянным модуль разности частот |b — a| = 1. Будем рассматривать отношение круговых частот b / a и начальную фазу d. Имеем для линии A = B d = 0, окружности , и параболы
. Основные отношения частот, удовлетворяющие условию, занесём во вложенный список m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]].
Код для построения графиков каждой из фигур на отдельных графиках
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sin,pi
import matplotlib.pyplot as plt
m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]]# отношение круговых частот
for i in m:
if i[0]==0:
a=1
x=[sin(a*t) for t in np.arange(0.,2*pi,0.01)]
y=[sin(a*t) for t in np.arange(0.,2*pi,0.01)]
plt.plot(x, y, 'r')# график для линии
plt.grid(True)
plt.show()
else:
a=i[0]
b=i[1]
d=0.5*pi
x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)]
y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)]
plt.plot(x, y, 'r') # график для различных отношений a/b
#круговых частот
plt.grid (True)
plt.show()
Результат не привожу, отдельные фигуры не впечатляют. Хочу коллаж из «кружев».
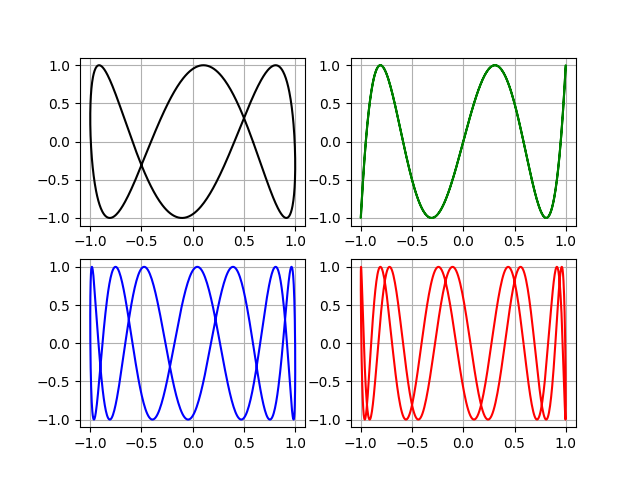
Код программы для построения на одной форме графиков для четырёх фигур при m= [3,4], [5,4],[5,6],[9,8]]
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sin,pi
import matplotlib.pyplot as plt
m=[[3,4],[5,4],[5,6],[9,8]] # отношение круговых частот
plt.figure(1)
for i in m:
a=i[0]
b=i[1]
d=0.5*pi
x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)]
y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)]
if m.index(i)==0:
plt.subplot(221)
plt.plot(x, y, 'k') # график для различных отношений a/b круговых частот
plt.grid(True)
elif m.index(i)==1:
plt.subplot(222)
plt.plot(x, y, 'g')
plt.grid(True)
elif m.index(i)==2:
plt.subplot(223)
plt.plot(x, y, 'b')
plt.grid(True)
else:
plt.subplot(224)
plt.plot(x, y, 'r')
plt.grid(True )
plt.show()
И вот они «кружева».
Что нельзя отнести к фигурам Лиссажу по определению о их замкнутости
Зачем нам |b — a| = 1, “за флажки!” попробуем например так m=[[1,3],[1,5],[1,7],[1,9]]
На втором графике при m=0,2 получена незамкнутая траектория, которая по определению не является фигурой Лbссажу.
В поисках механических аналогов
Поищем аналогии фигур в измерительной технике и вот вибрационный уровнемер с резонатором в виде эллиптической трубки [4].
Упруго закреплённая трубка эллиптического сечения с помощью систем возбуждения 5,6,7 совершает автоколебания в одной плоскости, а с помощью систем 8, 9, 10 в другой плоскости перпендикулярной первой. Трубка колеблется в двух взаимно перпендикулярных плоскостях с разными частотами близкими к собственным. Масса трубки зависит от уровня заполняющей её жидкости. С изменением массы меняются и частоты колебаний трубки, которые и являются выходными сигналами уровнемера. Частоты несут дополнительную информацию о мультипликативных и аддитивных дополнительных погрешностях, компенсируемых при обработке частот микропроцессором 11.
Условия адекватного моделирования
Для более-менее корректной привязки фигур Лиссажу к работе упомянутого уровнемера, следует учесть следующие обстоятельства. Во-первых, закреплённая одним концом трубка эллиптического сечения — это колебательная система с распределёнными параметрами, что сильно усложняет анализ её колебаний. Во-вторых, отношение частот колебаний трубки не может изменяться произвольно, оно зависит от эллипсности сечения и допустимых зазоров в системе возбуждения колебаний. Для отношения частот можно получить простое соотношение.
К чему принадлежат переменные, a, b, a0, b0 ясно из рисунка и кроме того формула для циклической частоты осциллятора известна из школьного курса физики. Для «реализации на Python в последнее отношение введём толщину стенки и показатель эллипсности внутреннего сечения трубки, тогда вместо четырёх переменных получим три.
Код программы для определения. допустимого изменения отношения частот
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
d=0.5
a=9
x=[w for w in np.linspace(0.8,0.95,15)]
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'r', label='Толщина стенки трубки в мм. -- %s' %str(d))
d=0.7
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'b',label='Толщина стенки трубки в мм.-- %s' %str(d))
d=1.0
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'g', label='Толщина стенки трубки в мм.-- %s' %str(d))
plt.ylabel('Отношение частот колебаний эллиптической трубки')
plt.xlabel('Отношение длин малой и большой полуосей')
plt.title('Определение допустимого диапазона для отношения частот')
plt.legend(loc='best')
plt.grid(True)
plt.show()
В результате работы программы получим график.
График построен для малой внутренней полуоси в 9 мм. Для конструктивно допустимого отношения малой к большой полуоси сечения в диапазоне от 0.8 до 0.95. Это основной фактор влияния на отношение частот, которое изменяется от 1.18 до 1.04. Толщина стенки влияет незначительно. Теперь у нас есть диапазон отношений и ним можно воспользоваться для дальнейшего моделирования.
Формы колебаний вертикальной оси трубки
Что касается распределённых механических параметров консольной трубки, то они при помощи равенства собственных частот и импеданса могут быть приведены к сосредоточенной массе жёсткости и демпфированию. Кроме того, для определения форм изгибных колебаний консольной трубки можно получить выражение для распределённых параметров. Уравнение для форм – балочные функции имеет вид:
где — корни уравнения:
Следует отметить что, не смотря на большое количество публикаций о формах и частотах колебаний консольного стержня, балки или трубки уравнения (4) нигде не приводяться, только рисунки без координат. Поэтому уравнение (4), я вывел через условия на концах и балочные функции, проверил по корням (5) и расположению узлов. Однако это тривиальное уравнение, о котором просто забыли.
Код программы для численного определения корней уравнения 1.1 и построения трёх форм изгибных колебаний оси трубки
1.1 —
#!/usr/bin/env python
#coding=utf8
from scipy.optimize import *
import numpy as np
from numpy import pi,cos,cosh,sin,sinh
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
d=[]
for i in range(0,4):
x=brentq(lambda x:cosh(x)*cos(x)+1,0+pi*i,pi+pi*i)
p=round(x,3)
if p not in d:
d.append(p)
x=[w for w in np.linspace(0,1,100)]
k=d[0]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)]
plt.plot(z, x, 'g', label='Первая форма для корня - %s' %str(k))
k=d[1]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)]
plt.plot(z, x, 'b', label='Вторая форма для корня - %s' %str(k))
k=d[2]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)]
plt.plot(z, x, 'r', label='Третья форма для корня - %s' %str(k))
plt.title('Первые три формы изгибных колебаний осевой линии трубки')
plt.xlabel(' Координата вдоль оси OX ')
plt.ylabel(' Координата положения осевой линии трубки вдоль оси OZ ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
В результате работы программы получим график построенный с учётом вертикального положения трубки.
На графике координата осевой линии приведена к длине трубки, а амплитуда нормирована. Положение узлов колебаний трубки относительно места её крепления в точности соответствует теории колебаний.
По каким траекториям движется конец трубки
Последнее препятствие — сложность получения осмысленного численного решения дифференциальных уравнений колебаний, при условии варьирования несколькими параметрами одновременно. Тут на помощь пришли две мои статьи о колебательном звене на Python [5,6], в которых приведена методика получения точных символьных решений дифференциальных уравнений.
Запишем два условно независимых уравнения для колебаний трубки в плоскости OX и OY с разными частотами a и b отношение между которыми выбрано из ранее установленного диапазона. Остальные параметры выбраны во правильной взаимосвязи, но произвольно для лучшей демонстрации результата.
Здесь введены следующие обозначения (для упрощения без индексов).
─ приведенная амплитуда силы,
─ коэффициент затухания,
─ собственная частота колебаний системы, m ─ сосредоточенная масса одинаковая для обоих уравнений,
─ сосредоточенные коэффициенты демпфирования, разные из-за разных амплитуд, а следовательно разных зазорах в системах возбуждения колебаний,
─ разные жёсткости из-за эллиптичности сечения трубки.
Код программы для решения каждого дифференциального уравнения системы (6), с последующем сложением для получения траектории движения конца трубки.
import numpy as np
from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
def solution(w,v,i,n1,n2,B,f,N):
t=Symbol('t')
var('t C1 C2')
u = Function("u")(t)
de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t+v))
des = dsolve(de,u)
eq1=des.rhs.subs(t,0)
eq2=des.rhs.diff(t).subs(t,0)
seq=solve([eq1,eq2],C1,C2)
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])
g= lambdify(t, rez, "numpy")
t= np.linspace(n1,n2,N)
plt.figure(1)
if i==1:
plt.subplot(221)
plt.plot(t,g(t),color='b', linewidth=3,label='x=%s*sin(%s*t+%s)' %(str(f),str(w),str(v)))
plt.legend(loc='best')
plt.grid(True)
else:
plt.subplot(222)
plt.plot(t,g(t),color='g', linewidth=3,label='y=%s*sin(%s*t+%s)' %(str(f),str(w),str(v)))
plt.legend(loc='best')
plt.plot(t,g(t),color='r', linewidth=3)
plt.grid(True)
return g(t)
N=1000#Число точек оцифровки временного интервала
B=0.2#Установка демпфирования
f=1#Установка амплитуды
n1=0#Нижняя граница временной развертки
n2=20#Верхняя граница временной развёртки
w1=5.0#Частота колебаний трубки вдоль оси ОХ
w2=10.0#Частота колебаний трубки вдоль оси ОУ
v1=0#Начальная фаза при колебании вдоль оси ОХ
v2=0#Начальная фаза при колебании вдоль оси ОУ
g1=solution(w1,v1,1,n1,n2,B,f,N)
g2=solution(w2,v2,2,n1,n2,B,f,N)
plt.subplot(223)
plt.plot(g1,g2,color='b', linewidth=3,label='w1/w2=%s'%str(w1/w2))
plt.legend(loc='best')
plt.grid(True)
plt.subplot(224)
x=[w for w in np.linspace(0,1,100)]
k=1.875
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)]
plt.plot(z, x, 'g',label='Форма -%s'%str(k))
plt.legend(loc='best')
plt.grid(True)
plt.show()
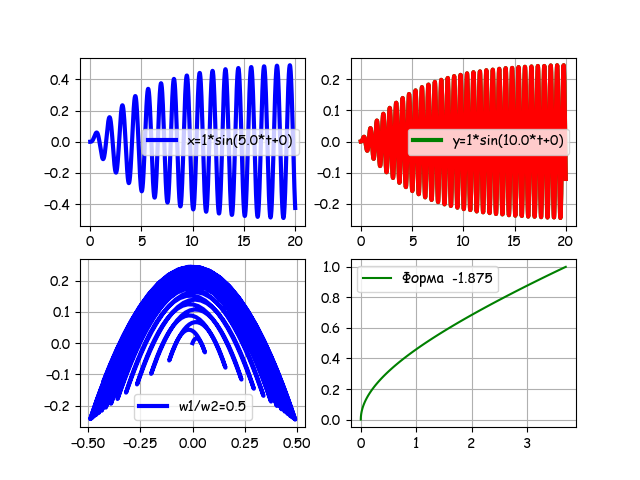
Программа позволяет менять все параметры модели, например, для:
N=1000, B=0.2, f=1, n1=0, n2=20, w1=5.0, w2=10.0, v1=0, v2=0
Для отношения частот 0.5 переходной процесс множит фигуры. Поставим “ворота” времени n15=0, n2=20, получим.
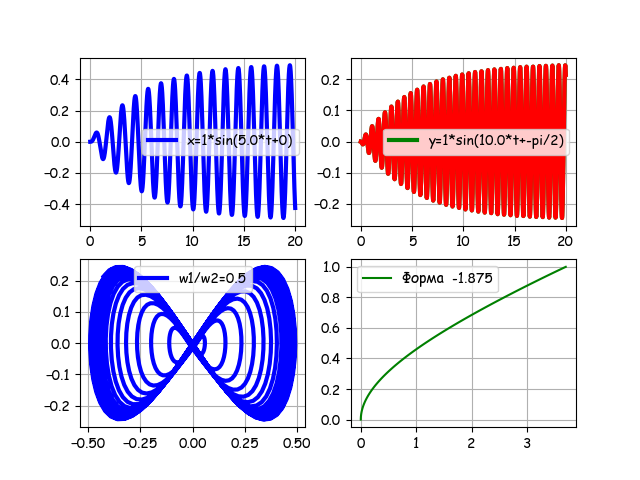
Снимем” ворота” и введём начальную фазу v2=-pi/2, получим:
С учётом изложенного выше, графики комментарий не требую.
Для интриги
Если эта статья найдёт своих читателей или читатели её найдут, не устрашившись теней прошлого, то я опубликую трёхмерные анимационные графики сложных пространственных колебаний трубки при изменении в ней уровня заполняющей жидкости.
Вместо выводов
Изобретение Жюля Антуана Лиссажу продолжает свой путь во времени, но уже и на Python. Надеюсь, что представленная интерпретация, конечно далёкая от совершенства, позволит продолжить знакомство с работами гениального математика Лиссажу.
Ссылки
- Биографии учёных физиков.
- Что такое фигуры Лиссажу?
- Фигуры Лиссажу.
- Вибрационный уровнемер.А.С.№777455
- Модель колебательного звена с применением символьного и численного решений дифференциального уравнения на SymPy и NumPy.
- Модель колебательного звена в режиме резонансных колебаний на Python.
Введение[править]
Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.
Простейшая физическая модель для этого — колебание грузика на пружинах, расположенных перпендикулярно друг другу.
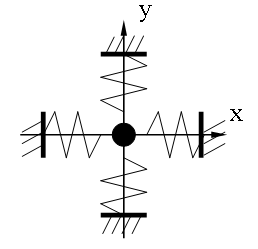
Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний.
Примеры графиков[править]

На данном изображение можно увидеть наиболее яркие примеры фигур Лиссажу (слева на право) :
- A/B = 1; d = 0.5;
- A/B = 1; d = 0;
- A/B = 1; d = 0.25;
- A/B = 1; d = 0;
- A/B = 3/2; d = 0;
- A/B = 0.9; d = 0;
Реализация[править]
Ссылки[править]
Автор проекта: Фомичева Мария