Примеры решения факториалов
Рассмотрим примеры решения примеров с факториалами. Зная что такое факториал числа и основную формулу его нахождения, легко решить большинство примеров.
СУММА ФАКТОРИАЛОВ
Начнем с суммы факториалов чисел. В таких примерах, просто вычисляем значения и складываем их. Значения факториалов легко найти в таблице факториалов или можно воспользоваться калькулятором факториалов.
Рассмотрим следующую задачу.
Решение: 5! + 4! = 1 · 2 · 3 · 4 · 5 + 1 · 2 · 3 · 4 = 120 + 24 = 144
Ответ: 5! + 4! = 144
В этом примере, сначала находятся значения факториалов чисел 5 и 4, которые равны 120 и 24 соответственно. Затем они складываются. Всё просто!
ДЕЛЕНИЕ ФАКТОРИАЛОВ
При решении задач на деление факториалов нужно вспомнить формулу факториала. А именно: n! = n · (n-1)!.
Разберем пример задачи на деление факториалов.
Разложим факториал числителя на следующие множители: 56! = 56 · 55 · 54!, а далее сокращаем 54! в числителе и знаменателе. Получаем, 55 · 56.
Как быстро решать факториалы?
Точно так же, как вы вычисляете факториалы? Говоря более математическим языком, факториал числа (n!) равно n(n-1). Например, если вы хотите вычислить факториал для четырех, вы должны написать: 4! = 4 х 3 х 2 х 1 = 24.
Как решить 6 факториалов?
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Как работают факториалы? факториал, в математике, произведение всех положительных целых чисел, меньших или равных данному положительному целому числу и обозначенных этим целым числом и восклицательным знаком. Таким образом, факториал семь записывается как 7 !, что означает 1 × 2 × 3 × 4 × 5 × 6 × 7. Факториал нуль определяется как равный 1.
Во-вторых, можно ли умножать факториалы? Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.
Как вы делаете факториалы в математике?
факториал в математике произведение всех положительных целых чисел, меньших или равных заданному положительному целому числу и обозначается этим целым числом и восклицательным знаком. Таким образом, факториал семь записывается как 7!, что означает 1 × 2 × 3 × 4 × 5 × 6 × 7.
тогда как факториалы используются в реальной жизни? Это очень полезно, когда мы пытаемся подсчитайте, сколько существует различных заказов на вещи или сколько различных способов мы можем комбинировать вещи. Например, сколькими различными способами мы можем расположить n вещей? У нас есть n вариантов для первого.
Как решить 6 факториалов?
Насколько велик факториал 52?
52! является приблизительно 8.0658e67. Чтобы получить точное представление, просмотрите факториальную таблицу или попробуйте калькулятор «новой школы», который понимает длинные целые числа.
Как решить факториальные задачи?
Что такое формула nCr?
Формула комбинаций: nCr = n! / ((п — г)! р!) n = количество элементов.
В каком классе вы изучаете факториалы? ИКЛ | факториалы | 7th класс математика
Вы умеете вычитать факториалы?
Как учить факториалы?
Чему равно произведение 2 факториалов? единственный известный факториал, который является произведением двух факториалов: 10! =6!
Умеете ли вы распределять факториалы? Факторное распределение имеет место, когда набор переменных — независимые события. Другими словами, переменные вообще не взаимодействуют; Учитывая два события x и y, вероятность x не изменится, если вы умножите y. Следовательно, вероятность x при условии, что произошло y — P(x|y) — будет такой же, как P(x).
Кто изобрел факториал?
Одним из самых основных понятий перестановок и комбинаций является использование факториальной записи. Используя понятие факториалов, многие сложные вещи упрощаются. Использование! был начат Кристиан Крамп в 1808 году.
Что такое факториал 100 говорить? Приблизительное значение 100! является 9.3326215443944E + 157. Количество завершающих нулей в 100! равно 24. Количество цифр в факториале 100 равно 158.
Какие приложения используют факториал?
отдельные объекты: есть. . В математическом анализе факториалы используются в степенных рядах для экспоненциальной функции и других функций, а также находят применение в алгебра, теория чисел, теория вероятностей и информатика.
Сколько стоит 8.06 е67? способами, которыми мы можем составить колоду карт. 52! чертовски большое число, равное 8.06e+67. 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 68 XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX, если быть точным. Это XNUMX-значный номер.
Что такое факториал 20?
Ответ: Факториал числа 20 равен 2432902008176640000.
Факториал n обозначается через n!
Факториал 52 верен? Количество возможных способов заказать колоду из 52 карт — 52! ‘(факториал 52), что означает умножение 52 на 51 by 50… вплоть до 1. Число, которое вы получите в конце, равно 8×10^67 (8 с 67 0 после него), по сути, это означает, что случайно перетасованную колоду никто никогда не видел раньше и никогда больше не увидит. .
Объясните, пожалуйста, как складывать и вычитать факториалы. Вот пример: 7!-5!/6!
Чтобы вычесть факториал из факториала, никакого общего правила нет: всё, что можно сделать, это вынести за скобки общий множитель, ну например:
Тут ничего хитрого нет. Ну и получается, что нужно считать факториал только меньшего числа. С суммой всё получится аналогично.
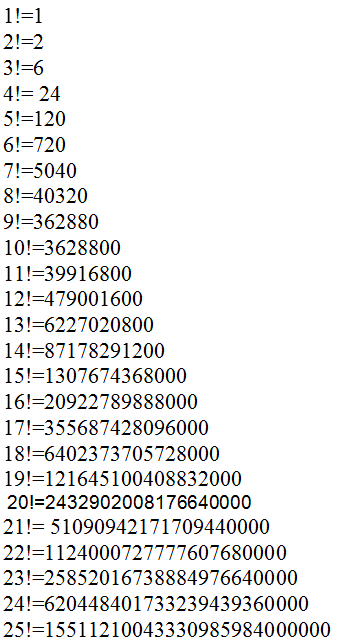
Однако, если факториалы большие, это не сильно упростит ситуацию. Кроме того, все маленькие факториалы обычно легко запомнить наизусть, и просто вычесть одно число из другого. Я приведу здесь специально список маленьких факториалов, их нужно запомнить:
Дальше знать необязательно.
А в приведённом тобой примере, вообще-то, первое действие — деление. На всякий случай.
#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
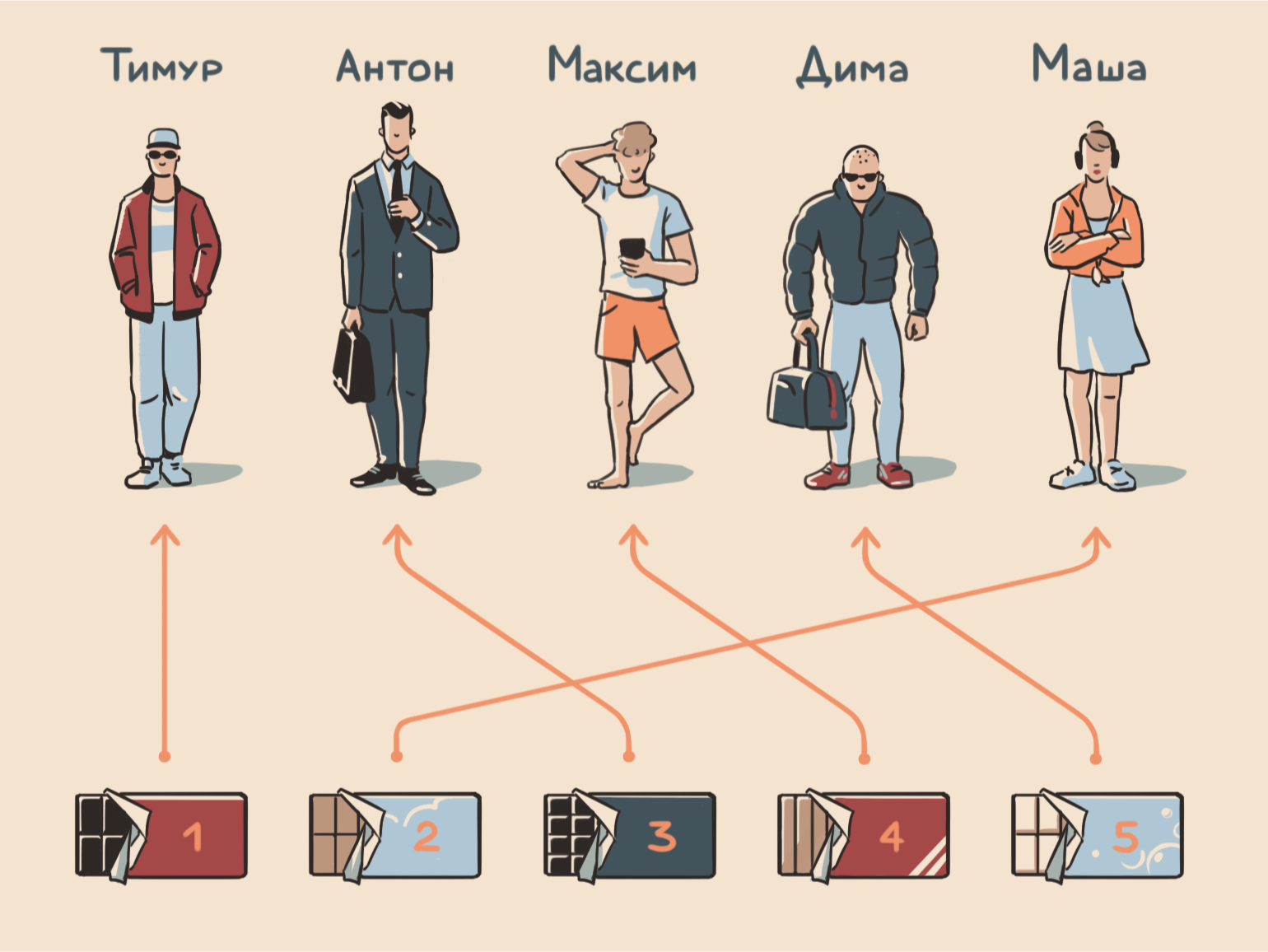
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
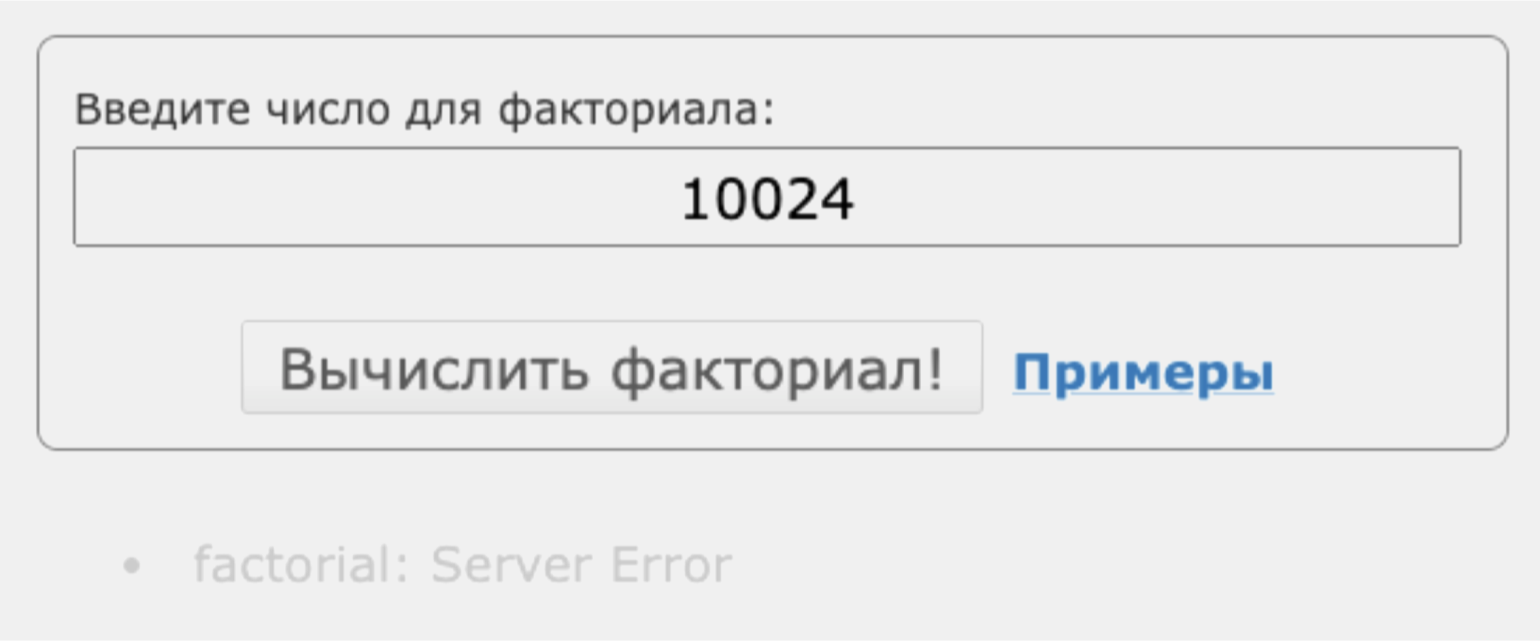
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
-
3! = 3 × 2! = 6;
-
41160 = 5! +8! + 6!
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
-
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
-
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
-
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).
Калькулятор факториалов
Калькулятор факториалов
Пользоваться нашим калькулятором факториалов предельно просто. Нужно нажать на клавиатуре !
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется
только переписать в тетрадь!
Пример:
Пример:
Пример:
Переменные:
Параметры:
Факториалы
Что такое факториалы и как их решать
Факториал числа n, который в математике обозначают буквой латиницы n, после которой следует
восклицательный знак !. Произносится голосом это выражение как “н факториал”. Факториал – это результат
последовательного умножения между собой последовательности натуральных чисел с 1 и до искомого числа n.
Например, 5! = 1 х 2 х 3 х 4 х 5=720Факториал числа n обозначается латинской буквой n! и произносится
как эн факториал. Представляет собой последовательное перемножение (произведение) всех натуральных чисел
начиная с 1 до числа n.
Например: 6! = 1 х 2 х 3 х 4 х 5=720
Факториал имеет математический смысл, только тогда, когда если это число целое и положительное
(натуральное). Этот смысл следует из самого определения факториала, т.к. все натуральные числа
неотрицательные и целые. Значения факториалов, а именно результат умножения последовательности от
единицы до числа n можно посмотреть в таблице факториалов. Такая таблица возможна, по причине того, что
значение факториала любого целого числа известно заранее и является, так сказать, табличным
значением.
По определению 0! = 1. То есть если имеется ноль факториал, то мы ничего не перемножаем и результат будет
первым натуральным существующим числом, то есть один.
Рост функции факториала можно отобразить на графике.
Это будет дуга, похожая на функцию икса в квадрате,
которая будет стремиться быстро вверх.
Факториал – является быстрорастущей функцией. Она растет по графику быстрее, чем функция многочлена любой
степени и даже экспоненциальная функция. Факториал растет быстрее многочлена любой степени и
экспоненциальной функции (но при этом медленнее двойной экспоненциальной функции). Именно поэтому, чтобы
посчитать факториал вручную могут быть сложности, так как результатом может получиться очень большое
число. Чтобы не считать факториал вручную, можно воспользоваться калькулятором подсчёта факториалов, с
помощью которого вы можете быстро получить ответ. Факториал применяется в функциональном анализе, теории
чисел и комбинаторике, в которой имеет большой математический смысл, связанный с числом всевозможных
неупорядоченных комбинаций объектов (чисел).
Чтобы быстро рассчитать число комбинаций n чисел, нужно всего лишь посчитать n!.
факториала калькулятором, искомое значение можно использовать в решении более сложных задач.
Вы можете посмотреть необходимый факториал в таблице: «Таблица
факториалов»
Бесплатный онлайн калькулятор факториалов
Наш бесплатный решатель позволяет расчитать факториалы онлайн любой сложности за считанные секунды. Все,
что вам необходимо
сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть
видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то
вы
можете задать их в нашей группе Вконтакте: pocketteacher.
Вступайте
в нашу группу, мы всегда рады помочь вам.
Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов.
Толяна Ромоданова светлой памяти — ЭСТ: Катюша — любил он эту песню.От проекта dpva.ru, команды Anonimous Freaks, родных, друзей, коллег и одноклассников — некоторые тоже уже ушли от нас R.I.P. |
|||
|
|
|||
|
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление
|
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник /
Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. |
|||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator |
Формула бинома
элементарная теория чисел — Факториал, выраженный через два других факториала
спросил
9 лет, 10 месяцев назад
Изменено
6 лет, 1 месяц назад
Просмотрено
4к раз
$begingroup$
Всегда ли факториал $N$ может быть выражен суммой (сложением и вычитанием) или произведением двух других факториалов?
Всегда ли существуют целые числа $A$ и $B$ такие, что $N! = А! + B!$ или $N! = А! — Б!$ или $N! = А!cdot В!$ ?
- элементарная теория чисел
- факториал
$endgroup$
4
$begingroup$
Если вы хотите $N! = А! + B!$, то $A,B Следовательно, $N! = А! + Б! leq 2(N-1)!$. Это возможно, только если $N =2$.
$endgroup$
$begingroup$
На этом сайте уже задавали вопрос об умножении. Общий пример
$$(n!-1)! cточка! = (н!)! $$ с такими примерами, как
$$ n=3; ; ; ; 5! cdot 6 = 6! $$
$$ n=4; ; ; ; 23! cdot 24 = 24! $$
$$ n=5; ; ; ; 119! cdot 120 = 120! $$
Единственный известный нетривиальный пример:
$$ 6! cdot 7! = 10! $$
Ну, может быть, я буду использовать для этого заглавные буквы. Если $К! cточка М! = N!$ и $K
$endgroup$
3
$begingroup$
Нет, на самом деле это редкость.
$endgroup$
0
$begingroup$
Если $N!=A!+B!$
, то
$A!=N!-B!$
и
$B!=N!-A!$
поэтому
$A !Б! = (N!-A!)(N!-B!)$
разделить обе части на A!B!
$1=(N!/A!-1)(N!/B!-1)$
$endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
теория чисел — Построение $mathbb N$ из набора факториалов
спросил
10 лет, 4 месяца назад
Изменено
8 лет, 9несколько месяцев назад
Просмотрено
755 раз
$begingroup$
Пусть S — множество ${0!, 1!, 2!, ldots}$. Можно ли построить любое натуральное число, используя только сложение, вычитание и умножение и используя любой элемент из S не более одного раза? Например:
$$ 3 = 2! + 1!$$
$$ 4 = 3! — 2! = 2! + 1! + 0!$$
$$ 146 = 4!cdot3! + 2!$$
и т.д. Моя интуиция подсказывает, что это неправда, но я не понимаю почему. Что-то вроде 8076 не имеет очевидного решения, но, возможно, вы можете получить его, вычитая огромный факториал из произведения двух меньших факториалов или что-то в этом роде.
РЕДАКТИРОВАТЬ: К сожалению, положительное целое, а не положительное число.
- теория чисел
- факториал
$endgroup$
9
$begingroup$
Позвольте мне предположить, что вам разрешено использовать только $0! = 1!$ один раз. В этом случае все факториалы после $4!$ делятся на $24$, поэтому, работая с $bmod 24$, вы можете использовать только числа $1, 2, 6$, каждое не более одного раза, и я достаточно уверен вы не можете получить никакие числа, конгруэнтные $10 bmod 24$ таким образом.
Редактировать: Если вы хотите использовать как $0!$, так и $1$, то все факториалы после $5!$ делятся на $120$, поэтому работая с $bmod 120$, вы можете использовать только числа $1 , 1, 2, 6, 24$.
Чтобы вычесть факториал из факториала, никакого общего правила нет: всё, что можно сделать, это вынести за скобки общий множитель, ну например:
Тут ничего хитрого нет. Ну и получается, что нужно считать факториал только меньшего числа. С суммой всё получится аналогично.
Однако, если факториалы большие, это не сильно упростит ситуацию. Кроме того, все маленькие факториалы обычно легко запомнить наизусть, и просто вычесть одно число из другого. Я приведу здесь специально список маленьких факториалов, их нужно запомнить:
Дальше знать необязательно.
А в приведённом тобой примере, вообще-то, первое действие — деление. На всякий случай.





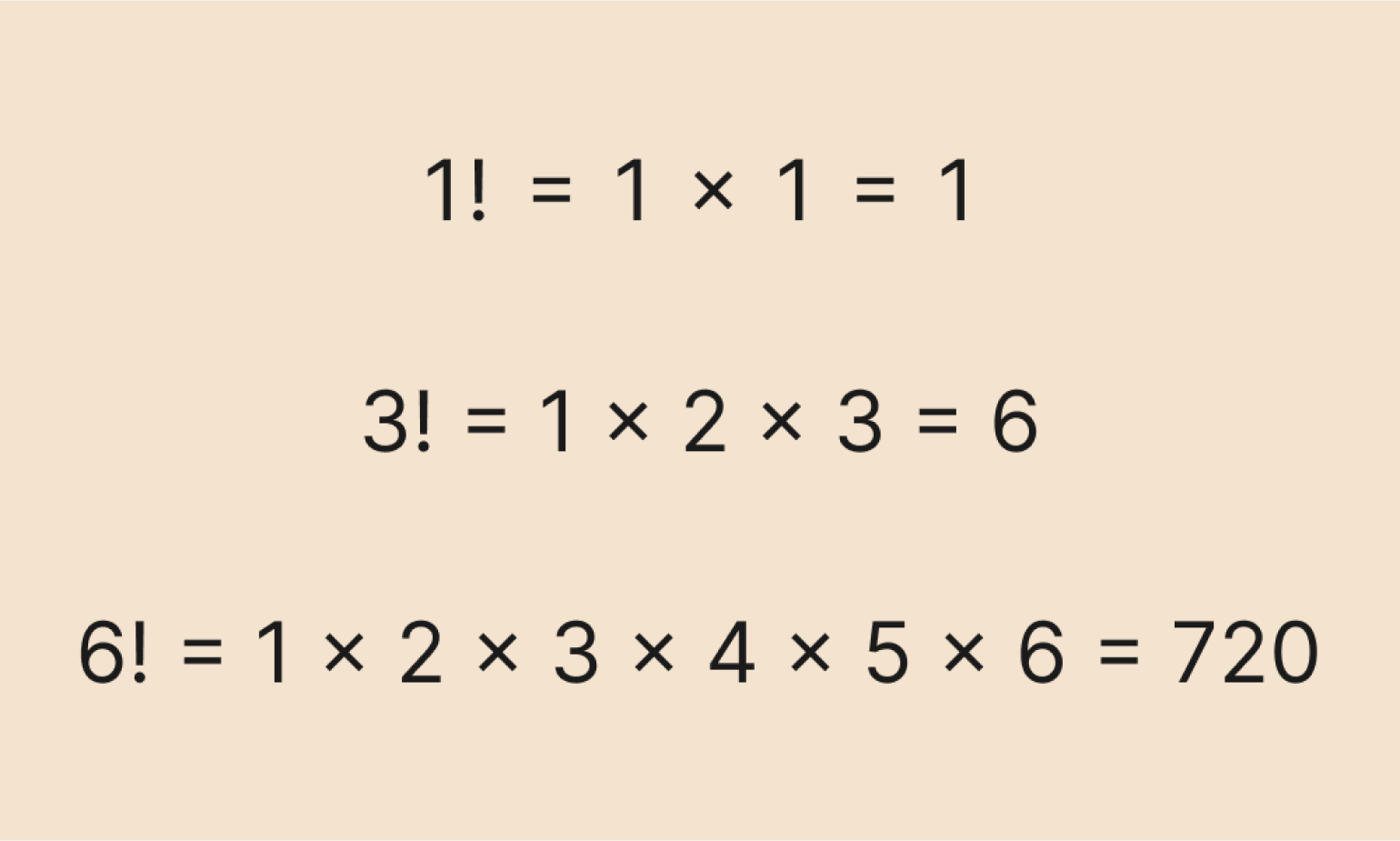

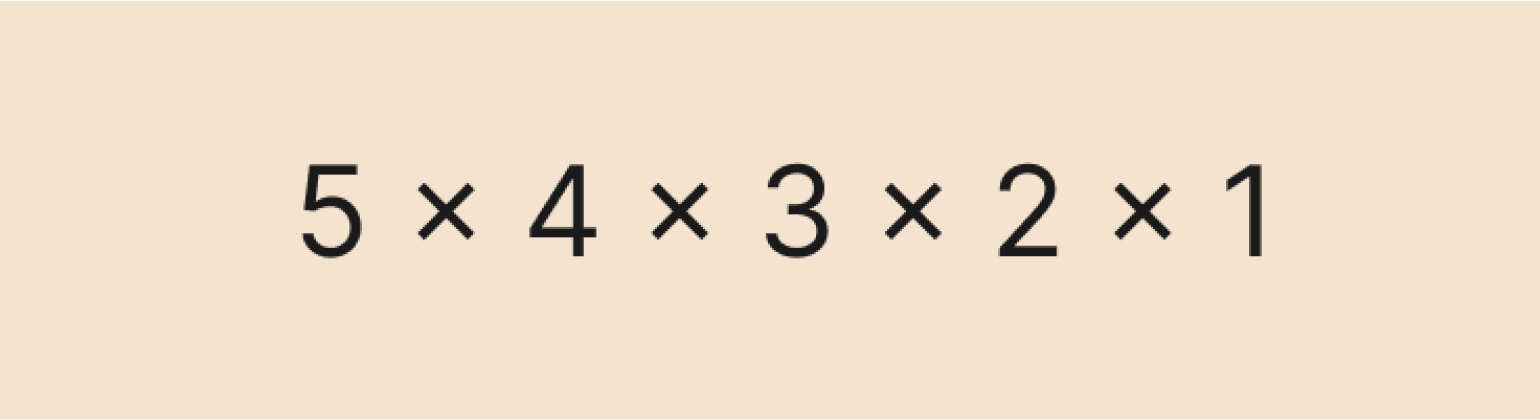
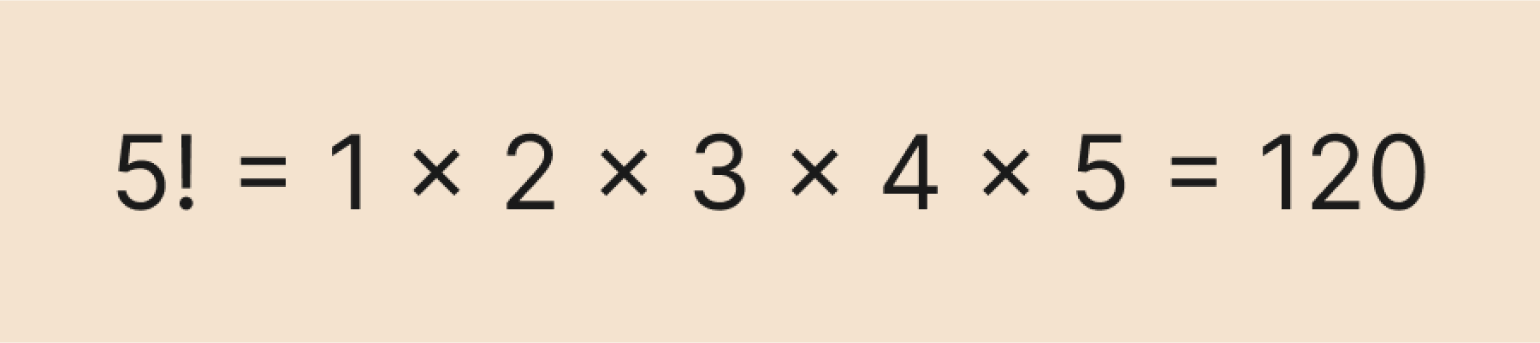
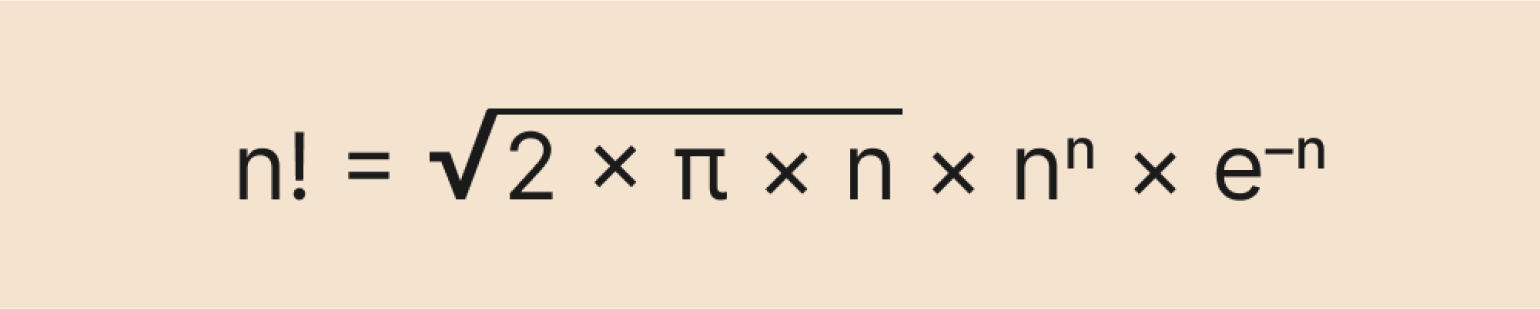
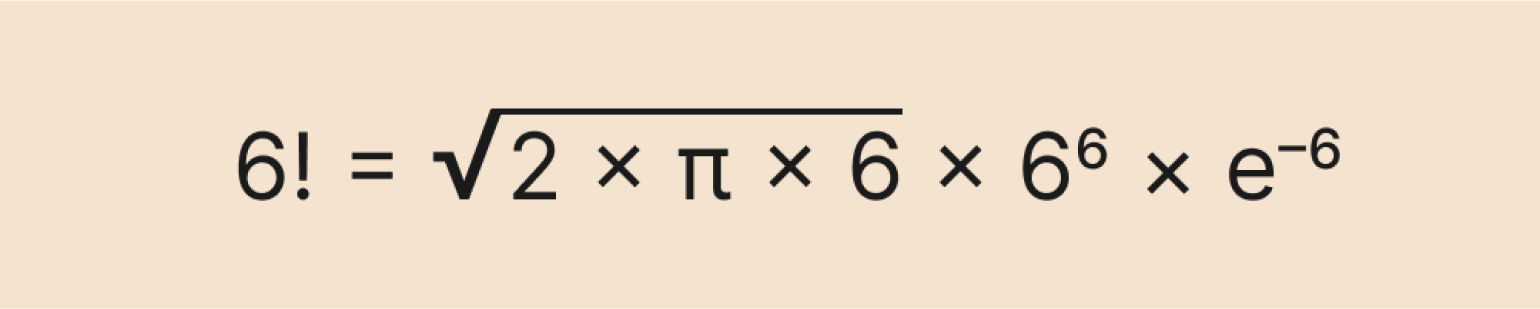
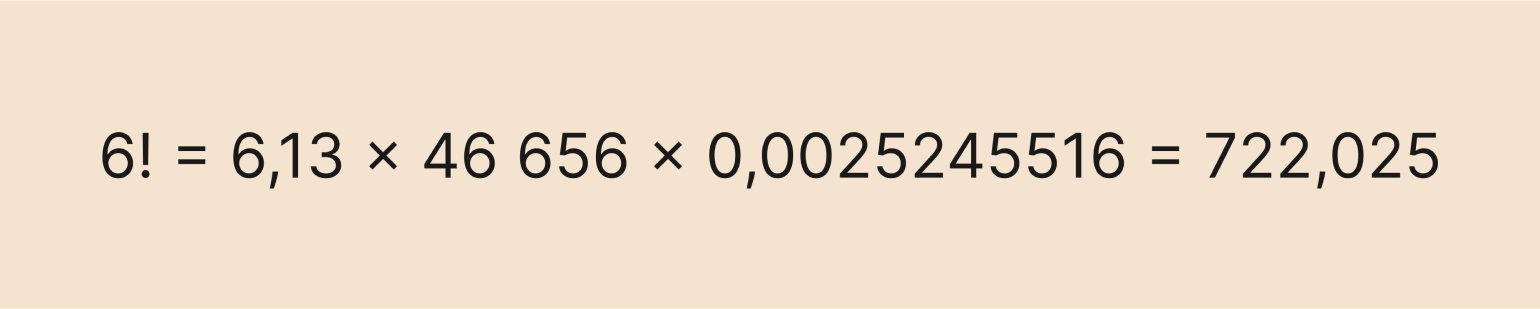

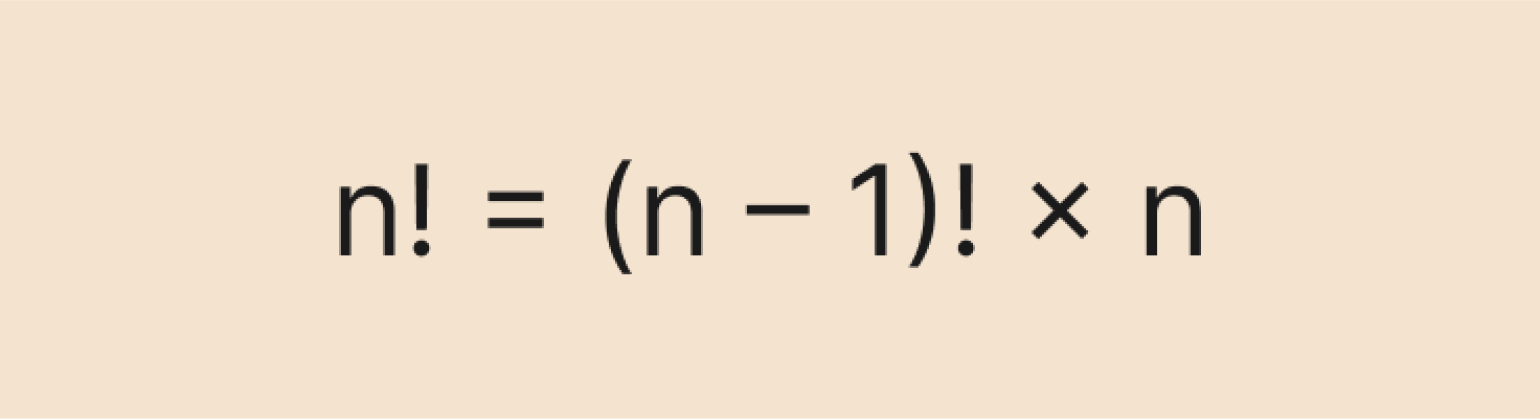

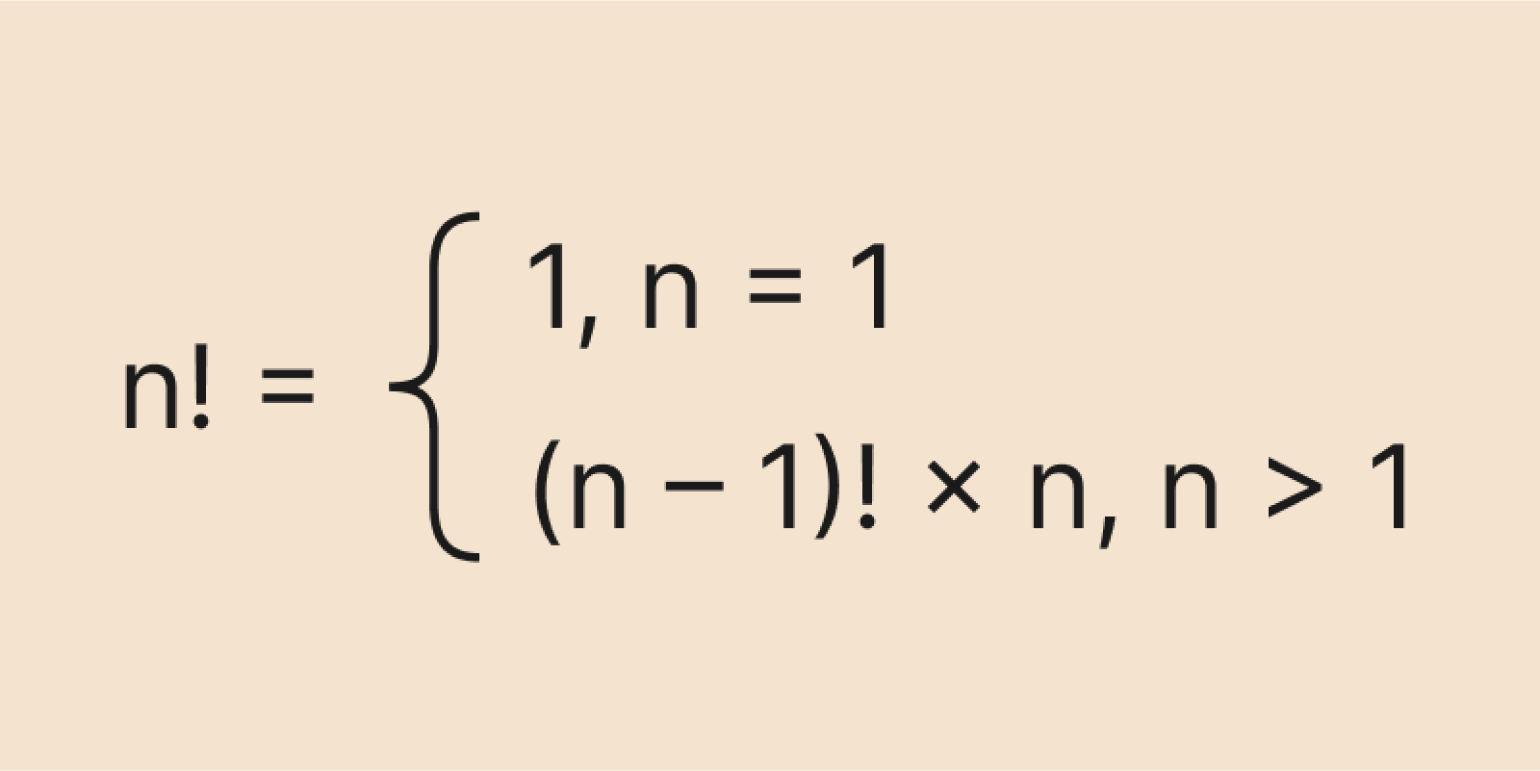
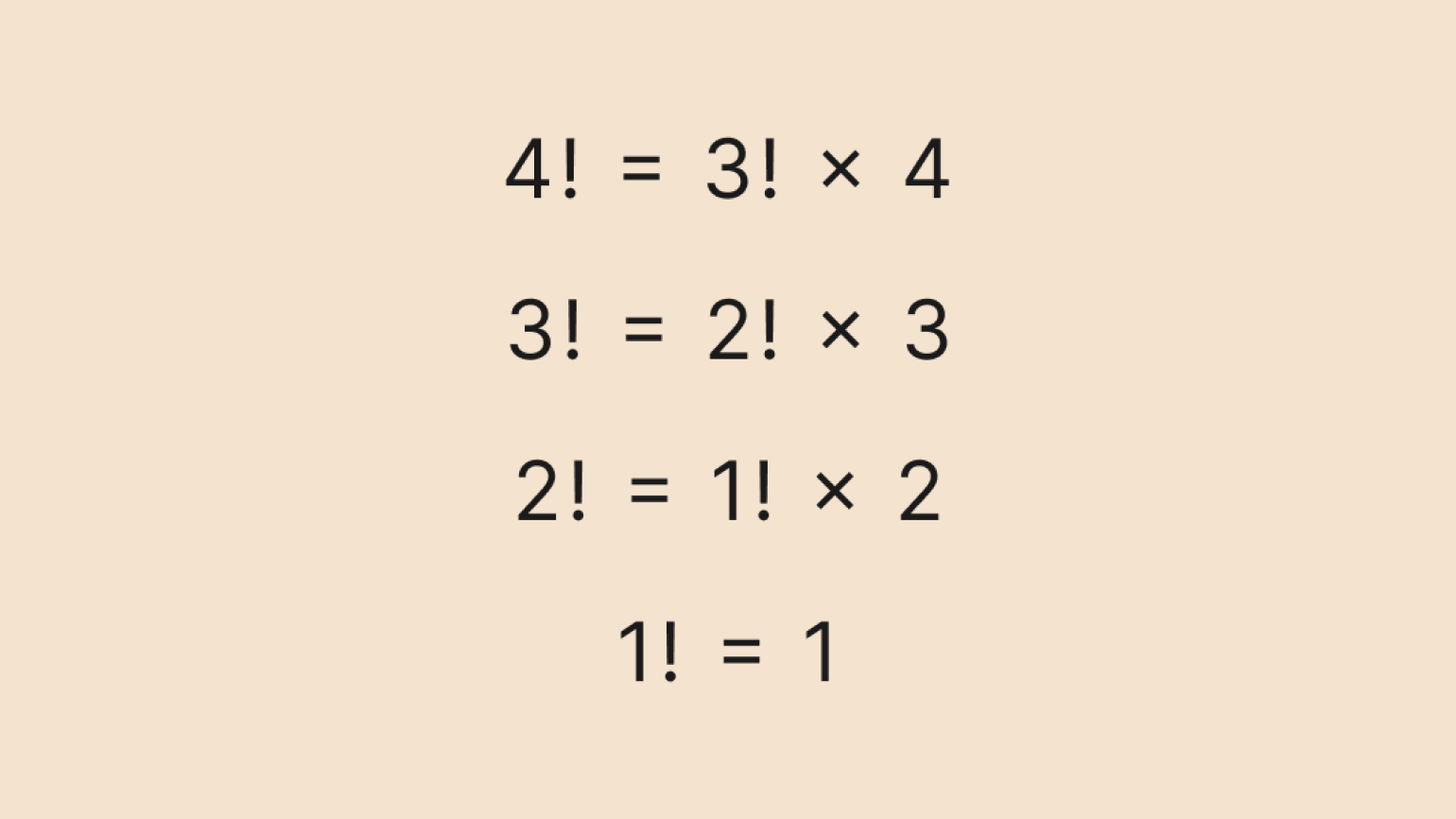
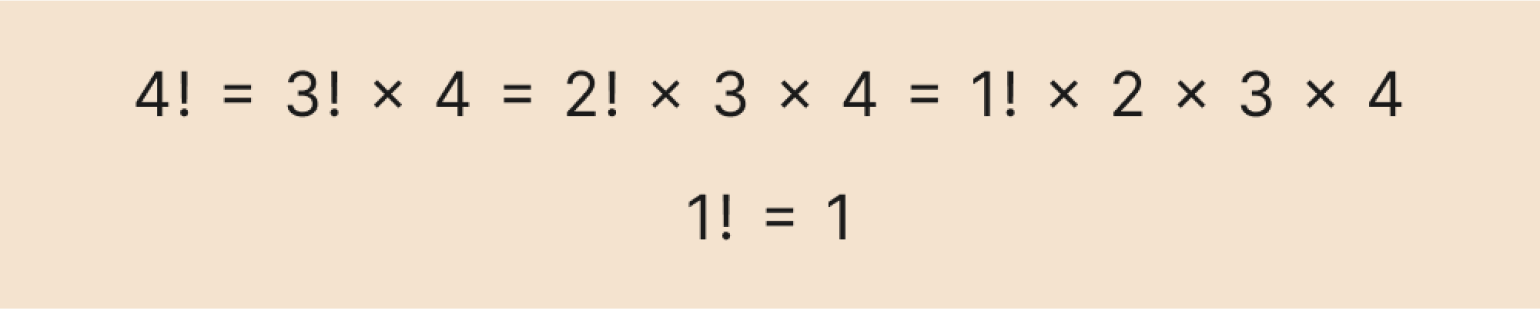
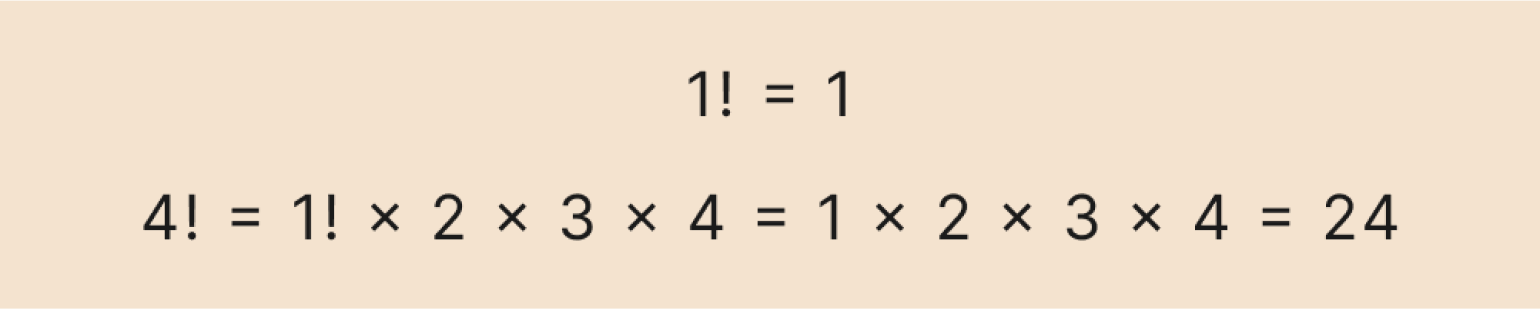


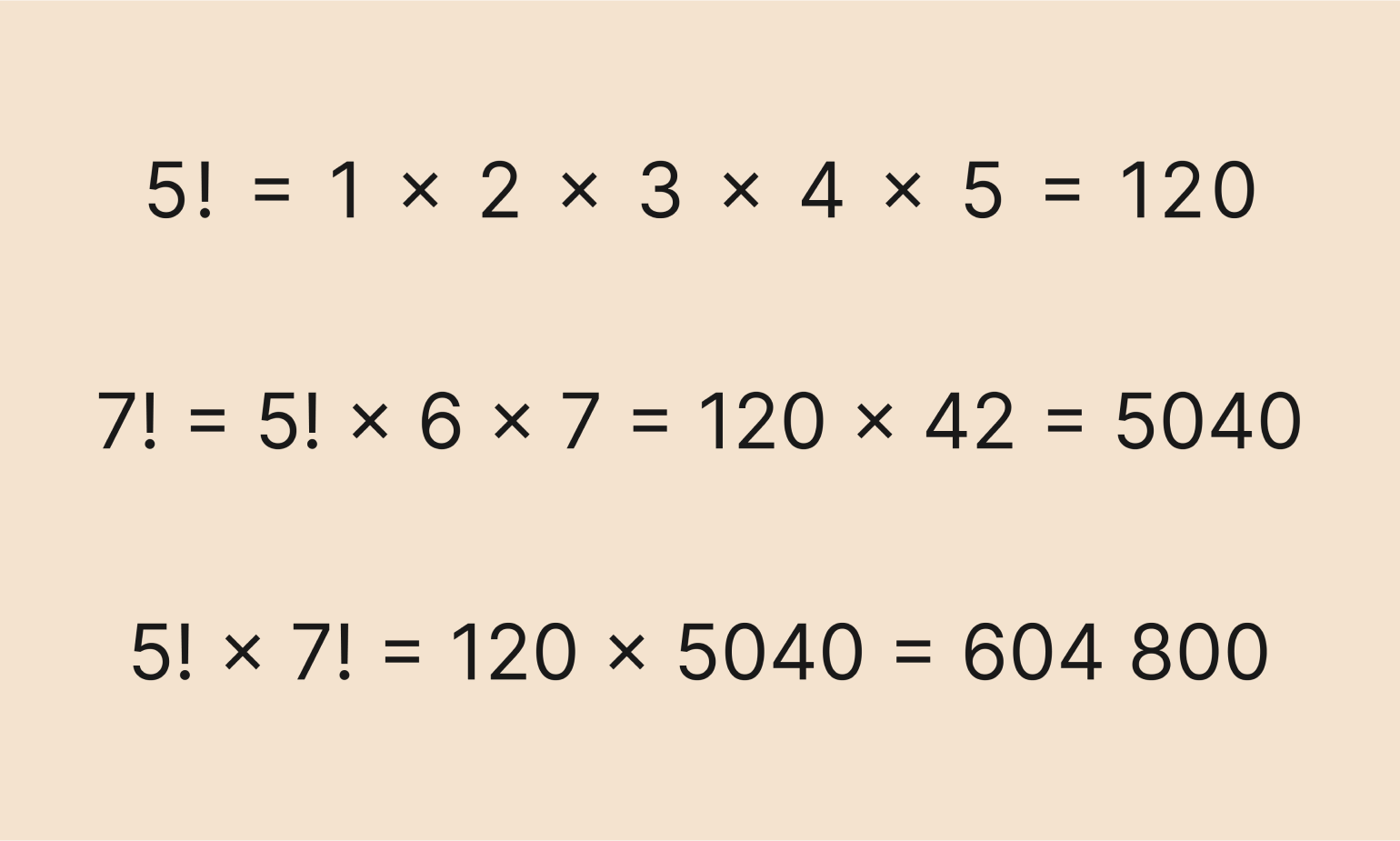

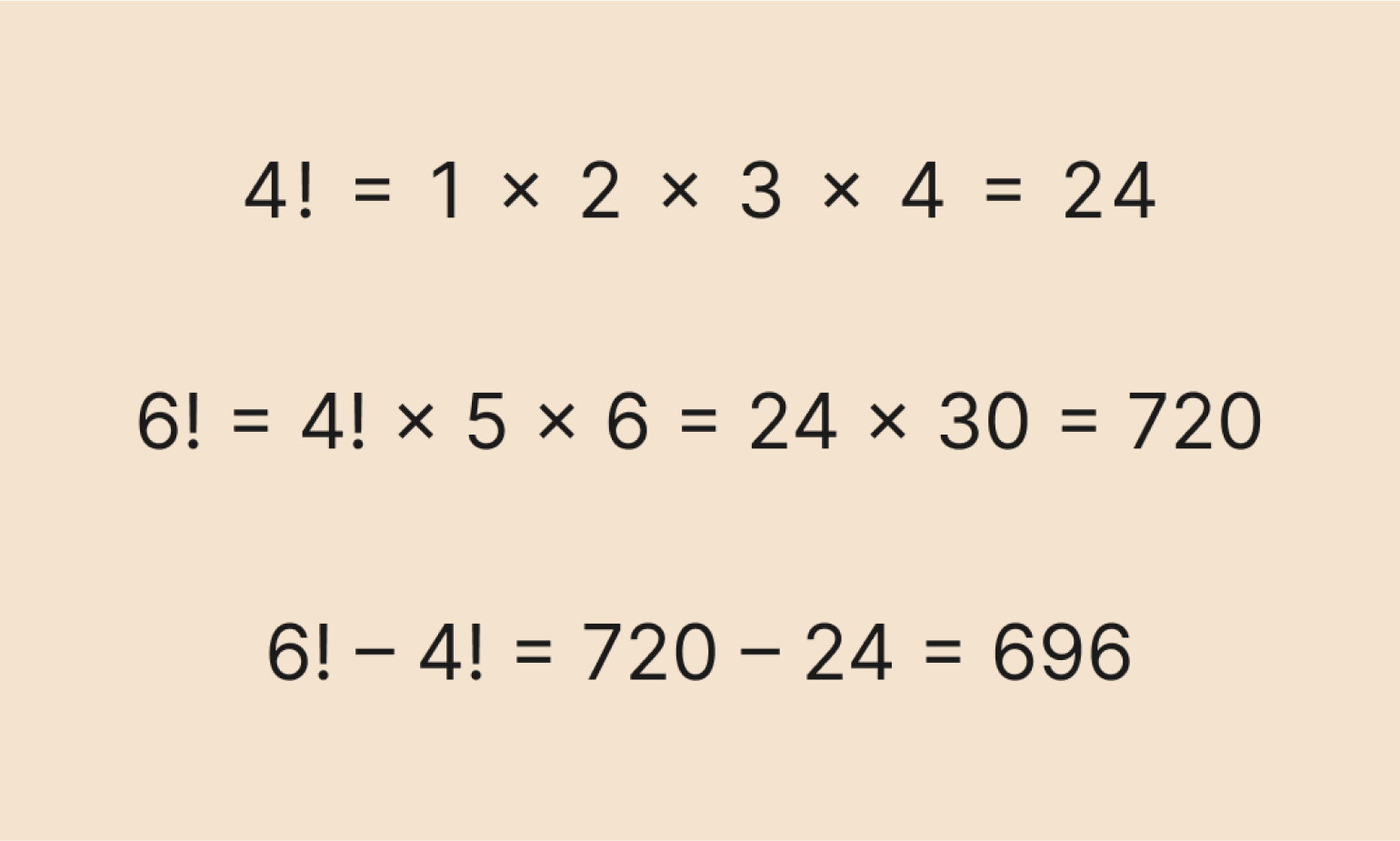

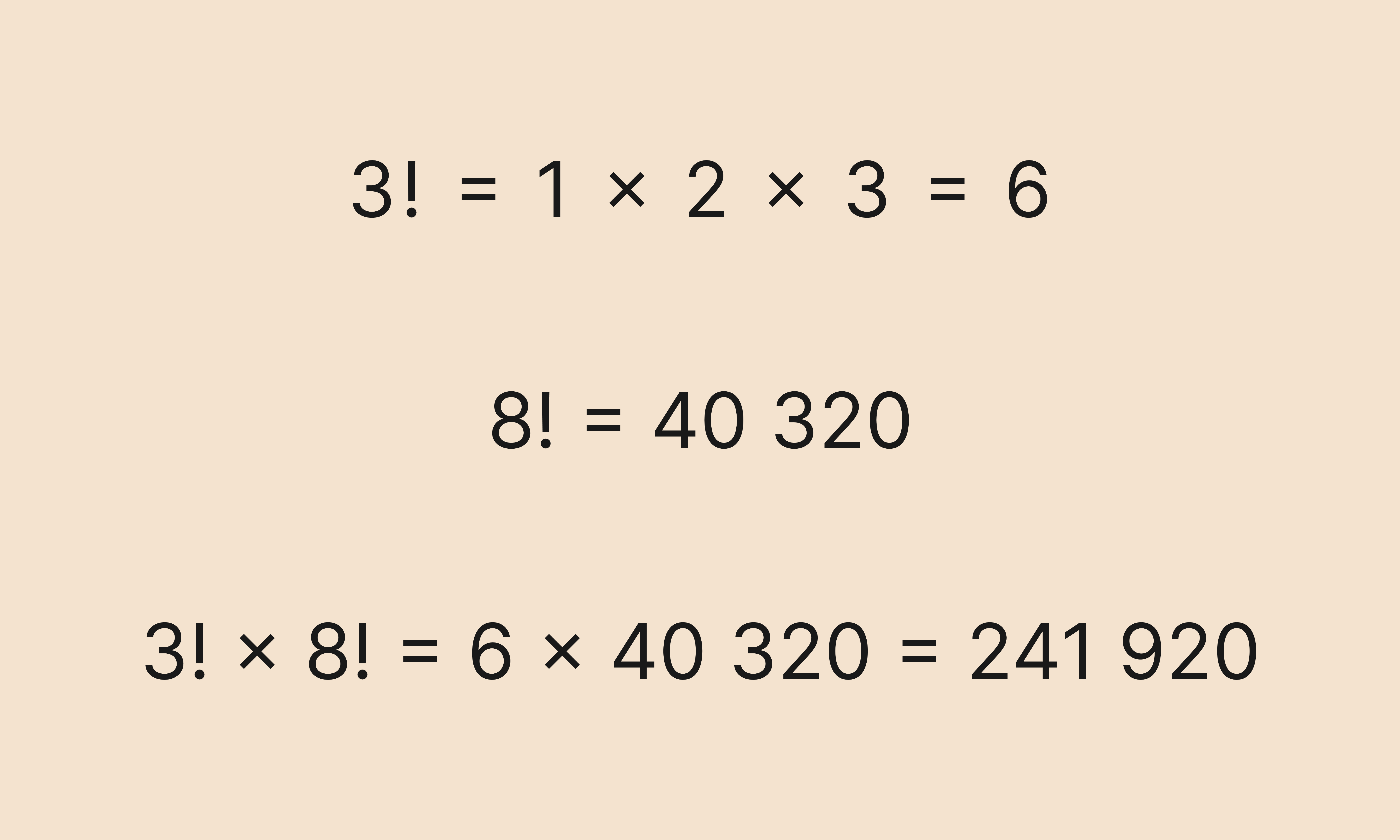

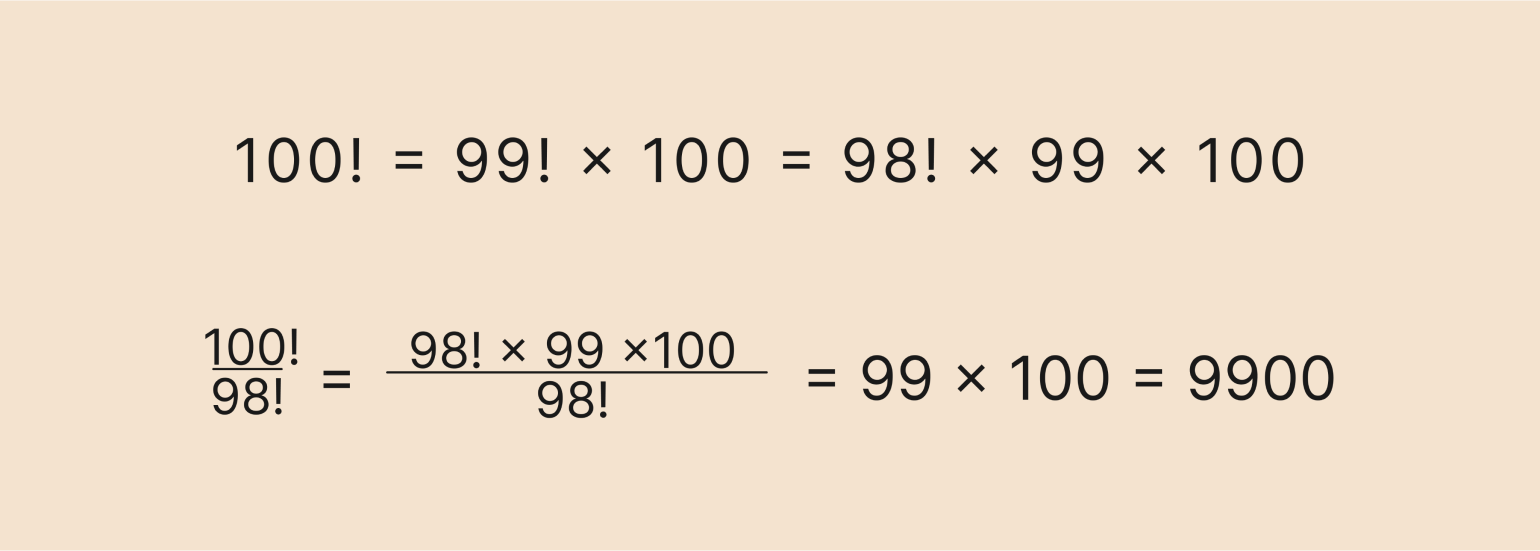
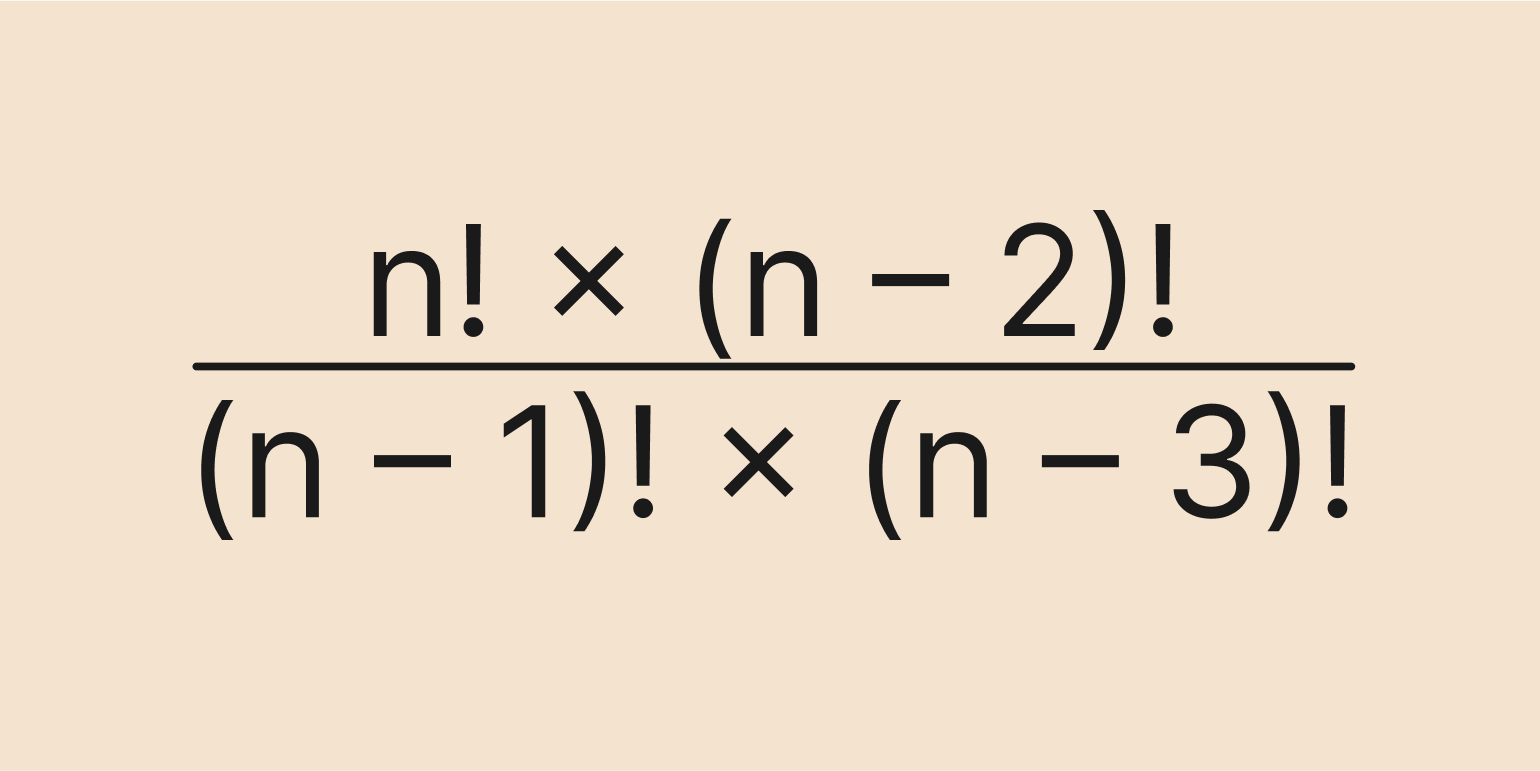
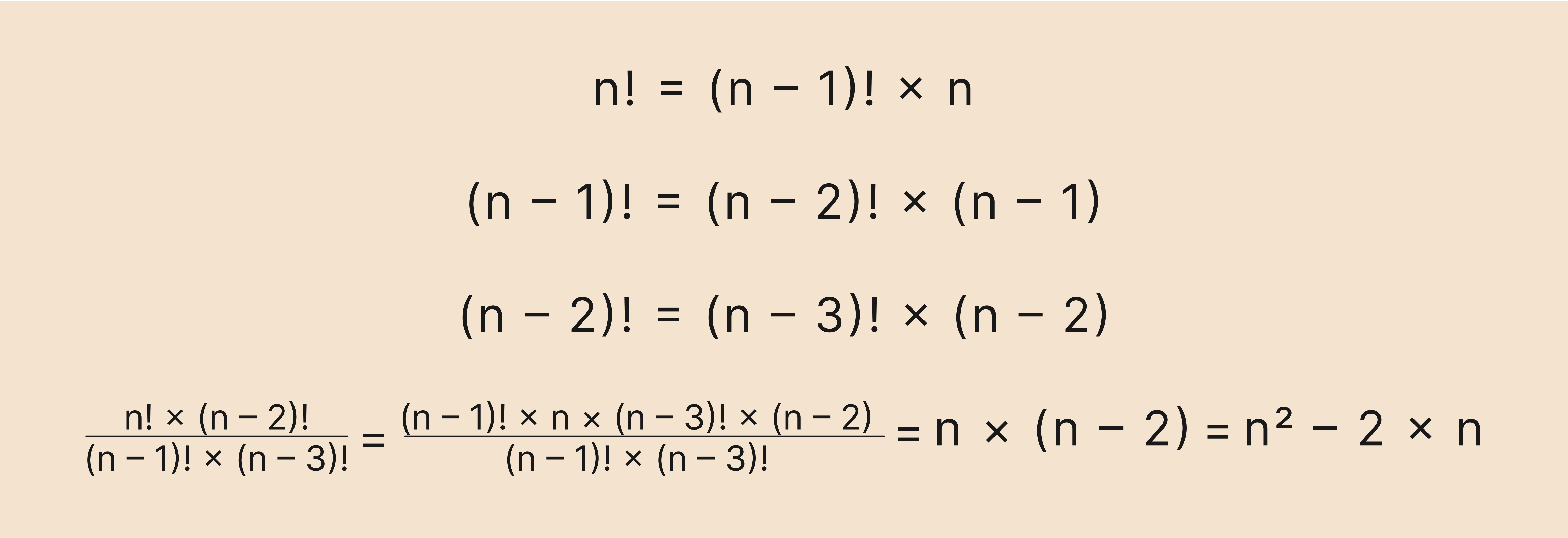
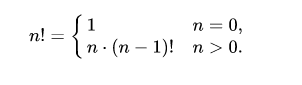
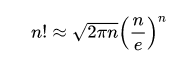


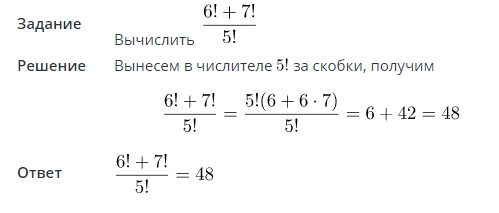



 Шпаргалки. Детский сад, Школа. / / Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов. Формула бинома
Шпаргалки. Детский сад, Школа. / / Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов. Формула бинома

