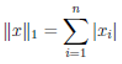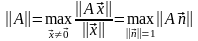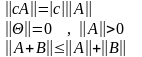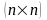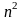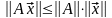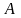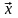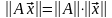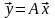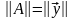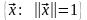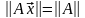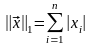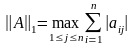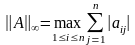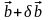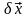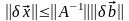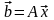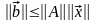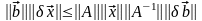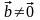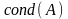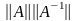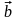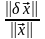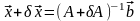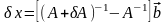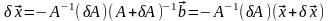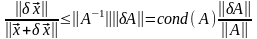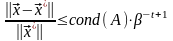Численные методы линейной алгебры
Основные положения численного анализа
Классическим средством изучения математических моделей и исследований на их основе свойств реальных объектов являются аналитические методы, позволяющие получать точные решения в виде математических формул. Эти методы дают наиболее полную информацию о решении задачи, и они до настоящего времени не утратили своего значения. Однако, к сожалению, класс задач, для которого они могут использоваться, весьма ограничен. Поэтому решение, как правило, осуществляется численными методами.
Численные методы — это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям. Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой. Численные методы, в отличие от аналитических, дают не общие, а частные решения. При этом требуется выполнить достаточное количество арифметических и логических действий над числовыми и логическими массивами.
В численном анализе используются два класса численных методов:
1. Прямые методы, позволяющие найти решение за определенное число операций.
2. Итерационные методы, основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию.
Решения, получаемые численными методами, в силу их приближенности содержат некоторые погрешности. Рассмотрим их источники и типы.
Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой. Неточность (неопределенность) задания исходных данных приводит также к неустранимым погрешностям.
Если мы устраним неопределенность в исходных данных и найдем решение с помощью какого-либо численного метода, то получим результат, не в точности соответствующий исходным данным в силу погрешности численного метода. В компьютере все числа представляются в конечном виде, и поэтому при использовании вычислительного алгоритма реализуются ошибки арифметических и других операций над числами, а также ошибки округления.
Дадим некоторые понятия из теории погрешностей вычислительных действий над приближенными величинами.
Пусть [math]x[/math] — точное, но, как правило, неизвестное значение некоторой величины, а [math]widehat{x}[/math] — ее известное приближенное значение.
Абсолютной погрешностью приближения [math]widehat{x}[/math] называется разность [math]Delta=bigl|x-widehat{x}bigr|[/math] (в общем случае [math]Deltawidehat{x}[/math] имеет размерность величины [math]x[/math]).
Относительная погрешность приближения [math]widehat{x}[/math] обозначается [math]delta[/math] и выражается отношением [math]delta= frac{Deltawidehat{x}}{|widehat{x}|}[/math] ([math]delta[/math] — безразмерная величина, [math]widehat{x}ne0[/math]). Часто величина [math]delta[/math] вычисляется в процентах, и тогда она умножается на сто.
Так как величина [math]x[/math], как правило, неизвестна, а погрешность необходимо определять, то в рассмотрение вводится предельная абсолютная погрешность [math]Delta(widehat{x}):[/math]
[math]Deltawidehat{x}= |x-widehat{x}|leqslant Delta(widehat{x}).[/math]
Раскрывая в этом неравенстве модуль, получаем соотношение, задающее отрезок, которому принадлежит точное значение: [math]widehat{x}-Delta(widehat{x}) leqslant xleqslant Delta(widehat{x})[/math]. Таким образом, величина [math]x[/math] находится в ∆-окрестности (дельта-окрестности), определяемой величинами [math]widehat{x}[/math] и [math]Delta(widehat{x})[/math].
Предельная относительная погрешность приближения [math]widehat{x}[/math] определяется отношением [math]delta(widehat{x})= frac{Delta(widehat{x})}{|widehat{x}|}[/math].
Такие погрешности оцениваются при рассмотрении численных методов. Эти оценки могут производиться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки).
Как правило, численный алгоритм решения задачи завершается, если погрешность меньше заданной заранее величины.
Норма матриц: понятие, определение, примеры
При решении многих практических задач необходимо как-то «измерять» матрицы, чтобы говорить, что одна матрица больше другой. Правило, по которому матрице (в частности, матрице-столбцу) ставится в соответствие некоторое неотрицательное число, имеющее смысл меры, определяет понятие норма матрицы.
Нормой матрицы-столбца [math]x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}[/math] называется функция [math]|x|[/math], удовлетворяющая следующим аксиомам:
1. [math]|x|geqslant0[/math] для любого столбца [math]x[/math], причем [math]|x|=0[/math] в том и только в том случае, если [math]x[/math] — нулевой столбец;
2. [math]|alpha x|=|alpha|cdot|x|[/math] для любого действительного числа [math]alpha[/math];
3. [math]|x+y|leqslant|x|+|y|[/math] для любых двух столбцов [math]x[/math] и [math]y[/math] размеров [math](ntimes1)[/math].
Аксиома 3 называется неравенством треугольника.
Примером нормы матрицы-столбца может быть семейство норм
[math]|x|= Biggl(sum_{i=1}^{n}|x_i|^pBiggr)^{1/p},[/math]
где при любом целом положительном [math]p[/math] определяется функция, удовлетворяющая условиям 1-3.
Приведем часто используемые нормы матриц-столбцов.
1. [math]|x|_1=max_{iinmathbb{N}}|x_i|[/math] — максимум среди модулей элементов столбца;
2. [math]textstyle{|x|_2=sumlimits_{i=1}^{n}|x_i|}[/math] — сумма модулей элементов столбца;
3. [math]textstyle{|x|_3=sqrt{sumlimits_{i=1}^{n}x_i^2}}[/math] — квадратный корень из суммы квадратов элементов.
Последняя норма называется евклидовой, так как совпадает с модулем столбца (длиной вектора), т.е. [math]|x|_3=|x|=sqrt{x^Tx}[/math].
Замечания 10.1
1. Можно показать, что справедливы следующие соотношения
[math]|x|_2geqslant|x|_3geqslant|x|_1[/math], а также [math]sqrt{n}cdot|x|_3geqslant|x|_2,~ sqrt{n}cdot|x|_1geqslant|x|_3[/math].
2. Норма может быть использована при анализе сходимости последовательностей матриц-столбцов.
Последовательность матриц-столбцов [math]bigl{x^{(1)},x^{(2)},ldots,x^{(k)},ldotsbigr}[/math] сходится к столбцу [math]x_{ast}[/math], если [math]lim_{kto+infty}x_i^{(k)}=x_{ast i}[/math], для всех [math]i=1,2,ldots,n[/math]. Для того чтобы последовательность [math]bigl{x^{(1)},x^{(2)}, ldots,x^{(k)},ldotsbigr}[/math] сходилась к столбцу х., необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|x^{(k)}-x_{ast}bigr|=0[/math].
3. Для определения псевдорешений систем линейных алгебраических уравнений ранее использовалась евклидова норма [math]|x|_3[/math].
4. Нормы позволяют оценить скорость сходимости последовательностей. Рассмотрим последовательность [math]bigl{x^{(k)}bigr}[/math], сходящуюся к [math]x_{ast}[/math]. Предположим, что все ее элементы различны и ни один из них не совпадает с [math]x_{ast}[/math]. Наиболее эффективный способ оценивания скорости сходимости состоит в сопоставлении расстояния [math]bigl|x^{(k+1)}-x_{ast}bigr|[/math] между [math]x^{(k+1)}[/math] и [math]x_{ast}[/math] с расстоянием [math]bigl|x^{(k)}-x_{ast}bigr|[/math] между [math]x^{(k)}[/math] и [math]x_{ast}[/math].
Последовательность [math]bigl{x^{(k)}bigr}[/math] называется сходящейся с порядком [math]{p}[/math], если [math]{p}[/math] — максимальное число, для которого
[math]0leqslant lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p} < +infty.[/math]
Поскольку величина [math]{p}[/math] определяется предельными свойствами [math]bigl{x^{(k)}bigr}[/math], она называется асимптотической скоростью сходимости.
Если последовательность [math]bigl{x^{(k)}bigr}[/math] — сходящаяся с порядком [math]{p}[/math], то число
[math]c=lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p},.[/math]
называется асимптотическим параметром ошибки. Если [math]p=1,~ c<1[/math], то сходимость линейная, если [math]p=2[/math] — квадратичная, если [math]p=3[/math] — кубическая и т.д. Если [math]p>1[/math] или [math]p=1,~c=0[/math], то сходимость сверхлинейная. Линейная сходимость является синонимом сходимости со скоростью геометрической профессии. Сверхлинейная сходимость является более быстрой, чем определяемая любой геометрической прогрессией.
Пример 10.1. Вычислить нормы матрицы-столбца [math]x=begin{pmatrix} 1&-2&3&-4 end{pmatrix}^T[/math].
Решение.
[math]begin{aligned} mathsf{1)}~, |x|_1&= max_{iinmathbb{N}}|x_i|= maxbigl{|1|,|-2|,|3|,|-4|bigr}=4,;\[5pt] mathsf{2)}~, |x|_2&= sum_{i=1}^{4}|x_i|= |1|+|-2|+|3|+|-4|=10,;\[5pt] mathsf{3)}~, |x|_3&= sqrt{sum_{i=1}^{4}x_i^2}= sqrt{1^2+(-2)^2+3^2+(-4)^2}=sqrt{30},. end{aligned}[/math]
Заметим, что свойство [math]|x|_2geqslant|x|_3geqslant|x|_1[/math], очевидно, выполняется.
Пусть [math]A[/math] — произвольная матрица размеров [math](mtimes n)[/math].
Нормой матрицы [math]A[/math] называется функция [math]|A|[/math], удовлетворяющая следующим аксиомам:
1) [math]|A|geqslant0[/math] для любой матрицы [math]A[/math], причем [math]|A|=0[/math] в том и только в том случае, если [math]A[/math] — нулевая матрица;
2) [math]|alphacdot A|=|alpha|cdot|A|[/math] для любого действительного числа [math]alpha[/math];
3) [math]|A+B|leqslant|A|+|B|[/math] для любых двух матриц [math]A[/math] и [math]B[/math] размеров [math](mtimes n)[/math] (неравенство треугольника);
4) [math]|Acdot B|leqslant|A|cdot|B|[/math] для любых двух матриц, у которых определено произведение.
Матричные нормы удобно определять через нормы матриц-столбцов. Для этого, задавшись какой-нибудь нормой для матриц-столбцов, рассматриваются значения [math]|Ax|[/math] при всевозможных х, удовлетворяющих условию [math]|x|=1[/math]. Максимальное из этих значений, которое найдется всегда, берется в качестве нормы матрицы [math]Acolon, |A|= max_{|x|=1}|Ax|[/math]. Такую матричную норму называют индуцированной.
Заметим, что в качестве определения индуцированной матричной нормы часто используется выражение [math]|A|=sup_{xne0}frac{|Ax|}{|x|}[/math], характеризующее максимальную величину, на которую преобразование, описываемое матрицей [math]A[/math], может растянуть любой ненулевой вектор в заданной норме.
Наиболее употребительными являются следующие формулы для вычисления значений норм матриц с действительными элементами.
1) [math]textstyle{|A|_1= maxlimits_{1leqslant ileqslant m}sumlimits_{j=1}^{n}|a_{ij}|}[/math] — максимум суммы модулей элементов в строке;
2) [math]textstyle{|A|_2= maxlimits_{1leqslant jleqslant n}sumlimits_{i=1}^{m}|a_{ij}|}[/math] максимум суммы модулей элементов в столбце;
3) [math]|A|_3=sqrt{lambda_{max}(A^TA)}[/math] — квадратный корень из максимального собственного значения [math]lambda_i[/math] матрицы [math]A^TA[/math];
4) [math]textstyle{|A|_4= sqrt{sumlimits_{i=1}^{m} sumlimits_{j=1}^{n} a_{ij}^2}}[/math] — квадратный корень из суммы квадратов элементов.
Заметим, что вычисление нормы [math]|A|_3= sqrt{lambda_{max}(A^TA)}[/math] связано с весьма трудоемкими операциями. Поскольку справедливо неравенство
[math]|A|_3=sqrt{lambda_{max}(A^TA)} leqslant |A|_4= sqrt{sumlimits_{i=1}^{m} sum_{j=1}^{n} a_{ij}^2},[/math]
то норма [math]|A|_4[/math] часто используется в оценках вместо [math]|A|_3[/math]. Норма [math]|A|_4[/math] возникает, если матрице [math]A[/math] поставить в соответствие «длинный столбец»:
[math]begin{pmatrix}a_{11},a_{21},ldots, a_{m1},a_{12},a_{22},ldots, a_{m2},ldots,a_{nn} end{pmatrix}^T[/math] и применить норму [math]|x|_3[/math].
Пример 10.2. Вычислить нормы матриц [math]A=begin{pmatrix}1&-2&3\ 4&5&-6\ -7&8&9 end{pmatrix}!,~ B=begin{pmatrix}1&0&0\ 0&1&0\ 0&0&1 end{pmatrix}[/math].
Решение. а)
[math]begin{aligned}|A|_1&= maxbigl{|1|+|-2|+|3|;, |4|+|5|+|-6|;, |-7|+|8|+|9|bigr}= max{6;,15;,24}=24;\[5pt] |A|_2&= maxbigl{|1|+|4|+|-7|;, |-2|+|5|+|8|;, |3|+|-6|+|9|bigr}= max{12;15;18}=18;\[5pt] |A|_4&= sqrt{1^2+(-2)^2+3^2+4^2+5^2+(-6)^2+(-7)^2+8^2+9^2}=\[2pt] &=sqrt{1+4+9+16+25+36+49+64+81}= sqrt{285};end{aligned}[/math]
б) [math]|B|_1=|B|_2=1,,~ |B|_4=sqrt{1+1+1}=sqrt{3}[/math].
Норма матриц может быть использована при анализе сходимости различных численных процедур. Пусть имеется последовательность матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] размеров [math]mtimes n[/math]. Матрица [math]A[/math] называется пределом последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math], если [math]lim_{kto+infty}a_{ij}^{(k)}=a_{ij}[/math] для всех [math]i=1,ldots,m[/math] и [math]j=1,ldots,n[/math]. Это обозначается [math]lim_{kto+infty}A^{(k)}=A[/math].
Для сходимости последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] к матрице [math]A[/math] необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|A^{(k)}-Abigr|=0[/math]. При этом последовательность, составленная из норм матриц [math]A^{(k)}[/math], сходится к норме матрицы [math]A[/math], т.е. [math]lim_{kto+infty} bigl|A^{(k)}bigr|=|A|[/math].
Отметим некоторые свойства предела матриц. Если [math]lim_{kto +infty}A^{(k)}=A,~ lim_{kto+infty}B^{(k)}=B[/math], то:
[math]begin{array}{ll}mathsf{1)}~ limlimits_{kto+infty}bigl[A^{(k)}pm B^{(k)}bigr]=Apm B;&qquad mathsf{2)}~ limlimits_{kto+infty}bigl[A^{(k)}cdot B^{(k)}bigr]=Acdot B;\\[-5pt] mathsf{3)}~ limlimits_{kto+infty}bigl[A^{(k)}bigr]^{-1}=A^{-1};&qquad mathsf{4)}~ limlimits_{kto+infty}bigl[CA^{(k)}bigr]=CA,~ limlimits_{kto+infty}bigl[A^{(k)}Dbigr]=AD.end{array}[/math]
где считается, что все операции определены.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Линейная алгебра для исследователей данных
Время на прочтение
5 мин
Количество просмотров 14K

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
-
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
-
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
-
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
-
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
-
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
-
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
-
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
-
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
-
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
и норма l∞
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство
для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
-
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
-
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Заметим, что
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
.
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
.
-
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
-
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
-
Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
-
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
и
.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
-
ЗАПИСАТЬСЯ НА ДЕМОУРОК
MathCAD — это просто! Часть 11. Продолжаем работать с матрицами
Матрицы — вещь важная, а потому было бы просто непростительно отводить на них всего одну статью из нашего цикла о работе в среде MathCAD. Узнав о том, как можно транспонировать матрицы, вычислять определители, обратные матрицы, а также перемножать и складывать их, сегодня мы с вами продолжим издевательства над этими важными в математике объектами. Думаю, что изложенные ниже сведения будут полезны и в практических вычислениях, производимых в среде MathCAD, ведь матрицы очень часто встречаются в реальных задачах.
Еще о вспомогательных функциях
В прошлый раз мы немного поговорили о специальных MathCAD’овских функциях, позволяющих разрезать матрицы на составные части или же склеивать их. Это не единственные из вспомогательных функций, действующих над матрицами, которые могут пригодиться в практике повседневной работы. Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.
Еще она по своему действию довольно близкая к Identity функция называется Diag. Она создает не матрицы, а векторы, состоящие из диагональных элементов квадратных матриц (т.е. из тех элементов, которые стоят на ее главной диагонали). Стоит при этом отметить, что размер вектора, получаемого на выходе, автоматически определяется размером входной матрицы.
Для определения размера матриц можно использовать функции Rows и Cols. Каждая из них имеет один-единственный входной параметр, которым является сама матрица, а на выходе выдают значения числа строк и столбцов соответственно. Для определения размера вектора можно использовать функцию length, которая работает аналогично указанным для матриц функциям.
Интересной также является предоставляемая MathCAD’ом функция для сортировки элементов векторов. Называется она просто и незатейливо — Sort. В качестве входного параметра этой функции нужно передать вектор, сортировкой которого мы будем заниматься, и на выходе получим почти такой же вектор, только его элементы будут упорядочены по возрастанию. Для сортировки строк и столбцов матрицы можно воспользоваться соответственно функциями Rsort и Csort, которым нужно передать в качестве параметров саму матрицу и номер того столбца или строки, которые должны быть отсортированы. Правда, работают эти функции несколько загадочно, иногда сортируя не только нужный столбец (строку), но и все остальные (см. соответствующую иллюстрацию). Чтобы изменить порядок следования чисел в векторе или порядок строк в матрице на противоположный, нужно воспользоваться функцией Reverse, в качестве аргумента для которой нужно передать изменяемые матрицу или вектор.
Ранг и норма матрицы
Два фундаментальных понятия, играющих очень важную роль в линейной алгебре — это ранг и норма матрицы. MathCAD позволяет пользователю вычислять эти характеристики матриц без лишних усилий, и сейчас я расскажу, как именно это делается.
Минором матрицы порядка k называется определитель, вычисленный для матрицы, образованной из k столбцов и k строк данной матрицы. Главным минором называется минор, для которого номера выбранных столбцов совпадают с номерами выбранных строк. Понимаю, это определение звучит несколько громоздко, но я думаю, если вы прочитаете его внимательно еще раз, то все станет просто и понятно. Рангом матрицы называется наибольший порядок среди всех ее ненулевых миноров. Ранг матрицы характеризует число линейно независимых столбцов или строк матрицы, а потому в матричной алгебре эта характеристика используется весьма широко. Для вычисления ранга матрицы в MathCAD’е используется функция Rank, которой в качестве аргумента передается та самая матрица, ранг которой нужно вычислить.
Норма матрицы — понятие более расплывчатое, чем ранг. Для полного определения нормы матрицы используется система ограничений, которым должен подчиняться строящийся по определенным правилам функционал. Вы можете найти подробное определение нормы матрицы в любом учебнике по линейной алгебре. Мы же сейчас удовлетворимся знанием того, что норма матрицы — это некоторый аналог величины, который для векторов называют длиной (норма вектора как раз и есть его длина). Впрочем, в отличие от длины вектора, где все понятно и определенно, норма матрицы может вычисляться несколькими разными способами, и в зависимости от способа вычисления ее величина может быть различной. Всем функциям для вычисления нормы матрицы, о которых здесь идет речь, требуется в качестве аргумента передавать ту матрицу, для которой будет вестись вычисление нормы. Функция Norm1 определяет норму путем складывания модулей элементов для каждого из столбцов и выбором наибольшей из получившихся для столбцов сумм. Функция Normi работает аналогичным образом, только для вычисления сумм там используются не столбцы, а строки. Функция Norme вычисляет норму матрицы по тому же алгоритму, по какому вычисляется норма вектора: квадраты всех элементов матрицы суммируются, а затем из полученного числа извлекается корень.
Собственные вектора и собственные значения матриц
Собственным вектором x и собственным значением ? матрицы X называются такие вектор и число соответственно, которые удовлетворяют соотношению xX = ?x. Обычно матрица имеет несколько собственных векторов и соответствующих им собственных значений, а потому мы будем рассматривать именно этот случай. Конечно, в MathCAD’е не слишком сложно с помощью некоторых преобразований рассчитать необходимые числа и вектора самостоятельно, однако можно еще больше упростить себе жизнь, воспользовавшись встроенными в эту среду функциями.
Функция Eigenvecs принимает в качестве входного параметра некоторую матрицу, а возвращает другую, содержащую собственные вектора исходной. При интерпретации результатов работы этой функции необходимо помнить, что в MathCAD’е вектора записываются в виде столбцов, так что и в этой матрице каждый из столбцов является собственным вектором первоначальной матрицы. Другая функция, Eigenvals, также принимает на вход некоторую матрицу, однако выдает для нее уже не собственные вектора, а собственные значения. Записываются они также в виде столбика. В этом столбце они идут в том же порядке, что и столбцы в матрице, возвращаемые первой функцией. То есть i-му столбцу матрицы, получаемой на выходе функцией Eigenvecs, соответствует i-е собственное значение в векторе. Впрочем, проследить соответствие собственных векторов и собственных значений для матрицы можно и более наглядным образом. Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.
Скалярное и векторное произведение векторов
Напоследок поговорим о вещах довольно простых, но очень распространенных в практике решения задач, а потому особенно важных. Сейчас мы рассмотрим, как с помощью MathCAD’а вычислять скалярное и векторное произведение векторов. Напомню, что скалярным произведением x.y называется число, равное x0y0 + x1y1 + x2y2 + … + xnyn, а вот с векторным все несколько сложнее. Оно определяется только для трехмерных векторов и вычисляется как определитель матрицы, составленной из базисных векторов (i, j и k) и элементов тех векторов, для которых вычисляется векторное произведение. Традиционно в математике векторное произведение обозначают c помощью крестика, который ставится между двумя перемножаемыми векторами.
Для вычисления скалярного и векторного произведения векторов обратимся снова к панели матричных вычислений, неоднократно выручавшей нас в наших упражнениях с MathCAD’ом. Скалярное произведение называется на ней Dot Product и обозначается как точка между двумя векторами, а векторное — Cross Product и обозначается крестиком, как я уже говорил выше. Чтобы перемножить два вектора, вы можете сначала обозначить их с помощью каких- либо символьных обозначений, а можете сразу записывать произведения между столбцами чисел.
Теперь, пожалуй, о матрицах самое основное и важное сказано. Как видите, в плане работы с векторами и матрицами MathCAD ничуть не менее мощный, чем во всем остальном. Поэтому использовать эту среду для матричных вычислений можно и нужно. Ну а как это делать, вы теперь уже знаете.
Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике soft
Как найти норму вектора в маткаде
Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и матричные функции Mathcad. В этих таблицах
- A и B — массивы (векторы или матрицы).
- v — вектор.
- M и N — квадратные матрицы.
- z — скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j — целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| identity(n) | n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0). |
| Re(A) | Массив, состоящий из элементов, которые являются вещественными частями элементов A. |
| Im(A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов A. |
| Е diag(v) | Диагональная матрица, содержащая на диагонали элементы v. |
| Е geninv(A) | Левая обратная к A матрица L такая, что LA = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. |
| Е rref(A) | Ступенчатая форма матрицы A. |
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
Возвращается.
| Имя функции | |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы M. |
| eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
| Е eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
| Е genvals (M,N) | Вектор v собственных значений, каждое из которых удовлетворяет обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. Вектор x — соответствующий собственный вектор. |
| Е genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции | Возвращается. |
| Е cholesky(M) | Нижняя треугольная матрица L такая, что LL T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T Mx>0 для любого вектора x 0. |
| Е qr(A) | Матрица, чьи первые n столбцов содержат ортогональную матрицу Q, а последующие столбцы содержат верхнюю треугольную матрицу R. Матрицы Q и R удовлетворяют равенству A=QR. Матрица A должна быть вещественной. |
| Е lu(M) | Матрица, которая содержит три квадратные матрицы P, L и U, расположенные последовательно в указанном порядке и имеющие с M одинаковый размер. L и U являются соответственно нижней и верхней треугольными матрицами. Эти три матрицы удовлетворяют равенству PM=LU . |
| Е svd(A) | Матрица, содержащая две расположенные друг над другом матрицы U и V. Сверху находится U — размера m x n, снизу V — размера n x n. Матрицы U и V удовлетворяют равенству A=Udiag(s)V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. |
| Е svds(A) | Вектор, содержащий сингулярные значения вещественнозначной матрицы размера m x n, где m>=n. |
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
Возвращается.
| Имя функции | |
| Е lsolve (M, v) | Вектор решения x такой, что Mx=v. |
Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как найти норму вектора в маткаде
Глава 3. Работа с векторами и матрицами
3.5 Транспонирование матрицы и вычисление определителя , нормы
Транспонированием называется операция, в результате которой столбцы исходной матрицы становятся строками, а строки – столбцами.
Для реализации этой и последующих операций выполните следующие действия:
– Наберите имя матрицы.
– Щелкните на кнопке со значком матрицы на математической панели.
– На панели Matrix (Матрицы) щелкните мышью на значке соответствующей операции, в данном случае М Т .
При вводе больших векторов из соображений экономии места удобно вводить их в виде строки с последующим транспонированием (рис. 3.8 ).
Транспонирование матрицы Определитель квадратной матрицы
D — неквадратная матрица
Ввод в виде строки
Вывод в виде строки
модуль вещественного числа
модуль комплексного числа
Рис. 3. 8 Транспонирование матрицы и вычисление ее определителя
Все матричные операторы и матричные функции работают только с векторами (в виде столбца), но не со строками, поэтому строки вначале приходится транспонировать в столбец, а после выполнения нужной операции вновь транспонировать в строку.
В MathCAD 12 при преобразовании строки и столбец имена строки и столбца должны быть разными.
Вычисление определителя матрицы
Для нахождения определителя заданной матрицы на панели Matrix выберите значок | X |, имеющий тройное значение:
– вычисление определителя матрицы, если Х – матрица;
– модуль числа, если Х– вещественное или комплексное число;
– длина вектора, если Х – вектор.
MathCAD 13 и 14 не может автоматически, как более старые версии, выбрать нужное действие. Необходимо в контекстном меню указать требуемую операцию.
Норма квадратной матрицы
Норма квадратной матрицы характеризует порядок величины элементов матрицы.
В MathCAD есть 4 функции для оценки нормы (рис. 3.9 ):
– norm 1( A ) – норма в пространстве L 1 ;
– norm 2( A ) – норма в пространстве L 2 ;
– norme(A) – евклидова норма;
– normi ( A ) – max – норма, или – норма.
Евклидова норма эквивалентна длине многомерного вектора .
Как видно на рис.4.12, величина нормы мало зависит от способа ее вычисления. При увеличении всех элементов матрицы в 100 раз все нормы также увеличиваются в 100 раз.
Рис. 3. 9 Функции для вычисления нормы матрицы матрицы
http://old.exponenta.ru/SOFT/MATHCAD/UsersGuide/chapter9/9_7.asp
http://www.math.mrsu.ru/text/courses/mcad/3.5.htm
-
-
May 28 2018, 08:04
- Наука
- Cancel
Норма Фробениуса
Норма Фробениуса или, как её ещё называют Евклидова норма, — это квадратный корень сумм квадратов модулей элементов матрицы размера m × n:
Простой пример. Есть матрица размера 3 × 3:
Она же, но с элементами, возведёнными в квадрат:
Сумма элементов этой матрицы будет равна 60. Квадратный корень из 60 примерно равен 7,746. Это число и есть норма Фробениуса для нашей матрицы.
Есть иной способ вычисления нормы Фробениуса: как квадратный корень произведения следа этой матрицы и эрмитово-сопряжённой матрицы:
https://ru.wikipedia.org/wiki/Норма_матрицы#Норма_Фробениуса
Поскольку
мы договорились оценивать погрешность
решения как расстояние между точным и
приближенным решениями системы, то нам
потребуется определить норму матрицы,
и ее определим, согласованно
с
определением нормы вектора:
(1).
Отсюда
непосредственно следует, что (1)
удовлетворяет аксиомам нормы
,
для
4.
Таким
образом, множество
матриц может быть интерпретировано как
нормированное векторное пространство
размерности
.
Также из (1) следует, что
.
(2)
Более
того, неравенство (2) является “неулучшаемым”,
в том смысле, что для каждой матрицы
найдется вектор
,
такой, что
.
Квадратная
матрица
задает линейное преобразование каждого
вектора
в вектор
,
можно считать, что формула (1) определяет
как наибольшую длину образа вектора
единичной сферы
при преобразовании
.
Если
выбрать евклидову норму в качестве
нормы вектора, то можно интерпретировать
норму матрицы следующим образом: При
выполнении линейного преобразования
единичная сфера деформируется в
эллипсоид5,
тогда норма матрицы
,
представляет собой длину максимальной
полуоси эллипсоида. Или, что норма
диагональной матрицы равна максимальному
по модулю элементу диагонали. Также
следует, что умножение матрицы на любую
ортогональную матрицу не изменяет ее
нормы.
Мы
интерпретировали только одну из возможных
норм векторов. Две другие, обычно
используемые в численном анализе нормы
таковы:
.
Эти
две нормы порождают соответствующие
матричные нормы:
.
Предлагается,
в качестве упражнения, интерпретировать
их в двух и трехмерном пространствах.
Для
расчета погрешности решений системы
будем вначале полагать, что матрица
системы задана точно, а вектор правых
частей приближенно
и выясним, как велико может быть
.
Имеем следующую цепочку соотношений:

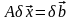
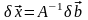
,
так
как
,
то
.
Перемножая, обе части последних
неравенств, имеем:
.
Предполагая,
что
,
получим
.
Для
любой невырожденной матрицы определим
сейчас ее число
обусловленности, обозначаемое
,
как произведение
6
и предыдущая формула перепишется в виде
.
(3)
Теперь
это соотношение можно интерпретировать
следующим образом:
есть мера относительной неопределенности
в задании вектора
.
Аналогично
можно интерпретировать как меру
относительной неопределенности вектора
решения системы. Поскольку неравенство
является не улучшаемым, то правая часть
(3) есть предельная относительная
погрешность.
До
сих пор мы предполагали, что матрица A
известна
точно, вектор правых частей имеет
неопределенность. Предположим теперь,
что матрица A
известна приближенно
,
тогда
,
после этого, воспользовавшись тождеством
,
найдем
.
Переходя в этой формуле к нормам: получаем
.
Объединяя
полученные результаты, мы будем иметь
соотношение для погрешности решения
системы вследствие представления данных
в арифметике с плавающей запятой7
,
где
-вычисленное
решение,
-основание
системы счисления,
-длина
разрядной сетки мантиссы. Следует
заметить, что этот вывод справедлив,
если мы пренебрегаем погрешностью
возникающей при выполнении арифметических
операций. Это предположение оправдано
тем обстоятельством, что если эта
погрешность и возникает, то она
минимизируется выбором ведущего элемента
при прямом ходе метода Гаусса.
Все
результаты рассмотрения можно
сформулировать в окончательном виде:
Предположим, что все элементы
и
точно представляются в арифметике с
плавающей запятой, и пусть вектор
,
получен на выходе подпрограммы решения
системы линейных уравнений. Предположим
также, что точная вырожденность матрицы,
если она имеет место, не была обнаружена,
и что не было ни машинных нулей, ни
переполнений. Тогда имеют место следующие
неравенства:
,
.
Здесь
—
основание системы счисления арифметики,
—
длина разрядной сетки мантиссы.
Второе
неравенство утверждает, что, как правило,
можно рассчитывать на то, что относительная
невязка будет
иметь величину, сравнимую с ошибкой
округления, независимо от того, насколько
плохо обусловлена матрица.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #