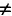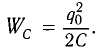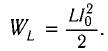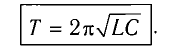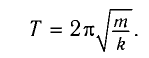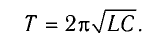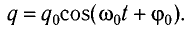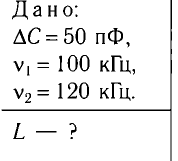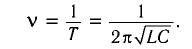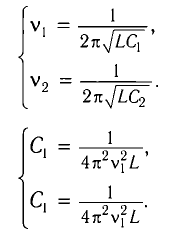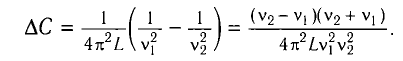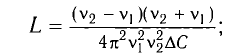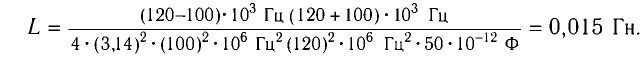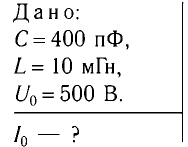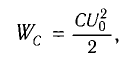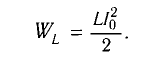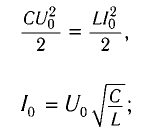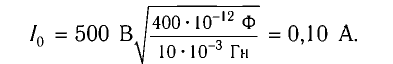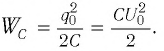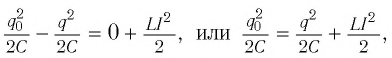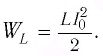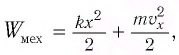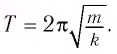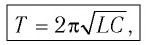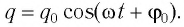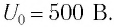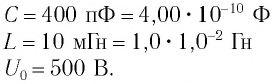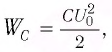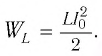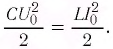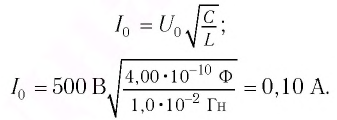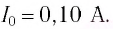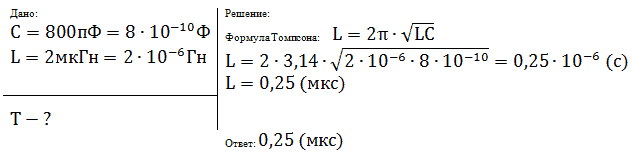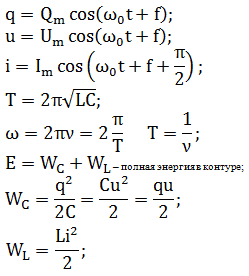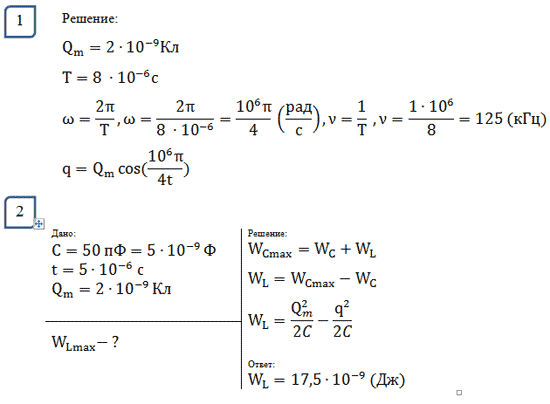Как найти энергию катушки в момент времени

Содержание

1 Колебательный контур
- 1.1 Энергии контура
- 1.2 Процессы в колебательном контуре
- 1.3 Свободные электромагнитные колебания
  - 1.3.1 *Вывод формулы Томсона
2 Литература

Колебательный контур

Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

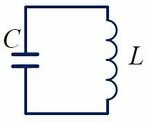
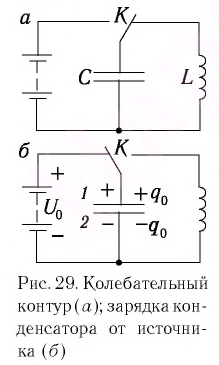
Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

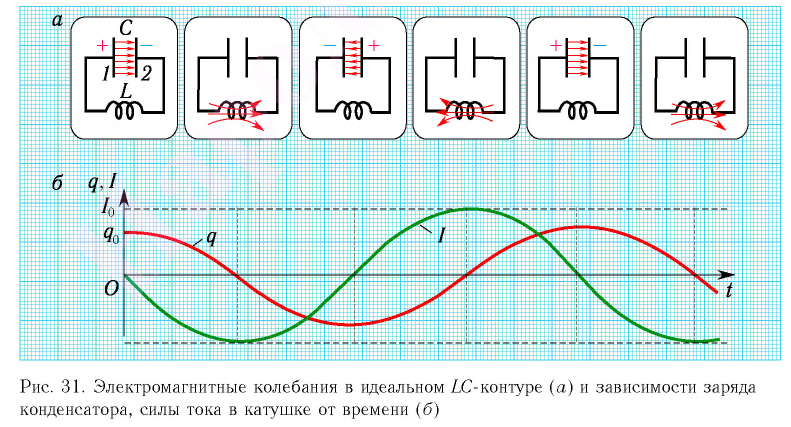
Рассмотрим процессы, которые возникают в колебательном контуре.

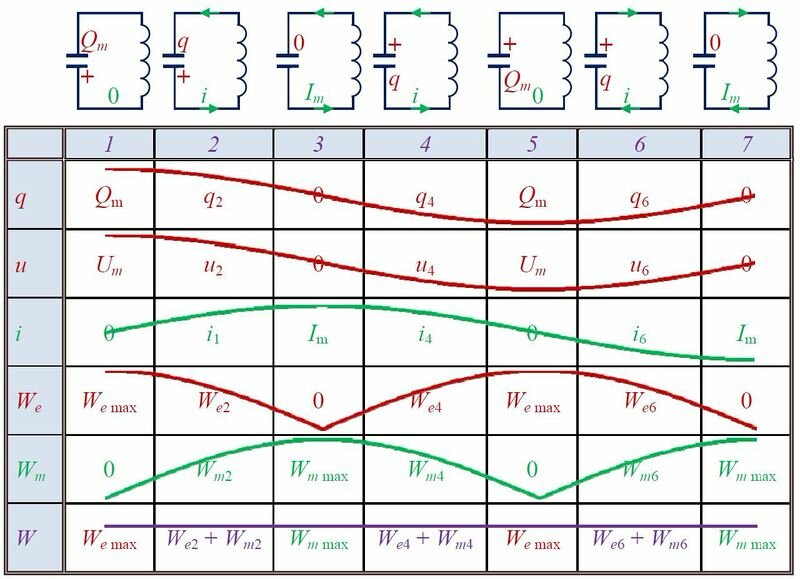
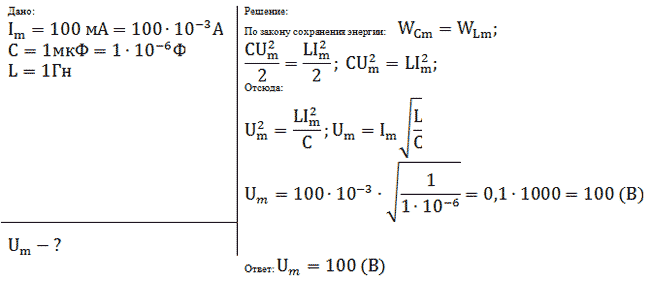
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

(W_{e, max } =dfrac{Q_{m}^{2} }{2C} =dfrac{Ccdot U_{m}^{2} }{2}, ; ; ; W_{e, 2} =dfrac{q_{2}^{2} }{2C} =dfrac{Ccdot u_{2}^{2} }{2}, ; ; ; W_{e, 4} =dfrac{q_{4}^{2} }{2C} =dfrac{Ccdot u_{4}^{2} }{2}, ; ; ; W_{e, 6} =dfrac{q_{6}^{2} }{2C} =dfrac{Ccdot u_{6}^{2} }{2},)

(W_{m; max } =dfrac{Lcdot I_{m}^{2} }{2}, ; ; ; W_{m2} =dfrac{Lcdot i_{2}^{2} }{2}, ; ; ; W_{m4} =dfrac{Lcdot i_{4}^{2} }{2}, ; ; ; W_{m6} =dfrac{Lcdot i_{6}^{2} }{2}.)

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

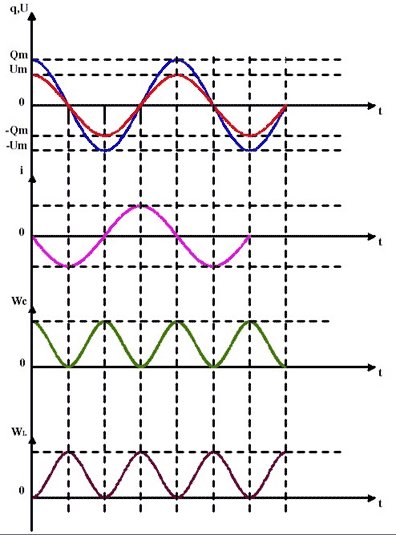
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q»,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

(left(dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} right)^{{‘} } =dfrac{q}{C} cdot q’+Lcdot icdot i’ = dfrac{q}{C} cdot q’+Lcdot q’cdot q»=0,)

(dfrac{q}{C} +Lcdot q»=0,; ; ; ; q»+dfrac{1}{Lcdot C} cdot q=0.)

Переписав его в виде:

(q»+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Источник

Печатать книгу

Сайт:	Профильное обучение
Курс:	Физика. 10 класс
Книга:	§ 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током
Напечатано::	Гость
Дата:	Понедельник, 29 Май 2023, 14:20

Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?

Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то

Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:

Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.

Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.

Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.

Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,

$calligraphic E subscript straight с equals negative fraction numerator increment straight Ф over denominator increment t end fraction equals negative fraction numerator increment open parentheses L I close parentheses over denominator increment t end fraction.$

Если индуктивность контура не изменяется во времени, т. е. L = const, то

$calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction.$

Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.

От теории к практике

Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции = 4,0 В?

Рис. 185

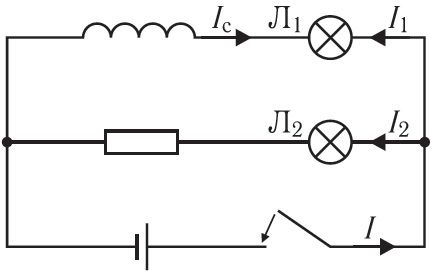
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л₂ начинает светиться практически сразу, а лампочка Л₁ — с заметным запаздыванием. При возрастании силы тока I₁, созданного источником на участке, образованном катушкой и лампочкой Л₁, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции I_с направлен навстречу току источника. В результате рост силы тока I₁ источника замедляется, и сила тока I₁ — |I_с| не сразу достигает своего максимального значения.

Рис. 185.1

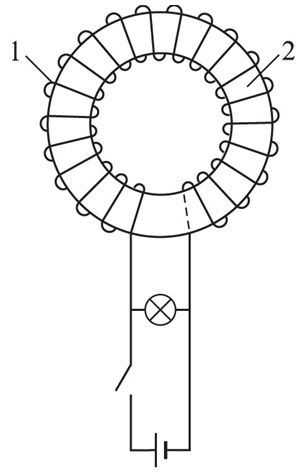
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.

Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений . Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.

Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.

При замыкании цепи, состоящей из источника тока с ЭДС , катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction$ .

Тогда в соответствии с законом Ома сила тока в цепи $I equals fraction numerator calligraphic E subscript 0 plus calligraphic E subscript straight с over denominator R end fraction$ .

Значит, $calligraphic E subscript 0 equals I R plus L fraction numerator increment I over denominator increment t end fraction$ .

Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: .

Рис. 185.2

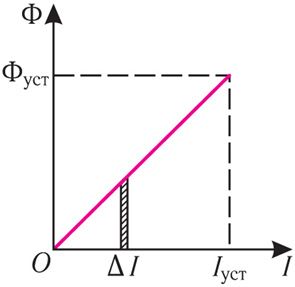
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):

δA_доп = ФΔI.

Полная дополнительная работа А_доп, равная сумме элементарных дополнительных работ δA_доп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).

$A subscript доп equals fraction numerator straight Ф subscript уст I subscript уст over denominator 2 end fraction equals fraction numerator L I subscript уст superscript 2 over denominator 2 end fraction.$

Эта работа превращается в энергию магнитного поля катушки, поэтому:

$W subscript straight м equals fraction numerator L I squared over denominator 2 end fraction comma$

где L — индуктивность контура; I — сила тока.

От теории к практике

Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки W_м = 1,2 Дж?

1. Что называют самоиндукцией?

2. В каких опытах можно наблюдать явление самоиндукции?

3. От чего зависит ЭДС самоиндукции?

4. Что называют индуктивностью? В каких единицах в СИ её измеряют?

5. Как вычислить энергию магнитного поля катушки с током?

6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?

Примеры решения задач

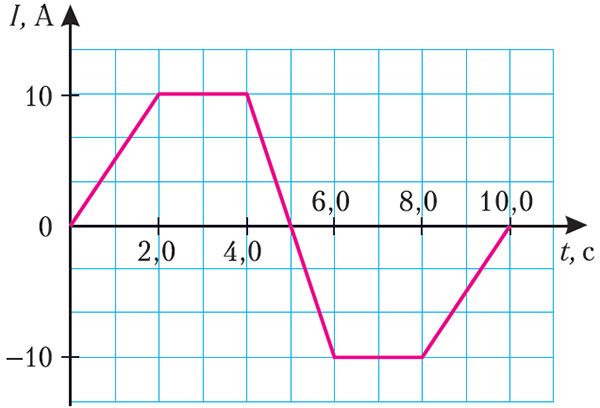
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.

Рис.

Рис. 186

Дано:
L = 40 мГн = 4,0 · 10^–2 Гн

— ?

Решение: ЭДС самоиндукции $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction$ . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:

1) от момента времени t₁ = 0,0 с до момента времени t₂ = 2,0 с сила тока изменяется на ΔI₁ = 10 А за промежуток времени Δt₁ = 2,0 с;

2) от момента времени t₃ = 4,0 с до момента времени t₄ = 6,0 с сила тока изменяется на ΔI₂ = –20 А за промежуток времени Δt₂ = 2,0 с;

3) от момента времени t₅ = 8,0 с до момента времени t₆ = 10,0 с сила тока изменяется на ΔI₃ =10 А за промежуток времени Δt₃ = 2,0 с.

Поскольку промежутки времени Δt₁ = Δ t₂ = Δ t₃ = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt₂ = 2,0 с (от t₃ = 4,0 с до t₄ = 6,0 с):

$open vertical bar calligraphic E subscript straight с close vertical bar subscript max equals L open vertical bar fraction numerator increment I subscript 2 over denominator increment t subscript 2 end fraction close vertical bar.$

Таким образом,

$open vertical bar calligraphic E subscript straight с close vertical bar subscript max equals 4 comma 0 times 10 to the power of negative 2 end exponent space Гн times fraction numerator open vertical bar negative 20 space straight А close vertical bar over denominator 2 comma 0 space straight с end fraction equals 0 comma 40 space straight В.$

Ответ: = 0,40 В.

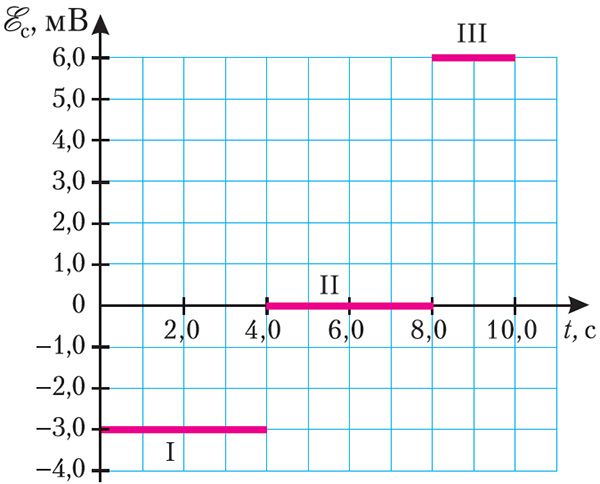
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?

Рис.

Рис. 187

Дано:
L = 2,0 мГн = 2,0 · 10^–3 Гн
t = 4,0 с

ΔI_I — ? ΔI_II — ?
ΔI_III — ? W_м — ?

Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции = –3,0 мВ, на участке III — = 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:

$calligraphic E subscript с equals negative L fraction numerator increment I over denominator increment t end fraction$ ; $increment I equals negative fraction numerator calligraphic E subscript с increment t over denominator L end fraction$ .

$increment I subscript straight I equals negative fraction numerator negative 3 comma 0 times 10 to the power of negative 3 end exponent space straight В times 4 comma 0 space straight с over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн end fraction equals 6 comma 0 space straight А$ ; $increment I subscript III equals negative fraction numerator 6 comma 0 times 10 to the power of negative 3 end exponent space straight В times 2 comma 0 space straight с over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн end fraction equals negative 6 comma 0 space straight А$ .

На участке II графика = 0, следовательно, сила тока не изменялась: ΔI_II = 0.

В момент времени t = 4,0 с энергия магнитного поля катушки $W subscript straight м equals fraction numerator L I squared over denominator 2 end fraction$ .

Следовательно,

$W subscript straight м equals fraction numerator 2 comma 0 times 10 to the power of negative 3 end exponent space Гн times open parentheses 6 comma 0 space straight А close parentheses squared over denominator 2 end fraction equals 36 times 10 to the power of negative 3 end exponent space Дж equals 36 space мДж$ .

Ответ: ΔI_I = 6,0 А; ΔI_II = 0; ΔI_III = –6,0 А; W_м = 36 мДж.

Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I₁ = 1,60 А до I₂ = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.

Дано:
Δt = 9,50 мс = 9,50 · 10^-3 с
I₁ = 1,60 А
I₂ = 2,40 А
= ‒14,0 В

Ф_с — ?
ΔW_м — ?

Решение: При изменении в катушке силы тока от I₁ до I₂ возникает собственный магнитный поток Ф_с = LI₂. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: $calligraphic E subscript straight с equals negative L fraction numerator increment I over denominator increment t end fraction equals negative L fraction numerator I subscript 2 minus I subscript 1 over denominator increment t end fraction$ . Следовательно,

$L equals negative fraction numerator calligraphic E subscript straight с increment t over denominator I subscript 2 minus I subscript 1 end fraction equals fraction numerator calligraphic E subscript straight с increment t over denominator I subscript 1 minus I subscript 2 end fraction$ . Тогда $straight Ф subscript straight с equals fraction numerator calligraphic E subscript straight с increment t I subscript 2 over denominator I subscript 1 minus I subscript 2 end fraction$ .

$straight Ф subscript straight с equals fraction numerator negative 14 comma 0 space straight В times 9 comma 50 times 10 to the power of negative 3 end exponent space straight с times 2 comma 40 space straight А over denominator 1 comma 60 space straight А minus 2 comma 40 space straight А end fraction equals 0 comma 399 space Вб equals 399 space мВб.$

Приращение энергии магнитного поля катушки

$increment W subscript straight м equals W subscript straight м 2 end subscript minus W subscript straight м 1 end subscript equals fraction numerator L I subscript 2 superscript 2 over denominator 2 end fraction minus fraction numerator L I subscript 1 superscript 2 over denominator 2 end fraction equals L over 2 open parentheses I subscript 2 superscript 2 minus I subscript 1 superscript 2 close parentheses equals fraction numerator negative calligraphic E subscript straight с increment t open parentheses I subscript 2 superscript 2 minus I subscript 1 superscript 2 close parentheses over denominator 2 open parentheses I subscript 2 minus I subscript 1 close parentheses end fraction equals fraction numerator negative calligraphic E subscript straight с increment t open parentheses I subscript 2 plus I subscript 1 close parentheses over denominator 2 end fraction.$

$increment W subscript straight м equals fraction numerator negative open parentheses negative 14 comma 0 space straight В close parentheses times 9 comma 50 times 10 to the power of negative 3 end exponent space straight с times left parenthesis 2 comma 40 space straight А plus 1 comma 60 straight А right parenthesis over denominator 2 end fraction equals 0 comma 266 space Дж space equals space 266 space мДж.$

Ответ: Ф_с = 399 мВб, ΔW_м = 266 мДж.

Упражнение 24

1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.

2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.

3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I₁ = 2,0 А до I₂ = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.

Рис. 188

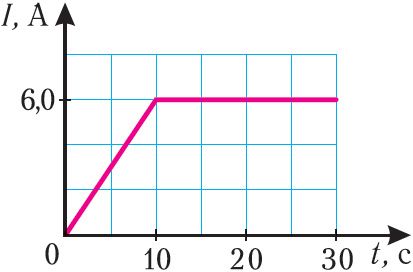
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t₁ = 10 с и t₂ = 20 с от момента начала отсчёта времени.

5. Сила тока в катушке равномерно уменьшилась от I₁ = 10 А до I₂ = 5,0 А. При этом энергия магнитного поля изменилась на ΔW_м = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.

6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I₁ = 8,0 А, если за промежуток времени t₁ = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.

7. Энергия магнитного поля катушки с индуктивностью L₁ = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L₂ в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, .

Источник

Электромагнитные колебания

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Колебательный контур
Энергетические превращения в колебательном контуре
Электромеханические аналогии
Гармонический закон колебаний в контуре
Вынужденные электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: t=0 . Заряд конденсатора равен q_0 , ток через катушку отсутствует (рис. 1). Конденсатор сейчас начнёт разряжаться.

Рис. 1. t=0

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину x_0 и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2).

Рис. 2.

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : t = T/4 . Конденсатор полностью разрядился. Сила тока достигла максимального значения I_0 (рис. 3). Сейчас начнётся перезарядка конденсатора.

Рис. 3. t = T/4

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения v_0 . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4).

Рис. 4.

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти t = T/2 . Конденсатор полностью перезарядился, его заряд опять равен q_0 (но полярность другая). Сила тока равна нулю (рис. 5). Сейчас начнётся обратная перезарядка конденсатора.

Рис. 5. t = T/2

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна x_0 .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6).

Рис. 6.

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен I_0 , но на сей раз имеет другое направление (рис. 7).

Рис. 7.

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью v_0 , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8).

Рис. 8.

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: t = T . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9).

Рис. 9. t = T

Данный момент идентичен моменту t = 0 , а данный рисунок — рисунку 1. Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

к оглавлению ▴

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен q_0 , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

$W = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}}.$

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен I_0 , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

$W = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

$W = frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Таким образом,

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}} = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Соотношение (1) применяется при решении многих задач.

к оглавлению ▴

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1):

$frac{displaystyle kx^2}{displaystyle 2 vphantom{1^a}} + frac{displaystyle mv^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle kx_0^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle mv_0^2}{displaystyle 2 vphantom{1^a}}.$ (2)

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, x_0 и v_0 — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2), мы видим следующие соответствия:

(3)

(4)

(5)

(6)

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

$T = 2 pi sqrt{frac{displaystyle m}{displaystyle k}}.$

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость 1/c . Получим:

(7)

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

к оглавлению ▴

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10).

Рис. 10. Положительное направление обхода

Сила тока считается положительной (I > 0) , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной (I < 0) .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если I > 0 , то заряд левой пластины возрастает, и потому .

Величины и меняются со временем, но энергия контура остаётся неизменной:

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = W = const.$ (8)

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8); не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ${(y^2)}$ ):

$frac{displaystyle 2q dot{q}}{displaystyle 2C vphantom{1^a}}+frac{displaystyle L cdot 2I dot{I}}{displaystyle 2 vphantom{1^a}} = W =0.$

Подставляя сюда и , получим:

$frac{displaystyle qI}{displaystyle C vphantom{1^a}} + LI ddot{q} = 0,$

$Ileft ( frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} right ) = 0.$

Но сила тока не является функцией, тождественно равной нулю; поэтому

$frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} = 0.$

Перепишем это в виде:

$ddot{q} + frac{displaystyle 1}{displaystyle LC vphantom{1^a}}q = 0.$ (9)

Мы получили дифференциальное уравнение гармонических колебаний вида $ddot{q} + omega^2_0 q = 0$ , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

$omega_0 = frac{displaystyle 1}{displaystyle sqrt{LC} vphantom{1^a}}.$ (10)

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

$T = frac{displaystyle 2 pi}{displaystyle omega_0 vphantom{1^a}}= 2 pisqrt{LC}.$

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

(11)

Циклическая частота omega_0 находится по формуле (10); амплитуда q_0 и начальная фаза alpha определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при t = 0 заряд конденсатора максимален и равен q_0 (как на рис. 1); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой q_0 :

$q = q_0 cos omega_0t = q_0 cos left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (12)

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12), опять-таки не забывая о правиле нахождения производной сложной функции:

$I = dot{q} = -q_0 omega_0 sin omega_0t.$

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

$I = -I_0 sin omega_0t = -I_0 sin left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (13)

Амплитуда силы тока равна:

$I_0 = q_0 omega_0 = frac{displaystyle q_0}{displaystyle sqrt{LC} vphantom{1^a}}.$

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2).

Ток течёт в отрицательном направлении: I < 0 . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13).

А теперь посмотрите на рис. 8. Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

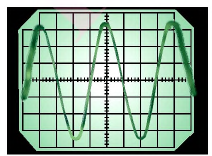
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13). Для наглядности представим эти графики в одних координатных осях (рис. 11).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

$cos left ( varphi + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = - sin varphi,$

запишем закон изменения тока (13) в виде:

$I = -I_0 sin omega_0 t = I_0 cos left ( omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная $omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}}$ , больше фазы заряда на величину pi/2 . В таком случае говорят, что ток опережает по фазе заряд на pi/2 ; или сдвиг фаз между током и зарядом равен pi/2 ; или разность фаз между током и зарядом равна pi/2 .

Опережение током заряда по фазе на pi/2 графически проявляется в том, что график тока сдвинут влево на pi/2 относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз pi/2 ).

к оглавлению ▴

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой omega (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте $omega_0 = 1/sqrt{LC}$ .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты omega : амплитуда тем больше,чем ближе omega к собственной частоте контура omega_0 .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитные колебания» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Колебательный контур:

Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.

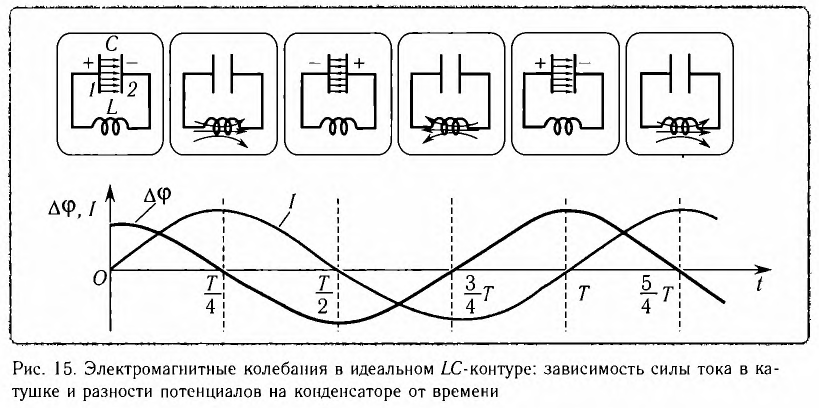
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.

В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R

Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +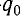, а на второй —. При этом конденсатор обладает энергией

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.

Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.

В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения . В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.

Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения . При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений и в различные моменты времени (см. рис. 15).

Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:

Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(1)

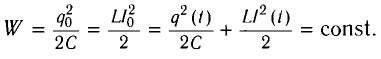
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.

Для пружинного маятника полная механическая энергия в любой момент времени 2 ,

(2)

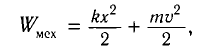
и период его колебаний

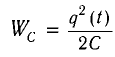
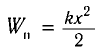
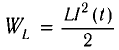
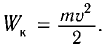
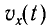
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора и потенциальной энергии упругой деформации пружины энергии магнитного поля катушки и кинетической энергии груза Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза служит сила тока I(t) в колебательном контуре.

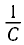
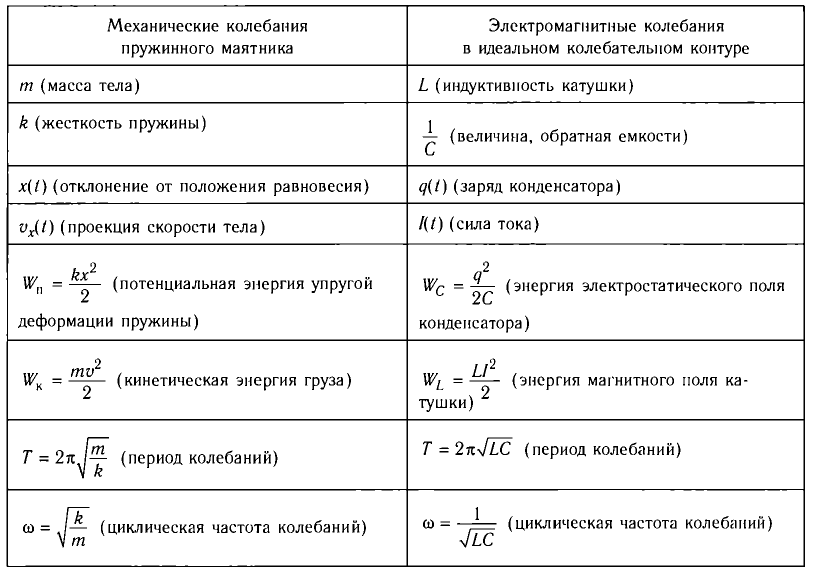
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на , тогда для периода свободных колебаний в LC-контуре получим формулу Томсона:

Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Таблица 4

Сопоставление физических величин, характеризующих электромагнитные и механические колебания

Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.

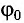
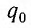
Для определения начальной фазы и амплитуды колебаний заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).

Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.

Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.

Пример №1

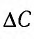
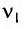
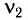
При изменении емкости конденсатора идеального LC-контура на = 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с = 100 кГц до = 120 кГц. Определите индуктивность L контура.

Решение

Частота колебаний в контуре

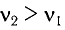
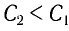
Поскольку частота колебаний в контуре увеличилась (), то электроемкость должна уменьшится, т. е. .

Из условия задачи получаем систему уравнений

Откуда

Вычитая из первого уравнения второе, получаем

Откуда находим

Ответ: L = 0,015 Гн.

Пример №2

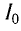
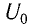
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе = 500 В.

Решение

Максимальная энергия электростатического поля конденсатора

а максимальная энергия магнитного поля катушки

Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 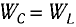, т. е.

откуда

Ответ: .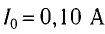

Колебательный контур и свободные электромагнитные колебания в контуре

Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.

Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.

Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.

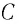
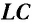
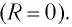
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью и катушки (соленоида) индуктивностью (рис. 29, а), называемую идеальным колебательным контуром или -контуром. Электрическое сопротивление идеального контура считают равным нулю Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.

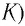
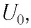
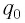
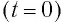
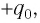
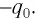
Подключив (при помощи ключа источник тока, зарядим конденсатор до напряжения сообщив ему заряд (рис. 29, б). Следовательно, в начальный момент времени конденсатор заряжен так, что на его обкладке 1 находится заряд а на обкладке 2 — заряд При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией

Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 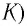(рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.

Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 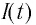которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.

Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 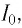определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).

При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):

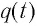
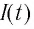
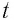
где — мгновенное значение заряда конденсатора и — сила тока в катушке в некоторый момент времени после начала разрядки конденсатора.

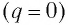
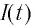
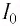
В момент полной разрядки конденсатора сила тока в катушке достигнет своего максимального по модулю значения (см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:

После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. 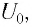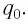Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.

Таким образом, в идеальном 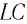-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.

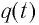
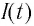
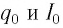
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд конденсатора и сила тока в катушке достигают своих максимальных значений в различные момента времени (см. рис. 31 а, б).

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

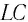
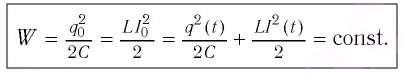
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство:

Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:

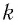
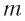
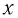
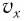
где — жесткость пружины, — масса груза, — проекция смещения тела от положения равновесия, — проекция его скорости на ось

Период его колебаний:

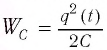
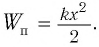
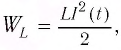
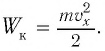
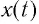
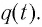
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора является аналогом потенциальной энергии упругой деформации пружины Соответственно, энергия магнитного поля катушки которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза Следовательно, аналогом координаты пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.

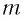
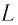
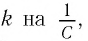
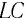
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу на индуктивность и жесткость тогда для периода свободных колебаний в -контуре получим формулу:

которая называется формулой Томсона.

Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:

Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.

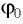
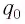
Для определения начальной фазы и максимального заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени

Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.

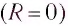
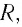
Полная энергия идеального колебательного контура с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.

Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.

Пример решения задачи:

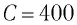
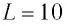
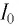
Идеальный колебательный контур состоит из конденсатора емкостью пФ и катушки индуктивностью мГн. Определите максимальное значение силы тока в контуре, если максимальное значение напряжения на конденсаторе
Дано:

Решение

Максимальная энергия электростатического поля конденсатора:

а максимальная энергия магнитного поля катушки:

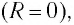
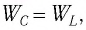
Так как контур идеальный то его полная энергия сохраняется с течением времени. По закону сохранения энергии т. е.

Отсюда

Ответ:

Исследовательские методы в физике
Вертикальное движение тел в физик
Неравномерное движение по окружности
Равномерное движение по окружности
Распространение механических волн в средах
Электромагнитное поле
Опыты Фарадея в физике
Электромагниты и их применение в физике

Источник

Слайд 1

Цели урока:

Образовательные: обобщение и
систематизация знаний по теме, проверка знаний,
умений, навыков. В целях повышения интереса к
теме работу вести с помощью опорных конспектов.
Воспитательные: воспитание
мировоззренческого понятия
(причинно-следственных связей в окружающем мире),
развитие у школьников коммуникативной культуры.
Развивающие: развитие самостоятельности
мышления и интеллекта, умение формулировать
выводы по изученному материалу, развитие
логического мышления, развитие грамотной устной
речи, содержащей физическую терминологию.

Тип урока:систематизация и обобщение
знаний.

Слайд 2

Техническая поддержка урока:

Демонстрации:
Плакаты.
Показ слайдов с помощью информационно –
компьютерных технологий.
Дидактический материал:
Опорные конспекты с подробными записями на
столах.
Оформление доски:
Плакат с кратким содержанием опорных
конспектов (ОК);
Плакат – рисунок с изображением колебательного
контура;
Плакат – график зависимости колебаний заряда
конденсатора, напряжения между обкладками
конденсатора, силы тока в катушке от времени,
электрической энергии конденсатора, магнитной
энергии катушки от времени.

Слайд 3

План урока:

1. Этап повторения пройденного материала.
Проверка домашнего задания.
Четыре группы задач по теме:

Электромагнитные колебания.
Колебательный контур.
Свободные колебания. Свободные колебания –
затухающие колебания
Характеристика колебаний.

2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.

ХОД УРОКА

Учитель: Темой урока является
«Решение задач по теме: «Электромагнитные
колебания и волны» на примере разбора задач ЕГЭ»

К доске вызываются 3 ученика для проверки
домашнего задания.

– Задания по этой теме можно разделить на
четыре группы.

Слайд 4

Четыре группы задач по теме:

1. Задачи с использованием общих законов
гармонических колебаний.
2. Задачи о свободных колебаниях конкретных
колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.

– Мы остановимся на решении задач 1 и 2 групп.

Урок начнем с повторения необходимых понятий
для данной группы задач.

Слайд 5

Электромагнитные колебания – это
периодические и почти периодические изменения
заряда, силы тока и напряжения.

Колебательный контур – цепь,
состоящая из соединительных проводов, катушки
индуктивности и конденсатора.

Свободные колебания – это колебания,
происходящие в системе благодаря начальному
запасу энергии с частотой, определяемой
параметрами самой системы: L, C.

Скорость распространения электромагнитных
колебаний равна скорости света: С = 3^.10⁸(м/с)

Основные характеристики колебаний

Амплитуда (силы тока, заряда, напряжения) –
максимальное значение (силы тока, заряда,
напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда,
напряжения) – i, q, u

Слайд 6

Схема колебательного контура

Учитель: Что представляют
электромагнитные колебания в контуре?

Слайд 7

Электромагнитные колебания представляют
периодический переход электрической энергии
конденсатора в магнитную энергию катушки и
наоборот согласно закону сохранения энергии.

Слайд 8

Задача №1 (д/з)

Колебательный контур содержит конденсатор
емкостью 800 пФ и катушку индуктивности
индуктивностью 2 мкГн. Каков период собственных
колебаний контура?

Слайд 9

Задача № 2 (д/з)

Колебательный контур состоит из конденсатора
емкостью С и катушки индуктивности
индуктивностью L. Как изменится период свободных
электромагнитных колебаний в этом контуре, если
электроемкость конденсатора и индуктивность
катушки увеличить в 3р.

Слайд 10

Задача № 3 (д/з)

Амплитуда силы тока при свободных колебаниях в
колебательном контуре 100 мА. Какова амплитуда
напряжения на конденсаторе колебательного
контура, если емкость этого конденсатора 1 мкФ, а
индуктивность катушки 1 Гн? Активным
сопротивлением пренебречь.

Слайд 11

Схема электромагнитных колебаний

Ученик 1 наглядно описывает процессы в
колебательном контуре.

Слайд 12

Ученик 2 комментирует электромагнитные
колебания в контуре, используя графическую
зависимость заряда, напряжения. Силы тока,
электрической энергии конденсатора, магнитной
энергии катушки индуктивности от времени.

Слайд 13

Уравнения, описывающие колебательные процессы
в контуре:

Обращаем внимание, что колебания силы тока в
цепи опережают колебания напряжения между
обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы
тока по гармоническому закону, необходимо
учитывать связь между функциями синуса и
косинуса.

Слайд 14

Задача № 1.

По графику зависимости силы тока от времени в
колебательном контуре определите, какие
преобразования энергии происходят в
колебательном контуре в интервале времени от
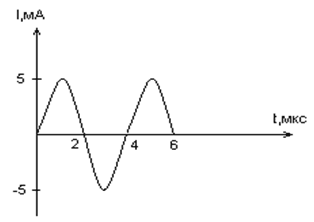
1мкс до 2мкс?

1. Энергия магнитного поля катушки
увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется
в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора
уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора
преобразуется в энергию магнитного поля катушки.

Слайд 15

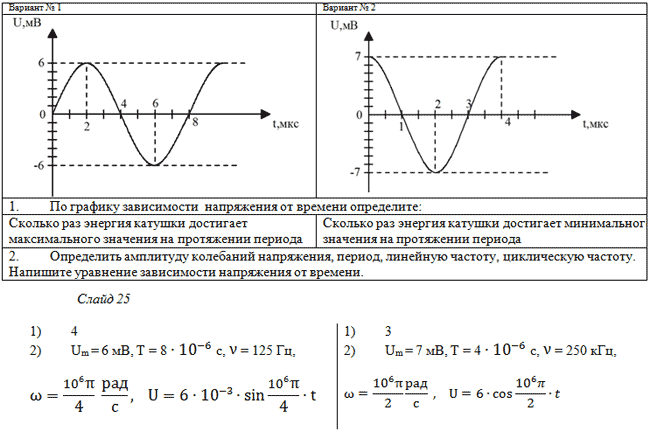
Задача № 2.

По графику зависимости силы тока от времени в
колебательном контуре определите:

а) Сколько раз энергия катушки достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
б) Сколько раз энергия конденсатора достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
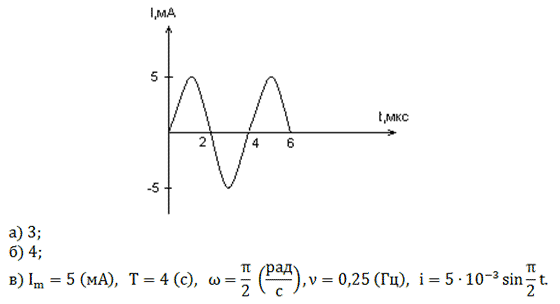
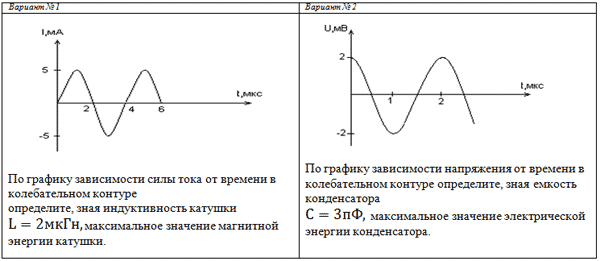
в) Определите по графику амплитудное значение
силы тока, период, циклическую частоту, линейную
частоту и напишите уравнение зависимости силы
тока от времени.

Слайд 16

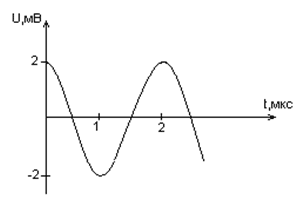
Задача № 3 (д/з)

Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите, какое преобразование энергии
происходит в интервале времени от 0 до 2 мкс?

Слайд 17

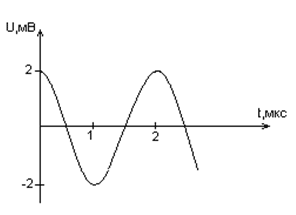
Задача № 4 (д/з)

Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите: сколько раз энергия конденсатора
достигает максимального значения в период от
нуля до 2мкс? Сколько раз энергия катушки
достигает наибольшего значения от нуля до 2 мкс?
По графику определите амплитуду колебаний
напряжений, период колебаний, циклическую
частоту, линейную частоту. Напишите уравнение
зависимости напряжения от времени.

Слайд № 18

К доске вызываются 2 ученика

Задача № 5, 6

Слайд 19

Слайд 20

Задача № 7

Заряд на обкладках конденсатора
колебательного контура изменяется по закону
q = 3·10^–7cos800πt. Индуктивность контура 2Гн.
Пренебрегая активным сопротивлением, найдите
электроемкость конденсатора и максимальное
значение энергии электрического поля
конденсатора и магнитного поля катушки
индуктивности.

Слайд 21

Слайд 22

Задача № 8

В идеальном колебательном контуре происходят
свободные электромагнитные колебания. В таблице
показано, как изменяется заряд конденсатора в
колебательном контуре с течением времени.

t, 10^–6(C)	0	1	2	3	4	5	6	7	8	9
q, 10^–9(Кл)	2	1,5	0	–1,5	–2	–1,5	0	1,5	2	1,5

1. Напишите уравнение зависимости заряда от
времени. Найдите амплитуду колебаний заряда,
период, циклическую частоту, линейную частоту.

2. Какова энергия магнитного поля катушки в
момент времени t = 5 мкс, если емкость конденсатора
50 пФ.

Домашнее задание. Напишите уравнение
зависимости силы тока от времени. Найдите
амплитуду колебаний силы тока. Постройте
графическую зависимость силы тока от времени.

Слайд 23

Слайд 24

Самостоятельная работа:

Приложение 1

Источник

Содержание

Колебательный контур

Энергии контура

Процессы в колебательном контуре

Свободные электромагнитные колебания

*Вывод формулы Томсона

Литература

Оглавление

Электромагнитные колебания

Колебательный контур

Энергетические превращения в колебательном контуре

Электромеханические аналогии

Гармонический закон колебаний в контуре

Вынужденные электромагнитные колебания

Колебательный контур и свободные электромагнитные колебания в контуре

Не пропустите также: