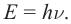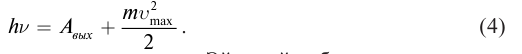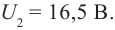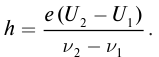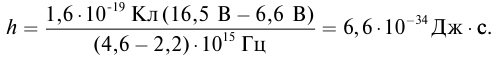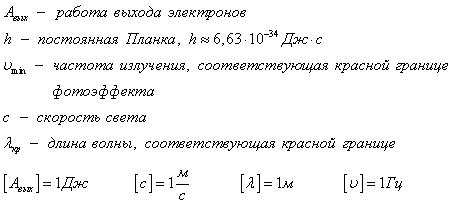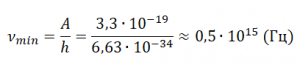Фотоэффект
-
Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.
-
Опыты Столетова
-
Зависимость фототока от напряжения
-
Законы фотоэффекта
-
Трудности классического объяснения фотоэффекта
-
Гипотеза Планка о квантах
-
Уравнение Эйнштейна для фотоэффекта
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.
Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.
Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.
к оглавлению ▴
Опыты Столетова
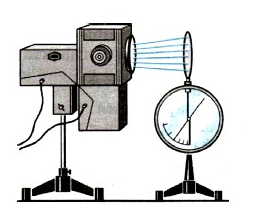
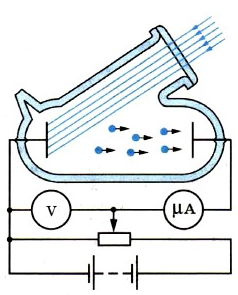
В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1.
Рис. 1. Фотоэлемент Столетова
В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод
. На катод и анод подаётся напряжение, величину
которого можно менять с помощью потенциометра и измерять вольтметром
.
Сейчас на катод подан «минус», а на анод — «плюс», но можно сделать и наоборот (и эта перемена знака — существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод (Поэтому поданное на электроды напряжение часто называют анодным напряжением). В данном случае, например, напряжение
положительно.
Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением
и летят на анод. Включённый в цепь миллиамперметр
регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.
В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.
к оглавлению ▴
Зависимость фототока от напряжения
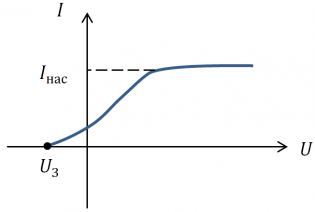
Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2.
Рис. 2. Характеристика фотоэлемента
Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .
Если напряжение отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает — электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод:
Здесь кг — масса электрона,
Кл — его заряд.
Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.
Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:
(1)
Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.
При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.
При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!
Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.
Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.
Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.
к оглавлению ▴
Законы фотоэффекта
Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.
Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).
Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.
А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.
Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3):
Рис. 3. Зависимость энергии фотоэлектронов от частоты света
Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если
, то фотоэффекта нет.
Если же , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.
Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при
: максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.
Все эти факты нашли отражение во втором и третьем законах фотоэффекта.
Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.
Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При
фотоэффект не наблюдается ни при какой интенсивности света.
к оглавлению ▴
Трудности классического объяснения фотоэффекта
Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?
Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.
В переменном электрическом поле световой волны электрон начинает совершать колебания.
И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.
Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.
Далее, откуда берётся красная граница фотоэффекта? Чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растёт и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.
Кроме того, неясна безынерционность фотоэффекта. Именно, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды.
Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.
Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.
Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.
Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.
к оглавлению ▴
Гипотеза Планка о квантах
Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).
Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.
В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.
Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:
(2)
Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.
Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:
Дж·с. (3)
Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.
к оглавлению ▴
Уравнение Эйнштейна для фотоэффекта
Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.
Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .
Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.
Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .
Каждый фотон монохроматического света, имеющего частоту , несёт энергию
.
Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.
Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.
Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода
по извлечению электрона из вещества и на придание электрону кинетической энергии
:
(4)
Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.
Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.
Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.
Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности.
Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.
Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.
1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.
Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.
2. Выразим из формулы (4) кинетическую энергию:
Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.
Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3.
3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота
, определяемая равенством
как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.
Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.
Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.
В ходе таких опытов было получено значение , в точности совпадающее с (3). Такое совпадение результатов двух независимых экспериментов — на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта — означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике — теории микромира, построение которой продолжается и сегодня.
Это была необходимая теория. Разберем задачи ЕГЭ по теме «Фотоэффект».
Задача 1. Поток фотонов с энергией 10 эВ выбивает из металла электроны. Какова максимальная кинетическая энергия электронов, если работа выхода электронов с поверхности данного металла равна 6 эВ?
Решение:
Eф = Авых + Ек.
Eк = Eф — Авых = 10 – 6 = 4 эВ.
Ответ: 4.
Задача 2. Когда на металлическую пластину падает электромагнитное излучение с длиной волны , максимальная кинетическая энергия фотоэлектронов равна 4,5 эВ. Если длина волны падающего излучения равна
,то максимальная кинетическая энергия фотоэлектронов равна 1 эВ. Чему равна работа выхода электронов из металла?
Решение:
Запишем уравнение фотоэффекта для двух случаев:
Домножим второе уравнение на 2 и вычтем из первого уравнения второе:
_________________________________
Ответ: 2,5.
Задача 3. Красная граница фотоэффекта исследуемого металла соответствует длине волны нм. Какова длина волны света, выбивающего из него фотоэлектроны, максимальная кинетическая энергия которых в 2 раза меньше работы выхода?
Решение:
По условию задачи,
Подставим это в уравнение фотоэффекта:
Ответ: 400.
Задача 4. Фотоны с энергией 2,1 эВ вызывают фотоэффект с поверхности цезия, для которого работа выхода равна 1,9 эВ. На сколько нужно уменьшить энергию фотона, чтобы максимальная кинетическая энергия фотоэлектронов уменьшилась в 2 раза?
Решение:
Запишем два уравнения фотоэффекта для двух случаев и учтём, что по условию задачи
Тогда получаем:
Из первого уравнения получаем, что
Тогда из второго уравнения получаем, что
Значит энергию падающих фотонов нужно уменьшить на
Ответ: 0,1.
Задача 5. Работа выхода электронов из металла равна Дж. Задерживающая разность потенциалов для фотоэлектронов, вылетевших с поверхности этого металла под действием излучения с некоторой длиной волны
, равна 3 В. Чему будет равна задерживающая разность потенциалов для фотоэлектронов в случае длины волны излучения
?
Решение:
Переведём работу выхода в электронвольты:
Теперь из уравнения фотоэффекта найдём энергию фотонов в первом случае:
Если длину волны увеличить в 2 раза, то энергия фотона уменьшится тоже в 2 раза, так как энергия фотона обратно пропорциональна длине волны. Тогда во втором случае энергия фотона будет равна:
Тогда:
Ответ: 1.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Фотоэффект» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
1.3.1.
Ток насыщения
Для
исследования силы фототока применяется
обычно схема, изображенная на рис. 1.3,а.
Здесь Р
–
освещаемая пластинка металла (фотокатод),
N
–
вторая пластинка (анод), присоединенная
через гальванометр G
к
соответствующему полюсу батареи В.
Электроны,
освобождаемые светом из пластины Р,
под
действием напряжения батареи В
движутся
к пластине N
и
далее через гальванометр, замыкают
электрическую цепь.
Уже
первые исследователи обнаружили, что
явление в высокой степени зависит от
чистоты
освещаемой
поверхности. Поэтому точные опыты
производятся со свежими поверхностями,
тщательно очищенными механическим
путем или, еще лучше, образованными
путем напыления металла в вакууме.
Высокий вакуум поддерживается между
электродами Р
и
N
во
время измерения, ибо присутствие газов
может сильно изменить свойстваповерхности
и, кроме того, осложняет условия выхода
и переноса зарядов. Поддерживая освещение
постоянным и изменяя напряжение батареи
мы будем в известных пределах изменять
силу тока в гальванометре. Но если опыт
производится в высоком вакууме и
электродам придана такая форма, что все
заряды,
вырванные
из освещенной поверхности, попадают на
второй сферический электрод даже без
помощи ускоряющего поля (рис. 1.3, б),
то сила фототока не будет возрастать
при увеличении поля. Если же на электрод
N
подавать отрицательный потенциал по
отношению к потенциалу электрода Р,
то
возникающее
поле тормозящее поле, направленное так,
что мешает движению электронов от
освещаемого электрода Р
к электроду N
, приводя фототок к нулю при достаточно
разности потенциалов между электродами.
б
в
а
г
Рис.
1.3. Законы фотоэффекта: а
– схема, для исследования фотоэффекта;
б
– схема опыта со сферическим анодом; в
– вольт амперные характеристики;
г
– зависимость фототока от освещенности
Действительно,
опыты со сферическим анодом показывают,
что в соответствии с этими рассуждениями
зависимость силы фототока I
от приложенной к электродам разности
потенциалов U
– так
называемая вольт амперная характеристика
фототока
–
имеет вид, изображенный на рис. 1.3, в
(сплошная кривая 1). При электродах, форма
и взаимное расположение которых не
удовлетворяют поставленным выше
требованиям, характеристика фототока
сильно изменяется (рис. 1.3, в,
пунктирная кривая 1). Однакосохраняются
ее существенные черты: при некоторой
не большой ускоряющей разности потенциалов
ток доходит до постоянной величины (ток
насыщения).
При
определенной тормозящей разности
потенциалов ток падает до нуля. На
стремление фототока к насыщению указал
А.Г. Столетов в своих опытах.
Так
как ток насыщения соответствует условиям,
при которых все
освобожденные
светом электроны проходят через цепь
гальванометра, то сила тока насыщения
и должна быть принята за меру
фотоэлектрического действия света. При
большей освещенности характер
вольтамперной характеристики сохранится,
но фототок насыщения увеличится (рис.
1.3 в,
кривые 2).
Тщательно
выполненные измерения показывают, что
сила тока насыщения строго пропорциональна
световому потоку, поглощенному металлом.
Так как интенсивность поглощенного в
металлах света пропорциональна
интенсивности падающего, то основной
закон фотоэффекта можно сформулировать
так:
сила
фототока насыщения прямо пропорциональна
падающему световому потоку
(рис. 1.3, г).
Этот
закон проверялся в очень широком
интервале интенсивностей света и
показано его строгое выполнение.
Благодаря этому закону фотоэлементыможно
использовать в качестве превосходных
объективных фотометров. Однако, выполнение
этого закона нарушается, если пространство
между электродами не будет вакуумировано.
Закон,
приведенный выше, выполняется с полной
строгостью в том случае, когда измеряемый
ток насыщения образован лишь электронами,
освобожденными светом. Это имеет место,
если чувствительная поверхность помещена
в вакуум. Приборы, наполненные газом,
являются более чувствительными, так
как в них к току фотоэлектронной эмиссии
прибавляется ток ионизации. Однако в
таких приборах могут возникать некоторые
отступления от простой пропорциональности
между силой тока насыщения и интенсивностью
света, поэтому ими надо пользоваться
для измерительных целей с известной
осмотрительностью.
1.3.2.
Скорости фотоэлектронов
Анализируя
вольтамперную характеристику фототока
(рис. 1.3, в),
мы обнаруживаем, что при подаче между
электродами тормозящего электрического
поля ток уменьшается до нуля. Отсюда
следует, очевидно, что часть электронов
обладает при вылете кинетической
энергией 1/2mV2,
которая
меньше работы, необходимой, для преодоления
приложенной разности потенциалов.
Подобрав такую разность потенциалов
UЗ,
при
которой ток обращается в нуль, мы
задерживаем все
электроны,
включая и самые быстрые. Таким образом,
Vm
–
максимальная
скорость электронов, освобожденных
светом в описанном опыте, –
определится из соотношения:
1/2
mVm
2
=
еUЗ. (1.1)
То
обстоятельство, что даже при наиболее
благоприятном расположении электродов
характеристика фототока не обрывается
сразу, а более или менее полого падает
до нуля, указывает, что скорости вылетающих
электронов различны: самые медленные
электроны задерживаются очень слабым
тормозящим полем, а для задержания самых
быстрых требуется встречная разность
потенциалов, равная UЗ
(см.
рис. 1.3,в).
Изучив закон уменьшения фототока с
ростом задерживающего поля, можно
определить распределение электронов
по скоростям. Причина такого разнообразия
скоростей заключается в том, что свет
может освобождать электроны не только
с поверхности металла, но и из некоторой
глубины. Эти последние электроны теряют
часть сообщенной им скорости раньше,
чем они выйдут на поверхность, вследствие
случайных столкновений внутри металла.
Поэтому
основной физический интерес представляет
максимальная
скорость,
определяемая при помощи соотношения
(1.1), ибо она характеризует энергию света,
сообщаемую электрону при его освобождении.
Было
бы, однако, ошибочным думать, что для
освобождения электрона со скоростью V
из
поверхности металла достаточно сообщить
ему энергию 1/2mV2.
Известно, что электрон при прохождении
через поверхность металла должен
преодолеть некоторое сопротивление
своему выходу, затратив определенную
работу А.
Эта
работа
выхода препятствует
в обычных условиях свободным электронам
металла покинуть последний. Она различна
для разных металлов, вследствие чего
между двумя соприкасающимися различными
металлами устанавливается контактная
разность потенциалов
(лабораторная
работа № 3).
Работу выхода можно также определить
по явлению термоэлектронной эмиссии,
ибо количество электронов, испускаемых
в течение секунды единицей поверхности
нагретого металла, сильно зависит от
величины работы выхода (лабораторная
работа № 5).
Таким
образом, энергия ε,
которую
нужно сообщить электрону для того, чтобы
он вырвался с максимальной скоростью
Vm
из
пластины, характеризуемой работой
выхода А
определяется
соотношением:
ε
=1/2
mVm
2
+ А = eU+eU0, (1.2)
где
U0
=А/e
–
потенциал
выхода.
При
помощи соотношения (1.2) можно найти
величину энергии ε,
получаемой
электроном при фотоэффекте. Исследования
Ленарда и ряда других ученых позволили
установить чрезвычайно важный закон:
энергия ε,
приобретаемая электроном, не зависит
ни от интенсивности падающего света,
ни от природы освещаемого вещества, ни
от его температуры, а энергия определяется
лишь частотой падающего монохроматического
света и растет с увеличением частоты.
1.3.3.
Уравнение Эйнштейна. Гипотеза световых
квантов.
Красная граница фотоэффекта
Еще
в тот период, когда указанный закон был
экспериментально установлен в качественной
форме, Эйнштейн (1905 г.) обосновал
теоретически количественную связь
между энергией, получаемой электроном
при его освобождении светом, и частотой
этого света. Согласно теории Эйнштейна
закон фотоэффекта имеет следующий вид:
ε
= 1/2
mVm
2
+ А = eU
+ А = hv, (1.3)
где
h=
6,626×10-34
Дж×с – постоянная теории квантов,
введенная Планком и носящая его имя.
Следуя
Эйнштейну, вся
энергия,
полученная электроном, поставляется
ему светом в виде определенной порции
hv
(световой
квант),
величина
которой зависит от частоты света,
и
поглощается им целиком (см. (1.3)). Таким
образом, электрон не заимствует энергию
от атомов вещества катода, благодаря
чему природа вещества определяет только
величину работы выхода.
Энергия
кванта очень велика по сравнению с
тепловой энергией электронов, и поэтому
изменение температуры должно лишь очень
слабо сказываться на скорости вылетающих
электронов (действительно, такое малое
влияние было обнаружено в работах
последнего времени). В рамках теории
Эйнштейна пропорциональность силы
фототока насыщения световому потоку
также легко объяснима. Действительно,
световой поток определяется числом
квантов света, падающих на поверхность
за единицу времени, а число освобожденных
электронов должно быть пропорционально
числу падающих квантов, при этом, как
показывает опыт, лишь малая часть квантов
передает свою энергию отдельным
электронам, остальные же расходуются
на нагревание металла в целом.
Теоретическая
формула Эйнштейна была блестяще
подтверждена десятилетие спустя опытами
Милликена (1916 г.). Измерения Милликена,
выполненные по схеме,
аналогичной схеме, представленной на
рис. 1.3, а,
чрезвычайно усложненной вследствие
применения ряда экспериментальных
предосторожностей (свеже очищаемая
поверхность металла в вакууме, учет
контактных разностей потенциалов между
различными частями аппаратуры и т. д.),
дали строго линейную зависимость между
задерживающим потенциалом UЗ
и
частотой падающего света v
для нескольких металлов (см. рис.1.4).
По
наклону этих прямых для ряда изученных
металлов (Na,
Mg,
А1, Си)
было определено значение постоянной
h.
Среднее
из этих измерений составляло h=
6,547×10-34
Дж×с, что хорошо совпадает со значениями
h,
полученными
из опытов иного рода.
Впоследствии
данный метод был улучшен и привел к еще
более точным определениям постоянной
Планка (h=
6,67×10-34
Дж×с, П.И.Лукирский, 1928 г., метод сферического
конденсатора).
Из
опытов Милликена можно, пользуясь
формулой Эйнштейна, определить также
и работу выхода. Найдем то значение
v
= v0,
которому
Рис.
1.4. Прямая Милликена: зависимость
задерживающего потенциала от частоты
падающего излучения
соответствует
UЗ
=
О, т. е. точку пересечения прямой Милликена
(рис. 1.4) с осью абсцисс, тогда работу
выхода металла можно определить:
А =
hv0.
Таким
образом, если освещать металл светом
частоты v0
(или меньшей), то UЗ
= 0,
т. е. электроны не выйдут из металла даже
при наличии некоторого ускоряющего
поля. Поэтому найденную таким образом
частоту v0
(или соответствующую длину волны λ0=c/v0)
называют граничной
частотой или
красной
границей
внешнего
фотоэффекта.
Она лежит в области тем более длинных
волн, чем электроположительнее металл,
т. е. чем легче отдает он свои электроны.
Так, например, для щелочных металлов
граница лежит в области видимого света,
тогда как для большинства других металлов
она находится в ультрафиолетовой области
спектра. Необходимо отметить также, что
присутствие примесей, например, газов,
растворенных в металле, нередко сильно
облегчает выход электронов, перемещая
границу в область более длинных волн.
В таблице 1 приведены значения красной
границы
для нескольких чистых
металлов:
Таблица
1
Красные
границы металлов
|
Металл |
К |
Na |
Li |
Hg |
Fe |
Ag |
Au |
Та |
|
λ0, |
550,0 |
540,0 |
500,0 |
273,5 |
262,0 |
261,0 |
265,0 |
305,0 |
1.3.4.
Обоснование гипотезы световых квантов
в явлениях фотоэффекта
Уравнение
Эйнштейна (1.3), которое можно также
записать в виде:
1/2тV2
=
h(v
– v0)
= eU, (1.4)
подтвержденное
опытами Милликена, подвергалось и в
дальнейшем разнообразным экспериментальным
проверкам. В частности, частота падающего
света варьировалась в очень широких
пределах – от видимого света до
рентгеновских лучей, и во всем интервале
опыт оказался в превосходном согласии
с теорией. В опытах с рентгеновскими
лучами проверка уравнения (1.4) упрощается
благодаря тому, что v
очень велико по сравнению с v0.
Поэтому соотношение (4) принимает вид
hv
=
eU
и
позволяет определить v,
если измерено U.
Таким
приемом пользуются даже для определения
длины волны очень жестких -лучей, для
которых метод дифракции на кристаллах
невозможно осуществить с достаточной
точностью из-за малости соответствующей
длины волны.
Фотоэлектрические
опыты с рентгеновскими лучами дают
возможность исследовать, распространяется
ли световая энергия равномерно во все
стороны, как следует из обычных волновых
представлений, или она идет то по одному,
то по другому направлению в виде
дискретных квантов. Действительно,
кванты видимого света обладают малым
запасом энергии (так, для желтого
излучения v
= 5×1014
с-1,
hv
=
3,31×10-19
Дж),
поэтому для регистрации их в большинстве
опытов приходится иметь дело с большим
числом квантов в единицу времени. В
соответствии с
этим
действие, производимое случайным
распределением летящих по всем
направлениям световых квантов, трудно
отличить от действия волны, равномерно
распространяющейся во все стороны. Чем
больше величина кванта, тем легче
наблюдать действие отдельного кванта
и легче, следовательно, осуществить
опыт наблюдения распространения световой
энергии не во все стороны равномерно,
а вспышками, то по одному, то по другому
направлению. Кванты рентгеновского
диапазона удовлетворяют этому условию.
Кроме того, с рентгеновскими лучами
легче осуществить условия, необходимые
для возбуждения небольшого числа актов
испускания в секунду. Известно, что для
получения рентгеновского излучения
нужно бомбардировать электронами анод.
Всякая остановка (или торможение)
электрона сопровождается испусканием
рентгеновского импульса. В рамках теории
световых квантов в самом благоприятном
случае вся кинетическая энергия электрона
после остановки перейдет полностью в
один-единственный квант, частота которого
v
определится из условия ε
=
hv.
Если
бомбардирующий электрон разгонялся
разностью потенциалов U
то
εкин
= eU,
и
условие максимальной частоты будет
иметь вид:
hv
= eU.
(1.5)
Действительно,
опыт подтвердил, что при испускании
рентгеновских волн наблюдается
максимальная частота (коротковолновая
граница), определяемая из условия (1.5),
где U
–
ускоряющая разность потенциалов, е
–
заряд электрона, v
–
частота границы и h
–
постоянная Планка. Волны более короткие
(большие v)
никогда не наблюдаются, волны же более
длинные соответствуют превращению лишь
части кинетической энергии электрона
в излучение. Определение коротковолновой
границы рентгеновского спектра может
быть выполнено весьма надежно, поэтому
такого рода опыты используются как один
из наиболее совершенных методов
определения значения постоянной Планка
с помощью соотношения (1.5).
Наилучшие
измерения, выполненные этим методом,
дали для постоянной Планка значение h
= 6,624×10-34
Дж×с.
Регулируя
число электронов, бомбардирующих анод,
можно менять число излучаемых рентгеновских
квантов. Если заставить такие рентгеновские
лучи воздействовать на металлическую
пластинку, вызывая внешний фотоэффект,
то, как показывает опыт, кинетическая
энергия испускаемых электронов равняется
энергии кванта. Таким образом, полная
схема превращения будет иметь вид:
eV
= 1/2mV2
= hv
= 1/2mV2,
(1.6)
т.
е. весь цикл превращений состоит из: 1)
превращения работы электрического поля
eU
в
кинетическую энергию 1/2mV2
электрона
в рентгеновской трубке, 2) превращения
кинетической энергии этого электрона
в рентгеновский квант hv,
и,
наконец, 3) превращение энергии кванта
полностью в кинетическую энергию 1/2mV2
электрона,
освобожденного этим квантом при
фотоэффекте. Такой цикл гораздо больше
походит на удар, чем на процесс постоянного
накопления в освобождаемом электроне
энергии, приносимой волнами.
Из
многочисленных опытов с рентгеновскими
лучами, обнаруживающих с большой ясностью
корпускулярные свойства этих лучей
следует отметить два: первый принадлежит
А.Ф.Иоффе и Н.И. Добронравову, второй –
Боте. Подробное описание этих опытов
можно найти в учебнике: Э.В. Шпольский
Атомная физика. т. I.
Осуществлены также опыты, показывающие,
что энергия рентгеновского излучения
распространяется в разные стороны не
одновременно, и что порции этого излучения
(кванты) летят
то
в ту, то в другую сторону.
Опыт
Боте был выполнен при помощи двух
счетчиков, достаточно чувствительных
для того, чтобы зарегистрировать действие
одного рентгеновского кванта, и достаточно
быстро фиксирующих его появление. Этот
опыт осуществлен Боте по схеме,
представленной на рис. 1.5.
Тонкая
фольга А,
освещенная
сбоку рентгеновскими лучами R,
сама
становится источником рентгеновских
лучей (рентгеновская
флуоресценция). Два
счетчика Cч1
и Cч2
расположены
симметрично. Попадание рентгеновского
излучения в каждый из них вызывает
немедленное (меньше чем через 0,001 с)
вздрагивание нити соединенного с ним
электрометра Э.
Эти вздрагивания регистрируются
автоматически на общей движущейся ленте
Л.
Если из фольги А
во
все стороны расходятся волны, то работа
обоих счетчиков должна происходить
одновременно, в такт (с малыми случайными
вариациями). Наоборот, если из А
летят
кванты то в ту, то в другую сторону, то
показания электрометров будут
беспорядочными и лишь случайно могут
оказаться близкими или одновременными.
Опыт совершенно отчетливо обнаружил
беспорядочность показаний электрометров,
т. е. доказал, что из фольги
летят
кванты то в одну, то в другую сторону.
R
Сч1
Сч2
А
Э1
Э2
Л
Рис.
1.5. Схема опыта Боте
Аналогичные
опыты с квантами видимого света затруднены
тем, что энергия этих квантов очень
мала. Однако к световым квантам очень
чувствителен глаз, хотя глаз не реагирует
на один отдельный квант, но опыты
показывают, что необходимое для
минимального светового ощущения число
квантов в секунду не очень значительно.
По измерениям С. И. Вавилова, в области
максимальной чувствительности глаза
(550 нм) для отдохнувшего глаза пороговая
чувствительность в среднем составляет
около 200 квантов, падающих за 1 с на зрачок
наблюдателя. В этих условиях, как показали
опыты Вавилова, удается наблюдать
флуктуационные колебания светового
потока, имеющие ясно выраженный
статистический характер. Хотя в таких
опытах и нельзя однозначно отделить
квантовые флуктуации светового потока
от флуктуации, связанных с физиологическими
процессами в глазу, тем не менее и они
могут рассматриваться как подтверждающие
квантовый характер явления, кроме того,
эти опыты дают результаты, существенные
для исследования свойств живого глаза.
В частности, с их помощью удалось
установить, что число квантов, которые
должны поглощаться в сетчатке
при
пороговом раздражении, приблизительно
на порядок меньше числа квантов, падающих
на зрачок, и составляет примерно 20
квантов в секунду.
Итак,
совокупность сведений о фотоэффекте,
изложенных выше, убедительно свидетельствует
в пользу представления о световых
квантах. Можно сказать, что свет частоты
v
не только покидает атом в виде порции
энергии, равной hv,
но
и в дальнейшем распространяется в
пространстве и вступает во взаимодействие
с веществом в виде такой порции,
локализованной и перемещающейся как
целое со скоростью света. Для таких
элементарных световых частиц Эйнштейн
ввел специальное название – фотон.
Энергия
фотона зависит от его частоты и равна
hv.
В
соответствии с одним из основных выводов
теории относительности энергия
неразрывно связана с понятием динамической
массы т,
причем
численное соотношение между ними
определяется
известным уравнением Эйнштейна
=
тс2.
Следуя
теории Эйнштейна, динамическая масса
фотона т
определяется выражением
m
=
hv/c2
=
m0
/(1-)1/2.
(1.7)
Так
как фотон движется со скоростью света,
то он обладает импульсом с абсолютной
величиной
p
= mc
= hv/c
(1.8)
и
направлением, совпадающим с направлением
распространения волны. Итак, энергия
фотона равна hv,
его
динамическая масса равна hv/c2,
величина
его импульса равна hv/c.
Корпускулярные
свойства фотона не должны заставить
нас забыть о том, что для огромного круга
явлений, волновые представления
оказываются справедливыми. Необходимо
отметить, что и в явлении фотоэффекта
есть свойства, говорящие в пользу
волновых представлений о свете. Эти
свойства особенно отчетливо выступают
при исследовании зависимости силы
фототока от длины волны.
1.3.5.
Зависимость силы фототока от длины
световой волны
Для
исследования зависимости силы фототока
от длины волны необходимо определить
силу тока насыщения, соответствующего
определенной лучистой энергии
монохроматического света. Результаты
подобных измерений приведены на рис.
6, где по оси ординат отложена сила тока
насыщения I0,
отнесенная к поглощенной лучистой
энергии, а по оси абсцисс – длина волны
.
Рисунок
1.6 показывает, что «красной границе»
0
Рис.
1.6. Зависимость силы Рис. 1.7.
Зависимость силы фототока
фототока
от длины волны от длины волны
щелочных металлов
соответствует
I0
= 0 и с уменьшением длины волны сила тока
на единицу поглощенной энергии возрастает.
Это значит, что свет с более короткой
длиной волны более эффективен. Если
принять во внимание, что чем короче
длина волны падающего света, тем «меньше»
квантов
содержится в единице поглощенной энергии
(ибо для коротких волн сами кванты,
равные hv
= hc/,
«больше»), то
из кривой рис. 1.6 ясно видно, как сильно
растет способность фотонов выбивать
электроны из вещества по мере перехода
к более «крупным» фотонам.
Опыт
показал, однако, что ход зависимости,
изображенный на рис. 1.6, не всегда имеет
место. У ряда металлов, особенно щелочных,
для которых красная граница лежит далеко
в видимой и даже в инфракрасной области
спектра и которые, следовательно,
чувствительны к более широкому интервалу
длин волн, наблюдается следующая
особенность: сила тока имеет резко
выраженный максимум для определенного
спектрального участка, быстро спадая
по обе его стороны (селективный,
или
избирательный,
фотоэффект,
рис. 1.7). Селективность фотоэлектрических
явлений очень напоминает резонансные
эффекты. Дело происходит так, как будто
электроны в металле обладают собственным
периодом колебаний, и по мере приближения
частоты возбуждающего света к собственной
частоте электронов амплитуда колебаний
их возрастает и они преодолевают работу
выхода.
Подтверждение
подобного взгляда можно было бы видеть
в том обстоятельстве, что явление
селективного фотоэффекта сильно зависит
от направления поляризации света и угла
падения. Если падающий свет поляризован
так, что вектор напряженности электрического
поля параллелен плоскости падения, то
эффект резко усиливается. Наоборот, при
повороте плоскости поляризации на 90°
селективный эффект исчезает. В первом
случае электрический вектор имеет
слагающую, перпендикулярная к поверхности
металла, тем больше, чем ближе угол
падения к прямому.
Следует
заметить, что легко наблюдаемый большой
селективный максимум щелочных металлов
принадлежит не чистому металлу,
а
соединениям,
обычно образующимся на поверхности
вследствие присутствия следов газа.
Для чистой поверхности металла, которая
получается с большим трудом, селективный
эффект выражен гораздо слабее. Тем не
менее существование селективного
фотоэффекта и его характер отчетливо
указывают на плодотворность волновых
представлений для понимания фотоэффекта.
Однако для полной количественной
трактовки этих явлений, включая и явление
селективного фотоэффекта, требуется
применение углубленных представлений
о металле, даваемых современной квантовой
теорией.
1.3.6.
Многофотонный фотоэффект
Рассмотренные
законы фотоэффекта были установлены
для сравнительно небольших интенсивностей
света. Интерпретация фотоэффекта,
основанная на квантовых представлениях,
связывает освобождение электрона с
передачей ему энергии одного фотона
падающего света. Однако известно, что
в случае очень больших интенсивностей
света оптический электрон атомов и
молекул может приобрести энергию
нескольких фотонов (многофотонные
поглощение и ионизация).
Аналогичное явление было обнаружено и
по отношению к свободным электронам
металлов (Фаркаш
с сотрудниками,1967 г.).
Если
при освещении поверхности металла
электрон способен приобрести энергию
N
фотонов
(т. е. энергию Nhv),
то
следует ожидать, очевидно, уменьшения
граничной частоты в N
раз
(смещения красной границы фотоэффекта
в сторону длинных волн) Наблюдению
фотоэффекта за красной границей,
требующему, как мы увидим, огромной
интенсивности света, длительное время
препятствовало сильное нагревание
металла, приводящее к термоэлектронной
эмиссии, для которой красная граница,
разумеется
не
существует. Маскирующее влияние
термоэлектронной эмиссии было почти
полностью устранено применением
сверхкоротких импульсов лазерного
излучения длительностью 10-11…10-12
с
и скользящим освещением фотокатода
(угол падения около 85°). И тот, и другой
прием приводят к уменьшению нагревания
и к подавлению термоэлектронной эмиссии.
В этих условиях фотоэлектроны были
надежно зарегистрированы далеко за
красной границей (вплоть до пятикратного
уменьшения частоты света в сравнении
с граничной частотой, определяемой
работой выхода).
Законы
многофотонного, или нелинейного,
фотоэффекта имеют много общего с законами
линейного (однофотонного) фотоэффекта,
рассмотренного выше. Пусть частота
света лежит в пределах
P/N<hv<P/(N-1),
(1.9)
Так
что для выхода фотоэлектрона необходимо
поглощение им не менее N
фотонов. При этом условии, как показывает
исследование распределения фотоэлектронов
по скоростям, выполняется соотношение
1/2mV2
+ А = Nhv,
(1.10)
вполне
аналогичное уравнению Эйнштейна (1.3) и
означающее, что фотоэлектрон действительно
приобрел энергию N
фотонов.
Число фотоэлектронов, характеризуемое
величиной тока насыщения, оказалось
пропорциональным интенсивности света,
возведенной в степень N.
Изменения
поляризации света и угла падения
позволили выяснить, что нелинейный
фотоэффект обусловливается исключительно
слагающей напряженности электрического
поля, перпендикулярной к поверхности
катода.
Перечисленные
свойства нелинейного фотоэффекта
установлены при
использовании
фотокатодов из различных материалов
(натрий, золото,
серебро и
др., а также полупроводники), для различных
значений N
=
2, 3, 4 и 5, в широком интервале изменения
интенсивности света
(от 0,1
до 103
МВт/см2).
При значении потока, примерно
равном
104
МВт/см2,
по-видимому,
имеет место еще одно нелинейное явление,
аналогичное автоэлектронной (или
холодной) эмиссии:
электрическое
поле волны изменяет потенциальный
барьер на
поверхности
металла, и электрон получает возможность
«просачиваться» через барьер, не
преодолевая энергии выхода. Такое
«просачивание» легко понять, если
вспомнить о волновых свойствах электрона
и принять во внимание, что прохождение
электрона через потенциальный барьер
аналогично проникновению электромагнитной
волны через тонкий слой оптически
плотного вещества при угле падения,
большем критического угла полного
внутреннего отражения.
1.3.7.
Безынерционность фотоэффекта
Можно
было бы попытаться дать качественное
объяснение фотоэффекта с волновой точки
зрения. Свободные электроны, в изобилии
имеющиеся в металле, удерживаются в нем
задерживающим полем, существующим на
границе металла. Работа выхода электрона
из металла составляет несколько
электрон-вольт. В электрическом поле
световой волны свободный электрон
приходит в колебания. Когда энергия
колебаний сделается достаточно большой,
электрон может преодолеть задерживающее
поле и уйти за пределы металла. Если же
электрон связанный, то все будет
происходить аналогично, но зависимость
энергии колебаний от частоты будет
носить более сложный, резонансный
характер. Однако такое объяснение не
согласуется с опытом. Кинетическая
энергия колеблющегося электрона
заимствуется от световой волны. Казалось
бы, что энергия вылетевшего электрона
должна быть тем больше, чем больше
интенсивность падающего света. Но опыты
Ленарда и многочисленные исследования
других ученых показали, что максимальная
скорость, с которой электроны вылетают
из тела, от интенсивности падающего
света совсем не зависит, а определяется
только его частотой. (Предполагается,
что материал тела и состояние освещаемой
поверхности остаются неизменными.)
Другое резкое расхождение с опытом
получится, если на основе приведенного
объяснения оценить время возникновения
фотоэффекта. Действительно, если взять,
например, изотропно излучающий точечный
источник света мощностью Р
= 100 Вт,
то по классической волновой теории
поток лучистой энергии распространяется
от источника света непрерывно во все
стороны. Пусть свет падает нормально
на плоский фотокатод из цинка, расположенный
на расстоянии r
от источника. Энергетическая освещенность,
создаваемая источником на фотокатоде,
будет Р/4r2.
Работа выхода электрона А
из цинка составляет около 3,74 эВ. Очевидно,
что для выхода электрона из металла
энергия, накопленная им при вынужденных
колебаниях, должна быть не меньше А.
Максимальная энергия, которую может
получить атом от излучения за время
t,
составляет мах
= (P/4r2)t,
где
– поперечное сечение атома. Энергия,
переданная электрону за то же время,
меньше мах,
но она должна быть не меньше А,
чтобы электрон мог выйти из металла, то
есть время должно быть t
>(4г2/P)A.
Учитывая, что среднее расстояние между
атомами цинка d
2,4910-8
см, сечение а можно оценить по формуле
d2
610-8
см2.
Для указанных условий получится t
> 1,25 с. Таким образом, по классической
волновой теории фотоэффект должен
протекать с запаздыванием. Если учесть,
что фотоэлементы реагируют на значительно
более слабые световые потоки, чем в
нашем примере, то и запаздывание
фотоэффекта может получиться много
больше. Между тем опыт показывает, что
фотоэффект протекает безынерционно,
т. е. фототок появляется мгновенно –
одновременно с освещением. Именно на
такой безынерционности основаны
практически все научно-технические
применения фотоэффекта. Указанные
трудности отпадают, если фотоэффект
рассматривать с фотонной точки зрения.
Взаимодействуя с электроном металла,
фотон может обмениваться с ним энергией
и импульсом. Такой процесс взаимодействия
напоминает удар шаров, а потому его
образно называют столкновением.
Фотоэффект возникает при неупругом
столкновении фотона с электроном. При
таком столкновении фотон поглощается,
а его энергия передается электрону.
Таким образом, электрон приобретает
кинетическую энергию не постепенно, а
сразу – в результате единичного акта
столкновения. Этим и объясняется
безынерционность фотоэффекта. Энергия
поглощаемого фотона может затрачиваться
на отрыв электрона от атома внутри
металла. Оторванный электрон может
взаимодействовать с атомом внутри
металла, растрачивая энергию на тепло.
Максимальной энергией вылетевший
электрон будет обладать тогда, когда
внутри металла он был свободен, т. е. не
связан с атомом, а при вылете наружу не
расходовал энергию на тепло.
-
Внутренний
фотоэлектрический эффект
Кроме
рассмотренного нами внешнего фотоэффекта
(называемого обычно просто фотоэффектом),
существует также внутренний фотоэффект,
наблюдаемый в полупроводниках и
диэлектриках. В этом случае под действием
оптического излучения происходит
изменение электрофизических параметров
материала, обусловленное образованием
дополнительных носителей заряда.
Внутренний фотоэффект, условно разделяют
на фотопроводимость
(фоторезистивный
эффект)
– он заключается в увеличении
электропроводности полупроводника или
диэлектрика под действием электромагнитного
излучения и фотогальванический
эффект
(вентильный
фотоэффект).
Фотогальванический эффект возникает
в полупроводниках с внутренним
потенциальным барьером (с р-n—переходом,
с переходом металл-полупроводник, с
гетеропереходом). При этом внутренне
электрическое поле перехода разделяет
возникшие под действием оптического
излучения неравновесные носители заряда
(дополнительные электроны и дырки).
Пространственно разделенные неравновесные
носители разных знаков – дырки и
электроны – создают фото-ЭДС.
Рассмотрим
процесс образования неравновесных
носителей заряда в полупроводниках при
поглощении его оптического излучения,
который приводит к увеличению
проводимости данного полупроводника.
Энергия фотонов может быть передана
электронам валентной зоны с переводом
этих электронов в зону проводимости,
т.е. энергия фотонов идет на отрыв
электрона от конкретного атома
полупроводника в кристаллической
решетке. Этот процесс называется эффектом
собственной фотопроводимости (рис. 2.1,
а).
Возможно
примесное поглощение, при котором под
действием света электроны могут
переходить с примесных донорных уровней
в зону проводимости (рис.2.1,б) или из
валентной зоны на уровни акцепторной
примеси (рис.2.1,в). В первом случае
возникает электронная (рис. 2.1, б),
во втором – дырочная (рис.
2.1, в)
фотопроводимость.
Фотопроводимость, возникающая в
результате двух последних процессов,
называется
примесной.
а б в
Рис.
2.1. Фотопроводимость полупроводников
и диэлектриков: cобственная
(а)
и примесная (б)
и (в)
Для
возникновения фотопроводимости
необходимо, чтобы энергия фотона
превышала либо ширину запрещенной зоны
(собственная фотопроводимость) или
энергетическое расстояние между одной
из зон и примесным уровнем ЕД,
ЕА
(примесная фотопроводимость). В
общем случае концентрация примесных
атомов существенно меньше концентрации
основных атомов, и они в основном
ионизованы уже при относительно низких
температурах. В этом случае собственная
фотопроводимость будет существенно
выше примесной и основная доля
фотоносителей – это собственные
фотоносители.
На
фоторезистивном эффекте основано
действие так называемых фотосопротивлений.
Фотосопротивление состоит из следующих
элементов (рис. 2.2): изолирующая подложка
1, на которую наносится тонкий слой
полупроводника 2 (такие слои получают
испарением в вакууме или химическим
осаждением) и металлические электроды
3, к которым подсоединяются провода для
включения в цепь. Для предохранения от
влияния воздуха фоточувствительная
поверхность фотосопротивления покрывается
тонкой пленкой лака. Лаковая пленка
должна обладать прозрачностью в той
области спектра, в которой работает
фотосопротивление.
Количество
образующихся носителей тока пропорционально
падающему световому потоку. Поэтому
фотосопротивления применяются для
целей фотометрии. Первым полупроводником,
нашедшим применение для этих целей, был
селен. В последнее время для видимой
части спектра стали широко применяться
фотосопротивления из CdS.
Фотосопротивления из полупроводников
PbS,
PbSe,
PbTe
и
InSb
используются в качестве детекторов
инфракрасного излучения. По чувствительности
они намного превосходят термоэлектрические
болометры, однако она существенно
зависит от длины волны падающего
излучения (этого нет для болометров)
Фотосопротивление
имеет ряд и других достоинств: малые
габариты, сравнительная простата
изготовления, высокие фотоэлектрические
свойства, практически неограниченные
сроки работы.
Рис.
2.2. Устройство фотосопротивления и схема
его включения
Работа
фотодиода основана на фотогальваническом
эффекте, фоточувствительный элемент
которого имеет структуру полупроводникового
диода. Упрощенная структура фотодиода
на основе р-n
перехода
изображена на рис. 2.3, а.
Пусть излучение воздействует в
направлении, перпендикулярном плоскости
р-n
перехода.
В результате поглощения фотонов с
энергией, большей, чем ширина запрещенной
зоны, в n—
слое полупроводника возникают
неравновесные электронно-дырочные пары
(фотоносители).
Фотоносители
диффундируют в глубь n-области.
Ширина n-области
W
такова, что основная доля созданных
излучением фотоносителей не успевает
рекомбинировать в n-области
и доходит до границы р-n
перехода
(x
= W).
Электроны и дырки разделяются электрическим
полем р-n
перехода
напряженностью Е0
, при этом дырки переходят в р-область,
а электроны не могу преодолеть поле
перехода и скапливаются у границы р-n
перехода
в n-области.
Таким образом, ток фотоносителей через
р-n
перехода
обусловлен дрейфом неосновных носителей
– дырок.
Качество
фотодиода определяется прежде всего
эффективностью управления фототоком
с помощью излучения. Именно оптическое
управление током фотодиода определяет
особенности его режимов работы. Сравним
с этих позиций принципы действия обычного
(выпрямительного) диода и фотодиода.
В
равновесном состоянии, когда поток
излучения отсутствует (Ф
= 0), зонные диаграммы диода и фотодиода
полностью совпадают. При этом уровень
Ферми одинаков для обеих областей и
диффузионная составляющая тока через
р-n
переход
– тока основных носителей – равна
дрейфовой составляющей тока неосновных
носителе (рис. 2.3, б).
В обычном диоде равновесие в структуре
нарушается при приложении к р-n
переходу
прямого напряжения (плюс к р-области,
минус к n-области)
– внутренний потенциальный барьер
снижается.
|
а |
б |
|
в |
+
n Ux – г |
Рис.
2.3. Структура фотодиода (а),
р-n
переход
в равновесном
состоянии (б),
р-n
переход
при воздействии излучения (в)
и конструкция солнечного элемента (г)
Равновесие
в потоках носителей через переход
нарушается в пользу диффузионной
составляющей тока, которая при достаточно
большом прямом напряжении определяет
значение тока через р-n
переход
в выпрямительном диоде является
фактически паразитной и должна быть
минимально возможной.
В
фотодиоде р-n
переход
разделяют созданные излучением
фотоносители (рис. 2.3, в).
Это приводит к снижению потенциального
внутреннего барьера в фотодиоде
(аналогично приложению прямого напряжения
в обычном диоде). Уровни Ферми в структуре
по обе стороны от р-n
перехода
уже не совпадают, а смещаются относительно
друг друга. Важно подчеркнуть, что в
фотодиоде равновесие под действием
излучения нарушается в «пользу» дрейфовой
составляющей тока через р-n
переход,
т.е. для эффективного управления током
с помощью излечения диффузионную
составляющую в фотодиоде необходимо
подавлять. В фотодиоде она – паразитная
составляющая тока через р-n
переход.
Дрейфовый
поток фотоносителей (дырок и электронов)
образует фоток Iф,
при этом дырки «заряжают»
р-область
положительно относительно n-области,
а электроны — n-область
отрицательно по отношению к р-области.
Возникшая таким образом разность
потенциалов, называемая фото-ЭДС Еф,
снижает внутренний потенциальный
барьер до значения ∆Е
(рис. 2.3, в).
Накопление
фотоносителей в соответствующих областях
имеет ограничение: одновременно с
накоплением (дырок в р-области
и электронов n-области)
происходит понижение потенциального
барьера Е0
на значение возникшей фото-ЭДС Еф.
очевидно, что Еф
должна быть меньше Е0,
так как разделение фотоносителей
возможно только при наличии некоторого
потенциального барьера ∆Е.
Уменьшение высоты потенциального
барьера и соответственно напряженности
электрического поля в р-n
переходе
ухудшает «разделительные свойства»
р-n
перехода.
Кроме
составляющей фото-ЭДС, которая возникает
из-за разделения носителей заряда полем
р-n
перехода
или другого потенциального барьера и
которая является основной, могут быть
и другие составляющие. Одна из них –
составляющая, которая называется
фото-ЭДС Дембера.
В
поверхностном слое освещаемого
полупроводника возникают фотоносители
– дополнительные дырки и электроны.
Коэффициент диффузии электронов больше
коэффициента диффузии дырок. Поэтому
при диффузии из места генерации
фотоносителей электроны опережают
дырки, происходит некоторое разделение
зарядов – поверхность полупроводника
приобретает положительный заряд по
отношению к объему. Возникает дополнительная
составляющая фото-ЭДС. Кроме того, при
наличии на поверхности ловушек захвата
носителей одного знака (только дырок
или только электронов) возникает
составляющая фото-ЭДС как итог диффузии
в глубь полупроводника носителей заряда
другого знака.
Для
обеспечения высокой чувствительности
к излучению необходимо, чтобы в фотодиоде
диффузионная составляющая тока была
минимальной. Поэтому фотодиод работает
или вообще без внешнего напряжения
(фотогальванический режим), или при
обратном внешнем напряжении (фотодиодный
режим).
На
описанном принципе работают солнечные
элементы, преобразующие энергию
солнечного света в электрическую
энергию. Данное устройство представляет
собой фотодиод с р-n—переходом
большой площади, способный преобразовывать
энергию падающего солнечного излучения
в энергию электрического тока с КПД,
достигающим 20%. Получать энергию
традиционными способами дешевле, чем
из солнечного излучения при таком КПД,
однако следует ожидать, что в ближайшее
время эта разница стоимостей будет
сокращаться.
Чаще
всего для изготовления солнечных
элементов используют кремний, а также
селен, арсенид
GaAs
и сернистый идий InS.
Конструкция солнечного элемента
приведена на рис. 2.3, г.
Полупроводниковые
фотоэлементы характеризуются не строгой
линейностью зависимости величины
электрического сигнала от освещения.
Содержание:
Фотоэффект:
Рассмотрим фотоэффект с точки зрения классической электродинамики.
На основе волновой теории света можно предположить, что:
- – свет любой длины волны должен вырывать электроны из металла;
- – на вырывание электрона из металла требуется определенное время;
- – число вырванных электронов и их энергия должны быть пропорциональны интенсивности света.
Александр Григорьевич Столетов (1839–1896) – русский физик. Исследовал внешний фотоэффект, открыл первый закон фотоэффекта. Исследовал газовый разряд, критическое состояние, получил кривую намагничивания железа.
Современная установка для исследования фотоэффекта
Современная установка для изучения фотоэффекта представляет собой два электрода, помещенных в стеклянный баллон, из которого выкачан воздух (рис. 210). На один из электродов через кварцевое «окошко» падает свет. В отличие от обычного стекла кварц пропускает ультрафиолетовое излучение. На электроды подается напряжение, которое можно менять с помощью потенциометра R и измерять вольтметром V. К освещаемому электроду К − катоду подсоединяют отрицательный полюс батареи. Под действием света катод испускает электроны, которые направляются электрическим полем к аноду, создается электрический ток. Значение силы тока фиксируется миллиамперметром.
Законы фотоэффекта Столетова
Исследования, проведенные русским ученым А.Г. Столетовым и немецким ученым Ф. Ленардом, показали, что законы фотоэффекта не соответствуют классическим представлениям.
На рисунке 211 представлена вольтамперная характеристика, полученная в результате измерений при различных значениях напряжения между электродами.
Из графика следует, что:
1. Сила фототока не зависит от напряжения, если оно достигает некоторого значения
Максимальное значение силы тока 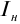
Сила тока насыщения − это максимальный заряд, переносимый фотоэлектронами за единицу времени:
где n − число фотоэлектронов, вылетающих с поверхности освещаемого металла за 1 с, е − заряд электрона.
2. Сила фототока отлична от нуля при нулевом значении напряжения.
3. Если изменить направление электрического поля, соединив катод с положительным полюсом источника тока, а анод − с отрицательным, то скорость фотоэлектронов уменьшится, об этом можно судить по показаниям миллиамперметра: сила тока уменьшается при увеличении отрицательного значения напряжения. При некотором значении напряжения 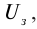
При известном значении 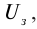
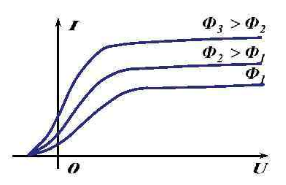
Исследование фотоэффекта при освещении катода световыми потоками равной частоты, но различной интенсивности дал результат, представленный вольтамперными характеристиками, изображенными на рисунке 212.
Сила фототока насыщения увеличивается с увеличением интенсивности падающего света.
Вспомните! Фотоэффект – это испускание электронов веществом под действием света или любого другого электромагнитного излучения.
Величина запирающего напряжения от интенсивности света не зависит, для всех потоков она имеет одно и то же значение.
Освещение катода светом одной и той же интенсивности, но разной частоты дало серию вольтамперных характеристик, представленных на рисунке 213. Как следует из графиков, величина задерживающего напряжения 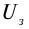
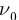
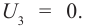
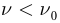
Минимальную частоту падающего света 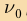
На основании экспериментальных данных Столетовым были сформулированы законы фотоэффекта:
- Сила фототока прямо пропорциональна интенсивности светового потока.
- Максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от интенсивности.
- Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света
(максимальная длина
), при которой возможен фотоэффект, если
то фотоэффект не происходит.
- Заказать решение задач по физике
Квантовая теория фотоэффекта
Теоретическое обоснование фотоэффекта было дано в 1905 г. А. Эйнштейном. Он предположил, что свет не только излучается квантами, как утверждал М. Планк, но и распространяется и поглощается порциями, представляет собой поток частиц − фотонов, энергия которых равна
Сам фотоэффект состоит в том, что световые частицы, сталкиваясь с электронами металла, передают им свою энергию и импульс и сами при этом исчезают. Если энергия квантов падающего света больше той работы, которую электрон должен совершить против сил притяжения к положительно заряженным частицам вещества, то электрон вылетает из металла. Становится понятным смысл красной границы фотоэффекта: для вырывания электрона из металла энергия квантов должна быть не меньше, чем 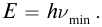
Это и есть формула Эйнштейна для фотоэффекта. Обычно ее пишут в виде:
Зависимость силы фототока от интенсивности света Эйнштейн объяснил следующим образом: число вылетающих в единицу времени электронов пропорционально интенсивности света, поскольку интенсивность определяется числом квантов, испускаемых источником в единицу времени. Мощная лампа испускает больше квантов, следовательно, число вырванных электронов светом такой лампы будет больше, чем светом менее мощной лампы.
Энергия вылетающих электронов зависит не от силы света лампы, а от того, какой частоты свет она испускает, от этого зависит энергия фотона и кинетическая энергия фотоэлектрона.
Фотоны, энергия, масса и импульс фотона
Фотон – это частица света. Он не делится на части: испускается, отражается, преломляется и поглощается целым квантом. У него нет массы покоя, неподвижных фотонов не существует.
Энергия фотона
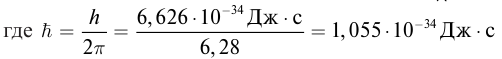
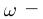
Масса фотона
Массу фотона определяют, исходя из закона о взаимосвязи массы и энергии:
Измерить массу фотона невозможно, ее следует рассматривать как полевую массу, обусловленную тем, что электромагнитное поле обладает энергией.
Импульс фотона
Фотон – частица света, следовательно, ее импульс равен:
Применение фотоэффекта в технике
Фотоэлементы:
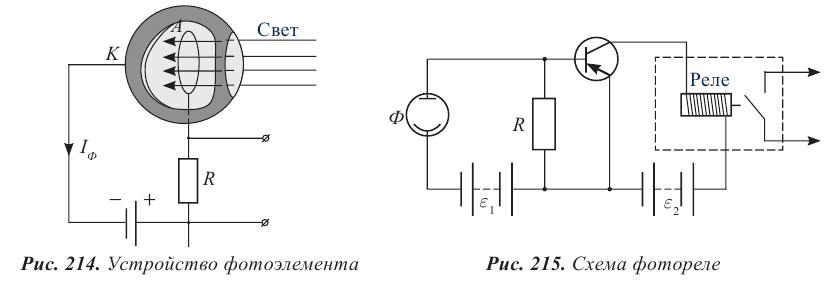
Приборы, принцип действия которых основан на явлении фотоэффекта, называют фотоэлементами. Устройство фотоэлемента изображено на рисунке 214. Внутренняя поверхность К (катод) стеклянного баллона, из которого выкачан воздух, покрыта светочувствительным слоем с небольшим прозрачным для света участком для доступа света внутрь баллона. В центре баллона находится металлическое кольцо А (анод). От электродов сделаны выводы для подключения фотоэлемента к электрической цепи. В качестве светочувствительного слоя обычно используют напыленные покрытия из щелочных металлов, имеющих малую работу выхода, т.е. чувствительных к видимому свету.
Фотоэлементы используют для автоматического управления электрическими цепями с помощью световых пучков.
Фотореле:
Фотоэлектрическое реле срабатывает при прерывании светового потока, падающего на фотоэлемент (рис. 215). Фотореле состоит из фотоэлемента Ф, усилителя фототока, в качестве которого используют полупроводниковый триод, и электромагнитного реле, включенного в цепь коллектора транзистора. Напряжение на фотоэлемент подают от источника тока 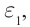
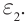
Когда фотоэлемент освещен, в его цепи, содержащей резистор R, идет слабый ток, потенциал базы транзистора выше потенциала эмиттера, и ток в коллекторной цепи транзистора отсутствует.
Если же поток света, падающий на фотоэлемент, прерывается, ток в его цепи сразу прекращается, переход эмиттер – база открывается для основных носителей, и через обмотку реле, включенного в цепь коллектора, пойдет ток. Реле срабатывает, и его контакты замыкают исполнительную цепь. Ее функциями могут быть остановка пресса, в зону действия которого попала рука человека, выдвигание преграды в турникете метро, автоматическое включение освещения на улицах.
Пример решения задачи
Определите постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой 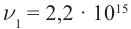
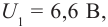
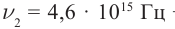
Дано:
U1 = 6,6 B
U2 = 16,5 B
h — ?
Решение: Запишем уравнение Эйнштейна для электрона, вырванного из металла светом с частотами 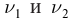
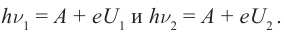
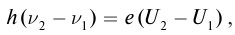
Выполним расчеты:
Ответ: h = 6,6 · 10–34 Дж · с.
- Оптические явления в природе по физике
- Оптические приборы в физике
- Оптика в физике
- Волновая оптика в физике
- Разложение белого света на цвета и образование цветов
- Давление света в физике
- Химическое действие света
- Корпускулярно-волновая природа света
VI. Квантовая физика
Тестирование онлайн
Фотоэлектрический эффект
Фотоэффектом называется явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передается электронам вещества. Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Уравнение Эйнштейна для фотоэффекта
На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии электрона:
Законы внешнего фотоэффекта
Столетовым Александром Григорьевичем (1839 — 1896) экспериментально были установлены законы внешнего фотоэффекта.
Первый закон фотоэффекта: фототок насыщения — максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, — прямо пропорционален интенсивности падающего излучения.
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля. Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового излучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.
Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.4k













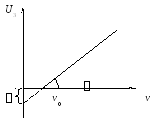












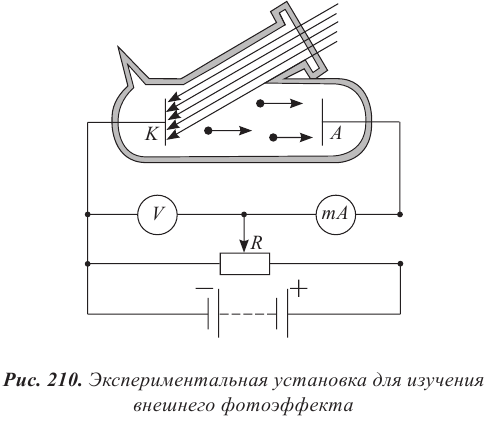
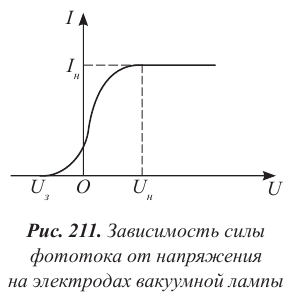
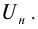
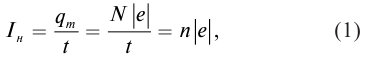
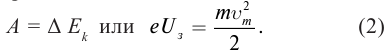
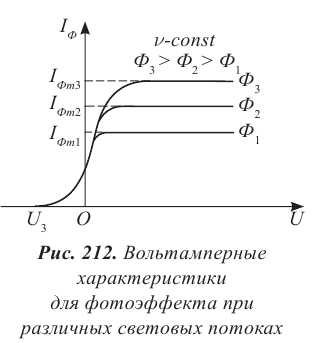
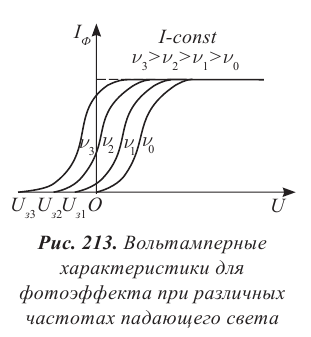
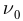 (максимальная длина
(максимальная длина 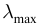 ), при которой возможен фотоэффект, если
), при которой возможен фотоэффект, если 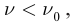 то фотоэффект не происходит.
то фотоэффект не происходит.