Решая совместно уравнения
(2),
(5), (9), получим выражение для полной
энергии электрона в атоме водорода:
| (10) |
Уравнение (10) определяет разрешенные
значения энергии электрона в атоме
водорода. Число n
принимает целые значения n =
1,2,3, …¥ .
Таким образом, энергия электрона в атоме
водорода может иметь не любые значения,
а только дискретный набор значений,
определяемых числом n,
или, как говорят, энергия электрона квантуется.
Подставляя значения
массы и
заряда электрона, постоянных 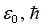
уравнение (10) и выражая энергию в электронвольтах
(эВ) (1эВ = 1,6.10-19
Дж), получим
формулу
| (11) |
Энергия основного состояния
(при n
= 1), равна E1=
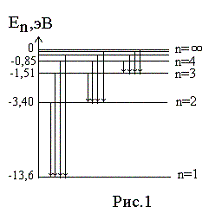
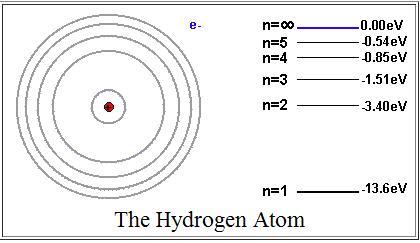
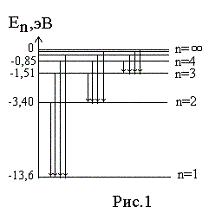
— 13,6 эВ. На рис. 1
приведена диаграмма энергетических
уровней электрона в атоме водорода, на
которой горизонтальными прямыми
отмечены разрешенные значения энергии.
Все состояния с величиной n= 1 … ¥ являются
связанными. При увеличении числа n
энергетические уровни сближаются все
больше и больше. При n ® ¥ E ®
0.
Энергетические состояния с энергией E ³
0
соответствуют тому, что электрон
становится свободным (не связанным с
ядром).
энергетических уровней (рис.1) позволяет
дать несколько важных определений.
Энергия возбуждения Евоз
– это энергия, которую необходимо
сообщить электрону, чтобы он из
основного состояния (n = 1)
перешел в возбужденное. Например, Евоз
= 10,2 эВ – энергия, необходимая для
перехода электрона в состояние,
соответствующее n =
2 (первое возбужденное состояние).
Энергия ионизации Еион
– энергия, необходимая для отрыва
электрона, находящегося в основном
состоянии (n
= 1), от ядра, т.е. для перевода электрона
на уровень с n = ¥ .
Для атома водорода энергия ионизации
равна 13,6 эВ.
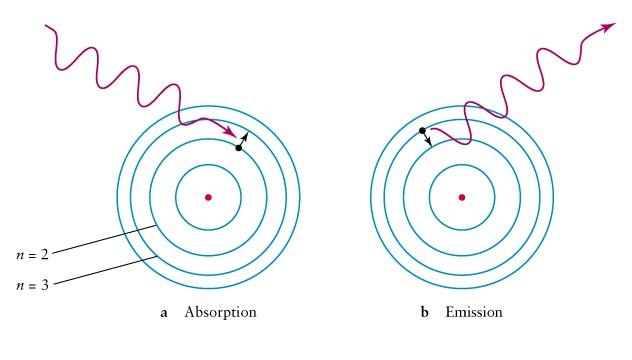
Согласно постулату Бора, при
переходе электрона из одного состояния (с
большей энергией) в другое (с меньшей
энергией) испускается фотон, частота
которого определяется формулой (8).
Учитывая выражение (10) для энергии
электрона в атоме, получим выражение для
частот испускаемых фотонов:
| (12) |
или, соответственно, для длин
волн испускаемых фотонов:
| (13) |
где Ry =
1,0974.107
м–1
– так называемая постоянная Ридберга.
Таким образом, модель атома Н.Бора
объясняет дискретный (линейчатый)
характер спектра испускания атома
водорода.
Спектральные
серии атома водорода
На диаграмме энергетических уровней (рис.1)
показаны возможные переходы электрона с
верхних уровней на нижние. При каждом
таком переходе излучается фотон с
частотой, определяемой формулой (12), или
длиной волны, определяемой формулой (13).
Переходы электрона с различных верхних
уровней на определенный нижний образуют
так называемые спектральные серии
атома водорода. Так, все переходы из
состояний с n
= 2, 3, 4, … в
состояние с n
= 1 образуют так называемую серию
Лаймана (ультрафиолетовое излучение).
Все длины волн этой серии лежат в
ультрафиолетовой области шкалы
электромагнитных волн. Переходы из
состояний с n
= 3, 4, 5, … в состояние с n
= 2 образуют серию Бальмера (видимый
свет). Переходы из состояний с n
= 4, 5, 6, … в состояние с n
= 3 образуют серию Пашена (инфракрасное
излучение). Длины волн всех остальных
серий (переходы на уровни с n
= 4, 5, и т.д.) лежат в инфракрасной области
спектра электромагнитного излучения.
Теория
Бора водородоподобных атомов.
Нильс
Бор создал теорию строения атома,
способную объяснить опыты Резерфорда
и спектр излучения паров водорода.
Спектр
характеризует распределение интенсивности
излучения по шкале частот (или по шкале
длин волн).

Постулаты
Бора.
1-й
постулат:
электрон
в атоме может двигаться только по
определенным стационарным орбитам,
находясь на которых, он не излучает и
не поглощает энергию. Момент импульса
электрона на этих орбитах кратен
постоянной Планка:
, (1)
me
– масса электрона,
— скорость электрона на орбите с номером
n,
rn
– радиус орбиты с номером n,
n
=1,2,3,….
Дж·с
– постоянная Планка.
2-й
постулат:
при
переходе электрона с одной стационарной
орбиты на другую излучается или
поглощается фотон, энергия которого
.
(2)
E
n1
и
E
n2
— энергия электрона в состоянии 1 и 2
(т.е. на орбитах 1 и 2),
— частота электромагнитных волн,
—
постоянная Планка.
Радиус
орбиты электрона в атоме водорода.
1-й
постулат Бора,
.
Выразим
скорость электрона:
.
(3)
Рассмотрим
круговые электронные орбиты. На электрон
с зарядом —e
со стороны ядра с зарядом +e
действует сила Кулона F,
сообщая электрону нормальное ускорение,
.
По
2-му закону Ньютона,
.
(4)
Сократим
и подставим скорость из (3):
.
Отсюда

Радиус
первой орбиты электрона (n
= 1), называется радиусом
Бора
,
=
0.53·10-10
м.
Радиус
орбиты электрона в атоме водорода
,
n
=1,2,3,…. – номер орбиты.
Энергия
электрона в атоме водорода.
Энергия
электрона представляет собой сумму
кинетической энергии
и
потенциальной
.
и
.
Потенциальная
энергия – это энергия электрона с
зарядом
в электрическом поле ядра. Из уравнения
(4) видно, что
.
Тогда
на n
–ой
орбите энергия электрона равна
=
=.
Т.е.
кинетическая энергия электрона равна
полной энергии, взятой со знаком «-».
Также
полную энергию можно записать через
потенциальную:
=
, или
.
Подставим
.
Тогда
=
.
Энергия
на первой орбите (на первом энергетическом
уровне) равна
=
= -13,6 эВ.
Величину
=
13,6 эВ = 2,18∙10-18
Дж
называют
энергией ионизации
(эта энергия необходима, чтобы перевести
электрон, находящийся на первом уровне,
в свободное состояние, т.е. чтобы
ионизовать атом). Окончательно, энергия
электрона на n
–ом
энергетическом уровне (на n
–ой
орбите) записывается как
=
.
Спектр излучения водорода.
Энергия
излучаемого или поглощаемого кванта:
.
Частота
,
длина волны,
— скорость света в вакууме.
=
+
=
,
=
.
=
—
формула Бальмера,
определяет
длины волн в спектре атома водорода.
=
1,1∙107
м-1
— постоянная Ридберга.
и
— номера энергетических состояний
(номера орбит) электрона.
Переходы
электрона с возбужденных энергетических
состояний на основной энергетический
уровень (
= 1) сопровождаются излучением в УФ
области
спектра (серия линий Лаймана),
переходы
на уровень с
= 2 приводят к линиям в
видимой области
(серия Бальмера),
переходы
на уровень с
= 3, 4, 5, … приводят излучению в ИК
области.
Теория
Бора не смогла объяснить строение
сложных атомов. Для объяснения поведения
микрочастиц была развита квантовая
механика.
Она
основана на том, что любая микрочастица,
наряду с корпускулярными, обладает
также волновыми свойствами (гипотеза
де Бройля).
Для
фотона, импульс
.
По
аналогии с фотоном, любую микрочастицу
можно рассматривать как волну с длиной
волны
,
—
длина волны де Бройля.
Гипотеза
де Бройля подтверждена экспериментально
наблюдением дифракции электронов, а
затем и протонов.
Принцип
неопределенностей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для описания положения электрона в электронной оболочке используют четыре квантовых числа. Здесь мы не будем углубляться в квантово-механические подробности и опишем только утилитарный смысл данных чисел. Набор, состоящий из четырёх квантовых чисел — это «адрес» электрона в электронной оболочке.
Главное квантовое число `n` — определяет полную энергию электрона на энергетическом уровне и показывает, из скольких энергетических уровней состоит электронная оболочка атома. Принимает целочисленные положительные значения от `1` до `oo`. В периодической таблице Д. И. Менделеева `n` равно номеру периода.
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n-1)`.
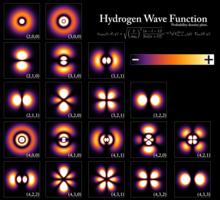
При `n=1`, `l` принимает только одно значение `0` (этому числовому значению соответствует буквенное `s`), следовательно, на первом энергетическом уровне только один подуровень — `s`. Орбиталь `s`-подуровня имеет сферическую форму (рис. 1).
При `n=2`, `l` принимает два значения: `0` `(s)` и `1` `(p)`. Энергетический уровень состоит из двух подуровней — `s` и `p`. Форма `p`-орбитали похожа на объёмную восьмёрку (рис. 1).
При `n=3`, `l` принимает уже три значения: `0` `(s)`; `1` `(p)` и `2` `(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещённых объёмных восьмёрок либо объёмной восьмерки с перемычкой (рис. 1).
При `n=4`, значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3` `(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения `-l` до `+l`, включая `0`.
При `l=0`, `m_l` принимает только одно значение — `0`. Следовательно, орбиталь, находящаяся на данном подуровне (`s`-подуровне), только одна. Мы уже знаем, что она имеет форму сферы с центром в начале координат.
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу (`p_x`, `p_y`, `p_z`).
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
При `l=3`, то есть на `f`-подуровне, орбиталей становится семь, так как `m_l` — принимает семь значений (от `−3` до `+3` через `0`). Орбитали являются более сложными объёмными структурами, и взаимное их расположение еще более сложно.
Спиновое квантовое число `m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Электронная ёмкость подуровня (максимальное количество электронов на подуровне) может быть рассчитана по формуле `2(2l+1)`, а уровня — по формуле `2n^2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n<=4`)
|
`n` |
`l` |
Обозначение орбитали |
`ml` |
Число орбиталей |
Число электронов на подуровне |
|
`1` |
`0` |
`1s` |
`0` |
`1` |
`2` |
|
`2` |
`0` `1` |
`2s` `2p` |
`0` `−1`; `0`; `+1` |
`1` `3` |
`2` `6` |
|
`3` |
`0` `1` `2` |
`3s` `3p` `3d` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` |
`1` `3` `5` |
`2` `6` `10` |
|
`4` |
`0` `1` `2` `3` |
`4s` `4p` `4d` `4f` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` `−3`; `−2`; `−1`; `0`; `+1`; `+2`; `+3` |
`1` `3` `5` `7` |
`2` `6` `10` `14` |
Химические свойства элементов и их соединений определяются электронным строением валентного уровня их атомов. Именно с участием электронов валентного уровня возникают химические связи между атомами и образуется соединение (вещество). Поэтому важно понимать правила заполнения электронных оболочек, строение валентного уровня и составлять электронную конфигурацию атомов элементов.
Energy levels for an electron in an atom: ground state and excited states. After absorbing energy, an electron may «jump» from the ground state to a higher energy excited state.
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.
In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom’s nucleus. The closest shell to the nucleus is called the «1 shell» (also called «K shell»), followed by the «2 shell» (or «L shell»), then the «3 shell» (or «M shell»), and so on farther and farther from the nucleus. The shells correspond with the principal quantum numbers (n = 1, 2, 3, 4 …) or are labeled alphabetically with letters used in the X-ray notation (K, L, M, N…).
Each shell can contain only a fixed number of electrons: The first shell can hold up to two electrons, the second shell can hold up to eight (2 + 6) electrons, the third shell can hold up to 18 (2 + 6 + 10) and so on. The general formula is that the nth shell can in principle hold up to 2n2 electrons.[1] Since electrons are electrically attracted to the nucleus, an atom’s electrons will generally occupy outer shells only if the more inner shells have already been completely filled by other electrons. However, this is not a strict requirement: atoms may have two or even three incomplete outer shells. (See Madelung rule for more details.) For an explanation of why electrons exist in these shells see electron configuration.[2]
If the potential energy is set to zero at infinite distance from the atomic nucleus or molecule, the usual convention, then bound electron states have negative potential energy.
If an atom, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher energy level, it is said to be excited, or any electrons that have higher energy than the ground state are excited. An energy level is regarded as degenerate if there is more than one measurable quantum mechanical state associated with it.
Explanation[edit]
Wavefunctions of a hydrogen atom, showing the probability of finding the electron in the space around the nucleus. Each stationary state defines a specific energy level of the atom.
Quantized energy levels result from the wave behavior of particles, which gives a relationship between a particle’s energy and its wavelength. For a confined particle such as an electron in an atom, the wave functions that have well defined energies have the form of a standing wave.[3] States having well-defined energies are called stationary states because they are the states that do not change in time. Informally, these states correspond to a whole number of wavelengths of the wavefunction along a closed path (a path that ends where it started), such as a circular orbit around an atom, where the number of wavelengths gives the type of atomic orbital (0 for s-orbitals, 1 for p-orbitals and so on). Elementary examples that show mathematically how energy levels come about are the particle in a box and the quantum harmonic oscillator.
Any superposition (linear combination) of energy states is also a quantum state, but such states change with time and do not have well-defined energies. A measurement of the energy results in the collapse of the wavefunction, which results in a new state that consists of just a single energy state. Measurement of the possible energy levels of an object is called spectroscopy.
History[edit]
The first evidence of quantization in atoms was the observation of spectral lines in light from the sun in the early 1800s by Joseph von Fraunhofer and William Hyde Wollaston. The notion of energy levels was proposed in 1913 by Danish physicist Niels Bohr in the Bohr theory of the atom. The modern quantum mechanical theory giving an explanation of these energy levels in terms of the Schrödinger equation was advanced by Erwin Schrödinger and Werner Heisenberg in 1926.
Atoms[edit]
Intrinsic energy levels[edit]
In the formulas for energy of electrons at various levels given below in an atom, the zero point for energy is set when the electron in question has completely left the atom, i.e. when the electron’s principal quantum number n = ∞. When the electron is bound to the atom in any closer value of n, the electron’s energy is lower and is considered negative.
Orbital state energy level: atom/ion with nucleus + one electron[edit]
Assume there is one electron in a given atomic orbital in a hydrogen-like atom (ion). The energy of its state is mainly determined by the electrostatic interaction of the (negative) electron with the (positive) nucleus. The energy levels of an electron around a nucleus are given by :
(typically between 1 eV and 103 eV),
where R∞ is the Rydberg constant, Z is the atomic number, n is the principal quantum number, h is Planck’s constant, and c is the speed of light. For hydrogen-like atoms (ions) only, the Rydberg levels depend only on the principal quantum number n.
This equation is obtained from combining the Rydberg formula for any hydrogen-like element (shown below) with E = h ν = h c / λ assuming that the principal quantum number n above = n1 in the Rydberg formula and n2 = ∞ (principal quantum number of the energy level the electron descends from, when emitting a photon). The Rydberg formula was derived from empirical spectroscopic emission data.
An equivalent formula can be derived quantum mechanically from the time-independent Schrödinger equation with a kinetic energy Hamiltonian operator using a wave function as an eigenfunction to obtain the energy levels as eigenvalues, but the Rydberg constant would be replaced by other fundamental physics constants.
Electron-electron interactions in atoms[edit]
If there is more than one electron around the atom, electron-electron-interactions raise the energy level. These interactions are often neglected if the spatial overlap of the electron wavefunctions is low.
For multi-electron atoms, interactions between electrons cause the preceding equation to be no longer accurate as stated simply with Z as the atomic number. A simple (though not complete) way to understand this is as a shielding effect, where the outer electrons see an effective nucleus of reduced charge, since the inner electrons are bound tightly to the nucleus and partially cancel its charge. This leads to an approximate correction where Z is substituted with an effective nuclear charge symbolized as Zeff that depends strongly on the principal quantum number.
In such cases, the orbital types (determined by the azimuthal quantum number ℓ) as well as their levels within the molecule affect Zeff and therefore also affect the various atomic electron energy levels. The Aufbau principle of filling an atom with electrons for an electron configuration takes these differing energy levels into account. For filling an atom with electrons in the ground state, the lowest energy levels are filled first and consistent with the Pauli exclusion principle, the Aufbau principle, and Hund’s rule.
Fine structure splitting[edit]
Fine structure arises from relativistic kinetic energy corrections, spin–orbit coupling (an electrodynamic interaction between the electron’s spin and motion and the nucleus’s electric field) and the Darwin term (contact term interaction of s shell[which?] electrons inside the nucleus). These affect the levels by a typical order of magnitude of 10−3 eV.
Hyperfine structure[edit]
This even finer structure is due to electron–nucleus spin–spin interaction, resulting in a typical change in the energy levels by a typical order of magnitude of 10−4 eV.
Energy levels due to external fields[edit]
Zeeman effect[edit]
There is an interaction energy associated with the magnetic dipole moment, μL, arising from the electronic orbital angular momentum, L, given by
with
.
Additionally taking into account the magnetic momentum arising from the electron spin.
Due to relativistic effects (Dirac equation), there is a magnetic momentum, μS, arising from the electron spin
,
with gS the electron-spin g-factor (about 2), resulting in a total magnetic moment, μ,
.
The interaction energy therefore becomes
.
Stark effect[edit]
Molecules[edit]
Chemical bonds between atoms in a molecule form because they make the situation more stable for the involved atoms, which generally means the sum energy level for the involved atoms in the molecule is lower than if the atoms were not so bonded. As separate atoms approach each other to covalently bond, their orbitals affect each other’s energy levels to form bonding and antibonding molecular orbitals. The energy level of the bonding orbitals is lower, and the energy level of the antibonding orbitals is higher. For the bond in the molecule to be stable, the covalent bonding electrons occupy the lower energy bonding orbital, which may be signified by such symbols as σ or π depending on the situation. Corresponding anti-bonding orbitals can be signified by adding an asterisk to get σ* or π* orbitals. A non-bonding orbital in a molecule is an orbital with electrons in outer shells which do not participate in bonding and its energy level is the same as that of the constituent atom. Such orbitals can be designated as n orbitals. The electrons in an n orbital are typically lone pairs.
[4]
In polyatomic molecules, different vibrational and rotational energy levels are also involved.
Roughly speaking, a molecular energy state, i.e. an eigenstate of the molecular Hamiltonian, is the sum of the electronic, vibrational, rotational, nuclear, and translational components, such that:
where Eelectronic is an eigenvalue of the electronic molecular Hamiltonian (the value of the potential energy surface) at the equilibrium geometry of the molecule.
The molecular energy levels are labelled by the molecular term symbols. The specific energies of these components vary with the specific energy state and the substance.
Energy level diagrams[edit]
There are various types of energy level diagrams for bonds between atoms in a molecule.
- Examples
- Molecular orbital diagrams, Jablonski diagrams, and Franck–Condon diagrams.
Energy level transitions[edit]
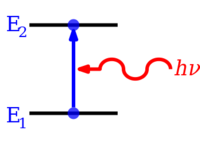
An increase in energy level from E1 to E2 resulting from absorption of a photon represented by the red squiggly arrow, and whose energy is h ν
A decrease in energy level from E2 to E1 resulting in emission of a photon represented by the red squiggly arrow, and whose energy is h ν
Electrons in atoms and molecules can change (make transitions in) energy levels by emitting or absorbing a photon (of electromagnetic radiation), whose energy must be exactly equal to the energy difference between the two levels.
Electrons can also be completely removed from a chemical species such as an atom, molecule, or ion. Complete removal of an electron from an atom can be a form of ionization, which is effectively moving the electron out to an orbital with an infinite principal quantum number, in effect so far away so as to have practically no more effect on the remaining atom (ion). For various types of atoms, there are 1st, 2nd, 3rd, etc. ionization energies for removing the 1st, then the 2nd, then the 3rd, etc. of the highest energy electrons, respectively, from the atom originally in the ground state. Energy in corresponding opposite quantities can also be released, sometimes in the form of photon energy, when electrons are added to positively charged ions or sometimes atoms. Molecules can also undergo transitions in their vibrational or rotational energy levels. Energy level transitions can also be nonradiative, meaning emission or absorption of a photon is not involved.
If an atom, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher energy level, it is said to be excited, or any electrons that have higher energy than the ground state are excited. Such a species can be excited to a higher energy level by absorbing a photon whose energy is equal to the energy difference between the levels. Conversely, an excited species can go to a lower energy level by spontaneously emitting a photon equal to the energy difference. A photon’s energy is equal to Planck’s constant (h) times its frequency (f) and thus is proportional to its frequency, or inversely to its wavelength (λ).[4]
- ΔE = h f = h c / λ,
since c, the speed of light, equals to f λ[4]
Correspondingly, many kinds of spectroscopy are based on detecting the frequency or wavelength of the emitted or absorbed photons to provide information on the material analyzed, including information on the energy levels and electronic structure of materials obtained by analyzing the spectrum.
An asterisk is commonly used to designate an excited state. An electron transition in a molecule’s bond from a ground state to an excited state may have a designation such as σ → σ*, π → π*, or n → π* meaning excitation of an electron from a σ bonding to a σ antibonding orbital, from a π bonding to a π antibonding orbital, or from an n non-bonding to a π antibonding orbital.[4][5] Reverse electron transitions for all these types of excited molecules are also possible to return to their ground states, which can be designated as σ* → σ, π* → π, or π* → n.
A transition in an energy level of an electron in a molecule may be combined with a vibrational transition and called a vibronic transition. A vibrational and rotational transition may be combined by rovibrational coupling. In rovibronic coupling, electron transitions are simultaneously combined with both vibrational and rotational transitions. Photons involved in transitions may have energy of various ranges in the electromagnetic spectrum, such as X-ray, ultraviolet, visible light, infrared, or microwave radiation, depending on the type of transition. In a very general way, energy level differences between electronic states are larger, differences between vibrational levels are intermediate, and differences between rotational levels are smaller, although there can be overlap. Translational energy levels are practically continuous and can be calculated as kinetic energy using classical mechanics.
Higher temperature causes fluid atoms and molecules to move faster increasing their translational energy, and thermally excites molecules to higher average amplitudes of vibrational and rotational modes (excites the molecules to higher internal energy levels). This means that as temperature rises, translational, vibrational, and rotational contributions to molecular heat capacity let molecules absorb heat and hold more internal energy. Conduction of heat typically occurs as molecules or atoms collide transferring the heat between each other. At even higher temperatures, electrons can be thermally excited to higher energy orbitals in atoms or molecules. A subsequent drop of an electron to a lower energy level can release a photon, causing a possibly colored glow.
An electron farther from the nucleus has higher potential energy than an electron closer to the nucleus, thus it becomes less bound to the nucleus, since its potential energy is negative and inversely dependent on its distance from the nucleus.[6]
Crystalline materials[edit]
Crystalline solids are found to have energy bands, instead of or in addition to energy levels. Electrons can take on any energy within an unfilled band. At first this appears to be an exception to the requirement for energy levels. However, as shown in band theory, energy bands are actually made up of many discrete energy levels which are too close together to resolve. Within a band the number of levels is of the order of the number of atoms in the crystal, so although electrons are actually restricted to these energies, they appear to be able to take on a continuum of values. The important energy levels in a crystal are the top of the valence band, the bottom of the conduction band, the Fermi level, the vacuum level, and the energy levels of any defect states in the crystal.
See also[edit]
- Perturbation theory (quantum mechanics)
- Computational chemistry
References[edit]
- ^ Re: Why do electron shells have set limits ? madsci.org, 17 March 1999, Dan Berger, Faculty Chemistry/Science, Bluffton College
- ^ Electron Subshells. Corrosion Source. Retrieved on 1 December 2011.
- ^ Tipler, Paul A.; Mosca, Gene (2004). Physics for Scientists and Engineers, 5th Ed. Vol. 2. W. H. Freeman and Co. p. 1129. ISBN 0716708108.
- ^ a b c d UV-Visible Absorption Spectra
- ^ Theory of Ultraviolet-Visible (UV-Vis) Spectroscopy
- ^ «Electron Density and Potential Energy». Archived from the original on 2010-07-18. Retrieved 2010-10-07.
Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
Планетарная модель атома Резерфорда позволила объяснить результаты опытов по рассеянию α-частиц вещества, но она не способна объяснить факт существования атома и его устойчивость.
В соответствии с планетарной моделью электроны атома должны двигаться вокруг неподвижного ядра. Двигаясь вокруг ядра с центростремительным ускорением под действием силы притяжения к ядру, электрон должен, как и всякий ускоренно движущийся электрический заряд, излучать электромагнитные волны с частотой, равной частоте обращения электрона вокруг ядра.
Энергия электрона в атоме должна при этом непрерывно уменьшаться за счёт излучения. Сам электрон должен с каждым оборотом приближаться по спирали к ядру и упасть на него под действием электрической силы притяжения. При этом атом потеряет всю электронную оболочку, а также присущие ему физические и химические свойства. Кроме того, атом должен потерять спектр излучения частоты, то есть атом должен давать излучение с непрерывным (сплошным) спектром частот.
Эти результаты, полученные с помощью классической механики и электродинамики, находятся в резком противоречии с опытом, который показывает, что
- Атомы являются весьма устойчивыми системами и в невозбуждённом состоянии могут существовать неограниченно долго, не излучая при этом электромагнитные волны
- Спектр излучения атома является линейчатым (дискретным) – образованным из отдельных линий (от латинского discretus – прерывистый, состоящий из отдельных значений)
Всё это свидетельствует о том, что законы классический физики применить к электронам в атомах нельзя, поэтому необходимы новые представления о механизме излучения и поглощения атомами электромагнитных волн. В основе современной теории атома лежитквантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов), а также связь величин, которые характеризуют частицы и системы, с физическими величинами, измеряемыми опытным путём.
В 1913 году датский физик Нильс Бор (1885 – 1962) ввёл идеи квантовой теории в ядерную модель атома Резерфорда и разработал теорию атома водорода, которая подтвердилась всеми известными тогда опытами. Бор сформулировал в виде постулатов основные положения новой теории, которые налагали лишь некоторые ограничения на допускаемые классической физикой движения. Однако последовательной теории атома Бор не дал. Впоследствии теория Бора была включена как частный случай в квантовую механику. В основе теории Бора лежат два постулата.
Первый постулат Бора: постулат стационарных состояний
Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия En. В стационарном состоянии атом не излучает.
Второй постулат Бора: правило частотe
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний:
hvkn = Ek — En
Частота излучения равна:
vkn = (Ek — En) / h = (Ek / h) — (En / h)
Или, длина волны излучения λ равна:
1 / λkn = (1 / hc) (Ek — En)
Где h – постоянная Планка, с – скорость света в вакууме.
Если Ek > En, то происходит излучение фотона, если Ek < En, то происходит поглощение фотона, при котором атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией. Таким образом, для каждого атома имеется ряд строго определённых дискретных значений энергии, которыми он может обладать. Физические величины, например энергия и импульс, которые могут принимать лишь дискретные (квантовые) значения, носят название квантованные физические величины (квантование физических величин). При этом энергетические уровни атома – это возможные значения энергии атома.
Правило квантования орбит позволяет определить радиусы стационарных орбит:
mvnrn = nh’
где n = 1, 2, 3…, m – масса электрона, rn – радиус n-ой орбиты, vn – скорость электрона на этой орбите.
Число n – положительное число, которое называется главное квантовое число.
Величина (mvn)rn – момент импульса электрона.
h’ – это величина, которая равна:
h’ = h/2π = 1,05445887•10-34 Дж•с
где h – постоянная Планка.
Главное квантовое число указывает номер орбиты, по которой может обращаться электрон.
Свои постулаты Н.Бор применил для построения теории простейшей атомной системы – атома водорода, состоящего из ядра – протона, и одного электрона. Эта теория также применима для водородоподобных ионов, то есть атомов с зарядом ядра Ze и потерявших все электроны, кроме одного (например, Li2+, Be3+ и т.п.). В предположении, что электрон движется по круговой орбите, постулаты Бора позволяют найти радиусы rn стационарных, возможных орбит электрона. На электрон действует кулоновская сила:
Fk = (1 / 4πε0) (ε2 / rn2)
Где е – модуль заряда электрона, равный заряду ядра, ε0 = 8,85418782 * 10-12 Ф/м – электрическая постоянная в единицах СИ.
Кулоновская сила сообщает электрону на орбите центростремительное ускорение:
aцс = (vn2) / rn
Согласно второму закону Ньютона:
Fk = maцс
Поэтому
(mvn2) / rn = e2 / (4πε0rn2)
Или
mvn2rn = e2 / (4πε0)
Используя правило квантования орбит mvnrn = nh’, можно получить выражения для возможных радиусов орбит. Исключая скорость vn из предыдущего выражения, получим:
rn = 4πε0n2h’ / me2 (так как h’ = h / 2π)
Таким образом, радиусы орбит электрона в атоме водорода прямо пропорциональны квадратам главного квантового числа n.
Наименьший радиус орбит при n = 1, то есть радиус первой орбиты в атоме водорода равен:
r1 = 4πε0h’ / me2 = 0,528 * 10-10 м = 0,528 Å
Радиус первой орбиты в атоме водорода носит название первый Боровский радиус и служит единицей длины в атомной физике.
Полная энергия Е электрона в атоме водорода, согласно механике Ньютона, равна сумме кинетической энергии Еk и потенциальной энергии П взаимодействия электрона с ядром:
E = Еk — П = (mvn2 / 2) — (e2 / 4πε0rn)
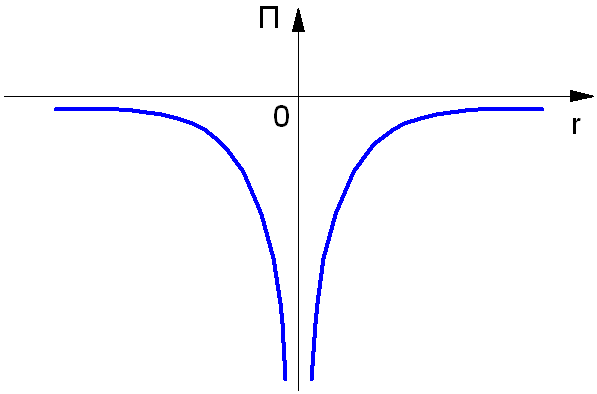
Потенциальная энергия электрона в атоме отрицательна:
П = — (e2 / 4πε0rn)
Так как нулевой уровень отсчёта берётся на бесконечности (рис. 1.3), а по мере приближения электрона к ядру его потенциальная энергия уменьшается. Взаимодействующие частицы – ядро и электрон – имеют заряды противоположных знаков.
Рис. 1.3. Потенциальная энергия электрона в атоме.
Подставляя значение скорости
vn2 = — e2 / 4πε0mrn
в выражение полной энергии, получим:
E = (m / 2) (e2 / 4πε0mrn) — (e2 / 4πε0rn)
Подставляя в эту формулу выражение для радиусов орбит, получим энергетические уровни электрона в атоме водорода (значения энергий стационарных состояний атома):
En = -(1 /(4πε0)2) me4 / 2h’2n2 = — (me4 / 8h2ε02) * (1 / n2), n = 1,2,3…
Энергия Еn электрона в атоме водорода зависит от главного квантового числа n, которое определяет энергетические уровни электрона в атоме водорода.
Основное энергетическое состояние атома (нормальное состояние атома) – это энергетический уровень при n = 1.
Значение энергии, соответствующее первому (низшему) энергетическому уровню в атоме водорода равно:
E1 = -(1 /(4πε0)2) me4 / 2h’2λ = -2,485 * 10-19 Дж = -13,53 эВ
В этом состоянии атом может находиться сколько угодно долго. Для того чтобы ионизировать атом водорода, ему нужно сообщить энергию 13,53 эВ, которая называется энергия ионизации.
Энергетические уровни при n > 1 – это возбуждённые энергетические состояния (возбуждённые состояния атома). Возбуждённое состояние атома является менее устойчивым, чем основное состояние. Время жизни атома в этом состоянии имеет порядок 10-8 секунд. За это время электрон успевает совершить около ста миллионов оборотов вокруг ядра.
При переходе электрона с удалённой от ядра стационарной k-орбиты на ближайшую n-ую орбиту атом излучает фотон, энергия которогоhvnk согласно второму постулату Бора определяется:
hvkn = Ek — En = -(1 / (4πε0)2) * (me4 / 2h’2) * [(1 / n2) — (1 / k2)] = (me4 / 8h2ε02) * [(1 / n2) — (1 / k2)]
Частота излучения атома водорода:
vkn = (1 / (4πε0)2) * (me4 / h’3) * [(1 / n2) — (1 / k2)] = R[(1 / n2) — (1 / k2)]
Где
R = (me4 / (4πε0)2) * 4πh’3) = (me4 / 8h3ε02) = 3,288 * 1015 c-1— постоянная Ридберга
Постоянная Ридберга определяется через постоянную Планка, массу и заряд электрона.
Длина волны излучения определяется соотношением:
1 / λnk = vnk / c = (me4 / 8ε02h3c) * [(1 / n2) — (1 / k2)] = Rc[(1 / n2) — (1 / k2)]
Где
Rc = R / c = 1,0974 * 107 м-1 — также постоянная Ридберга
с = 3*108 м/с – скорость света в вакууме.
Теоретическое значение R совпадает с экспериментальным значением, полученным из спектроскопических измерений.
Энергия обычно измеряется в электронвольтах (эВ). Электронвольт– это значение энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В:
1 эВ = 1,6 * 10-19 Кл * 1В = 1,6 * 10-19 Дж