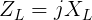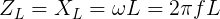Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
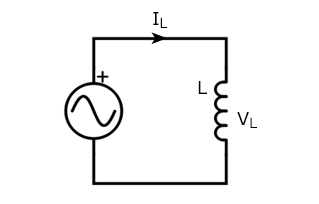
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС,
равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения,
что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС,
равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая
пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток 
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока 
сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать 
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома,
где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда –
накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное.
Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю.
Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току,
обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее
уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt)
запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений 
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчитать реактивное сопротивление ёмкости или индуктивности:
Реактивное сопротивление ёмкости
XC = 1 /(2πƒC)
Реактивное сопротивление индуктивности
XL = 2πƒL
Расчитать ёмкость и индуктивность от сопротивления:
Расчёт ёмкости: C = 1 /(2πƒXC)
Расчёт индуктивности: L = XL /(2πƒ)
Похожие страницы с расчётами:
Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.
Физика
– какая ёмкость слова,
Физика
для нас не просто звук,
Физика
– опора и основа,
Всех
без исключения наук!
Задача
1.
В цепи переменного тока с частотой 50 Гц при напряжении 220 В возникает сила
тока 4 А. Известно, что в эту цепь включена катушка с ничтожно малым активным
сопротивлением. Какова индуктивность катушки?
|
ДАНО: |
РЕШЕНИЕ Индуктивное сопротивление Циклическую частоту можно Запишем закон Ома для Приравняем две последних |
|
|
Ответ:
175 мГн.
Задача
2.
. При увеличении частоты от 50 Гц до 60 Гц, ёмкостное сопротивление конденсатора
с постоянной ёмкостью уменьшилось на 10 Ом. Найдите электроёмкость
конденсатора.
|
ДАНО: |
РЕШЕНИЕ Ёмкостное сопротивление Циклическую частоту можно Тогда ёмкостное Применим данную формулу для Изменение ёмкостного Тогда электроёмкость |
|
|
Ответ:
53 мкФ.
Задача
3.
Известно, что через катушку, включенную в цепь переменного тока с частотой 200 Гц,
проходит ток не более 3 А. Найдите напряжение на катушке, в момент времени
t = 0,2 мс,
если в начальный момент времени оно максимально. Индуктивность катушки равна 5 мГн.
|
ДАНО: |
СИ |
РЕШЕНИЕ Из закона Ома для участка цепи следует Индуктивное сопротивление определяется по формуле Амплитудное напряжение рассчитывается по выражению Запишем уравнение гармонических колебаний напряжения Циклическая частота равна Тогда уравнение гармонических колебаний напряжения будет Тогда в момент времени t = 0,2 мс напряжение будет равно |
|
|
Ответ:
18,3 В.
Задача
4.
Докажите, что если частота переменного тока равна собственной частоте, то по
катушке индуктивности и конденсатору будет протекать одинаковый ток, а также на
катушке и на конденсаторе будет одинаковое напряжение.
|
ДАНО: |
РЕШЕНИЕ Собственная циклическая По определению, собственная Таким образом, имеется два Рассмотрим параллельное Из закона Ома для участка Индуктивное сопротивление Ёмкостное сопротивление С учётом двух последних Теперь рассмотрим При последовательном Из закона Ома для участка Индуктивное сопротивление Ёмкостное сопротивление С учётом двух последних |
|
Доказать |
Ответ:
доказано.
Виды сопротивления и их особенности
Если в цепи постоянное напряжение, то, зная её сопротивление, можно узнать силу тока при помощи закона Ома. Он говорит о том, что сила тока пропорциональна напряжению, которое является его причиной. Коэффициент пропорциональности представляет обычное сопротивление. Его принято называть активным.
Если напряжение является постоянным, то сопротивление будет только активным. Его значение определяет, сколько энергии электрического поля преобразовано в тепло, то есть, безвозвратно утрачено. Поэтому при работе с кабелями СИП-3 1×50, СИП-2 3×70 и другими нужно помнить, что потери энергии из-за активного сопротивления могут быть значительными.

Более распространено использование переменного тока. Он возникает под воздействием напряжения, циклически изменяющегося по синусоидальному закону. Такой ток порождает реактивное сопротивление, которое дополняет действие активного. Существует две разновидности реактивного сопротивления различной природы — на основе индуктивности или емкости. Их отличительной особенностью является то, что они способствуют не трате электроэнергии, а преобразованию её в другую форму.
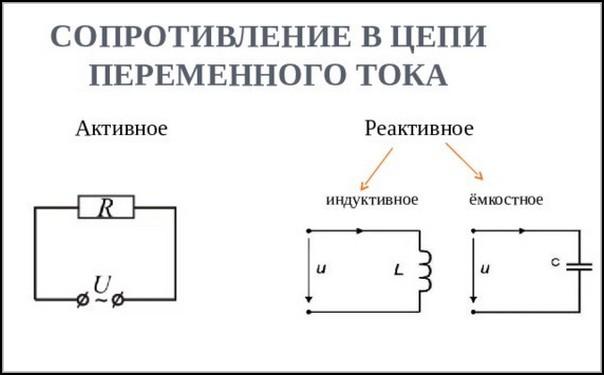
Нужно учитывать, что применение различных видов кабелей связано не только с наличием активного сопротивления, но и реактивного. Например, кабели СИП-3 1×50, СИП-2 3×70, АС-95 могут использоваться в электросетях и с активным, и индуктивным, и емкостным сопротивлениями.
Чтобы понять, что собой представляет индуктивное сопротивление, можно представить цепь, в которой имеется катушка, подключённая к источнику переменного тока. Как известно, напряжение меняется по синусоидальному закону. При этих изменениях катушка будет создавать магнитное поле, которое будет, в частности, влиять на текущий через него ток. Согласно природе магнитного поля, при уменьшении тока магнитное поле способствует его увеличению, а при усилении наблюдается противоположный эффект. Кроме того, цепь переменного тока с активным сопротивлением тратит энергию на выделение тепла.
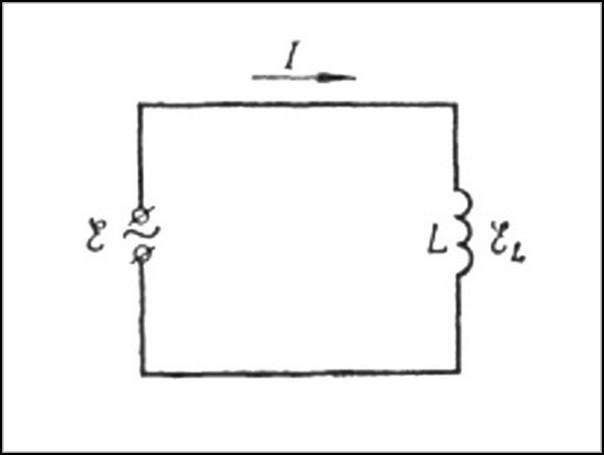
На практике речь идёт о действии индуктивного сопротивления, обеспечивающего сдвиг фазы между током и напряжением. Движение зарядов создаёт поле, которое в свою очередь препятствует изменению тока. Такое сопротивление присутствует не только в катушках, но и, например, при использовании кабеля СИП-2 3×70.
Емкостное сопротивление имеет другую природу. Для объяснения следует рассмотреть цепь, состоящую из источника переменного тока и конденсатора. Последний представляет собой деталь, в которой две поверхности параллельны друг другу и не имеют непосредственного электрического контакта.
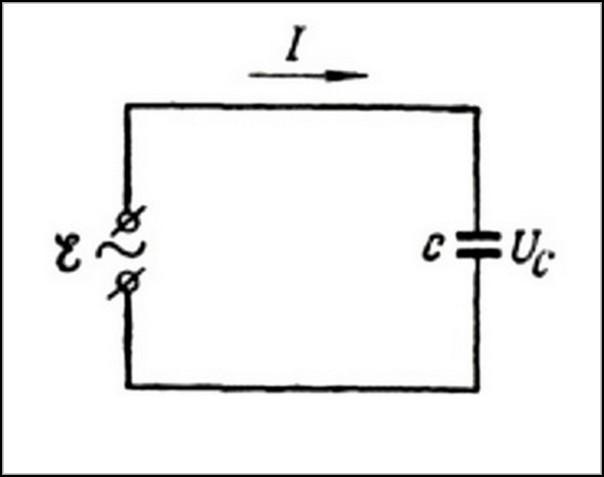
При использовании постоянного тока на обкладках конденсатора накапливаются заряды: на одной — положительный, а на второй — отрицательный. Электрополе за счет накопленного заряда представляет собой источник, противодействующий току. Поэтому конденсатор в цепи постоянного тока является бесконечно большим сопротивлением. Ток не проходит сквозь диэлектрик, разделяющий обкладки конденсатора.
В цепи переменного тока конденсатор циклически заряжается и разряжается, обеспечивая движение электрозарядов. Данный процесс в цепи переменного тока с активным и реактивным сопротивлением будет происходить с опозданием относительно синусоидального изменения напряжения. Таким образом, конденсатор представляет собой конечное сопротивление, получившее название емкостного.
Разница между емкостным и индуктивным сопротивлением заключается в том, что через индуктивную катушку постоянный ток протекает, а при использовании конденсатора пройти не может. Однако переменный ток в обеих цепях может течь без каких-либо проблем.

Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.
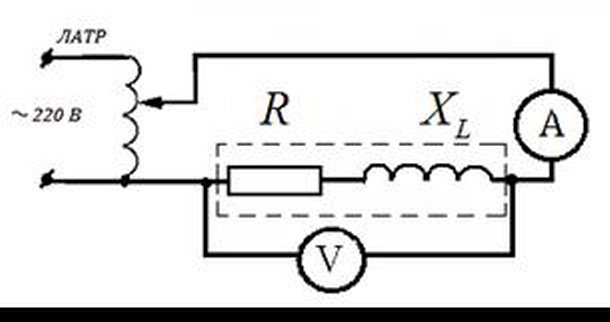
Схема для измерения
В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

Определение индуктивности
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение 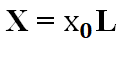
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
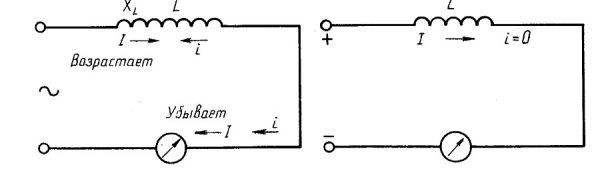
Принцип действия электродвижущей силы
Катушка индуктивности
Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.
Обычно каркас имеет цилиндрическую или тороидальную форму.
Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.
Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.

Катушки индуктивности
Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.
Калькулятор импеданса катушки индуктивности
Калькулятор определяет импеданс катушки индуктивности для заданной частоты синусоидального сигнала. Определяется также угловая частота.
Пример. Рассчитать импеданс катушки индуктивности 10 мкГн на частоте 25 МГц.
Входные данныеИндуктивность, Lгенри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)Частота, fгерц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данныеУгловая частотаω= рад/сИндуктивное реактивное сопротивлениеXL= Ом
Введите значения индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Для ввода значения бесконечность наберите inf.
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Здесь
XL — реактивное сопротивление катушки в омах (Ом),
ZL — импеданс катушки в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
L — индуктивность в генри (Гн),
j — мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
График зависимости реактивного сопротивления катушки XL индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.
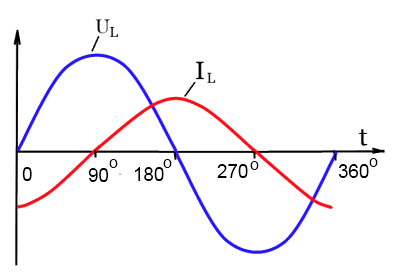
В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности XL велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Катушки индуктивности в высокочастотном модуле телевизионного приемника
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуляПростой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Полное сопротивление
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума — 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Единицы индуктивного реактивного сопротивления | Единица СИ индуктивного реактивного сопротивления
Индуктивное реактивное сопротивление противодействует протеканию тока в цепи. Таким образом, единица измерения индуктивного сопротивления в системе СИ такая же, как и у сопротивления, то есть Ом.
Символ индуктивного сопротивления
Индуктивное сопротивление обозначается ?Lor XL.
Индуктивность в цепи постоянного тока

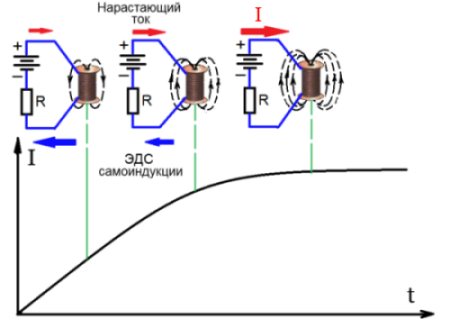
При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле.
Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции.
Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону.
Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения.
Продолжительность нарастания тока в секундах определяется по формуле:
t=3L/R,
где L – индуктивность катушки в генри, а R – общее сопротивление всей цепи в омах.
Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна:
t=3•0,6/60=0,03 сек.
При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице “Электромагнетизм” рис.е).
В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.
Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания.
Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток.
Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.
Индуктивность в цепи переменного тока
Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков.
Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть.
Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.
Будет иначе, если в цепь катушки подать переменный ток.
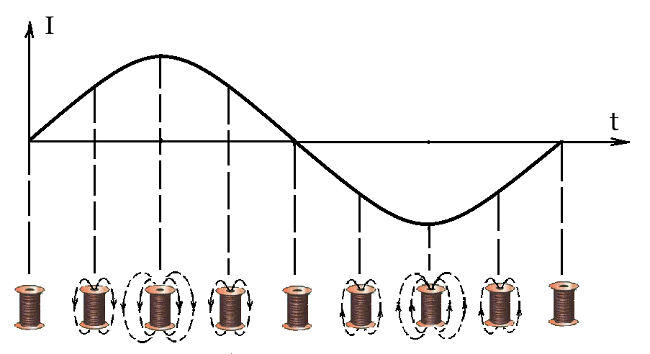
При этом магнитное поле катушки индуктивности становится тоже переменным.
На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.
Рассмотрим график происходящих процессов в катушке индуктивности.
При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º) на катушку поступает нарастающее напряжение и ее магнитное поле “расширяется”, накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке.
За другую четверть периода (90º-180º), когда напряжение на катушке индуктивности уменьшается, магнитное поле “сворачивается”, индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже “помочь” уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору.
Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю.
Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление, как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе – наоборот.
Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления, не вызывает безвозвратных потерь энергии.
Допустим, возьмем идеальную катушку, в которой не учитываются сопротивления провода и другие потери.
Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL,которое измеряется в омах и вычисляется по формуле:
где f – частота тока в герцах (Гц), а L – индуктивность катушки в генри (Г).
Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.
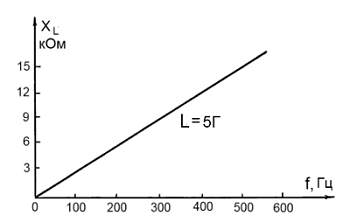
К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц.
XL=2π•50•5=1570 Ом.
На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц – 31МОм. На графике показана зависимость упомянутой катушки от частоты.
Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку:
Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц.
I= 0,4/2•3,14•5•103•500•10-6=0,25 мА
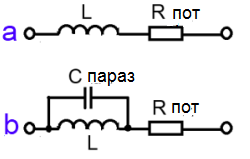
В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот.
На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис.а).
Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно:
и называется импедансом.
На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз, которая шунтирует индуктивность (рис.b).
Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость.
Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки.
Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь:
Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200.
Чтобы достигнуть такого качества используют следующие средства:
– применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода);
– увеличение толщины провода, что, правда, увеличит габариты катушки;
– в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга.
Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки.
Одним из способов является перекрестная намотка типа “универсаль” (рис.c). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис.d,e).
Что называется индуктивным и емкостным сопротивлением?
Сопротивление индуктивное — величина, характеризующая сопротивление, оказываемое переменному току индуктивностью цепи (её участка), измеряется в омах. Ёмкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка).
Что такое емкостное сопротивление и как оно определяется?
— емкостное сопротивление — это проводник, включенный в цепь переменного тока и неимеющий заметного сопротивления и индуктивности, но имеющий заметную емкость С. — емкостное сопротивление проводника переменному току. — действующие значения силы тока и напряжения связаны соотношением, аналогичным закону Ома.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Емкостное и индуктивное сопротивление в цепи
Содержание
- 1 Виды сопротивления и их особенности
- 2 Полное сопротивление
- 3 Пример использования
- 4 Видео по теме
Разность потенциалов между точками электрической цепи порождает ток, который представляет собой упорядоченное движение электронов под действием электрополя. В том случае, когда напряжение постоянное, в цепи будет только активное сопротивление. Если же напряжение переменное, то появляется еще реактивное сопротивление, которое определяется индуктивностью и емкостью компонентов используемой схемы.
Виды сопротивления и их особенности
Если в цепи постоянное напряжение, то, зная её сопротивление, можно узнать силу тока при помощи закона Ома. Он говорит о том, что сила тока пропорциональна напряжению, которое является его причиной. Коэффициент пропорциональности представляет обычное сопротивление. Его принято называть активным.
Если напряжение является постоянным, то сопротивление будет только активным. Его значение определяет, сколько энергии электрического поля преобразовано в тепло, то есть, безвозвратно утрачено. Поэтому при работе с кабелями СИП-3 1×50, СИП-2 3×70 и другими нужно помнить, что потери энергии из-за активного сопротивления могут быть значительными.
Более распространено использование переменного тока. Он возникает под воздействием напряжения, циклически изменяющегося по синусоидальному закону. Такой ток порождает реактивное сопротивление, которое дополняет действие активного. Существует две разновидности реактивного сопротивления различной природы — на основе индуктивности или емкости. Их отличительной особенностью является то, что они способствуют не трате электроэнергии, а преобразованию её в другую форму.
Нужно учитывать, что применение различных видов кабелей связано не только с наличием активного сопротивления, но и реактивного. Например, кабели СИП-3 1×50, СИП-2 3×70, АС-95 могут использоваться в электросетях и с активным, и индуктивным, и емкостным сопротивлениями.
Чтобы понять, что собой представляет индуктивное сопротивление, можно представить цепь, в которой имеется катушка, подключённая к источнику переменного тока. Как известно, напряжение меняется по синусоидальному закону. При этих изменениях катушка будет создавать магнитное поле, которое будет, в частности, влиять на текущий через него ток. Согласно природе магнитного поля, при уменьшении тока магнитное поле способствует его увеличению, а при усилении наблюдается противоположный эффект. Кроме того, цепь переменного тока с активным сопротивлением тратит энергию на выделение тепла.
На практике речь идёт о действии индуктивного сопротивления, обеспечивающего сдвиг фазы между током и напряжением. Движение зарядов создаёт поле, которое в свою очередь препятствует изменению тока. Такое сопротивление присутствует не только в катушках, но и, например, при использовании кабеля СИП-2 3×70.
Емкостное сопротивление имеет другую природу. Для объяснения следует рассмотреть цепь, состоящую из источника переменного тока и конденсатора. Последний представляет собой деталь, в которой две поверхности параллельны друг другу и не имеют непосредственного электрического контакта.
При использовании постоянного тока на обкладках конденсатора накапливаются заряды: на одной — положительный, а на второй — отрицательный. Электрополе за счет накопленного заряда представляет собой источник, противодействующий току. Поэтому конденсатор в цепи постоянного тока является бесконечно большим сопротивлением. Ток не проходит сквозь диэлектрик, разделяющий обкладки конденсатора.
В цепи переменного тока конденсатор циклически заряжается и разряжается, обеспечивая движение электрозарядов. Данный процесс в цепи переменного тока с активным и реактивным сопротивлением будет происходить с опозданием относительно синусоидального изменения напряжения. Таким образом, конденсатор представляет собой конечное сопротивление, получившее название емкостного.
Разница между емкостным и индуктивным сопротивлением заключается в том, что через индуктивную катушку постоянный ток протекает, а при использовании конденсатора пройти не может. Однако переменный ток в обеих цепях может течь без каких-либо проблем.
Полное сопротивление
На практике необходимо учитывать как активное, так и индуктивное и емкостное сопротивления. Это особенно важно при выборе компонентов для электрических сетей. Например, активное, емкостное и индуктивное сопротивления кабелей СИП-3 зависят от их номинального сечения. Поэтому при создании электролинии следует выбрать правильный диаметр проводника, чтобы в будущем не возникало аварийных ситуаций.
При наличии нескольких разновидностей сопротивления возникает понятие полного сопротивления. Графически его представляют в виде прямоугольного треугольника. Длина одного его катета представляет величину активного сопротивления, а другого — разницу между значениями индуктивного и емкостного сопротивлений. Полное сопротивление в этом случае будет измеряться гипотенузой. В соответствии с теоремой Пифагора она определяется по следующей формуле:
Пример использования
Если в сети необходимо регулировать силу тока, удобно использовать реостат (переменное сопротивление). При использовании этой детали, действие которой основано на омическом сопротивлении, можно видеть, как расходуется энергия на нагрев. Таким образом, его можно включать в цепь с активным сопротивлением и индуктивностью с целью регулировки обоих видов сопротивления.
Если вместо реостата используется катушка с изменяемыми параметрами, она позволяет легко произвести регулировку и при этом избежать нагрева. Такое решение особенно удобно, если используется электрическая цепь со значительным напряжением. Когда присутствует активное, емкостное и индуктивное сопротивление, регулировать можно любое из них.
При использовании проводов или обычных радиодеталей в электрической цепи на самом деле измеряется и индуктивное, и ёмкостное сопротивления. Каждое из них зависит от частоты тока, а также от физических и геометрических особенностей используемых схем. Например, провод АС 50 или АС 70 может иметь индуктивное сопротивление в пределах 0.392–0.435 Ом/км. У А 50 аналогичная величина составляет от 0.297 до 0.468 Ом/км. Изолированный кабель АВБбШв 4х240 характеризируется величиной сопротивления всего 0.077 Ом/км.
При выборе проводов необходимо учитывать особенности соответствующих марок. Например, в наименованиях АС 95, АС 120 и других цифра указывает толщину проводов, от которой зависят их электрические свойства. При работе с изолированными самонесущими кабелями СИП-2 3×70, СИП-3 1×50, СИП-3 1×70, СИП-3 1×95, СИП-3 1×120 нужно помнить, что их характеристики зависят не только от физических показателей, но и от номинального напряжения.
Видео по теме
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
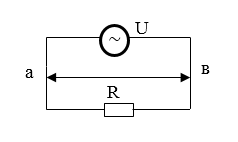
Активное сопротивление
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
[Ileft(tright)=I_m{sin left(omega tright) left(1right). }]
Рисунок 1.
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
[U=IR=I_m{Rsin left(omega tright) left(2right), }]
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
[U_m=RI_mleft(3right),]
где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
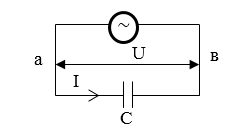
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
Рисунок 2.
Мы можем использовать следующие соотношения:
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
«Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока» 👇
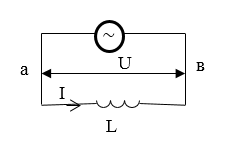
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
Рисунок 3.
Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
По условию $R=0. mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в данном случае равна:
где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
Определение 2
Выражение вида:
[I_m=frac{U_m}{sqrt{R^2+{left(omega L-frac{1}{omega C}right)}^2}}left(12right).]
где
[Z=sqrt{R^2+{left(omega L-frac{1}{omega C}right)}^2}(13)]
называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Пример 1
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $nu$.
Решение:
Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
[I_m=frac{U_m}{sqrt{R^2+{left(omega L-frac{1}{omega C}right)}^2}}left(1.1right)]
оно связано с действующим значением силы тока как:
[I=frac{I_m}{sqrt{2}}left(1.2right).]
В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
[U=frac{U_m}{sqrt{2}}to U_m=sqrt{2}Uleft(1.3right).]
Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
[I=frac{1}{sqrt{2}}frac{sqrt{2}U}{sqrt{R^2+{left(omega L-frac{1}{omega C}right)}^2}}=frac{U}{sqrt{R^2+{left(omega L-frac{1}{omega C}right)}^2}}=frac{U}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}},]
где $omega =2pi nu .$
Ответ: $I=frac{U}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}}.$
Пример 2
Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
Решение:
Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:
[U_L=Iomega L=2 pi nu Lfrac{U}{sqrt{R^2+{left(2 pi nu L-frac{1}{2 pi nu C}right)}^2}}.]
Напряжение на активном сопротивлении ($U_R$) равно:
[U_R=IR=frac{UR}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}}.]
Напряжение на конденсаторе ($U_C$) определяется как:
[U_C=frac{I}{C2 pi nu}=frac{1}{C2 pi nu}frac{U}{sqrt{R^2+{left(2 pi nu L-frac{1}{2 pi nu C}right)}^2}}.]
Ответ: $U_L=2pi nu Lfrac{U}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}}, U_R=frac{UR}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}},U_C=frac{1}{C2pi nu }frac{U}{sqrt{R^2+{left(2pi nu L-frac{1}{2pi nu C}right)}^2}}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме