Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L,
обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром.
В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот.
Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока.
При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает.
При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное — растет.
При некоторой частоте ƒ0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки
становятся численно равными: Xc = XL.
При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.
Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве
емкостного и индуктивного сопротивлений, называют режимом резонанса токов.
Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты.
Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.
Расчет частоты резонанса параллельного LC-контура описывается формулами:
XL
— индуктивное реактивное сопротивление, Ом;
XС
— ёмкостное реактивное сопротивление, Ом;
ƒ0
— резонансная частота, Гц;
Расчет частоты резонанса LC-контура
Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура,
или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.
XL =
XC =
ƒ0 =
φ = °
XL
>
XC
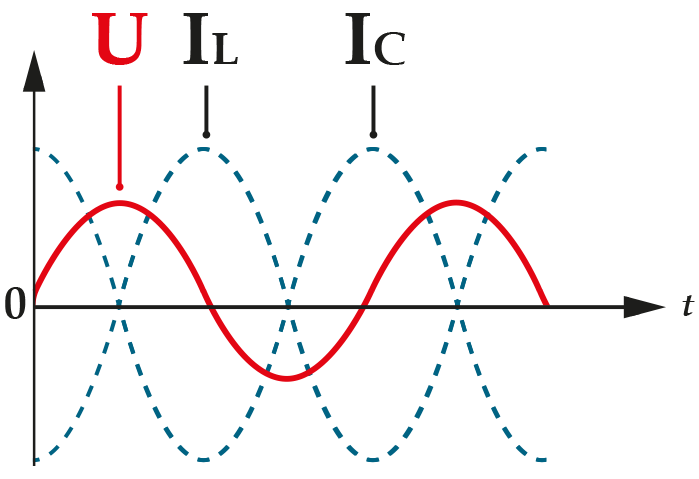
Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного.
Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс,
тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.
Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.
Подбор конденсатора на сайте
Подбор катушки индуктивности на сайте
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).
Емкость плоского конденсатора, состоящего из п пластин площадью пластины
где d — расстояние между пластинами, м.
Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:
где R1 — радиус внутренней обкладки (жилы), м;
R2 — радиус внешней обкладки, м.
Емкость прямолинейного провода длиной / и радиусом поперечного сечения г (м) (второй провод — в бесконечности), Ф:
Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:
Индуктивность кольца со средним радиусом R и радиусом сечения кольца г (м), Гн:
Индуктивность многослойной катушки толщиной обмотки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн
Индуктивность тороидальной катушки кругового сечения (рис. 1.2, б), Гн:
где w — число витков катушки,
D — средний диаметр тора, м;
d — диаметр среднего витка, м.
Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:
Рис. 1.3. Концентрически расположенные катушки индуктивности
Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примыкающих друг к другу (рис. 1.3), Гн:
где L12 — индуктивность катушки, состоящей из первой и второй катушек;
L1, L2 — собственные индуктивности катушек.
После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией 
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.
Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = 
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний 
Частота свободных колебаний контура ƒ = 1 / T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
По формуле циклической частоты свободных электромагнитных колебаний , где L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V — «ню» частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:
В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем:
Условие задачи:
Определить емкость конденсатора фильтра выпрямителя, если частота тока 50 Гц, а емкостное сопротивление 230 Ом.
Задача №9.10.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=50) Гц, (X_C=230) Ом, (C-?)
Решение задачи:
Емкостное сопротивление конденсатора (X_C) определяют по следующей формуле:
[{X_C} = frac{1}{{omega C}};;;;(1)]
В этой формуле (omega) – циклическая частота колебаний, которая связана с частотой (nu) по формуле:
[omega = 2pi nu;;;;(2)]
Подставив выражение (2) в формулу (1), получим:
[{X_C} = frac{1}{{2pi nu C}}]
Откуда электроемкость конденсатора (C) равна:
[C = frac{1}{{2pi nu {X_C}}}]
Посчитаем численный ответ задачи:
[C = frac{1}{{2 cdot 3,14 cdot 50 cdot 230}} = 1,38 cdot {10^{ – 5}};Ф = 13,8;мкФ]
Ответ: 13,8 мкФ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.10.8 При включении конденсатора на синусоидальное напряжение 220 В с частотой 50 Гц
9.10.10 Конденсатор емкостью 10 мкФ включен в цепь, в которой мгновенное значение
9.10.11 Емкостное сопротивление конденсатора на частоте 50 Гц равно 100 Ом. Каким оно
Расчёт ёмкости колебательного контура
Расчёт ёмкости колебательного контура (L,C)
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
Формула расчета ёмкости колебательного контура
- C = 1/(4π²F²L)
Где:
- F — Резонансная частота, Гц)
- L — Индуктивность, (Гн)
- C — Ёмкость, (Ф)
Онлайн-калькулятор для расчёта ёмкости колебательного контура
Индуктивность:
Частота:
Ёмкость:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
-
Определяем емкость и индуктивность контура, учитывая, что на резонансной частоте должно выполняться условие:
|
|
(2) |
где
− круговая частота;
− волновое (или характеристическое)
сопротивление контура.
При
заданной резонансной частоте контура
уменьшению индуктивности соответствует
увеличение емкости, и наоборот.
Одновременно
изменяется
и величина
.
Увеличение индуктивности требует
намотки большого количества витков
провода. При уменьшении индуктивности
возрастают геометрические размеры
конденсатора. При слишком большом
значении
междувитковая емкость катушки становится
соизмеримой с основной емкостью контура.
Поэтому ухудшается стабильность
резонансной частоты и возрастает
антенный эффект контура, т.е. способность
контура реагировать на внешние поля.
При малой величине
возникают затруднения в согласовании
контура с транзистором и нагрузкой.
С
учетом этих противоречивых требований
наилучшей величиной волнового
сопротивления низкочастотного
колебательного контура следует считать
.
Тогда
емкость конденсатора:
|
|
(3) |
По
табл. 1, приложение 3 выбираем конденсатор
с емкостью
с минимальным рабочим напряжением.
Находим индуктивность контура:
|
|
(4) |
-
Число
витков W
катушки индуктивности определяем по
формуле:
|
|
(5) |
где
− коэффициент, приведенный в табл. 2,
приложение 2 для альсиферовых сердечников;
− индуктивность,
.
-
Исходя
из средней длины витка
для данного типоразмера сердечника,
приведенной в табл. V,
определяем длину обмоточного провода:.
(6)
-
Пользуясь
данными табл. Б.2, находим диаметр
провода (с изоляцией):
|
|
(7) |
По
табл. 1, приложение 4, выбираем тип
провода с диаметром равным,
-
Рассчитываем
полное сопротивление провода
по формуле:
|
|
(8) |
где
– длина провода,
;
− сопротивление 1
провода выбранного диаметра, Ом.
По
справочнику [1] находим
.
и полное сопротивление провода.
-
Определяем
сопротивление потерь в сердечнике на
вихревые токи
:
|
|
(9) |
где
− коэффициент потерь на вихревые токи,
табл.1, приложение 2.
-
Сопротивление
потерь в сердечнике на последействие
равно
|
|
(10) |
где
– коэффициент потерь на последействие,
табл. 1, приложение 2.
-
Сопротивление
потерь в конденсаторе
определяется тангенсом угла
,
имеющим для металлобумажных конденсаторов
величину порядка
:
.
(11)
-
Общее
сопротивление потерь в контуре без
учета влияния нагрузки и потерь в
сердечнике на гистерезис равно:.
(12)
-
Находим
оптимальную величину нагрузочного
сопротивления
в коллекторной цепи транзистора. Эту
величину должно иметь сопротивление
резонансного контура между выводами,
подключаемыми к коллектору транзистора
и к источнику питания:
|
|
(13) |
-
Определяем
потери в сердечнике на гистерезис. Для
этого предварительно рассчитываем
вспомогательный коэффициент
:
|
|
(14) |
где
− коэффициент, зависящий от типа
сердечника (табл. Б.2),
,
(15)
где
− сопротивление нагрузки, пересчитанное
в контур параллельно его реактивным
элементам;
− эквивалентное
сопротивление контура на резонансной
частоте (без учета влияния нагрузки).
Следует
иметь в виду, что при малом значении
возрастает добротность системы контур
– нагрузка и уменьшается КПД каскада.
При
()
добротность нагруженного контура
вдвое меньше добротности ненагруженного,
а мощность при резонансной частоте
распределяется поровну между нагрузкой
и контуром.
Пользуясь
номограммой, приведенной на рис. 4,
находим величину сопротивления потерь
в сердечнике на гистерезис как функцию
коэффициента
и
сопротивления
.
Для пользования номограммой необходимо
отложить по вертикальной оси значение
,
а по верхней горизонтальной оси значение
.
На пересечении перпендикуляра,
восстановленного к точке А и кривой,
соответствующей точке Б, находим точку
В. Опуская из этой точки перпендикуляр
на нижнюю горизонтальную ось, находим
величину
.
.
Рисунок
4 – Номограмма на определения сопротивления
потерь в сердечнике контура на гистерезис
-
Находим
полное сопротивление потерь в контуре:.
(16)
-
Определяем
собственную добротность контура
:
.
(17)
-
Эквивалентная
добротность системы контур – нагрузка
:.
(18)
-
Определяем
полосу пропускания усилителя
|
|
(19) |
-
Находим
эквивалентное сопротивление нагруженного
контура на резонансной частоте:.
(20)
-
Коэффициент
подключения контура к транзистору
рассчитываем по формуле:
|
|
(21) |
Отсюда
число витков обмотки
:
|
|
(22) |
-
Коэффициент
подключения нагрузки к контуру:.
(23)
-
Число
витков обмотки
определяется
соотношением:
|
|
(24) |
-
Реализация
модели схемы с использованием программы
Multisim. Построение АЧХ в заданном диапазоне
частот.
Соседние файлы в папке ЛабЫ_ТОР
- #
- #
- #
- #
- #
- #
- #















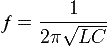

 ,
,
 .
.