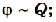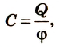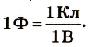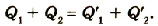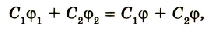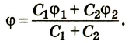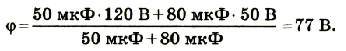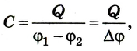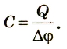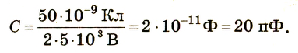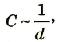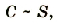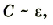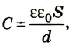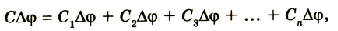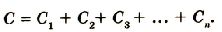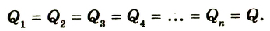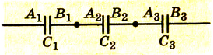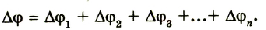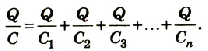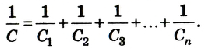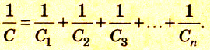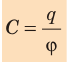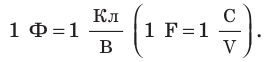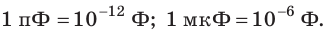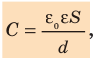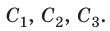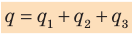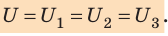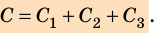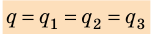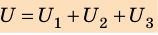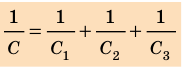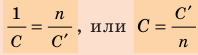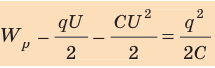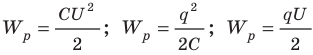Как найти электроемкость конденсатора формула томсона

Найди верный ответ на вопрос ✅ «Как найти емкость конденсатора через формулу Томпсона? Очень прошу …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Конденсатор – пассивный электронный компонент, главной характеристикой которого является емкость. Предназначен в основном для накопления энергии, разделения цепей постоянного тока, фильтрации помех, создания резонансных цепей и т.п. Чтобы применение конденсаторов на практике было осознанным, следует ознакомиться с их основными параметрами, методами измерения и изменения емкости.

От чего зависит и в чем измеряется емкость конденсатора

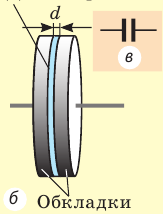
Конденсатор в общем случае состоит из двух проводящих обкладок, разделенных диэлектриком. Если к обкладкам приложить напряжение, такое устройство запасает электрическую энергию путем накопления заряда. (говорят, что конденсатор заряжается). Количественно запасенная конденсатором электрическая энергия выражается формулой , где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.

Единицей измерения емкости в СИ является фарад (1 Ф) (устаревшее название – фарада). Для практических целей это слишком большая единица. Так, земной шар имеет ёмкость менее 1 Ф, поэтому в технике используют, в основном, дольные единицы:

• пикофарады – 1 пФ (1 pF) =10^-12 Ф;
• нанофарады – 1 нФ (1 nF) =10^-9 Ф;
• микрофарады – 1мкФ (1 µF) = 10^-6 Ф.

Более крупные единицы до недавнего времени не использовались, так как емкости порядка больших дольных единиц были труднодостижимыми. Лишь с появлением ионисторов появилась возможность оперировать величинами порядка единиц и даже десятков фарад.

Как узнать емкость конденсатора

Чтобы использовать конденсатор для практических целей, надо знать его емкость. Выяснить эту величину можно различными способами.

По маркировке

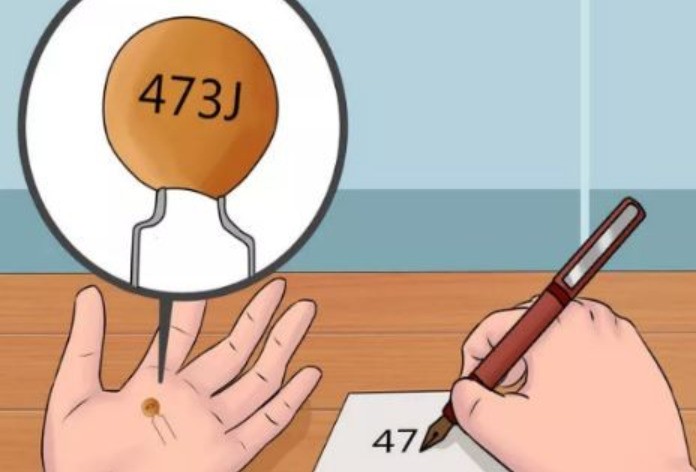
В первую очередь, надо попробовать определить параметры конденсатора по его маркировке. На оксидные конденсаторы, имеющие емкость которых составляет от долей до нескольких тысяч микрофарад, эта характеристика наносится на корпус в виде цифры, обозначающей емкость в микрофарадах, с индексом uF (для отечественных изделий предыдущих годов выпуска после цифры стоит индекс мкФ).

Конденсаторы, обладающие емкостью от единиц пикофарад до единиц микрофарад маркируют тремя цифрами:

• первые два символа — мантисса;
• третья цифра – множитель.

Попросту говоря, к первым двум цифрам надо приписать количество нулей, обозначаемое третьей цифрой.

Например, на конденсатор на рисунке нанесено обозначение 473. К цифрам 47 надо приписать три нуля, тогда получится 47000 пФ. Удобнее представить это значение в виде 47нФ или 0,047 мкФ.

Такое обозначение применяется не всегда (особенно, на старых типах отечественных изделий). Иногда на корпусе наносят явное значение ёмкости с единицей измерения.

Но и единицу измерения указывают не всегда. Принцип таков:

• если нет множителя или не указана единица, считается, что ёмкость в пикофарадах;
• если есть множитель, он указывается одной буквой (n – нанофарады, µ — микрофарады и т.п.).

На зарубежных конденсаторах выпуска до 70-х годов можно встретить обозначение µµF. Так маркировалась ёмкость в пикофарадах («микро-микрофарады»).

Если емкость неизвестна, надпись но корпусе отсутствует или есть сомнения, лучше провести измерения одним из известных способов.

Мультиметром

Сделать это можно, например, с помощью цифрового тестера. Многие современные мультиметры имеют функцию измерения емкости конденсаторов. Надо всего лишь выбрать соответствующий режим, обычно обозначаемый символом конденсатора или буквами Cx, и подключить конденсатор к щупам или специально выделенным гнездам. При измерении надо иметь в виду, что:

1. Нижний предел измеряемой величины довольно большой, и для большинства распространенных приборов составляет не менее 1000 пФ.
2. Измерительные провода со щупами имеют собственную ёмкость (до 100 пФ), и ее надо учитывать при измерениях.

Поэтому тестеры, у которых для измерения ёмкости предназначен отдельный выход, измеряют параметры более точно.

Чтобы обмерить конденсатор с меньшей ёмкостью, лучше воспользоваться специализированным тестером (можно приобрести на интернет-площадках, расположенных в Юго-Восточной Азии). Они позволяют измерять ёмкость от десятков или даже единиц пикофарад.

Осциллографом

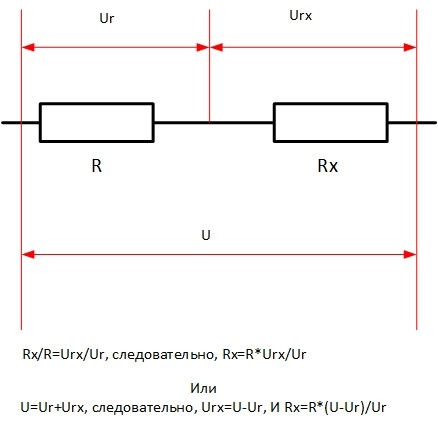
Если есть два резистора – один с известным сопротивлением R, а другой с неизвестным Rx, их можно соединить последовательно (сделать делитель напряжения), подать на него напряжение, и измерить падение на каждом элементе или на общей цепи. Измерения можно провести тестером в режиме вольтметра. Тогда Rx можно вычислить по одной из формул, указанных на рисунке.

Известно, что конденсатор обладает сопротивлением переменному току, которое зависит от частоты по формуле Xc=1/(2*π*f*C), где:

• f – частота тока в Герцах;
• С – ёмкость конденсатора в Фарадах.

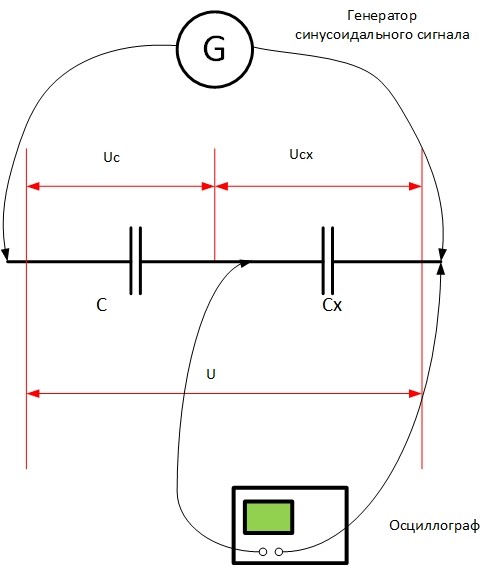
Можно сделать подобный делитель из конденсаторов, и сравнить сопротивление неизвестного прибора Xcx с сопротивлением эталонного конденсатора Xc, откуда легко вычислить неизвестную ёмкость:

откуда

Далее несложно найти С.

При этом возникают две проблемы:

1. Измерения нельзя проводить на постоянном токе – сопротивление реального конденсатора при f=0 близко к бесконечности.
2. При измерении переменного напряжения достаточно высокой частоты тестер будет давать значительную погрешность.

Поэтому в качестве источника тока надо использовать генератор сигнала высокой частоты (чем меньше предполагаемая ёмкость, тем выше должна быть частота, в противном случае точность замеров будет невысокой), а в качестве измерительного прибора – осциллограф.

В качестве эталонного элемента для делителя можно взять резистор с известным сопротивлением (вместо Xc в формулу надо подставить R) или катушку (дроссель) с известной индуктивностью. В этом случае вместо Xc в формулу надо подставить X_L (вычисляется, как X_L=2* π*f*L).

Если имеется эталонная индуктивность, можно найти емкость, составив колебательный контур. Его надо подключить по указанной схеме, а затем, перестраивая генератор, найти резонансную частоту (при ней амплитуда сигнала на осциллографе будет максимальной). Ёмкость можно рассчитать по известной формуле Томсона .

Формулы для расчета емкости

Хотя общая зависимость ёмкости от геометрических размеров и свойств диэлектрика определена выше, для конкретных типов конденсаторов удобнее пользоваться приведенными формулами.

Электроемкость плоского конденсатора

Самый распространённый тип конденсатора, применяемый в технике – плоский. Его обкладки состоят из двух параллельных пластин, между которыми находится диэлектрик. Чтобы уменьшить габариты такого прибора, обкладки с диэлектриком между ними сворачивают в рулон или складывают в прямоугольный пакет. Емкость такого конденсатора рассчитывается по формуле , где:

• С – ёмкость, Ф;
• S – площадь обкладок, кв.м;
• d – расстояние между обкладками;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что емкость тем больше, чем больше площадь обкладок и меньше расстояние между ними. Кроме того, можно выбрать диэлектрик с высоким ε и пропорционально увеличить ёмкость в тех же габаритах.

Электроемкость сферического конденсатора

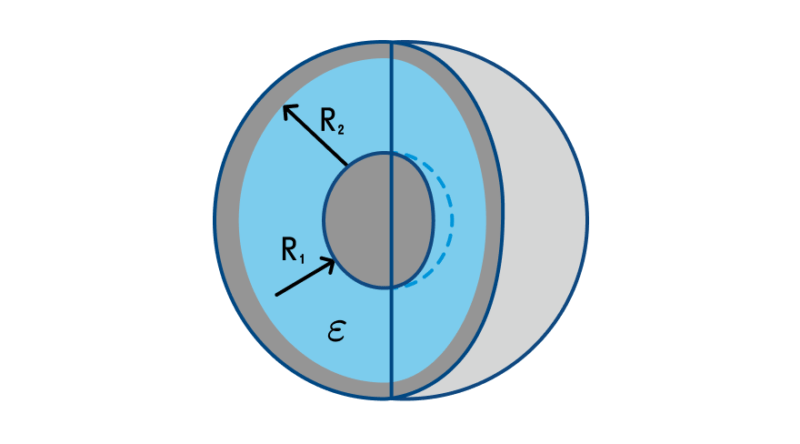
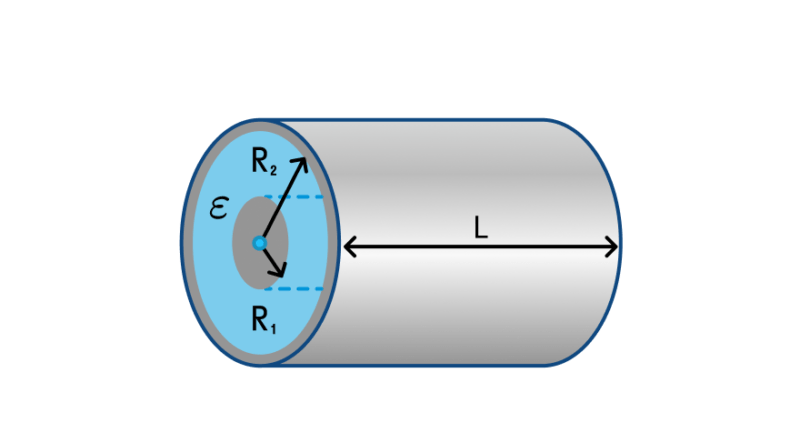
Сферическим конденсатором называется устройство, состоящее из двух проводящих сфер – большой радиусом R1 и малой радиусом R2. Малая сфера вложена в большую. Поверхности сфер служат обкладками. Пространство между сферами может заполняться твердым, жидким диэлектриком или воздухом (воздушный сферический конденсатор). Такие приборы используются для лабораторных исследований (например, для изучения фотоэлектрических явлений).

Формула емкости для такого прибора выглядит, как , где:

• С – ёмкость, Ф;
• R1 – радиус внутренней сферы;
• R2 – радиус внешней сферы;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что зависимость емкости от геометрии подобна плоскому конденсатору. Емкость увеличивается при увеличении площади поверхностей сфер (которые зависят от квадрата радиусов) и уменьшается при увеличении расстояния между обкладками (R2-R1).

Электроемкость цилиндрического конденсатора

У цилиндрического конденсатора обкладки представляют собой два коаксиальных (расположенных на общей оси) цилиндра длиной l каждый с радиусами R1 (меньший) и R2 (больший). Пространство между ними также может быть заполнено либо воздухом, либо другим диэлектриком. Такие приборы используют в масс-спектрометрии и в некоторых типах счетчиков заряженных частиц. Формула для емкости будет выглядеть, как .

Здесь также прослеживается зависимость от площади (при росте длины увеличивается площадь обкладок, следовательно, растет емкость) и расстояния между обкладками. При росте отношения R2/R1 расстояние увеличивается, а ёмкость падает.

Как изменится емкость при параллельном и последовательном соединении

В реальных схемах конденсаторы могут быть включены последовательно или параллельно. При этом суммарная емкость будет разной.

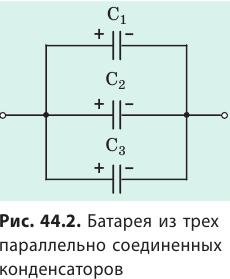
Если включить n конденсаторов параллельно, то в этом случае:

• к каждой ячейке прикладывается одно и то же напряжение (U₁=U₂=..=U_n=U);
• запасенные в каждом конденсаторе заряды складываются.

Тогда общая емкость равна С=U*q=U*(q₁+q₂+..+q_n)=U*q₁+U*q_2+..+ U*q_n=C1+C2+..+Cn. То есть, при параллельном включении ёмкость батареи равна сумме ёмкостей всех элементов. Это эквивалентно сложению площадей всех пластин.

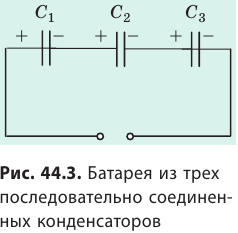
Батарею можно собрать и последовательно, при этом одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

При этом действуют следующие соотношения (в качестве примера рассмотрена батарея из трех элементов):

• заряды –q1 и q2, -q2 и q3 равны, так как обкладки с этими зарядами соединены между собой;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по модулю, но их знак противоположен.

Заряды каждого конденсатора одинаковы и равны q, но при различной емкости разности потенциалов между обкладками каждого элемента определяются из соотношений:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Следовательно, напряжения на ячейках батареи распределяются пропорционально емкостям. Суммарная емкость равна С=q/(U₁+U₂+U₃), следовательно 1/С=(U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, включенных последовательно, выполняется равенcтво:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула достаточно громоздка, но если последовательная цепь состоит из двух элементов, соотношение приводится к виду С= С₁* С₂/( С₁+ С₂).

Последовательное соединение на практике обычно применяется не для снижения общей ёмкости, а для уменьшения напряжения на каждом элементе при использовании конденсаторов в высоковольтных цепях.

Разобравшись с факторами, влияющими на ёмкость конденсатора и способами изменения этого параметра, можно научиться анализировать не только пассивные, но и активные (содержащие полупроводниковые приборы) цепи. Это позволит сделать шаг на пути к развитию навыков и повышению квалификации специалиста.

Содержание:

Электроемкость:

Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.

Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).

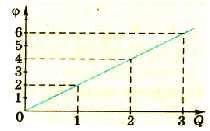
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).

Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.

Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.

Рис. 130. Электризация шара большего диаметра

Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.

Анализируя результаты опытов и соответствующие графики, можно сделать выводы:

1. потенциал каждого шара пропорционален его заряду: 
2. для тел различных размеров коэффициент пропорциональности разный.

Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.

где C — электроемкость проводника; Q — заряд; φ — потенциал.

Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).

Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:

Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.

• 1Ф — довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 10⁴ Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
• 1 микрофарад = 1 мкФ = 10^-5 Ф.
• 1 пикофарад = 1 пФ = 10^-12 Ф.

Пример:

Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.

После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов

Отсюда

или

Подставив значения физических величин и произведя расчеты, получим:

Ответ: после соединения шары будут иметь потенциал 77 В.

Конденсатор

Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.

Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.

Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара

Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.

Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.

Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:

где Q — заряд одной пластины; (φ_l— φ₂) и ∆φ — разность потенциалов между пластинами.

Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».

Пример:

Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?

Подставим значения физических величин:

Ответ: электроемкость данного конденсатора 20 пФ.

Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).

Питер ван Мушенбрук (1692-1781) — голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор — лейденскую банку и провел опыты с ней.

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки

Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.

Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.

В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.

Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком

Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.

Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов

Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.

Электроемкость плоского конденсатора

Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.

Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.

При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.

Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.

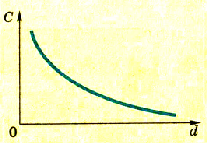
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.

где d — расстояние между обкладками.

Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).

Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.

Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами

Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.

Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин

Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении — наоборот.

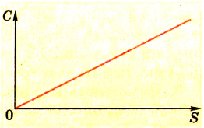
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.

где S — площадь пластин, которые перекрываются.

Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.

Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).

Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин

Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.

Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.

где ε — диэлектрическая проницаемость диэлектрика.

Эта зависимость изображена графиком на рисунке 1.40.

Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика

Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора

где ε — относительная диэлектрическая проницаемость диэлектрика; ε₀— электрическая постоянная; d — расстояние между пластинами; S — площадь пластины.

Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.

Соединение конденсаторов в батареи

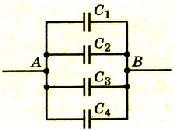
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.

При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.

Pиc 1.41. Схема параллельного соединения конденсаторов

Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:

Если учесть, что 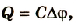 то

или

Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.

При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B₁ будет соединена с пластиной A₂, пластина B₂ -с пластиной А₃ и т. д. (рис. 1.43).

Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A₁ и обкладка B₁ будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:

Pиc. 1.42. Последовательное соединение конденсаторов

Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:

Учитывая, что 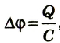 будем иметь

Разделим левую и правую части равенства на Q:

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с

При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.

При последовательном соединении конденсаторов разной электроемкости C₁, C₂, C₃, … С_n общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C₁ < C₇ < C₉ < … < C_n, то C < C₁.

Электроемкость

То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?

Что такое электроемкость

Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.

Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:

Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).

1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл;

1 Ф — очень большая единица емкости, поэтому используют дольные единицы:

Что такое конденсатор

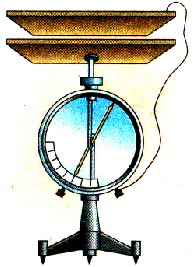
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).

Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах

Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.

Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.

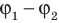
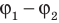
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов () между его обкладками не зависит ни от значения q, ни от разности потенциалов (), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:

где U — напряжение между обкладками: .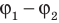

Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.

Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:

где 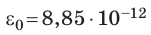Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.

Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.

Как рассчитывают электроемкость батареи конденсаторов

Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.

Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями

При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:

Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:

Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.

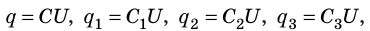
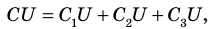
Поскольку то следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:

При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:

Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:

Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:

При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.

Приведенные соотношения можно обобщить для любого количества конденсаторов.

Обратите внимание!

• Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
• Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:

Энергия заряженного конденсатора

Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.

Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.

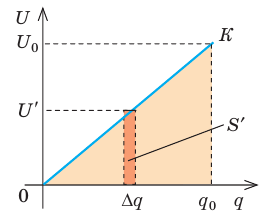
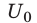
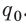
Вычислим энергию заряженного до напряжения конденсатора емкостью С, на котором накоплен заряд . Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.

При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 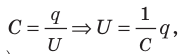поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.

Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке

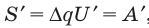
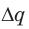
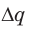
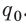
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: , где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда ; A′ — работа, которую совершило поле при потере конденсатором заряда . Полная работа, которую совершило поле при уменьшении заряда конденсатора от до 0, определяется площадью выделенного на рис. 44.4 треугольника.

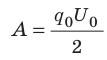
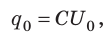
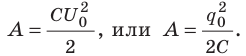
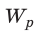
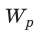
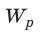
Следовательно,. Учитывая, чтополучим: С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от до нуля: A= − 0 = W. Таким образом, энергия заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:

Для чего нужны конденсаторы

В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио­ и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.

В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).

Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:

• по назначению — постоянной и переменной емкости;
• по форме обкладок — плоские, сферические, цилиндрические и др.;
• по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.

Выводы:

• Энергию заряженного конденсатора можно вычислить по формулам:
• Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).

Электроемкость конденсатора – физическая величина, характеризующая процесс заряда проводников, разделенных слоем диэлектрика. Используется многочисленными математическими расчетами, маркируется на корпусе изделия.

Формулы

Электроемкость конденсатора принято выражать через запасаемый заряд q при приложенном напряжении U подобным образом:

C = q/U.

Происхождение формулы – загадка. Известно только: из теоремы Гаусса по напряженности электрического поля найдем электроемкость конденсатора. Кто провел расчет, нигде не говорится. Физическая величина фарад изначально в системе СГС отсутствовала, в 1861 году ввела специальная комиссия, сформированная физиками.

По отдельным сведениям, впервые электроемкость конденсатора определил введший термины в обиход. Подразумеваем Алессандро Вольту. Поздние 70-е (XVIII века) ученый уделил исследованиям вопроса, установил: электроемкость можно выразить через накапливаемый заряд, приложенное к электродам напряжение.

Вдобавок удаётся часто встретить формулу электроемкости плоского конденсатора:

Авторы избегают судить, кто занимался расчетами выражения. Рассуждая логически, мало кого интересовала электроемкость плоского конденсатора до появления на свет изобретения Полака. Лейденские банки по-другому распределяют заряд. Рассуждения приводят к началу XX века. Возможно, вопросом занимались Тесла, Герц. С меньшей вероятностью – Попов.

Фамилии названы по критериям заинтересованности переменным током. Тесла изучал вопросы безопасности электричества, передачи на расстояние, конструировал двигатели. Герц и Попов исследовали антенны, заведомо настраиваются на некую длину волны, которую проще получить, применяя колебательный контур. Следовательно, ученые обязаны иметь представление об электроемкости конденсатора, катушках индуктивности.

Джеймс Максвелл, лорд Кельвин, Вильгельм Вебер много внимания уделяли совершенствованию единых систем измерения физических величин. Вероятно, кто-то приложил руку к исследованию конденсаторов. Ясно одно – в мировой истории естественных наук масса белых пятен, когда дело касается русскоязычных источников. Портал ВашТехник одним из первых начнёт публиковать новейшие исследования в области правильного понимания произошедших событий.

История

Нетерпеливым читателям докладываем: Алессандро Вольта ввел собственно термин емкости. Неизвестно точно, употреблял ли кто раньше, но в своей работе итальянский ученый, называя электрофорус конденсатором, одновременно применяет к нему термин емкости. Как сосуду, куда можно «налить» заряд из емкости. Конденсатором зовет за схожесть процесса с осаждением паров: понемногу наберем произвольное количество электричества. По большому счету, это верно.

Термин конденсатор

Исторически первым конденсатором считают лейденскую банку. Поныне ходят споры, кто изобрел прибор, поскольку оба ученых, увлеченных событиями, избегали ведения аккуратных записей. Бесспорно одно – электроемкость прибора измерить было нельзя, отсутствовало соответствующее понятие «электроемкость конденсатора».

Придумавший термин бессилен произнести слово раньше, нежели Алессандро Вольта в 1782 году, докладывая Королевскому Научному обществу изыскания в области электростатики, чтобы понять, откуда берется электричество. Известно, в течение следующих пяти лет Луиджи Гальвани откроет «животное электричество», приведшее Вольту прямиком к созданию первого элемента питания. Докладывая обществу, молодой ученый лишен упомянутых знаний, светило пытается понять, откуда появляется заряд. Рассуждает приблизительно так: «К настоящему времени немало свидетельств существования атмосферного электричества. Люди бессильны найти следы присутствия. Вероятно, означает: созданные электроскопы слишком слабы, неспособны уловить столь тонкую материю. Следовательно, требуется найти способ забрать из воздуха флюиды».

Выполняя сказанное, Алессандро Вольта предлагает приспособление, называемое электрофорусом (не путать с электрофорной машиной). Прибор захватывает флюиды атмосферного проводника (воздуха). Принцип служения Вольте напоминает процесс конденсации: собирает электричество.

Электрофорус

Запад электрофорус называет генератором емкостного типа. Указанное выше позволяет полагать: подобное определение прилепилось благодаря написанному Английскому Королевскому обществу Вольтой. Устройство придумано другим человеком – шведским физиком Джоном Кларком Вилке. Случилось двумя десятилетиями ранее – 1762 год.

Ныне считается, популярность прибору придал Вольта, называя любимца вечным генератором электричества. Тоже по сути правильно, тереть резину можно тысячелетиями. Больше «конденсатор» напоминает (см. рис.) здоровенную печать. Сверху, помимо основной центральной ручки, стоит боковая – снятия отрицательного потенциала. Видим три слоя:

1. Подложка необязательна, на нее наклеивается резина.
2. Тонкий слой резины служит телом электризации трением.
3. Сверху – тонкий лист металла, снабженный двумя рукоятками, одна (центральная) изолирована.

Начав работы, нужно убрать «печать», натереть резину шерстью. Затем гладкий диск ставится обратно. Площадь соприкосновения с резиной невелика из-за присутствующих шероховатостей, положительный заряд приобретается нескоро. Нужно выждать. Оператор на короткий миг заземляет крышку боковой ручкой, снимая отрицательный заряд, снизу остается положительный. Прикасаясь одной рукой к металлу, можно слышать хорошо различимый треск. Резина после поднятия крышки несет избыток электронов, позволяющий повторить опыт несколько раз (верится с трудом, некоторые источники говорят о сотне повторений).

Разнимая тела, резким движением потянув изолирующую рукоятку, оператор получает статическое электричество. Изобретение революционное, примечательно, появилось в считанные годы после отмены закона охоты на ведьм. По заявлению Вольты, круг резины делается по возможности тонким, в пределах 50-й доли дюйма. Удается получить наилучший результат. Лист металла фактически становится пластиной. В противном случае долго придётся ждать наполнения объема проводника. В простонародье «конденсатор» называют резиновым пирогом. Пирогом, покрытым металлической начинкой.

Действительно ли электрофорус является неисчерпаемым источником энергии? В идеальных условиях, хотя верится с трудом. Отрицательный заряд резины поляризует металлическую пластину, создавая некий потенциал. Вытесненные на внешнюю поверхность электроны снимаются прикосновением заземлителя. Остается разнять составные части электрофоруса. Уничтожив положительный заряд прикосновением, услышав звук проскочившей искры, можно заново начинать опыт.

Электрофорус действительно напоминает конденсатор. После снятия лишнего отрицательного заряда превращается фактически в упомянутый прибор. Долго храниться конденсатор не может, поскольку электроны с резины понемногу будут стекать на металл. Устройство разрядится. Фактически резина, металл отделены друг от друга воздухом, служащим диэлектриком. Вместо резины используем различные полимеры, например, Тефлон.

Осталось заметить: во времена Вольты не знали методов избавления резины от статического заряда. «Обкладка» конденсатора могла долгое время хранить груз электронов. Вольта предлагает для разрядки поместить образец под солнечные лучи, либо поводить рядом горящей свечой. Через ионизированное пламя электроны покидают конденсатор. Сегодня понятно, достаточно вымыть резину, чтобы следов не осталось статического напряжения. Для работы потребуется вновь высушить.

Лейденская банка

Считается, что Феликс Савари обнаружил колебания резонансного контура. Разряжая лейденскую банку через витую нить меди, наблюдал беспорядочное снование стрелки компаса. 1826 год, когда Англия, Франция, Германия, частично Италия лихорадочно исследовали новое явление, привнесенное в научный мир Эрстедом.

Историю создания лейденской банки можно прочитать в соответствующем обзоре. Следует сказать, никто не пытался толком понять, какова электроемкость конденсатора. Не нужно по очевидным соображениям: лейденскую банку преимущественно использовали научные круги, решая специфические задачи. Опыт Феликса Савари надолго остался без внимания…

В 1842 году колебательным контуром, электроемкостью конденсатора занялся наш старый знакомый, сэр Джозеф Генри, изобретатель электромагнитного реле, любитель телеграфа. Изложил письменно после опробования заметок Савари практикой:

«Аномалия, остающаяся столь долго без объяснения, которая на первый взгляд представляется существующей наперекор нашей теории электричества и магнетизма, после тщательного изучения мною отнесена к доселе неизведанным явлениям. Разряд происходит странно (вразрез теории Франклина), ощущение, что, выходя из банки, флюид начинает странствовать взад-вперед. Увиденное принуждает признать: процесс начинается нормальным образом, затем происходит несколько смен направлений, каждый раз амплитуда становится меньше, пока движения затухнут вовсе. Судя по всему, феномен сегодня не может быть объяснен, физики встречались с ним (Савари), но оказались бессильны».

Очевидно, ученого совершенно не интересует электроемкость конденсатора – мысли поглощены аномалией, которую хотелось бы разведать. Пятью годами позже, ознакомившийся с отчетом Генри физик Гельмгольц на встрече Физического общества Берлина, говорит:

«Проводя электролиз, заметил необычные колебания. Такое ощущение, процесс колебаний продолжается, пока само vis viva не исчезнет навсегда, поглощенное суммарным сопротивлением цепи. Создается впечатление, по контуру текут два тока противоположных направлений, верх берет то один, то другой».

Конец спорам положил знаменитый Вильям Томсон, нареченный лорд Кельвин. Математически исследовав процесс, заявил: в цепи очевидно присутствуют две вещи: электроемкость конденсатора и индуктивность свернутой медной проволоки. Работа On Transient Electric Currents стала классической. Хотя лорд Томсон зовет индуктивность электродинамической емкостью, смысл формулы однозначный. Ученый первым заявил: энергия передается меж конденсатором и катушкой индуктивности, постепенно затухая на активном сопротивлении цепи.

Формула, приведенная на рисунке, дана в современных величинах, обозначения стандартные. С – электроемкость конденсатора, L – индуктивность катушки, q – величина заряда, I – ток цепи. Прочие символы относятся к операциям дифференцирования. Термин индуктивность введен намного позже – в 1886 году Оливером Хэвисайдом. Формула резонансной частоты, зависящей от электроемкости конденсатора и индуктивности катушки, выведена Джеймсом Максвеллом в 1868 году.