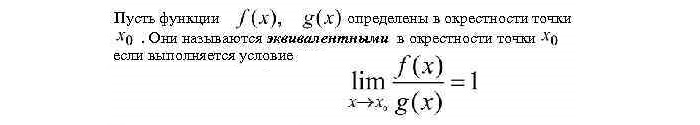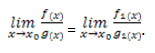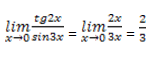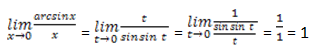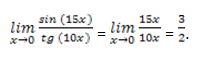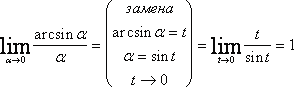Заказать задачи по любым предметам можно здесь от 10 минут
Таблица эквивалентности пределов
Для раскрытия неопределенностей ноль делить на ноль $[frac{0}{0}]$ очень удобно использовать таблицу эквивалентности пределов. Важно, чтобы аргумент функции стремился к нулю. Только в этом случае возможно делать замену.
| Формулы эквивалентности пределов | |
| $ sin x sim x $ | $ e^x — 1 sim x $ |
| $ tg ;x sim x $ | $ a^x — 1 sim xln a $ |
| $ arcsin x sim x $ | $ ln (1+x) sim x $ |
| $ arctg ; x sim x $ | $log_a (1+x) sim frac{x}{ln a}$ |
| $ 1- cos x sim frac{x^2}{2} $ | $(1+x)^a — 1 sim ax $ |
| Пример 1 |
| Найти пределы используя эквивалентные бесконечно малые функции $limlimits_{xto 0} frac{x sin x^2}{arcsin x} $ |
| Решение |
|
Подставляем точку $x=0$ в предел и получаем неопределенность. $$limlimits_{xto 0} frac{x sin x^2}{arcsin x} = bigg [frac{0}{0} bigg ] $$ Замечаем под пределом две функции, для которых можно использовать формулы эквивалентных бесконечно малых функций. Но перед этим проверим, что аргументы их стремятся к нулю. $$ sin 0^2 = sin 0 = 0 $$ $$ arcsin 0 = 0 $$ Значит для нашей задачи получаем следующие замены. $$ sin x^2 sim x^2 $$ $$ arcsin x sim x $$ Подставим эквивалентности в предел, чтобы вычислить ответ. $$limlimits_{xto 0} frac{x sin x^2}{arcsin x} = lim limits_{x to 0} frac{x cdot x^2}{x} = $$ Сокращаем знаменатель и подставляем в оставшееся выражение под числителем $x=0$. $$ = limlimits_{xto 0} x^2 = 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{xto 0} frac{x sin x^2}{arcsin x} = 0 $$ |
| Пример 2 |
| Заменяя эквивалентными бесконечно малыми найдите предел $ limlimits_{xto 0} frac{1-cos 4x}{x} $ |
| Решение |
|
В пределе получаем неопределенность ноль делить на ноль $[frac{0}{0}]$. Замечаем, что числитель похож на формулу из таблицы эквивалентности пределов. Подставим в него точку $x=0$. $$ 1- cos (4 cdot 0) = 1-cos 0 = 1 — 1 = 0 $$ Получили, что числитель равен нулю при $x=0$, а это значит допустима замена на бесконечно малую функцию. $$ 1-cos 4x = frac{(4x)^2}{2} = frac{16x^2}{2} = 8x^2 $$ Возвращаемся к пределу, подставляя в него полученное выражение для числителя. $$limlimits_{xto 0} frac{1-cos 4x}{x} = limlimits_{xto 0} frac{8x^2}{x} = limlimits_{xto 0} 8x = 0 $$ |
| Ответ |
| $$ limlimits_{xto 0} frac{1-cos 4x}{x} = 0 $$ |
| Пример 3 |
| Вычислить предел функции используя эквивалентно малые величины $limlimits_{xto 1} frac{sin (x-1)}{x^2-1} $ |
| Решение |
|
Подставив $x=1$ получаем неопределенность $[ frac{0}{0} ] $. Замечаем, что в числителе присутствует синус, который есть в таблице эквивалентностей. По необходимому условию аргумент синуса должен стремиться к нулю, чтобы применить формулу эквивалентности. Проверим это подставив $x=1$ в него. $$ sin (1-1) = sin 0 = 0 $$ Проверка показала, что формулу можно применить, так как аргумент равен нулю. $$ sin (x-1) sim x-1 $$ $$limlimits_{xto 1} frac{sin (x-1)}{x^2} = limlimits_{xto 1} frac{x-1}{x^2-1} = $$ Применяя формулу разности квадратов $a^2-b^2 = (a-b)(a+b)$ для знаменателя упрощаем его. $$ = limlimits_{xto 1} frac{x-1}{(x-1)(x+1)} = limlimits_{xto 1} frac{1}{x+1} = frac{1}{2} $$ |
| Ответ |
| $$ limlimits_{xto 1} frac{sin (x-1)}{x^2-1} = frac{1}{2} $$ |
Содержание:
- Таблица эквивалентных б.м. функций
- Предельные равенства для эквивалентных б.м. функций
Определение
Б.м. функции $alpha(x)$ и $beta(x)$ называются эквивалентными или равносильными б.м.
одного порядка при $x rightarrow a$, если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=1$
Обозначают: $alpha(x) sim beta(x)$ при
$x rightarrow a$.
Пример
Задание. Проверить, являются ли функции $alpha(x) = 5(x^2-5x+6)$ и
$beta(x) = x^2-x-6$ эквивалентными бесконечно малыми при
$x rightarrow 3$.
Решение. Проверим вначале, что данные функции являются
бесконечно малыми функциями в точке
$x=3$:
$$begin{aligned} lim _{x rightarrow 3} alpha(x) &=lim _{x rightarrow 3} 5left(x^{2}-5 x+6right)=0 \ lim _{x rightarrow 3} beta(x) &=lim _{x rightarrow 3}left(x^{2}-x-6right)=0 end{aligned}$$
Найдем предел отношения этих функций:
$$begin{aligned}
lim _{x rightarrow 3} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 3} frac{5left(x^{2}-5 x+6right)}{x^{2}-x-6} &=lim _{x rightarrow 3} frac{5(x-3)(x-2)}{(x-3)(x+2)}=\
&=lim _{x rightarrow 3} frac{5(x-2)}{x+2}=frac{5}{5}=1
end{aligned}$$
Ответ. Заданные функции $alpha(x) = 5(x^2-5x+6)$ и
$beta(x) = x^2-x-6$ являются эквивалентными бесконечно малыми.
Таблица эквивалентных б.м. функций
Таблица эквивалентных б.м. функций при $x rightarrow 0$
$$begin{array}{|l|c|c|c|}
hline 1 . & sin x sim x & 6 . & ln (1+x) sim x \
hline 2 . & arcsin x sim x & 7 . & log _{a} x sim frac{x}{ln a} \
hline 3 . & operatorname{tg} x sim x & 8 . & a^{x}-1 sim x ln a \
hline 4 . & operatorname{arctg} x sim x & 9 . & e^{x}-1 sim x \
hline 5 . & 1-cos x sim frac{x^{2}}{2} & 10 . & (1+x)^{m}-1 sim m x \
hline
end{array}$$
Предельные равенства для эквивалентных б.м. функций
Теорема
Предел отношения двух б.м. функций $alpha(x)$ и
$beta(x)$ при
$x rightarrow a$ равен пределу отношения эквивалентных им б.м.
функций $alpha^{*}(x)$ и $beta^{*}(x)$ при
$x rightarrow a$, то есть верны предельные равенства:
$$lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=lim _{x rightarrow a} frac{alpha^{*}(x)}{beta(x)}=lim _{x rightarrow a} frac{alpha(x)}{beta^{*}(x)}=lim _{x rightarrow a} frac{alpha^{*}(x)}{beta^{*}(x)}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти предел $lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}$
Решение. При $x rightarrow 0$:
$sin 2 x sim 2 x$
$$lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}=lim _{x rightarrow 0} frac{x(3+7 x)}{2 x}=lim _{x rightarrow 0} frac{3+7 x}{2}=frac{3}{2}$$
Ответ. $lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}=frac{3}{2}$
Теорема
Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.
Верно и обратное утверждение.
Теорема
Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.
Слагаемое, которое эквивалентно сумме б.м. функций, называется главной частью указанной суммы.
Замена суммы б.м. функций ее главной частью называется отбрасыванием б.м. высшего порядка.
Пример
Задание. Найти предел $lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}$
Решение. При $x rightarrow 0$:
$5 x-6 x^{3} sim 5 x,$ tg $3 x sim 3 x$
$lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}left[frac{0}{0}right]=lim _{x rightarrow 0} frac{5 x}{3 x}=lim _{x rightarrow 0} frac{5}{3}=frac{5}{3}$
Ответ. $lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}=frac{5}{3}$
Читать дальше: признаки существования пределов.
Эквивалентные функции
Содержание:
- Что такое эквивалентные функции
-
Эквивалентные функции и их применение к нахождению пределов
- Свойства функций
- Применяемые определения
- Применяемые теоремы
-
Сравнение функций
- Сравнение бесконечно малых функций
- Сравнение бесконечно больших функций
- Примеры решения пределов с помощью эквивалентных функций
Что такое эквивалентные функции
Определение
Эквивалентность — равнозначность в каком-либо отношении.
Эквивалентные функции позволяют облегчить процесс вычисления пределов с помощью замены множителей в примерах с дробями и произведениями.
Функции α(x) и β(x) называются эквивалентными при x→α, если ( lim_{xrightarrowalpha}frac{alpha(x)}{beta(x)}=1.)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Данное определение применимо к бесконечно большим и малым функциям.
Эквивалентность обозначается знаком ∼, т.е. чтобы показать, что функции α(x) и β(x) эквивалентны, нужно оформить запись следующим образом: α(x)∼β(x)
Для удобства следует использовать специальную таблицу.
Эквивалентные функции и их применение к нахождению пределов
Свойства функций
Основные свойства бесконечно малых функций:
- (alphasimalpha,;(lim_{xrightarrow a})fracalphaalpha=1.)
- Если (alphasimbeta и betasimgamma, то alphasimgamma,;(lim_{xrightarrowalpha}fracalphagamma=lim_{xrightarrowalpha}(fracalphabetatimesfracbetagamma)=1times1=1).)
- Если (alphasimbeta и betasimgamma и betasimgamma, то (lim_{xrightarrowalpha}fracbetaalpha=lim_{xrightarrowalpha}frac1{displaystylefracalphabeta}=1).)
- Если (alphasimalpha_1 и betasimbeta и lim_{xrightarrowalpha}fracalphabeta=kappa, то и lim_{xrightarrowalpha}frac{alpha_1}{beta_1}=kappa или lim_{xrightarrowalpha}fracalphabeta=lim_{xrightarrowalpha}frac{alpha_1}{beta_1}.)
Основные свойства эквивалентных бесконечно больших функций:
- (frac{alpha(x)-beta(x)}{alpha(x)}=(1-frac{beta(x)}{alpha(x)})overset{x-alpha}{rightarrow0}.)
- (x = {-b pm sqrt{b^2-4ac} over 2a}alpha(x)simlambdabeta(x), где lambda=lim_{xrightarrowalpha}frac{alpha(x)}{beta(x)}.)
- (alpha(x)+beta(x)simalpha(x).)
Применяемые определения
Основные определения:
- Функции (alpha(x) и beta(x)) бесконечно малы при (xrightarrowalpha.)
- Если есть (lim_{xrightarrowalpha}frac{alpha(x)}{beta(x)}=Cneq0,;infty, то alpha(x) и beta(x)) бесконечно малые одного и того же порядка при (xrightarrowalpha )
- Если есть (lim_{xrightarrowalpha}frac{alpha(x)}{beta(x)}=0) , то (alpha(x))— величина более высокого порядка малости, чем (beta(x)) при (xrightarrowalpha.)
- Если (notnilim_{xrightarrowalpha}frac{alpha(x)}{beta(x)}), то бесконечно малые (alpha(x) и beta(x)) несравнимы при (xrightarrowalpha.)
- Суммой двух бесконечно больших функций при (xrightarrowalpha) является неопределенность.
- Произведением бесконечно большой функции и функции, имеющей в точке α конечный ненулевой предел, является бесконечно большая функция при (xrightarrowalpha.)
Данных определений будет достаточно для решения пределов с применением понятия эквивалентности.
Применяемые теоремы
Теорема 1 (о замене эквивалентными в произведении и отношении):
Если (alpha_1(x),;alpha_2(x),;beta_1(x),;beta_2(x)) являются бесконечно малыми при (xrightarrowalpha и alpha_1(x)simbeta_1(x),;alpha_2(x)simbeta_2(x)) при (xrightarrowalpha), то
- (alpha_1(x)timesalpha_2(x)simbeta_1(x)timesbeta_2(x);)
- (frac{alpha_1(x)}{alpha_2(x)}simfrac{beta_1(x)}{beta_2(x)}) при (xrightarrowalpha;)
- (lim_{xrightarrowalpha}frac{alpha_1(x)}{alpha_2(x)}=lim_{xrightarrowalpha}frac{beta_1(x)}{beta_2(x)}.)
Теорема 2:
Для того чтобы бесконечно малые функции α(x) и β(x) были эквивалентными при (xrightarrowalpha), нужно, чтобы при (xrightarrowalpha) выполнялось любое из равенств:
- (alpha(x)-beta(x)=circ(alpha(x));)
- (alpha(x)-beta(x)=circ(beta(x)).)
Теорема 3:
Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них.
Верно и обратное утверждение.
Теорема 4:
Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Теорема 5 (о замене эквивалентных функций в пределах частного):
Если при (xrightarrow x_0, alpha(x)simalpha_1(x), beta(x)simbeta_1(x)) существует предел (lim_{xrightarrow x_0}frac{a_1(x)}{beta_1(x)},) то существует и предел (lim_{xrightarrow x_0}frac{a(x)}{beta(x)}=lim_{xrightarrow x_0}frac{a_1(x)}{beta_1(x)}.)
Сравнение функций
Сравнение бесконечно малых функций
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) есть конечное ненулевое число, то (alpha(x)) и (beta(x)) называются бесконечно малыми одного и того же порядка.
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) есть ноль, то (alpha(x)) по сравнению с (beta(x)) является бесконечно малой более высокого порядка при (xrightarrowalpha), а (beta(x)) по сравнению с (alpha(x) )— бесконечно малой меньшего порядка.
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) есть бесконечность, то (beta(x)) по сравнению с (alpha(x)) является бесконечно малой более высокого порядка при (xrightarrowalpha), а (alpha(x)) по сравнению с (beta(x)) — бесконечно малой меньшего порядка.
Сравнение бесконечно больших функций
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) больше нуля и меньше бесконечности, то (alpha(x)) и (beta(x)) называются бесконечно большими одного и того же порядка.
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) есть бесконечность, то (alpha(x)) по сравнению с (beta(x)) является бесконечно большой более высокого порядка, при (xrightarrowalpha). При этом (beta(x)) имеет меньший порядок роста.
- Если (lim_{xrightarrowalpha}frac{a(x)}{beta(x)}) есть ноль, то (beta(x)) по сравнению с (alpha(x)) является бесконечно большой более высокого порядка при (xrightarrowalpha.)
- Если (alpha(x) и beta^n(x)) являются бесконечно большими функциями одного и того же порядка, то функция (alpha(x)) по сравнению с (beta^n(x)) называется бесконечно большой n-ного порядка.
Примеры решения пределов с помощью эквивалентных функций
Пример 1
Найти предел:
(lim_{xrightarrow0}frac{lnleft(1+4xright)}{sinleft(3xright)} )
Решение
Воспользуемся таблицей эквивалентных функций.
(lnleft(1+alpharight)simalpha,;sinleft(alpharight)simalpha)
Следовательно,
(lim_{xrightarrow0}frac{lnleft(1+4xright)}{sinleft(3xright)}=lim_{xrightarrow0}frac{4x}{3x}=frac43)
Пример 2
Найти предел:
(lim_{xrightarrow0}frac{sqrt[3]{1+x}-1}x)
Решение
Воспользуемся таблицей эквивалентных функций.
(sqrt[3]{1+x}sim1+frac x3)
Следовательно,
(lim_{xrightarrow0}frac{sqrt[3]{1+x}-1}x=lim_{xrightarrow0}frac{{(1+x)}^{displaystylefrac13}-1}x=lim_{xrightarrow0}frac{1+{displaystylefrac x3}-1}x=frac13lim_{xrightarrow0}frac xx=frac13)
Пример 3
Найти предел:
(lim_{xrightarrowmathrmpi}frac{1+cosleft(xright)}{{(x-mathrmpi)}^2})
Решение
Произведем замену переменной
((x-mathrmpi)=y, где yrightarrow0, если xrightarrowmathrmpi)
Преобразуем выражение.
(L=lim_{xrightarrowmathrmpi}frac{1+cosleft(xright)}{{(x-mathrmpi)}^2}=lim_{yrightarrow0}frac{1+cosleft(y+mathrmpiright)}{y^2})
Применим формулу приведения:
(cosleft(y+mathrmpiright)=-cosleft(yright))
Получим:
(L=lim_{yrightarrow0}frac{1-cosleft(yright)}{y^2})
Воспользуемся таблицей эквивалентных функций.
(1-cosleft(yright)simfrac{y^2}2)
Следовательно,
(L=lim_{yrightarrow0}frac{1-cosleft(yright)}{y^2}=lim_{yrightarrow0}frac{displaystylefrac{y^2}2}{y^2}=frac12)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Определение эквивалентных функций
Эквивалентные функции — это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.
Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.
Теорема о замене функций эквивалентными в пределе частного
Если при x1, стремящимся к x2, f(x)~f1(x) и g(x)~g1(x) существует предел:
то существует и предел:
Доказательство
Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:
в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:
при этом:
f(x) ~ f1(x), p(x) ~ p1(x), … , r(x) ~ r1(x), g(x) ~ g1(x), q(x) ~ q1(x), … , s(x) ~ s1(x).
Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.
Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.
Таблица эквивалентных функций
Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x0:
|
Эквивалентность при t → 0 |
Равенство при t → 0 |
|
sin t ~ t |
sin t = t + 0(t) |
|
arsin t ~ t |
arsin t = t + 0(t) |
|
tg t ~ t |
tg t = t + 0(t) |
|
artg t ~ t |
artg t = t + 0(t) |
|
1-cos t ~ |
1-cos t = + 0(t2) |
|
et – 1 ~ t |
et — 1 = t + 0(t) |
|
at – 1 ~ t ln a |
at – 1 = t ln a + 0(t) |
|
ln (1 + t) ~ t |
ln (1 + t) = t + 0(t) |
|
loga (1 + t) ~ |
loga (1 + t) = + 0(t) |
|
(1 + t)b — 1 ~ bt |
(1 + t)b — 1 = bt + 0(t) |
|
sh t ~ t |
sh t = t + 0(t) |
|
arsh t ~ t |
arsh t = t + 0(t) |
|
th t ~ t |
th t = t + 0(t) |
|
arsh t ~ t |
arsh t= t + 0(t) |
|
ch t – 1 ~ t2/2 |
ch t – 1 ~ t2/2 + 0(t2) |
Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.
В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.
Примеры решения пределов с помощью эквивалентных функций
Для сравнения рассмотрим несколько примеров.
Пример 1
Вычислить
Начнём решение, учитывая, что tg2x ~ 2x, sin3x ~ 3x при x → 0, тогда
Пример 2
Найти
Пусть arcsin x = t, тогда x = sin t и t → 0 при x → 0. Исходя из этого:
Значит, arcsin x ~ x при x → 0.
Пример 3
Вычислить
Решение: если sin (15x) ~ 15x, tg (10x) ~ 10x, тогда
Для решения пределов можно использовать онлайн калькуляторы, размещенные на ресурсах в свободном доступе.
Функции и
называют бесконечно
малыми при ,
если и
Функции и
называют эквивалентными
бесконечно малыми при ,
если
Очень
удобно пользоваться заменой
эквивалентных бесконечно малых при
нахождении пределов. Замена производится
на основе таблицы.
Таблица
эквивалентных бесконечно малых.
Пусть —
бесконечно малая при .
Эквивалентность
всех величин таблицы можно доказать,
основываясь на равенстве .
52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
При
вычислении пределов часто применяется
следующая Теорема.
Предел отношения двух бесконечно малых
(неопределенность )
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
Отметим
также: если ,
то.
3.2. Основные формулы эквивалентности бесконечно малых.
Известна
формула первого замечательного предела:
Используя
это равенство, получим
Отсюда
получаем первую группу формул
эквивалентности бесконечно малых.
При
. (1)
Вторая
группа формул связана с логарифмической
функцией.
Имеем:
Если
при ,
то
Получаем
вторую группу формул:
(2)
Третья
группа формул связана с показательной
функцией. Имеем:
Отсюда
Тогда
Итак,
третья группа формул эквивалентности
бесконечно малых
,
,
(3)
Четвертая
группа формул связана со степенной
функцией.
Имеем:
Итак,
четвертая группа формул эквивалентности
бесконечно малых
,
,
(4)
53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
Определение. Предела
слева (справа)
Число
А(В) по определению называется пределом
функции f(x)
в точке х0 слева
(справа), если
>0 >0
: x из x0-<x<x0 (x0<x<x0+)
f(x)-A< (f(x)-B<),
при
этом пишут:
Пример.

Справедлив
критерий 2 существования предела функции
в точке.
Теорема.
Для
того, чтобы у функции f(x)
существовал предел при хх0 необходимо
и достаточно, чтобы существовал
левосторонний предел в т. х0,
существовал правосторонний предел в
т. х0 и
они были бы равны между собой.
Определение. Непрерывности
функции слева (справа).
Функция f(x)
определенная в левосторонней окрестности
т. х0 (или
в правосторонней окрестности т.х0) и
в самой точке х0 называется
непрерывной в т. х0 слева
(справа), если
>0 >0
: x из x0-<xx0 (x0x<x0+)
f(x)-f(x0-0)< (f(x)-f(x0+0)<)
При
этом значения f(x0-0)
(f(x0+0))
называют значениями функции в точке
х0 слева
(справа).
Пример
.
f(-0)=0.
Теорема.
Критерий непрерывности функции в точке.
Для
того чтобы функция f(x)
была непрерывной в т. х0 необходимо
и достаточно, чтобы она была непрерывна
слева в т. х0,
справа в т. х0 и
при этом выполнялось соотношение :
f(x0-0)=f(x0+0)=f(x0)
54. Точки разрыва функции и их классификация.
Определение. Разрывной
функции в т. x0.
Функция f(x)
не являющаяся непрерывной в т. x0 называется
разрывной в т. x0.
При
этом точки разрыва функции подразделяются
на точки разрыва I рода
и II рода.
Определение. Точка
разрыва I рода.
Если
у функции f(x) и
они конечны, то говорят, что точка x0—
точка разрыва первого рода.
При
этом, если ,
то говорят, что точкаx0—
точка устранимого
разрыва.
Если
же ,
то говорят, что точкаx0—
точка разрыва с конечным
скачком.
-разрывная
функция.
Если
положить — то
произойдет устранение разрыва и функция
станет непрерывной.
У
функции так
как

имеется конечный скачок.
Определение. Точка
разрыва II рода.
Если
у функции f(x)
хотя бы один из односторонних пределов
не существует или равен , то говорят,
что т. х0—
точка разрыва II рода.
Пример
Если
устремить х к 0 разными способами, то
получим различные значения пределов:
, kN, x0
, а ;
kN, x0
, а ,
значит
функция f(x)
не имеет предела â т. х0=0,
то есть т. х0 точка
разрыва II рода.