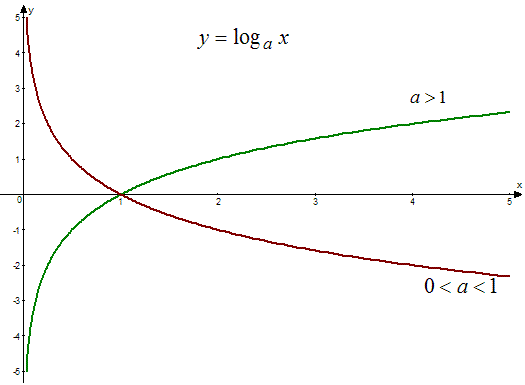Как найти экстремумы логарифмической функции

   Здравствуйте, Дорогие друзья! Продолжаем рассматривать задания связанные с исследованием функций. Рекомендую повторить теорию, необходимую для решения задач на нахождение максимального (минимального) значения функции и на нахождение точек максимума (минимума) функции.

Задачи с логарифмами на нахождение наибольшего (наименьшего) значения функции мы уже рассмотрели. В этой статье рассмотрим три задачи, в которых стоит вопрос нахождения точек максимума (минимума) функций, при чём в заданной функции присутствует натуральный логарифм.  

Теоретический момент:

По определению логарифма – выражение стоящее под знаком логарифма должно быть больше нуля. *Это обязательно нужно учитывать не только в данных задачах, но и при решении уравнений и неравенств содержащих логарифм.

Алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни отмечаем на числовой прямой. *Также на ней отмечаем точки, в которых производная не существует. Получим интервалы, на которых функция возрастает или убывает.

4. Определяем знаки производной на этих интервалах (подставляя произвольные значения из них в производную).

5. Делаем вывод.

Найдите точку максимума функции у = ln (х–11)–5х+2

Сразу  запишем, что х–11>0 (по определению логарифма), то есть х > 11.

Рассматривать функцию будем на интервале (11;∞).

Найдём производную заданной функции:

Нахождение точек максимума (минимума) функции

Найдем нули производной:

Точка х = 11 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки 11 и 11,2. Определим знаки производной функции, подставляя произвольные значения из интервалов (11;11,2) и (11,2;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х=11,2 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 11,2  

Решите самостоятельно:

Найдите точку максимума функции у=ln (х+5)–2х+9.

Посмотреть решение

Найдите точку минимума функции у=4х– ln (х+5)+8

Сразу запишем, что х+5>0 (по свойству логарифма), то есть х>–5.

Рассматривать функцию будем на интервале  (– 5;+∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = –5  не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки –5 и –4,75. Определим знаки производной функции, подставляя произвольные значения из интервалов (–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х= –4,75  производная функции меняет знак с отрицательного на положительный,  значит это искомая точка минимума.

Ответ: – 4,75   

Решите самостоятельно:

Найдите точку минимума функции у=2х–ln (х+3)+7.

Посмотреть решение

Найдите точку максимума функции у = х2–34х+140lnх–10

По свойству логарифма выражение, стоящее под его знаком больше нуля, то есть х > 0.

Функцию будем рассматривать на интервале (0; +∞).

Найдём производную заданной функции:

Найдем нули производной:

Решая квадратное уравнение, получим: D = 9    х1 = 10   х2 = 7.

Точка х = 0  не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси три точки 0, 7 и 10.

Ось ох разбивается на интервалы:  (0;7),  (7;10), (10; +∞).

Определим знаки производной функции, подставляя произвольные значения из полученных интервалов в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х = 7 производная функции меняет знак с положительного на  отрицательный,  значит это искомая точка максимума.

Ответ: 7

Решите самостоятельно:

Найдите точку максимума функции у = 2х2 –13х+9lnх+8

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом всё. Успехов вам!

С уважением, Александр Крутицких 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Уважаемый пользователь! Для получения полного доступа ко всем функциями сайта, пожалуйста, пополните счёт

690 руб.

+ 1 месяц

Получите 1 месяц полного доступа

Пополнить счёт

1400 руб.

+ 3 месяца

Вы экономите 625₽!

Получите 3 месяца полного доступа

Пополнить счёт

3890 руб.

+ 9 месяцев

Вы экономите 2119₽!

Получите 9 месяцев полного доступа

Пополнить счёт

Если вы хотите использовать платформу как репетитор или как учитель, пожалуйста, свяжитесь с нами

Источник

Нахождение
точек минимума логарифмической функции.

Краткие
теоретические сведения

Определение.  Точки,
в которых производная функции равна 0 или не существует называются критическими.

  Среди этих точек могут быть точки максимума ( max ) и  минимума ( min ), которые называются точками экстремума       ( Xmax и Xmin ).  Значения функции в
этих точках называют экстремумами функции   и обозначают fmax (Xmax)  и  fmin (Xmin). 

Необходимым условием существования экстремумов является
равенство нулю производной или если производная не существует, то есть
необходимое условие – это наличие критических точек. (Это теорема Ферма), но
этого условия еще не достаточно. Чтобы функция имела экстремум в некоторой
точке, надо, чтобы при переходе через эту точку производная меняла свой знак,
то есть надо, чтобы возрастание менялось на убывание, или убывание на
возрастание. Если такой смены нет, то в этой критической точке не будет
экстремума.

Если
знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- )
на (+ ) – это точка min.

Вывод. Для существования
экстремумов необходимо выполнение двух условий:

1.       Существование критических точек.

2.       Смена знака производной при переходе через критическую точку.

Ответить на
вопросы.

1.    
Что такое критические точки,  как их
находят?

2.    
Какие бывают точки экстремума?

3.    
Что такое экстремумы функции?

4.    
 Какие существуют экстремумы функции?

5.    
Что является необходимым условием
существования экстремума?

6.    
Что является достаточным условием
существования экстремума?

7.    
В каком случае функция будет иметь
максимум?

8.    
В каком случае функция будет иметь
минимум?

Нахождение точек экстремумов функции осуществляют по следующему
плану:

1.     
Найти
область определения функции.

2.     
Найти
производную.

3.     
Найти
критические точки ( приравнять производную к нулю).

4.     
На
числовой прямой отметить найденные критические точки, выделить           
полученные числовые промежутки и проверить знак производной в каждом из них.

5.     
Записать,
где получились точки максимума или минимума, (а может быть и перегиба, если
знак производной не менялся при переходе через точку, или разрыва).

Самостоятельная
работа.

Вариант
1.

1.Найдите
точку минимума функции y~=~4x-ln (x+11)+12.

2.
Найдите точку минимума функции y=7x-ln(x+4)^{7}+8.

3.
Найдите точку минимума функции y=2x-ln(x+8)^{2}.

4.
Найдите точку минимума функции y=7x-7ln(x+9)+6.

5.
Найдите точку минимума функции y=0,5x^2-16x+63ln x -2.

6.
Найдите точку минимума функции y=log_5(x^2-30x+249)+8.

7.
Найдите точку минимума функции y=log_4(x^2+16x+75)-6.

Вариант
2.

1.
Найдите точку минимума функции y~=~2x-ln (x+2)+13.

2.
Найдите точку минимума функции y=6x-ln(x+8)^{6}+3.

3.
Найдите точку минимума функции y=2x-ln(x+7)^{2}+4.

4.
Найдите точку минимума функции y=x-ln(x+6)+3.

5.
Найдите точку минимума функции y=0,5x^2-17x+72ln x +5.

6.
Найдите точку минимума функции y=log_6(x^2+24x+147)+2.

7.
Найдите точку минимума функции y=log_6(x^2-12x+59)+7.

Вариант
3.

1.Найдите
точку минимума функции y~=~10x-ln (x+9)+6.

2.
Найдите точку минимума функции y=9x-ln(x+5)^{9}+2.

3.
Найдите точку минимума функции y=11x-ln(x+13)^{11}+7.

4.
Найдите точку минимума функции y=7x-7ln(x+9)+6.

5.
Найдите точку минимума функции y=1,5x^2-57x+270ln x +6.

6.
Найдите точку минимума функции y=log_2(x^2+2x+30)+10.

7.
Найдите точку минимума функции y=log_3(x^2-16x+76)+8.

Вариант
4.

1.Найдите
точку минимума функции y~=~4x-ln (x+8)+12.

2.
Найдите точку минимума функции y=11x-ln(x+8)^{11}+6.

3.
Найдите точку минимума функции y=2x-ln(x+4)^{2}+2.

4.
Найдите точку минимума функции y=x-ln(x+6)+3.

5.
Найдите точку минимума функции y=1,5x^2-21x+30ln x +6.

6. Найдите точку минимума функции y=log_3(x^2-12x+41)+1.

7.
Найдите точку минимума функции y=log_9(x^2+16x+87)+7.

Источник

Лучшие онлайн-курсы для подготовки к ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Логарифмические функции»

Открытый банк заданий по теме логарифмические функции. Задания B12 из ЕГЭ по математике (профильный уровень)

Тригонометрические уравнения

Задание №1132

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=5x^2-12x+2ln x+37 на отрезке left[frac35; frac75right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 10x-12+frac{2}{x}= frac{10x^2-12x+2}{x}.

Определим нули производной: y'(x)=0;

frac{10x^2-12x+2}{x}=0,

5x^2-6x+1=0,

x_{1,2}= frac{3pmsqrt{3^2-5cdot1}}{5}= frac{3pm2}{5},

x_1=frac15notinleft[frac35; frac75right],

x_2=1inleft[frac35; frac75right].

Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом промежутке.

Знаки производной и промежутки монотонности функции на отрезке

Из рисунка видно, что на отрезке left[frac35; 1right]исходная функция убывает, а на отрезке left[1; frac75right]возрастает. Таким образом, наименьшее значение на отрезке left[frac35; frac75right]достигается при x=1 и равно y(1)= 5cdot 1^2-12cdot 1+2 ln 1+37= 30.

Ответ

30

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=4x^2-19x+11ln x+715 на отрезке left[frac34; frac54right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 8x-19+frac{11}{x}= frac{8x^2-19x+11}{x}.

Определим нули производной: y'(x)=0;

frac{8x^2-19x+11}{x}=0,

8x^2-19x+11=0,

x_{1,2}= frac{19pmsqrt{19^2-4cdot8cdot11}}{2cdot8}= frac{19pm3}{16},

x_1=1,

x_1in left[frac34; frac54right],

x_2=frac{22}{16}=frac{11}{8}>frac{10}{8}=frac{5}{4},

x_2notin left[frac34; frac54right].

Расставим знаки производной и определим промежутки монотонности исходной функции.

Знаки производной и промежутки монотонности функции

Из рисунка видно, что на отрезке left[frac34; 1right] исходная функция возрастает, а на отрезке left[1; frac54right] убывает. Таким образом, наибольшее значение на отрезке left[frac34; frac54right] достигается при x=1 и равно y(1)= 4cdot 1^2-19cdot 1+11 ln 1+715= 700.

Ответ

700

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1116

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=7x-ln(x+11)^7 на отрезке [-10,5;,,0].

Показать решение

Решение

ОДЗ: (x+11)^7>0, x+11>0, x>-11. На ОДЗ исходная функция примет вид:y=7x-7 ln (x+11).

Найдём производную: y’=7-frac{7}{x+11}. Определим нули производной: 7-frac{7}{x+11}=0,

frac{1}{x+11}=1,

x=-10.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Знаки производной и промежутки монотонности функции

Из рисунка видно, что на отрезке [-10,5; -10] исходная функция убывает, а на отрезке [-10; 0] возрастает. Таким образом, наименьшее значение на отрезке [-10,5; 0] достигается при x=-10 и равно y(-10)= 7cdot (-10)-ln (-10+11)^7= -70.

Ответ

-70

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №952

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+7)^9-9x на отрезке [-6,5; 0].

Показать решение

Решение

ОДЗ. (x+7)^9>0,  x+7>0,  x>-7.

Так как на ОДЗ ln(x+7)^9=9ln(x+7), то исходная функция примет вид: y=9ln(x+7)-9x. Найдём производную: y’=frac{9}{x+7}-9.

Определим нули производной

frac{9}{x+7}-9=0,

frac{1}{x+7}=1,

x=-6.

Расставим знаки производной и определим промежутки монотонности исходной функции

Поведение функции на числовой оси со знаками производной

Из рисунка видно, что на отрезке [-6,5; -6] исходная функция возрастает, а на отрезке [-6; 0] — убывает. Таким образом, наибольшее значение на отрезке [-6,5; 0] достигается при x=-6 и равно y(-6)=ln(-6+7)^9-9cdot(-6)=54.

Ответ

54

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №336

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=12x-ln(12x)+100 на отрезке left [frac{1}{36}; frac34 right ].

Показать решение

Решение

y’=(12x-ln(12x)+100)’=12-frac{12}{12x}=frac{12x-1}{x}.

y’=0 при x=frac{1}{12}, причем y’ меняет знак в этой точке с «−» на «+». Это означает, что x=frac{1}{12} является точкой минимума.

yleft ( frac{1}{12} right )=12cdotfrac{1}{12}-lnleft ( 12cdotfrac{1}{12} right )+100=1-0+100=101.

Ответ

101

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №125

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+8)^3-3x на отрезке [−7,5; 0]

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=3ln(x+8)-3x

y’=frac{3}{x+8}-3

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{3}{x+8}=3

x+8=1

x=-7

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

Поведение функции на числовой оси со знаками производной

При переходе через точку x = −7 производная меняет знак с плюса на минус. Значит x = −7 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −7.

y(-7)=3ln1+21=21

Наибольшее значение функции равно 21.

Ответ

21

Задание №124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите точку максимума функции y=log_2(4+10x-x^2)-71.

Показать решение

Решение

Определим область допустимых значений функции.

4+10x-x^2>0

x^2-10x-4<0

5-sqrt{29}<x<5+sqrt{29}

Вычислим производную функции.

y’=frac{10-2x}{(4+10x-x^2)ln2}

Найдем точки экстремума, в которых производная функции обращается в нуль.

10-2x=0

x = 5

На числовой оси отложим граничные точки ОДЗ и точку экстремума и посмотрим как ведет себя функция.

Граничные точки отрезка и точка экстремума на числовой оси

При переходе через точку x = 5 производная меняет знак с плюса на минус. Значит x = 5 – точка максимума функции.

Ответ

5

Задание №123

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+5)^4-4x на отрезке [−4,5; 0].

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=4ln(x+5)-4x

y’=frac{4}{x+5}-4

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{4}{x+5}=4

x+5=1

x=-4

На числовой оси отложим граничные точки отрезка и точку экстремума и посмотрим как ведет себя функция.

Граничные точки отрезка и точка экстремума на числовой оси

При переходе через точку x = −4 производная меняет знак с плюса на минус. Значит x = −4 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −4.

y(-4)=ln(-4+5)^4-4cdot(-4)=16

Наибольшее значение функции равно 16.

Ответ

16

Лучшие репетиторы для сдачи ЕГЭ

Источник

Содержание:

  • Определение
  • Свойства логарифмической функции

Определение

Функция, которую можно записать формулой $y=log _{a} x$,
называется логарифмической функцией. Здесь $x>0$ —
аргумент, $a>0, a neq 1$ — основание
логарифма.

Логарифмическая функция является обратной функцией к показательной $y=a^{x}$.
Поэтому графики этих функций симметричны относительно биссектрисы первой и третьей координатных четвертей.

Свойства логарифмической функции

1  Область определения — $D[y] : x in(0 ;+infty)$

2  Область значений — $E[y] : y in(-infty ;+infty)$

3  Четность/нечетность — функция общего вида (функция ни четная, ни нечетная)

4  Нули функции — $x=1$

5  Интервалы монотонности, экстремум функции — график
функции возрастает на $(0 ;+infty)$ при
$a>1$; убывает на $(0 ;+infty)$
при $0 lt a lt 1$; точек экстремума нет.

6  Интервалы выпуклости/вогнутости — Функция выпукла на промежутке $(0 ;+infty)$ при
$a>1$;
функция вогнута на промежутке $(0 ;+infty)$
при $0 lt a lt 1$; точек перегиба нет.

7  График логарифмической функции:

График логарифмической функции, при разных значениях основания

Читать дальше: логарифмические уравнения.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти октмо организации по адресу
  • Failed to initialize nvidia with error csgo как исправить
  • Как составить список всех файлов в каталоге
  • Делфи как найти да нет
  • Как найти центральный угол через хорду

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии