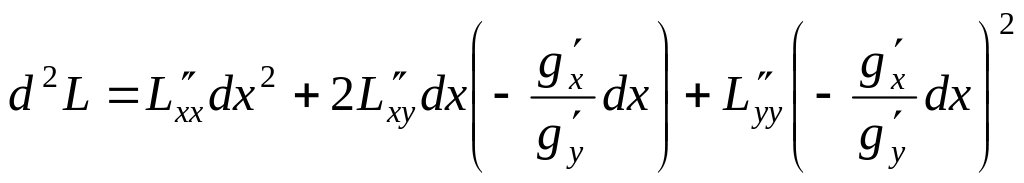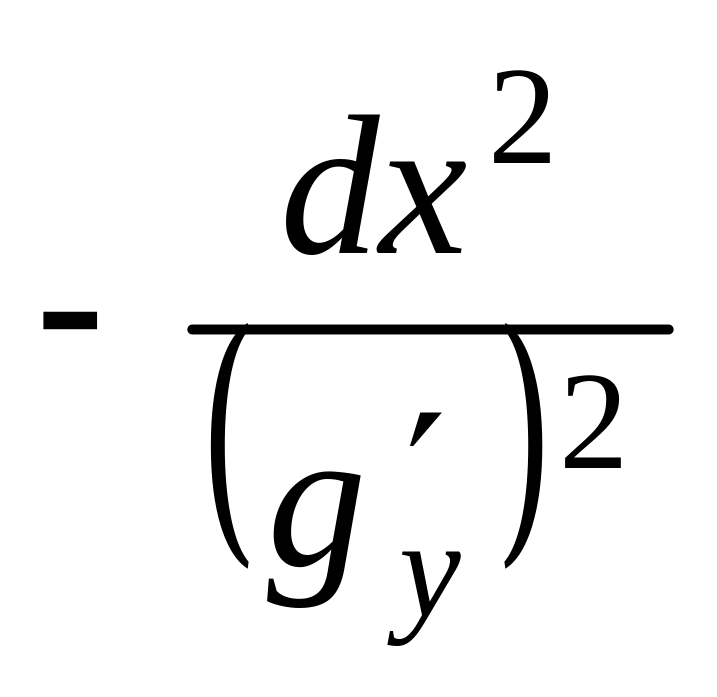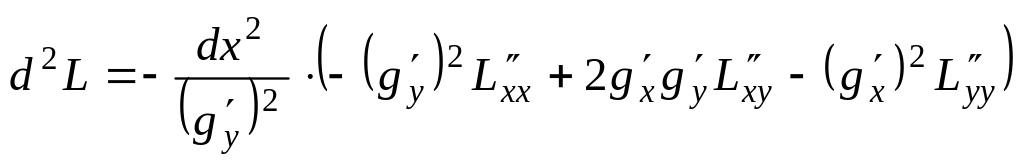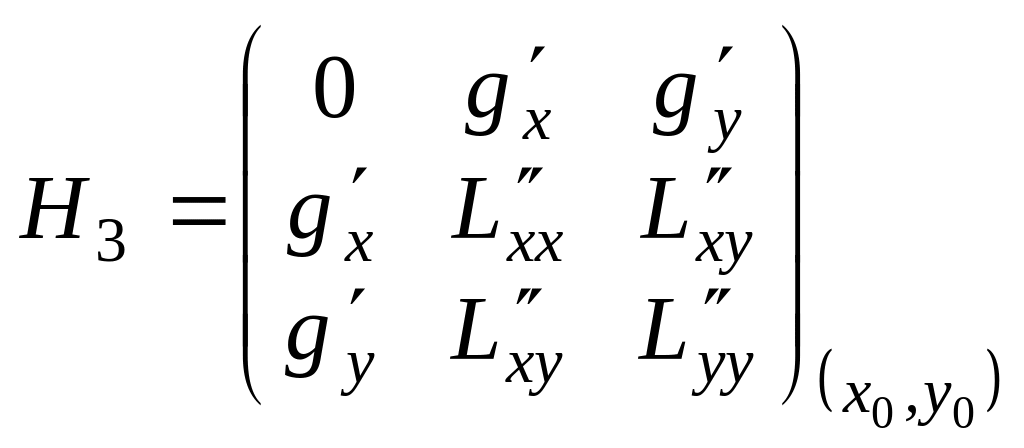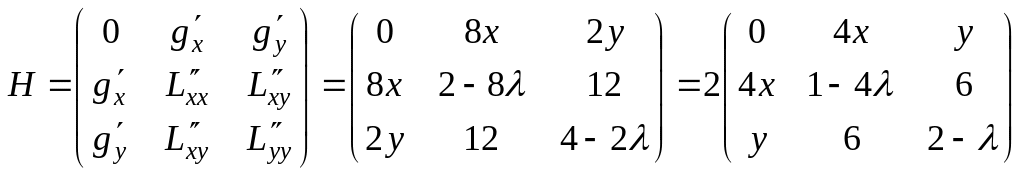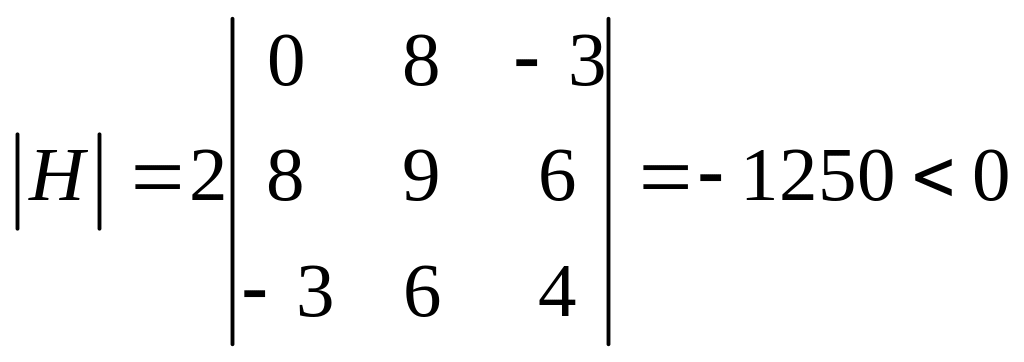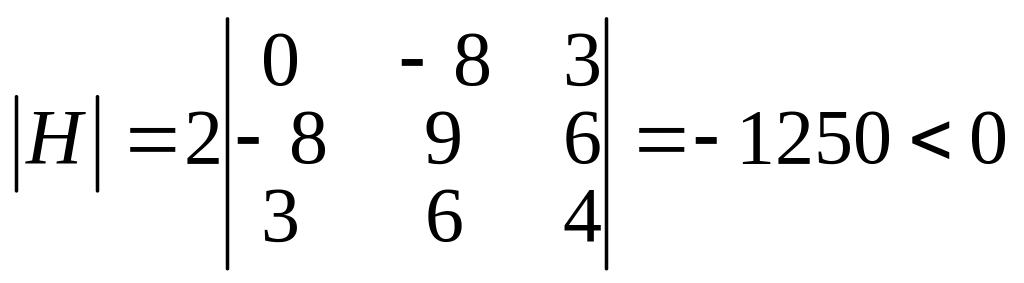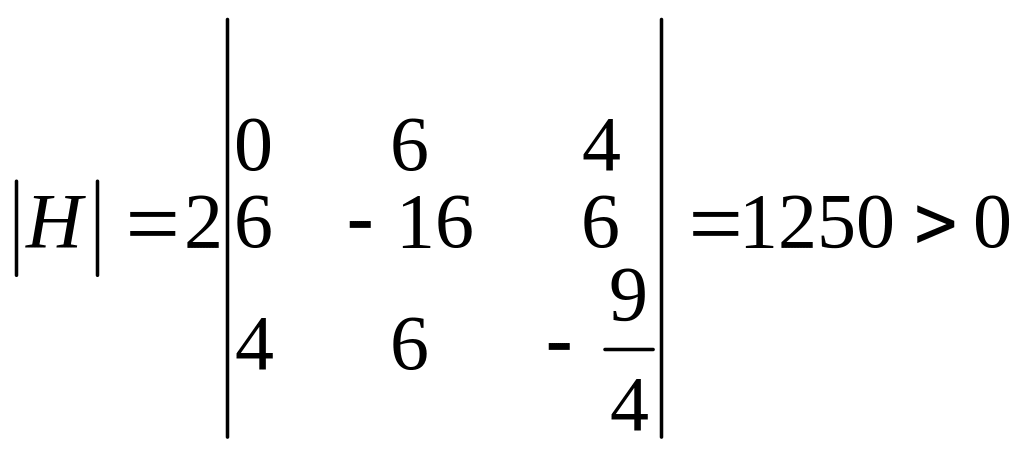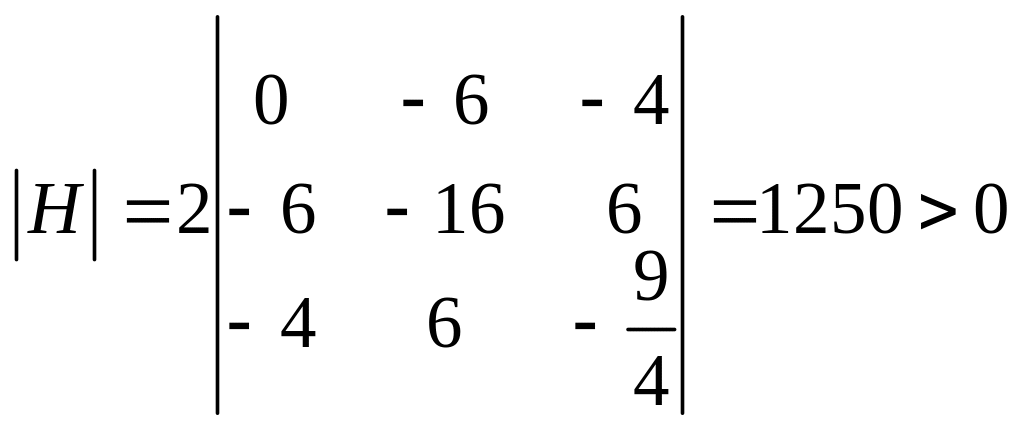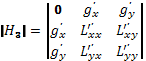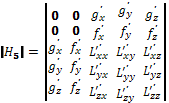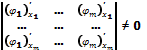Условный экстремум. Метод множителей Лагранжа. Первая часть.
Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.
Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.
Метод множителей Лагранжа для функций двух переменных.
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$
Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.
Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:
$$d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=F_{xx}^{»}dx^2+2F_{xy}^{»}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{»}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{»}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{»}-(varphi_{x}^{‘})^2 F_{yy}^{»} right)$$
Второй сомножитель (расположенный в скобке) можно представить в такой форме:
$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{»}} & normred{F_{xy}^{»}} \
varphi_{y}^{‘} & normred{F_{xy}^{»}} & normred{F_{yy}^{»}} end{array} right|
$$
Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{»} & F_{xy}^{»} \ F_{xy}^{»} & F_{yy}^{»} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.
Примечание относительно формы записи определителя $H$. показатьскрыть
Алгоритм исследования функции двух переменных на условный экстремум
- Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
- Решить систему $
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.$ - Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
- Составить определитель $H$ и выяснить его знак
- С учетом уравнения связи вычислить знак $d^2F$
Метод множителей Лагранжа для функций n переменных
Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):
$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$
Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:
$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:
$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$
Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы
$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$
выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
Пример №1
Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.
Решение
Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.
Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.
Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:
$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$
Запишем систему уравнений для определения стационарных точек функции Лагранжа:
$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$
Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:
$$
left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$
Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.
$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{»}=2lambda;; F_{xy}^{»}=0;; F_{yy}^{»}=2lambda.\
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{»} & F_{xy}^{»} \ varphi_{y}^{‘} & F_{xy}^{»} & F_{yy}^{»} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$
В точке $M_1(1;3)$ получим:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$
Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.
Аналогично, в точке $M_2(-1;-3)$ найдем:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$
Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.
Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.
Запись определителя $H$ в общем виде. показатьскрыть
Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:
$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=2lambda left( dx^2+dy^2right)
$$
Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.
Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.
Пример №2
Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.
Решение
Первый способ (метод множителей Лагранжа)
Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:
$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$
$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\
left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.
$$
Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.
$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{»} & F_{xy}^{»} \ varphi_{y}^{‘} & F_{xy}^{»} & F_{yy}^{»} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$
В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:
$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=8dx^2-2dxdy+18ydy^2
$$
Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.
$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$
Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.
Второй способ
Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:
$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$
Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.
$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$
Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{»}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{»}$:
$$u_{xx}^{»}=-18x+10;\
u_{xx}^{»}(M_1)=10;;u_{xx}^{»}(M_2)=-10.$$
Так как $u_{xx}^{»}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{»}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.
Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.
Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.
Пример №3
Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.
Решение
Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:
$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\
left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$
Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.
Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.
$$
F_{xx}^{»}=frac{lambda}{4}; ; F_{xy}^{»}=5; ; F_{yy}^{»}=lambda.
$$
Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:
$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$
В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:
$$
F_{xx}^{»}=frac{-5}{2}; ; F_{xy}^{»}=-10; ; dy=-frac{dx}{2}.\
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.
$$
Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:
$$
d^2 F=F_{xx}^{»}dx^2+2F_{xy}^{»}dxdy+F_{yy}^{»}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$
Подставляя $x=2$, $y=1$, $lambda=-10$, получим:
$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$
Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.
Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.
В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.
Условный экстремум
4 раздела
от теории до практики
2 примера
Примеры решения задач
видео
Примеры решения задач
-
Понятие условного экстремума.
Начать изучение
-
Прямой метод отыскания точек условного экстремума.
Начать изучение
-
Метод множителей Лагранжа.
Начать изучение
-
Несколько замечаний о методе множителей Лагранжа.
Начать изучение
Понятие условного экстремума.
Пусть на открытом множестве (G subset boldsymbol{R}^{n}) заданы функции (f_{0}(x)), (f_{1}(x), ldots, f_{m}(x)), причем (m < n), и пусть (E) — множество точек множества (G), удовлетворяющих системе уравнений
$$
f_{1}(x) = 0, ldots, f_{m}(x) = 0.label{ref1}
$$
Уравнения eqref{ref1} будем называть уравнениями связей (или просто связями).
Определение 1.
Точка (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in G) называется точкой условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in G cap S_{delta}(x^{0})) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Определение 2.
Точка (x^{0} in G) называется точкой строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in dot{S}_{delta}(x^{0}) cap G) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Аналогично определяются точки условного максимума. Точки условного максимума и минимума называются точками условного экстремума.
Прямой метод отыскания точек условного экстремума.
Предположим, что из системы уравнений eqref{ref1} можно выразить какие-либо (m) переменных (x_{i}) через остальные переменные. Тогда, подставив вместо соответствующих переменных (x_{i}) их выражения через остальные (n-m) переменных в функцию (f_{0}(x)), получим функцию (F) от (n-m) переменных.
Задача о нахождении точек экстремума функции (f_{0}(x)) при наличии связей eqref{ref1} сведется к задаче нахождения обычного (безусловного) экстремума функции (F), зависящей от (n-m) переменных.
Пример 1.
Найти точки условного экстремума функции (z = 1-x^{2}-y^{2}), если (x+y = 1).
Решение.
(vartriangle) Уравнение связи (x+y = 1) легко разрешается относительно переменной (y), а именно (y = 1-x). Подставив это выражение для (y) в функцию (z = 1-x^{2}-y^{2}), получаем, что (z = 1-x^{2}-(1-x)^{2} = 2x-2x^{2}). Функция (2x-2x^{2}) имеет максимум при (x = frac{1}{2}). Точка ((frac{1}{2}, frac{1}{2})) является точкой условного максимума функции (z(x, y)) при наличии связи (x+y = 1), причем (z_{max} = displaystylefrac{1}{2}). (blacktriangle)
Замечание 1.
Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.
Метод множителей Лагранжа.
Определение 3.
Рассмотрим функцию (n+m) переменных
$$
L(x, lambda) = f_{0}(x)+lambda_{1}f_{1}(x)+ldots+lambda_{m}f_{m}(x),nonumber
$$
где (x in G), а (lambda = (lambda_{1}, ldots, lambda_{m}) in boldsymbol{R}^{m}). Числа (lambda_{1}, ldots, lambda_{m}) называются множителями Лагранжа, а функция (L(x, lambda)) называется функцией Лагранжа.
Будем говорить, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, если
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{1}} (x^{0}, lambda^{0}) = 0, ldots, frac{partial L}{partial x_{n}} (x^{0}, lambda^{0}) = 0\
&\
& displaystylefrac{partial L}{partial lambda_{1}} (x^{0}, lambda^{0}) = f_{1}(x^{0}) = 0, ldots, frac{partial L}{partial lambda_{m}} (x^{0}, lambda^{0}) = f_{m}(x^{0}) = 0.
end{array}label{ref2}
$$
Теорема 1.
(Теорема Лагранжа).
Пусть (x^{0}) — точка условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{0, m}), непрерывно дифференцируемы в окрестности точки (x^{0}), причем в точке (x^{0}) ранг матрицы Якоби
$$
A = begin{pmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{1}}{partial x_{n}}(x)\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{m}}{partial x_{n}}(x)end{pmatrix}label{ref3}
$$
равен (m).
Тогда найдутся такие множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}), что ((x^0, lambda^0)) будет стационарной точкой функции Лагранжа.
Доказательство.
(circ) Так как (m < n), а ранг матрицы Якоби в точке (x^{0}) равен (m), то хотя бы один из миноров этой матрицы порядка (m) отличен от нуля.
Без ограничения общности можно считать, что
$$
begin{vmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{1}}{partial x_{m}}(x^{0})\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{m}}{partial x_{m}}(x^{0})end{vmatrix} neq 0,label{ref4}
$$
так как выполнения условия eqref{ref4} всегда можно добиться, перенумеровывая переменные и уравнения связей в нужном порядке.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)). Тогда существует окрестность (K'(x^{0}) = K’_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) такая, что
$$
f_{0}(x)-f_{0}(x^{0}) geq 0 mbox{при всех} x in E cap K’ (x^{0}).label{ref5}
$$
В силу непрерывности частных производных и выполнения условия eqref{ref4} можно применить теорему о неявных функциях. В силу этой теоремы найдется такая окрестность
$$
K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}) subset K'(x^{0}),nonumber
$$
в которой система уравнений связей eqref{ref1} определяет переменные (x_{1}, ldots, x_{m}) как неявные функции переменных (x_{m+1}, ldots, x_{m}). Это означает, что найдется единственный набор непрерывно дифференцируемых в окрестности (K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) функций (varphi_{i}(x_{m+1}, ldots, x_{n})), (i = overline{1, m}), таких, что
$$
varphi_{i}(x_{m+1}^{0}, ldots, x_{m}^{0}) = x_{i}^{0}, i = overline{1, m};label{ref6}
$$
$$
f_{i}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n}) equiv 0,label{ref7}
$$
$$
(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n})) in K_{1}(x_{1}^{0}, ldots, x_{m}^{0})nonumber
$$
при ((x_{m+1}, ldots, x_{n}) in K_{2}(x_{1}^{0}, ldots, x_{m}^{0})), (i = overline{1, m}).
Другими словами, множество (E cap K(x^{0})) можно задать следующим образом:
$$
begin{array}{cc}
& E cap K(x^{0}) = {x: x = (x_{1}, ldots, x_{n}), (x_{m+1}, ldots, x_{n}) in K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}),\
& \
& x_{i} = varphi_{i}(x_{m+1}, ldots, x_{n}), i = overline{1, m}}.
end{array}label{ref8}
$$
Так как (K(x^{0}) subset K'(x^{0})), то из неравенства eqref{ref5} следует, что функция (f_{0}(x)) принимает на множестве (E cap K(x^{0})) наименьшее значение в точке (x^{0}). Если взять представление множества (E cap K(x^{0})) в виде eqref{ref8}, то сложная функция
$$
F(x_{m+1}, ldots, x_{n}) = f_{0}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n})label{ref9}
$$
определена в окрестности (K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) и принимает в этой окрестности наименьшее значение в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Следовательно, в силу необходимых условий экстремума должно выполняться равенство (dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = 0). Воспользовавшись инвариантностью формы первого дифференциала и равенством eqref{ref9}, получаем, что
$$
sum_{k=1}^{n} frac{partial f_{0}(x^{0})}{partial x_{k}} dx_{k} = 0.label{ref10}
$$
В равенстве eqref{ref10} (dx_{m+1}, ldots, dx_{n}) есть дифференциалы независимых переменных, a (dx_{1}, ldots, dx_{n}) — дифференциалы функций (varphi_{i}, ldots, varphi_{m}), зависящих от (x_{m+1}, ldots, x_{n}). Для краткости будем говорить о независимых и зависимых дифференциалах.
Найдем связи между зависимыми и независимыми дифференциалами. Дифференцируя тождества eqref{ref7} в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} dx_{k} = 0, i = overline{1, m}.label{ref11}
$$
Умножая равенства eqref{ref11} на множители (lambda_{i}) и складывая полученные равенства с равенством eqref{ref10}, находим
$$
0 = sum_{k=1}^{n} left(frac{partial f_{0}}{partial x_{k}}+sum_{i=1}^{m} frac{partial f_{i}}{partial x_{k}} lambda_{i}right)_{x = x^{0}} dx_{k} = sum_{k=1}^{n} frac{partial L(x^{0}, lambda)}{partial x_{k}} dx_{k},label{ref12}
$$
где (L(x^{0}, lambda)) есть функция Лагранжа.
Подберем множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}) так, чтобы коэффициенты при зависимых дифференциалах в равенстве eqref{ref12} обратились в нуль, то есть
$$
frac{partial L(x^{0}, lambda)}{partial x_{k}} = frac{partial f_{0}(x^{0})}{partial x_{k}}+sum_{i=1}^{m} lambda_{i}^{0} frac{partial f_{i}(x^0)}{partial x_{k}} = 0, k = overline{1, m}.label{ref13}
$$
Система уравнений eqref{ref13} единственным образом определяет множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}), так как ее определитель eqref{ref4} отличен от нуля.
При выполнении условий eqref{ref13} уравнение eqref{ref12} примет вид
$$
sum_{k=m+1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} dx_{k} = 0.label{ref14}
$$
Так как дифференциалы независимых переменных (dx_{m+1}, ldots, dx_{n}), могут принимать любые значения, то из eqref{ref14} следует, что
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = m+1, ldots, n.label{ref15}
$$
Объединяя равенства eqref{ref13} и eqref{ref15}, получаем
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = overline{1, n}.nonumber
$$
Так как точка (x^{0} in E) и, следовательно, удовлетворяет уравнениям связей, то
$$
frac{partial L(x^{0}, lambda^{0})}{partial lambda_{j}} = f_{i}(x^{0}) = 0, j = overline{1, m}.nonumber
$$
Таким образом, ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)). (bullet)
Второй дифференциал функции Лагранжа, вычисленный при фиксированных (lambda_{1}^{0}, ldots, lambda_{m}^{0}) по переменным ((x_{1}, ldots, x_{n})) в точке ((x_{1}^{0}, ldots, x_{n}^{0})), будем обозначать через (d_{xx}^{2}L(x^{0}, lambda^{0})).
Таким образом,
$$
d_{xx}^{2}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}.label{ref16}
$$
Иногда вместо (d_{xx}^{2}L(x^{0}, lambda^{0})) будем писать (d^{2}L(x^{0}, lambda^{0})).
Обозначим через (E_{T}) следующее линейное многообразие в (boldsymbol{R}^{n}):
$$
E_{T} = left{xi = (xi_{1}, ldots, xi_{n}) in boldsymbol{R}^{n}: sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} xi_{k} = 0, i = overline{1, m}right}.label{ref17}
$$
Равенства eqref{ref11} означают, что (dx = (dx_{1}, ldots, dx_{n}) in E_{T}).
Теорема 2.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{1, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0}), причем в точке (x^{0}) ранг функциональной матрицы eqref{ref3} равен (m).
Тогда найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, a (d^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}).
Доказательство.
(circ) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) будет стационарной точкой функции Лагранжа, то есть выполняются условия eqref{ref2}. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию eqref{ref9}, имеющую безусловный экстремум в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие (d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) geq 0).
Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой eqref{ref9}, находим, что
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{0}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{0}}{partial x_{k}}(x^{0}) d^{2}x_{k} geq 0.label{ref18}
$$
Дифференцируя два раза в точке (x_{m+1}^{0}, ldots, x_{n}^{0}) тождества eqref{ref7}, получаем равенства
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{i}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{i}}{partial x_{k}}(x^{0}) d^{2}x_{k} = 0.label{ref19}
$$
Если умножить каждое из равенств eqref{ref19} на соответствующий множитель Лагранжа (lambda_{i}^{0}) и сложить с неравенством eqref{ref18}, то получаем неравенство
$$
d_{xx}^{2}L(x^{0}, lambda^{0})+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} geq 0.label{ref20}
$$
Последняя сумма в неравенстве eqref{ref20} равна нулю, так как ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа и в ней выполняются условия eqref{ref2}. Таким образом, (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}). (bullet)
Теорема 3.
(Достаточные условия условного экстремума).
Пусть функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0} in boldsymbol{R}^{n}), причем в точке (x^{0}) ранг функциональной матрицы (3) равен (m), и пусть ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)).
Тогда если (d_{xx}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) является точкой условного строгого минимума функции (f_{0}(x)) при наличии связей eqref{ref1}. Если (d_{xx}L(x^{0}, lambda^{0})) есть отрицательно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) — точка условного строгого максимума. Если (d_{xx}L(x^{0}, lambda^{0})) есть неопределенная квадратичная форма при (dx in E_{T}), то (x^{0}) не есть точна условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Доказательство.
(circ) Пусть
$$
E = {x: f_{i}(x) = 0, i = overline{1, m}}.label{ref21}
$$
По условию теоремы функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы eqref{ref3} равен (m). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие eqref{ref4} и что найдется такая окрестность (K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})), что множество (E cap K(x^{0})) можно задать формулой eqref{ref8}. На (E cap K(x^{0})) функция (f_{0}(x)) становится функцией (n-m) переменных (F(x_{m+1}^{0}, ldots, x_{n}^{0})), определенной формулой eqref{ref9} и имеющей непрерывные частные производные второго порядка.
По условию теоремы ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, то есть
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{k}} (x^{0}, lambda^{0}) = 0, k = overline{1, n};\
&\
& displaystylefrac{partial L}{partial lambda_{i}} (x^{0}, lambda^{0}) = f_{i}(x^{0}) = 0, i = overline{1, m}.
end{array}label{ref22}
$$
Из формул eqref{ref22} следует, что (x^{0} in E) и что
$$
d_{x}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = 0.label{ref23}
$$
Рассмотрим функцию (L(x, lambda^{0})) на множестве (E cap K(x^{0})). Очевидно, что
$$
L(x, lambda^{0}) = f_{0}(x) = F(x_{m+1}, ldots, x_{n}) mbox{при} x in E cap K(x^{0}).label{ref24}
$$
В силу инвариантности формы первого дифференциала из формулы eqref{ref24} следует, что
$$
dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = d_{x}L(x^{0}, lambda^{0}) = 0.label{ref25}
$$
Находя второй дифференциал от обеих частей равенства eqref{ref24} и используя равенства eqref{ref22}, получаем
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{j} partial x_{k}} dx_{j} dx_{k}+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = d_{xx}^{2}L(x^{0}, lambda^{0}).label{ref26}
$$
Пусть (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Так как множество (E cap K(x^{0})) можно задать в форме eqref{ref8}, то, выбирая (dx_{m+1}, ldots, dx_{n}) произвольным образом, получим, что дифференциалы (dx_{1},…, dx_{m}) зависят от ((dx_{m+1}, ldots, dx_{n})). Дифференцируя тождества eqref{ref7} в точке (x^{0}), получаем соотношения eqref{ref11}, которые означают, что (dx in E_{T}).
Из формулы eqref{ref26} тогда следует, что
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) > 0 mbox{при} dx_{m+1}^{2}+ldots+dx_{n}^{2} > 0.label{ref27}
$$
Из eqref{ref25} и eqref{ref27} получаем, что ((x_{m+1}^{0}, ldots, x_{n}^{0})) есть точка строгого минимума функции (F(x_{m+1}, ldots, x_{n})), то есть (x^{0}) есть точка строгого минимума функции (f_{0}(x)) на множестве (E cap K(x^{0})). Таким образом, (x^{0}) есть точка строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Аналогично рассматривается случай, когда (d_{xx}^{2}L(x^{0}, lambda^{0}) < 0), (dx in E_{T}), (dx neq 0). Если же (d_{xx}^{2}L(x^{0}, lambda^{0})) при (dx in E_{T}) есть неопределенная квадратичная форма, то не выполняется условие (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при (dx in E_{T}), являющееся, в силу теоремы 2, необходимым условием минимума. Поэтому (x^{0}) не есть точка условного минимума функции (f_{0}(x)) при связях eqref{ref1}. Аналогично доказывается, что (x^{0}) не может быть точкой условного минимума функции (-f_{0}(x)), а следовательно, и точкой условного максимума функции (f_{0}(x)) при связях eqref{ref1}. (bullet)
Замечание.
Если окажется, что (d_{xx}^{2}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма на всем пространстве (boldsymbol{R}^{n}), то (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Поэтому в этом случае в квадратичной форме (d_{xx}^{2}L(x^{0}, lambda^{0})) не нужно исключать зависимые дифференциалы.
Пример 1.
Найти экстремумы функции (x-2y+2z = u) и на сфере (x^{2}+y^{2}+z^{2} = 1).
Решение.
(vartriangle) Строим функцию Лагранжа
$$
L(x, y, z, lambda) = x-2y+2z+lambda(x^{2}+y^{2}+x^{2}-1)nonumber
$$
Стационарные точки функции Лагранжа находим, решая систему уравнений
$$
frac{partial L}{partial x} = 1+2lambda x = 0,quad frac{partial L}{partial y} = -2+2lambda y = 0,quad frac{partial L}{partial z} = 2+2lambda z = 0,nonumber
$$
$$
frac{partial L}{partial lambda} = x^{2}+y^{2}+z^{2}-1 = 0.nonumber
$$
Исключая из этой системы (x, y, z), получаем (displaystyleleft(frac{1}{2lambda}right)^{2}+left(frac{1}{lambda}right)^{2}+left(frac{1}{lambda}right)^{2}-1 = 0), откуда (lambda_{1} = displaystylefrac{3}{2}), (lambda_{2} = -displaystylefrac{3}{2}).
У функции Лагранжа есть две стационарные точки,
$$
M_{1} = left(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)quad mbox{и}quad M_{2} = left(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right).nonumber
$$
Так как (d^{2}L(M_{1}) = 3(dx^{2}+dy^{2}+dz^{2}) > 0), a (d^{2}L(M_{2}) = -3(dx^{2}+dy^{2}+dz^{2}) < 0) при (dx^{2}+dy^{2}+dz^{2} > 0), тo (displaystyleleft(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)) — точка условного минимума, a (displaystyleleft(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right)) — точка условного максимума функции (u = x-2y+2x) при наличии ограничения (x^{2}+y^{2}+z^{2}-1 = 0), Причем (u_{min} = -3), (u_{max} = 3). (blacktriangle)
Пример 2.
Найти условные экстремумы функции (f_{0}(x, y) = e^{axy}), (a neq 0), при наличии ограничения (f_{i}(x, y) = x^{3}+y^{3}+x+y-4 = 0).
Решение.
(vartriangle) Построим функцию Лагранжа:
$$
L(x, y) = e^{axy}+lambda(x^{3}+y^{3}+x+y-4).nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x} = aye^{axy}+lambda(3x^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial y} = axe^{axy}+lambda(3y^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial lambda} = x^{3}+y^{3}+x+y-4 = 0.
end{array}label{ref28}
$$
Умножая первое уравнение на (x), а второе на (y) и вычитая, получаем
$$
lambda(3x^{3}-3y^{3}+x-y) = lambda(x-y)(3x^{2}+3xy+3y^{2}+1) = 0.label{ref29}
$$
Если (lambda = 0), то из первых двух уравнений eqref{ref28} получаем (x = y = 0). Но (x = y = 0) не удовлетворяет уравнению связи. Итак, (lambda neq 0), поэтому из eqref{ref29} следует, что (x = y) (второй сомножитель всегда положителен: (3(x^{2}+xy+y^{2})+1 > 0)). Подставляя (x = y) в уравнение связи, получаем (x^{3}+x = 2), (x = y = 1). Первое из уравнений eqref{ref28} дает при (x = y = 1) значение (lambda = -displaystylefrac{a}{4} e^{a}).
Итак, ((1, 1, -displaystylefrac{a}{4} e^{a})) есть единственная стационарная точка функции Лагранжа.
Так как
$$
d(e^{axy}) = a(x dy+y dx) e^{axy},nonumber
$$
$$
d^{2}(e^{axy}) = a^{2}(x dy+y dx)^{2} e^{axy}+2a dx dy e^{axy},nonumber
$$
$$
d^{2}(x^{3}+y^{3}+x+y-4) = 6x dx^{2}+6y dy^{2},nonumber
$$
то для второго дифференциала функции Лагранжа при (lambda_{0} = -displaystylefrac{a}{4} e^{a}) и (x = y = 1) получается следующее выражение:
$$
d^{2}L(1, 1, lambda_{0}) = ae^{a}left[a(dx+dy)^{2}+2 dx dy-frac{3}{2}(dx^{2}+dy^{2})right].label{ref30}
$$
Дифференцируя уравнение связи при (x = y = 1), получаем, что (dy+dx = 0). Подставляя (dy = -dx) в уравнение eqref{ref30}, получаем равенство
$$
d^{2}L(1, 1, lambda_{0}) = -5ae^{a}dx^{2}.label{ref31}
$$
Поэтому при (a < 0) в точке (1,1) будет условный минимум, а при (a > 0) — условный максимум функции (f_{0}(x, y)) при наличии связи (x^{3}+y^{3}+x+y = 4), причем экстремальное значение функции равно (e^{a}). (blacktriangle)
Замечание.
Уравнение связи (x^{3}+y^{3}+x+y = 4) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.
Несколько замечаний о методе множителей Лагранжа.
Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.
В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.
|
Определение условного экстремума Первый Второй Геометрическая Окаймленный Последовательность |
Определение
условного экстремума
Определение.
Условным экстремумом функции
называется максимум или минимум функции,
достигнутый при условии, что ее аргументы
связаны некоторым уравнением
:
В дальнейшем экстремумы, не являющиеся
условными, будем называть безусловными.
П
ри
нахождении условных экстремумов функции
аргументы
и
уже нельзя рассматривать как независимые
переменные. Они связаны между собой
соотношением
,
которое называется уравнением связи.
Для пояснения различия между локальным
(безусловным) и условным экстремумом
рассмотрим функцию
.
Она описывает так называемый параболоид
вращения и имеет безусловный минимум
в точке, указанной темной стрелкой (рис.
7.7). Добавим уравнение связи (ограничение
в виде равенства)
,
описывающее плоскость. Задача теперь
формулируется так: найти экстремум
функции
,
рассматривая среди всех значений
только те, которые в совокупности
образуют плоскость
.
Другими словами, экстремум следует
искать среди точек, принадлежащих
одновременно обеим поверхностям,
изображенным на рис. 7.7. Эти точки образуют
красную линию. Минимальное значение
(условный минимум) достигается в точке,
указанной белой стрелкой.
З
амечание.
Условный экстремум может существовать
не в одной точке. В частном случае это
может быть линия, как представлено на
рис. 7.8. Здесь стрелкой указан достигаемый
на отрезке прямой условный минимум
функции
при дополнительном условии связи
.
Локальный минимум функции
также существует. Он находится в точке
с координатами
.
Опишем два метода поиска условного
экстремума.
Первый метод
нахождения условного экстремума
Пусть уравнение связи
может быть разрешено относительно
зависимой переменной:
.
Подставим функцию
в исследуемую на экстремум функцию
.
Получим функцию одного аргумента
,
в которой учтено условие связи. Далее
надо исследовать функцию
на локальный экстремум, который будет
являться для функции
условным экстремумом.
ПРИМЕР 1. Исследовать
на условный экстремум функцию
при условии
.
Решение. Из уравнения
связи найдем
и подставим в исследуемую функцию
.
Исследуем ее на
экстремум:
.
Критическая точка
.
Вторая производная
.
Поэтому в точке
существует минимум функции
,
соответственно в точке с координатами
,
— условный минимум функции
.
Его значение
.
На рис. 7.9 представлены описываемые
обеими функциями пересекающиеся
поверхности. На точку условного минимума
указывает стрелка.
ПРИМЕР 2. Исследовать
на условный максимум функцию
при условии
.
Решение. Подставим
в исследуемую функцию величину
из уравнения связи. Получим
.
1. Если
,
то
.
2
.
Если
,
то
,
причем значение
больше либо равно значению
в любой точке
при условии
.
Следовательно, 1 будет максимальным
значением функции
,
аргументы которой связаны уравнением
,
т.е.
.
Условный минимум равен нулю при
.
Поверхность
и плоскость
представлены на рис. 7.10. Линии их
пересечения, где функция
достигает максимального значения,
выделены белым цветом.
Непосредственная
подстановка используется в простейших
случаях. Часто подобная подстановка
приводит к громоздким выражениям для
исследуемой функции, или бывает
невозможно решить уравнение связи
относительно зависимой переменной. В
этих случаях используется эффективный
метод, предложенный французским
математиком Жозефом Луи Лагранжем
(1736-1813).
Замечание. Рассмотренная нами в
последнем примере функция является
обобщением двухфакторной (зависящей
от двух переменных) производственной
функции Леонтьева, которая имеет вид:
.
Здесь переменные
полагаются неотрицательными и обозначают
соответственно затраты капитала и
затраты труда, параметры
являются положительными и отвечают
соответственно за фондоемкость продукции
и трудоемкость продукции.
Второй метод
нахождения условного экстремума (метод
Лагранжа)
Идея метода состоит в замене функции
,
исследуемой на условный экстремум, на
функцию, которая может быть исследована
на локальный экстремум. Эта функция
,
называемая функцией Лагранжа, составлена
из функции
,
функции ограничения
и некоторого коэффициента
,
их соединяющего (множителя Лагранжа)
Варьируя величину
,
можно добиться совпадения условного
экстремума функции
со стационарной точкой функции Лагранжа.
Д
ля
иллюстрации сказанного рассмотрим
задачу,
На рис. 7.11. изображены функции Лагранжа
при различных значениях коэффициента
(
).
Это параболоиды вращения. Кроме того,
изображено множество точек
в виде плоскости, а также функция
(частный случай функции Лагранжа при
).
Меняя
,
находим ту из функций
,
локальный экстремум которой совпадает
с условным экстремумом функции
.
Как видно из рисунка, это достигается
при
.
Для лучшего обзора картины на рисунке
вырезаны части параболоидов.
Перейдем к обоснованию метода. Уравнение
связи
определяет величину
как функцию
от переменной
.
При подстановке
в исследуемую функцию
получим функцию одной переменной
,
производная которой в точке возможного
условного экстремума
равна
нулю, или, что равносильно этому, должен
быть равен нулю дифференциал функции:
, (2)
причем
отличны от нуля.
Из уравнения связи
соотношение между дифференциалами
аргумента и функции в любой точке, а
следовательно, и в точке
,
определяется равенством
. (3)
Умножим равенство (3) на некоторое число
(множитель Лагранжа), которое определим
позже, и сложим с равенством (2)
. (4)
Слева в равенстве (4) стоит дифференциал
функции
,
которую называют функцией Лагранжа.
Равенство
при изучении нами локального экстремума
получалось исходя из того, что
.
Это давало необходимые условия локального
экстремума. В рамках логической цепочки
рассуждений о локальном экстремуме
функции
,
потребуем выполнения условий
в точке
.
С этой целью выберем множитель
так, чтобы было выполнено равенство
. (5)
Тогда из соотношения
получим
. (6)
Теперь можно сказать, что равенства (5)
и (6) выражают необходимые условия
локального экстремума в точке
функции Лагранжа
.
Иногда говорят, что система
определяет условия первого порядка при
нахождении условного экстремума.
Геометрическая
интерпретация необходимых условий
локального экстремума
Интересна геометрическая интерпретация
решений системы. Введем векторы
и
.
Из системы легко получить равенство
,
откуда следует коллинеарность векторов
и
.
Построим фрагмент карты линий уровня
функции
(рис. 7.12). Пунктиром обозначен график
функции
.
Градиенты
и
перпендикулярны линиям уровня в точках
и
соответственно. Векторы
и
перпендикулярны к линии
также в точках
и
.
При движении справа налево вдоль кривой
пересекаются линии уровня функции
,
причем каждое следующее пересечение
происходит с линией более низкого
уровня. Градиенты
и
в каждой точке направлены под разными
углами, как это имеет место, например,
в точке
.
Коллинеарность векторов
и
возникает в точке
.
Следовательно, в этой точке выполнены
необходимые условия локального экстремума
функции Лагранжа. При дальнейшем движении
вдоль кривой уравнения связи
пересекаются линии более высокого
уровня. Можно заключить, что в точке
имеется минимум. Если бы кривая уравнения
связи, выйдя из точки
,
продолжала пересекать линии все более
низкого уровня, точка
оказалась бы седловой (или точкой
минимакса).
Окаймленный гессиан
Для функции Лагранжа
получены необходимые условия локального
экстремума. Теорема о достаточных
условиях локального экстремума функции
подобна ранее сформулированной теореме
о достаточных условиях локального
экстремума для функции
,
но между ними существуют отличия.
Замечание. Следует учитывать, что
условный минимум функции
может и не соответствовать безусловному
минимуму функции Лагранжа в той же
точке. Условному экстремуму с ограничением
типа равенства соответствует лишь
стационарность функции Лагранжа.
(об исследовании на экстремум по
окаймленному гессиану)
Пусть всюду в окрестности точки
:
1. определена функция
;
2. обе частные производные первого
порядка
непрерывны, причем
;
3. все частные производные второго
порядка
непрерывны;
4. дифференциалы
и
связаны между собой соотношением
,
причем
;
5. второй дифференциал
в точке
является знакоопределенной квадратичной
формой.
Тогда функция
имеет в точке
локальный экстремум, а функция
условный экстремум:
а) при
локальный минимум,
б) при
локальный максимум.
◄ Доказательство теоремы заключается
в обосновании использования в данной
теореме выводов ранее рассмотренной
теоремы о достаточных условиях для
функции
при исследовании на локальный экстремум.
Уравнение связи
приводит к существованию зависимости
между дифференциалами
и
.
Как известно, второй дифференциал не
обладает инвариантностью формы. Поэтому
выражение для
требует уточнения. Найдем дифференциал
от дифференциала
в точке
,
считая
зависимой переменной:
.
Здесь
в силу непрерывности вторых производных,
в стационарной точке
.
Поэтому второй дифференциал функции
Лагранжа в точке
будет совпадать со вторым дифференциалом
функции Лагранжа двух независимых
переменных
.
Следовательно, можно воспользоваться
выводами о знакоопределенности
и соответственно знаке
по знакам угловых миноров матрицы Гессе:
1. если
,
функция
имеет в точке
минимум;
2. если
,
функция
имеет в точке
максимум.
Если сделать вывод о наличии экстремума
невозможно при произвольных
и
,
найдем
из равенства
и подставим в
:
.
Вынесем за скобки множитель
:
.
Эта формула может быть приведена к
удобному для использования виду. Второй
сомножитель в произведении вычисляется
как определитель матрицы в точке
.
Матрица
называется
окаймленной матрицей Гессе, а определитель
— окаймленным гессианом. Если гессиан
,
то
,
что указывает на безусловный максимум
функции
и условный максимум функции
.
Если
,
то
.
Это соответствует безусловному минимуму
функции
и условному минимуму функции
.
Обоснование закончено. ►
Замечание 1. Если
,
метод не работает. Поскольку точка
является стационарной для функции
Лагранжа, в этой точке возможен уcловный
экстремум функции
.
Замечание 2. Метод Лагранжа не указывает
условий, при которых условный экстремум
отсутствует.
Замечание 3. При составлении функции
Лагранжа можно брать неопределенный
множитель с любым знаком. Выбор
определяется соображениями удобства.
З
амечание
4. Вычисляемый неопределенный
множитель
может оказаться любым действительным
числом, включая иррациональное число.
В частном случае при
условный экстремум исследуемой функции
совпадает с ее локальным экстремумом,
если таковой существует. На рис. 7.13
представлено графическое решение задачи
на условный экстремум функции
с уравнением связи
.
Линия пересечения изображена красным
цветом. Стрелкой указан условный
экстремум функции
,
совпадающий с ее локальным максимумом.
Вычисленное значение множителя
.
Последовательность
действий при отыскании условных
экстремумов функции двух переменных
Задача. Найти условный экстремум функции
при наличии уравнения связи
.
Краткая формулировка:
(7)
Решение.
1) Составляем функцию Лагранжа
.
2) Находим производные функции
и приравниваем их нулю. Присоединяем
уравнение связи, получая систему из
трех уравнений для определения координат
возможных точек экстремума
и множителя Лагранжа
.
3) Строим окаймленную матрицу Гессе,
вычисляем окаймленный гессиан в точке
и делаем вывод о наличии условного
экстремума. Находим значение функции
в точке условного экстремума.
ПРИМЕР. Провести
исследование на условный экстремум
Решение. Составим
функцию Лагранжа
и запишем систему
уравнений из первых производных и
уравнения связи:
(8)
Из первых двух
уравнений получаем
(9)
Очевидно, что точка
с координатами
является решением системы (9), но не
удовлетворяет последнему уравнению
системы (8). Полагая теперь
,
разделим первое уравнение системы (9)
на второе
и решим полученное
уравнение. Корни уравнения
.
Подставив
в первое или второе уравнения системы
(8), найдем связь между переменными
и
:
.
Подстановка выражения
в третье уравнение системы (7) дает
.
Соответственно
.
Для
получим
.
Итак, получены четыре стационарные
точки
,
:
,
,
,
.
Найдем все вторые
производные функции Лагранжа:
.
Составим матрицу
Гессе из вторых производных
.
Подстановка любого
значения множителя из
приводит к равенству нулю минора
.
Поэтому обратимся к окаймленной матрице
Гессе
.
Рассмотрим
последовательно четыре стационарные
точки.
1)
.
.
В точке
достигается условный минимум
.
2)
.
.
Здесь условный
минимум
.
3)
.
.
В точке
достигается условный максимум
.
4)
.
.
Здесь условный
максимум
.
Н
а
рисунках 7.14 и 7.15 представлено графическое
решение задачи на условный экстремум.
Пересечения
поверхностей изображены с двух точек
обзора, отличающихся приблизительно
на
.
Стрелками показан один из минимумов
(рис. 7.14) и один из максимумов (рис. 7.15).
Для случая трех переменных исследование
функции на условный экстремум при одном
уравнении связи
методом Лагранжа приводит к окаймленной
матрице Гессе 4-го порядка

В стационарной точке
рассматриваются окаймленные гессианы
3-го
и 4-го
порядков, где
и
.
Условия
,
являются достаточными для достижения
в данной точке условного минимума.
Условия
,
являются достаточными для достижения
в данной точке условного максимума.
Условие
является достаточным для утверждения
об отсутствии в данной точке экстремума.
Условный экстремум может существовать
при наличии нескольких уравнений связи.
Задача нахождения условного экстремума
функции 3-х переменных с 2-мя уравнений
связи формулируется следующим образом
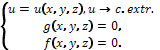
Если решение системы из уравнений связи
с последующей подстановкой результатов
в исследуемую функцию затруднено,
строится функция Лагранжа в виде
Необходимые условия содержат 5 уравнений
c 5-ю переменными
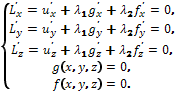
Решив систему уравнений и найдя
стационарные точки, исследуем окаймленный
гессиан
.
Если
в рассматриваемой стационарной точке,
то достигается минимум, если
,
то максимум.
Условный экстремум
функции n
переменных с m
уравнениями связи
Найдем экстремум скалярной функции
векторного аргумента
,
аргумент которой удовлетворяет уравнению
связи
,
представляющему собой равенство нулю
векторной функции векторного аргумента.
Здесь
,
,
причем
Задача на условный экстремум формулируется
так
Будем полагать, что производные
,
непрерывно дифференцируемы по вектору
,
градиенты функции
линейно независимы
при
одновременно, где
Составим функцию Лагранжа
.
где
,
скалярное произведение вектор-множителя
Лагранжа на вектор-функцию ограничений.
Рассмотрим векторную систему
которая состоит из двух векторных
равенств с двумя векторными переменными
и
и содержит в координатах
векторов
равенств с
переменными. Из первых n
равенств с
переменными выберем m
соотношений (например, первые m
равенств) и подберем для них m
координат вектора
так, чтобы правые части равенств
обратились в нуль.
Подобрать соответствующие m
значений
можно, используя правило Крамера
Определитель
в силу линейной независимости столбцов
определителя (независимости градиентов
функции
).
Значения
подставим в следующие
соотношений 1-го векторного равенства
и потребуем обращения их в нуль. Эти
равенства составят
уравнений для переменных
Добавим m уравнений
связи. Получится система из n
уравнений с n переменными
для нахождения координат вектора
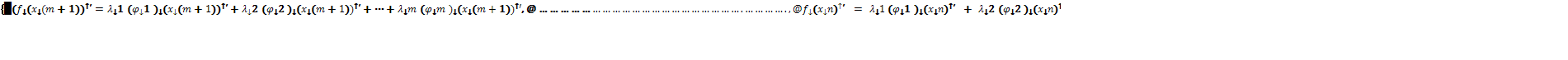
Подобный алгоритм нахождения
позволяет утверждать, что в формуле
разложения функции Лагранжа в ряд
Тейлора в окрестности точки
1-й дифференциал функции Лагранжа
обращается в нуль. Действительно,
Поведение приращения функции Лагранжа
будет определяться вторым дифференциалом
.
Следовательно, в точке
разыскивается локальный экстремум
функции Лагранжа, а значит, условный
экстремум функции
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #