Как найти экстремум функции в excel - Avtoru.top - решение различных проблем

history 14 января 2021 г.

Группы статей

Надстройка «Поиск решения»

Пусть дана функция с несколькими переменными F(x1, x2, …)=a1*x1+a2*x2+… Также даны граничные условия в виде b1*x1+b2*x2+…<=c (несколько условий). Нужно найти экстремум функции F (минимум или максимум). Это классическая задача для Поиска решения MS EXCEL, кроме того это линейная модель. Сделаем удобную форму для таких задач и покажем как настроить Поиск решения.

Задача

Пусть дана явная функция с 4 переменными:

Также даны несколько (семь) граничных условий (англ: restrictions, constraints):

Требуется найти максимум функции F.

Создание модели

Решим задачу с помощью инструмента MS EXCEL

Поиск решения

, хотя можно ее решить и другим способом, например аналитически.

На рисунке ниже приведена модель, созданная для решения задачи (см.

файл примера

).

Переменные (выделено зеленым)

. В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с

оптимизацией затрат

. Хотя математически — это эквивалентные задачи, только количество переменных разное.

После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).

Ограничения (выделено серым)

. Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4<=-3. В первом случае х1>=0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).

Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы =

СУММПРОИЗВ($D$19:$D$22;C26:C29)

. В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).

Целевая функция (выделено красным)

.

Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про

пропускную способность трубопровода

Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.

Источник

Экстремум функции

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство(f(x₁) < f (x₂) (f(x₁) >f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a,b] возрастает (убывает), то ее производная на этом отрезке f ‘ (x) > 0 , (f ‘ (x) < 0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность x_о, для всех точек которой верно неравенство f(x) ≤ f(x_о), (f(x) ≥f(x_о)).

Точки максимума и минимума называются точками экстремума, значения функции в них — ее экстремумами.

Точки экстремума

Необходимые условия экстремума. Если x_о является точкой экстремума функции f(x), то либо f ‘ (x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в них определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о — критическая точка. Если f ‘ (x) при переходе через x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную f ‘ (x) в окрестности x_о и вторую производную f » (x₀) в самой точке x_о. Если f ‘ (x_о) = 0, f » (x₀)>0, (f » (x₀) <0), то x_о является точкой локального минимума (максимума) функции f(x). Если же f » (x₀)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y =f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 1. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.

Задачи на нахождения экстремума функции

Пример 3. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR 2 Н Þ Н = V/pR 2 =16p/ pR 2 = 16/ R 2 . Значит, S(R) = 2p(R 2 +16/R). Находим производную этой функции:
S ‘ (R) = 2p(2R- 16/R 2 ) = 4p (R- 8/R 2 ). S ‘ (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.

Пример 4. Найти экстремумы функцииf(x) = 2x 3 — 15x 2 + 36x — 14.

Пример 5. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется c погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

[expert_bq id=»1570″]Найти наибольшее и наименьшее значения функции z 5xy-4 , если переменные x и y положительны и удовлетворяют уравнению связи frac frac-1 0. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Продолжим разбор примеров на нахождение условного экстремума функций нескольких переменных. В первой части мы работали с функциями двух переменных, а здесь обратимся к функциям трёх переменных. Если понадобятся примеры для функций большего количества переменных, отпишите мне, пожалуйста, на форум или в комментариях.

Условный экстремум функций многих переменных. Метод множителей Лагранжа. Первая часть.

Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
[expert_bq id=»1570″]Определяем положение глобального минимума модельной функции , который или принимается в качестве глобального минимума функции f x , или уточняется с помощью какого-либо метода локальной оптимизации. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Рассмотрим одномерную задачу условной глобальной оптимизации: найти минимум одномерной многоэкстремальной функции f ( x ), определенной в замкнутой области допустимых значений D = [ a ; b ] и имеющей в этой области конечное число минимумов (4.1).

Второй способ

Напомню, что значения функции $f(z)$ при заданных условиях связи совпадают с значениями функции $u(x,y,z)$, т.е. найденный экстремум функции $f(z)$ и есть искомым условным экстремумом функции $u(x,y,z)$. В принципе, несложно также указать остальные координаты точки условного экстремума:

Источник

Обновлено: 24.05.2023

VBA Excel. Нахождение экстремума функции Методом Золотого Сечения.

О методе Золотого Сечения:

Безусловно, простой и быстрый метод. И как водится, скорость не способствует аккуратности. Это я о том, что если на заданном интервале поиска будут находиться несколько минимумов (максимумов), то данный алгоритм легко может вернуть локальный (не самый большой, не абсолютный) экстремум.

Задание:

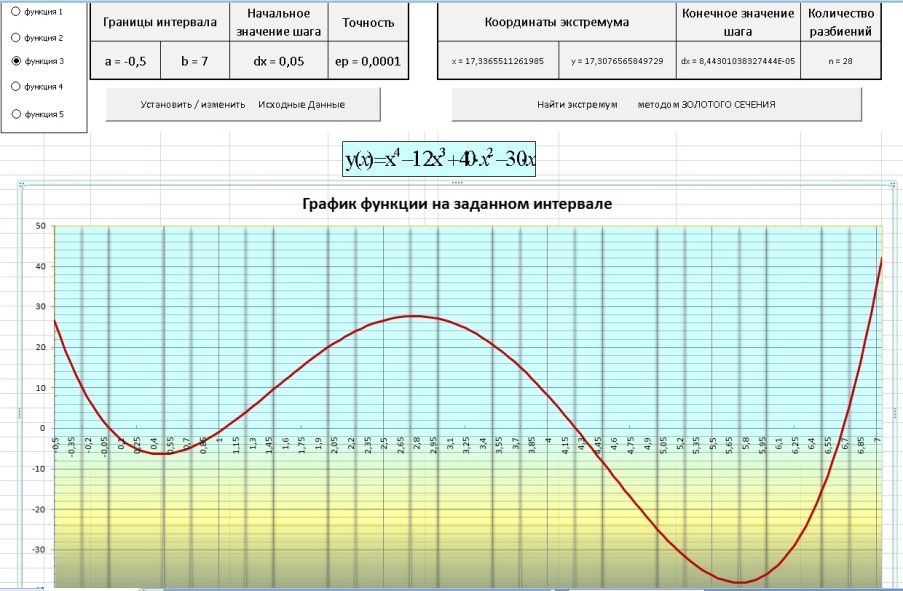
Составить программу позволяющую протестировать алгоритм поиска экстремума методом Золотого Сечения на примере пяти произвольных функций. Исходными данными для поиска должны являться границы интервала, точность и тип экстремума (MAX или MIN). Программа должна отображать график функции на заданном интервале и координаты точки экстремума.

Модуль листа Excel (SheetGoldCutting), на котором как на форме будут располагаться необходимые органы управления ходом тестирования;
Форма для ввода данных FormDann;
Класс ExtremGC, вычисляющий координаты точки экстремума с заданной точностью, а также массив точек графика функции на заданном интервале (для отображения на диаграмме);
Стандартный модуль GoldCutting для описания глобальных констант, переменных и функций.

Например, так.

Рис.1 Рабочий лист Excel с диаграммой, двумя командными кнопками и кнопками выбора функции

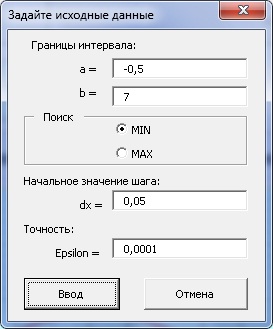
Рис.2 Форма для ввода исходных данных

Данная форма вызывается явно при щелчке по первой командной кнопке (расположенной на листе Excel) или косвенно, если в момент нажатия на вторую командную кнопку (расположенную на листе Excel), исходные данные не обеспечивают необходимых условий начала выполнения алгоритма.
Для удобства пользователя, все элементы TextBox допускают ввод только числовых значений.
При щелчке по кнопке «Отмена» все переменные получат значения, которые существовали на момент открытия формы.

При открытии файла (если макросы включены) или включении макросов (если они были отключены на момент открытия файла) выполняется обработчик события с целью задать (определить) одну из заготовленных функций, как функцию для тестирования по умолчанию. Для этого достаточно отметить одну (например, первую) OptionButton (или как часто называют — радиокнопку) и вызвать макрос назначенный этой кнопке.

Private Sub Workbook_Open()
‘ радиокнопки нумеруются в этой книге от 5 до 9.
‘ Поэтому по умолчанию выделяю первую кнопку.
Sheets(1).Shapes(«Option Button 5»).ControlFormat.Value = 1
SheetGoldCutting.OptBut1_Click
End Sub

Метод theAlgoritm класса ExtremGC, который, собственно, и выполняет определение координат точки экстремума выглядит приблизительно так:

‘Нахождение экстремума функции на отрезке. Метод золотого сечения
Public Sub theAlgoritm(v1 As Double, v2 As Double, v3 As Double, v4 As Double, findMax As Boolean)
Dim x1 As Double, x2 As Double, y1 As Double, y2 As Double, sme As Double
FullArrayOnly v1, v2, v3, v4 ‘для проверки допустимости аргумента

If Not BadDann Then

zc = (1 + Sqr(5)) / 2
n = 0 ‘количество разбиений (переменная модуля класса)
Do While b — a > ep
sme = (b — a) / zc
x1 = b — sme: x2 = a + sme
y1 = theFunc(x1): y2 = theFunc(x2)
If findMax Then
‘поиск максимума
If y1 = y2 Then
a = x1
Else
b = x2
End If
End If
n = n + 1 ‘количество разбиений (переменная модуля класса)
Loop
dxk = Abs(b — a) ‘ конечное значение шага
xe = (a + b) / 2: ye = theFunc(xe) ‘ результат: координаты точки экстремума

Кому интересен остальной код – обращайтесь…
Если нужно что-то изменить в проекте под Ваши требования (например, заменить функции) – пожалуйста, проблем не будет!

исходный код уже открыт. Используйте !

Если у Вас не появляется форма ввода данных, значит вы забыли включить макросы…

Хочу обратить внимание, что для первой функции значения аргумента не могут быть меньше или равны нулю.

Чтобы увидеть, как ошибается алгоритм и находит локальный экстремум вместо абсолютного, задайте достаточно большой интервал (например: от 0 до 25) для 4 или 5 функций, имеющих явную периодичность…

Область определения функции (-∞;+∞)
Составим таблицу знаков функции f(x), полагая x равным:
a) критическим значениям функции (корням производной) или близким к ним;
b) граничным значениям (исходя из области допустимых значений неизвестного).
Имеем: 3х2+2х
Производная имеет 2 корня: x1=0; x2=-2/3

знак f(x)

Из таблицы видно, что функция 1 раз меняет знак, значит уравнение имеет 1 корень.
Уменьшим промежуток, в котором находится корень:

знак f(x)

Следовательно, x1 принадлежит промежутку ( -2; -2/3 ) . Используя процедуру Поиск решения найдем
а) все корни данного уравнения
Найдем значение функции по формуле =A1^3+A1^2+3. Эту формулу вставим в ячейку В1
Выберем Сервис→Поиск решения. Установим параметры:

параметры окна Поиск решения

Получим корень уравнения x1=-1.864 y=0

б) все экстремумы данной функции.
Найдем экстремумы функции с помощью команды Данные→Поиск решения. Установим параметры для поиска максимума:

поиск максимума с помощью процедуры Поиск решения

максимум функции

Найдем минимум функции с помощью процедуры Поиск решения. Введем параметры:

параметры окна поиск решения для нахождения минимума функции

Получим минимум в точке х=0, y=3.

значение минимума функции, найденное с помощью Поиска решений

Введем таблицу значений функции на промежутке [-2;1] с шагом 0,2. На основании данных таблицы построим график функции f(x). Для этого выберем команду главного меню Вставка→Диаграмма.
Получим график функции

Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).

Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.

Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).

Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).

Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).

Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

Найти минимум функции методом золотого сечения.
Помогите пожалуйста. Нужно найти минимум функции у=х*х-sinх методом золотого сечения. в СИ.

Найти максимум функции методом золотого сечения
Здравствуйте, в университете задали задачу, которую необходимо сделать в Mathcad’е. Необходимо.

Найти минимум функции x^2-sinx методом золотого сечения
Найти минимум функции x^2-sinx методом золотого сечения

«Помогите» = «сделайте всё за меня»?
Как насчёт график нарисовать в том же Экселе и определить пределы расположения локальных экстремумов? Сколько их вообще будет?
Вот блок-схема нахождения локального минимума функции на отрезке [a;b] с заданной точностью
jogano, К сожалению, я абсолютно ничего не понимаю в этом.. Это так решается? К примеру в решении приводится один из локальных экстремумов — min функции

Если решение верное, то мне надо таким же образом получить max функции, хотя я не уверен, что именно так должно решаться, даже не имею представления

Хочу сообщить, что тема все еще АКТУАЛЬНА. Спасибо!

jogano, а как быть, если в условии задачи не указаны отрезки [a;b]?

Вот блок-схема нахождения локального минимума функции на отрезке [a;b] с заданной точностью
Добрый вечер, jogano, хочу уточнить одну вещь. В блок-схеме приводится метод решения задачи, при известных отрезках (интервалах) [a;b]. В моем же случае отрезки не указаны, как мне определить эти отрезки, для дальнейшего решения задачи? Спасибо!

Dr_Mann, вам уже промолчали по этому поводу. Намёков вы, видимо, не понимаете. Отвечаю прямо — когда я делал вашу задачу, я сначала нарисовал график в Экселе, и визуально определил нужный отрезок. Как это сделать без графика, я не знаю. Надеюсь, больше вопросов вида «а если не рисовать?», «а как можно по другому?» не будет.
Добрый вечер, jogano, хочу уточнить одну вещь. В блок-схеме приводится метод решения задачи, при известных отрезках (интервалах) [a;b]. В моем же случае отрезки не указаны, как мне определить эти отрезки, для дальнейшего решения задачи? Спасибо!
Постройте график функции в том же самом табличном редакторе которым вы пользуетесь, Excel или Calc из libreOffice / OpenOffice.
WH, Получилось вот так, по-моему не совсем правильно..

Потому что для построения тоже нужны значения для аргумента x. Я ввел значения от 0 до 10, наверно нужны другие значения..
Нужно просто взять большее чило значений, не через 1, а к примеру через 0,1, и копированием формулы построить ряд данных, секундное дело. И подобрать подходящий вид графика и его тип. Если Вам нужно в пределах 0. 10, то вот что у меня получилось в программе Calc, все выглядит вполне нормально.
Ответ у Вас должен получиться такой
х = 2.3896
f(x) = 0.5979
правда я не в табличном редакторе считал, так что не спрашивайте меня как это сделать в таблицах.
WH, Так получается я могу любые значения х ввести и всегда будет разный график и соответственно разные интервалы. Возвращаясь к самой задачи, какие значения х мне следует вводить, чтобы получить верный график функции и его верные интервалы [a;b], для дальнейшего решения моей задачи? От 0 до 10 я ввел рандомно.

Решение

У Вас в условиях задачи сказано — найти локальные экстремумы. Строим график функции что бы понять где они находятся. Видим, что экстремумов 3, причем 2 из них являются еще и глобальными и равными друг другу (это будет понятно если построить графики в более широком диапазоне значений X и более узких границах, а так же и по формуле функции). Теперь методом золотого сечения находим значения:

Глобальные экстремумы выделил красными кружочками, находятся в диапазонах X где то между -4. -1 и между 1. 4.
Локальный экстремум можно выделить в диапазоне значений Х на промежутке -1. 1 (синий кружочек), находится он по оси X в районе нуля.

Результат который у Вас должен получиться.

WH, Спасибо большое, что не прошли мимо и помогли разобраться. Теперь у меня есть понимание решения этой задачи.. Думаю, тему следует закрывать

Минимизация функции методом золотого сечения
Здравствуйте, помогите с лабораторной. Нужно написать код, исходя из следующей блок схемы.

Минимизировать Функции методом золотого сечения
Минимизировать Функции f(x) = |x| + e^10x методом золотого сечения Отрезок неопределнности .

Определить минимум функции методом золотого сечения
Ребята помогите с решением задачи в маткаде по золотому сечению: Определить методом золотого.

Поиск экстремума функции методом золотого сечения
Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей.

Читайте также:

Как сделать поверхность в фотошопе

Docs for microsoft office ms word powerpoint excel document templates что это

Toshiba 32av933rb прошивка usb

Какие виды учета ведутся в программе 1с зуп корп

Malwarebytes удалить полностью утилита

Источник

history 14 января 2021 г.

Задача

Создание модели

Экстремум функции

Точки экстремума

Задачи на нахождения экстремума функции

Условный экстремум функций многих переменных. Метод множителей Лагранжа. Первая часть.

Второй способ

VBA Excel. Нахождение экстремума функции Методом Золотого Сечения.

Решение

Не пропустите также: