Цель этой работы: с помощью экспериментальной
установки определить электрическое сопротивление резистора при заданном
значении силы тока.
Для выполнения этой работы мы будем использовать оборудование
из комплекта № 3 в составе: источник тока, двухпредельный
вольтметр, амперметр двухпредельный, ключ, реостат,
соединительные провода и резистор, обозначенный R2.
Прежде чем
приступить к работе давайте с вами вспомним, что электрическое сопротивление
— это скалярная физическая величина, характеризующая свойства проводника
препятствовать прохождению электрического тока в нём.
Ещё в 1826
году Георг Ом экспериментально установил, что сила тока на участке цепи прямо
пропорциональна напряжению на концах этого участка и обратно пропорциональна
его сопротивлению:
Зная
величину напряжения на концах проводника и ток в нём, по закону Ома можно
вычислить электрическое сопротивление проводника, как отношение напряжения на
концах проводника к силе тока в проводнике:
Именно сопротивление проводника нам и предстоит определить в
сегодняшней работе. Приступим к выполнению.
Итак, первое, что мы с вами сделаем, — это соберём
экспериментальную установку. Для этого последовательно с источником тока
соединим ключ (следите за тем, чтобы он находился в разомкнутом состоянии),
исследуемый резистор, амперметр на предел измерения 3 А и реостат. А чтобы
измерить напряжение на концах исследуемого резистора параллельно к нему
подключим вольтметр, подключённый на предел измерения 6 В.
Далее мы с вами нарисуем электрическую схему нашей установки.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, согласно закону Ома, сила тока на участке цепи прямо
пропорциональна напряжению на концах этого участка и обратно пропорциональна
его сопротивлению:
Отсюда
находим, что электрическое сопротивление проводника равно отношению напряжения
на концах проводника к силе тока в проводнике:
Прежде чем приступить непосредственно к работе ещё раз
внимательно проверьте вашу электрическую цепь. Особое внимание обратите на то,
чтобы амперметр был включён последовательно в цепь, вольтметр — параллельно, а
также на соблюдение полярности подключения обоих приборов.
Если всё в порядке, то включаем источник питания и замыкаем
ключ. Далее, с помощью ползунка (если в вашем комплекте ползунковый реостат)
или вращая ручку реостата, устанавливаем в цепи заданную нам по условию силу
тока. При этом не забываем, что на прибор мы должны смотреть перпендикулярно
шкале прибора.
Установив требуемое значение силы тока, снимаем показания с
вольтметра. Итак, у нас напряжение на концах резистора оказалось равным
примерно 2,4 В.
В бланк ответов значения силы тока в цепи и напряжения на
концах резистора мы должны записать с учётом погрешности измерения, данной нам
по условию задания.
Закончив с прямыми измерениями, приступаем к нахождению
сопротивления заданного резистора. Для этого в расчётную формулу подставляем
наши значения силы тока и напряжения:
В выводе напишем, что сопротивление резистора R2 равно 6 Ом.
Загрузить PDF
Загрузить PDF
Измерительный мост — это устройство, используемое для определения электрического сопротивления; его можно найти во многих физических лабораториях.
Шаги
-
1
Проверьте, замкнут ли провод измерительного моста. Если нет, прочно закрепите оба конца проволоки. Устройство имеет 5 мест для подсоединения. Эти контакты расположены выше провода измерительного моста, по два с каждой стороны и один посередине.
-
2
Представьте 5 точек на бумаге, расположенных вдоль прямой линии, и линию под ними, длина которой немного больше, чем расстояние между крайними точками, как изображено на рисунке выше.
-
3
Подсоедините известное сопротивление к одной стороне моста и неизвестное — ко второй, заняв таким образом 4/5 контактов моста. К оставшемуся контакту подключите последовательно гальванометр, высокое сопротивление и щуп.
-
4
Перемещая щуп вдоль провода измерительного моста, отметьте показание, при котором гальванометр покажет нулевое значение.
-
5
Допустим, это показание равно R1. Теперь найдите R2=100-R1.
-
6
Подобным образом найдите показание моста, поменяв местами известное и неизвестное сопротивления.
-
7
Пусть это значение, то есть расстояние на проводе моста, соответствующее нулевому току на гальванометре, равно R3. Найдите R4: R4=100-R3.
-
8
Сложите R1 и R3 и поделите сумму на два. Обозначим результат как L. Найдите среднее величин R2 и R4. Обозначим его M.
-
9
Можете повторить процедуру с разными известными сопротивлениями. Неизвестное сопротивление находится по формуле: неизвестное сопротивление(a)=известное сопротивление(b)*L/M. Искомая величина должна быть одинаковой для всех величин известных сопротивлений, использованных для ее определения.
Реклама
Об этой статье
Эту страницу просматривали 3364 раза.
Была ли эта статья полезной?
Цель:
Измерить
сопротивление участка электрической
цепи с параллельным соединением
проводников и доказать справедливость
равенства
.
Оборудование:
источник тока, два резистора с различным
сопротивлением, амперметр, ключ,
соединительные провода.
Порядок
выполнения работы:
-
Собрать
электрическую цепь согласно схеме 1.

Схема 1 Схема 2
Схема
3
-
Амперметром
измерить
силу тока, а вольтметром — напряжение
на первом резисторе. -
Р
ассчитать
по закону Ома сопротивление на первом
резисторе
. -
Аналогично,
используя схему 2 рассчитать
,
а используя схему 3 — экспериментальное
значение сопротивления всей цепи
. -
Рассчитать
теоретическое значение общего
сопротивления цепи по формуле
или
-
Сравнить
экспериментальное и расчетное значение
общего сопротивления.
Вывод:
В
ходе работы мы экспериментально
определили и теоретически рассчитали
сопротивление параллельного участка
электрической цепи (
,
что в свою очередь подтверждает
справедливость равенства
.
Примечание:
Небольшая разница значений объясняется
погрешностями эксперимента.
Билет №7. Изучение обратимости световых лучей
Ц
ель:
Доказать
справедливость принципа обратимости
световых лучей.
Оборудование:
плоское
зеркало, лазерная указка, булавки
(иголки) для обозначения хода лучей,
лист
картона.
Порядок
выполнения работы:
-
Направить
на зеркало луч света под произвольным
углом. Зафиксировать направление
падающего (АО) и отраженного (ОВ) луча
с помощью булавок. -
Н
аправить
на зеркало падающий луч света вдоль
линии ВО и убедиться, что отразившись,
он пройдет вдоль ОА.
Вывод:
Луч света, направленный по линии ОВ,
отразившись, распространится вдоль
линии ОА, т.е. по линии хода падающего
луча в первом случае, что подтверждает
принцип обратимости световых лучей.
Билет №8. Изучение зависимости гидростатического давления от глубины погружения в жидкость
Цель:
Доказать, что давление жидкости на
погружённое в неё тело, прямо пропорционально
глубине его погружения.
Оборудование:
Широкий сосуд с водой, линейка, датчик
с мембраной, жидкостный манометр.
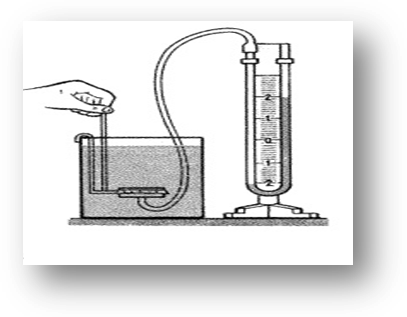
Примечание.
Принцип действия
манометра, используемого в данной
работе, основан на уравновешивании силы
давления неподвижного столба жидкости
в сосуде с силой давления, создаваемого
разностью уровней жидкости в манометре
(U-образной
трубке).
Порядок
выполнения работы:
-
Опуская
датчик с мембраной в сосуд с водой,
измеряем глубину его погружения h.
С помощью манометра измеряем давление
столба воды р
на данной глубине. -
По
полученным данным строим график
зависимости давления от глубины.

Вывод:
В
результате исследования получена
зависимость
близкая
к линейной, что не противоречит теории,
ведь гидростатическое давление можно
рассчитать из соотношения
,
где
плотность жидкости, а
ускорение свободного падения. Значит
Билет №9. Определение показателя преломления стекла
Цель:
Экспериментально
доказать закон преломления света.
Теория
вопроса:
-
Л
уч,
падающий и преломлённый, лежат в одной
плоскости с перпендикуляром, проведённым
в точке падения луча к плоскости границы
раздела двух сред. -
Отношение
синуса угла падения α
к синусу угла преломления γ
есть величина постоянная для двух
данных сред,
Оборудование:
призма, 4 иголки, картон, линейка,
транспортир, карандаш.
Порядок
выполнения работы:
-
На
картон поместить призму и обвести ее
контур карандашом. -
Не
удаляя призму воткнуть иголки 1 и 2 в
картон так, чтобы, проведённый через
них луч не был перпендикулярен верхней
грани призмы. -
На
картоне через точку падения луча
построить перпендикуляр к верхней
грани призмы, продлив его за нижнюю
грань призмы. -
Р
асположить
иголки 3 и 4 так, чтобы глядя на них
через призму, казалось, что иголки 4, 3,
2 и 1 установлены вдоль одной прямой.
Так, с помощью иголок 3 и 4 можно
зафиксировать преломлённый луч. -
Обозначить
углы падения
и преломления γ. -
Измерить
углы α и γ с помощью транспортира.
Определить показатель преломления
стекла по формуле
. -
Сравнить
полученное значение показателя
преломления стекла с табличными данными.
Выводы:
Измерив, угол падения и угол преломления,
согласно закону преломления света, мы
определили показатель преломления
стекла из которого изготовлена данная
призма. При α=19°
и γ=12°,
n=1,56,
что соответствует табличным данным и
подтверждает справедливость закона
преломления света.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрическое сопротивление проводника

4.3
Средняя оценка: 4.3
Всего получено оценок: 175.
4.3
Средняя оценка: 4.3
Всего получено оценок: 175.
Электрический ток в проводнике возникает в результате силового воздействия электрического поля на заряженные частицы. Скорость частиц, достигнув определенной, конечной величины, далее не возрастает. Способность проводника ограничивать скорость движения электронов называется электрическим сопротивлением.
Основной механизм сопротивления проводников
Ток в проводнике создается направленным движением свободных электронов. Электроны, ускорившись в электрическом поле, продолжают одновременно участвовать в тепловом хаотическом движении, сталкиваясь с нейтральными и заряженными атомами, расположенными в узлах кристаллической решетки. Излишки приобретенной кинетической энергии электроны отдают (“тормозятся”) более тяжелым по массе атомам (нейтральным и ионизированным).
Таким образом возникает сопротивление однонаправленному движению свободных электронов. Отличия в структуре решеток, размерах и массах атомов разных веществ являются причинами того, что электрические сопротивления проводников могут значительно отличаться друг от друга.
Как определить величину сопротивления
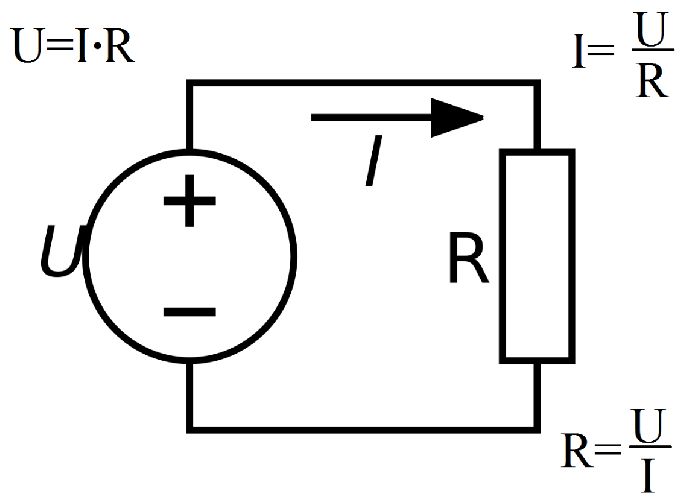
Эту задачу в 1826 г. решил немецкий ученый Георг Ом. Он провел большое число экспериментов с образцами разных проводников. С помощью набора источников тока он подавал напряжение U на исследуемые образцы и, одновременно измерял c помощью амперметра электрический ток I. Полученные результаты позволили ему вывести формулу, названную законом Ома:
$ U = I * R $ (1)
где:
U — напряжение, В;
I — сила тока, А.
Величина R была названа электрическим сопротивлением. Пользуясь формулой (1) можно получить уравнение для вычисления R по результатам измерения напряжения U и тока I:
$ R={U over I} $ (2)
Единица измерения электрического сопротивления
Единицу измерения сопротивления назвали в честь Георга Ома. В Международной интернациональной системе единиц СИ электрическое сопротивление 1 Ом имеет участок цепи, на котором падает напряжение равное 1 В при силе тока 1 А:
$ 1 Ом = { 1 Вover 1 A} $ (3)
Для определения сопротивления с помощью закона Ома требуется измерить предварительно напряжение и ток. Двух измерений можно избежать с помощью прибора, разработанного для непосредственного измерения сопротивления. Прибор называется омметром.
На практике большинство используемых в электрических схемах и приборах сопротивлений гораздо больше, чем 1 Ом. Поэтому чаще применяются кратные единицы измерений : килоом и мегом:
- 1 кОм = 1000 Ом;
- 1 МОм = 1000 000 Ом.
Удельное электрическое сопротивление
Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.
Эта функциональная связь хорошо описывается следующей формулой:
$ R = ρ *{ Lover S} $ (4)
Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества. Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:
$ ρ = R*{ Sover L } $ (5)
Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 200С)
|
Серебро |
0,016 |
Бронза (сплав) |
0,1 |
|
Медь |
0,017 |
Олово |
0,12 |
|
Золото |
0,024 |
Сталь (сплав) |
0,12 |
|
Алюминий |
0,028 |
Свинец |
0,21 |
|
Иридий |
0,047 |
Никелин (сплав) |
0,42 |
|
Молибден |
0,054 |
Манганин (сплав) |
0,45 |
|
Вольфрам |
0,055 |
Константан (сплав) |
0,48 |
|
Цинк |
0,06 |
Титан |
0,58 |
|
Латунь (сплав) |
0,071 |
Ртуть |
0,958 |
|
Никель |
0,087 |
Нихром (сплав) |
1,1 |
|
Платина |
0,1 |
Висмут |
1,2 |
Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается. При приближении к температуре абсолютного нуля, которая равна -2730 С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.
Что мы узнали?
Итак, мы узнали, что способность проводника ограничивать величину электрического тока называется сопротивлением. Величину сопротивления проводника можно определить с помощью закона Ома, измерив напряжение и ток. Если известно удельное сопротивление проводника, его длина и поперечное сечение, то сопротивление можно вычислить с помощью формулы (4), не измеряя ток и напряжение.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Марина Ковтун
10/10
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 175.
А какая ваша оценка?
2.5 Расчёт сопротивления проводника. Удельное сопротивление
Причиной электрического сопротивления является взаимодействие электронов с ионами кристаллической решётки. Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, на опытах изучил Г. Ом. Он установил, что сопротивление проволоки длиной `l` и площадью поперечного сечения `S` определяется по формуле
где `rho` – удельное сопротивление вещества, из которого изготовлен проводник. Эту величину определяют экспериментально, результаты измерений удельного сопротивления приводят в физических справочниках (и в справочных разделах задачников по физике).
В соответствии с формулой (12) единицей удельного сопротивления в СИ служит Ом`*`м.
Удельное сопротивление вещества зависит от температуры. Для металлов с ростом температуры растёт и удельное сопротивление. У электролитов наблюдается обратная зависимость. Эти обстоятельства следует учитывать на практике при расчётах спиралей электронагревательных приборов, нитей лампочек накаливаний и т. д.
Резистор сопротивлением `R=38` Ом изготовлен из медного провода кругового сечения массой `m=11,2` г. Найдите длину `l` провода. Удельное сопротивление меди `rho=1,7*10^(-8)` Ом`*`м, плотность меди `delta=8,9*10^3 «кг»//»м»^3`. Обратите внимание, что в настоящем примере приняты обозначения: `delta` – плотность, `rho` – удельное сопротивление.
Обозначим площадь поперечного сечения проводника `S`. Тогда объём проводника равен `V=S*l`, его масса `m=delta*V=delta*S*l`. По формуле (12) сопротивление проводника равно `R=rhol/S`.
Исключая `S` из двух последних соотношений, приходим к ответу на вопрос задачи:
`l=sqrt((mR)/(rho delta))=sqrt((11,2*10^(-3)*38)/(1,7*10^(-8)*8,9*10^3))~~53` м.