Как найти дробную часть отрицательного числа

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Нахождение дроби от числа

Поддержать сайт

Превышение неотрицательного действительного числа за его целой частью

дробная часть или десятичная часть не -Negative вещественное число x { displaystyle x}— это превышение над целой частью этого числа. Если последнее определяется как наибольшее целое число, не превышающее x, называемое floor of x или ⌊ x ⌋ { displaystyle lfloor x rfloor}, его дробная часть можно записать как:

гидроразрыв ⁡ (x) = x — ⌊ x ⌋, x>0 { displaystyle operatorname {frac} (x) = x- lfloor x rfloor, ; x>0}.

Для положительного числа, записанного в традиционной позиционной системе счисления (такой как двоичная или десятичная ), его дробная часть, следовательно, соответствует цифры, стоящие после точки счисления.

Содержание

• 1 Для отрицательных чисел
• 2 Отношение к непрерывным дробям
• 3 См. также
• 4 Ссылки

Отрицательные числа

Однако в случае отрицательных чисел существуют различные противоречивые способы расширения функции дробной части на них: либо она определяется так же, как и для положительных чисел, i. е., по frac ⁡ (x) = x — ⌊ x ⌋ { displaystyle operatorname {frac} (x) = x- lfloor x rfloor}(Graham, Knuth Patashnik 1992), или как часть числа справа от точки счисления frac ⁡ (x) = | х | — ⌊ | х | ⌋ { displaystyle operatorname {frac} (x) = | x | — lfloor | x | rfloor}(Daintith 2004), или нечетной функцией :

frac ⁡ (x) = {x — ⌊ x ⌋ x ≥ 0 x — ⌈ x ⌈ x < 0 {displaystyle operatorname {frac} (x)={begin{cases}x-lfloor xrfloor xgeq 0\x-lceil xrceil x<0end{cases}}}

, где with x ⌉ { displaystyle lceil x rceil}как наименьшее целое число не меньше x, также называемый потолком x. Как следствие, мы можем получить, например, три разных значения для дробной части только одного x: пусть это будет -1,3, его дробная часть будет 0,7 в соответствии с первым определением, 0,3 в соответствии со вторым определением и -0,3 согласно третьему определению, результат которого также может быть получен прямым способом с помощью

frac ⁡ (x) = x — ⌊ | х | ⌋ ⋅ sgn ⁡ (x) { displaystyle operatorname {frac} (x) = x- lfloor | x | rfloor cdot operatorname {sgn} (x)}.

x — ⌊ x ⌋ { displaystyle x- lfloor x rfloor}и определения «нечетной функции» позволяют однозначно разложить любое действительное число x на сумму его целой и дробной частей, где «целая часть» относится к ⌊ x ⌋ { displaystyle lfloor x rfloor}или ⌊ | х | ⌋ ⋅ sgn ⁡ (x) { displaystyle lfloor | x | rfloor cdot operatorname {sgn} (x)}соответственно. Эти два определения функции дробной части также обеспечивают идемпотентность.

Дробная часть, определенная через отличие от ⌊ ⌋, обычно обозначается фигурными скобками :

{x}: = x — ⌊ x ⌋. { displaystyle {x }: = x- lfloor x rfloor.}

Его диапазон представляет собой полуоткрытый интервал [0, 1). Для противоположных чисел дробные части дополняются следующим образом:

{x} + {- x} = {0, если x ∈ Z, 1, если x ∉ Z. { displaystyle {x } + {- x } = { begin {cases} 0 { t_dv {if}} x in mathbb {Z} \ 1 { t_dv {if}} x not in mathbb {Z}. end {cases}}}

Связь с непрерывными дробями

Каждое действительное число может быть однозначно представлено как непрерывная дробь, а именно как сумма его целой части и , обратная его дробной части, которая записывается как сумма его целой части и обратной дробной части, и так далее.

См. Также

Ссылки

Целая часть числа (floor)

Как наверное многие знают,
целой частью вещественного числа $a$ называется наибольшее целое число, не превосходящее $a$. Целую часть числа мы будем обозначать нижними квадратными скобками $lfloor a rfloor$, так как
целая часть всегда округляет число в меньшую сторону, то есть вниз. Такое обозначение введено канадским ученым
Кеннетом Айверсоном (K.Iverson), который для целой части ввел в употребление термин floor (англ. «пол»),
в противоположность функции ceil (англ ceiling — «потолок»), рассмотренной ниже.

Примеры: $lfloor 5 rfloor = 5$, $lfloor 5,8 rfloor = 5$, $lfloor 0,3 rfloor = 0$, $lfloor -0,3 rfloor = -1$, $lfloor -5,8 rfloor = -6$. Как видим, для неотрицательных чисел достаточно просто отбросить дробную часть. Для отрицательных чисел так не получается, поскольку, отбрасывая дробную часть от например $-5.8$, мы получим число $-5$, превышающее первоначальное число, тогда как, согласно определению, целая часть не может быть больше самого числа.

Для обозначения целой части также используются обычные квадратные скобки $[text{…}]$,
встречаемые еще в трудах короля математиков Карла Фридриха Гаусса (C. Gauß) в начале XIX века.
Однако $[…]$ используются также в другом смысле (скобки Айверсона, наименьшее общее кратное, векторное произведение),
поэтому многие склоняются к тому, что от использования обычных квадратных скобок для целой части следует отказаться.
В старых книгах на русском языке широко используется обозначение Лежандра (A.-M. Legendre) Е(x) от французского entière — целое.

Свойства целой части.

Свойство 1. Для $n = lfloor a rfloor$ необходимо и достаточно, чтобы $n$ было целым числом и удовлетворяло неравенству: $n leqslant a lt n+1$.

Число $n = lfloor a rfloor$, является целым по определению. Неравенство следует из того, что во-первых $n$ не превосходит $a$, а во-вторых, так как $n$ — наибольшее из таких чисел, число $n+1$ обязано быть больше $a$. Наоборот, выполнение неравенства для целого $n$ означает, что $n$ – наибольшее целое число, не превосходящее $a$, то есть $n = lfloor a rfloor$.

Неравенство свойства 1 можно записать так:  $lfloor a rfloor leqslant a lt lfloor a rfloor + 1$. Отсюда: $0 leqslant a — lfloor a rfloor lt 1$,   а также   $a-1 lt lfloor a rfloor leqslant a$.

Свойство 2. $a=lfloor a rfloor$ тогда и только тогда, когда $a$ — целое число.

Если $a=lfloor a rfloor$, то, поскольку $lfloor a rfloor$ — целое число, то таким же должно быть $a$. Наоборот, если $a$ — целое, то оно подходит под определение собственной целой части.

Свойство 3а. Если $m$ — целое число и $m;leqslant;a$, то $m;leqslant;lfloor a rfloor$.

Свойство 3b. Если $m$ — целое число и $m gt a$, то $m geqslant lfloor a rfloor$ + 1.

Свойство 3a вытекает из максимальности целой части. Свойство 3b следует из неравенства $m gt a geqslant lfloor a rfloor$.

Свойство 4. Если $a leqslant b$, то $lfloor a rfloor leqslant lfloor b rfloor$. Другими словами, функция $lfloor x rfloor$ является монотонно-неубывающей.

Следует из свойства 3a в силу того, что $lfloor a rfloor$ — целое число и $lfloor a rfloor leqslant a leqslant b$.

Поменяв местами $a$  и  $b$, затем прочтя каждое неравенство справа налево, получим: если $a geqslant b$, то $lfloor a rfloor geqslant lfloor b rfloor$

Свойство 5. Если $m$ — целое число, to $lfloor m + a rfloor = m + lfloor a rfloor $.

Из свойства 1 (необходимость) следует $lfloor a rfloor leqslant a lt lfloor a rfloor+1$. Прибавляя $m$ к каждой части, получаем
$m + lfloor a rfloor leqslant m + a lt (m + lfloor a rfloor) +1 $, откуда снова в силу свойства 1 (но достаточности) следует требуемое утверждение.

Свойство 6. $lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor leqslant lfloor a_1 + a_2 + … + a_n rfloor leqslant lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor + n;-;1$ .

Сложив неравенства $lfloor a_i rfloor leqslant a lt lfloor a_i rfloor+1$ для $i$ от $1$ по $n$, получим:
$$
lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor leqslant a_1 + a_2 + … + a_n lt lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor + n
$$

Из левого неравенства согласно свойству 3a вытекает
$$
lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor leqslant lfloor a_1 + a_2 + … + a_n rfloor
$$
тогда как из правого неравества, согласно свойству 3b следует
$$
lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor + n > lfloor a_1 + a_2 + … + a_n rfloor
$$
или (поскольку в обоих частях неравенства целые числа)
$$
lfloor a_1 rfloor + lfloor a_2 rfloor + … + lfloor a_n rfloor + n — 1 geqslant lfloor a_1 + a_2 + … + a_n rfloor
$$
что завершает доказательство утверждения.

Свойство 6а. $lfloor a rfloor + lfloor b rfloor leqslant lfloor a + b rfloor leqslant lfloor a rfloor + lfloor b rfloor +1 $

Частный случай свойства 6 при $n=2$.

Свойство 6b. $n lfloor a rfloor leqslant lfloor na rfloor leqslant n (lfloor a rfloor + 1) — 1$

Частный случай свойства 6 при $a_1=a_2=…=a_n=a$.

График функции $lfloor x rfloor $

Как видно из чертежа, график функции $y = lfloor x rfloor$ состоит из горизонтальных отрезков единичной длины, включая их левые концы
(обозначенные темными кружками) но исключая правые концы (обозначенные контурами окружностей, иногда вместо этого используются стрелки, направленные к отсутствующему концу). Функция разрывна для целых значений аргумента.
Функция, график которой состоит из горизонтальных отрезков (другими словами, ее область определения можно разбить на отрезки,
на каждом из которых функция принимает постоянное значение), называется кусочно-постоянной или ступенчатой.

График функции $y=lfloor x rfloor$

Функция «потолок» (ceil)

Кроме целой части», рассматривается (хотя и не так часто) парная функция, округляющая число в бо́льшую сторону, то есть вверх. Такая функция
именуется «потолок» (англ ceil, сокращение от ceiling) «Потолком» вещественного числа $a$ называется наименьшее целое число, не меньшее $a$.

Для функции «потолок» используются верхние квадратные скобки: $lceil…rceil$. Примеры: $lceil 5 rceil = 5$, $lceil 5,8 rceil = 6$, $lceil 0,3 rceil = 1$, $lceil -0,3 rceil = 0$, $lceil -5,8 rceil = -5$.

Свойства функции ceil

Так как функция «потолок» является парной функцией, каждое свойство функции «целая часть» (floor) имеет аналог для функции ceil. Свойства $lceil…rceil$ перечислены ниже.

Свойство 1^c. Для $n = lceil a rceil$ необходимо и достаточно, чтобы $n$ было целым числом и удовлетворяло неравенству: $n-1 lt a leqslant n$.
По-другому $lceil a rceil-1 lt a leqslant lceil a rceil$,   откуда  
$0 leqslant lceil a rceil — a lt 1$,   а также   $a leqslant lceil a rceil lt a+1 $

Свойство 2^c. $a=lceil a rceil$ тогда и только тогда, когда $a$ — целое число.

Свойство 2a^c. $lfloor a rfloor leqslant a leqslant lceil a rceil $, причем неравенства обращаются в равенства тогда и только тогда, когда $a$ — целое число.

Свойство 3а^c. Если $m$ — целое число и $m;geqslant;a$, то $m;geqslant;lceil a rceil$.

Свойство 3b^c. Если $m$ — целое число и $m lt a$, то $m leqslant lceil a rceil-1$.

Свойство 4^c. Если $a geqslant b$, то $lceil a rceil geqslant lceil b rceil$.

Поменяв местами $a$  и  $b$, затем прочтя каждое неравенство справа налево получим: если $a leqslant b$, то $lceil a rceil leqslant lceil b rceil$,
поэтому функция $lceil x rceil$ также является монотонно-неубывающей.

Свойство 5^c. Если $m$ — целое число, to $lceil m + a rceil = m + lceil a rceil $.

Свойство 6^c. $lceil a_1 rceil + lceil a_2 rceil + … + lceil a_n rceil — n;+;1 leqslant lceil a_1 + a_2 + … + a_n rceil leqslant lceil a_1 rceil + lceil a_2 rceil + … + lceil a_n rceil $ .

Свойство 6а^c. $lceil a rceil + lceil b rceil — 1 leqslant lceil a + b rceil leqslant lceil a rceil + lceil b rceil $

Свойство 6b^c. $n (lceil a rceil — 1) + 1 leqslant lceil na rceil leqslant n lceil a rceil $

График функции ceil

Функция $y = lceil x rceil$ также является ступенчатой.
Ее график можно получить из графика функции $y = lfloor x rfloor$,если исключить левые концы отрезков,
добавив вместо них правые концы, после чего сдвинуть график на единицу вверх.

График функции $y=lceil x rceil$

Дробная часть числа

Согласно определению, дробной частью вещественного числа называется разница между числом и его целой частью, то есть ${a}=a-lfloor a rfloor$, где фигурные скобки ${..}$ используются для обозначения дробной части.

Примеры: ${5}=0$, ${5,8}=0,8$, ${0,3}=0,3$, ${-0,3}=0.7$, ${-5,8}=0.2$. Хотя для отрицательных чисел дробная часть возможно не совсем то, что следует из «здравого смысла», это вполне согласуется с определением целой части.

Свойства дробной части

Свойство 1^f. $gamma = {a}$ тогда и только тогда, когда $(a-gamma)$ — целое число и $0 leqslant gamma lt 1$.

Если $gamma = {a}$, то $(a-gamma) = lfloor a rfloor = n$ — целое число. Кроме того, согласно свойству 1 (необходимость),  $n leqslant a lt n + 1$, откуда, вычитая $n$, получаем  $0 leqslant a — n lt 1$, или $0 leqslant gamma lt 1$.

Наоборот, если $a-gamma = n$ — целое число и $0 leqslant gamma lt 1$, то прибавив $n$ получим $n leqslant a lt n+1$, откуда из свойства 1 (достаточность) $n = lfloor a rfloor$, следовательно $gamma = a-n = {a}$.

Отсюда следует, что нуль — единственно возможное целое значение дробной части.

Свойство 2^f. ${a}=0$ тогда и только тогда, когда $a$ — целое число.

В самом деле ${a}=0$ эквивалентно $lfloor a rfloor = a$, что согласно свойству 2 имеет место тогда и только тогда, когда когда $a$ — целое число.

Свойство 3^f. Функция ${x}$ является периодической с наименьшим положительным периодом равным единице.

Если $m$ — целое число, то согласно свойству 5,
$$
{m+x} = (m+x) — lfloor m+xrfloor = (m+x)-(m+lfloor xrfloor) = x — lfloor xrfloor = {x},
$$
следовательно, любое целое число (в том числе единица) является периодом функции ${x}$.

С другой стороны, если $r$ — положительное число, меньшее 1,
то $lfloor r rfloor = 0$, откуда ${r} = r > 0$. Таким образом ${0+r} ne {0}$, поэтому $r$ не может быть периодом функции ${x}$.

Свойство 4^f. Дробная часть суммы равна дробной части суммы дробных частей: $
{a_1 + a_2 + … + a_n} = left { {a_1} + {a_2} + … + {a_n} right }$.

Сложив равенства $a_i = lfloor a_i rfloor + {a_i}$ для всех $i$ от 1 по $n$, получаем: $a_1 + a_2 + … + a_n = P + Q$,
где $P=lfloor a_1 rfloor + lfloor a_2 rfloor + … lfloor a_n rfloor$ — целое число, a $Q = {a_1} + {a_2} + … + {a_n}$.
Отсюда, в силу периодичности дробной части, ${a_1 + a_2 + … + a_n} = {Q} = left { {a_1} + {a_2} + … + {a_n} right }$,
что и требовалось доказать.

Следствие. Полагая $a_1 = a_2 = … = a_n = a$,  получаем:   ${na}={n{a}}$.

График функции ${x}$

График функции $y = { x }$ нетрудно построить, учитывая периодичность функции, а также ${x}=x$ при $0leqslant x lt 1$.
Он также состоит из отрезков, включая их левые концы.

График функции $y={ x }$

ЗАДАЧИ

Вертикальные линии $|…|$ используются для обозначения абсолютной величины.

Часть 1

1.1 Доказать что для равенства целых частей двух чисел, необходимо, чтобы разность этих чисел была меньше единицы:
из $lfloor a rfloor = lfloor b rfloor$ (а также из $lceil a rceil = lceil b rceil$) следует $|a-b|lt 1$. Является это условие достаточным?

1.2Как вы заметили, $lfloor -a rfloor = — lfloor a rfloor$ лишь тогда, когда $a$ — целое число. Исправьте правую часть этого равенства, чтобы оно имело место при любых $a$.

1.3Постройте графики функций $lfloor |x| rfloor$ и $|lfloor x rfloor|$. В каких случаях эти значения равны между собой?

1.4Доказать, что если $n$ — целое число, то  
$leftlfloor dfrac{lfloor a rfloor}{n} right rfloor = left lfloor dfrac{a}{n} right rfloor $.

1.5Выразить ${-a}$ через ${a}$.

1.6Обозначим через $lfloor a rceil$ — ближайшее целое число, то есть число, полученное
по обычным правилам округления (например $lfloor 0,8 rceil=lfloor 1,3 rceil=1$,  $lfloor -0,8 rceil=lfloor -1,3 rceil=-1$). При этом, числа вида $n+frac{1}{2}$, где $n$ — целое («точные половины») округляются до ближайшего четного числа (например $lfloor 0,5 rceil=lfloor -0,5 rceil=0$,  $lfloor 1,5 rceil=lfloor 2,5 rceil=2$,  $lfloor -1,5 rceil=lfloor -2,5 rceil=-2$).

   
а) Доказать, что функция $y = lfloor x rceil$ — нечетна (то есть $lfloor -x rceil = -lfloor x rceil)$;
   
b) Построить график функции.

1.7Обозначим через ${{a}}$ расстояние от $a$ до ближайшего целого числа: ${{a}} = |a-lfloor a rceil|$,  где  $lfloor a rceil$ — величина, определенная в предыдущей задаче. Например, ${{3,2}}={{4,8}}={{-4,8}}=0,2$.

   Доказать, что:
   
a) ${{a}}=left| left{ a+dfrac{1}{2} right} — dfrac{1}{2} right |$;
   
b) функция ${{x}}$ непрерывна;
   
c) функция ${{x}}$ четна (то есть ${{-x}}={{x}}$).

   Построить график функции ${{x}}$.

1.8Жидкость налита в бутыли вместимостью 40л, при этом одна из бутылей оказалась неполной. Если тот же объем жидкости перелить в бутыли вместимостью 50л, все они будут заполнены, причем понадобится на 5 бутылей меньше. Если использовать бутыли вместимостью 70л, то понадобится еще меньше на 4 бутыли, но опять одна бутыль будет неполной. Определить объем жидкости.

1.9Указать на координатной плоскости множество пар точек $(x,y)$, таких что:
   
a) $lfloor x rfloor = lfloor y rfloor$;
   
b) ${ x } = {y };$
   
c) $lfloor x + y rfloor = lfloor x rfloor + lfloor y rfloor$.

1.10Найти значения интегралов: a)$int_{0}^{x}{lfloor t rfloor};dt$; b) $int_{0}^{x}{lceil t rceil};dt$; c)$int_{0}^{x}{{t }};dt$. Построить графики.

Решения задач части 1.

Часть 2

Стандартный способ решения уравнений, содержащих целую часть, сводится к приведению уравнения к системе неравенств. Эта часть демонстрирует такой подход. Возможен также графический метод, примеры которого даны в решениях задач 2.1 — 2.4.

Решить уравнения:

2.1$left lfloor dfrac{x-1}{3} right rfloor = x + 5$

2.2$left lfloor dfrac{2x-3}{5} right rfloor = dfrac{3x+2}{11}$

2.3$left lfloor dfrac{x-3}{2} right rfloor = left lfloor dfrac{x-2}{3} right rfloor$

2.4$x^2 — 10lfloor x rfloor + 9 = 0$

2.5$x^4 — 2x^2 — lfloor x rfloor = 0$

2.6$x^3 — lfloor x rfloor — 7 = 0$

2.7$1-|x+1| = dfrac{lfloor x rfloor — x}{|x-1|}$

Решения задач части 2.

Часть 3

Для задач этой части стандартные методы не работают, а если даже и применимы, то требуют определенной изобретательности.

Решить уравнения:

3.1$leftlfloor dfrac{2x-1}{3} rightrfloor + leftlfloor dfrac{4x+1}{6} rightrfloor = dfrac{5x-4}{3}$

3.2$|sin x + cos x| = 5 — 4lfloor x rfloor$

3.3a) $left{ x + dfrac{1}{x} right} = {x} + dfrac{1}{{x}}$;
   b) $leftlfloor x + dfrac{1}{x} rightrfloor = lfloor x rfloor + dfrac{1}{lfloor x rfloor}$

3.4$lfloor x rfloor + dfrac{1}{lfloor x rfloor} = {x} + dfrac{1}{{x}}$

3.5$x^2+{x}^2=50$

3.6${(x+1)^3} = x^3$

3.7$lfloor x^3 rfloor — 3lfloor x rfloor^2 + 3lfloor x rfloor = {x} + 2$

3.8Решить систему уравнений:
$qquadqquad
left { begin{matrix}
x + lfloor y rfloor + {z} = 1,1 \
y + lfloor z rfloor + {x} = 2,2 \
z + lfloor x rfloor + {y} = 3,3
end{matrix}
right .
$

3.9Сколько целых чисел $n$, удовлетворяющих условию
$displaystyle qquadqquad
leftlfloorsqrt{leftlceilsqrt{n},rightrceil}rightrfloor = leftlceilsqrt{leftlfloorsqrt{n}rightrfloor},rightrceil
$
   существует в диапазоне от 1 до 10000 включительно?

Решения задач части 3.

Часть 4

Целая и дробные части всегда были излюбленным способом бросить вызов участникам различных математических олимпиад, заставляя проявить чудеса находчивости в короткое время. У вас однако времени предостаточно, поэтому не спешите заглядывать в ответы.

4.1 Решить систему уравнений:
$qquadqquad
left { begin{matrix}
x^2 + lfloor y rfloor = 10 \
y^2 + lfloor x rfloor = 13
end{matrix}
right .
$

4.2Решить уравнение в целых положительных числах:
$qquadqquadlfloorsqrt[3]{1}rfloor + lfloorsqrt[3]{2}rfloor + … + lfloorsqrt[3]{x^3-1}rfloor = 400$

4.3Доказать что для целого положительного  $n$
$qquadqquadleft{sqrt{1}right} + left{sqrt{2}right} + … + left{sqrt{n^2}right} leqslant dfrac{n^2-1}{2}$,
   причем равенство имеет место тогда и только тогда, когда  $n=1$.

4.4Доказать, что если $p$ и $q$ — взаимно-простые числа, то:
$qquadqquadleftlfloor dfrac{p}{q} rightrfloor + leftlfloor dfrac{2p}{q} rightrfloor … leftlfloor dfrac{(q-1)p}{q} rightrfloor = dfrac{(p-1)(q-1)}{2}$

4.5Доказать, что для целого положительного $n$:
$qquadqquadlfloor x rfloor + leftlfloor x+dfrac{1}{n} rightrfloor … leftlfloor x+dfrac{n-1}{n} rightrfloor = lfloor nx rfloor $

4.6Для целого неотрицательного $n$ и целого положительного $k$ доказать тождество:
$qquadqquadleftlfloor dfrac{n}{k}rightrfloor + leftlfloor dfrac{n+1}{k}rightrfloor + dots + leftlfloor dfrac{n+k-1}{k}rightrfloor = n$

4.7Доказать тождество для целого неотрицательного $n$:
$qquadqquad lfloor sqrt{n} + sqrt{n+1} rfloor = lfloor sqrt{4n+2} rfloor$

4.8Доказать, что уравнение:
$qquadqquadlfloor x rfloor + lfloor 2x rfloor + lfloor 4x rfloor + lfloor 8x rfloor + lfloor 16x rfloor + lfloor 32x rfloor = 12345$

   не имеет решений.

Решения задач части 4.

Целые числа

Представьте плитку шоколада или пиццу, они могут быть целыми или разрезанными на части, так же и с числами! Узнайте, что такое целые числа и как часто мы их используем в нашей жизни.

Что такое целые числа

Целые числа — это все положительные, все отрицательные числа и ноль. Никаких дробных частей в целых числах не бывает!

Например, к целым будут относиться числа: -12, -381, -5, 0, 32, 164, 978.

Как вы помните, в математике числа, которые мы используем для счета называются натуральными. Таким образом, можно сказать, что целые числа — это натуральные числа, ноль и отрицательные числа.

Выведем основные заключения:

• Целое число может быть не только положительным. 
• Число 0 – целое число.
• Целое число не может включать дробную часть. Значит, такие числа, как 1½, 3 ¼ и 7 ⅚, не являются целыми числами, а 1, 3 и 7 — целыми.
• Целое число не может включать десятичный элемент. Это означает, что такие числа как 3,5 или 9,12 не являются целыми, а 3 или 9 — целые числа.

Как обозначаются целые числа

Множество целых чисел обозначается буквой «Z».

Z = {∞ … -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, … ∞}

Множество целых чисел бесконечно, поэтому нельзя определить, сколько всего существует целых чисел. По этой же причине нельзя назвать наибольшее целое число либо наименьшее целое число.

Положительные и отрицательные целые числа

Множество целых чисел состоит из положительных и отрицательных чисел. Рассмотрите числовой луч: справа от нуля находятся положительные числа, а слева — отрицательные числа.

Отрицательные целые числа — это целые числа, которые меньше нуля. Записывают отрицательные числа всегда со знаком минус.
Например: — 12, — 135, — 74, — 3009.

Положительные целые числа — это целые числа, которые больше нуля. Записывают положительные числа без какого-то знака.
Например: 35, 14, 1004, 7286.

Свойства целых чисел при сложении и умножении

Закономерности при выполнении арифметических действий с целыми числами определяют основные свойства целых чисел. Все свойства сложения и умножения натуральных чисел будут подходить и для целых чисел.

Сумма и произведение двух целых чисел всегда будет целым числом. Например, два целых числа 2 и 6.

2 + 6 = 8 — целое число;

2 × 6 = 12 — целое число.

Переместительное свойство

Сумма или произведение целых чисел будут одинаковы, даже если порядок чисел поменять местами.

a + b = b + a

2 + 6 = 6 + 2

 8 = 8

a ⋅ b = b ⋅ a

2 ⋅ 6 = 6 ⋅ 2

12 = 12

Это свойство работает независимо от знака.

( — 2) + 6 = 6 + ( — 2)

4 = 4

2 ⋅ ( — 6) = ( — 6) ⋅ 2

 — 12 = — 12.

Сочетательное свойство

Сложение целого числа с суммой двух целых чисел равно сложению суммы двух первых чисел с третьим.

a + (b + c) = (a + b) + c

5 + (2 + 3) = (5 + 2) + 3

Умножение целого числа на произведение двух целых чисел равно произведению суммы двух первых чисел с третьим.

a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c

5 ⋅ (2 ⋅ 3) = (5 ⋅ 2) ⋅ 3

Умножение целого числа на сумму двух целых чисел равно сумме произведений первого со вторым и первого с третьим числом.

a ⋅ (b + c) = a ⋅ b + a ⋅ c

5 ⋅ (2 + 3) = 5 ⋅ 2 + 5 ⋅ 3

25 = 25

При умножении целого числа на ноль результат будет всегда равен нулю.

a ⋅ 0 = 0 или — a ⋅ 0 = 0

5 ⋅ 0 = 0 или — 5 ⋅ 0 = 0

Свойства целых чисел при вычитании

Разность равных целых чисел будет всегда равна нулю.

a — a = 0

Распределительное свойство

Вычитание суммы двух целых чисел из другого целого числа.

a — (b + c) = (a — b) — c

Вычитание целого числа из суммы двух целых чисел.

(a + b) — c = (a — с) + b = a + (b — c)

Сочетательное свойство

Умножение целого числа на разность двух целых чисел равно разности произведений первого и второго числа с первым и третьим числом.

a ⋅ (b — c) = a ⋅ b — a ⋅ c

5 ⋅ (6 — 4) = 5 ⋅ 6 — 5 ⋅ 4

10 = 10
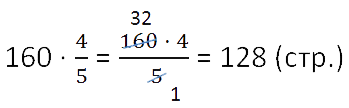