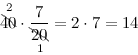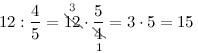В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
План урока:
Умножение обыкновенных дробей
Нахождение дроби от числа
Деление обыкновенных дробей
Нахождение числа по заданному значению его дроби
Дробные выражения
Умножение обыкновенных дробей
Разберем ситуацию.
На уроке технологии девочки занимались выпечкой. Они готовили печенье. По рецепту на изготовление одного килограмма печенья уходит 3/8 килограмма сахара. Сколько сахара необходимо принести детям, чтобы приготовить 1/2 килограмма печенья?
Чтобы ответить на главный вопрос задачи, нам необходимо узнать количество сахара нужное для изготовления 1/2 килограмма печенья. По условию, мы знаем, что для выпечки 1 кг лакомства требуется 3/8 кг сахара. Следовательно, чтобы вычислить требуемую массу сахарного песка необходимо найти произведение 3/8 и 1/2 . Известные множители представлены в виде обыкновенных дробей. Чтобы выполнить умножение обыкновенных дробей нужно использовать правило:
числитель умножаем на числитель, а знаменатель на знаменатель. Первый результат пишем над чертой дроби, второй под чертой:
Получается, чтобы испечь нужное количество печенья школьницы должны подготовить 3/16 килограмма сахарного песка.
Нахождение дроби от числа
Разберем следующую ситуацию и узнаем, как найти дробь от числа.
Вениамин очень любит уроки изобразительного искусства. В его альбоме для рисования 48 листов. Мальчик удивленно заметил, что своими рисунками уже заполнил 7/8 альбома. Сколько всего рисунков получилось у школьника?
Задачу можно решить двумя способами. Подробно рассмотрим каждый из них.
Способ 1.
Чтобы ответить на главный вопрос задачи нам нужно узнать, сколько листов соответствует записи 7/8. Для этого давайте вспомним, о чем нам говорят компоненты дробных выражений:
Теперь, можно сказать, что весь альбом разделили на 8 частей, а использовали только 7. Попробуем посчитать. Вначале, делим 48 на 8:
48 : 8 = 6.
6 листов приходится на 1/8 часть альбома. Зная, что таких частей было взято 7, найдем произведение 6 и 7 :
6 × 7 = 42.
Мы выяснили, что Вениамин нарисовал 42 рисунка.
Для решения задачи таким способом, нужно выполнить два действия, а это не всегда удобно. Так же, такой способ может вызывать трудности при вычислениях, если компоненты не делятся нацело.
В таких ситуациях, логичнее будет использование второго способа.
Способ 2.
По условию нам известно число и часть этого числа, выраженная обыкновенной дробью. Нужно найти числовое значение соответствующее данной дроби. Задания такого вида имеют собственное название «Нахождение дроби от числа» и правило, используя, которое можно с легкостью вычислить любое числовое значение соответствующее дробному выражению:
Применим изученное правило на практике. Чтобы найти 7/8 от 48 нам нужно, просто умножить 7/8 на 48:
Мальчик нарисовал 42 рисунка.
Запомните оба способа, и применяйте их для решения различных заданий.
Деление обыкновенных дробей
Разберем пример.
Строительная бригада выполняла ремонт городской дороги.На ремонт определенного участка дороги, рабочие потратили 7/9 тонны асфальта. Определите, сколько километров дороги отремонтировали рабочие, если на ремонт одного километра уходит 3/7 тонны строительного материала.
По условию нам известно, что всего было использовано 7/9 тонны материала, при этом мы знаем, что на один километр требуется 3/7 тонны. Чтобы ответить на главный вопрос задачи нужно количество использованного асфальтаразделить на количество строительного материала, необходимое для починки одного километра. В результате мы получим число отремонтированных километров. В данном случае, в качестве делимого и делителя выступают обыкновенные дроби. И перед нами возникает проблема «Как же выполнить деление обыкновенных дробейс разными знаменателями?».
В арифметике на этот случай имеется определенное правило, которое расскажет, как выполнить деление обыкновенных дробей.
Выполним деление имеющихся чисел с применением рассмотренного правила
Выполним деление, имеющихся дробных чисел с применением рассмотренного правила. Разделим 7/9 на 3/7. Делимое 7/9 оставляем без изменений, а делитель 3/7 переворачиваем, и получаем 7/3. Находим произведение данных выражений:
Все очень просто. Главное помните, что при выполнении деления дробей с разными знаменателями делитель переворачиваем и находим произведение перевернутого делителя и делимого!
Нахождение числа по заданному значению его дроби
В школе проходила неделя экологии. Учащиеся шестого класса были приглашены лесничеством на высадку деревьев. До обеда, ребята высадили 6/11 всех саженцев. Сколько растений осталось высадить школьникам, если до обеда дети высадили 54 дерева?
Чтобы ответить на главный вопрос задачи, нужно определить число по заданному значению его дроби. В арифметике существует правило, используя, которое возможно с легкостью найти любое число по значению его дроби:
Теперь мы знаем, что для вычисления общего количества саженцев, нужно известное значение дроби разделить на саму дробь. Зная, что число – 54, а дробь – 6/11, имеем:
В результате получили неправильную дробь. Выделим из полученного произведения целую часть.Для этого разделим числитель на знаменатель:
594 : 6 = 99.
Выходит, что за целый день школьникам нужно высадить 99 растений.
В математике часто встречаются задания, в которых требуется вычислить значение «многоэтажных» дробей. Как называются такие дробные выражения, каким способом их вычислять рассмотрим далее.
Дробные выражения
Когда ученик видит в учебнике задание в виде выражения:
то желание заниматься математикой сразу пропадает. Сегодня мы узнаем,как решать дробные выражения и докажем, что даже такие выражения совершенно не сложные, и выполнить вычисления сможет каждый желающий после изучения нашего урока!
Никого не пугает запись обыкновенной дроби – 3/7, 4/15, 8/14.
Каждый понимает, что дробная черта заменяет привычный знак деления – : .
Например:
10/21 = 10 : 21 или 7/18 = 7 : 18.
Выходит, что частное чисел или выражений, в случае замены знака деления чертой дроби, называют дробным выражением.
Вот так, проведя два простых вычисления, мы выполнили задание, вызывающее недоумение у школьников. Математика интересная и простая наука. Если приложите немного внимания и терпения, то результат не заставит себя ждать!
Знаешь ли ты?
1) Ученые – селекционеры вывелиновый вид яблонь. Удивительным является то, что корни растения уходит в землю более чем на 49/50километра (около 980 метров), а общая длина корневища достигает 4000 метров.
2) За всю жизнь человек выпивает примерно 75 тонн воды. Подсолнечнику, например, достаточно 1/4 тонны(250 литров), чтобы вырасти и принести семена.
3) Италия в который раз удивила весь мир. Около вулкана Этна растет каштан, диаметр ствола которого, составляет,3/50 километра (около 60 метров),это чуть ли не половина футбольного стадиона.
4) Пальма Рафия Тедигера встречается только в Бразилии. Она интересна тем, что её листья имеют гигантские размеры. Черенок листка достигает1/200 километра (5 метров), длина листика – более1/50 километра (более 20 метров), ширина – более 5 метров (1/200 километра).
5) По сообщениям ихтиологов(ученых, занимающихся изучением рыб), самую большую длину в мире,имеют ремень-рыбы. Во взрослом возрасте они достигают длины более 1/100километра(более 10 метров), а длина молодых особей находится в пределах 0,003 километра или 3 метров.
Скачать материал

Скачать материал


- Сейчас обучается 41 человек из 29 регионов


- Сейчас обучается 49 человек из 26 регионов


- Сейчас обучается 48 человек из 25 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
«Как находить дробь от числа и число по его дроби, соблюдая правила дорожного движения».
Тема урока:
1
Сергиенко В.А. Дробь от числа. -
2 слайд
Чтобы найти
дробь от числа,
нужно умножить число
на эту дробь.
Чтобы найтиЧисло по данному
значению его дроби,
надо это значение
разделить на дробь.правила
-
3 слайд
Прочитай задачи и определи:
к какому виду они относятся.
разминка -
4 слайд
В дачном поселке 30 домов.
от всех домов -двухэтажные.
Сколько двухэтажных домов? -
5 слайд
В конюшне стоят лошади.
0,2 всех лошадей — вороные.
Сколько лошадей в конюшне,
если вороных в ней 14?14:0,2=140:2=70 (лошадей)-в конюшне.
Ответ: 70 лошадей.
-
6 слайд
В 6 классе 25 учащихся. Девочки составляют 0,8 всех учащихся.
Сколько в классе мальчиков? -
7 слайд
От трубы отрезали 6 метров,
что составляет длины всей
трубы.
Найдите длину трубы. -
8 слайд
Сведения госавтоинспекции
За 9 месяцев по Московской области произошло 10862 ДТП.
Погибло – 2126 человек,
из них – 58 детей.
Ранено 13510 человек,
из них – 968 детей. -
-
10 слайд
РЕШЕНИЕ ЗАДАЧ
НАХОЖДЕНИЕ
ДРОБИ ОТ ЧИСЛА
И ЧИСЛА ПО ЕГО ДРОБИ. -
11 слайд
Задача №1.
Из 120 опрошенных школьников не выполняютправила дорожного движения учащихся и
не всегда соблюдают всех учащихся.
Сколько детей выполняют ПДД, если они
составляют остальную часть?СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ
-
12 слайд
КРАТКАЯ ЗАПИСЬ
Задача №1Ответ:
54 ученика выполняют ПДД.
1 способ
2 способ
Решите задачу №1 двумя способами -
13 слайд
задача № 2.
Из 120 опрошенных школьников не выполняютправила дорожного движения учащихся и
не всегда соблюдают оставшихся
учащихся.
Сколько детей выполняют ПДД, если они
составляют остальную часть? -
14 слайд
Задача №1.
Из 120 опрошенных школьников не выполняютправила дорожного движения учащихся и
не всегда соблюдают
Сколько детей выполняют ПДД, если они
составляют остальную часть?всех учащихся.
оставшихся учащихся.
Задача № 2.
СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ -
15 слайд
КРАТКАЯ ЗАПИСЬ
Задача №1Задача №2
Ответ:
54 ученика выполняют ПДД.
Ответ:
63 ученика выполняют ПДД.
РЕШЕНИЕ -
16 слайд
Домашнее задание:
Решить задачу №2
другим способом -
17 слайд
Нарушения, которые чаще всего допускают дети:
Переход улицы перед близко движущимся транспортом – 27%.
Переход улицы на красный сигнал светофора – 27%.
Невнимательность при переходе улицы – 17%.
Неожиданный выход из-за транспортных средств — 9%
Игры на проезжей части-20% -
18 слайд
РЕШЕНИЕ ЗАДАЧ
НАХОЖДЕНИЕ
ДРОБИ ОТ ЧИСЛА
И ЧИСЛА ПО ЕГО ДРОБИ. -
19 слайд
Задача №1.
Из 120 опрошенных школьников не выполняютправила дорожного движения учащихся и
не всегда соблюдают всех учащихся.
Сколько детей выполняют ПДД, если они
составляют остальную часть?Ответ:
54 ученика выполняют ПДД.
Составить к задаче №1 обратную задачу -
20 слайд
Задача №1.
Из опрошенных школьников не выполняютправила дорожного движения учащихся и
не всегда соблюдают всех учащихся.
Сколько детей выполняют ПДД, если они
составляют остальную часть?Ответ:
54 ученика выполняют ПДД.54 ученика выполняют ПДД.
Сколько детей было опрошено?
Обратная задача
СОСТАВИТЬ КРАТКУЮ ЗАПИСЬ -
21 слайд
КРАТКАЯ ЗАПИСЬ
Задача №1Обратная задача
Ответ:
54 ученика выполняют ПДД.
Ответ:
120 учеников опрошено.
РЕШИТЬ
ДВУМЯ
СПОСОБАМИ -
22 слайд
Придумайте задачу заданного типа, используя данные:
и решите ее любым способом.
задание
-
23 слайд
Задача№1
Ответ:16
Задача №2Ответ:28
Задача №3Ответ:400
Бонус -
24 слайд
1.Главная автомагистраль.
2.Штрихи на дороге, обозначающие пешеходный переход.
3.Дорога для пешеходов.
4.Край дороги.
5.Пересечение двух улиц.
6.Сотрудник милиции, работающий на дороге.
7.Место ожидания транспорта.
8.Наказание за нарушение ПДД.
1.Шоссе.2.Зебра.
3.Тротуар.4.Обочина.
5.Перекресток.6.Регулировщик.
7.Остановка.
8.Штраф.
ВИКТОРИНА -
25 слайд
Спасибо за урок!
-
26 слайд
Решение задачи №1
(1 способ)
Ответ: 54 человека выполняют ПДД. -
27 слайд
Решение задачи №1
(2 способ)
Ответ: 54 человека выполняют ПДД. -
28 слайд
Решение задачи №2
Ответ:63 человека выполняют ПДД.
Краткое описание документа:
Саша Чернов сел делать домашнее задание и сидел за столом 2 часа. 20 минут из них он ковырял в носу и думал о мороженом. 10 минут искал в ящике стола ластик, чтобы стереть с учебника истории неприличную картинку, на рисование которой затратил перед этим 40 минут. Остальное время Саша спрягал немецкие глаголы. Сколько глаголов проспрягал Саша, если на каждый глагол у него ушло по 25 минут
Как находить дробь от числа и число по его дроби, соблюдая правила дорожного движения».В дачном поселке 30 домов. от всех домов -двухэтажные.
l Сколько двухэтажных домов? В 6 классе 25 учащихся. Девочки составляют 0,8 всех учащихся.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 267 603 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 08.03.2015
- 938
- 2
Задачи на смекалку. 6 класс.
- Учебник: «Математика (в 2 частях)», Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
- Тема: 7. Наименьшее общее кратное
- 08.03.2015
- 4784
- 31


- 08.03.2015
- 1596
- 4
Рейтинг:
4 из 5
- 08.03.2015
- 17787
- 174
- 08.03.2015
- 773
- 2
- 08.03.2015
- 6797
- 0
- Категория: Математика

Разберем на примере задачи нахождение дроби от числа.
От дома до школы 560 м. Саша прошел 2/5 этого пути. Сколько метров прошел Саша?
Весь путь — это 5 частей или одно целое (5/5). Найдем одну часть:
1) 560 : 5 = 112 (м) — составляет одна часть Сашиного пути. А он прошел 2 таких части
2) 112 * 2 = 224 (м) — составляет 2/5 пути.
Ответ: 224 м.
А теперь ту же задачу превратим в нахождение числа по его дроби.
Саша прошел 224 м, что составляет 2/5 всего пути от дома до школы. Найди расстояние от дома до школы?
224 м — это часть пути, значит весь путь будет больше. Эта информация нужна для самопроверки. Найдем сначала 1/5 пути
1) 224 : 2 = 112 (м) — составляет 1/5 пути
2) 112 * 5 = 560 (м) — составляет весь путь
Ответ: 560 м.
Проверим себя. При нахождении дроби от числа результат будет меньше этого числа, если у нас правильная дробь, и больше, если неправильная (то есть целое + еще какая-то часть).
При нахождении числа от дроби — все наоборот, результат будет больше этого числа, если у нас правильная дробь, и меньше, если неправильная.
Калькулятор на нахождения дроби от числа и числа по его дроби
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 — это заданное число, $frac{7}{20}$ — дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
Итак, получили, что $frac{7}{20}$ от 40 равно 14 — искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.