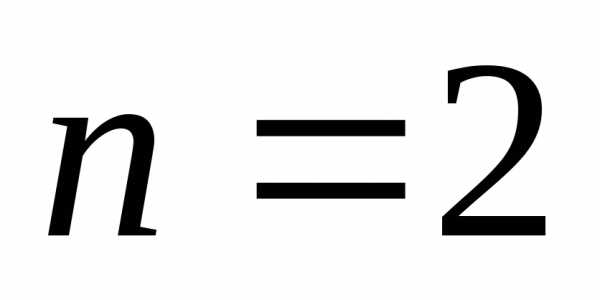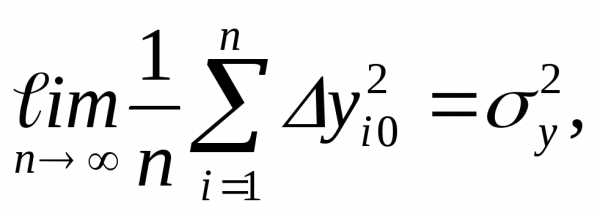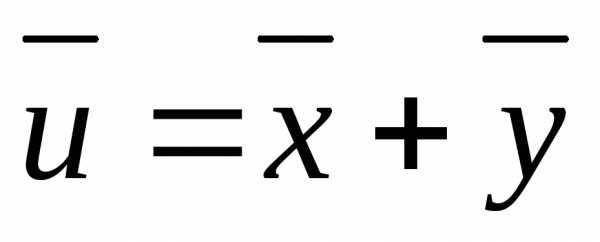Доверительная вероятность и доверительная погрешность
При
обработке результатов измерений любой
физической величины возникают две
задачи. Первая состоит в нахождении по
набору данных наилучшей оценки измеряемой
величины ,
которую с наибольшим основанием можно
принять за приближенное значение
величины .
Вторая – в определении точности
полученного результата.
Результат
измерения физической величины представляют
в виде
Приведенная
запись означает, что существует
определенная степень уверенности в
том, что значение измеряемой величины
находится в пределах рассчитанного по
результатам наблюдений интервала
,
называемогодоверительным.
Величина
называетсядоверительной
погрешностью.
Указание
значения доверительной
вероятности
означает, что при проведении большого
числа наблюдений вслучаев результаты наблюдений измеряемой
физической величины, выполненные с
одинаковой тщательностью и одними и
теми же измерительными приборами,
попадут внутрь доверительного интервала.
Значения доверительной
погрешности и доверительной вероятности
однозначно связаны друг с другом, а
именно: чем больше погрешность, тем
больше вероятность того, что результат
измерений находится в указанных пределах,
и наоборот.
Виды погрешностей
По
характеру, происхождению, а также по
способам оценки и исключения влияния
на результат измерений погрешности
делят на три основные группы: случайные,
систематические и грубые (промахи).
Систематические
и грубые погрешности
определяются факторами, чуждыми условиям
и проведению эксперимента. Погрешности
такого рода могут быть исключены путем
тщательных проверок. Систематические
погрешности связаны с ограниченной
точностью прибора и метода измерений,
а также округлением при считывании
значения со шкалы. Когда причины,
вызывающие эти погрешности, известны,
их можно исключить, уточняя метод
измерения и вводя поправки к показаниям
приборов. Систематические погрешности
не уменьшаются с увеличением числа
измерений.
Грубые
погрешности
(промахи) обычно связаны с отсутствием
достаточной квалификации экспериментатора,
неправильным отсчетом по прибору,
неправильной записью результата
наблюдения, невнимательностью и т.п.
Обычно грубые погрешности хорошо
заметны, т.к. при многократно проделанных
измерениях соответствующие промахам
результаты резко отличаются от остальных.
Такие погрешности могут возникать в
результате неустойчивой работы установки
или отдельного прибора. Они могут быть
устранены путем повторных измерений
или снятием показаний другим
экспериментатором.
Случайные
погрешности
обусловливаются большим количеством
трудноучитываемых факторов, влияющих
как на измерительные устройства,
исследуемый физический объект или
процесс, так и на самого экспериментатора.
Такими факторами могут быть, например,
колебания температуры элементов
установки, напряженностей электрического
и магнитного полей, движение воздуха,
вибрация зданий и приборов, трение в
движущихся элементах, погрешности при
отсчете делений шкалы и т.п. Исключить
случайные погрешности отдельных
измерений невозможно, но величину таких
погрешностей можно оценить, проводя
повторные (многократные) измерения.
Оценка величины случайных погрешностей
производится с помощью аппарата
математической статистики и теории
вероятностей.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Доверительная вероятность и доверительный интервал.
- Доверительный интервал — формула и примеры определения вероятности
- Общая схема построения
- Точный интервал
- Асимптотическое приближение
- Доверительная вероятность. Доверительный интервал.
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
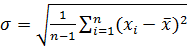
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 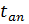
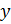
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 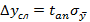
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Источник
Доверительный интервал — формула и примеры определения вероятности
В математической статистике при анализе и систематизации различных данных для подведения практических выводов часто используют метод доверительных интервалов. С его помощью выполняют определённую выборку среднего или доли с учётом стандартной ошибки. Благодаря этому достоверность вероятности увеличивается, так как оценка расширяется в обе стороны от исследуемой величины.
Общая схема построения
По сути, метод основан на модели классической математической статистики, подразумевающей бесконечно возможные выборки в генеральной совокупности. Пусть имеется главная выборка эпсилон с функцией распределения известной до некого параметра тау (Fe (x, τ)). Из этой генеральной совокупности получена выборка объёмом эн, включающая диапазон от x1 до xn. Этот параметр можно считать одномерным и принадлежащим диапазону от τ до R. Математически такое положение описывают как τ є T c R.
Если предположить, что для некоторого интервала йод, лежащего от нуля до единицы, существуют статистики S-(X|n|, J) и S+(X|n|, J), при этом им соответствует неравенство P< S-(X|n|, J) Свойство статистики и распределения
Таким образом, определить доверительную вероятность попадания тэта в интервал от S- до S+ можно от значения обратной функции в точках, равняющихся квантили статистики игрек порядка j/2 и 1 — j/2. При этом когда рассматриваемая функция монотонно убывает, знаки в неравенстве меняются на противоположные.
Пользуясь общим подходом расчёта доверительных интервалов, можно посчитать вероятность для нормальной генеральной совокупности, опираясь на ряд утверждений. Пусть известна выборка X|n,| взятая из совокупности E
N (j, ς 2 ), то есть имеющей нормальный закон распределения с математическим ожиданием j и дисперсией сигма в квадрате. Для такого состояния справедливо следующее:
Точный интервал
Существует ряд правил, позволяющих построить точные интервалы для математического ожидания и дисперсии нормально распределённой случайной величины. Есть два случая — при одном дисперсия может быть известной, а при другом нет. Следует обратить внимание, что точная доверительная вероятность строится с помощью общей схемы. Используют следующие правила для предоставления точных прогнозов:
Асимптотическое приближение
Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P< S-(X|n|, j) Примеры решения задач
Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = — m / p2 — (n — m) / (1 — p)2 Использование онлайн-калькулятора
На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.
Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.
Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:
Они доступны на русском языке, их интерфейс интуитивно понятен, поэтому воспользоваться их услугами сможет любой заинтересованный, имеющий доступ к интернету. Автоматический расчёт занимает буквально секунды, что составляет существенную разность по сравнению с затратой времени при самостоятельном вычислении.
Источник
Доверительная вероятность. Доверительный интервал.
Δr – доверительный интервал
Интервал значений случайной величины внутри которого с заданной вероятностью находится истинное значение измеряемой величины, называется доверительны интервалом, а соответствующая ей вероятность – доверительной вероятностью (Pд)
В соответствии со стандартом, принимают 4 градации доверительной вероятности
| Рд | 0.9 | 0.95 | 0.975 | 0.99 |
| q | 0.1 | 0.05 | 0.025 | 0.01 |
q – уровень значимости результата.
0,9;0,1 – для оценочных расчетов
0,95;0,05 – для технически расчетов
0,975 – для точных технических расчетов
0,99 – для особо ответственных расчетов
19. Статистические методы исключения грубых промахов.
Методика применяется к многократным измерениям
Оценка грубых промахов реш. методом мат. статистики.
Суть метода: выдвигается нулевая гипотеза, что сомнительных результат принадлежит к совокупности измерений, а затем пользуясь статистическими критериями опровергают данную гипотезу, и результат отбрасывается.
Методы подбора критериев:
1) Критерий позволяет отбросить результат резко отличающийся от среднего арифметического

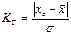
ZГ(n,q) = f(q,n)– теор. знач. критер. Греббса
q – уровень значимости
КГ>ZГ – результат отбрасывается
Формулу f(q,n) придумал Гребс для больших n, Шарле и Шавене для малых
2) Критерий позволяет отбросить результат резко отличающийся от соседних результатов


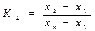
Если КΔ>ZΔ, то результат отбрасывается
20. Статистические методы исключения систематических погрешностей.
Есть случайные и систематические составляющие. Сначала надо определить есть ли систематическая составляющая
Критерий для оценки наличия систематической прогрессирующей погрешности (критерий Аббе)
Но это всё определяется не точно на 100%, а с некоторой доверительной вероятностью
Метод наименьших квадратов (исключение систематической составляющей)
Нужно, чтобы сумма квадратов разности была минимальной
21. Методика оценки погрешности при прямых измерениях с однократным наблюдением.
Для оценки точности при однократных измерениях надо иметь информацию об измерительном средстве, о методе измерения, об условиях измерения и об опыте оператора.
Расчёт погрешности на основе допустимых предельных погрешностей, без учёта разбиения погрешности на случайную и систематическую составляющие.
В основе методики – принцип наихудшего случая, т.е. что погрешность носит систематический характер и имеет один знак.
Методика даёт завышенный, но надёжный результат с вероятностью ≈ 1
Расчёт погрешности с учётом систематической и случайной составляющей
K – коэффициент, зависящий от уровня значимости результата и числа n.
n – число измерений
r – число интервалов
23. Правила округлений результатов измерений.
1) Погрешность результатов измерений указывается 2-мя значащими цифрами, если первая из них 1 или 2 и одной цифрой в остальных случаях.
2) Результат измерения округляют до того же десятичного знака, кот. оканчивается округленное значение абс. погрешности.
24. Средства измерений. Их классификация.
Средства измерений – техническое устройство предназначенное для измерений, имеющее нормированные метрологические характеристики воспроизвод. и хранящее ед. физ. вел, размер кот. принимается неизменным в теч. известного интервала времени.
1.по метролог. назначению
-метролог.(для работы метролог. служб)
2.по конструктивному исполнению
Мера – средство измерения, предназначенное для хранения и воспроизведения размера физ. вел.
Измерительный преобразователь – средство измерения, предназначенное для получения значения измеряемой величины в сигнал, удобный для передачи, хранения, обработки.
Он может быть отдельным прибором, тогда это датчик, но чаще он встроен в измерительный прибор
Измерительный прибор – средство измерения, предназначенное для измерения в заданном диапазоне, имеющее нормированные метролог. характеристики.
Измерительные системы – совокупность средств измерений и вычислительных средств, объединённых в единую систему.
3.по уровню автоматизации
ГОСТ дел. все приборы на 20 групп
М – измерит. мощности
У – измерит. усилители
Ц – комбинированные приборы
25. Основные метрологические характеристики электро-радиоизмерительных приборов.
Метрологическая хар-ка – это свойство средства измерения, влияющая на погрешность измерения.
1)Погрешность измеряемого средства
2)Диапазон показаний и измерений
Диапазон измерений – часть диапазона показаний, где обеспечивается нормированная точность.
3)Предел измерений – наим. и наиб. значение диапазона измерений
4)Градуированная характеристика – зависимость измерения показаний от измеряемой величины.
5)Чувствительность измерит. прибора- отношение измеренного сигнала на выходе к вызывающему его входному сигналу.
6)Разрешающая способность – min изменение входного сигнала, кот. различимо по показанию прибора
7)Быстродействие – число измерений в ед. времени
8)Внутреннее сопротивление (для приборов подключённых последовательно)
9)Входное сопротивление прибора (для приборов подключённых ||)
Может быть активным и реактивным
10)Вариация показаний – разница, показаний при плавном подходе к измеряемой точке при изменении измеряемой вел (Гистерезис). Характерно для динамических измерений
11)Мощность потребляемая от измерительной цепи
Она должна стремиться к 0.
26. Нормирование инструментальной погрешности
Нормировать можно в формах:
Основная и дополнительная погрешности нормируются отдельно
Типовые метрологические характеристики:
Обычно нормирование производится первой партии выпускаемых приборов (испытание на точность)
Измерение производятся в нормальных условиях
Измерения повторить для точек диапазона и некоторых точек в диапазоне.
Дополнительная погрешность измеряется так же, как и основная, но измеряются условия измерения (по каждому параметру измеряется отдельно)
27. Классы точности средств измерений.
Класс точности прибора- это основная метрологическая характеристика.
Класс точности количественно выражается в форме предела допустимой абс., относит. или приведенной погрешности.
Для радиоизмерит. приборов класс точности выражается пределом относит. или приведенной погрешности. Формулу для расчета погрешности приводят в паспорте на прибор. Используются одночленные формулы (погрешность имеет аддитивную составляющую) и двучленные (аддитивная составл. + мультипликативная)
28. Измерение напряжения и других параметров электрической цепи. Измеряемые значения переменного напряжения.
Напряжения и токи могут быть постоянными и переменными. При измерении постоянного напряжения прибор будет указывать на его действительное значение. При измерении переменного напряжения в зависимости от применяемого прибора для измерений может быть получена одна из следующих величин:
-амплитудное значение переменного напряжения,
-среднеквадратичное значение (действительное значение).
Мгновенное значение напряжения переменного тока является функцией времени и определяется следующей формулой:
Где:
ω- круговая частота,
Среднее значение напряжения определяется по формуле:
Для симметричного синусоидального переменного (гармонического) напряжения это значение будет равно нулю. Поэтому для оценки гармонического переменного напряжения эта характеристика не применяется. Она может быть применена для выделения постоянной составляющей негармонического переменного напряжения.
Средневыпрямленное значение напряжения определяется по формуле:
Выпрямление может быть однополупериодное и двухполупериодное. При однополупериодном выпрямлении в формулу ( 3 ) надо добавить коэффициент 0,5.
Среднеквадратичное значение напряжения определяется по формуле:
ния называют также действующим значением переменного напряжения или тока.
Амплитудное, средневыпрямленное и среднеквадратичное значения напряжения связаны между собой коэффициентами амплитуды и формы.
Для гармонического напряжения Ка = 1,41, а Кф =1,11. То есть различные значения напряжения для гармонического сигнала связаны соотношениями:
29. Приборы для измерения напряжения и других параметров электрической цепи.
Измерение напряжения – наиболее популярный способ измерения так как :
1) Напряжение наиболее полно характеризует режим работы электрической схемы
2) При измерении напряжения не необходимости разрыва электрической цепи
3) Измеряя напряжение, косвенным методом можно измерить другие параметры (I,R)
Токи и напряжение могут быть постоянными и переменными. Когда напряжение постоянное, то прибор показывает его действующее значение, когда переменное – прибор может измерять разные значения. В этом случае надо знать какой прибор как работает
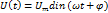
Характеристики переменного напряжения :
1) Амплитудное значение
2) Среднее значение
4) Действующее значение среднеквадратичное
Для гармонического сигнала Uср в = 0,637 Um
Для оценки формы сигнала:
Коэффициент амплитуды : Ка = Um / U =1,41
Коэффициент формы : Кф = U/ Uср в = 1,11
Классификация приборов для измерения напряжения
По виду измеряемого параметра приборы могут быть:
-измерители ёмкости, индуктивности
Если прибор измеряет несколько параметров он называется мультиметром
Все измеряющие приборы
Электромагнитные приборы относятся к приборам непосредственной оценки. Обычно в таких приборах электрическая энергия преобразуется в механическую энергии. (?в част.? Во вращательное движение стрелочного механизма)
Они строятся по следующим измерительным схемам: машинно-электрическая, электромагнитная, электростатичесая, электродинамическая, магнитноэлектрическая
Высокая точность, высокая чувствительность (класс 0,1; 0,5)
Все остальные измеряемые системы более грубые
Используется для точных механических приборов
Недостатки: Большое потребление энергии от источника
Электростатические системы используются для высокочастотных измерений (используется конденсатор)
Электродинамические системы потребляют много энергии, для измерителей мощности, счётчиков электрической энергии
Электронноаналоговые приборы – используются те же принципы как и в электромеханических
Основной недостаток электрических систем – большое ….
Потребление мощности от измеряемой цепи, что ведет к методической погрешности
Треугольник-усилитель переменного напряжения
УПТ-усилитель постоянного тока
Достоинство: за счет усилителей данный прибор не отнимает энергию от измеряемой цепи. Имеет высокую чувствительность и точность. В основном используется для измерения малых величин.
Цифровые приборы:
ЦОУ-цифровое отсчетное устройство
30. Осциллографы. Назначение и классификация осциллографов.
Для измерения параметров динамических сигналов используют специальные приборы. Для детерминированных сигналов используют осциллографы, для случайных сигналов –измерители параметров случайных сигналов. (Измерение математического ожидания, дисперсии, среднего квадратичного отклонения, корреляционных характеристик и др.).
Электронный осциллограф предназначен для визуального отображения формы и приближенного измерения параметров периодических сигналов сложной формы.
Наряду с тестерами, цифровыми вольтметрами и импульсными генераторами осциллографы являются наиболее распространенными измерительными приборами и очень широко применяются на всех стадиях проектирования, производства и обслуживания ЭВМ.
Осциллограф позволяет получить на экране электронно-лучевой трубки график одного или нескольких периодов входного сигнала в координатах «время – напряжение», т.е. график функции y=f(t). Пример такого графика показан на рис.
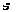
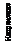
1. Универсальные О. 100МГц
2. Стробоскопические О. – Они используются для измерения высокочастотных сигналов, либо кратковременных повторений сигналов до 10МГц работ.
3. Запоминающие О. для исследования однократных, редко повторяющихся процессов.
4. Специальные О. – О. Целевого назначения, снятие видеосигнала; для переходных процессов.
2) многоканальные (2,4…)
Осциллографы делятся по исполнению:
1) аналоговые на ЭЛТ
2) цифровые с использованием матричных экранов
3) виртуальные приборы
31. Назначение и классификация измерительных генераторов.
Измерительные генераторы подразделяются на несколько групп (см. рис. 2.1).
Наиболее распространенными являются генераторы звуковой частоты ГЗ, высокой частоты Г4, прямоугольных импульсов Г5, качающейся частоты Г2.
Источник сигналов разнообразных форм и частот, предназначенные для регулирования, настройки и измерений в электронных схемах.
Они должны обладать:
1) возможностью регулировки выходных параметров
2) высокую стабильность
3) стандартные средства связи с др. измерительными устройствами
В зависимости от формы сигнала, генераторы делятся:
— генератор сигналов произвольной формы
— генератор случайных сигналов
— генератор стандартной частоты
По принципу пострения:
Практические рекомендации по работе с измерительными генераторами сводятся к следующему:
а) перед подключением генератора к нагрузке следует убедиться, что её сопротивление не меньше, чем минимально-допустимое по «Техническое описанию»,
б) соединять выход генератора с нагрузкой следует только входящими в комплект коаксиальными радиочастотными кабелями,
в) генераторы импульсов обеспечивают гарантированную по «Техническому описанию» форму только при работе на согласованную нагрузку.
г) прежде чем устанавливать длительность импульса и его задержку, необходимо приближенно вычислить длительность периода».
32. Измерение частоты и интервалов времени.
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.
2.1 Случайная величина
Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.
Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].
Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δx] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δx: x∈[x0,x0+δx].
Устремим интервал
δx к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w(x0)=P[x0,x0+δx]δx будет оставаться конечным.
Функцию w(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.
Замечание. В математической литературе распределением часто называют не функцию
w(x), а её интеграл W(x)=∫w(x)𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.
Гистограммы.
Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[kh,(k+1)h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.
σ=1,0, h=0,1, n=104)
Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w(x).
Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.
Свойства распределений.
Из определения функции w(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:
| Px∈[a,b]=∫abw(x)𝑑x. | (2.1) |
Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w(x) по всей области
значений x (то есть суммарная площадь под графиком w(x)) равен единице:
Это соотношение называют условием нормировки.
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения
случайной величины:
где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину
| σ2=(x-x¯)2¯=∫(x-x¯)2w𝑑x | (2.3) |
называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.
Доверительный интервал.
Обозначим как P|Δx|<δ вероятность
того, что отклонение от среднего Δx=x-x¯ составит величину,
не превосходящую по модулю значение δ:
| P|Δx|<δ=∫x¯-δx¯+δw(x)𝑑x. | (2.4) |
Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.
2.2 Нормальное распределение
Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
| w𝒩(x)=12πσe-(x-x¯)22σ2. | (2.5) |
Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.
Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩(x)).
При значительном отклонении x от среднего величина
w𝒩(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.
Замечание. Точки x=x¯±σ являются точками
перегиба графика w(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w(x¯±σ)/w(x¯)=e-1/2≈0,61
от высоты вершины.
Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.
x-x0σ2=2w(x)σ1=1
Доверительные вероятности.
Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.
Замечание. Значение интеграла вида ∫e-x2/2𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.
Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна
| P|Δx|<σ=∫x¯-σx¯+σw𝒩𝑑x≈0,68. |
Вероятность отклонения в пределах x¯±2σ:
а в пределах x¯±3σ:
Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2σ;x¯+2σ],
и лишь 0,27% окажутся за пределами
[x¯-3σ;x¯+3σ].
Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.
Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись
означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δx;x¯+δx] с
вероятностью 68%. Таким образом погрешность ±δx считается
равной одному среднеквадратичному отклонению: δx=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δx=2σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.
Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.
Сравнение результатов измерений.
Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.
Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2σ.
Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если
Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.
Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.
Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.
2.3 Независимые величины
Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:
Обозначим отклонения величин от их средних как Δx=x-x¯ и
Δy=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δx¯=x¯-x¯=0,
Δy¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δx⋅Δy¯
равно произведению средних Δx¯⋅Δy¯
и, следовательно, равно нулю:
| Δx⋅Δy¯=Δx¯⋅Δy¯=0. | (2.6) |
Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:
Найдём дисперсию σz2. В силу независимости имеем
| Δz2¯=Δx2¯+Δy2¯+2Δx⋅Δy¯≈Δx2¯+Δy2¯, |
то есть:
Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.
Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.
Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2x=2σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2x=2σx.
Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.
Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.
Пример. Пусть σy=σx/3,
тогда σz=σx1+19≈1,05σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.
2.4 Погрешность среднего
Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.
Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых
Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать
| σZ=σx12+σx22+…+σxn2=nσx, |
поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем
Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.
Подчеркнём отличия между σx и σ⟨x⟩:
величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;
величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.
2.5 Результирующая погрешность опыта
Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?
Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:
Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δxслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δxсист=x¯-xист=const:
Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:
| σполн2=⟨δxсист2⟩+⟨δxслуч2⟩≤Δсист2+σслуч2. | (2.9) |
Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.
Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.
Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:
Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)
d=386±6мкм,εd=1,5%.
Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=162,0м/с,
среднеквадратичное отклонение σv=13,8м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δv, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6м/с
(ε≈4%), так и значение σv≈14м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=163,3м/с,
σv=12,1м/c, σ⟨v⟩=5м/с,
σполн≈11,2м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f(x).
В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:
Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δx=x-x⋆, и пользуясь определением производной,
при условии, что функция y(x) — гладкая
вблизи x≈x⋆, запишем
где f′≡dydx — производная фукнции f(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δy2⟩,
σx2=⟨Δx2⟩), и затем снова извлечём
корень. В результате получим
Пример. Для степенной функции
y=Axn имеем σy=nAxn-1σx, откуда
σyy=nσxx,или εy=nεx,
то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.
Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.
Упражнение. Найдите погрешность логарифма y=lnx, если известны x
и σx.
Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.
2.6.2 Случай многих переменных
Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:
Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:
где символом fx′≡∂f∂x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f(x,y,…):
| σu2=fx′2σx2+fy′2σy2+… | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.
Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …
Остановимся на некоторых важных частных случаях формулы
(2.11).
Пример. Для суммы (или разности) u=∑i=1naixi имеем
σu2=∑i=1nai2σxi2.
(2.12)
Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что
σu2u2=α2σx2x2+β2σy2y2+…
или через относительные погрешности
εu2=α2εx2+β2εy2+…
(2.13)
Пример. Вычислим погрешность произведения и частного: u=xy или u=x/y.
Тогда в обоих случаях имеем
εu2=εx2+εy2,
(2.14)
то есть при умножении или делении относительные погрешности складываются
квадратично.
Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу
u=arctgyx.
В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′zx′=-yx2+y2,
uy′=uz′zy′=xx2+y2, и наконец
σu2=y2σx2+x2σy2(x2+y2)2.
Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.
По итогам данного раздела можно дать следующие практические рекомендации.
-
•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью. -
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной. -
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.
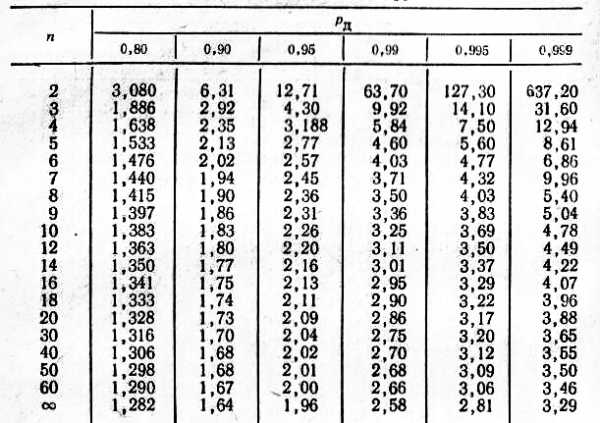
Надежность результата многократных измерений. Коэффициент Стьюдента.
Доверительной
вероятностью или надежностью
P
серии измерений называется вероятность
попадания истинного значения измеряемой
величины в данный интервал (выражается
в долях единицы или в процентах).
Интервал
(<x>±-
∆x)
в который попадает истинное значение
искомой величины с заданной доверительной
вероятностью P(∆x)
, называют доверительным
интервалом или интервалом надежности
и для краткости обозначают как ∆x.
Чем
больше доверительный интервал, тем
больше доверительная вероятность того,
что результат измерения попадет в него.
Величина доверительного интервала,
рассчитывается методами теории
вероятностей и математической статистики
и определяется выбором вида функции
распределения случайных величин f(∆x).
Для
всех функций распределения, базовым
является распределение
Гаусса,
справедливое для большого количества
равноточных
измерений

[1.5]
где
величина
называется среднеквадратичным
или стандартным отклонением
от среднего
значения <x>
а,
распределения.
Распределение
Гаусса показывает, что вероятность
появления малых случайных погрешностей
больше вероятности появления больших
погрешностей, при этом случайные
погрешности равные по абсолютной
величине, но противоположные по знаку
встречаются одинаково часто.
При
лабораторных измерениях (n
< 20) для расчета интервала надежности
используется распределение
Стьюдента (при
распределение Стьюдента переходит в
распределение Гаусса),
которое
позволяет по заданной величине надежности
P(∆x)
найти величину доверительного интервала
∆x,
с помощью поправочных коэффициентов
Стьюдента:
где
— коэффициент
Стьюдента, зависящий от выбора
доверительной вероятности p
и числа измерений n,
S
– среднеквадратичное отклонение –
(СКО), вычисляемое по формуле:
[1.7]
Величина
интервала ∆x,
рассчитанная при помощи формулы [1.6]
стремится к нулю при увеличении числа
опытов.
Коэффициенты Стьюдента
|
Число измерений n |
Доверительная |
|||
|
0,90 |
0,95 |
0,99 |
0,999 |
|
|
2 |
6,314 |
12,706 |
63,657 |
636,619 |
|
3 |
2,920 |
4,303 |
9,925 |
31,598 |
|
4 |
2,353 |
3,182 |
5,841 |
12,941 |
|
5 |
2,132 |
2,776 |
4,604 |
8,610 |
|
6 |
2,015 |
2,571 |
4,032 |
6,859 |
|
7 |
1,943 |
2,447 |
3,707 |
5,959 |
|
8 |
1,895 |
2,365 |
3,499 |
5,405 |
|
9 |
1,860 |
2,306 |
3,355 |
5,041 |
|
10 |
1,833 |
2,262 |
3,250 |
4,781 |
Очевидно, что число
опытов имеет смысл выбрать таким, чтобы
случайная погрешность среднего сравнялась
с погрешностью прибора либо стала меньше
ее. Дальнейшее увеличение числа измерений
теряет смысл, так как не увеличит точность
получаемого результата
Расчет погрешности прямых измерений
Прежде,
чем приступить к измерениям, необходимо
предварительно определить пределы
точности данных приборов (инструментальные
погрешности
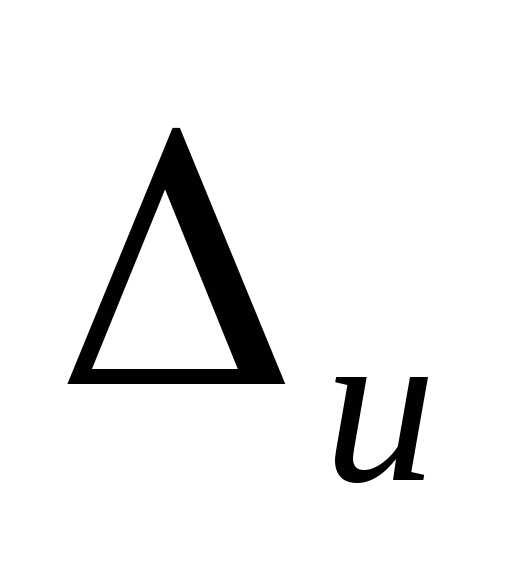
Равноточные
измерения любой физической величины
делаются не менее трех раз и заносятся
в таблицу, с учетом инструментальной
погрешности. В зависимости от поведения
значений результатов измерения, возникают
две различные схемы:
Случайная
погрешность много меньше инструментальной
Если
оказывается, что все время получается
один и тот же результат (нет разброса),
то в качестве интервала надежности
берется стандартная (инструментальная)
погрешность прибора ∆и,
рассчитанная по его классу точности
(или погрешность градуировки прибора)
и результат записывается в виде:
При
этом доверительная вероятность
(надежность) равна
и, как правило, не указывается.
Случайная
погрешность сравнима с инструментальной
Если
разброс значений физической величины
x
превышает погрешность градуировки, то
количество измерений n
увеличивают до тех пор, пока они не
окажутся величинами одного порядка.
Интервал надежности вычисляют в следующей
последовательности:
-
Находят
среднее значение: -
Оценивают
среднеквадратичное отклонение — СКО:
-
По
заданному значению надежности p
и числу измерений n,
находят
случайную составляющую погрешности:
-
Полную
погрешность вычисляют как корень
квадратный из суммы квадратов случайной
∆хсл
и инструментальной ∆xи
составляющих:
-
Находят
относительную погрешность: -
Результат
записывают в виде: ,
,
р
= …
studfiles.net
Коэффициент Стьюдента
Пример
Определить
достоверность
измерений для
установленного доверительного интервала.
По формуле (1.2)
имеем:
.
По табл.1.1для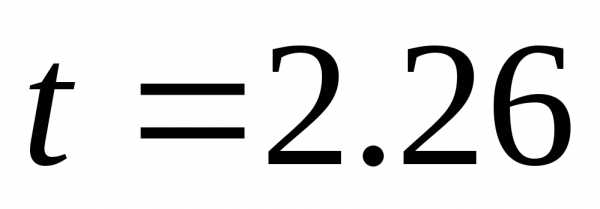
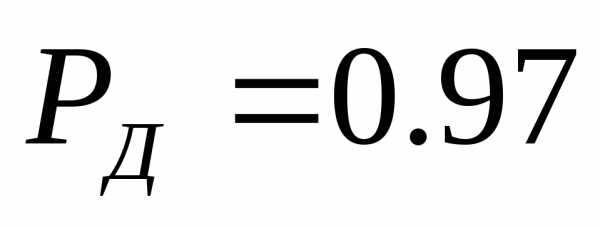
Это означает, что
в заданный доверительный интервал из
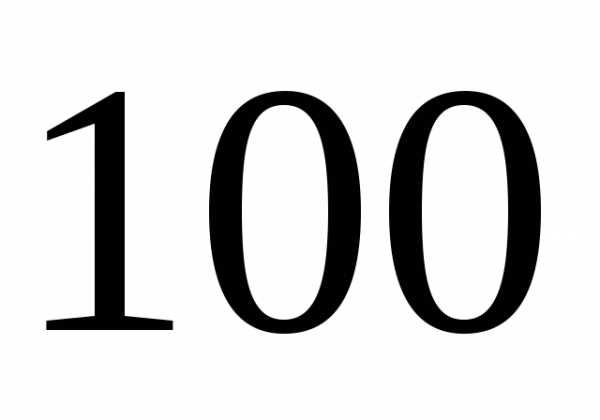

Значение
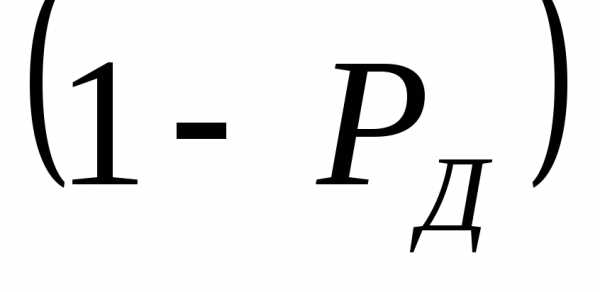
уровнем
значимости.
Из него следует,
что при нормальном законе распределения
погрешность, превышающая доверительный
интервал, будет встречаться один раз
из
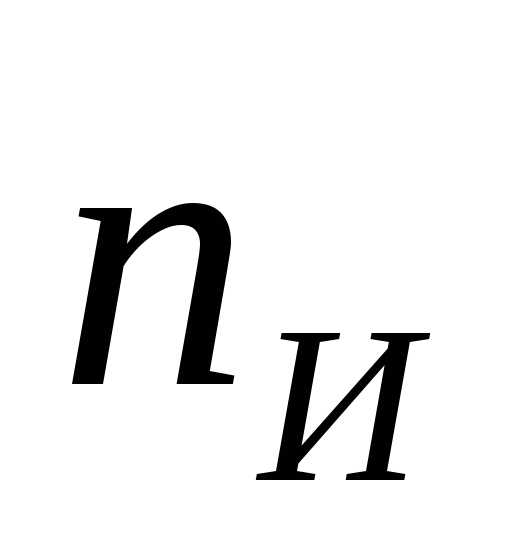
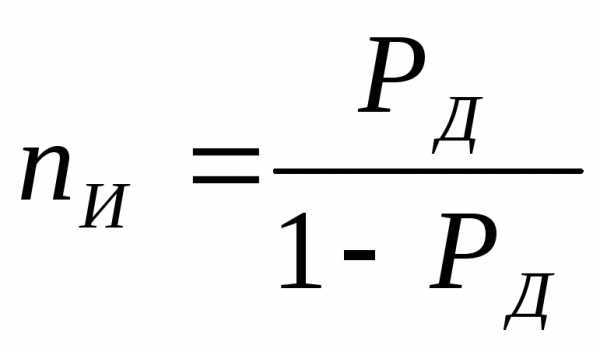
(1.4)
Это означает, что
приходится браковать одно из
измерений.
По данным приведенных
выше примеров можно вычислить количество
измерений, из которых одно измерение
превышает доверительный интервал.
Если
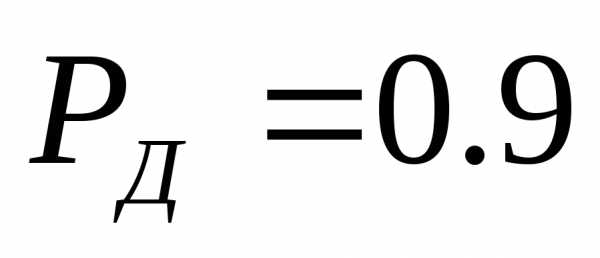
то по формуле (1.4) определяетсяизмерений.
Если
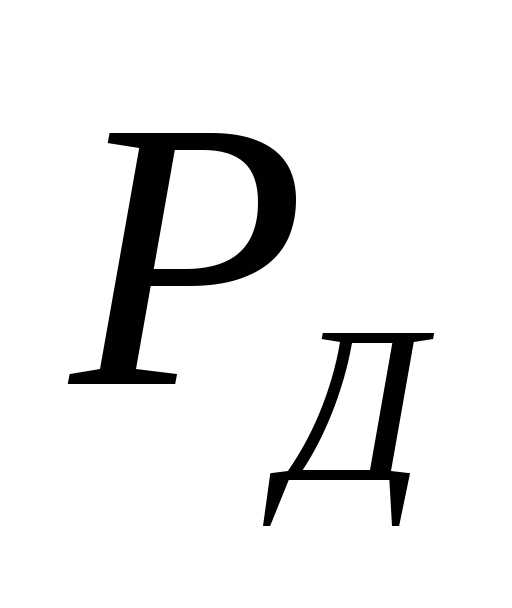
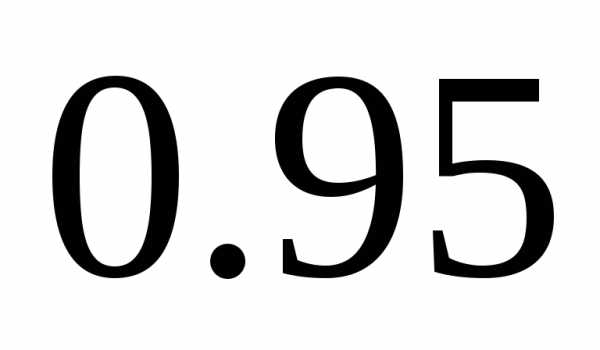
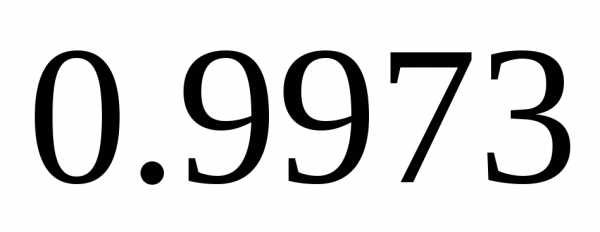
соответственно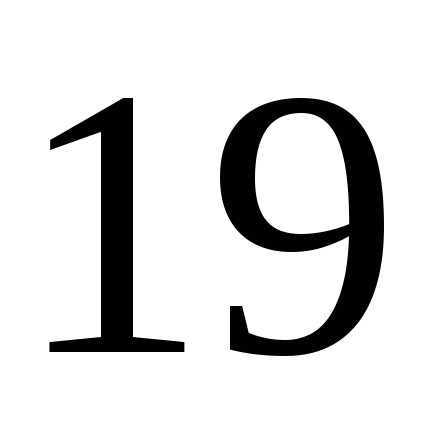

2. Определение минимального количества измерений
Для проведения
опытов с заданной точностью и достоверностью
необходимо знать то количество измерений,
при котором экспериментатор уверен в
положительном исходе.
В связи с этим
одной из первоочередных задач при
статистических методах оценки является
установление минимального, но достаточного
числа измерении для данных условий.
Задача сводится
к установлению минимального объема
выборки (числа измерении)
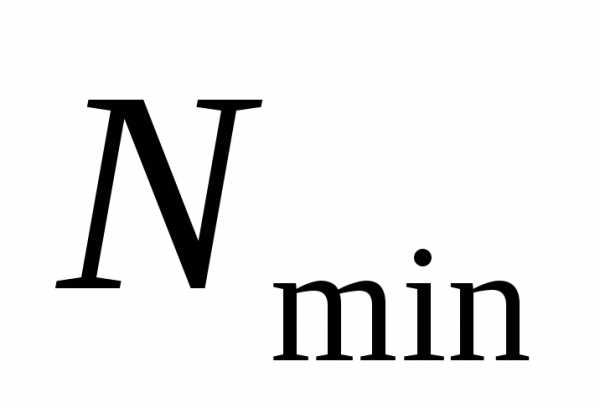
интервала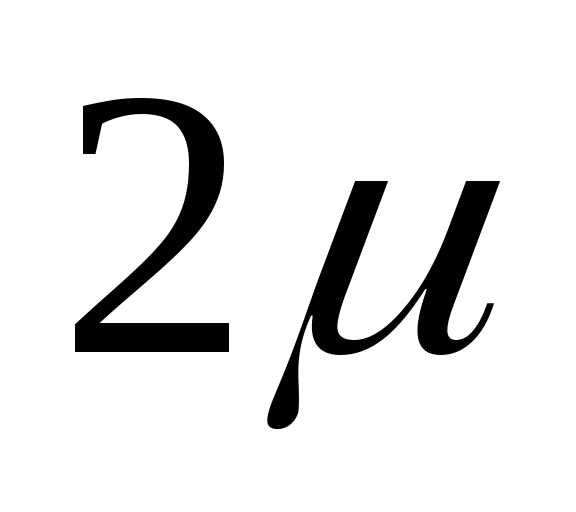
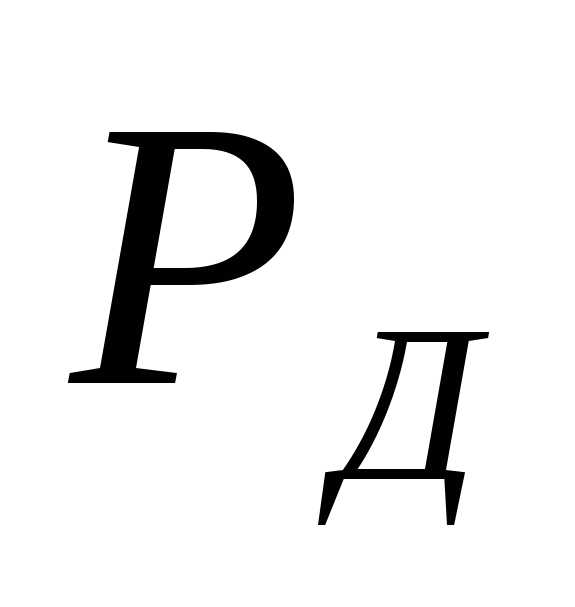
При выполнении
измерений необходимо знать их точность:
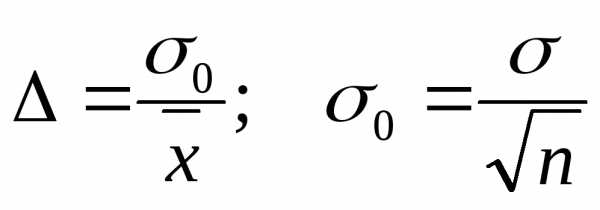
(2.1)
где
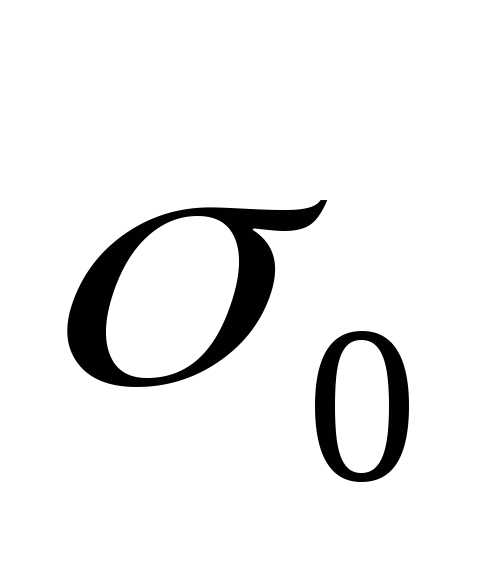
среднеквадратического отклонения
Значение
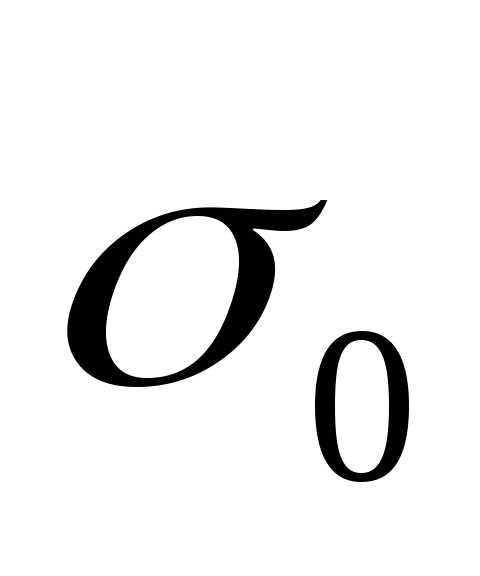
ошибкой.
Доверительный
интервал ошибки измерения

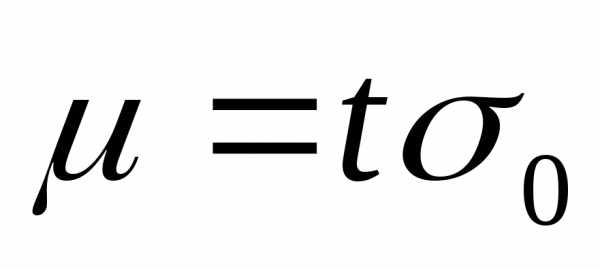
С помощью
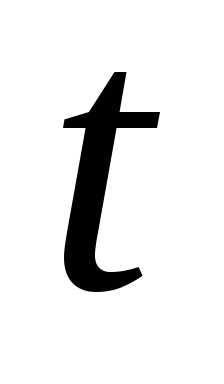
вероятность ошибки измерений потабл.1.1.
В исследованиях
часто по заданной точности

определяют минимальное количество
измерений, гарантирующих требуемые
значения
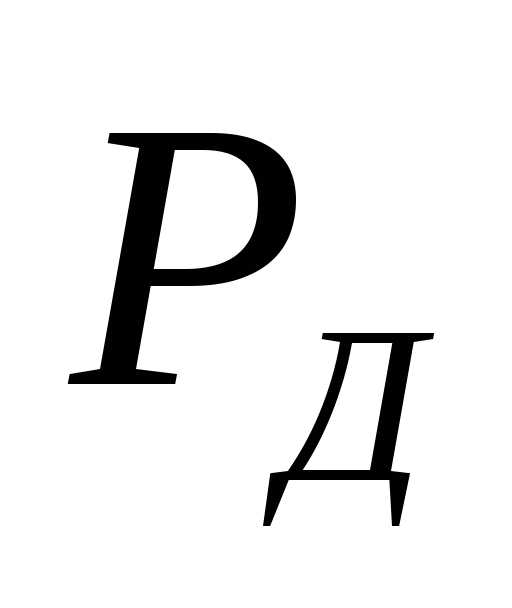
При получаем
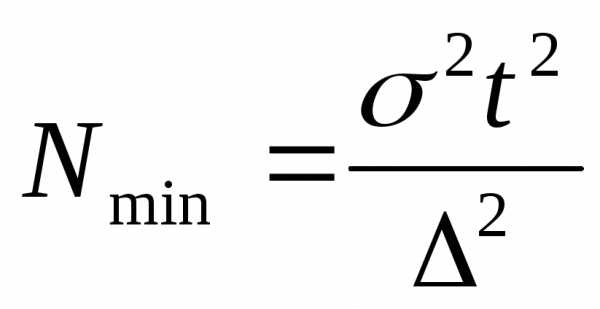
(2.2)
Для определения
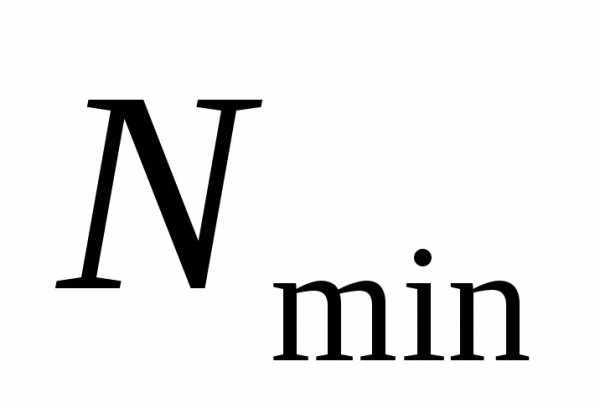
вычислений.
1.
Проводится предварительный эксперимент
с количеством измерений
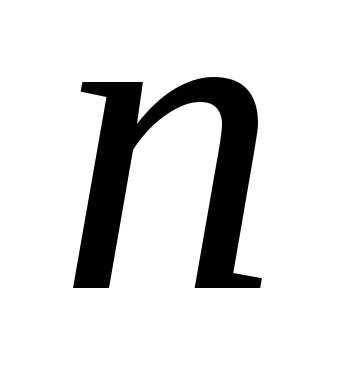
которое составляет в зависимости от
трудоемкости опыта от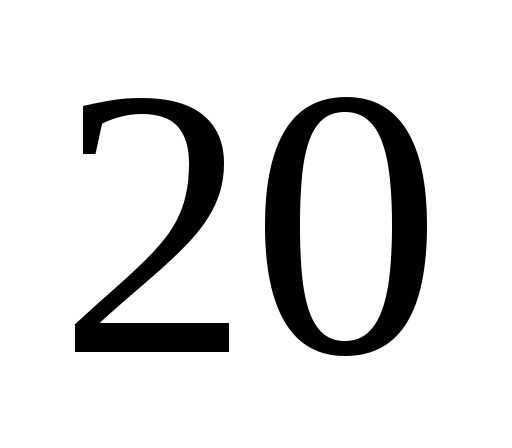

2.
Вычисляется среднеквадратическое
отклонение

3.
В соответствии с поставленными задачами
эксперимента устанавливается требуемая
точность измерений

которая не должна превышать точности
прибора.
4.
Устанавливается нормированное отклонение
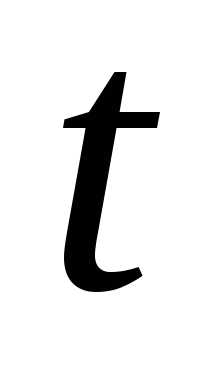
значение которого обычно задается
(зависит также от точности метода).
5.
По формуле (2.2) определяют
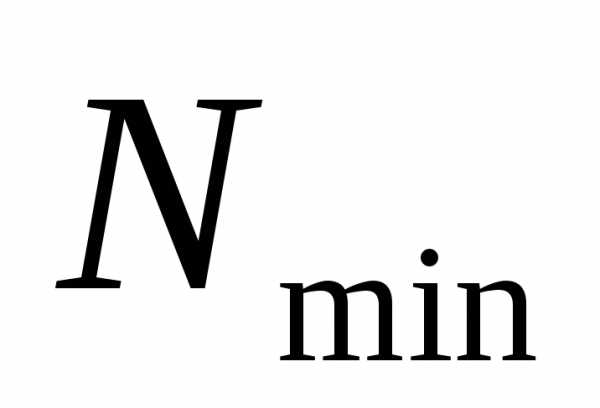
число измерений не должно быть меньше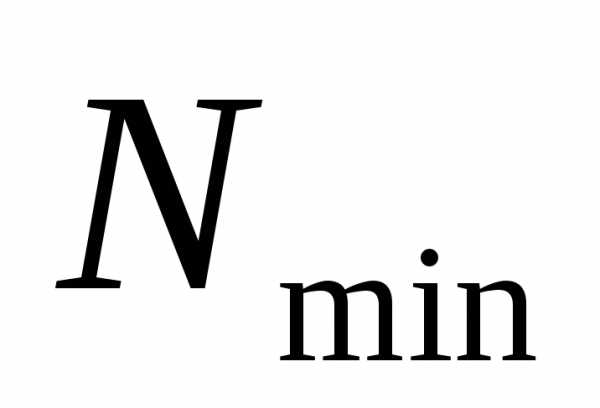
Пример
При приемке
сооружений комиссия в качестве одного
из параметров замеряет их ширину.
Согласно инструкции требуется выполнять

параметра.
Если предварительно вычисленное значение,
то можно определить, с какой достоверностью
комиссия оценивает данный параметр.
Из формулы (2.2)
можно записать
.
В соответствии с
табл.10.1
доверительная вероятность для
.
Это низкая
вероятность.
Погрешность,
превышающая доверительный интервал
,
согласно выражению (1.4) будет встречаться
один раз из,
т.е. из четырех измерений. Это недопустимо.
В связи с этим
необходимо вычислить минимальное
количество измерений с доверительной
вероятностью
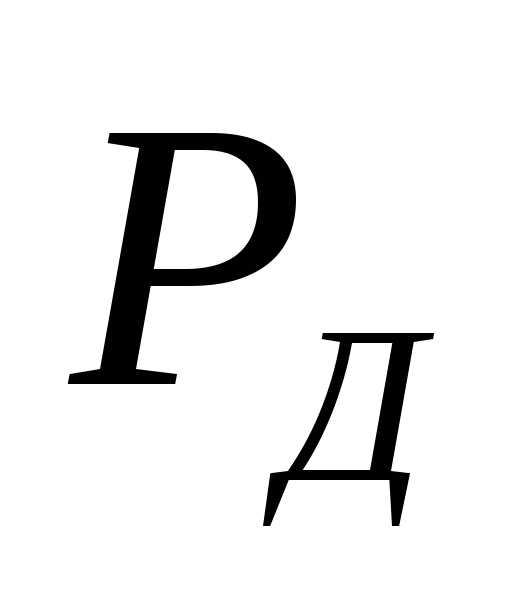
равной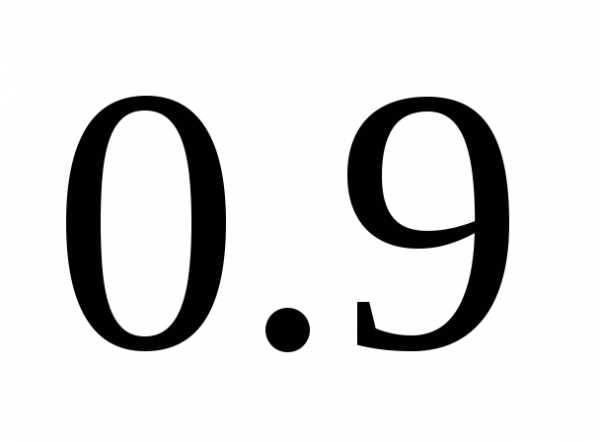
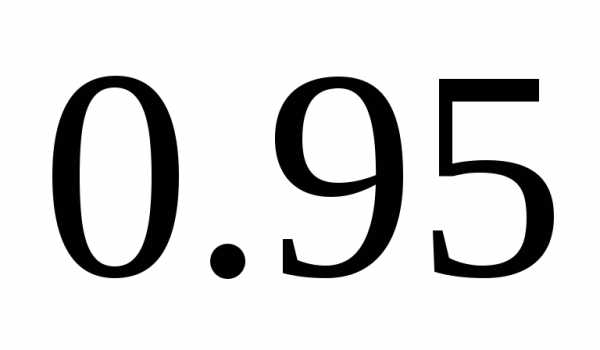
По формуле (2.2)
имеем
измерения при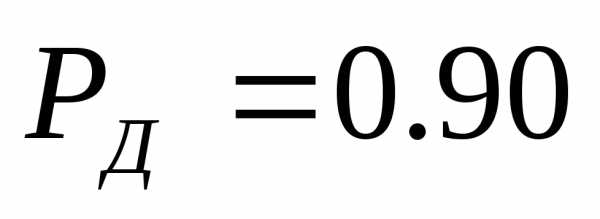

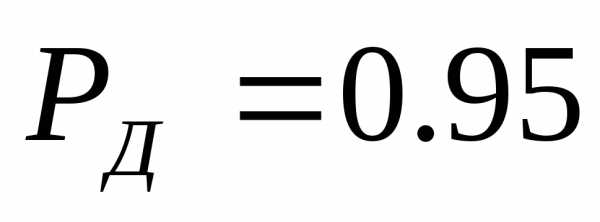
что значительно превышает установленные
Для нахождения
границы доверительного интервала при
малых значениях (
применяют метод, предложенный в 1908 г.
английским математиком Госсетом В.С.
(псевдоним Стьюдент).
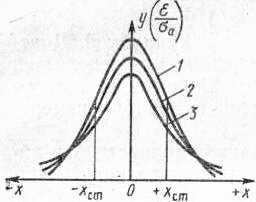
Кривые распределения
Стьюдента в случае
(практически при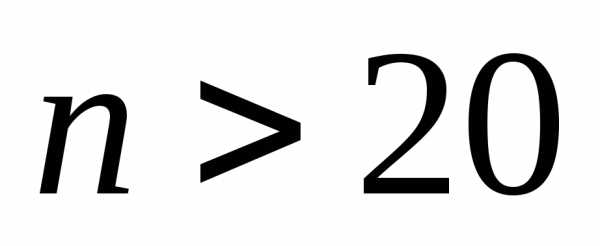
переходят в кривые нормального
распределения (рис.10.1).
Рис.2.1. Кривые
распределения Стьюдента для различных
значений:
1
— при
;2
— при
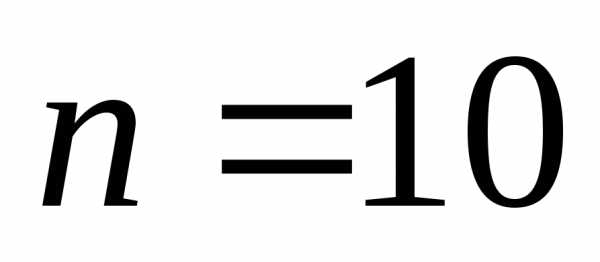
— при
studfiles.net
Коэффициенты Стьюдента
|
Число |
Надежность Р |
||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,99 |
|
|
2 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
637 |
|
3 |
0,82 |
1,06 |
1,5 |
1,9 |
2,9 |
4,3 |
35 |
|
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
12,9 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
8,6 |
|
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
6,9 |
|
7 |
0,72 |
0,91 |
1,1 |
1,4 |
1,9 |
2,4 |
6,0 |
|
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
5,4 |
|
9 |
0,71 |
0,89 |
1,1 |
1,4 |
1,9 |
2,3 |
5,0 |
|
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
4,8 |
2.2. Расчет случайной погрешности
При обработке прямых измерений результаты
наблюдений и вычислений удобно оформлять
в виде табл. 2.
Таблица 2
Расчет среднего значения и случайной погрешности по методу Стьюдента
|
№ |
ai |
|
ai |
ai2 |
|
P |
tPN |
aсл |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
В колонке 1указывается номер опыта
по порядку (обычно проводится 3-7
измерений).
В колонке 2 записываютсязначения
измеряемой величины.
В колонку 3вноситсясреднее
значениеизмеряемой величины,
рассчитанное по формуле:
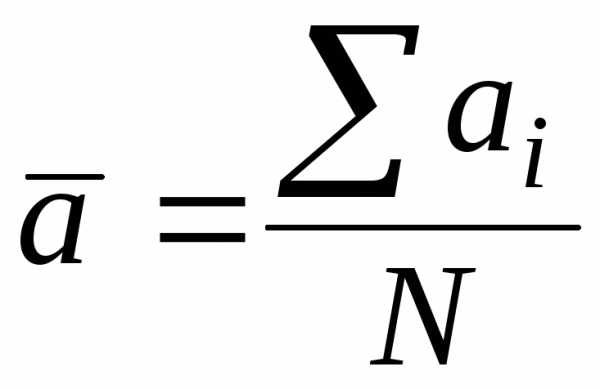
В колонке 4представленыотклонениякаждого значенияизмеряемой величины от среднего:
.
(2)
Каждый результат, полученный по последней
формуле, возводится в квадрат и заносится
в колонку 5.
В колонке 6следует расположитьсреднеквадратичную погрешность ,
рассчитанную по формуле:
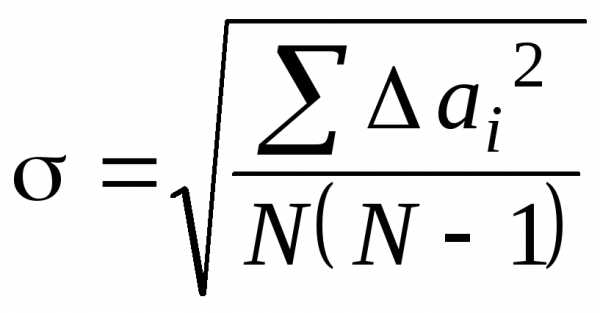
Она характеризует разброс средних
значений измеряемой величины.
Среднеквадратичная погрешность тем
больше, чем сильнее измеренные величины
отличаются друг от друга.
В колонку 7заносится значение
доверительной вероятности (или надежности)
Обычно достаточно выбрать значениеР= 0,95 (или, что то же самое, 95%).
Коэффициент Стьюдента, учитывающий
заданную доверительную вероятность и
число измерений tPN
,находится по табл. 1 и располагаетсяв
колонке 8.
Случайная погрешностьрассчитывается
по формуле
aсл=tPN
S(4)
и заносится в колонку 9.
2.3. Учет систематических погрешностей
К учитываемым систематическим погрешностям
относятся погрешности средств измерения
и погрешности отсчета.
В форме абсолютных погрешностейзадаются погрешности линеек,
штангенциркулей, секундомеров, термометров
и т.п. Абсолютная погрешность средства
измерения в этом случае может быть
вычислена по формуле
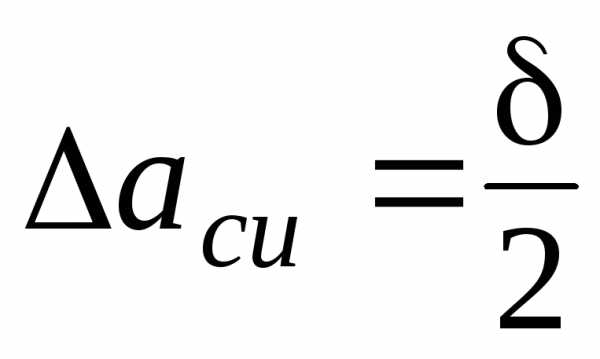
где -
цена деления прибора.
В форме приведенных погрешностейзадаются пределы допускаемых погрешностей
электроизмерительных приборов,
манометров. Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле
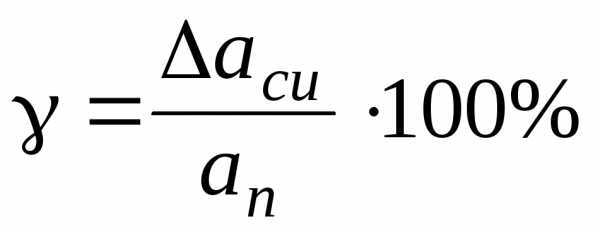
где ап—нормирующее
значениеприбора илипредел измерений;
— предел допускаемой приведенной
погрешности прибора в процентах от
нормирующего значения;
аси— абсолютная погрешность
прибора.
Пользуясь этой формулой, можно определить
абсолютную погрешность измерительного
прибора:
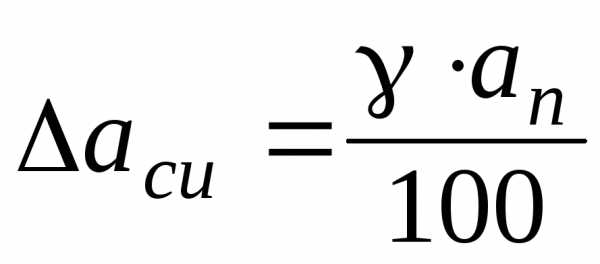
Полная абсолютная погрешностьпрямых измерений рассчитывается по
формуле
. (7)
Чаще всего случайная погрешность и
погрешность средств измерения — величины
разных порядков; в таких случаях меньшей
погрешностью пренебрегают. Например,
если
,
то
studfiles.net
Коэффициенты Стьюдента — это… Что такое Коэффициенты Стьюдента?
- Коэффициенты Стьюдента
-
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Определение
Пусть Fn — функция распределения Стьюдента t(n) с n степенями свободы, и . Тогда α-квантилью этого распределения называется число tα,n такое, что
- .
Замечания
- .
- Функция не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение t(n) симметрично. Следовательно,
- t1 − α,n = − tα,n.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета tα,n, необходимо найти строку, соответствующую нужному n, и колонку, соответствующую нужному α. Искомое число находится в таблице на их пересечении.
Пример
- t0.2,4 = 0.2707;
- t0.8,4 = − t0.2,4 = − 0.2707.
См. также
Квантили tα,n
two-tailed test 1-0.9/2 1-0.8/2 1-0.7/2 1-0.6/2 1-0.5/2 1-0.4/2 1-0.3/2 1-0.2/2 1-0.1/2 1-0.05/2 1-0.02/2 one-tailed test 1-0.9 1-0.8 1-0.7 1-0.6 1-0.5 1-0.4 1-0.3 1-0.2 1-0.1 1-0.05 1-0.02 1 0.1584 0.3249 0.5095 0.7265 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 2 0.1421 0.2887 0.4447 0.6172 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 3 0.1366 0.2767 0.4242 0.5844 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 4 0.1338 0.2707 0.4142 0.5686 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 5 0.1322 0.2672 0.4082 0.5594 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 6 0.1311 0.2648 0.4043 0.5534 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 7 0.1303 0.2632 0.4015 0.5491 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 8 0.1297 0.2619 0.3995 0.5459 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 9 0.1293 0.2610 0.3979 0.5435 0.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 10 0.1289 0.2602 0.3966 0.5415 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 11 0.1286 0.2596 0.3956 0.5399 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 12 0.1283 0.2590 0.3947 0.5386 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 13 0.1281 0.2586 0.3940 0.5375 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 14 0.1280 0.2582 0.3933 0.5366 0.6924 0.8681 1.0763 1.3450 1.7613 2.1448 2.6245 15 0.1278 0.2579 0.3928 0.5357 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 16 0.1277 0.2576 0.3923 0.5350 0.6901 0.8647 1.0711 1.3368 1.7459 2.1199 2.5835 17 0.1276 0.2573 0.3919 0.5344 0.6892 0.8633 1.0690 1.3334 1.7396 2.1098 2.5669 18 0.1274 0.2571 0.3915 0.5338 0.6884 0.8620 1.0672 1.3304 1.7341 2.1009 2.5524 19 0.1274 0.2569 0.3912 0.5333 0.6876 0.8610 1.0655 1.3277 1.7291 2.0930 2.5395 20 0.1273 0.2567 0.3909 0.5329 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 21 0.1272 0.2566 0.3906 0.5325 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 22 0.1271 0.2564 0.3904 0.5321 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 23 0.1271 0.2563 0.3902 0.5317 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 24 0.1270 0.2562 0.3900 0.5314 0.6848 0.8569 1.0593 1.3178 1.7109 2.0639 2.4922 25 0.1269 0.2561 0.3898 0.5312 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 26 0.1269 0.2560 0.3896 0.5309 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 27 0.1268 0.2559 0.3894 0.5306 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 28 0.1268 0.2558 0.3893 0.5304 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 29 0.1268 0.2557 0.3892 0.5302 0.6830 0.8542 1.0553 1.3114 1.6991 2.0452 2.4620 30 0.1267 0.2556 0.3890 0.5300 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 31 0.1267 0.2555 0.3889 0.5298 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 32 0.1267 0.2555 0.3888 0.5297 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 33 0.1266 0.2554 0.3887 0.5295 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 34 0.1266 0.2553 0.3886 0.5294 0.6818 0.8523 1.0525 1.3070 1.6909 2.0322 2.4411 35 0.1266 0.2553 0.3885 0.5292 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 36 0.1266 0.2552 0.3884 0.5291 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 37 0.1265 0.2552 0.3883 0.5289 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 38 0.1265 0.2551 0.3882 0.5288 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 39 0.1265 0.2551 0.3882 0.5287 0.6808 0.8509 1.0504 1.3036 1.6849 2.0227 2.4258 40 0.1265 0.2550 0.3881 0.5286 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 41 0.1264 0.2550 0.3880 0.5285 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 42 0.1264 0.2550 0.3880 0.5284 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 43 0.1264 0.2549 0.3879 0.5283 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 44 0.1264 0.2549 0.3878 0.5282 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2.4141 45 0.1264 0.2549 0.3878 0.5281 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 46 0.1264 0.2548 0.3877 0.5281 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 47 0.1263 0.2548 0.3877 0.5280 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 48 0.1263 0.2548 0.3876 0.5279 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 49 0.1263 0.2547 0.3876 0.5278 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 50 0.1263 0.2547 0.3875 0.5278 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 100 0.1260 0.2540 0.3864 0.5261 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 1000 0.1257 0.2534 0.3854 0.5246 0.6747 0.8420 1.0370 1.2824 1.6464 1.9623 2.3301
Wikimedia Foundation.
2010.
- Коэффициенты Ламэ
- Коялович, Войцех
Смотреть что такое «Коэффициенты Стьюдента» в других словарях:
-
Процентили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез. Содержание 1 … Википедия
-
Квантили распределения Стьюдента — Квантили (процентили) распределения Стьюдента (коэффициенты Стьюдента) числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.… … Википедия
-
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
-
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
-
Наименьших квадратов метод — один из методов ошибок теории (См. Ошибок теория) для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближённого представления заданной функции другими (более простыми)… … Большая советская энциклопедия
-
Математи́ческие ме́тоды — в медицине совокупность методов количественного изучения и анализа состояния и (или) поведения объектов и систем, относящихся к медицине и здравоохранению. В биологии, медицине и здравоохранении в круг явлений, изучаемых с помощью М.м., входят… … Медицинская энциклопедия
-
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
-
РДМУ 109-77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов — Терминология РДМУ 109 77: Методические указания. Методика выбора и оптимизации контролируемых параметров технологических процессов: 73. Адекватность модели Соответствие модели с экспериментальными данными по выбранному параметру оптимизации с… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации
-
Нахождение дисперсии ошибки определения коэффициента регрессии — 3.9.3. Нахождение дисперсии ошибки определения коэффициента регрессии При равном числе параллельных опытов (m0) во всех точках плана матрицы дисперсию ошибки определения коэффициента регрессии определяют по формуле… … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
КОЭФФИЦИЕНТЫ Стьюдента t p 2
КОЭФФИЦИЕНТЫ
СТЬЮДЕНТА tp,n
(n от 1 до 30)
р — надежность,
n – число измерений
|
n |
p |
|||||||
|
0,80 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,998 |
0,999 |
|
|
2 |
3,077 |
6,313 |
12,706 |
31,820 |
63,656 |
127,656 |
318,306 |
636,619 |
|
3 |
1,885 |
2,920 |
4,302 |
6,964 |
9,924 |
14,089 |
22,327 |
31,599 |
|
4 |
1,638 |
2,353 |
3,182 |
4,540 |
5,840 |
7,458 |
10,214 |
12,924 |
|
5 |
1,533 |
2,132 |
2,776 |
3,746 |
4,604 |
5,597 |
7,173 |
8,610 |
|
6 |
1,476 |
2,015 |
2,570 |
3,649 |
4,032 |
4,773 |
5,893 |
6,863 |
|
7 |
1,439 |
1,943 |
2,446 |
3,142 |
3,707 |
4,316 |
5,207 |
5,958 |
|
8 |
1,415 |
1,895 |
2,365 |
2,998 |
3,500 |
4,229 |
4,785 |
5,408 |
|
9 |
1,397 |
1,860 |
2,306 |
2,897 |
3,355 |
3,832 |
4,501 |
5,041 |
|
10 |
1,383 |
1,833 |
2,262 |
2,821 |
3,250 |
3,690 |
4,297 |
4,780 |
|
11 |
1,372 |
1,813 |
2,228 |
2,764 |
3,169 |
3,581 |
4,144 |
4,587 |
|
12 |
1,363 |
1,795 |
2,201 |
2,718 |
3,105 |
3,496 |
4,024 |
4,437 |
|
13 |
1,356 |
1,782 |
2,179 |
2,681 |
3,085 |
3,428 |
3,929 |
4,178 |
|
14 |
1,350 |
1,771 |
2,160 |
2,650 |
3,112 |
3,373 |
3,852 |
4,220 |
|
15 |
1,345 |
1,761 |
2,145 |
2,625 |
2,976 |
3,326 |
3,787 |
4,140 |
|
16 |
1,341 |
1,753 |
2,131 |
2,603 |
2,947 |
3,286 |
3,732 |
4,072 |
|
17 |
1,336 |
1,745 |
2,119 |
2,583 |
2,920 |
3,252 |
3,686 |
4,015 |
|
18 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
3,222 |
3,646 |
3,965 |
|
19 |
1,330 |
1,734 |
2,101 |
2,551 |
2,878 |
3,197 |
3,611 |
3,922 |
|
20 |
1,328 |
1,729 |
2,093 |
2,540 |
2,861 |
3,174 |
3,579 |
3,883 |
|
21 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
3,153 |
3,552 |
3,850 |
|
22 |
1,323 |
1,720 |
2,079 |
2,517 |
2,831 |
3,135 |
3,527 |
3,819 |
|
23 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
3,119 |
3,505 |
3,792 |
|
24 |
1,320 |
1,714 |
2,069 |
2,500 |
2,807 |
3,104 |
3,485 |
3,768 |
|
25 |
1,138 |
1,711 |
2,064 |
2,492 |
2,797 |
3,091 |
3,467 |
3,745 |
|
26 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
3,078 |
3,450 |
3,725 |
|
27 |
1,315 |
1,705 |
2,056 |
2,478 |
2,778 |
3,066 |
3,436 |
3,706 |
|
28 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
3,057 |
3,421 |
3,690 |
|
29 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
3,047 |
3,408 |
3,674 |
|
30 |
1,311 |
1,699 |
2,045 |
2,462 |
2,756 |
3,036 |
3,396 |
3,849 |
КОЭФФИЦИЕНТЫ
СТЬЮДЕНТА tp,n
(n от 30 до 500)
р — надежность,
n – число измерений
|
N |
p |
|||||||
|
0,80 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,998 |
0,999 |
|
|
31 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
3,030 |
3,385 |
3,646 |
|
33 |
1,308 |
1,693 |
2,036 |
2,440 |
2,738 |
3,014 |
3,365 |
3,621 |
|
35 |
1,307 |
1,691 |
2,032 |
2,441 |
2,728 |
3,952 |
3,348 |
3,601 |
|
37 |
1,305 |
1,688 |
2,028 |
2,435 |
2,720 |
9,490 |
3,333 |
3,582 |
|
39 |
1,304 |
1,686 |
2,024 |
2,429 |
2,712 |
3,981 |
3,319 |
3,566 |
|
41 |
1,303 |
1,684 |
2,021 |
2,423 |
2,705 |
3,971 |
3,307 |
3,551 |
|
43 |
1,320 |
1,682 |
2,018 |
2,418 |
2,698 |
2,693 |
3,296 |
3,537 |
|
45 |
1,301 |
1,680 |
2,015 |
2,414 |
2,692 |
3,956 |
3,286 |
3,526 |
|
47 |
1,300 |
1,677 |
2,013 |
2,410 |
2,687 |
3,949 |
3,277 |
3,515 |
|
49 |
1,299 |
1,677 |
2,011 |
2,406 |
2,682 |
3,943 |
3,269 |
3,505 |
|
51 |
1,298 |
1,676 |
2,009 |
2,403 |
2,678 |
3,937 |
3,261 |
3,406 |
|
56 |
1,297 |
1,673 |
2,004 |
2,396 |
2,668 |
2,924 |
3,256 |
3,476 |
|
61 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
3,915 |
3,232 |
3,460 |
|
66 |
1,295 |
1,669 |
1,997 |
2,385 |
2,654 |
3,906 |
3,220 |
3,447 |
|
71 |
1,294 |
1,669 |
1,994 |
2,381 |
2,648 |
3,899 |
3,211 |
3,435 |
|
81 |
1,292 |
1,664 |
1,990 |
2,373 |
2,638 |
2,887 |
3,195 |
3,416 |
|
91 |
1,291 |
1,662 |
1,987 |
2,389 |
2,632 |
2,878 |
3,183 |
3,402 |
|
101 |
1,290 |
1,660 |
1,984 |
2,364 |
2,626 |
2,871 |
3,174 |
3,391 |
|
121 |
1,289 |
1,658 |
1,972 |
2,358 |
2,617 |
2,860 |
3,160 |
3,374 |
|
151 |
1,287 |
1,655 |
1,976 |
2,352 |
2,609 |
2,848 |
3,146 |
3,357 |
|
201 |
1,286 |
1,653 |
1,972 |
2,345 |
2,601 |
2,839 |
3,132 |
3,340 |
|
251 |
1,285 |
1,651 |
1,970 |
2,341 |
2,597 |
2,822 |
3,123 |
3,330 |
|
301 |
1,284 |
1,650 |
1,968 |
2,339 |
2,592 |
2,828 |
3,118 |
3,323 |
|
401 |
1,284 |
1,649 |
1,966 |
2,336 |
2,588 |
2,823 |
3,111 |
3,315 |
|
501 |
1,283 |
1,647 |
1,964 |
2,333 |
2,785 |
2,819 |
3,106 |
3,310 |
studfiles.net
Коэффициент Стьюдента
|
n |
a |
||||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
31,6 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
8,6 |
|
10 |
0,7 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
3,3 |
4,8 |
Таким образом,
порядок расчета случайной ошибки
измерения должен быть следующим:
а) производят n
измерений искомой физической величины
и вычисляют ее среднее значение
;
б) находят абсолютные
погрешности отдельных измерений
;
в) рассчитывают
среднюю квадратическую погрешность
среднего арифметического
;
г)
по заданной доверительной вероятности
a
и числу измерений n
находят из табл. 1.1 коэффициент Стьюдента
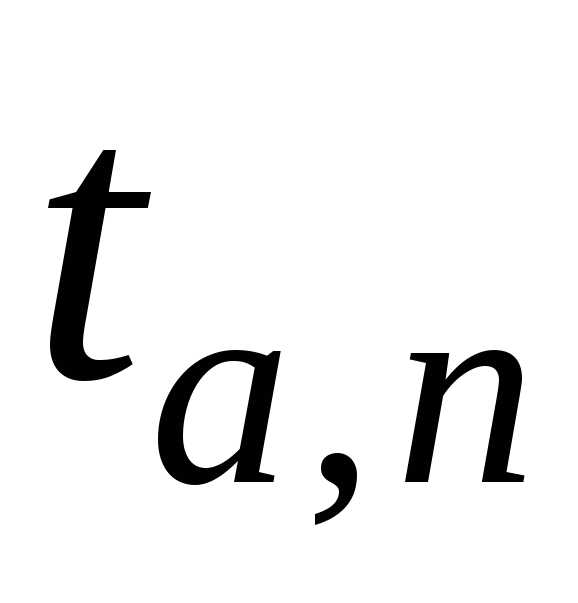
д) рассчитывают
доверительный интервал
;
е) окончательный
результат записывают в виде
при
.
Замечания.
Так как при малом числе измерений
является
случайной величиной и определяется с
большой погрешностью, то при записи
числового значения доверительного
интервала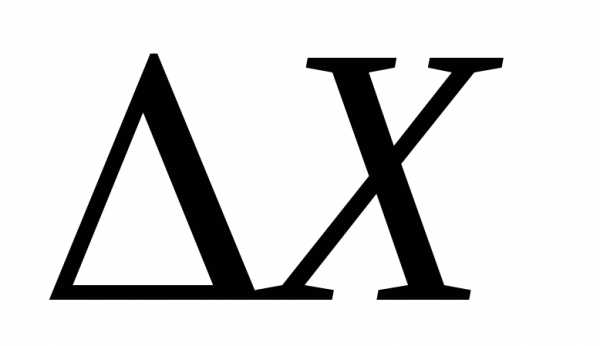
учитывать это обстоятельство. В теории
ошибок доказано, что при числе измеренийn
£
10
в числовом значении
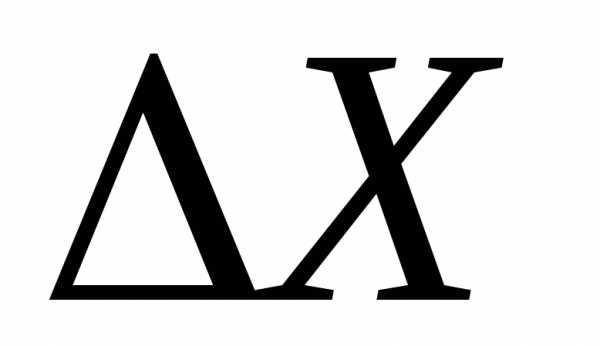
оставить одну значащую цифру, если она
больше трех (),
и две, если первая из них меньше четырех
().
Затем числовое значение <X
>
округляют до разряда ошибки, например:
.
Точность вычислений
при обработке результатов измерений
нужно согласовать с точностью самих
измерений, ошибка вычислений должна
быть на порядок меньше ошибки измерений.
Систематические ошибки. Соотношение случайной и систематической ошибок
Систематические
ошибки могут существенно исказить
результат измерения, поэтому перед
началом измерений необходимо выявить
систематические ошибки и, если возможно,
исключить их. С этой целью проверяют
исправность используемых приборов,
правильность их установки, анализируют
метод измерения и т. д. Чаще всего
источником систематических погрешностей
являются неточности, допущенные при
изготовлении измерительных приборов,
такие погрешности называют инструментальными,
или приборными. Эти ошибки при изготовлении
приборов не определяют, а лишь
устанавливают, не превышают ли они
допустимые пределы. Предельная погрешность
d
обычно указывается в паспорте или
обозначается соответствующим условным
знаком на шкале прибора. Например, для
микрометра предельная погрешность
равна 0,004 мм,
для штангенциркуля –
0,05 мм
и
т. д.
Таким
образом, в результате обработки данных,
полученных при измерении, мы находим
случайную ошибку, величина которой
определяется полушириной доверительного
интервала
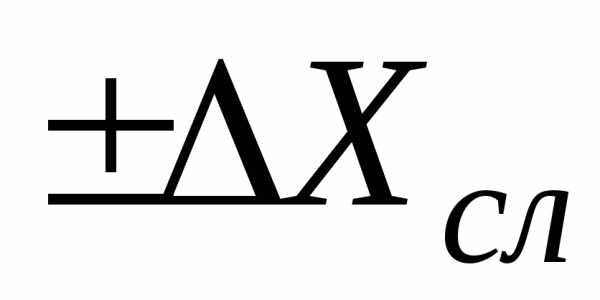
и ситематическую ошибку, равную предельной
погрешности:Если предельная допустимая погрешность
измерительного прибора не указана, то∆Хпр
берут равной половине цены наименьшего
деления шкалы прибора.
К
какому же отношению между величинами
случайной и систематической погрешностей
следует стремиться при проведении
измерений? По-видимому, определяющей
должна быть систематическая ошибка,
т.е., выбирая метод измерения и необходимое
число измерений, нужно добиваться, чтобы
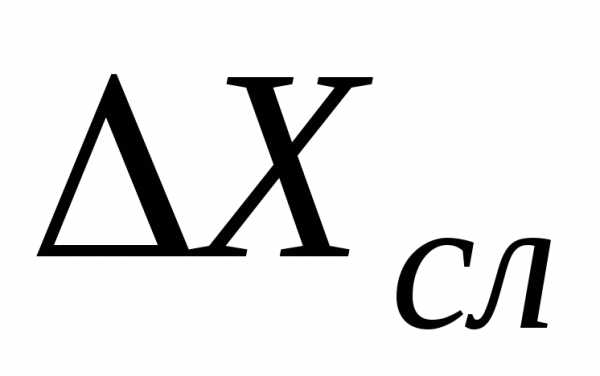
меньше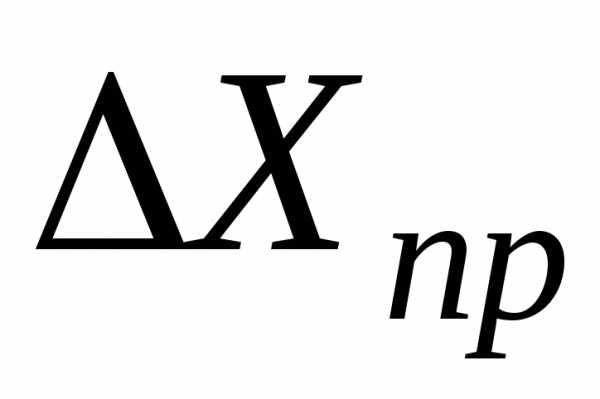
Если,
то пренебрегают систематической ошибкой,
прирассматривают только систематическую
ошибку. Может оказаться, что случайная
ошибка сравнима по величине с
систематической, тогда находят суммарную
ошибку
.
studfiles.net
Значения коэффициентов Стьюдента
|
n |
0,9 |
0,95 |
0,99 |
0,999 |
|
1 |
2 |
3 |
4 |
5 |
|
2 3 4 5 6 7 8 9 10 ∞ |
6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,65 |
12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 1,96 |
63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 2,58 |
636,62 31,60 12,84 8,61 6,86 5,96 5,40 5,04 4,78 3,29 |
Например,
задавая доверительную вероятность δ
=0.95, по числу проведенных измерений n=5
по табл. 2 можно найти
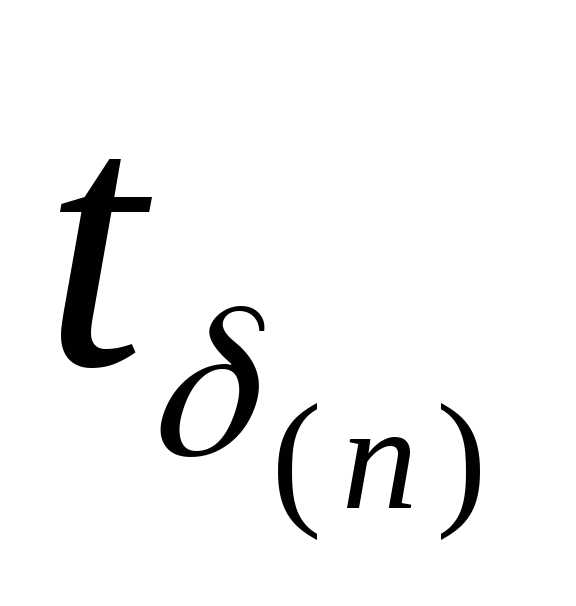
2,78. Тогда, определив предварительно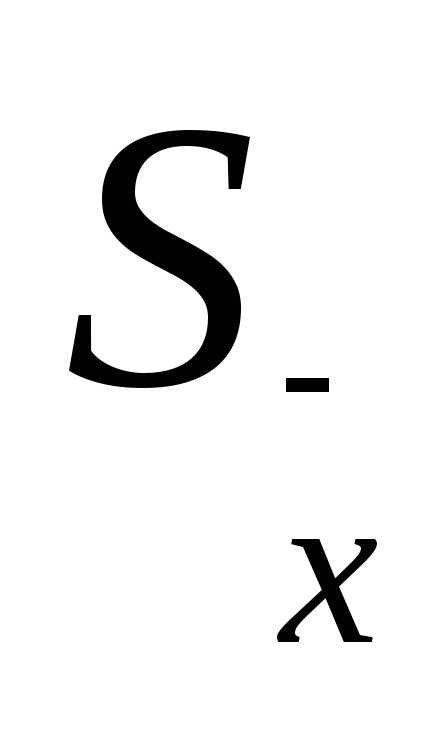
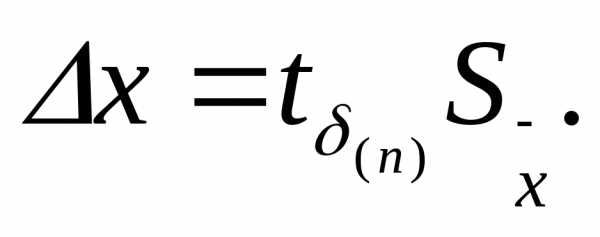
Выражение
(41) ввиду малого объема информации дает
границы доверительного интервала более
широкими.
Результат
измерения можно представить в виде:
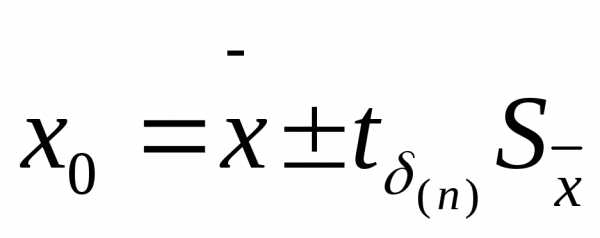
δ=0,95, n=5.
(42)
Конечно,
оценка (42) еще не дает представления об
общей погрешности измерения, в
которую
входит и систематическая ошибка.
Совместный
учет случайных
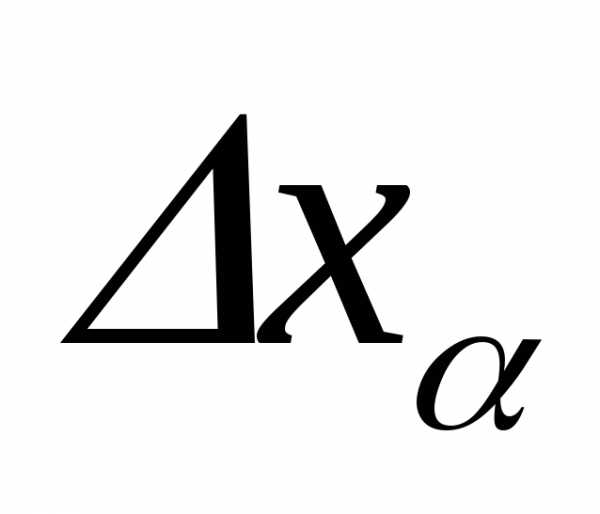
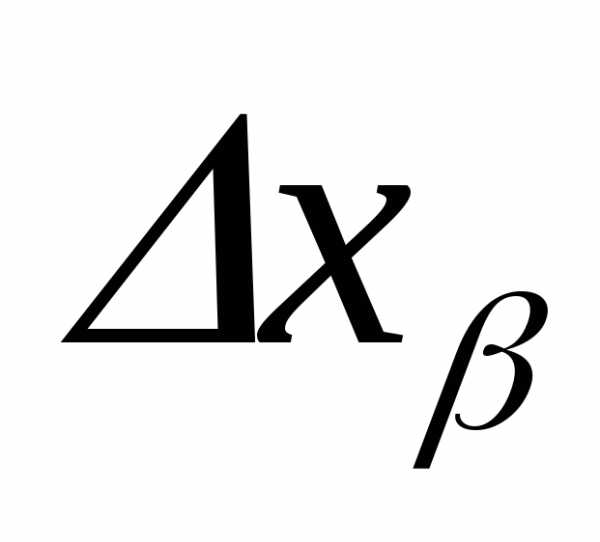
При
этом следует принять во внимание, что
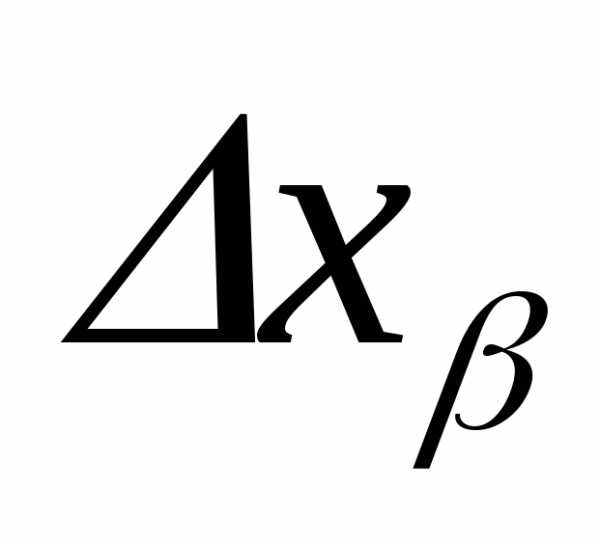
Максимальное же значение случайных
ошибок равно 3σ . Следовательно, для их
равноправного учета необходимо
предположить, что приборная погрешность
β (или ∆пр)
равна утроенной дисперсии распределения
погрешностей прибора 3σпр
,т.е. погрешности соответствующей
надежности δ =0.997. Тогда за систематическую
ошибку можно принять
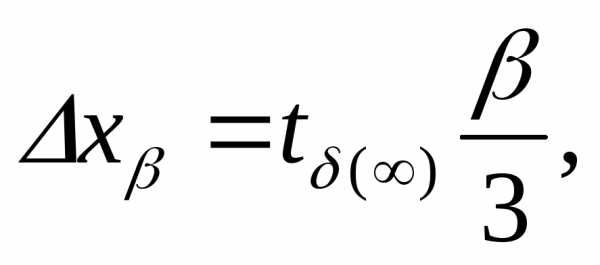
(43)
Коэффициенты
Стьюдента для проведенного числа
измерений


заданной надежности
δ.
Погрешности косвенных измерений
Часто
приходится вычислять искомую величину
по результатам измерений других величин,
связанных с этой величиной определенной
функциональной зависимостью. Например,
объем шара
можно вычислить, измерив его радиусR
. Также измерения называются косвенными.
Рассмотрим
конкретный пример. Допустим, что величины
Х0,
У0
и U0
связаны равенством
.
(44)
Непосредственно
измеряются величины Х0
и У0,
и по этим измерениям мы судим об U0,
считая
(45)
измерением
величины U0.
Предполагается,
что измерения Хi
и yi
независимы друг
от
друга, и распределены нормально с
дисперсиями
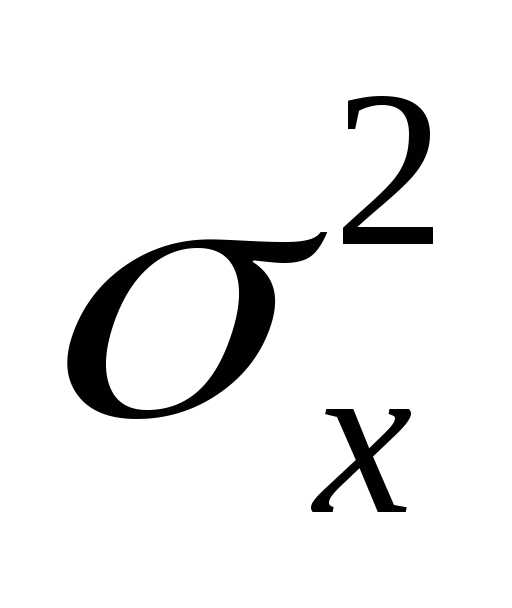
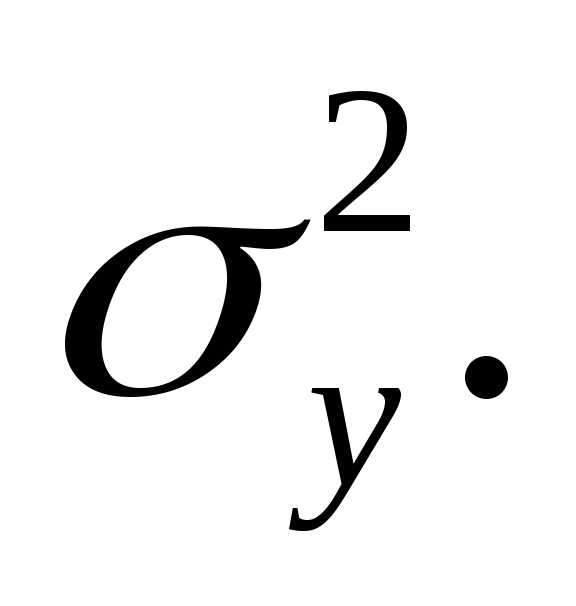
заключается в том, как по известным
значениям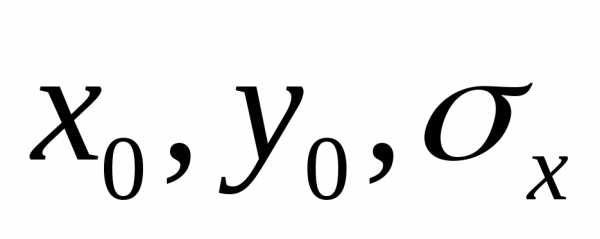

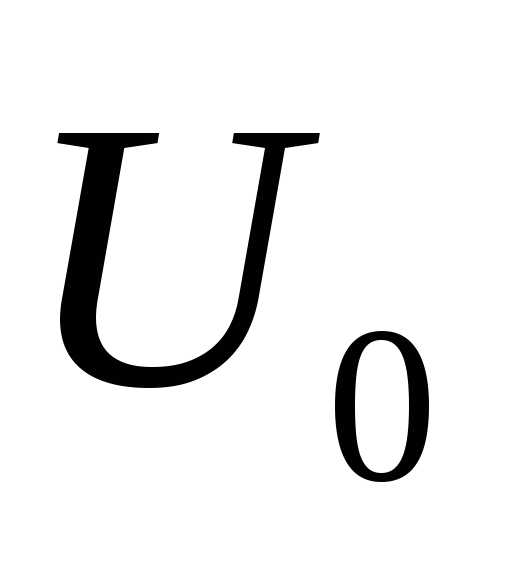
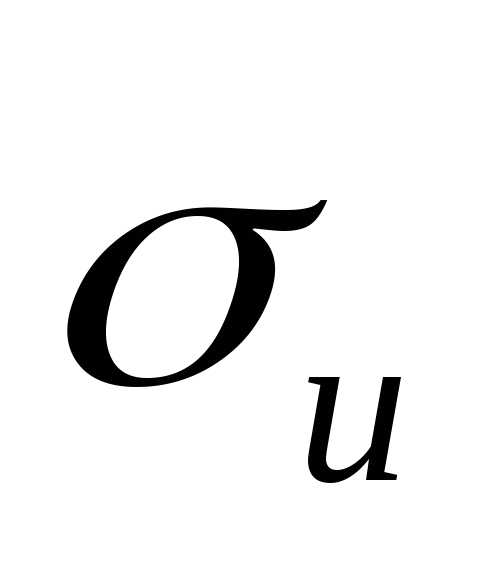
Очевидно,
что погрешность косвенного измерения
обусловлена
погрешностями отдельных измерений
и.
Поэтому выражение (45) можно переписать
в виде:
(46)
Вычитая
почленно левые и правые части уравнений
(46) и (44). для погрешности косвенного
измерения получим:
(47)
Тогда
для дисперсии результатов косвенного
измерения можно записать выражение:
Здесь
член
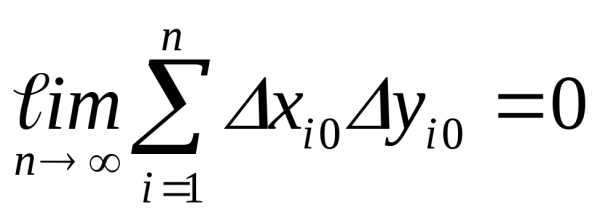
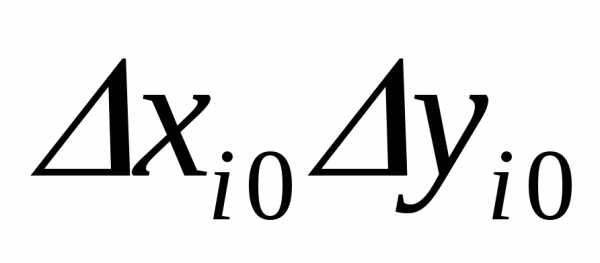
положительным, или отрицательным.
Учитывая,
что
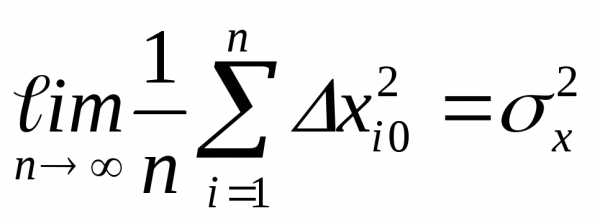
получим
(48)
или
(49)
Равенство
(49) определяет соотношение средних
квадратичных ошибок прямых и косвенных
измерений. Это выражение для частного
случая имеет весьма общий характер и
называется законом сложения дисперсий.
Следовательно,
при измерении нескольких неизвестных
величин складываются дисперсии этих
величин (не ошибки, а именно дисперсии).
Средние
квадратичные ошибки средних арифметических
связаны
аналогичным образом
(50)
Рассмотрим
общий случай, когда u
— функция двух переменных х и y:
(51)
Ошибки
в величинах х и у такова:
,
где Х0
и У0
— истинные значения величин Х в У. Тогда
для результата отдельного измерения
можно записать
(52)
Если
‘та функция непрерывна и имеет
производные, то ее можно разложить в
ряд Тейлора. Рассматривая только члены
c
нулевыми и первыми степенями малых
погрешностей

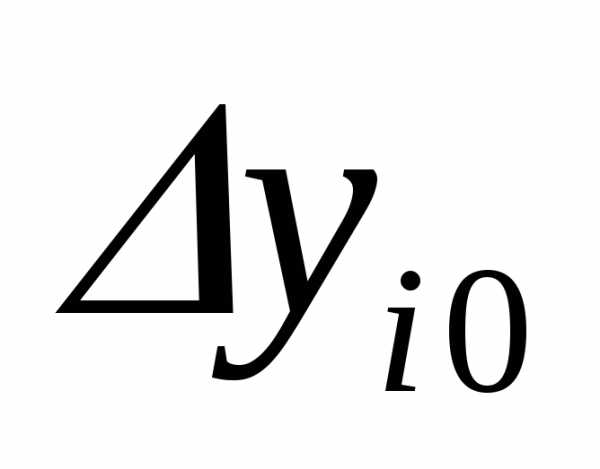
получим:
или
поскольку
(53)
Частные
производные здесь вычисляются при Х=Х0
и У=У0.
Запишем выражение для дисперсии
результатов косвенного измерения:
Учитывая,
что
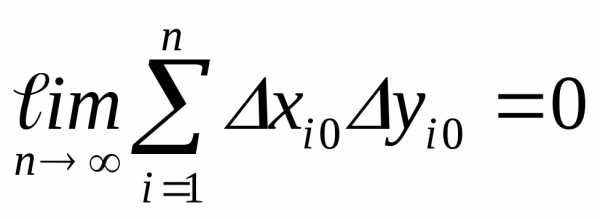
получим
(54)
или
(55)
Для
относительной погрешности косвенного
измерения
учитывая,
что
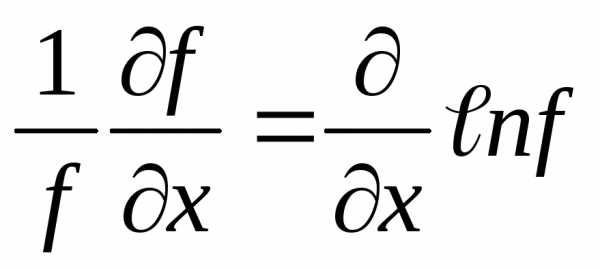
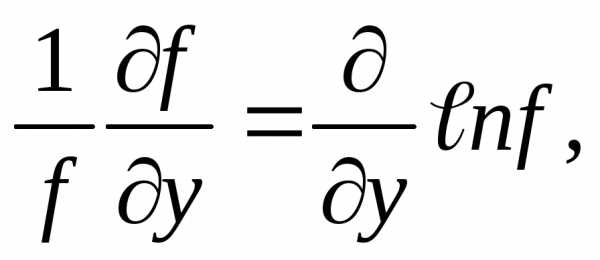
(56)
studfiles.net

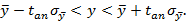
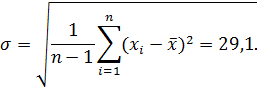








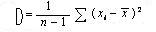
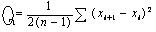
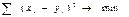
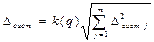
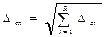
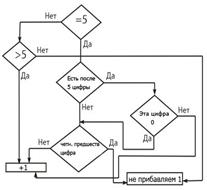
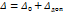
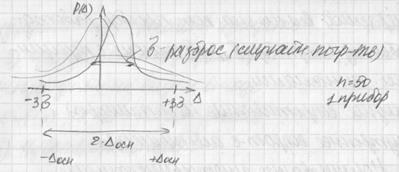

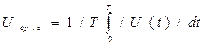

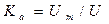
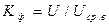
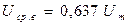
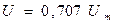
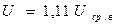


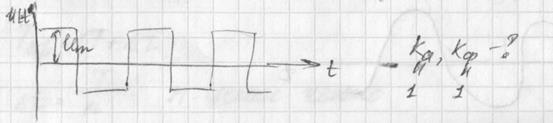
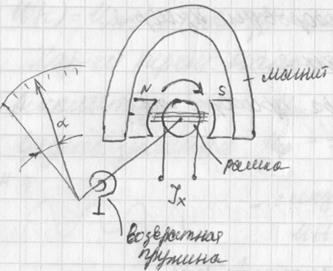
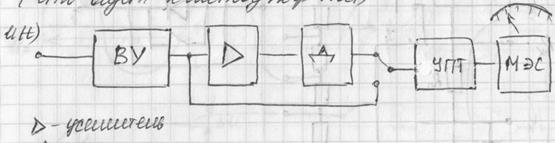

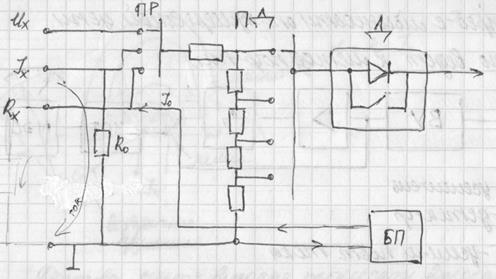








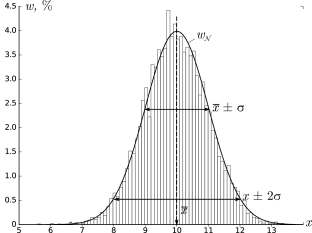

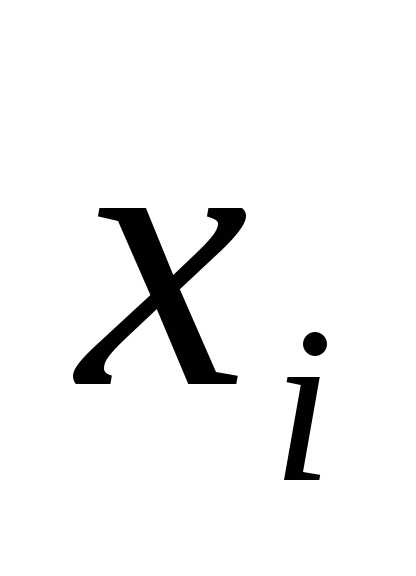
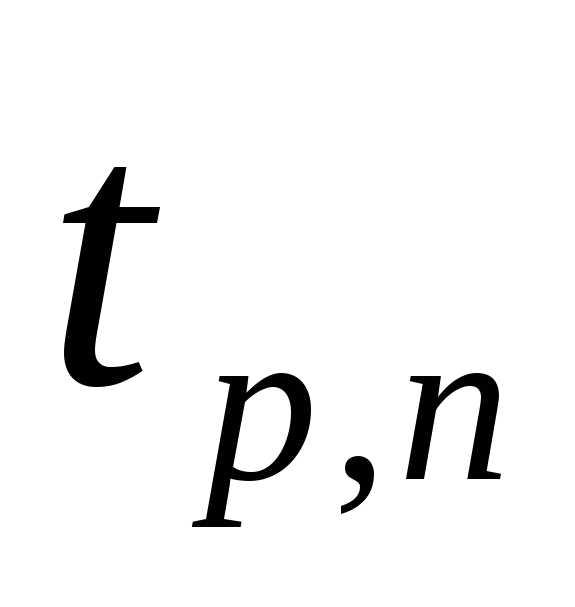
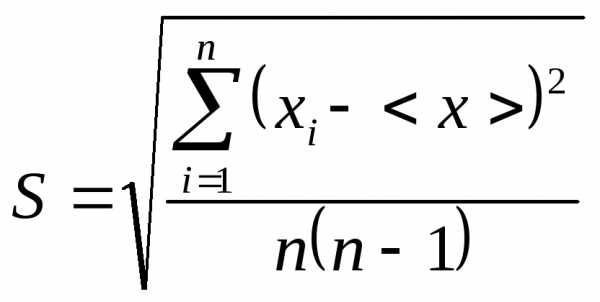
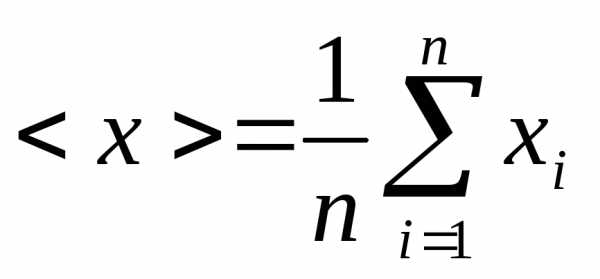
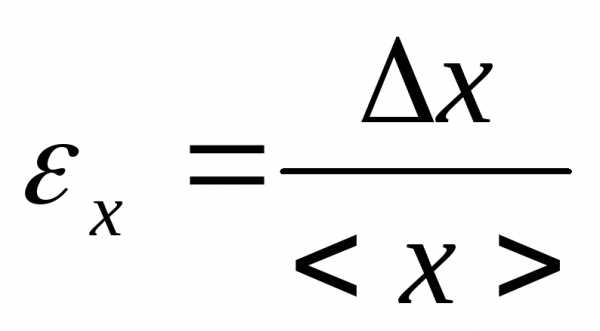
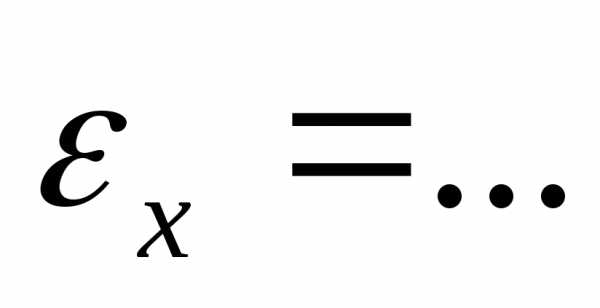 ,
,