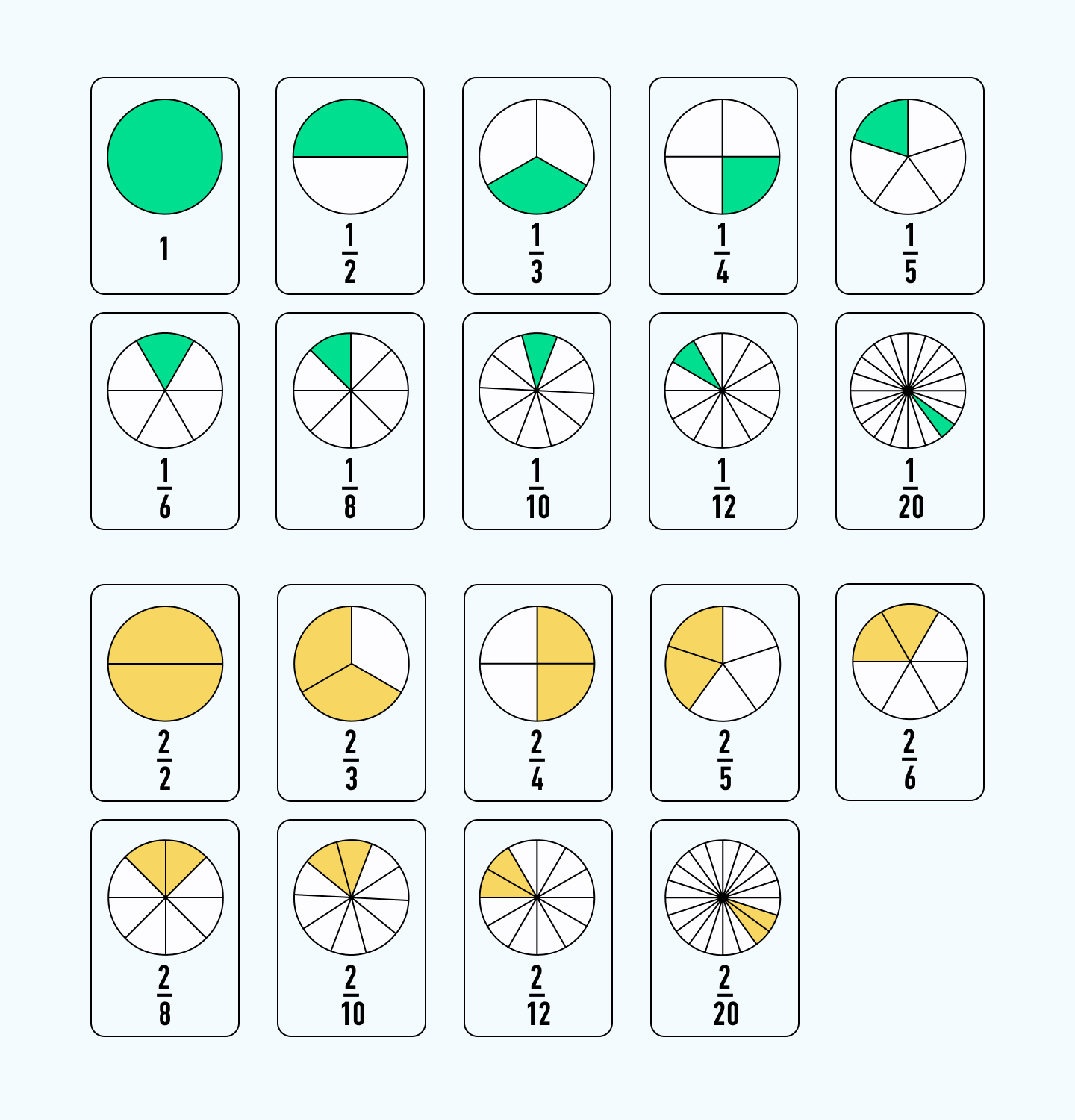
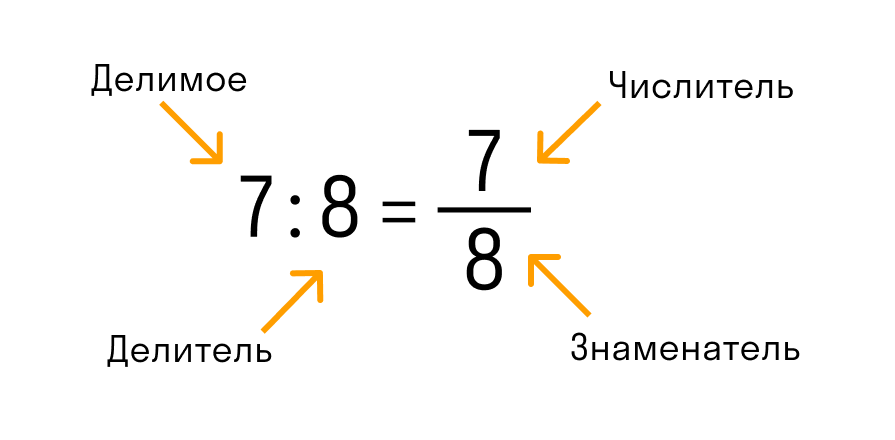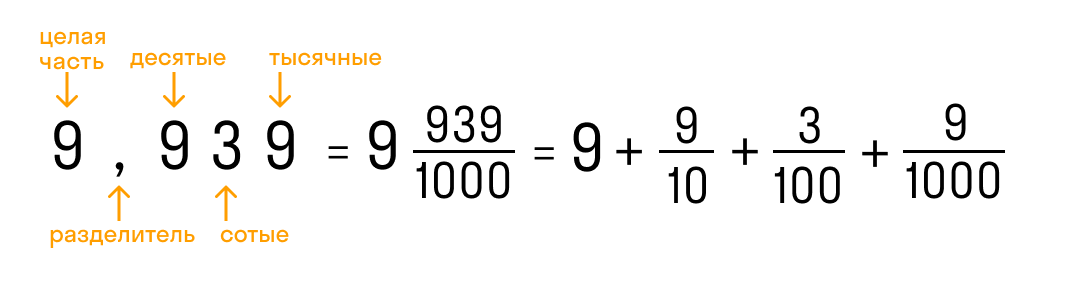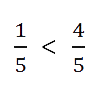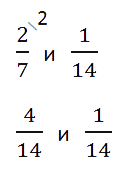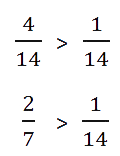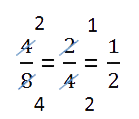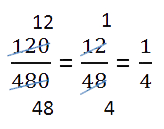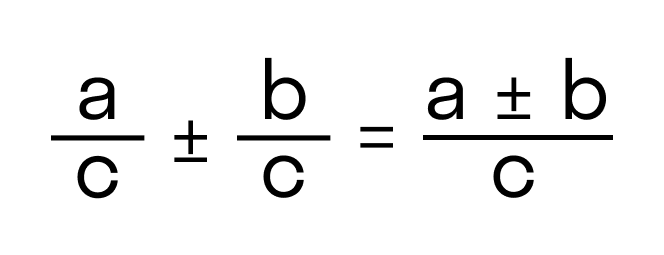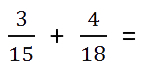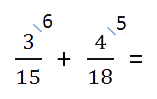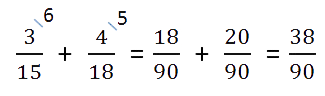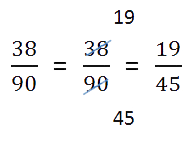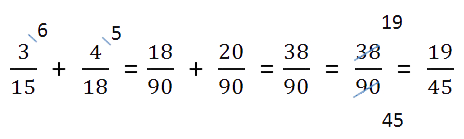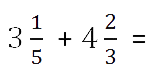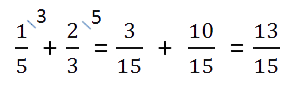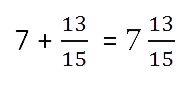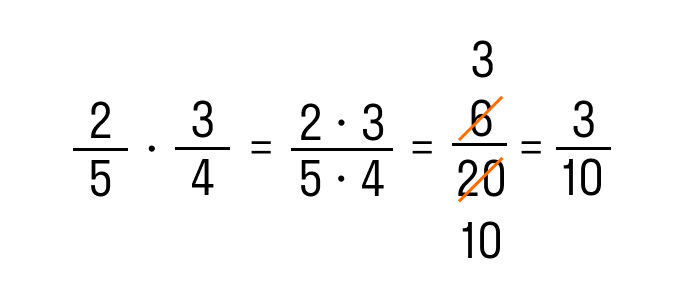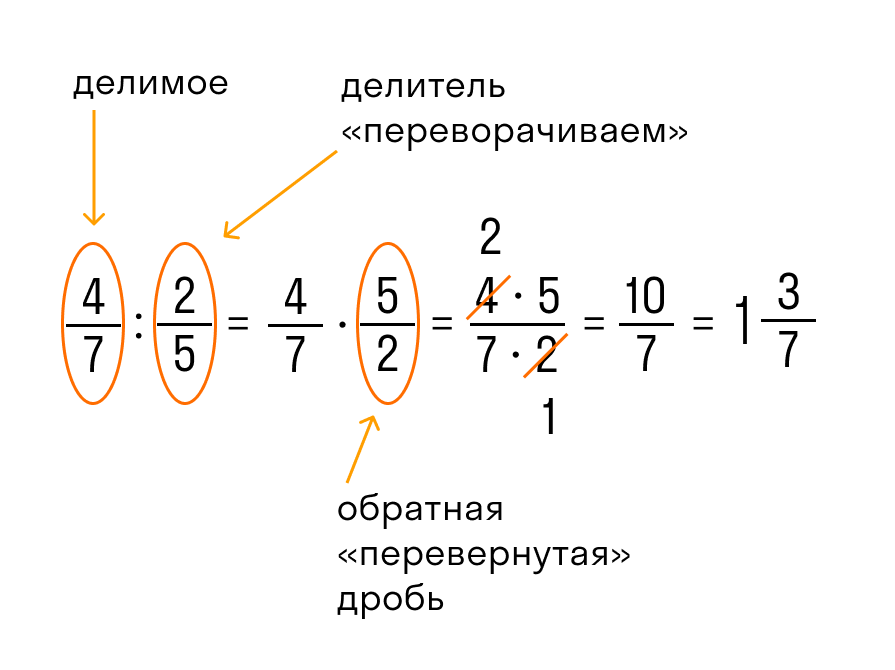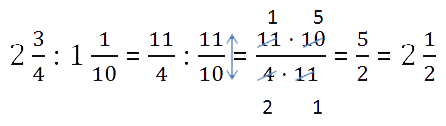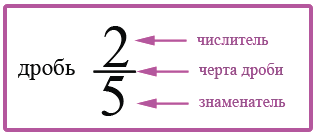Доля целого
Доля это каждая из равных частей, на которые поделено целое.
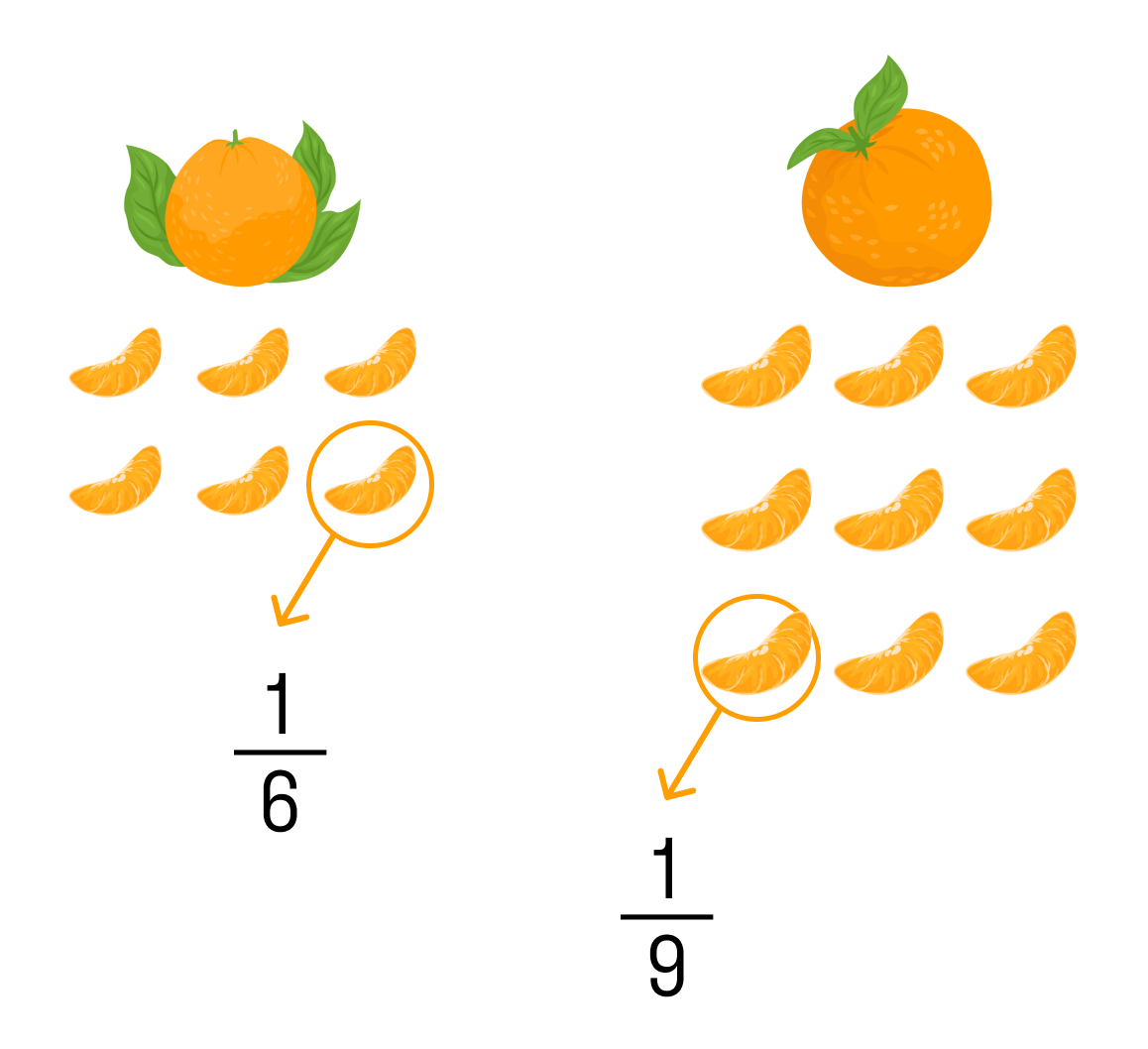
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
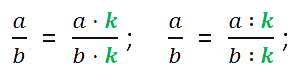
- Дробь не имеет значения, если знаменатель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4
- Поэтому первая дробь 1/5 меньше второй 4/5.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Как рассуждаем:
- Приведем дроби к общему знаменателю:
- Сравним дроби с одинаковыми знаменателями:
Ответ: 2/7 > 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к общему знаменателю, нужно:
- Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
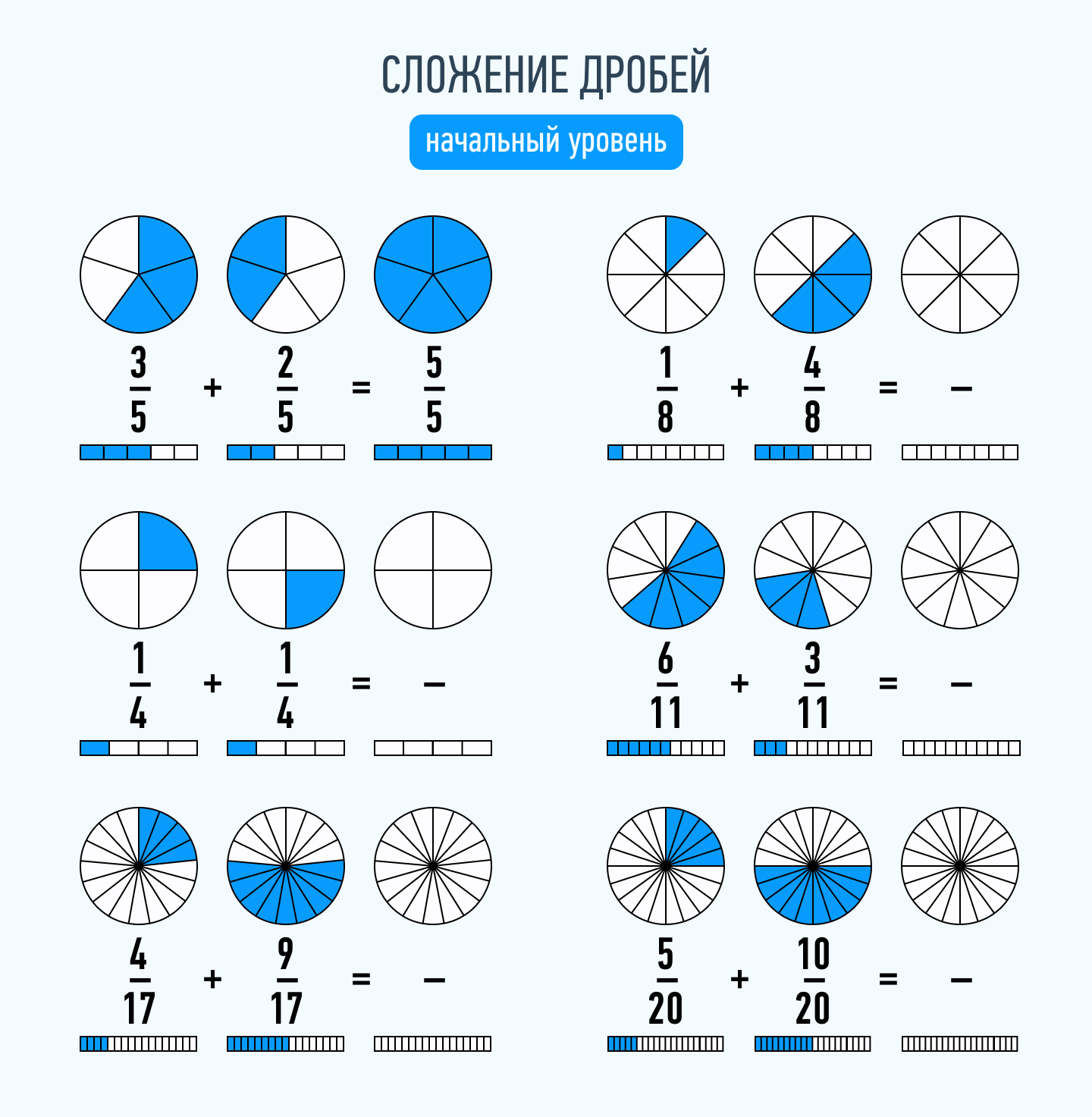
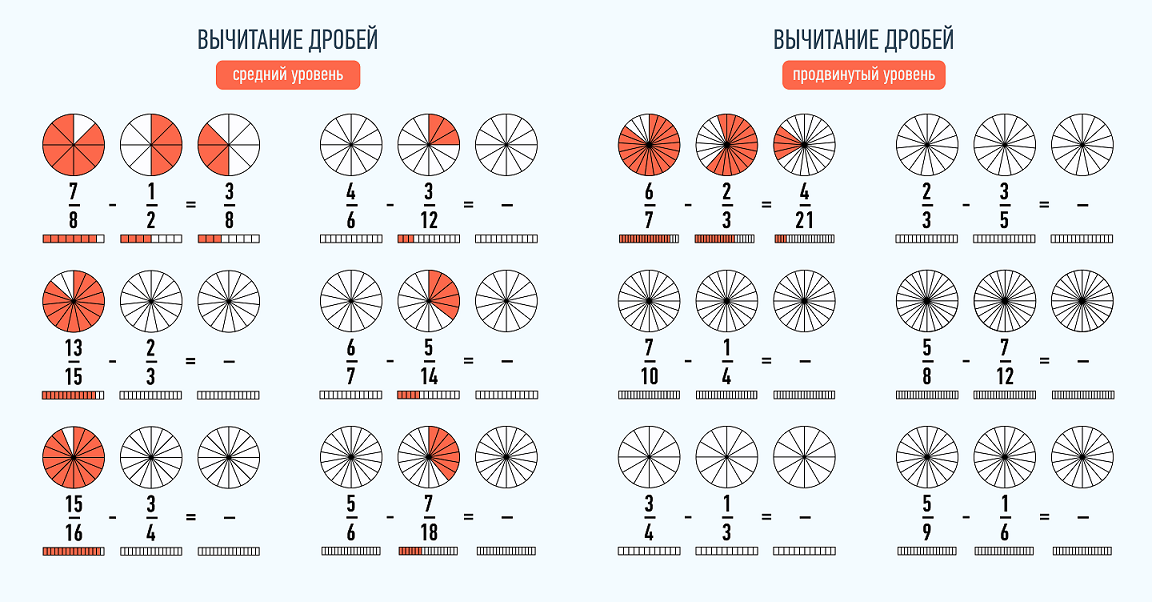
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
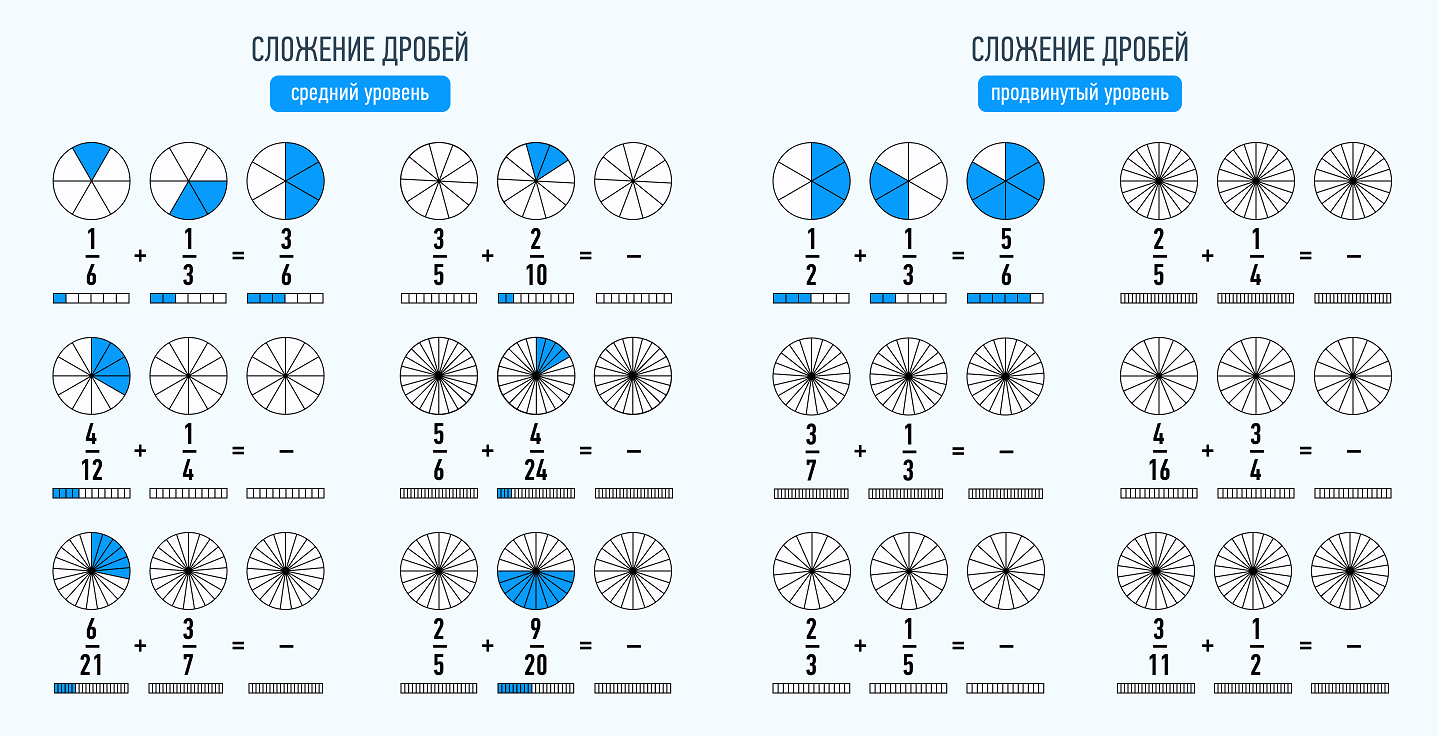
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
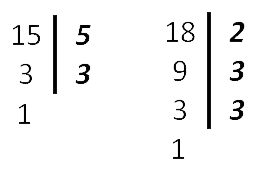
- Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
- Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
- Проверим полученный результат:
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
- Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
Обыкновенные дроби
- Доли единицы
- Обыкновенные дроби
Доли единицы
Единицу можно разделить на равные части.
Пример. Изобразим единицу отрезком и разделим его на три равных части:
Каждую из этих равных частей, на которые разделена единица, называют долей единицы, долей целого или просто долей.
Доля единицы — это каждая из равных частей, на которые разделена единица.
При делении единицы на равные части, доли получают название, которое зависит от того, на сколько частей была разделена единица.
Пример. Если единица разделена на 5 равных частей, то каждая доля называется пятой (частью), а все вместе — пятые (части):
Название доли указывает, какая это часть единицы, а также даёт понять, на сколько равных частей была разделена единица.
Обыкновенные дроби
Для описания количества долей используются обыкновенные дроби.
Обыкновенная дробь — это число, выражающее количество долей. Обыкновенная дробь иначе называется простой дробью или просто дробью.
Дробь устно и письменно выражается двумя числами. Первое число указывает количество долей (например, три), второе — каких долей (например, пятых).
Записывается обыкновенная дробь так: пишут число, показывающее количество долей:
m.
Под этим числом проводят горизонтальную черту и под чертой пишут второе число, показывающее, какие это доли:
где m — нуль или натуральное число, n — натуральное число.
Таким образом, математическая запись обыкновенной дроби состоит из двух чисел, которые отделяются друг от друга горизонтальной чертой.
Пример. Изобразим единицу отрезком, который разделён на 9 долей. Отметим на нём одну, две и четыре доли:
Выразим выделенные количества долей дробями. Одна доля выражается дробью 


Некоторые обыкновенные дроби имеют свои названия, которые часто используются в обиходе. Так, одна вторая доля называется иначе половиной, одна третья доля — третью, одна четвёртая доля — четвертью:
План урока:
Понятие доли и обыкновенной дроби
Правильные и неправильные дроби
Минутка истории
Без знания дробей никто не может признаваться знающим арифметику! (Цицерон)
Дробные числа сопровождают нас в течение всей жизни, они помогают строить, лечить, сочинять музыку, писать стихи. Их можно найти везде, нужно только задуматься над этим – начиная от покупки продуктов в магазине (½ кг сахара), кулинарных рецептов и заканчивая спокойствием в доме (честно разделить между всеми домочадцами мамин пирог). Поэтому стоит внимательно и вдумчиво отнестись к изучению данной темы!
Понятие доли и обыкновенной дроби
Новый год – любимый праздник многих. Дед мороз, праздничный стол, подарки, веселье. Ассоциации у всех разные. И только мандарин, вызывает у каждого праздничное настроение.
Изображение взято с фотостока
Вот именно на примере мандарина и рассмотрим, что такое доли.
Представьте, что праздники закончились, а в вазе остался только один мандарин. Как же разделить его на всех, как сделать так, чтобы все получили одинаковую долю?
Очень просто! Мандарин следует поделить на дольки, и раздать желающим.
На рисунке, фрукт состоящий из 8 долек, то есть 8 человек могут взять по 1 дольке. Делаем вывод, что доля – это одна из одинаковых частей чего-либо. Каждый гость получил по 1 из 8 долек, значит, получил по 1/8 всего мандарина.
Если бы гостей было двое, то фрукт пришлось делить на 2 части, при этом, каждый взял бы по однойиз двух половинок, то есть по ½ мандарина или половину.
Запомни!1/2 – половина,1/3 часть называют – треть, а ¼ – четверть.
Например:яблоко разрезали на 3 кусочкаи раздали 3 детям, получается, что каждому ребенку досталась треть яблока.
Для письменного обозначения количества долей, используются обыкновенные дроби.В записи которой, содержится два числа и черта, которая их разделяет. Черта бывает горизонтальной и вертикальной.
Помни! Обыкновенная дробь – число вида c/k, где обязательно с и к натуральные числа.
Числовое значение, расположенное над чертой, или слева от неё, называют числителем. Числителем обыкновенной дроби c/k называют натуральное число с.
Числовое значение, расположенное под чертой или справа от неё, называют знаменателем.
Знаменателем обыкновенной дроби c/k, называют натуральное число к.
Давайте разберемся, какую информацию несет числитель и знаменатель?
Запомни! Знаменатель указывает на количество равных долей в предмете.
Например: в дробном числе 5/6, знаменатель 6 говорит, что предмет состоит из 6 долей.
Запомни! Числитель показывает, количество используемых долей.
Например: в записи 5/6, числитель 5 показывает, что используется 5 долей.
Получается, 5/6 говорит о том, что предмет разделен на 6 долей, но используется только 5 из них.
Если пока не получается запомнить из каких компонентов состоит дробь, то просто сохрани табличку и пользуйся!
Теперь давайте рассмотрим, как же выполнить сравнение обыкновенных дробей.
Представим такую ситуацию:
Мама испекла пирог и разделила его на 3 части. Дети съели лакомство. Миша съел 2/3 пирога, а Васе досталась 1/3. Как определить, кому достался больший кусок пирога?
На рисунке видно, что порция Миши оказалась больше.
Значит, 2/3>1/3.
Сформулируем правило сравнения обыкновенных дробей.
Помни! Чтобы сравнить дроби, имеющие равные знаменатели, достаточно сравнить только числители. Больший числитель соответствует большему числу.
Например:
Довольно часто, возникает необходимость, найти сумму или разность обыкновенных дробей. Как правильно выполнять действия сложения и вычитания обыкновенных дробей?
Рассмотрим сложение дробей:
Назару задали 15 примеров, он сначала решил 2 примера, а потом ещё 1 пример. Мама поинтересовалась у него, какая часть домашнего задания выполнена? Назар задумался. Давайте подумаем и мы:
Все задание состоит из 15 примеров – это количество долей, на которое разбито все задание, или знаменатель. Сначала мальчик вычислил 2 примера – это часть задания, которая взята к рассмотрению, или числитель. Получаем 2/15. Позже он решил еще один пример, значит, выполнил еще 1/15 всей работы. Чтобы определить, какая часть задания выполнена, необходимо сложить полученные выражения: 2/15 + 1/15.
Помни! При сложении обыкновенных дробей, достаточно суммировать числители, а цифру под чертой записать без изменений.
2/15 + 1/15 = (2+1)/15 = 3/15.
Получается, что мальчик выполнил 3/15 всего задания, значит, 3 задания из 15.
Теперь давайте узнаем, как необходимо выполнять вычитание обыкновенных дробей, имеющих равные знаменатели.
Важно! Чтобы найти разностьдвух дробей, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель записать без изменений.
Например: 5/8 — 2/8 = (5-2)/8 = 3/8
Правильные и неправильные дроби
Все обыкновенные дробные выражения делятся на правильные и неправильные дроби:
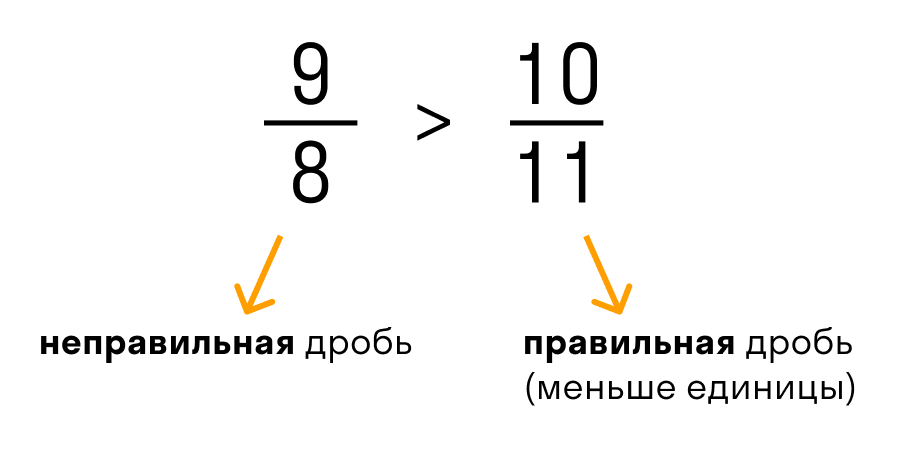
- Правильные дроби,всегда имеют числитель меньший, чем знаменатель: ¾,2/7.Такие дроби < 1.
- Неправильные дроби, всегдаимеют знаменатель меньший или равный числителю,Такие дроби ≥ 1.
Примеры неправильных дробей: 4/3,9/8, 10/10
В нашей повседневной жизни, возникают разные ситуации, и часто именно знания связанные с дробными выражениями, помогают найти правильное решение. Например:
Маша съела 5/3 яблока. Как узнать, сколько яблок съела Маша?
Если исходить из определений компонентов дробного выражения, получается,что яблоко разделили на 3 кусочка, но съедено было 5 таких кусочков, значит, фрукт был не один.
В таком случае поможет использование правила выделения целой части из неправильной дроби, то есть определения количества целых предметов:
- найти частное числителя и знаменателя;
- целое частное, создает целую часть;
- остаток записывается над чертой, а под чертой остается прежний знаменатель.
Зная, как найти количество целых предметов, давайте узнаем, сколько же яблок съела Маша. Для этого делим числитель на знаменатель (5:3=1(ост.2)), получается 1 и востатке 2.
Единица показывает количество целых предметов, остаток записываем над чертой, а под чертой записываем делитель – 1+2/3. Следовательно, Маша съела 1 целое яблоко и 2/3 второго яблока.
Выполнив все расчеты, мы получили запись нового числового значения, состоящего изцелой и дробной части. Числовые значения такого виданазывают смешанными числами. Примеры смешанных чисел:
Важно! Любое смешанное число всегда переводится в неправильную дробь!
Для этого существует специальный алгоритм действий:
- Перемножаем целую часть и знаменатель.
- Суммируем произведение с числителем.
- Суммазаписывается числителем, а знаменатель не меняется.
Например:3 + 4/5 = (3*5+4)/5 = 19/5
Запомни очередность действий, и тогда, даже самое сложное домашнее задание не огорчит тебя!
Часто возникает необходимость в сложении и вычитании смешанных чисел. Как это правильно сделать?
Важно! При сложении смешанных чисел, сначала суммируются целые части слагаемых, а потом дробные части.
Например: 4+2/7 + 6+3/7 = 10+(2+3)/7 = 10+5/7
Важно! При вычитании смешанных чисел, от целой части уменьшаемого отнимается целая часть вычитаемого, а после отнимаются дробные части.
Например: 14+6/11 – 8+4/11 = 6+(6-4)/11 = 6+2/11
Минутка истории
Точное время появления дробных выражений пока не установлено. Но исторические находки предполагают, что они возникли в связи с жизненной необходимостью. Задания с использованием дробей считались самыми сложными, и выполнять их могли, только люди, обладающие огромным умственным потенциалом. За такие знания, мудрецов почитали на уровне бога. Ведь без их помощи невозможно было разделить добычу между всеми охотниками поровну, уловмежду рыбаками, урожай между соседями. До сих пор в Германии существует поговорка «Оказаться в дробях», – это значит попасть в попасть в непонятную, запутанную ситуацию.
На Русь, понятие «дробь»пришлов начале 9 века. Источником этого понятия стало выражение «дробить» (разделять, разламывать). На протяжении длительного времени,разные народы называли такие числа ломаными, ведь при разделении любого предмета (конфета, яблоко, хлеб) его приходилось разламывать.
В России существовала отдельная единица измерения для определения размеров земельных наделов, она состояла из четверти и получетверти. Еще эту единицу называли осьмина. Это была дробь, которая использовалась только для измерения земельных угодий. Осьминой невозможно измерить другие величины, скорость или количество прибыли. Гораздо позже эта единица измерения преобразовалась в 1/8, которую можно применять для измерения любой величины.
В произношении дробных чисел на Руси, были свои правила. В название, дробного числа,знаменатель которого больше 5, и меньше 11 добавлялось окончание «ина»: 1/6– шестина, 1/9– девятина, 1/10– десятина. Если дробь имела в знаменателе число больше 10, то в названии дроби обязательно произносились слово «жеребей»: 4/13 – четыре тринадцатых жеребьев.
Число, которое записывалось над чертой, называли верхнее число, а число под чертой – исподнее число.
Где в жизни мы можем встретить дроби:
— При использовании мер измерения: 1 грамм=1/1000 килограмма=1/100000 центнера
— Охотники,используют дробь.
— В медицине. Каждое лекарственное средство, в своем составе, содержит различные компоненты, измеряющиеся дробями.
— Быструю, резкую игру на барабанах называют барабанной дробью.
— По команде капитана корабля «дробь» сразу прекращается огонь.
— При нумерации домов использование дробей уместно на двух пересекающихся улицах.
— Основными движениями в русских народных танцах является дробь и бег.
— Во всех кулинарных рецептах, необходимые пропорции указаны дробными числами: 2/3 стакана муки или 3/4 яблока.
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
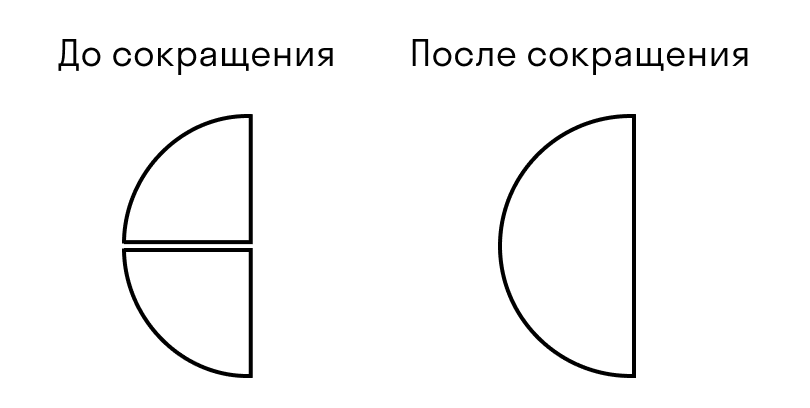
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
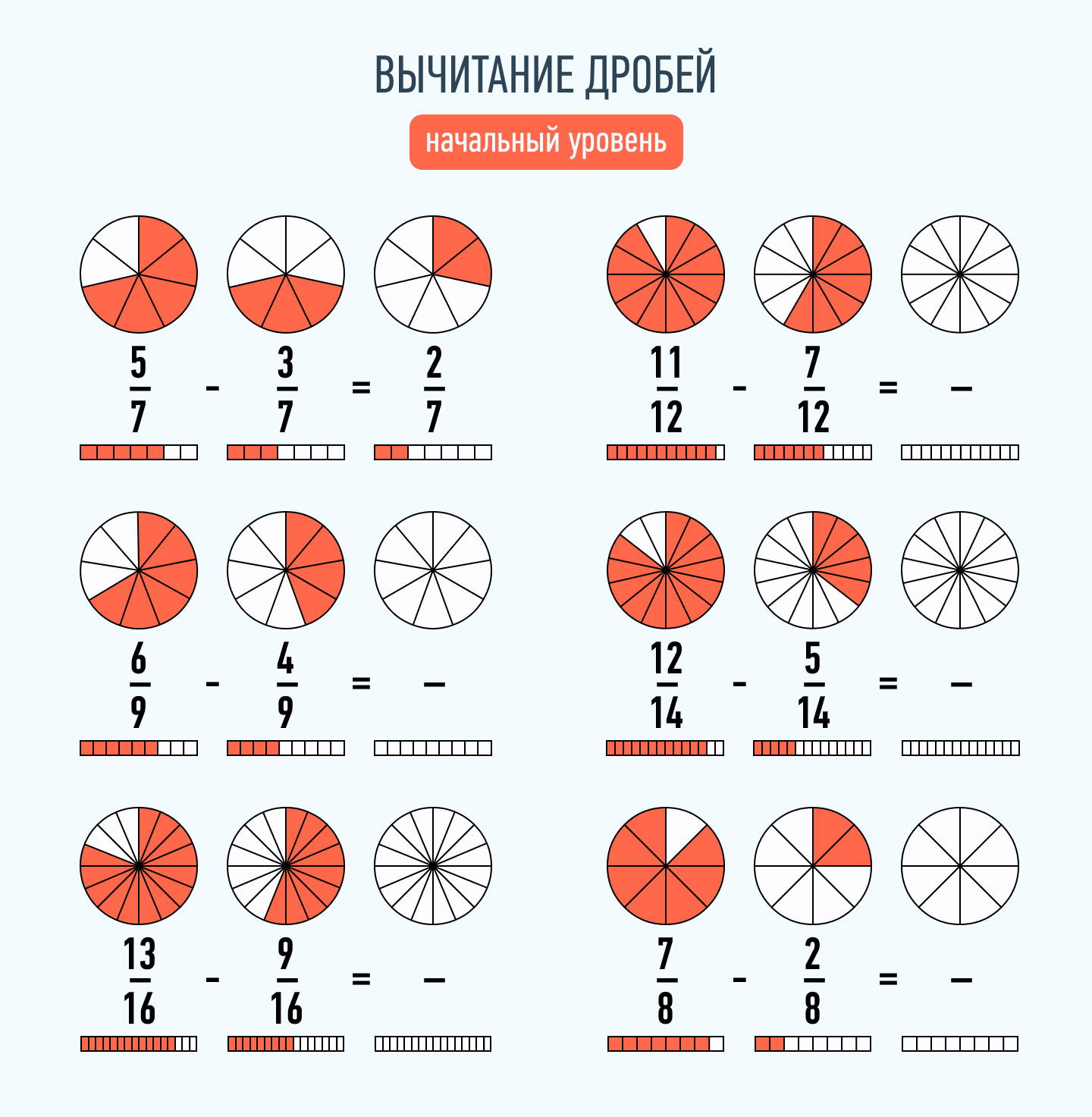
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
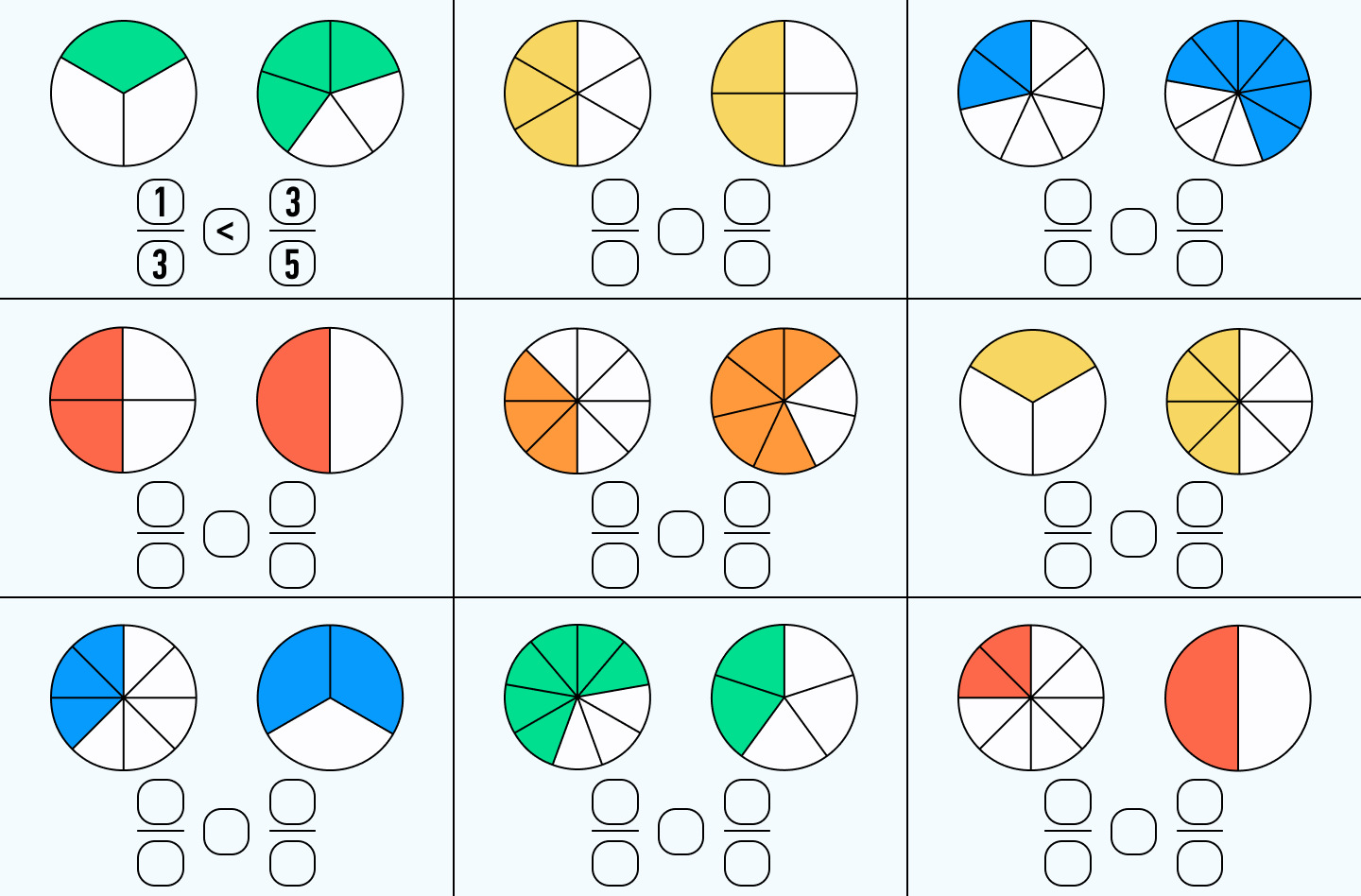
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Доли. Обыкновенные дроби
Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:
Допустим, нам надо разделить апельсин на 6 равных частей:
В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:
=
Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.
Например, рассмотрим брусок:
Разделим его на 5 частей:
То есть мы получим пятые доли бруска. Закрасим две части красным:
Мы закрасили две пятые доли. Для обозначения долей используют специальную двухэтажную запись, состоящую из двух натуральных чисел и черты дроби, которую называют обыкновенной дробью (дробным числом или просто дробью). Над чертой число называется числитель, под чертой знаменатель. Знаменатель дроби показывает, на сколько равных частей разделили нечто целое, а числитель — сколько таких частей взяли. То есть в рассматриваемом случае числитель равен 2, а знаменатель — 5, и дробь записывается так: 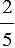
Теперь закрасим три части бруска:
Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: 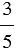
Теперь закрасим желтым цветом пять частей бруска:
Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: 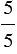
Рассмотрим рисунок ниже:
Нам даны два одинаковых бруска, которые разделены на 5 равных частей каждый. На первом закрашено 5 частей фиолетовым цветом, на втором — 2 части. То есть мы можем сказать, что мы закрасили семь пятых долей. Дробь, обозначающая эти доли, записывается так: 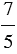
Определения
Правильная дробь – это дробь, числитель которой меньше знаменателя.
Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.
При чтении дробей надо помнить: числитель дроби — количественное числительное женского рода (одна, две, девять и т.д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т.д.)
Советуем посмотреть:
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 904,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1007,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1379,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1594,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1734,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1791,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1829,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 988,
Мерзляк, Полонский, Якир, Учебник
Номер 1018,
Мерзляк, Полонский, Якир, Учебник
Номер 1024,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 473,
Мерзляк, Полонский, Якир, Учебник
Номер 542,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Задание 698,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 839,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1070,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1164,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1192,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1198,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1256,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 5,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 537,
Мерзляк, Полонский, Якир, Учебник
Номер 574,
Мерзляк, Полонский, Якир, Учебник
Номер 640,
Мерзляк, Полонский, Якир, Учебник
Номер 845,
Мерзляк, Полонский, Якир, Учебник
Номер 1101,
Мерзляк, Полонский, Якир, Учебник
Номер 1127,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 50,
Мерзляк, Полонский, Якир, Учебник
Номер 52,
Мерзляк, Полонский, Якир, Учебник
Номер 140,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 226,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 251,
Мерзляк, Полонский, Якир, Учебник
Номер 253,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 280,
Мерзляк, Полонский, Якир, Учебник