Как найти длительность паузы импульса - Avtoru.top

Расчёт скважности и длительности импульсов

Одним из важных параметров периодического сигнала является скважность импульсов

Основы скважности и длительности импульсов

Частота повторения импульсов F — это количество импульсов, генерируемых в течении одной секунды.
Период импульсной последовательности Т – это время импульса t_H, сложенное со временем паузы t_L:
T = t_H + t_L = 1 / F

Скважность S импульсной последовательности — это отношение периода к длительности импульса:
S = T / t_H (S > 1)

Обратная величина скважности — это коэффициент заполнения D:
D = t_H / T
Коэффициент может быть выражен в процентах:
D = (t_H / T) × 100%

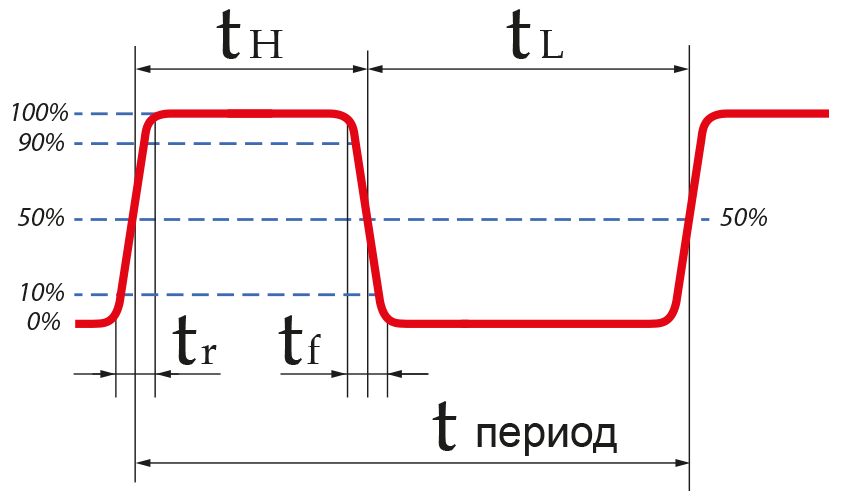
Длительность прямоугольного импульса определяется на уровне 50% его амплитуды.
Время нарастания импульса t_r — это интервал времени, измеренный между моментами, когда амплитуда изменяется от 0,1 до 0,9 установившегося значения. Между этими же уровнями измеряется и время спада импульса t_f.
Сигнал идеальной формы имеет значение равное нулю для t_r и t_f.

Расчет скважности и длительности импульса

Введите любые два значения

Длительность импульсов 1

Длительность импульсов 2

Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!

Источник

Рассмотрим
передачу информации импульсными
сигналами. Для импульсов
прямоугольной формы постоянная
составляющая X₀=X_mt_и/T₀
а
амплитуда n-й гармоники выражается
формулой

. (1.7)

Отдельные
составляющие спектра отстоят друг от
друга на частоту
импульсов, т. е. в спектре содержатся
только частоты f₀,
2f₀,
Зf₀
и т. д. Амплитуды гармоник пропорциональны
амплитуде импульсов,
но на частотах, где аргумент синуса
равен k(k
— целое
число). А на частотах nf₀
=
1/t_и,
2/t_и,
3/t_и,
…,
они обращаются в нуль.

При
уменьшении частоты импульсов интервалы
между отдельными гармониками
сокращаются. Положение же нулевых
амплитуд остается неизменным, поскольку
оно определяется только длительностью
импульсов. Следовательно, уменьшение
частоты f₀
ведет к обогащению спектра гармониками,
спектр становится гуще.
Амплитуда
каждой гармоники и постоянная составляющая
при этом уменьшаются.

При
увеличении периода импульсов до
бесконечности интервалы между гармониками
стремятся к нулю. Число гармоник
стремится к бесконечности, спектр
становится
сплошным, как это показано на
рис. 1.3,г.

При
увеличении частоты импульсов
f
интервалы
между гармониками возрастают,
спектр обедняется гармониками.
При
уменьшении длительности импульсов
нулевые амплитуды спектра отодвигаются
вправо, в сторону больших
частот. Положение гармоник на частотной
оси при этом не меняется.
Следовательно, число гармоник
с амплитудами, превышающими некоторый
определенный уровень, возрастает,
т. е. спектр колебаний расширяется. Чем
уже импульс, тем шире его спектр, и
наоборот.

Суммарная
энергия всех колебаний, составляющих
спектр импульса,
равна энергии, сосредоточенной в
импульсе. Зависимость относительной
энергии W
колебаний
ограниченной полосы частот для импульсов
разных типов приведена на рис. 1.7. Видно,
например,
что для прямоугольного импульса (кривая
1) в полосе частот 0
< f< 2/t_и
заключено примерно 95
%
всей энергии импульса, а
на остальную часть спектра приходится
только 5 % энергии. Большей
сосредоточенностью энергии в спектре
обладают импульсы треугольной
формы (кривая 2)
и
колокольной формы (кривая 3). Отсюда
следует, что электронное устройство,
предназначенное для воспроизведения
периодической последовательности
импульсов, должно
без искажений передавать частоты от f
до
(1-2)/t_и.
Например,
при f
=1 кГц и t_u=1
мкс полоса воспроизводимых частот
простирается от 1 кГц до 1-2 МГц. Для
одиночных импульсов нижняя
граница полосы пропускания доходит
вплоть до нуля.

При
постепенном уменьшении длительноcти
импульса, но сохранении
его площади (равной единице) спектр
импульса непрерывно расширяется
и в пределе, когда импульс описывается
δ-функцией,
t_и
стремится
к нулю, а амплитуда Х_т
—
к
бесконечности,
спектр становится
равномерным и простирается в бесконечность.

Когда,
например, требуется определить частотную
характеристику
электронной схемы, то удобно использовать
воздействие, описываемое
δ
— функцией. Благодаря равномерности
спектра δ
-функции
спектр выходного сигнала повторит
частотную характеристику
устройства. Возможен и другой подход к
оценке временных параметров сигналов
и воздействий, основанный на оценке их
формы кривой. Чаще
всего речь идет об импульсах, которые
по форме близки к простым геометрическим
фигурам (рис. 1.8).Различают
импульсы: прямоугольные
(а); трапецеидальные (б); треугольные
(в); пилообразные (г); экспоненциальные
(д); колоколообразные
(е).
У
реального
импульса переходы между
его отдельными участками плавные, что
не позволяет четко фиксировать
длительность
участков. Поэтому
прибегают к понятию активной
длительности, которым
пользуются в экспериментах и при учете
реальной формы импульсов
(рис. 1.9).

Активной
длительностью прямоугольного импульсаt_и
называют
промежуток времени между началом
нарастания и окончанием спада
импульса, отсчитанными по уровню 0,1Х_m,
где Х_т
—
амплитуда
импульса. Активная длительность
нарастания импульса t_фи
спада его t_c
определяется
интервалом времени между моментами, в
которые высота импульса принимает
значения 0,9Х_т
и
0,1Х_т.
Время
задержки импульса t_зд—
время от момента, когда
высота импульса равна нулю, до момента,
когда она станет равной
0,1Х_m
. Степень негоризонтальности вершины
(длительность
последней равна t_и—
t_ф—
t_c)
характеризуется сколом
(неравномерностью). Скол Х_m
определяется
как разность амплитуды
импульса и высоты его в начале спада.
После
спада импульса часто образуется обратный
выброс с полярностью,
противоположной полярности основного
импульса, амплитудой
Х_в
и
длительностью t_в.
Это
так называемый хвост импульса. Хвост
может быть как апериодического, так и
колебательного характера.
Время t_в
называют
временем восстановления. В
большом числе практических случаев
нарастание импульсов носит
экспоненциальный характер (рис. 1.9) и
описывается уравнением х
= Х_m
[1 —
ехр (-t/τ)].
Спад
импульса описывается уравнением
экспоненты х=
Х_т
ехр
(-t/τ),
где τ
— постоянная времени экспоненты.
Значения активной длительности импульса
находят после
решения этих уравнений относительно
t:

(1-8)

Подставляя
сюда значения х
=
0,1Х_т
и
0,9Х_m,
найдем время нарастания t_ф=t(0,9Х_m)
—
t(0,lX_m)
2,2τ
и
время спада
t_c

2,2τ.

Для
управления цифровыми устройствами
часто используются перепады напряжения,
которые представляют собой скачкообразные
изменения напряжения между двумя
уровнями. Перепад от низкого уровня к
высокому называют положительным и,
наоборот, если напряжение изменяется
от высокого уровня к низкому — отрицательным.

Вимпульсной технике часто приходится
иметь дело с последовательностями
импульсов, которые периодически
повторяются через промежуток времениТ,
который называют периодом следования
(рис. 1.10). Интервал времени между импульсами
называется длительностью паузы t_п.
Последовательность импульсов
характеризуется также частотой
повторения
f
= 1/T,
скважностью
Q
= T/t_и
и
коэффициентом
заполнения
k₃
=
t_и/T
=
1/Q.
Дополнительными параметрами для
последовательности импульсов являются
также среднее значение напряжения или
тока за период Т:

и
действующее значение

Для
последовательности прямоугольных
импульсов U_cp
= U_m/Q,
U_Д=U_m/Q,
т.е. —
действующее значение U_Д
напряжения последовательности
прямоугольных импульсов больше
среднего значения в

раз.
Кроме
последовательностей одиночных импульсов
в цифровой технике широко используются
также последовательности пачек импульсов
(рис. 1.11), каждая из которых состоит из
нескольких импульсов. Длительность
паузы между импульсами в одной пачке
иногда бывает переменной и является
важным параметром импульсного сигнала,
образуемого пачкой импульсов.

Ч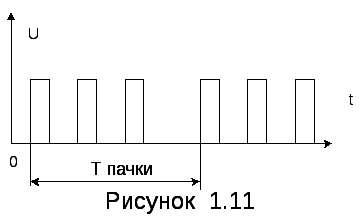тобы
судить о возможностяхформирования,
передачи и приема сигналов
и воздействий с помощью той
или иной аппаратуры, прибегают
к исследованию ее переходных характеристик.
Переходная
характеристика
представляет
собой зависимость выходного параметра
(тока, напряжения) от времени при
скачкообразном входном воздействии.
Такое воздействие дает возможность
выяснить реакцию устройства сразу в
двух режимах: при мгновенном изменении
входного
сигнала (переходный режим) и при постоянном
его значении (статический режим). Иначе
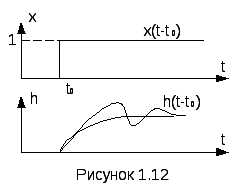
говоря, переходная функция h(t-t₀)
находится
как нормальная реакция системы (т. е.
реакция при
нулевых начальных условиях) на воздействие
в виде единичной ступенчатой функции
(рисунок 1.12)

или,
что тоже самое,
(1.9)

Напомним,
что -функция
или импульсная
функция может быть найдена из единичной
ступенчатой
путем дифференцирования: (t)
= d1(t)/dt.

Нормальную
реакцию (t)
на
импульсное воздействие называют
импульсной
переходной функцией. Нормальная
реакция устройства на произвольное
воздействие х(t)
выражается
через импульсную переходную функцию
с помощью интеграла.

(1.10)

где
(τ)
играет роль весовой функции.

Очевидно,
что реальные входные сигналы имеют
меньшую крутизну
нарастания и спада, чем переходная
характеристика, и ограниченную
длительность вершины.

Контрольные
вопросы

1. Какие
сигналы называются детерминированными
и случайными?

2.
Какими
параметрами характеризуются
электрические сигналы?

3. Что такое активная
длительность импульса?

4. Как определяются
длительность фронта и среза импульса?

5. Что такое спад
вершины импульса?

7. Что такое
коэффициент заполнения?

11.
Какими параметрами импульсов и
импульсных последовательностей
передаваться
информация?

12.
Какими параметрами гармонических
сигналов может передаваться реформация?

13. Для
чего применяют модуляцию?

14.
Какие физические носители информации
применяют в автоматике?

15 . Что
понимают под воздействием, и какие
воздействия применяют в электронных
элементах автоматике?

16. Выберете тип
модуляции для передачи информации от
датчиков по силовому кабелю электробура
глубинной скважины.

17. С какой частотой
необходимо производить дискретизацию?

18. Определите,
какая часть спектра сигнала связана с
искажениями фронта и плоской вершины
импульса.

19. Как будет
изменяться спектр сигнала, если
длительность прямоугольного импульса
будет приближаться к длительности
паузы?

20. Какой сигнал
обладает самым узким и самым широким
спектром?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Общая информация

К основным параметрам последовательности импульсов относятся:

амплитуда импульса – Um,
длительность импульса – tu,
длительность паузы – tn,
период следования T или частота f = 1/T следования.

Если длительность tu всех импульсов, входящих в состав последовательности, и всех пауз tn постоянна в течение времени, то она называется периодической.

Важным параметром периодического импульсного процесса является скважность импульсов S. Скважность импульсов – это отношение периода следования к длительности импульса, рассчитывается по формуле:

Эффективность S при управлении устройства достигается при стабильной частоте сигнала. Иногда используют обратную величину D – коэффициент заполнения, рассчитывается по формуле:

При равенстве tu и tn скважность равна 2, и сигнал называется меандром. S и D – безразмерные величины, так как время делится на время. В цифровых устройствах применяются импульсы различной формы. Формой импульса называется графическое изображение закона изменения импульсного напряжения во времени. На рис. ниже показаны формы сигналов:

а – прямоугольная,
б – трапецеидальная,
в – экспоненциальная,
г – колокольная,
д – ступенчатая,
е – пилообразная.

Виды импульсных сигналов

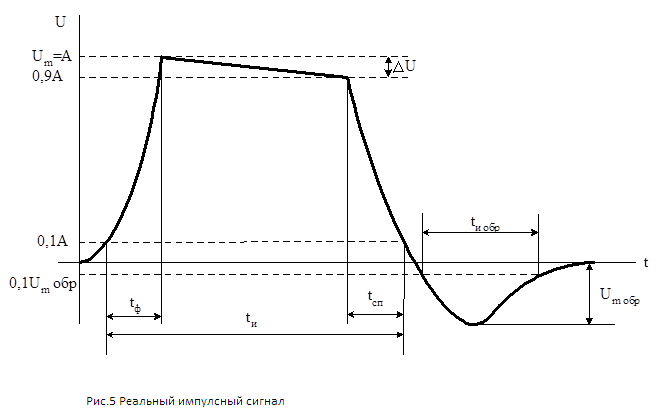
Техническая характеристика формы импульсов связана с количественной оценкой основных параметров импульса, свойств отдельных его участков, которые играют разную роль при воздействии импульса на устройство. На рис. выше изображены идеализированные формы импульса. Из-за переходных процессов в устройствах (формирования и усиления импульсов) существует реальная форма, например, прямоугольного импульса (рис. ниже).

Реальная форма импульса

Основные параметры импульса– это:

Размах импульса – Um,
Длительность импульса – tи,
Длительность переднего фронта – tф,
Длительность заднего фронта – tсп,
Спад вершины – ΔU,
Размах выброса заднего фронта – Um обр,
Длительность выброса заднего фронта – tи обр.

Указанные величины считываются между уровнями 0.1 и 0.9 от амплитуды в микросекундах, в зависимости от частоты сигнала. Амплитудные – в вольтах.

Определить параметры импульсного сигнала можно с помощью осциллографа, частотомера или мультиметра.

Характеристики скважности

Коэффициент заполнения и показатель скважности зависят от уровня получаемого колебания, при этом его частота определяется параметрами генератора. Для вычисления скважности имеют наибольшее значение два основных критерия:

Период Т.
Длительность импульса t1.

Принцип действия

Для формирования прямоугольного колебания в устройствах-модуляторах имеется специальная микросхема-контроллер либо аналоговая микросхема. Подключение происходит посредством цепи на полупроводнике. Полупроводник имеет только два состояния:

Закрытое
Открытое.

Важно! Работа всей цепи зависит от характера колебаний. Следовательно, если лампа подключена через полупроводниковый прибор, она начнёт мерцать с заданной частотой.

Однако, когда частота превышает 50 Гц, из-за особенностей глаз человека, мигание сливается в единое свечение. Но таким образом можно регулировать и яркость свечения. Снижение коэффициента повлечет за собой уменьшение яркости света, выдаваемой лампой.

Подобную схему можно использовать для постоянных двигателей. Уменьшение частоты провоцирует снижение скорости вращения двигателя, а высокие – к большей мощности агрегата.

В аналогичных устройствах применяется полупроводниковый переключатель, который имеет высокую скорость срабатывания и низкую проводимость, поскольку в противном случае устройство может запаздывать.

Как обозначается

Скважность обозначается английской буквой S, величина, обратная ей – коэффициент заполнения – буквой D. Данные обозначения используются и в русской, и в англоязычной литературе.

Формы сигналов

Сигналы различаются по форме и характеристикам:

Синусоида. Переменный ток на выходе из дома представляет собой синусоидальную волну, которая изменяется во времени с частотой 50 Гц. Для синусоидального колебания период можно выражать не в секундах, а в градусах или в радианах. При этом, необходимо учитывать, что полный период равен 360 ° (при использовании градусной меры) или 2п (если применяется радианная мера)

Вам это будет интересно Требуемая освещенность в помещении

Важно! Период и частота математически зависят друг от друга. По мере того, как период уменьшается, частота увеличивается, и наоборот.

Поскольку меандры имеют симметричные прямоугольные волны, периоды T и t1 которых равны, они широко используются в электронных цепях часов и сигналов синхронизации. На входе и выходе практически всех цифровых логических схем используются такие сигналы. Поскольку они симметричны, длительность положительной части равняется временному промежутку, когда импульс отрицательный (ноль). У сигналов, используемых в качестве тактовых сигналов в цифровой технике, длительность положительного импульса называется временем заполнения цикла.
Разница между прямоугольным сигналом и меандром заключается в том, что длительности положительной и отрицательной частей периода не равны друг другу. Поэтому прямоугольные сигналы классифицируются как несбалансированные.
Важно! Сигнал может принимать и положительные, и отрицательные значения, подвергаясь изменениям. В показанном потоке время положительного импульса больше, чем длительность отрицательного импульса, хотя бывает и наоборот.

Применение

Для формирования прямоугольных колебаний применяется микросхема аналогового типа или чип-контроллер. Сами колебания управляют только нагрузкой, идущей от источника тока. Подключение производится через ключевую схему на полупроводнике. Ключ имеет всего два состояния: либо он включён в сеть, либо размыкает её.

Грубо говоря, все зависит от характеристик колебаний. Так, если светильник подключен через подобную схему, то при низкой частоте работы устройства лампа будет мигать с определенной периодичностью, но при превышении её сверх 50Гц в человеческих глазах отдельные всплески света сольются в одно ровное свечение. Это особенность человеческого глаза, который не улавливает колебания свыше этого значения. Но и яркость свечения можно регулировать. Чем ниже коэффициент заполнения, а, следовательно, и значение, обратное ему, тем меньше яркость свечения источника.

Аналогичный пример можно использовать и с двигателем постоянного тока, под управлением широтно-импульсного регулятора. При этом низкая частота приведёт к снижению оборотов двигателя, в то время как высокая – к его эффективной работе. Для её достижения используются ключи-полупроводники, обладающие значительным быстродействием и низким коэффициентом проводимости, так как в противном случае возможно запаздывание сигнала.

При необходимости сигналы схемы импульсного регулятора можно усреднять, для этого используются фильтры низких частот, но при подключении двигателя с большой механической инерцией и хорошим значением индуктивности. В этом случае снижение амплитуды и частоты происходит самопроизвольно.

Скважность, а также её обратное значение зависят от уровня моделирующего сигнала, частота таких устройств определяется частотой дублирующего генератора, подающего дополнительный сигнал.

Чем отличается скважность и коэффициент заполнения импульсов

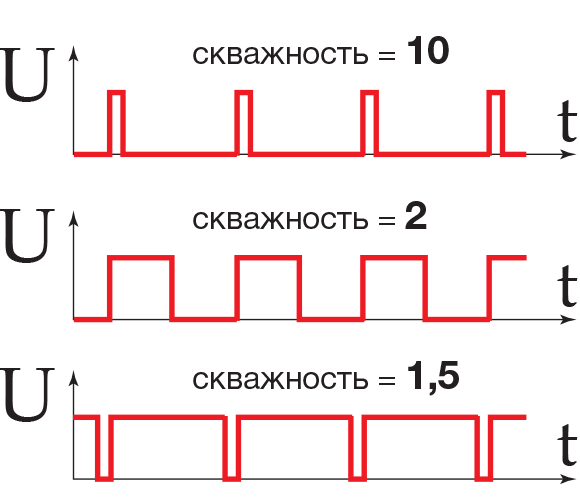
Одной из наиболее важных величин в импульсной электронике – это скважность, обозначаемая латинской буквой S. Она дает характеристику импульсам прямоугольной формы и показывает, как относится их период T ко времени t1. К примеру, коэффициент меандра равен 2, поскольку время t1 в этой последовательности составляет половину периода: S = T / t1 = 2. И в числителе, и в знаменателе находится время, выраженное в секундах. При вычислениях они сокращаются, поэтому коэффициент является величиной, не имеющей единиц измерения.

Генератор скважности

Меандр представляет собой поток импульсов, в котором отрицательные и положительные части имеют одинаковую продолжительность. Инверсия скважности имеет название коэффициент заполнения. Следовательно, скважность способна принимать множество значений от бесконечности до единицы, а рабочий цикл этого же потока импульсов, как еще могут называть коэффициент заполнения, способен принимать значения от 0 до 1. Часто удобней записывать не данный коэффициент, измерение которого производится десятичными дробями, а скважность, которая равна, чаще всего, целому числу. Например: D = 0,5 или S = 2 – эти две записи означают одно и то же, но вторую читать легче. Рабочий цикл S = 10 соответствует показателю D = 0,1 – это означает, что длительность импульса в 10 раз меньше его периода. В широтно-импульсной модуляции (сокращенно, ШИМ) прибор изменяет ширину или продолжительность импульса, при этом будет соответственно изменяться и коэффициент. Частота при этом будет постоянной. В таком случае, чем больше величина, показывающая скважность, тем более узким будет импульс, и, наоборот – при минимальной скважности будет достигаться максимальная ширина. При изучении данного явления просматривается этимологическая связь с словом «скважина» из русского языка: широкая скважина (на самом деле, это промежуток между импульсами в потоке) – положительные части узкие, узкая скважина – положительные части широкие (но свободное пространство между ними мало).

Важно: У англоязычных авторов термин «скважность» не встречается вовсе, а для его замены применяют понятие «рабочий цикл» – аналогичный российскому коэффициенту заполнения (D). Однако в английской литературе он выражается не дробным числом, а процентом. Например, если D = 0,5 в западных пособиях будет указано: D = 50%.

Как измерить скважность с помощью формулы

Скважность прямоугольных импульсов S – это отношение периода T ко времени импульса, обозначаемого буквой t1. Также, стоит отметить, что рабочий цикл D – это значение обратное скважности:

Скважность формула

Скважность сигнала – одна из самых важных характеристик в импульсной технике. Ее основные характеристики – это период и время численного значения импульса. Изменяя эти характеристики, можно повлиять на всю цепь.

Как рассчитать коэффициент заполнения?

Коэффициент заполнения — прямоугольный импульс

Она получается делением секунд на секунды. Иногда удобно измерять коэффициент заполнения в процентах. Тогда нужно приведенное в определении отношение умножить на 100%. Как мы видим, чем короче импульс, тем меньше коэффициент заполнения.

Расчет коэффициента заполнения печатной платы

Расчет коэффициента заполнения печатной платы можно сделать по сборочному чертежу платы. Для этого надо измерить площадь, занимаемую элементом вместе с выступающими за корпус выводами.(Посадочное место). В плане (плоскости) все посадочные места можно рассматривать как прямоугольники и окружности. Как известно, площадь прямоугольника равна произведению длины на ширину прямоугольника, а площадь круга

S = πD²/4 , где

D – диаметр круга, а π – физическая константа, равная 3,14

Расчет следует вести с использованием таблицы 3.4.1

Наименование элемента	Площадь занимаемая элементом	Количество однотипных элементов	Площадь занимаемая всеми элементами
Резистор МЛТ 0,125	13,2 мм²	37	488,4 мм²
Резистор СП3-4аМ	78,5 мм²	6	471 мм²
Резистор СП3-38б	50,24 мм²	1	50,24 мм²
Транзистор КТ3102А	21,23 мм²	3	63,68 мм²
Транзистор КТ837Ф	43,77 мм²	3	131,31 мм²
Конденсатор К50-35	15,9 мм²	5	79,5 мм²
Конденсатор К53-14	40 мм²	2	80 мм²
Микросхема К561ЛН2	144,3 мм²	1	144,3 мм²
Микросхема К561ИЕ10	162,8 мм²	2	325,6 мм²
Диод КД521В	7,22 мм²	17	122,74 мм²
Оптрон АОД109	144,3 мм²	1	144,3 мм²

Таблица заполняется, после чего надо сложить все цифры последнего столбца. Таким образом будет найдена площадь, занимаемая всеми элементами схемы S элемент.

Площадь печатной платы — S платы равна произведению ее длины на ширину. Коэффициент заполнения печатной платы

S элемент = 2101,1 мм²

К зап = S элемент / S платы х 100%

К зап = 2101,1 / 4516,2 х 100% = 214,94

Управление скважностью

С помощью цифровых сигналов происходит управление разнообразными устройствами. Первое применение такого управления использовалось при передаче информации кодом Морзе. Сигнал передаётся короткими и длинными импульсами. Каждой букве соответствует определённый набор точек и тире. Сегодня этот метод управления используется для ШИМ-управления.

При изменении D (коэффициент заполнения) от 0 до 1 добиваются нужного напряжения на выходе электронного устройства. Таким образом, можно управлять оборотами двигателя, освещением, яркостью дисплея и т.д. При формировании прямоугольных импульсов используются специально разработанные микросхемы, например, NE555, NL494, КР1006ВИ1, IR2153, и микроконтроллеры: Arduino, AVR, SG2525A.

Для обеспечения надёжной работы управляемых устройств к параметрам импульсного сигнала предъявляются жестокие требования по их стабильности. Это достигается применением кварцевого генератора и хорошей переходной характеристикой схемы формирования управляющих импульсов.

Источники

https://rentps3.ru/sovety/skvazhnost-impulsov-eto.html
https://ElectroInfo.net/raznoe/chto-takoe-skvazhnost-skvazhnost-impulsov.html
https://RadioLisky.ru/pribory-i-ustrojstva/skvazhnost-formula.html
https://elquanta.ru/teoriya/skvazhnost-impulsov.html
https://kmd-mk.ru/chto-takoe-skvazhnost-signala/

[свернуть]

Источник

радиоликбез

Для периодической последовательности импульсов (рис, 151, а) свойственно следование импульсов через равные промежутки времени. Ее характеризуют следующие параметры.

Период следованияТ_и — интервал времени от момента появления одного импульса до момента появления следующего импульса той же полярности.

Частота следования F_и, являющаяся величиной, обратной периоду следования, т. е.

Длительность паузы Т_и — время между моментом окончания одного импульса и началом другого:

Скважность импульсов Q, определяемая как отношение периода следования Т_и к длительности t_и

Среднее значение импульсного тока (напряжения) получается, если ток (напряжение) импульса равномерно распределить на весь период так, чтобы площадь прямоугольника I_срT_и (рис. 151,б) была равновелика площади импульса S_и

Коэффициент заполнения — величина, обратная скважности, показывающая, какую часть периода занимает импульс:

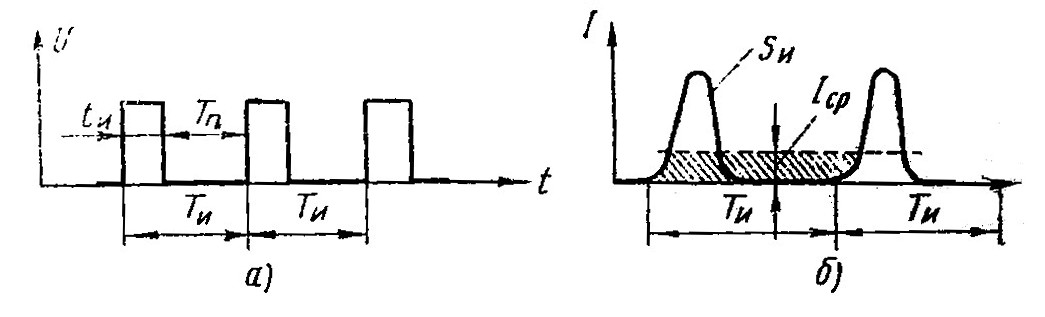Параметры периодической последовательности импульсного сигнала

Рис. 151. Периодическая последовательность импульсов:

а — прямоугольных, б — колоколообразных

Средняя мощность P_Ср определяется отношением энергии W, выделенной в цепи за период следования импульса T_и, к длительности этого периода:

Очевидно, Р_срТ_и=P_иt_и, откуда

Электронные приборы для импульсных схем очень часто выбирают по средней мощности.

Читайте также: Общая характеристика импульсного сигнала
Прохождение импульсов через линейные цепи

Источник

Общая информация

К основным параметрам последовательности импульсов относятся:

l амплитуда импульса – Um,
l длительность импульса – tu,
l длительность паузы – tn,
l период следования T или частота f = 1/T следования.

Важным параметром периодического импульсного процесса является скважность импульсов S. Скважность импульсов – это отношение периода следования к длительности импульса, рассчитывается по формуле:

Эффективность S при управлении устройства достигается при стабильной частоте сигнала. Иногда используют обратную величину D – коэффициент заполнения, рассчитывается по формуле:

При равенстве tu и tn скважность равна 2, и сигнал называется меандром. S и D – безразмерные величины, так как время делится на время. В цифровых устройствах применяются импульсы различной формы. Формой импульса называется графическое изображение закона изменения импульсного напряжения во времени. На рис. ниже показаны формы сигналов:

а – прямоугольная,
б – трапецеидальная,
в – экспоненциальная,
г – колокольная,
д – ступенчатая,
е – пилообразная.

Основные параметры импульса – это:

l Размах импульса – Um,
l Длительность импульса – tи,
l Длительность переднего фронта – tф,
l Длительность заднего фронта – tсп,
l Спад вершины – ΔU,
l Размах выброса заднего фронта – Um обр,
l Длительность выброса заднего фронта – tи обр.

Определить параметры импульсного сигнала можно с помощью осциллографа, частотомера или мультиметра.

Виды импульсов и их параметры.

Под импульсом понимают кратковременное отклонение напряжения или тока от некоторого постоянного уровня, в частности, от нулевого.

Существует два вида импульсов: видеоимпульсы и радиоимпульсы.

Видеоимпульсы представляют собой кратковременное изменение напряжения или тока в цепи постоянного тока. Видеоимпульсы имеют прямоугольную, трапецеидальную, треугольную, экспоненциальную и колоколообразную формы (рис.15.1).

Рис. 15.1. Идеализированная форма импульсов прямоугольной (а), трапецеидальной (б), треугольной (в), экспоненциальной (г) и колоколо-образной (д) форм.

Следует иметь в виду, что реальные импульсы не имеют формы, строго соответствующей названию. Так, например, прямоугольные импульсы имеют форму, близкую к трапецеидальной, а треугольные – к экспоненциальной.

Различают импульсы положительной и отрицательной полярности, а также двухсторонние (разнополярные) импульсы («меандр»).

Рис. 15.2. Двухсторонние (разнополярные) импульсы.

Наиболее часто применяются прямоугольные импульсы.

Радиоимпульсы представляют собой кратковременные посылки синусоидального напряжения или тока. Они снимаются с выхода высокочастотного генератора, который управляется (модулируется) видеоимпульсами. Поэтому форма огибающей радиоимпульсов соответ-ствует форме модулирующих видеоимпульсов (рис. 15.3).

Введём понятие об основных параметрах импульса на примере реального прямоугольного импульса. Как показано на рис. 15.4 такие импульсы имеют передний фронт, срез (задний фронт) и плоскую вершину (участок импульса между фронтами). На рисунке показан также спад плоской вершины (∆U) и как следствие небольшой выброс напряжения. Параметрами реального импульса являются: амплитуда импульса, его длительность и крутизна фронтов, а также мощность в импульсе.

Рис. 15.4. Импульс напряжения прямоугольной формы.

Амплитуда импульса

– это наибольшее значение напряжения или тока. Амплитуда напряжения или тока выражается в вольтах, киловольтах, милливольтах, микровольтах или амперах, миллиамперах, микроамперах.

Длительность импульса

. За активную длительность импульса принимают промежуток времени, измеренный на уровне, соответствую-щем половине амплитуды. Иногда длительность импульса определяют на уровне 0,1 (0,1 или по основанию импульса. В дальнейшем, если это не оговорено, длительность импульса будет определяться по основанию и обозначаться . Длительность импульса выражается в единицах времени: секундах, миллисекундах, микросекундах и нано-секундах.

Длительность и крутизна фронта (спада) импульса

. Длительность переднего фронта импульса определяется временем нарастания импульса, а длительность среза – временем спада импульса. Наиболее часто пользуются понятием активной длительности фронта , за которую принимают время нарастания импульса от 0,1 до 0,9 . Аналогично, длительность среза – время спада импульса от 0,9 до 0,1 .

Обычно длительность и составляет единицы процента от . Чем меньше и по сравнению с длительностью импульса, тем больше форма импульса приближается к прямоугольной. Иногда, вместо и фронты импульса характеризуют скоростью нарастания (спада). Эту величину называют крутизной фронта (спада) S

и выражают в вольтах в секунду. Для прямоугольного импульса приближённо:

S = (15.1)

Мощность в импульсе

. Энергия W импульса отнесённая к его длительности определяет мощность в импульсе:

= (15.2)

Эта мощность выражается в ваттах, киловаттах, мегаваттах.

2. Параметры импульсных последовательностей.

Импульсы, повторяющиеся через равные промежутки времени, образуют периодическую последовательность. Такая последовательность, параметры которой изменяются в соответствии с передаваемой инфор-мацией, является сигналом.

Кроме параметров, присущих одиночному импульсу, импульсная последовательность характеризуется дополнительными параметрами: периодом повторения импульсов, частотой повторения импульсов, коэффициентом заполнения, скважностью импульсов, а также средним значением мощности импульсного колебания .

Период и частота повторения импульсов

. Промежуток времени между началом двух соседних однополярных импульсов называют периодом повторения (следования) импульсов. Он выражается в единицах времени: секундах, миллисекундах, микросекундах. Величину, обратную периоду повторения, называют частотой повторения (следо-вания) импульсов. Частота повторения импульсов определяет количество периодов в течение одной секунды и выражается в герцах, килогерцах, мегагерцах (рис. 15.5).

Рис. 15.5. Последовательность треугольных импульсов.

Коэффициент заполнения и скважность импульсов

. Часть периода Т занимает пауза – это отрезок времени между окончанием и началом двух соседних импульсов, т.е.:

= — (15.3)

Отношение длительности импульса к периоду повторения называют коэффициентом заполнения:

γ = (15.4)

Коэффициент заполнения – величина безразмерная меньше единицы.

Величину обратную коэффициенту заполнения называют скважностью импульсов:

q = = (15.5)

Скважность величина безразмерная больше единицы.

Среднее значение напряжения (тока) импульсного колебания

. При определении среднего за период значения напряжения (тока) импульсного колебания ( ), напряжение или ток распределяют рав-номерно на весь период так, чтобы площадь прямоугольника была равна площади импульса .

Так как для прямоугольного импульса:

= (15.6)

и = = γ = (15.7)

т.е. среднее значение напряжения (тока) прямоугольного импульсного колебания в q раз меньше амплитудного.

Средняя мощность

. Энергия W импульса, отнесённая к периоду импульсов определяет среднюю мощность импульса:

= (15.8)

Сравнивая выражения и , получим:

= (15.9)

= = q (15.10)

= = (15.11)

Т.е. средняя мощность и мощность в импульсе отличаются в q раз. Отсюда следует, что мощность в импульсе, которую обеспечивает генератор, может в q раз превосходить среднюю мощность генератора.

Управление скважностью

Блокинг генератор: принцип работы

Как_определить_длительность_импульса

Импульсные процессы

Источниками колебаний в форме импульсов чаще всего являются импульсные генераторы — автономные преобразователи энергии источника питания, в энергию разрывных колебаний требуемой формы. Другим способом получения импульсов является их формирование путем изменения параметров колебаний иной формы, например синусоидальной.

Для этого используют формирующие устройства — ограничители амплитуды, схемы дифференцирования и другие устройства, которые изменяют параметры колебания — амплитуду, период следования, форму и т.п.

Электрическим импульсом называют напряжение или ток, отличающиеся от нуля или постоянного значения только в течение короткого промежутка времени, который меньше или сравним с длительностью установления процессов в электрической системе, в которой они действуют. Импульсы могут быть как периодическими, так и одиночными (рис. 1)

Рис. 1. Импульсы различной формы

В случае следующих друг за другом импульсов (т.е. периодических) обычно предполагается, что интервал между ними существенно превышает длительность процессов установления. В противном случае этот сигнал называют несинусоидальным напряжением или током. Такое определение не отличается строгостью, ибо переходные процессы протекают, как известно, бесконечно долго. Однако оно позволяет отличать импульсы в общепринятом смысле от напряжения сложной формы.

Параметры электрического импульса

Импульсы и импульсные последовательности характеризуются рядом параметров (длительность импульса, длительность паузы, время фронта, период следования и др). Методика измерения этих параметров представлена на рис 2.

Рис. 2. Основные параметры импульсов

Um – амплитуда импульса. Это наибольшее отклонение напряжения от исходного, установившегося значения Uo;

tфр – длительность фронта импульса (или время фронта). Это временной интервал, в течение которого напряжение возрастает от 0,1Um до 0,9Um. Иными словами, время фронта измеряется не по максимальному и минимальному значению напряжений, а по уровням 0.1-0.9 от максимального значения.

tcп – длительность спада импульса (или время спада). Это временной интервал, в течение которого напряжение спадает от 0,9Um до 0,1Um. Его иногда еще называют временем среза импульса.

tи – длительность импульса. Это временной интервал между моментами на соседних интервалах tфр и tcп, для которых u = 0,5Um. Иными словами, длительность импульса измеряется на уровне половины амплитуды.

Видео

RS триггер

1305 ₽ Подробнее

435 ₽ Подробнее

Hi-Res плееры

novice_chips #9. Введение в теорию импульсов. Часть I. Одиночные импульсы.

Я продолжаю рубрику фин_чипсы для новичков (novice_chips), в которой размещаю свои размышления о рыночном мироздании (улыбаюсь) с расчетом, что она будет полезной именно новичкам, а также тем, кто хотел бы погрузиться в биржевую торговлю системно и последовательно.

novice_chips — те важные выводы, к которым придут многие в течение первых 3-5 лет торговли. Но можно получить эти знания быстрее.

Предыдущий novice_chips здесь

В прошлых чипсах мы рассмотрели общий подход к анализу рыночной ситуации в целом. Переходим к более подробной оценке спекулятивных рыночных предпосылок.

Инвестиции и спекуляции означают принципиально разные подходы к извлечению денег, и являются противоположными по своей сути. Поэтому следует отличать:

Ø рынок в широком смысле – рынок инвесторов, функционирующий как открытая система;
Ø рынок в узком смысле как замкнутое сообщество, рынок профессионалов-спекулянтов.

Суть рынка профессионалов заключается в смене (манипуляции) и повторяемости ценовых уровней, в отличие от рынка инвесторов, на котором желательны большие поступательные восходящие движения.

Вследствие появления персональных компьютеров, интернета, развития средств передачи и обработки информации стало возможным играть более короткие торговые периоды (таймфреймы), отыгрывая уже не ежегодные, а эпизодически появляющиеся новости. Таким образом, биржевая торговля стала развиваться преимущественно в одном направлении – повышение доходности на единицу времени.

И теперь большую силу представляют собой крупные спекулянты — банки, управляющие компании, которые оперирует горизонтом в полгода-год, и стремятся создать дополнительные колебания цены в течение этого периода, на которых они зарабатывают вне зависимости от общего тренда в мировой экономике.

У спекулянта другая реальность, которая выпала из поля зрения нобелевских лауреатов.

Во-первых, спекулянту важен торговый период (таймфрейм), с которым он работает.

В широком смысле таймфрейм (ТФ) – это масштаб ожидаемого движения цены, а в узком — масштаб вашей доходности, так как вы (в идеале, конечно) получаете запланированную прибыль в определенные вами сроки.

Во-вторых, спекулянту важны новости. Рынок профессионалов (фондовый рынок в узком смысле) использует предполагаемую (будущую) информацию для того, чтобы играть ее на опережение, и этого не учитывает традиционная информационная матрица. Также для игры используются и сложившиеся информационные тренды, которые чаще всего играют в противоположном направлении.

В-третьих, спекулянтам важно опередить инвесторов. Крупные спекулянты консультируют и эмитентов, и инвесторов, лучше других информированы, имеют значительные средства, чтобы начинать рыночные движения. Поэтому для ликвидных бумаг первые плюс-минус 20-30% к цене правильно считать «спекулянтской пенкой».

Задача спекулянта — иметь деньги практически в любой момент, готовые к выводу с прибылью. Ему не нужно 10 000% годовых за 10-20 лет, ему нужно +40+80% годовых, и каждый год чтобы можно было их вывести и потратить.

Именно этими соображениями и обусловлена теория импульсов, к изучению которой мы приступаем.

ВВЕДЕНИЕ В ТЕОРИЮ ИМПУЛЬСОВ

Характеристика базовых рыночных движений (импульс и коррекция)

Разберем базовые рыночные движения – импульс и коррекцию к импульсу. Понимание сути этих движений особенно полезно и в боковике, когда рынок движется внутри определенного диапазона, от его верхней границы к нижней и наоборот, так и при движении через границы диапазонов.

(Примечание: мы рассмотрим идеальные, академические модели, иллюстрирующие суть обсуждаемых движений, в реальной жизни может быть множество нюансов на графиках, которые, тем не менее, не означают другую рыночную логику).

Мы уже говорили, что рынок профессионалов обеспечивает смену и повторяемость ценовых уровней. Инициируя рыночные движения, отдельные крупные игроки получают торговое преимущество перед остальными, совершая сделки по более выгодным уровням раньше других и в большем объеме.

Смена уровней происходит манипулятивно, а именно посредством импульсного движения, у которого есть инициатор. Возврат и повторяемость уровней происходит как правило в рамках коррекций к явленным импульсам. Очевидно, что коррекция по величине меньше импульса.

Описывая импульс как феномен, мы фиксируем нарушение обычного рыночного оборота: в какой-то отрезок времени вдруг кем-то акций покупается/продается больше, чем обычно по статистике за это время, за счет чего происходит значительный сдвиг цены.

То есть кто-то решает купить нужный ему объем не медленно, а быстро, на опережение удовлетворения спроса, атакуя при этом выставленные заявки на продажу, и не дожидаясь, пока ему «нальют» в биды. Тем более что продавцы обычно не спешат продать весь свой объем по одной цене, и выставляют заявки «лесенкой». Поэтому инициатору импульса, чтобы купить большой объем, приходится незамедлительно переходить на более высокие уровни покупки, где еще есть предложение.

Например, на текущем рынке (2017 год) в акциях Лукойла за час покупается и продается примерно 50 000 акций. При этом цена колеблется в пределах полпроцента. Если кто-то захочет купить эти 50 000 акций агрессивно, не за час, а за 15 минут, то цена вырастет больше чем на процент. Если при этом через процент покупатель продолжит скупку, то к концу часа пройдет объем 100 или 150 тысяч акций, а цена изменится на +1.5+2%. Так на графиках белой свечой будет оформлен импульс на «часовике», равный по величине и объему обычному движению «4-часовика» (более старшего таймфрейма).

Импульс служит трём целям (на примере импульса вверх):

1.Привлекается внимание к бумаге. Игроки начинают анализировать причину агрессивной скупки, если находят ее, пытаются купить на откате, если нет, увеличивают продажи. В любом случае оборот в акции резко возрастает, что играет на руку инициатору импульса.

2.Быстро покупается повышенный объем акций.

3.Происходит положительный сдвиг цены в сторону покупателя, выводя все его покупки в плюс. В этом и суть манипуляции – если вы купили в основном внизу и в середине движения, и вам удалось протолкнуть цену еще выше, то все ваши покупки окажутся в плюсе.

На часовых графиках цен для российских голубых фишек величина импульса из ТФ+1 составит +1+1.5% (размах 4-часовика), на дневных графиках +3+6% (недельный размах), на недельных +7+12% (месячный размах). Для месячных графиков понятие импульс теряет свое значение, так как движения в одном направлении размером больше +12% и более, как правило, являются сложносоставными, включают в себя совокупность импульсов, и их стоит рассматривать как трендовые.

Первое отступление: необходимо смотреть все основные таймфреймы, оценивая движение бумаги.

Второе отступление: силу импульса мы оцениваем по степени возмущения рыночной среды в наблюдаемом таймфрейме. Для этого нам необходимо сравнить явленный импульс с обычными движениями на соседних и более старших таймфреймах. Мы оцениваем амплитуду импульса, его денежный объем, и уровни закрытия.И в этом нам поможет понятие среднего диапазона или, говоря очень упрощенно, амплитуда или «размах» цены.

Таким образом, под импульсом мы понимаем возмущение рыночной среды в виде безоткатного движения в одну сторону, величина которого соизмерима со среднестатистической амплитудой движений в более старшем таймфрейме (ТФ+1).

Импульс обладает тремя важными признаками в совокупности.

Если какого-то признака нет, то это движение не импульс, и может не породить последствия, вызываемые импульсом.

Вот эти признаки:

1.Цена проходит увеличенное расстояние (ТФ+1 или как минимум удвоенный размах играемого ТФ)

2.Повышенный объем (как минимум удвоенный объем играемого ТФ)

3.Закрытие происходит недалеко от вершины, т.к. откат в импульсе (хвост свечи) означает начало коррекции внутри импульса, что говорит о большом противодействии, которое может закончить игру раньше времени.

Импульсы бывают одиночными, двойными и сложносоставными.

Импульсы, имеющие кратковременную манипуляцию, как правило, одиночные, с длительной манипуляцией – чаще всего двойные, с небольшой внутренней коррекцией.

Одиночный импульс (на примере вздерга)

Это импульс, имеющий для его инициатора (ИИ) целью кратковременное и значительное повышение (перестановку) цены без дальнейших попыток продолжения роста. Как правило, одиночный импульс подгадывается под определенное время – закрытие сессии, квартала, года или торгового периода (часа, дня, недели, месяца), под выход важных статданных.

Это может быть:

Ø Утренний гэп
Ø Корректирующий импульс
Ø Импульс открытия или закрытия
Ø Новостной импульс
Ø Импульс следования
Ø Обманный импульс

Общее правило – одиночные импульсы закрываются (аннулируются) в ближайшем времени.

Исключения есть: после утреннего гэпа цены в среднем продолжают двигаться в его направлении. Играть на закрытие гэпов – уязвимая идея.

Очень часто возвратное движение уже не уходит ниже высокой цены открытия. И чем сильнее гэп, тем сильнее последующее движение.

Статистически целесообразнее играть не против гэпа, а использовать движение на закрытие гэпа (откат к цене открытия) для открытия позиции в направлении гэпа.

Дальше мы поговорим про двойные импульсы.

СЛЕДУЮЩИЙ ЧИПС УЖЕ НАПИСАН И РАЗМЕЩЕН ЗДЕСЬ

Если мои novice_chips (финансовые чипсы для новичков) вызвали ваш интерес, пожалуйста, напишите об этом в комментариях или поставьте лайк.

Источник

Расчёт скважности и длительности импульсов

Одним из важных параметров периодического сигнала является скважность импульсов

Основы скважности и длительности импульсов

Расчет скважности и длительности импульса

Общая информация

Характеристики скважности

Принцип действия

Как обозначается

Формы сигналов

Применение

Чем отличается скважность и коэффициент заполнения импульсов

Как измерить скважность с помощью формулы

Как рассчитать коэффициент заполнения?

Расчет коэффициента заполнения печатной платы

Управление скважностью

Общая информация

Виды импульсов и их параметры.

Управление скважностью

Как_определить_длительность_импульса

Видео

novice_chips #9. Введение в теорию импульсов. Часть I. Одиночные импульсы.

Не пропустите также: