Enter the total energy of a photon into the calculator to determine the wavelength.
- De Broglie Wavelength Equation Calculator
- Wavelength Calculator
- Photon Energy Calculator
- Peak Wavelength (Wien’s Law) Calculator
- Wavelength to Energy Calculator
- Wave Energy Calculator
Energy to Wavelength Formula
The following equation can be used to convert energy into a wavelength for photons.
- Where w is the wavelength
- h is the Planck constant (6.6261*10^-34)
- c is the speed of light (299,792,458 m/s)
- E is the energy
To calculate wavelength from energy, divide the product of the Planck constant and speed of light by the energy.
Energy To Wavelength Definition
Energy to wavelength is defined as the conversion of the total energy contained within a photon into the wavelength.
Energy to Wavelength Example
How to calculate energy to wavelength?
- First, determine the speed of light.
This will be constant at the value of (299,792,458 m/s)
- Next, determine the plank constant.
This will be constant at (6.6261*10^-34)
- Next, determine the total energy.
Calculate the total energy of the photon.
- Finally, calculate the wavelength.
Convert the energy to wavelength using the equation above.
FAQ
What is a wavelength?
A wavelength is a distance a photon travels as it completes one full-wave or frequency.
What is the planck constant?
The Planck constant is a universal constant of energy*time that describes energy waves.

В этой статье мы собираемся обдумать взаимосвязь энергии и длины волны вместе с примерами и решить некоторые задачи, чтобы проиллюстрировать то же самое.
Энергия находится в прямой зависимости от частоты электромагнитных излучений. Если длина волны увеличивается, это означает, что повторяемость волны будет уменьшаться, что непосредственно влияет на энергию частицы в волне.
Формула соотношения энергии и длины волны
Энергия частицы может быть связана с ее скоростью во время распространения. Скорость частицы дает представление о частоте и длине волны. Если длина волны мала, то частота и, следовательно, энергия частицы будут увеличиваться.
Если колебания частицы больше в траектории пути, то возвратность частицы в волну больше и длина волны мала, это означает, что энергия, которой обладает частица, больше.
Энергия любого тела связана с его длиной волны уравнением
E=hc/λ
Где «h» — постоянная Планка h = 6.626 * 10-34Js
C — скорость света c=3 *108 м/с и
λ — длина волны света
Энергия обратно пропорциональна длине волны света. Чем меньше длина волны, тем больше энергия частицы в волне.
Задача 1: Рассчитать энергию фотонов, испускающих красный свет. Считайте длину волны луча красного света равной 698 нм. Какова будет энергия, если длина волны уменьшится до 500 нм, то есть если источник излучает зеленый свет?
Данный:λ1=698нм
λ2=500 нм
ч = 6.626 * 10-34 Js
с=3 * 108 м/с
У нас есть,
E=hc/λ1
E = 6.626 * 10-34 Дж* 3 * 108 м/с/698* 10-9m
=0.028* 10-17=28* 10-20Дж
Энергия красной длины волны 28* 10-20Джоули.
Если длина волны λ2=500 нм
Тогда энергия, связанная с зеленым светом, равна
E=hc/λ2
E = 6.626 * 10-34 Дж* 3 * 108 м/с / 500* 10-9m
= 0.03910-17=39* 10-20Дж
Мы видим, что энергия увеличилась до 39*10-20 Джоулей при уменьшении длины волны.
Подробнее о Влияние преломления на длину волны: как, почему, подробные факты.
График взаимосвязи энергии и длины волны
По мере увеличения длины волны частота волны падает, тем самым уменьшая энергию, которой обладает волна. Если мы построим график зависимости энергии от длины волны появляющейся частицы, то график будет выглядеть так, как показано ниже.
Приведенный выше график ясно показывает, что по мере увеличения длины волны энергия, связанная с частицей, уменьшается экспоненциально.
Связь кинетической энергии и длины волны
Если скорость частицы больше, то очевидно, что кинетическая энергия частицы велика. Кинетическая энергия определяется уравнением
КЭ=1/2мВ2
Где m — масса объекта или частицы
V — скорость массы
Мы можем записать приведенное выше уравнение как
2E=мв2
Умножение «m» в обеих частях уравнения
2mE=(мВ)2
Импульс объекта определяется как произведение массы объекта на скорость, с которой он движется.
p = mv
Следовательно, приведенное выше уравнение становится
P2=2 мВ
P=√2mE
Согласно де Бройлю,
λ =h/p
Подставляя приведенное выше уравнение, мы имеем
λ =h/ √2mE
Приведенное выше уравнение дает связь между энергией и длиной волны частицы.
Подробнее о Что такое кинетическая энергия света: подробные факты.
Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10-31 кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.
Данный: λ = 293 нм
м = 9.1 × 10-31 kg
ч = 6.626 * 10-34Js
с=3 *108 м/с
У нас есть,
λ =h/ √2mE
λ2=h2/ 2мЕ
Е = ч2/ 2мλ2
=(6.626 * 10-34 Дж)2/2* 9.1* 10-31* (293*10-9) 2
= 0.28 * 10-23
Кинетическая энергия, связанная с частицей, равна 0.28*10-23 Джоули.
Теперь, чтобы вычислить скорость частицы, выведем формулу скорости из кинетической энергии:
КЕ=1/2 мВ2
2E= мв2
v=√(2Е/м)
= √(2(0.28*10-23)/(9.8*10-31))
= 0.24 * 104= 2400 м / с
Скорость частицы с длиной волны 298 нм составляет 2400 м/с.
Связь энергии электрона и длины волны
Энергия электрона определяется простым уравнением:
Е=чню
Где «h» — постоянная Планка, а
nu — частота появления электрона
Частота электрона определяется как
ню = v / λ
Где v — скорость электрона и
λ — длина волны электронной волны
Следовательно, энергия связана с длиной волны электрона как
E=hv/λ
Это соотношение позволяет найти энергию, связанную с распространением одиночного электрона с определенной длиной волны, скоростью и частотой. Энергия обратно пропорциональна длине волны. Если длина волны электрона уменьшается, энергия волны должна быть больше.
Изображение Фото: Pixabay
Получив энергию в той или иной форме, электрон переходит из более низкого энергетического состояния в более высокое энергетическое состояние. Для перехода электронов из одного состояния в другое энергия электрона определяется уравнением
Э=РE(1/нf– 1/нi)
Где RE=-2.18* 10-18m-1 является константой Ридберга
nf это конечное состояние электрона
ni это начальное состояние электрона
Мы можем далее переписать приведенное выше уравнение как
ч ню = RE(1/нf– 1/нi)
hc/λ =RE(1/нf– 1/нi)
1/λ =REhc(1/nf– 1/нi)
1/λ =R(1/nf– 1/нi)
Где,
Р=РEчс=1.097* 107
По мере того, как электрон получает энергию, электрон переходит и перескакивает в более высокое состояние энергетического уровня и высвобождает энергию электронам, присутствующим в этом состоянии, и либо становится стабильным, либо высвобождает количество энергии и возвращается в более низкие энергетические состояния.
Подробнее о 16+ Пример амплитуды волны: подробные пояснения.
Задача 3: Если электрон переходит из состояния ni=1, чтобы указать nf=2, затем рассчитайте длину волны электрона.
Данный:
ni=1
nf=2
1/λ =RE(1/нf– 1/нi)
1/λ=-1.097*107 * ( 1/2-1/1 )
1/λ=0.5485* 107
Следовательно,
λ = 1/0.5485* 107
λ =1.823*10-7
λ =182.3*10-9=182.3нм
Длина волны света, излучаемого при переходе электрона с одного энергетического уровня на другой, равна 182.3 нм.
Связь лучистой энергии и длины волны
Каждый объект поглощает световые лучи в дневное время в зависимости от его формы, размера и состава. Если температура поверхности объекта достигает температуры выше абсолютного нуля, объект будет излучать излучения в виде волн.
Это испускаемое излучение пропорционально четвертой степени абсолютной температуры объекта и определяется уравнением
U=ɛΣ Т4A
Где U — излучаемая энергия
ɛ — коэффициент излучения излучения от объекта
Σ — постоянная Стефана-Больцмана, равная Σ=5.67*10-8Вт / м2K4
T — абсолютная температура
А — площадь объекта
Объект с высокой температурой излучает излучение с короткими длинами волн, а более холодные поверхности излучают волны с большей длиной волны. В зависимости от испускаемого излучения и длины волны испускаемого излучения волны классифицируются в соответствии с приведенной ниже таблицей.
| Имя и фамилия | Радиоволны | Микроволны | Инфракрасный порт | Видимый | Ультрафиолетовое | рентген | Гамма излучение |
| Длина волны | > 1м | 1mm-1m | 700нм-1мм | 400nm-700nm | 10nm-380nm | 0.01nm-10nm | <0.01 нм |
| частота | <300 МГц | 300MHz-300GHz | 300ГГц-430ТГц | 430ТГц-750ТГц | 750ТГц-30ФГц | 30PHz-30EHz | >30 Гц |
По мере уменьшения длины волны излучения частота волны возрастает. Длина волны напрямую связана с температурой, поэтому, если частота испускаемого излучения больше, это означает, что энергия объекта высока.
Гамма-лучи, рентгеновские лучи и ультрафиолетовые лучи имеют очень короткую длину волны, поэтому энергия этих волн очень высока по сравнению с видимым, инфракрасным, микроволнами или радиоволнами. Кроме того, чем выше излучение, полученное объектом, тем больше он будет излучать в зависимости от коэффициента излучения объекта.
Ниже приведен график зависимости энергии от длины волны в секунду для разных температур. График показывает, что по мере повышения температуры системы энергия испускаемого излучения также увеличивается с температурой.
Для длины волны в видимой области эмиссия излучения максимальна. Это связано с тем, что Солнце излучает УФ-лучи вместе с инфракрасными лучами и видимыми лучами, а эти лучи представляют собой электромагнитные волны дальнего действия. Озоновый слой Земли защищает земную атмосферу от этого вредного излучения и либо отражается обратно, либо задерживается в облаках.
В видимом диапазоне в дневное время излучается больше излучений, поскольку в дневное время от Солнца поступает все больше и больше излучений, а испускается меньше ИК-лучей по сравнению с видимым спектром. Ночью температура снижается, длина волны излучения увеличивается, и объект излучает больше ИК-лучей.
Подробнее о Свойства преломления: волна, физические свойства, исчерпывающие факты.
Задача 4: Коробка длиной 11 см, шириной 2 см и воздухом 7 см нагревается до температуры 1200 Кельвинов. Если коэффициент излучения ящика равен 0.5, то рассчитайте скорость излучения энергии из ящика.
Данный:л=11см
ч=2см
б = 7cm
е =0.5
Σ=5.67* 10-8Вт / м2K4
Т=1200 К
Общая площадь ящика составляет
A=2(фунт+чб+гл)
=2(11*7+7*s 2+2*11)
=2 (77+14+22)
=0.0226 кв.м
Энергия, излучаемая коробкой, равна
U=ɛ Σ T4A
=0.5* 5.67* 10-8* 12004* 0.0226
=1328.6 Вт
Связь частоты энергии и длины волны
Чем больше частота волны, тем больше энергия, связанная с частицей. Энергия связана с частотой волны как
E=ч/ню
Где «h» — постоянная Планка.
nu — частота волны
Частота волны определяется как скорость волны в среде и длина волны.
ню = v / λ
Где v — скорость волны
λ — длина волны
Следовательно,
λ=v/ну
Это дает связь между частотой и длиной волны волны. Это говорит о том, что длина волны и частота обратно пропорциональны друг другу. Если длина волны увеличивается, частота волны уменьшится.
Подробнее о Влияние преломления на частоту: как, почему нет, подробные факты.
Задача 5. Скорость луча света, испускаемого источником, равна 1.9 × 108 РС. Частота возникновения излучаемой волны составляет 450ТГц. Найдите длину волны испускаемого излучения.
Данный: v=1.9*108 м/с
F=450ТГц=450*1012Hz
Длина волны луча света равна
λ = v/f
=1.9* 108/ 450* 1012
= 0.004222 * 10-4
=422.2* 10-9=422.2нм
Луч света имеет длину волны 422.2 нм.
Связь энергии фотона и длины волны
Энергия, которой обладает фотон, называется энергией фотона и обратно пропорциональна электромагнитной волне фотона по соотношению
E=hc/λ
Где «h» — постоянная Планка.
С — скорость света
λ — длина волны фотона
Частота фотона определяется уравнением
f=с/λ
Где f — частота
Следовательно, фотон с большей длиной волны обладает небольшой единицей энергии, тогда как фотон с меньшей длиной волны дает большое количество энергии.
Подробнее о Какова длина волны фотона: как найти, несколько идей и фактов.
Задача 6: Рассчитать энергию фотона, распространяющегося в электромагнитной волне с длиной волны 620 нм.
Данный: Длина волныλ =620 нм
ч = 6.626 * 10-34 js
с=3 *108 м/с
У нас есть,
E=hc/λ
Е=6.626 * 10-34 Дж*3 * 108 м/с/620* 10-9m
= 0.032 * 10-17= 32 * 10-20 Дж
Энергия, связанная с фотоном, равна 32* 10-20Джоули.
Часто задаваемые вопросы
Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 106 м/с
Данный: v=6.35*106м/с
м=9.1*10-31kg
ч=6.62* 10-34 Js
Кинетическая энергия электрона равна
КЕ=1/2 мВ2
=1/2 * 9.1*10-31* (6.35* 106)2
=1.83* 10-17Дж
Импульс электрона равен
P=√2mE
=√2* 9.1* 10-31* 1.83 * 10-17
= 5.7 * 10-24кг.м / с
Теперь длина волны электрона
λ =h/√2mE
= 6.62 * 10-34/ 5.7 * 10-24
= 4.8 * 10-10m
=48нм
Длина волны электрона, движущегося со скоростью 6.35*106м/с составляет 48 нм.
Q2. Черный объект площадью 180 кв.м находится при температуре 550К. Какова скорость излучения энергии от объекта?
Данный: А=180 кв.м
Т=550К
Поскольку объект имеет черный цвет, коэффициент излучения равен 1.
е =1
У нас есть,
U=ɛΣT4A
=1*с 5.67* 10-8* 5504* 180
= 0.93 * 106МОЩНОСТЬ
Мощность излучения от выброса излучения от объекта составляет 0.93*106Вт.
Какова абсолютная температура системы?
Это неизменное и совершенное значение температуры системы.
Абсолютная температура системы измеряется по шкале градусов Цельсия, Фаренгейта или Кельвина, которые измеряют ноль как абсолютный ноль градусов.
Как длина волны фотона зависит от температуры?
Температура системы определяет подвижность частиц системы.
Чем больше излучений получает система при более высоких температурах, тем больше излучения будет излучаться системой. При более высоких температурах излучаются более короткие волны, а при более низких температурах излучаются более длинные волны.
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие «длина волны» ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-
1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-
2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-
3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-
4
Воспользуйтесь приведенной формулой, чтобы вычислить скорость или частоту. Формулу можно переписать в другом виде и вычислить скорость или частоту, если дана длина волны. Чтобы найти скорость по известным частоте и длине волны, используйте формулу:
. Чтобы найти частоту по известным скорости и длине волны, используйте формулу:
.[5]
Реклама
-
1
-
2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-
3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-
1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-
2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-
3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 238 раз.
Была ли эта статья полезной?
Условие задачи:
Найти длину волны светового излучения с энергией фотонов 2·10-19 Дж?
Задача №11.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(E=2 cdot 10^{-19}) Дж, (lambda – ?)
Решение задачи:
Согласно формуле Планка, энергия фотона (E) пропорциональна частоте колебаний (nu) и определяется следующим образом:
[E = hnu;;;;(1)]
В этой формуле (h) – это постоянная Планка, равная 6,62·10-34 Дж·с.
Известно, что частоту колебаний (nu) можно выразить через скорость света (c), которая равна 3·108 м/с, и длину волны (lambda) по следующей формуле:
[nu = frac{c}{lambda };;;;(2)]
Подставим выражение (2) в формулу (1), тогда получим:
[E = frac{{hc}}{lambda }]
Отсюда искомая длина волны светового излучения (lambda) равна:
[lambda = frac{{hc}}{E}]
Мы получили решение задачи в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[lambda = frac{{6,62 cdot {{10}^{ – 34}} cdot 3 cdot {{10}^8}}}{{2 cdot {{10}^{ – 19}}}} = 9,93 cdot {10^{ – 7}};м = 0,993;мкм]
Ответ: 0,993 мкм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
11.1.11 Во сколько раз масса фотона, соответствующего видимой части спектра (lambda_1=0,6 мкм)
11.1.13 Какой массой обладает фотон с длиной волны 0,6 мкм?
11.1.14 Найти массу фотона излучения с длиной волны 1 мкм
Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
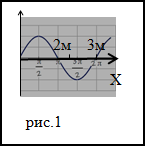
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.