Как найти длину волны зная амплитуду

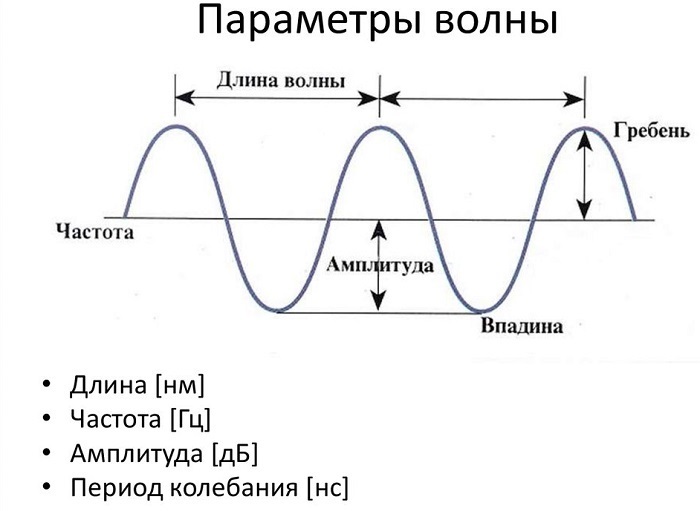
Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной. 

Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества. 

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

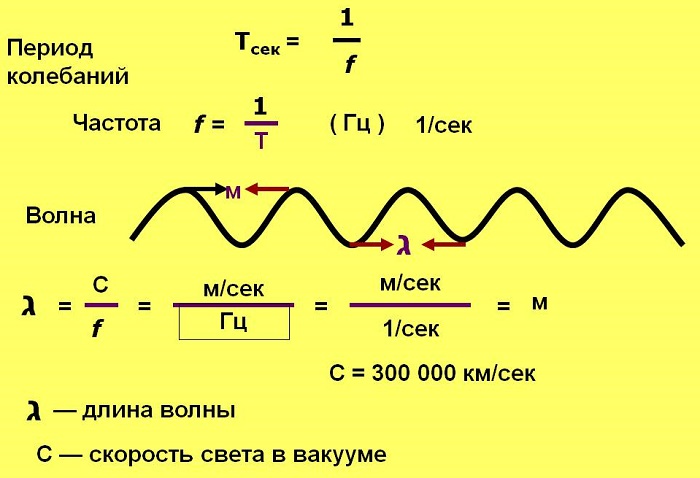
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10⁸ м/с поделить на длину в метрах.

Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

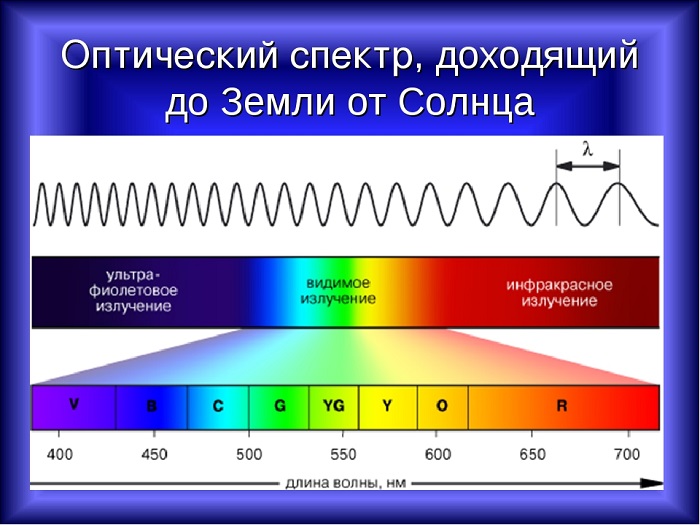
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

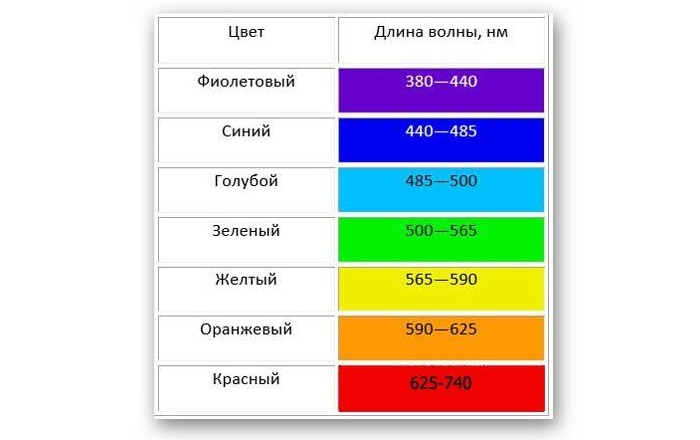
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

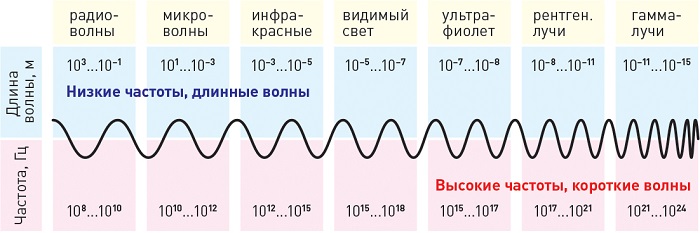
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания. 

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Что такое длина волны 

Волна — изменение характеристик физического поля или среды, способное удаляться от места возникновения или колебаться внутри ограниченной области пространства.

​Длина волны — расстояние между точками, которое волна проходит за одно колебание.

Если точки отстоят на расстояние (lambda) друг от друга, их смещения из положений равновесия будут одинаковы, и колебания в них будут происходить в одинаковой фазе.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В системе СИ длина волны измеряется в метрах.

Чем меньше длина волны, тем легче сконцентрировать ее энергию в заданном направлении. Поэтому, например, в эхолокации используют ультразвук. Поскольку ультразвуковые волны в воде затухают гораздо слабее, чем в воздухе, эхолокацию особенно широко используют в гидроакустике.

Физические характеристики волны

Два главных параметра волны — частота колебаний f (число полных циклов колебаний в секунду) и длина волны (lambda) — зависят друг от друга.

Зная эти параметры, можно произвести вычисления, чтобы выяснить период повторения колебаний Т и скорость распространения волны v.

Интенсивность волны описывается такими параметрами, как:

• амплитуда;
• плотность энергии;
• плотность потока мощности.

Геометрически волна состоит из гребней и ложбин.

Для продольных волн чаще используют понятия точек максимального сжатия и максимального растяжения.

Для стоячих волн — понятия пучности и узла, характеризующие участки с максимальной и минимальной амплитудой колебаний.

Виды волн, какие бывают

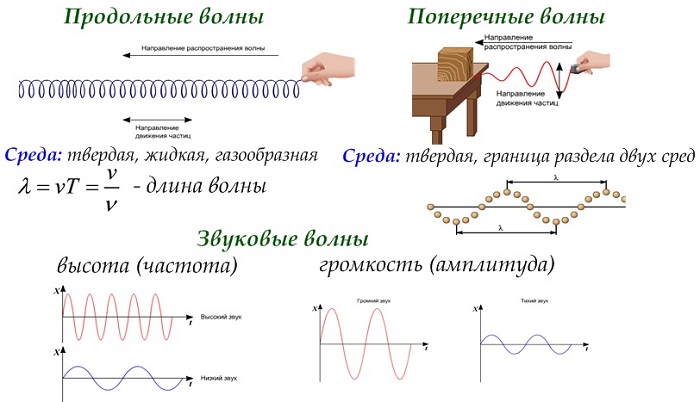
Продольные волны

Продольные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.

Они возникают при сопротивлении среды изменению ее объема, их причина — деформация сжатия/растяжения (в твердой среде) или уплотнения/разрежения (в газах и жидкостях).

Продольная волна заставляет частицы среды колебаться у своих положений равновесия, и этот процесс перемещается параллельно направлению распространения волны. Частицы сдвигаются строго по одной линии.

Чтобы узнать длину волны, нужно измерить расстояние между ближайшими точками сжатия или растяжения. Продольные волны могут распространяться в любой среде: твердой, жидкой, газообразной. Во время этого процесса непрерывно изменяется давление в каждой точке среды.

Поперечные волны

Поперечные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.

Они возникают при сдвиге слоев среды относительно друг друга. В поперечной волне колебания элементов происходят в направлениях, перпендикулярных направлению распространения волны. Среда стремится вернуть деформированные частицы на место, при этом на несмещенные частицы рядом со смещенными воздействуют силы упругости и отклоняют их от положения равновесия. Жидкости и газы не сопротивляются изменению формы, поэтому поперечные волны возможны только в твердых средах.

Длина поперечной волны — расстояние между двумя ближайшими ее впадинами или горбами.

Стоячие волны

Стоячие волны — волновые процессы в распределенных колебательных системах с устойчивым в пространстве расположением участков с максимальной и минимальной амплитудой.

Самую простую одномерную стоячую волну можно возбудить, запустив колебательный процесс с одного конца стержня или гибкой струны. Добравшись до конца стержня или струны, волна отразится, что вызовет наложение.

Бегущие волны

Бегущие волны — процессы последовательного изменения (с определенным запаздыванием) состояния взаимодействующих тел, когда они друг за другом приходят в движение.

Ее можно запустить, например, в системе из косточек домино, выстроенных строго друг за другом на ровной поверхности. Если осторожно толкнуть первую, она, падая, уронит вторую, та — следующую, и в результате такого последовательного падения по ряду побежит волна.

Формулы длины волны

Длина стоячей и бегущей волны

(lambda_{};=;v;times;T;=;frac vf;=;frac{2mathrm{πv}}omega)

v здесь — фазовая скорость волны, Т — период колебаний, f — частота, (omega) — круговая частота.

Длина стоячей волны — это расстояние между двумя пучностями или двумя узлами, которое можно рассчитать с помощью формулы:

(lambda_{ст};=;fraclambda2.)

Длина стоячей волны равна половине длины соответствующей бегущей волны, так как возникает при наложении двух волн, падающей и отраженной, и сумма их амплитуд равна нулю.

Длина электромагнитной волны

Электромагнитная волна — это электрическое и магнитное поля, взаимно превращающиеся друг в друга.

В случае электромагнитных волн колебания совершают векторы электрического и магнитного полей. Механического колебания не происходит, но электромагнитные волны, например, световые, принято относить к поперечным.

Частоты и длины электромагнитных волн изменяются в очень широких пределах: от нескольких колебаний в секунду до (10^{27}), от размеров, сопоставимых с размерами атомов, до миллионов километров в безвоздушном пространстве. Поэтому электромагнитные излучения принято делить на частотные диапазоны в порядке возрастания длины волны, от гамма-лучей к радиоволнам. Границы между выделенными диапазонами условны.
Длина электромагнитной волны обратно пропорциональна частоте и вычисляется через скорость света:

(nutimeslambda;=;с.)

Скорость распространения излучения, она же скорость света, равна:

(3;times;10^8;frac мс.)

Длина звуковой волны

Колебания частотой от 16 до 20 000 Гц воспринимаются ухом человека. Колебания источников звуковых волн, например, струн или голосовых связок, создают в среде последовательно сменяющие друг друга сжатия и разрежения.

Когда периодические изменения давления достигают барабанной перепонки, она совершает вынужденные колебания. Эти колебания анализирует по амплитуде и частоте внутреннее ухо, имеющее форму улитки, рецепторы которого настроены на различные звуковые частоты. Затем колебания передаются в мозг по слуховому нерву и воспринимаются как слышимые звуки.

Длину звуковой волны вычисляют по общей формуле:

(lambda;=;v;times;T;.)

Расчет длины волны через энергию фотона

Электромагнитное излучение испускается не непрерывно, а отдельными порциями, которые называют квантами или фотонами. Их энергия пропорциональна частоте и высчитывается по формуле:

(E;=;htimesnu)

Где h — постоянная Планка, равная (6,6;times;10^{-34};Джtimes с.)

Очевидно, что наибольшую энергию несут кванты коротковолнового излучения. За единицу измерения энергии фотонов обычно принимают электронвольт, его обозначение — эВ. Это энергия, которую приобретает свободный электрон, ускоренный электрическим полем с разностью потенциалов в 1 вольт.

1 электронвольт равен (1,6;times;10^{-19};Дж.)

Кванты видимого излучения обладают энергиями 2–3 эВ и занимают лишь небольшую область исследуемого в астрофизике электромагнитного спектра, который простирается от значений энергии порядка миллионных долей электронвольта для метровых радиоволн до миллионов электронвольт для гамма-излучения.

Так как частота равна скорости распространения излучения, деленной на длину волны, длину волны можно вычислить, зная энергию фотона и частоту.

(lambda;=frac{;htimes;c;}E)

Примеры решения задач

Решение:

(lambda;=;v;times;T;)

Для нахождения периода Т воспользуемся формулой (Т;=frac{;1;}f.)

Следовательно, (lambda;=;frac{v;}f.)

Подставив известные данные, получим (lambda;=;frac{340;}{440};=;0,78;м.)

Ответ: 78 см.

Решение:

(lambda;=;v;times;T;)

1 час = 3600 секунд

Подставив известные данные, получим (lambda;=;8;times;3600;=;28800;м.)

Ответ: 28800 м.

Длина волны. Связь длины волны со скоростью ее распространения. Уравнение волны

Как уже отмечалось, возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит не мгновенно, а с определенной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости (vec upsilon) направлен по нормали к волновой поверхности в сторону распространения волны и в однородной изотропной среде совпадает с направлением луча. Следует отличать скорость распространения волны от скорости колебания частиц среды около своих положений равновесия.

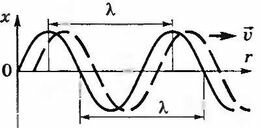
Пусть волна распространяется вдоль горизонтальной оси (например, вдоль упругого горизонтального шнура). В данный момент времени форма волны повторяется в пространстве вдоль шнура через определенные отрезки. На рисунке 15.7 показан профиль волны в определенный момент времени. С течением времени вся эта картина перемещается со скоростью (upsilon) слева направо (штриховая линия).

Расстояние между ближайшими точками, колеблющимися в одинаковых фазах (рис. 15.7), называется длиной волны. Длина волны (~lambda) равна расстоянию, на которое распространяется фронт волны за время, равное периоду (~T) колебаний источника волн[~lambda = upsilon T.]

Так как (T = frac{1}{nu};) (nu = frac{omega}{2 pi},) то скорость волны связана с частотой колебаний уравнением (~upsilon = lambda nu.) Отсюда (lambda = frac{upsilon}{nu} = frac{2 pi upsilon}{omega},) где (~omega) — циклическая частота колебаний, (~nu) и (~omega) зависят только от свойств источника волны.

При возникновении волн в среде их частота определяется частотой колебаний источника, а скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.

Выведем уравнение плоской волны.

Пусть источник совершает гармонические колебания по закону

(~x = A sin omega t,)

где х — смещение, А — амплитуда, (~omega) — циклическая частота, t — время.

В точках, отстоящих на расстоянии r от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать во времени от колебаний источника на (Delta t = frac{r}{upsilon}.)

Тогда смещение точки среды с координатой r в момент времени t

(x = A sin omega Bigr( t-frac{r}{upsilon} Bigl),) или (x = A sin Bigr( omega t-frac{omega r}{upsilon} Bigl).)

Это и есть уравнение плоской бегущей монохроматической волны (при этом предполагают, что затуханием волны в процессе ее распространения можно пренебречь). Смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени t и расстояния r до равновесного положения точки среды.

Из уравнения волны следует:

1. Амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника.

2. Любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления r данной точки от источника колебаний:

(~x = A sin(omega t + alpha),) где (alpha = -frac{omega r}{upsilon}.)

3. Положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением

(x = A sin Bigr( frac{omega r}{upsilon} + beta Bigl),) где (~beta = -omega t)

имеет разное значение в разные моменты времени.

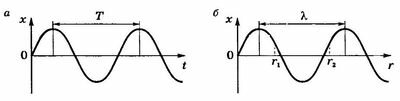
На рисунке 15.8, б приведен график этой функции при t = 0, представляющий собой «моментальный снимок» волны, т.е. положение всех частиц среды, в которой распространяется волна, в момент времени t = 0 — график волны. В отличие от графика колебаний (рис. 15.8, а), который показывает зависимость смещения одной частицы от времени в данной точке среды, график волны (рис. 15.8, б) показывает зависимость смещения всех частиц среды из положения равновесия от расстояния г до источника колебаний в некоторый фиксированный момент времени.

Найдем разность фаз колебаний двух точек среды, находящихся на расстоянии (~Delta r = r_2 — r_1) друг от друга (рис. 15.8, б). Колебания этих точек описываются уравнениями:

(x_1 = A sin omega Bigr( t — frac{r_1}{upsilon} Bigl);) (x_2 = A sin omega Bigr( t — frac{r_2}{upsilon} Bigl).)

Разность фаз (Delta varphi_1 = varphi_1 — varphi_2) будет равна

(Delta varphi = omega Bigr( t — frac{r_1}{upsilon} Bigl) — omega Bigr( t — frac{r_2}{upsilon} Bigl) = frac{omega}{upsilon}(r_2-r_1) = frac{2 pi}{T upsilon}(r_2 — r_1) = frac{2 pi}{lambda} Delta r.)

Если две точки находятся на расстоянии (~Delta r = lambda,) то разность фаз колебаний этих точек (Delta varphi = 2 pi,) что соответствует данному выше определению длины волны.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 428-430.

Была ли эта статья полезной?