Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
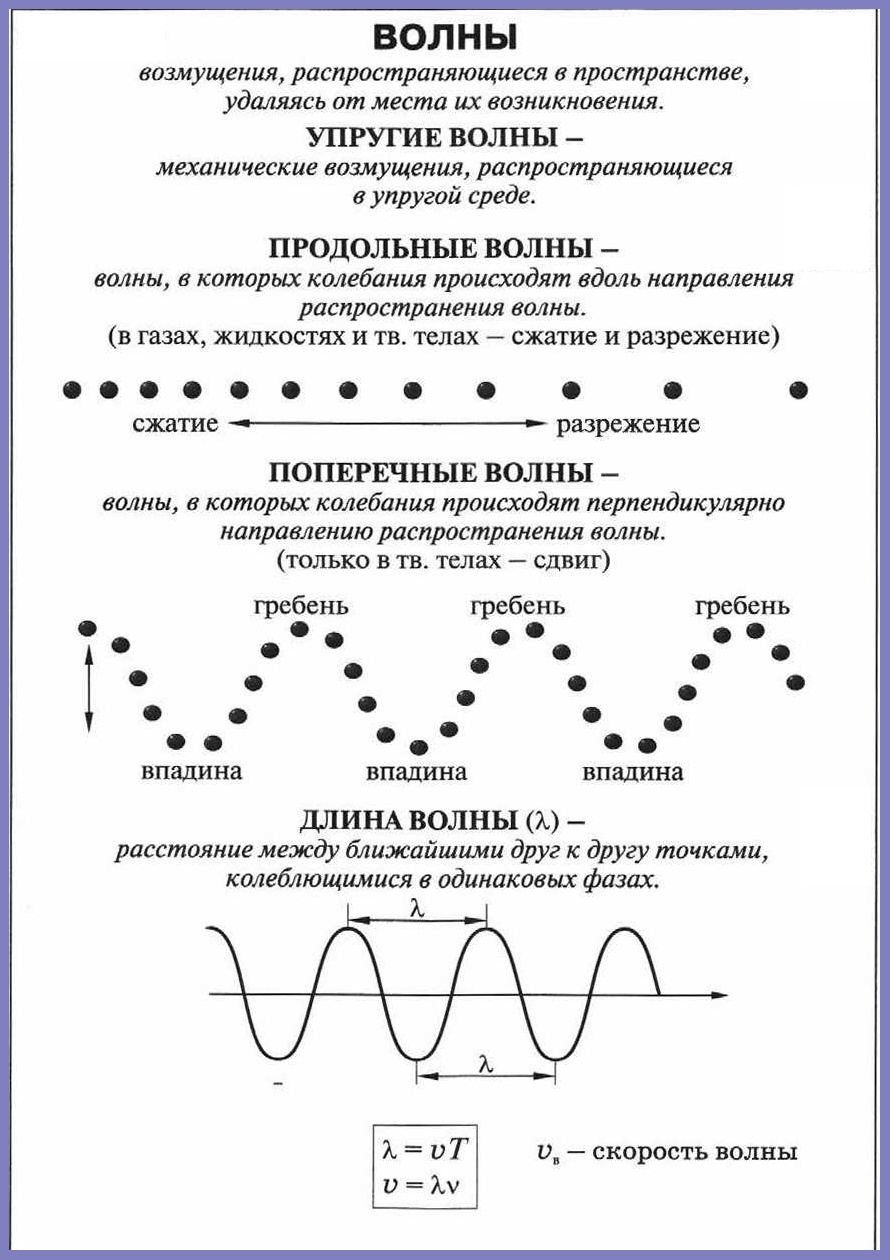
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?
Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?
Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?
Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.
Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.
Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.
Краткая теория для решения Задачи на Механические волны.
Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
- Подробности
- Обновлено 30.05.2018 20:13
- Просмотров: 1500
Задачи по физике — это просто!
Вспомним
Формула длины волны:
Период колебаний:
А теперь к задачам!
Элементарные задачи из курса школьной физики на механические колебания и волны.
Задача 1
Определить длину волны с частотой 300 Гц, которая распространяется в воздухе со скоростью 340 м/с.
Задача 2
Найти период колебания плота на волнах озера, если длина волны составляет 4 метра, а скорость распространения волн равна 2,5 м/с.
Задача 3
Определить сколько колебаний за 1 минуту совершает буек на воде, если скорость распространения волн составляет 3 м/с, а длина волны равна 5 метрам.
Задача 4
По поверхности воды идут волны. Определить параметры волны (период колебания, длину волны, скорость распространения), если расстояния между 1 и 4 гребнями волн составляет 9 метров, а мимо наблюдателя за 10 секунд проходят 5 гребней волн.
Задача 5
Поплавок удочки рыбака за 40 секунд сделал 20 колебаний, а расстояние между соседними гребнями волн составило 2 метра. Какова была скорость распространения волны?
Задача 6
С лодки в воду бросили камень. По воде пошли круги-волны. Расстояние между соседними гребнями волн составило 1 метр, а время за которое волна дошла до берега — 1 минута. Причем волны накатывались на берег с интервалом в 2 секунды. На каком расстоянии от берега бросили камень?
Задача 7
За время полета 30 секунд муха делает 15000 взмахов крыльями, а период колебания крыла комара составляет 1,6 миллисекунд. Во сколько раз отличаются частоты колебаний крыльев мухи и комара?
Успех в решении физических задач зависит не только от способностей в физике, но и от того, как часто вы решаете задачи. Сегодня в нашей регулярной рубрике «Физика для чайников» решаем задачи на электромагнитные волны.
Подпишитесь на нас в телеграме, там есть много полезного для всех учащихся, и так вы не пропустите ничего важного. А тем, кто хочет получить скидку на наши услуги, обязательно стоит заглянуть на наш второй канал с акциями и приятными бонусами.
Электромагнитные волны: решение задач
Сначала скажем, что решение задач по любой теме начинается с повторения теории. А если что-то не получается, помните: не нужно брать задачу «с наскока». Лучше почитайте общую памятку по решению физических задач, держите под рукой полезные формулы, и решение обязательно придет (если подумать).
Задача №1 на электромагнитные волны
Условие
Радиостанция работает на частоте 12 МГц. Какова длина излучаемых радиоволн?
Решение
Длина волны и частота и период связаны соотношениями:
ϑ=сλ ; λ=сϑ=сT
В соответствии с этим, рассчитаем:
λ=3·10812·106=25 м
Ответ: 25 м.
Задача №2 на электромагнитные волны
Условие
Электромагнитная волна с Земли долетает до Марса за 3 минуты и 6 секунд. Каково расстояние до Марса?
Решение
Зная скорость света (скорость электромагнитной волны) и время, вычислим расстояние по простейшей формуле из механики:
S=ctS=3·108·186=56·106 км
Не забываем переводить значения в систему СИ. 3 минуты =180 секунд.
Ответ: 56 миллионов километров.
Задача №3 на электромагнитные волны
Условие
На каком расстоянии s от антенны радиолокатора А находится объект, если отражённый от него радиосигнал возвратился обратно через промежуток времени τ = 200 мкс?
Решение
За время τ сигнал проходит путь 2s (до объекта, и обратно):
2s=cτs=cτ2
Подставим значения, и найдем ответ:
s=3·108·200·10-62=30·103 м=30 км
Ответ: 30 км.
Задача №4 на электромагнитные волны
Условие
Определить длину электромагнитных волн в воздухе, излучаемых колебательным контуром с емкостью 3 нФ и индуктивностью 0,012 Гн. Активное сопротивление контура принять равным нулю.
Решение
Применим формулу для периода колебаний колебательного контура:
T=2πLC
А теперь вспомним, как длина волны связана с периодом колебаний:
λ=сT
Отсюда:
λ=2πсLC
λ=2·3,14·3·108·0,012·3·10-9=11,304·103 м
Ответ: 11304 м.
Задача №5 на электромагнитные волны
Условие
В каком диапазоне длин волн может работать приёмник, если ёмкость конденсатора в его колебательном контуре плавно изменяется от C1 = 50 пФ до С2 = 500 пФ, а индуктивность катушки постоянна и равна L = 20 мкГн?
Решение
Длина волны, которую воспринимает радиоприемник, равна:
λ=2πсLC
Соответственно, чтобы узнать диапазон, нужно найти максимальную и минимальную длины волн, соответствующие минимальной и максимальной емкостям конденсатора:
λ1=2πсLC1=2·3,14·3·108·50·10-12·20·10-6=60 мλ2=2πсLC2=2·3,14·3·108·500·10-12·20·10-6=188 м
Приемник работает в диапазоне ультракоротких радиоволн (УКВ).
Ответ: от 60 до 188 м.
Вопросы на тему «Электромагнитные волны»
Вопрос 1. Что такое электромагнитная волна?
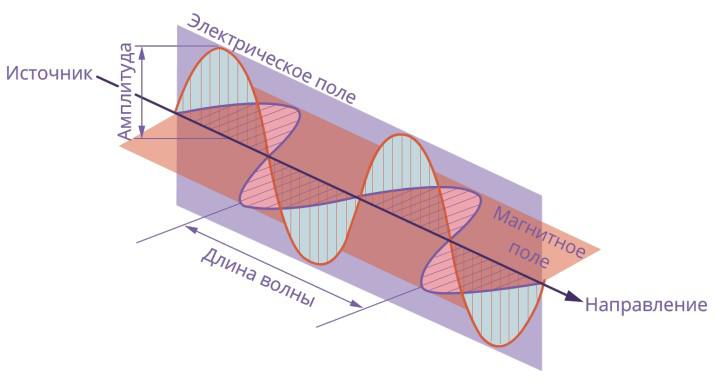
Ответ. Электромагнитная волна – это распространяющееся в пространсте возмущение (изменение) электромагнитного поля. Другими словами:
Электромагнитные волны – это электромагнитные колебания, которые распространяются в пространстве с конечной скоростью.
Вопрос 2. Можно ли увидеть электромагнитную волну?
Ответ. Да, можно. Ведь видимый человеческим глазом свет представляет собой ни что иное, как электромагнитные волны опрделенного диапазона (от 400 до 760 нанометров).
Вопрос 3. Какова скорость электромагнитных волн в вакууме?
Ответ. Электромагнитная волна в вакууме распространяется со скоростью с=300 000 км/с. Это фундаментальная физическая постоянная.
В других прозрачных средах скорость света будет меньше.
Вопрос 4. Какие бывают электромагнитные волны?
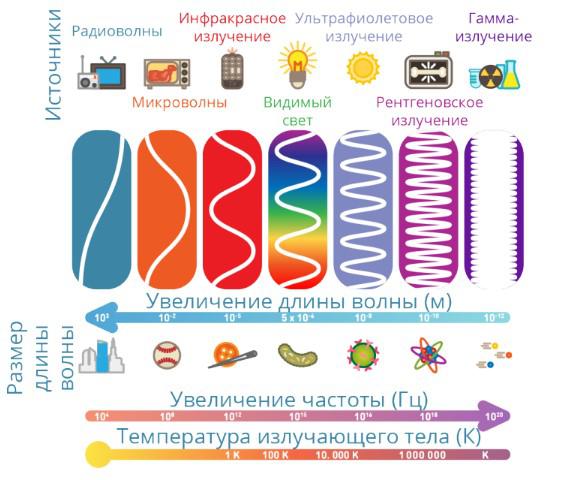
Ответ. В зависимости от диапазона длин волн, электромагнитное излучение делится на:
- радиоволны;
- оптическое излучение;
- ионизирующее электромагнитное излучение.
Вопрос 5. Какие волны самые опасные для здоровья человека?
Ответ. Гамма-излучение, рентгеновские лучи, УФ-излучение.
Нужна помощь в решении задач и других заданий? Обращайтесь в специальный сервис для учащихся в любое время.
Длина волны .
( lambda =vT )
(lambda) — Длина волны (метры)
(v) — Скорость распространения волны
(T) — Период
Наиболее простой пример волн это волны на поверхности воды
( T=dfrac{t}{N} )
(T) — период колебаний ( время за которое совершается одно колебание )
(N)- общее количество колебаний за все время
Задача 1.
Поплавок колеблется на волнах, причем за время (t=8 c ), он совершает (N=10 ) колебаний .
Расстояние между соседними гребнями волн составляет ( lambda=0,8 м ).
Найти скорость распространения волны.
Показать ответ
Показать решение
Видеорешение
Дано:
(t=8 c)
(N=10 )
( lambda=0,8 м )
(v-? )
( T=dfrac{t}{N}= dfrac{8 c}{10}=0,8 c )
( lambda =vT )
(v= dfrac{lambda}{T}=dfrac{0,8 м}{0,8 c}=1 м/с )
Ответ: ( v= 1 м/с )
Задачи на колебания и волны с решениями
Механические гармонические колебания
9.1.1 Уравнение гармонических колебаний имеет вид x=4*sin(2*pi*t) (м). Определить
9.1.2 Материальная точка совершает гармонические колебания. Период колебаний 0,5 с
9.1.3 За какое время от начала движения точка, колеблющаяся по закону x=7*sin(0,5*pi*t) (м)
9.1.4 Две точки совершают гармонические колебания. Максимальная скорость первой точки
9.1.5 За какой промежуток времени маятник, совершающий гармонические колебания
9.1.6 Тело совершает гармонические колебания. Период колебаний 0,15 с, максимальная
9.1.7 Определите смещение от положения равновесия материальной точки, совершающей
9.1.8 За равные промежутки времени первое тело совершило 100, а второе – 400 колебаний
9.1.9 Материальная точка совершает гармонические колебания с периодом 0,8 с
9.1.10 При гармонических колебаниях вдоль оси ox координата тела изменяется по закону
9.1.11 Уравнение движения колеблющейся точки имеет вид x=0,05*cos(2*pi*t/3) (м)
9.1.12 Уравнение движения точки x=0,05*cos(3*pi*t) (м). Чему равна амплитуда
9.1.13 Найти максимальное значение скорости точки, уравнение движения которой
9.1.14 Во сколько раз изменится амплитуда колебаний ускорения гармонически колеблющейся
9.1.15 Материальная точка совершает гармонические колебания по закону
9.1.16 Найти период гармонического колебания, фаза которого увеличивается
9.1.17 При фазе pi/3 смещение частицы, колеблющейся по закону косинуса, было равно 1 см
9.1.18 Материальная точка совершает гармонические колебания с периодом 0,5 с. Амплитуда
9.1.19 Уравнение колебаний материальной точки имеет вид x=0,02*sin(pi*t/2+pi/4)
9.1.20 Маятник массой 5 кг и длиной 0,8 м совершает колебательное движение с амплитудой
9.1.21 Тело совершает гармонические синусоидальные колебания с нулевой начальной фазой
9.1.22 Материальная точка совершает синусоидальные колебания с амплитудой 8 см
9.1.23 Найти период гармонического колебания, изображенного на рисунке
9.1.24 T=0,2 с – период гармонического колебания с амплитудой 10 см. Найти смещение тела
9.1.25 Материальная точка совершает гармонические колебания. Если при неизменной
9.1.26 Материальная точка совершает гармонические колебания. Если при неизменной амплитуде
Математический маятник
9.2.1 Во сколько раз изменится частота колебаний математического маятника
9.2.2 Амплитуда колебаний математического маятника 10 см. Наибольшая скорость 0,5 м/с
9.2.3 Частота гармонических колебаний математического маятника возрастает в 2 раза
9.2.4 Период колебаний маятника на Земле равен 1 с. Каким он будет на Луне, если ускорение
9.2.5 Какова длина математического маятника, совершающего колебания по закону
9.2.6 Два математических маятника с периодами колебаний 6 и 5 с соответственно одновременно
9.2.7 Два маятника начинают одновременно совершать колебания. За время первых
9.2.8 При опытном определении ускорения свободного падения учащийся за 5 мин насчитал
9.2.9 Маятник установлен в кабине автомобиля, движущегося прямолинейно со скоростью
9.2.10 Один математический маятник имеет период 3 с, а другой – 4 с. Каков период
9.2.11 Математический маятник длиной 0,01 м имеет ту же частоту колебаний, что и шарик
9.2.12 Математический маятник длиной 2,45 м совершает 100 колебаний за 314 с. Определите
9.2.13 Какова длина математического маятника, совершающего колебания по закону
9.2.14 Маятник состоит из металлического шарика массой 1 г и нити. На шарик поместили
9.2.15 Определите длину математического маятника, который за 10 с совершает на 4 полных
9.2.16 Математический маятник длиной 1 м совершает гармонические колебания
9.2.17 Во сколько раз время прохождения колеблющейся точки первой половины амплитуды
9.2.18 К потолку подвешены два маятника. За одинаковое время первый маятник совершил
9.2.19 Первый шарик, подвешенный на нити длиной 1 м, отклонили от положения равновесия
9.2.20 Математический маятник совершает колебания. В положении наибольшего отклонения
9.2.21 Кубик совершает малые колебания в вертикальной плоскости, двигаясь без трения
9.2.22 Небольшой металлический шарик массой 10 г, подвешенный на нити длиной 0,1 м
9.2.23 Математический маятник с длиной нити L совершает свободные колебания вблизи стены
9.2.24 В неподвижном лифте период собственных колебаний математического маятника
Пружинный маятник
9.3.1 Шарик массой 5 г колеблется по закону x=0,04*sin(2*pi*(t/T+0,5))
9.3.2 Шарик на пружине сместили на 1 см от положения равновесия и отпустили
9.3.3 Определить амплитуду колебаний, если для фазы 45 градусов смещение частицы
9.3.4 Частота колебаний шарика, прикрепленного к вертикальной пружине, равна 2,8 Гц
9.3.5 Найти массу груза, который на пружине жесткостью 25 Н/см делает 20 колебаний
9.3.6 Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период
9.3.7 Груз, подвешенный к пружине, совершает 10 колебаний в минуту. Определите жесткость
9.3.8 Пружина под действием груза массой 10 кг совершает 50 колебаний в минуту
9.3.9 Уравнение колебаний пружинного маятника массой 200 г имеет вид
9.3.10 Груз, подвешенный к пружине, вызвал её удлинение на 4 см. Найти период собственных
9.3.11 Автомобильные рессоры имеют жесткость 20 кН/м. Каким будет период колебаний
9.3.12 Длина пружинного маятника увеличилась в 4 раза. Во сколько раз изменится период
9.3.13 Висящий на пружине груз массой 0,1 кг совершает вертикальные колебания
9.3.14 Тело совершает гармонические колебания в горизонтальной плоскости на пружине
9.3.15 Найти массу груза, который на пружине с жесткостью 250 Н/м совершает 100 полных
9.3.16 Невесомая пружина жесткостью 100 Н/м подвешена за один из концов так
9.3.17 На пружине подвешена чаша весов с гирями. При этом период вертикальных колебаний
9.3.18 Грузы массы 200 г, подвешенный к пружине, колеблется с такой же частотой
9.3.19 Как изменится период вертикальных колебаний груза, подвешенного на двух
Энергия механических колебаний
9.4.1 Груз, подвешенный на пружине, жесткость которой 1 кН/м, совершает косинусоидальные
9.4.2 Во сколько раз изменится полная механическая энергия колеблющегося маятника
9.4.3 Найти потенциальную энергию математического маятника массой 200 г в положении
9.4.4 Груз массой 0,2 кг колеблется на пружине жесткостью 500 Н/м. Чему равна полная
9.4.5 Смещение груза, подвешенного на пружине, в зависимости от времени задается законом
9.4.6 Найти кинетическую энергию груза, совершающего косинусоидальные колебания
9.4.7 Груз массой 0,2 кг, подвешенный на пружине, совершает 30 колебаний за 1 минуту
9.4.8 Пружинный маятник вывели из положения равновесия и отпустили. Через какое время
9.4.9 Пружинный маятник совершает косинусоидальные колебания, после того как его вывели
9.4.10 Материальная точка совершает гармонические колебания. Как изменится кинетическая
9.4.11 Максимальная кинетическая энергия материальной точки массы 10 г, совершающей
9.4.12 Тело массы 5 кг совершает гармонические колебания с амплитудой 10 см
9.4.13 Тело массы 5 кг совершает гармонические колебания с частотой 2,5 Гц
Механический резонанс
9.5.1 При какой скорости поезда маятник длиной 10 см, подвешенный в вагоне, особенно
9.5.2 Ведра с водой на коромысле имеют частоту собственных колебаний 0,625 Гц. При какой
9.5.3 Автомобиль движется по неровной дороге, на которой расстояние между буграми
9.5.4 Трактор оставил на грунтовой дороге следы в виде углублений на расстоянии 0,3 м
Механические волны
9.6.1 Точки, находящиеся на одном луче и удаленные от источника колебаний на 12 и 14,7 м
9.6.2 Какую разность фаз будут иметь колебания двух точек, находящихся на расстоянии
9.6.3 Эхо от оружейного выстрела дошло до стрелка через 6 с после выстрела. На каком
9.6.4 Скорость распространения волн, качающих лодку, 1,5 м/с. Расстояние между
9.6.5 Во сколько раз изменится длина звуковой волны при переходе из воздуха в воду
9.6.6 Плоская волна, возбуждаемая источником, колеблющимся по закону x=0,2sin(62,8t) (м)
9.6.7 В струне, закрепленной с двух концов, возбуждены колебания. На рисунке показаны
9.6.8 Волна с частотой 5 Гц распространяется в пространстве со скоростью 3 м/с
9.6.9 Волны распространяются в упругой среде со скоростью 100 м/с. Наименьшее расстояние
9.6.10 На озере в безветренную погоду с лодки бросили тяжелый якорь. От места бросания
9.6.11 Рассчитать длину звуковой волны в воде, если частота колебаний 440 Гц
9.6.12 Определить расстояние между двумя ближайшими точками бегущей волны
9.6.13 Найти разность фаз колебаний между двумя точками звуковой волны, отстоящими
9.6.14 Длина волны 60 см. На каком расстоянии друг от друга находятся точки волны
9.6.15 Вдоль резинового шнура распространяется волны со скоростью 3 м/с при частоте 2 Гц
9.6.16 Скорость звука в воздухе 330 м/с. Какова частота звуковых колебаний, если длина
9.6.17 Рыболов заметил, что за 10 с поплавок совершил на волнах 20 колебаний
9.6.18 На рисунке приведена “мгновенная фотография” участка струны, по которой
9.6.19 У звуковой волны частоты 2 кГц при переходе из стали в воздух длина волны
9.6.20 Звуковая волна с частотой колебаний 500 Гц распространяется в стальном стержне
9.6.21 Стальную деталь проверяют ультразвуковым дефектоскопом с частотой 1 МГц
9.6.22 Сигнал ультразвукового эхолота возвратился на корабль через 0,4 с после излучения
9.6.23 Какова длина волны ультразвукового сигнала, посланного корабельным гидролокатором
9.6.24 Толщина стального листа контролируется генератором, излучающим ультразвуковые
Колебательный контур
9.7.1 Собственные колебания тока в контуре протекают по закону I=0,01*cos(1000*pi*t) (А)
9.7.2 Изменение заряда конденсатора в колебательном контуре происходит по закону
9.7.3 Индуктивность колебательного контура 500 мкГн. Какую емкость следует выбрать
9.7.4 Необходимо изготовить колебательный контур, собственная частота которого 15 кГц
9.7.5 Мгновенное значение силы синусоидального тока через 1/3 периода равно 2,6 А
9.7.6 Колебательный контур состоит из катушки индуктивности и плоского воздушного
9.7.7 В колебательном контуре к конденсатору подсоединили параллельно другой конденсатор
9.7.8 Колебательный контур состоит из катушки индуктивности и двух одинаковых конденсаторов
9.7.9 Напряжение на конденсаторе в идеальном колебательном контуре изменяется
9.7.10 К конденсатору с зарядом 0,25 нКл подключена катушка индуктивности. Каков
9.7.11 Частота собственных колебаний в колебательном контуре увеличилась в 3 раза
9.7.12 Чему равен период собственных колебаний в колебательном контуре, индуктивность
9.7.13 Во сколько раз изменится период свободных электрических колебаний
9.7.14 Заряд на обкладках конденсатора колебательного контура изменяется по закону
9.7.15 Во сколько раз изменится амплитуда колебаний силы тока, протекающего
9.7.16 Во сколько раз изменится частота колебаний в колебательном контуре, при увеличении
9.7.17 Сила тока изменяется со временем по закону I=2*cos(10*t) (А). Чему равен
9.7.18 В колебательном контуре конденсатор емкостью 50 нФ заряжен до максимального
9.7.19 Батарею из двух одинаковых конденсаторов емкостью 10 нФ каждый, заряженную
9.7.20 Колебательный контур составлен из индуктивности 0,1 Гн и конденсатора емкостью 10 мкФ
9.7.21 Колебательный контур составлен из дросселя с индуктивностью 0,2 Гн и конденсатора
9.7.22 В колебательном контуре совершаются незатухающие электромагнитные колебания
9.7.23 Электрический колебательный контур содержит катушку индуктивности 10 мГн
9.7.24 Ток в идеальном колебательном контуре изменяется по закону I=0,01cos(1000t) (А)
9.7.25 Как изменится частота колебаний в идеальном колебательном контуре
Затухающие колебания
9.8.1 Сила тока в сети изменяется по закону I=4,2sin(omega*t) (А). Какое количество теплоты
9.8.2 В колебательном контуре происходят затухающие электромагнитные колебания
9.8.3 Конденсатор емкостью 10 мкФ зарядили до напряжения 400 В и подключили к катушке
Энергия электромагнитных колебаний
9.9.1 Определить силу тока в колебательном контуре в момент полной разрядки конденсатора
9.9.2 Полная энергия колебаний в контуре равна 5 Дж. Найти максимальную силу тока
9.9.3 Уравнение колебаний электрического заряда в колебательном контуре (L=2 Гн)
9.9.4 Через поперечное сечение катушки индуктивностью 12 мГн проходит заряд 60 мКл
9.9.5 В колебательном контуре сила тока изменяется по закону I=-0,02*sin(400*pi*t) (А)
9.9.6 В колебательном контуре индуктивность катушки равна 0,2 Гн. Амплитуда силы тока
9.9.7 Заряженный конденсатор замкнули на катушку индуктивности. Через какое время
9.9.8 В электрическом колебательном контуре индуктивность катушки 4 мГн, а максимальный
Переменный ток
9.10.1 Сила тока изменяется по формуле I=8,5*sin(314t+0,651) (А). Определить
9.10.2 Катушка индуктивностью 20 мГн включена в сеть промышленного переменного тока
9.10.3 Мгновенное значение ЭДС синусоидального тока 120 В для фазы 45 градусов
9.10.4 Напряжение на концах участка цепи, по которой течет переменный ток, изменяется
9.10.5 В цепь переменного тока включены последовательно конденсатор емкостью 1 мкФ
9.10.6 Вольтметр, включенный в цепь переменного тока, показывает 220 В. На какое
9.10.7 Максимальное напряжение в колебательном контуре, состоящем из катушки
9.10.8 При включении конденсатора на синусоидальное напряжение 220 В с частотой 50 Гц
9.10.9 Определить емкость конденсатора фильтра выпрямителя, если частота тока 50 Гц
9.10.10 Конденсатор емкостью 10 мкФ включен в цепь, в которой мгновенное значение
9.10.11 Емкостное сопротивление конденсатора на частоте 50 Гц равно 100 Ом. Каким оно
9.10.12 К зажимам генератора присоединен конденсатор с емкостью 0,1 мкФ. Найти
9.10.13 В сеть переменного тока напряжением 220 В и частотой 50 Гц включен конденсатор
9.10.14 ЭДС в цепи переменного тока выражается формулой E=120*sin(628*t) (В). Определить
9.10.15 Длина воздушной линии передачи равна 300 км, частота тока 50 Гц. Найдите сдвиг
9.10.16 В цепь переменного тока включены последовательно сопротивление 100 Ом
Трансформаторы
9.11.1 Трансформатор включен в сеть с напряжением 120 В. Первичная обмотка его
9.11.2 Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на её концах 220 В
9.11.3 ЭДС первичной и вторичной обмоток трансформатора соответственно равны 220 и 20 В
9.11.4 Понижающий трансформатор с коэффициентом трансформации 10 включен в сеть
9.11.5 Сила тока в первичной обмотке трансформатора 0,6 А, напряжение на её концах 120 В
9.11.6 Трансформатор повышает напряжение с 220 до 660 В и содержит в первичной
9.11.7 Обмотка трансформатора со стальным сердечником имеет индуктивность 0,6 Гн
9.11.8 Первичная обмотка трансформатора, включенного в сеть 380 В, имеет 2400 витков
9.11.9 На первичную обмотку понижающего трансформатора с коэффициентом трансформации
9.11.10 В сердечнике трансформатора, включенного в сеть переменного тока частотой 50 Гц
9.11.11 Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть
Резонанс в колебательном контуре
9.12.1 В катушке индуктивности сила тока линейно увеличивается со скоростью 10 А/с
9.12.2 В цепь включены конденсатор 2 мкФ и индуктивность 0,05 Гн. Какой частоты ток надо
9.12.3 Параметры контуров таковы: C1=120 пФ, L1=3,5 мГн, C2=150 пФ, L2=5 мГн. На сколько
9.12.4 Резонанс в колебательном контуре с конденсатором 1 мкФ наступает при частоте
9.12.5 При изменении емкости конденсатора на 100 пФ резонансная частота
Электромагнитные волны
9.13.1 Колебательный контур имеет емкость 2,6 пФ и индуктивность 0,012 мГн. Какой длины
9.13.2 Найти емкость конденсатора колебательного контура, если при индуктивности
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.4 Определите максимальный ток в контуре, если длина электромагнитной волны
9.13.5 В каком диапазоне длин волн можно улавливать радиопередачи приемником
9.13.6 Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц
9.13.7 Максимальная величина заряда на конденсаторе колебательного контура 1 мкКл
9.13.8 Колебательный контур создает в воздухе электромагнитные волны длиной 150 м
9.13.9 Если конденсатор с расстоянием между пластинами 1 см определенным образом
9.13.10 Как нужно изменить емкость конденсатора в колебательном контуре радиоприемника
9.13.11 Индуктивность катушки пропорциональна квадрату числа ее витков. Как следует
9.13.12 Электрический колебательный контур радиоприемника содержит катушку индуктивности
9.13.13 Колебательный контур радиоприемника содержит конденсатор емкости 1 нФ
( 32 оценки, среднее 4.78 из 5 )