Содержание: [Скрыть]
-
- 1. Постановка задачи
- 2. Основные положения гидравлического расчета
- 3. Подбор оптимального диаметра трубопровода
- 4. Расчет падения напора и гидравлического сопротивления
- 5. Расчет потерь давления
- 6. Примеры задач гидравлического расчета трубопровода с решениями
Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:
Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
- переходный режим (2300<Re<4000), который характеризуется нестабильной структурой потока, когда отдельные слои жидкости перемешиваются;
- турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.
Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.
Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.
Подбор оптимального диаметра трубопровода
Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.
Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:
При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).
Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:
Расчет падения напора и гидравлического сопротивления
Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.
Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.
Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.
Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.
Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:
В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы:

Расчет потерь давления
Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.
Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:
Примеры задач гидравлического расчета трубопровода с решениями
Задача 1
В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м3/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.
Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.
Исходные данные:
Расход Q = 80 м3/час = 80·1/3600 = 0,022 м3/с;
эффективный диаметр d = 24 мм;
длина трубы l = 32 м;
коэффициент трения λ = 0,028;
давление в аппарате Р = 2,2 бар = 2,2·105 Па;
общий напор Н = 20 м.
Решение задачи:
Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:
w=(4·Q) / (π·d2) = ((4·0,022) / (3,14·[0,024]2)) = 48,66 м/с
Потери напора жидкости в трубопроводе на трение определяются по уравнению:
HТ = (λ·l) / (d·[w2/(2·g)]) = (0,028·32) / (0,024·[48,66]2) / (2·9,81) = 0,31 м
Общие потери напора носителя рассчитываются по уравнению и составляют:
hп = H — [(p2-p1)/(ρ·g)] — Hг = 20 — [(2,2-1)·105)/(1000·9,81)] — 0 = 7,76 м
Потери напора на местные сопротивления определяется как разность:
7,76 — 0,31=7,45 м
Ответ: потери напора воды на местные сопротивления составляют 7,45 м.
Задача 2
По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.
Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10-5.
Исходные данные:
Скорость потока жидкости W = 2,0 м/с;
диаметр трубы d = 100 мм;
общий напор Н = 8 м;
относительная шероховатость 4·10-5.
Решение задачи:
Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.
Значение скоростного напора определяется по соотношению:
w2/(2·g) = 2,02/(2·9,81) = 0,204 м
Потери напора воды на местные сопротивления составят:
∑ζМС·[w2/(2·g)] = (4,1+1)·0,204 = 1,04 м
Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):
hп = H — (p2-p1)/(ρ·g) — = 8 — ((1-1)·105)/(1000·9,81) — 0 = 8 м
Полученное значение потери напора носителя на трение составят:
8-1,04 = 6,96 м
Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10-3 Па·с, плотность воды – 1000 кг/м3):
Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10-3) = 200000
Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):
λ = 0,316/Re0,25 = 0,316/2000000,25 = 0,015
Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:
l = (Hоб·d) / (λ·[w2/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м
Ответ:требуемая длина трубопровода составит 213,235 м.
Задача 3
В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м3/час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.
Исходные данные:
Расход Q = 18 м3/час = 0,005 м3/с;
длина трубопровода l=26 м;
для воды ρ = 1000 кг/м3, μ = 653,3·10-6 Па·с (при Т = 40°С);
шероховатость стальной трубыε = 50 мкм;
коэффициент трения λ = 0,026;
Δp=0,01 МПа;
ΔH=1,2 м.
Решение задачи:
Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:
∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d5 = (8·26·0.005²)/(9,81·3,14²)· λ/d5 = 5,376·10-5·λ/d5
Выразим диаметр:
d5 = (5,376·10-5·λ)/∆H = (5,376·10-5·0,026)/1,2 = 1,16·10-6
d = 5√1,16·10-6 = 0,065 м.
Ответ: оптимальный диаметр трубопровода составляет 0,065 м.
Задача 4
Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q1 = 18 м3/час и Q2 = 34 м3/час. Трубы для обоих трубопроводов должны быть одного диаметра.
Определите эффективный диаметр труб d, подходящих под условия данной задачи.
Исходные данные:
Q1 = 18 м3/час;
Q2 = 34 м3/час.
Решение задачи:
Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:
d = √(4·Q)/(π·W)
Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.
Для первого трубопровода с расходом Q1 = 18 м3/час возможные диаметры составят:
d1min = √(4·18)/(3600·3,14·1,5) = 0,065 м
d1max = √(4·18)/(3600·3,14·3.0) = 0,046 м
Для трубопровода с расходом 18 м3/час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.
Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q2 = 34 м3/час:
d2min = √(4·34)/(3600·3,14·1,5) = 0,090 м
d2max = √(4·34)/(3600·3,14·3) = 0,063 м
Для трубопровода с расходом 34 м3/час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.
Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.
Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.
Задача 5
В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м3/час. Определите режим течения потока воды в трубе.
Дано:
диаметр трубы d = 0,25 м;
расход Q = 100 м3/час;
μ = 653,3·10-6 Па·с (по таблице при Т = 40°С);
ρ = 992,2 кг/м3 (по таблице при Т = 40°С).
Решение задачи:
Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:
W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c
Значение числа Рейнольдса определим по формуле:
Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10-6) = 216422
Критическое значение критерия Reкр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.
Ответ: режим потока воды – турбулентный.
В курсовой работе
проектируют круглые безоголовочные
трубы. Предварительно проверяют
достаточность заданной насыпи по двум
условиям: по засыпке над трубой; по
возвышению над уровнем воды перед трубой
в расчетный паводок.
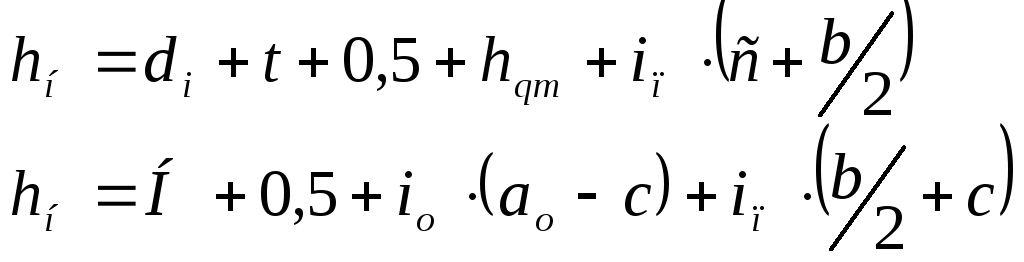
(2.5.1)
где d,
t
– диаметр и толщина стенки круглой
трубы (таблица 2.5.1);
hqm
– толщина монолитных слоев дорожной
одежды, (по заданию);
iп,
iо
– поперечный уклон проезжей части,
обочин;
с
– ширина укрепленной или остановочной
полосы;
а
– ширина обочины;
b
– ширина проезжей части двухполосной
дороги или одного направления дороги
I
категории;
Н
– глубина воды перед трубой, определяется
по заданному расходу и заданному
отверстию трубы по таблице 2.4.
Если окажется, что
полученная по формуле (2.5.1) высота насыпи
больше, чем по заданию, то для дальнейших
расчетов принимают большую высоту.
Высота откоса
насыпи:
,
(2.5.2)
Длина трубы зависит
от ширины дорожного полотна, высоты hон
и заложения откосов m
насыпи.
По ТКП [ ] заложение
откоса принимается 1:4 для дороги категории
I-а,
1:3 для категорий I-б,
I-в,
II,
III,
IV
при высоте насыпи до 3м на дорогах I
и II
категорий и до 2м на дорогах III,
IV
категорий. При большей высоте насыпи
(до 6м) заложение откоса принимается
равным m=1,5
при мелких и пылеватых песках и m=1,75
при супесях, суглинках. При высоте откоса
насыпи более 6м заложение откоса в нижней
части принимается 1:2 при суглинках и
супесях и не изменяется (m=1,5)
при мелких и пылеватых песках.
При применении
звеньев труб длиной 2,5м необходимо
обеспечить засыпку стыка крайних звеньев
грунтом насыпи.
В связи с этим для
труб с отверстием 1,6 и 1,4м заложение
откоса на входе и выходе трубы должно
быть 1:1,5.
Для труб с отверстием
1,0м заложение откоса на входе или на
выходе может быть принято не круче
1:2,1, для труб с отверстием 1,2м не круче
1:1,8.
2.5.1 Определение
длины трубы при заложении откоса насыпи
m=1,5
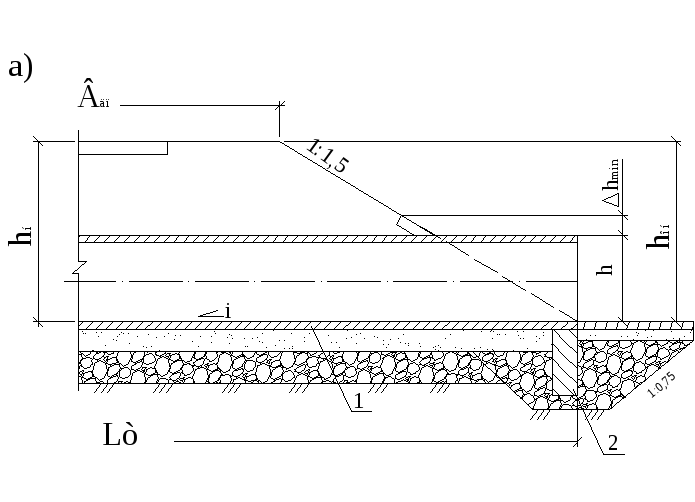
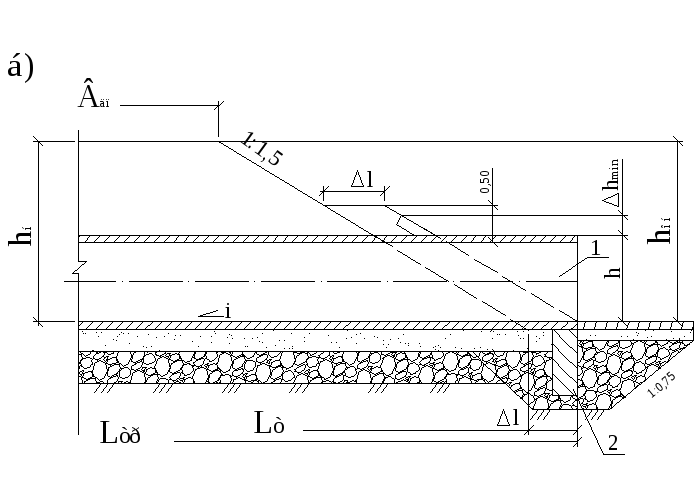
Рисунок 2.5.1 Схема
к определению длины трубы при заложении
откоса m=1,5:
а) теоретической; б) фактической: 1 –
звено трубы; 2 – противофильтрационный
экран
Теоретическая
длина трубы (рис.2.5.1) с откосом насыпи
1:1,5 вычисляется по формуле:
,
(2.5.3)
где
– ширина дорожного полотна, зависит от
категории дороги;
hон
– высота откоса насыпи, определятся по
формуле (2.5.2);
Длина трубы
определяется по формуле:
,
(2.5.4)
где n
– число звеньев трубы.
|
n |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Lтр |
10,12 |
12,62 |
15,12 |
17,62 |
20,12 |
22,02 |
25,12 |
Число звеньев
трубы назначается из условия, чтобы
фактическая длина трубы была равна или
больше теоретической.
Если Lтр
> LT,
то принимают длину трубы равной
фактической Lтр,
полученной по формуле (2.5.4), отодвигая
противофильтрационный экран от подошвы
насыпи на входе на величину
(рисунок 2.5.1), равную
,
(2.5.5)
Если полученное
значение
больше 1,5м, то целесообразно вход и выход
трубы отодвинуть от подошвы насыпи на
расстояние:
,
(2.5.6)
Вычислим верховую
и низовую часть трубы. При смещении
трубы на входе длина трубы от оси дороги
до входа определяется по формуле (2.5.7),
а до выхода по формуле (2.5.8) с учетом
продольного уклона трубы i
и заложения откосов.
,
(2.5.7)
,
(2.5.8)
где i
– продольный уклон трубы (по заданию);
m
– заложение откоса насыпи у трубы.
При смещении трубы
от подошвы на входе и на выходе верховая
и низовая части трубы вычисляются по
формулам:
,
(2.5.9)
,
(2.5.10)
Пример 2.5.1
Исходные данные:
дорога III
технической категории (=12,0м).
Высота насыпи 4,16м. Заложение откоса
1:1,5. Уклон трубы 0,010.
Требуется определить
общую длину трубы и ее составляющие
(верховую и низовую).
По формуле (2.5.2)
вычислим высоту откоса насыпи:
.
Теоретическую
длину трубы по формуле (2.5.3):
.
Из формулы (2.5.4)
следует, что при 9 звеньях длина трубы
Lтр
= 22,02м , что
недостаточно. При n=10
длина трубы Lтр
= 25,12м, что
больше теоретической на
.
Сместим начало трубы от подошвы насыпи
на.
Тогда длина верховой части трубыL1
и низовой L2:
,
.
2.5.2 Определение
длины трубы при заложении откоса m>1,5
Заложение откосов
низких насыпей принимают по безопасности
движения m=3
или m=4,
высоких насыпей по устойчивости откосов
при глинистых грунтах m=1,75
при высоте насыпи до 6м и m=2
при высоких насыпях (нижняя часть).
Предельная крутизна
укрепленного откоса m=1,5,
поэтому для уменьшения длины трубы
перемещаем ее начало и конец от подошвы
насыпи к оси дороги (рис. 2.5.2), принимая
откос насыпи у трубы с заложением 1:1,5.
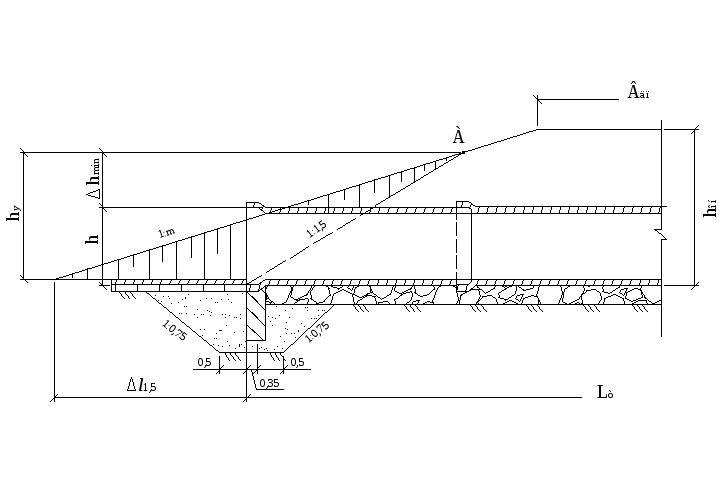
Рисунок 2.5.2 Схема
к определению длины трубы при m>1,5
Высота укрепления
откоса насыпи у трубы на выходе:
,
(2.5.11)
где d,
t
– внутренний диаметр трубы, толщина
стенки, определяется по таблице 2.5.1.
Таблица 2.5.1
|
Диаметр |
1,0 |
1,2 |
1,4 |
1,6 |
2,0 |
|
Толщина |
13 |
14 |
15 |
16 |
15 |
|
Толщина |
23 |
23 |
23 |
21 |
22 |
Если глубина воды
перед трубой
,
то и на входе высота укрепления откоса
определяется по формуле (2.5.10). Если же,
то высота укрепленного откоса на входе
определяется по формуле:
,
(2.5.11)
При вычислении
теоретической длины трубы примем
.
Назначим сопряжение откосов с заложением
1:m
и 1:1,5 (точка А
на рис.2.5.2) на высоте укрепления откоса
с заложением 1:1,5. Тогда теоретическая
длина трубы при высоте откоса насыпи
до 6м определяется по формуле:
,
(2.5.12)
где Вдп
– ширина дорожного полотна, зависит от
категории дорог;
hон
– по формуле (2.5.2);
hy,1
– высота укрепления откоса ().
Если высота откоса
насыпи у трубы
hон>6м,
,
то теоретическая длина трубы:
,
(2.5.13)
где m,
m1
– заложение откоса верхней части насыпи
и нижней (m1=1,75,
m2=2,0).
Если высота откоса
насыпи
и
,
то теоретическая длина трубы:
,
(2.5.14)
Фактическую длину
трубы вычислим по формуле:
,
(2.5.15)
где n
– число звеньев, определяется подбором.
При подборе числа
звеньев возможны два варианта, отличающиеся
по длине трубы на 2,5м (на одно звено).
Вариант 1. Длина
трубы меньше теоретической
.
Смещаем точку пересечения откосов вверх
(рис. 2.5.3) на величину.
,
(2.5.16)
Проверяют
достаточность высоты откоса для
размещения точки сопряжения А:
,
(2.5.17)
Длина верховой
части трубы (до оси дороги) и низовой
вычисляется по формулам:
;
,
(2.5.18)
Если условие
(2.5.17) не выполнено, то рассматривают
вариант 2,
когда длина
трубы больше теоретической, определенной
по формуле (2.5.12)
.
При варианте 2 и
отверстии трубы 1,6 или 1,4м отодвигают
противофильтрационный экран к подошве
насыпи на величину
.
Длина части трубы на входе и на выходе
считается от оси дороги, определяется
по формулам (2.5.9) и (2.5.10).
В случае отверстия
1,0 и 1,2м уполаживают откос от точки А
(рис. 2.5.2) до начала (конца) трубы.
Пример 2.5.2
Исходные данные:
дорога II
технической категории. Высота откоса
насыпи 3,0м. заложение откоса 1:3. отверстие
трубы 1,2м, глубина воды перед трубой
1,2м.
Требуется определить
длину трубы.
Высота укрепления
откоса насыпи на входе:
;
.
Принимаем
.
На выходе
,
.
Примем заложение
откоса на высоту укрепления 1:1,5, а на
остальной части 1:3.
Теоретическая
длина трубы:
.
Если принять 10
звеньев, то длина трубы 25,12м. что меньше
теоретической
на величину
.
Примем длину трубы 25,12м, придвинув откос
с заложением 1:1,5 на величину.
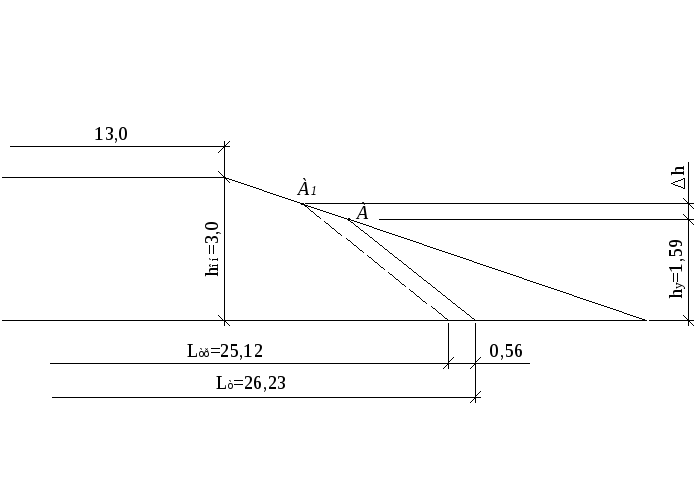
Рисунок 2.5.3 Схема
к примеру 2.5.2
Откос с заложением
1:1,5 к оси на величину
(рис. 2.5.2). Точка сопряжения откосов с
заложением 1:3 и 1:1,5 поднимется на величину:
.
Она находится ниже
бровки обочины, так как выполняется
условие:
,
т.е. 3,0 >
1,96м
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
31.05.2015401.92 Кб55n1.doc
- #
- #
- #
- #
Расчёт линейного теплового расширения труб выполняется для определения прироста длины участка трубопровода при нагреве, необходимости устройства компенсатора температурных удлинений и определения потребной компенсирующей способности.
Прирост длины участка трубопровода при температурном расширении определяется по формуле:
dL = a · l · (tmax – tc), мм
a – коэффициент линейного теплового расширения, °C-1, его величина зависит от физических свойств материала.
tmax — максимальная температура теплоносителя в трубопроводе, °C.
tс — температура окружающей среды в момент монтажа трубопровода, °C.
l — длина участка трубопровода, м.
Водопроводные, отопительные, канализационные, дымоходные, обсадные, медные, стальные, пластиковые, металлопластиковые, узкие, широкие — трубы разного назначения из различных материалов окружают нас повсюду. Необходимость проложить новые коммуникации или заменить старые возникает и во время строительства дома, и при текущем ремонте. Составляя проект предстоящих работ, не помешает вооружиться калькулятором, чтобы провести расчет веса трубы, ее массы, объема и прочих параметров.
Зачем нужно рассчитывать параметры труб?
Предварительный расчет параметров труб необходим во многих случаях. Например, для правильной коммуникации трубопровода с другими элементами системы. Проектировщики и монтажники при работе с трубами используют такие показатели, как:
- проходимость трубопровода;
- потери тепла;
- количество утеплителя;
- количество материала для защиты от коррозии;
- шероховатость внутренней поверхности трубы и т. п.
В результате можно определить точное количество труб, необходимых для конкретной системы, а также их оптимальные характеристики. Правильные расчеты избавляют от избыточных расходов на приобретение и транспортировку материала, позволяют веществам, которые находятся в трубопроводе, перемещаться с заданной скоростью для максимально эффективного использования системы.
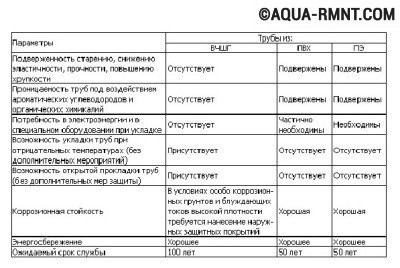
В этой таблице приведены некоторые полезные сведения о характеристиках труб разного вида, которые помогут выбрать подходящие конструкции, необходимые для создания трубопровода
В отопительных системах диаметр труб существенно зависит от допустимой скорости. Пример такого рода расчетов представлен на видео:
Расчеты различных параметров трубы
Для того, чтобы правильно рассчитать основные параметры труб, следует определить следующие показатели:
- материал, из которого изготовлена труба;
- тип сечения трубы;
- внутренний и внешний диаметр;
- толщина стенок;
- длина трубы и т. п.
Часть данных можно получить, просто измерив конструкцию. Множество полезных сведений содержится в сертификационных документах, а также в различных справочниках и ГОСТах.
Как узнать диаметр и объем трубы?
Некоторые формулы расчетов знакомы каждому школьнику. Например, если нужно уточнить диаметр конкретной трубы, следует измерить ее окружность. Для этого можно воспользоваться сантиметровой лентой, которой пользуются швеи. Или же следует обернуть трубу другой подходящей лентой, а затем измерить полученный отрезок с помощью линейки.
Далее используем формулу длины окружности:
L=πD, где:
- L — длина окружности круга;
- π — постоянное число «пи», равное примерно 3,14;
- D — диаметр окружности круга.
Достаточно проделать несложное преобразование, чтобы вычислить с помощью этой формулы внешний диаметр трубы:
D=L/π.
Измерив толщину стенок трубы, легко рассчитать также внутренний диаметр круга. Для этого от значения внешнего диаметра трубы следует отнять удвоенное значение толщины стенок трубы.
Расчет сечения трубы
Чтобы рассчитать сечение трубы, следует вычислить площадь круга. При этом учитывается разница между наружным диаметром трубы и толщиной ее стенок, проще говоря — внутренний диаметр трубы.
На этом рисунке наглядно представлены такие показатели как наружный диаметр трубы и толщина ее стенки. Разница между наружным диаметром и толщиной позволяет вычислить внутренний диаметр трубы
Формула площади круга выглядит так:
S=πR², где:
- S — площадь круга;
- π — число «пи»;
- R — радиус круга, рассчитывается как половина диаметра.
Если используются сведения о наружном диаметре и толщине стенок трубы, то формула может выглядеть следующим образом:
S=π(D/2-T)², где:
- S — площадь сечения;
- π — число «пи»;
- D — наружный диаметр трубы;
- T — толщина стенок трубы.
Допустим, имеется труба, внешний диаметр которой составляет 1 метр, а толщина стенок равна 10 мм. Для начала следует согласовать все единицы измерения. Толщина стенок составит 0,01 метра. Согласно приведенной выше формуле рассчитаем сечение такой трубы:
S=3,14Х(1м/2-0,01м)²=0,75м²
Таким образом, сечение трубы с указанными параметрами будет равно 0,75 кв. м.
Как известно, точность вычислений с числом «пи» зависит от количества знаков после запятой, которые используются при применении этой константы. Однако в строительстве обычно нет нужды в сверхточных расчетах, и число «пи» принимается равным 3,14. Конечный результат также имеет смысл округлять до двух знаков после запятой.
Как рассчитать объем трубы?
На этой схеме наглядно отражено использование таких данных как радиус сечения трубы и ее длина для определения объема трубы
Выполнить расчет объема конкретного отрезка трубы также не сложно. Для этого нужно сначала найти площадь окружности трубы по ее внешнему диаметру по формуле, приведенной выше:
S=π(D/2)² или S=πR²
В этом случае D — это внешний диаметр трубы, а R – внешний радиус, т. е. половина диаметра. После этого полученное значение нужно умножить на длину отрезка трубы, получив объем, который выражается в кубических метрах. Формула расчета объема трубы может выглядеть так:
V=SH, где
- V — объем трубы, куб. м.
- S — площадь внешнего сечения, кв.м.;
- H — длина отрезка трубы, м.
Допустим, имеется труба с внешним диаметром 50 см и длиной 2 метра. Сначала следует согласовать все единицы измерения. D=50 см=0,5 м. Подставим это значение в формулу площади круга:
S=π(D/2)²=3,14(0,5/2)²=0,0625 м²
Теперь можно вычислить объем:
V=SH=0,0625Х2=0,125 м³.
Все эти расчеты можно легко проделать с помощью обычного калькулятора, однако гораздо более удобно использовать соответствующую вычислительную машину, осуществляющую расчёт в режиме онлайн: https://calcsoft.ru/obyom-cilindra.
Калькулятор проводит вычисления в зависимости от начальных данных: радиус основания и высота, диаметр основания и высота или площадь основания и высота.
Как рассчитать массу трубы?
Информация о весе конкретного количества труб необходима, чтобы спрогнозировать расходы на их транспортировку. Если используется большая конструкция, ее вес не помешает соотнести с несущей способностью фундамента знания.
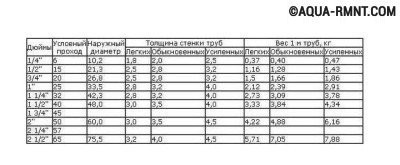
В этой таблице указаны справочные данные о весе стальных труб различного вида с учетом их размеров и особенностей технологии производства
Ученикам средних классов хорошо известно, что найти массу объекта можно путем умножения его объема на плотность вещества, из которого этот объект состоит. Строители избавлены от утомительных вычислений массы конкретного отрезка трубы, поскольку в различных строительных справочниках содержится информация о весе погонного метра самых различных видов труб. Проще всего выполнить расчет массы трубы с помощью соответствующих ГОСТов, используя информацию о:
- материале, из которого изготовлена труба;
- ее внешнем диаметре;
- толщине стенок;
- внутреннем диаметре и т. п.
Выяснив вес одного погонного метра трубы, следует умножить полученное значение на общее количество погонных метров. Сложность задачи соответствует уровню четвертого-пятого класса общеобразовательной школы.
Для выяснения веса труб предлагаем вам воспользоваться нашим онлайн-калькулятором. В соответствующие поля вводят необходимые сведения, после чего программа выдает значение веса заданного количества труб.
Как определить площадь внешней поверхности трубы?
При монтаже самых различных систем может потребоваться утепление трубопровода. Чтобы максимально точно определить необходимое количество теплоизолирующего материала или другого необходимого покрытия (антикоррозионного, гидроизоляционного и т.п.), рекомендуется вычислить площадь внешней поверхности трубы.
Чтобы правильно рассчитать количество материала, необходимого для утепления трубы, следует вычислить площадь ее наружной поверхности. Для этого длину окружности наружного сечения следует умножить на длину трубы
Любую трубу круглого сечения можно мысленно представить как прямоугольник, который свернули в трубочку. Площадь прямоугольника определяется как произведение его длины и ширины. В случае с трубой длине прямоугольника будет соответствовать длина трубы, а его ширине — длина ее внешней окружности.
Формула длины окружности уже упоминалась в начале, она выглядит как L=∏D. Обозначим длину отрезка трубы как H. Тогда площадь наружной поверхности трубы будет равна:
St=πDH, где:
- St — площадь внешней поверхности трубы, кв.м.;
- π — постоянное число «пи», равное 3,14;
- D — внешний диаметр трубы, м;
- H — длина трубы, м.
Например, если имеется труба диаметром 30 см и длиной 5 метров, площадь ее поверхности будет равна:
St=πDH=3,14Х0,3Х5=4,71 кв.м.
Используя приведенные выше формулы, можно без труда сделать расчет объема внутреннего пространства трубы и площадь ее внутренней поверхности. Для этого в расчетах достаточно заменить значение внешнего диаметра трубы на величину ее внутреннего диаметра.
А если сечение трубы не круглое?
Все формулы и расчеты, описанные ранее, рассматривают исключительно трубы с круглым сечением. Действительно, в современном строительстве чаще всего используются именно такие конструкции. Однако существуют трубопроводы с:
- прямоугольным;
- овальным;
- трапециевидным сечением и т. п.
Для расчета таких нестандартных труб рекомендуется использовать ряд простых формул. Так, площадь квадратного или прямоугольного сечения определяется как произведение длины и ширины. Умножив площадь на длину отрезка трубы, можно вычислить объем трубы. Чтобы найти площадь поверхности трубы прямоугольного сечения, следует перемножить длину отрезка трубы и периметр сечения. Периметр, как известно, это сумма всех сторон прямоугольника.
Трубы с прямоугольным или трапециевидным сечением чаще всего применяются при создании дымоходов и канализационных систем. Для расчета основных параметров таких труб используют несколько простых формул
Периметр трапеции также вычисляется как сумма всех ее сторон. Умножаем эти данные на длину отрезка трубы и получаем площадь поверхности трубы. Чтобы рассчитать объем трубы с трапециевидным сечением, нужно сначала найти площадь трапеции. Она рассчитывается как произведение полусуммы ее оснований и высоты:
S=0,5(A+B)H, где:
- А и В — длина оснований трапеции, т. е. ее параллельных сторон;
- Н — высота трапеции, т. е. перпендикуляр, проведенный от одного основания к другому.
Умножив площадь трапециевидного сечения на длину отрезка трубы, получаем ее объем.
Чтобы рассчитать параметры трубы с овальным сечением, действуют примерно так же. Вычисляют длину окружности овала, а также его площадь. Умножив длину окружности на длину отрезка трубы, получим поверхности трубы. Произведение площади овального сечения и длины отрезка трубы даст значение объема трубы.
Овал имеет две оси: большую и малую. Длина окружности овала (или эллипса) рассчитывается как произведение числа «пи» на сумму длин его полуосей:
L=πХ(А+В), где:
- ∏ — постоянное число «пи», равное 3,14;
- А и В — длина полуосей овала.
Площадь овала рассчитывается как произведение его полуосей и числа «пи»:
S=πАВ.
Чтобы избежать сложных расчетов, можно воспользоваться многочисленными он-лайн калькуляторами, которые позволяют рассчитать параметры труб самых разных конфигураций.
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(4 голоса, среднее: 5 из 5)
Поделитесь с друзьями!