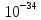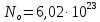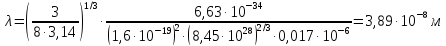Пример
решения задачи
Задача.
Вычислить длину свободного пробега
электронов в меди при T=300
К, если ее удельное сопротивление при
этой температуре равно 0,017 мкОм/м.
Дано:
Решение:
T=300
К Согласно представлениям
квантовой теории,
ρ=0,017мкОм/м
удельная проводимость металлов γ
связана с длиной
λ
— ? свободного пробега
электронов λ соотношением
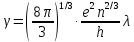
а
по определению ρ
=
Следовательно,
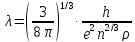
где
е = 1,6∙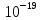
h
= 6,63∙
Дж∙с – постоянная Планка
Концентрация
свободных электронов в меди равна
концентрации атомов

где
d
– плотность меди, d
= 8920
– число
Авогадро,
А
– атомная масса, А = 63,54∙
Ответ:
λ=3,89∙
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- | Печать |
Вместо того чтобы использовать площадь для описания взаимодействия мы можем использовать длину, так как расстояние которое проходит электрон между взаимодействиями с атомами имеет большое значение, когда мы используем тонкие образцы. Этот новый параметр является тем средним расстоянием, которое электрон проходит между актами рассеяния. Это расстояние важно, зная его, мы можем вычислить насколько тонкие мы должны сделать наш образцы, так чтобы множественное рассеяние не является значительным, что позволяет легче интерпретировать получаемые изображения и спектроскопические данные с использованием теории однократного рассеяния. Термин σtotal может быть выражен как обратная длина свободного пробега λ. Поскольку размерность σtotal являются м-1, есть простое выражение для длины свободного пробега, которое имеет размерность длины

Типичные значения λ для рассеяния при типичных для ПЭМ ускоряющих напряжениях составляют порядка десятков нанометров, поэтому приближение однократного рассеяния применимо для образов толщиной этого порядка. К сожалению, для длины свободного пробега принято использовать обозначение λ, не надо путать это обозначение с длиной волны электрона. Из уравнения 2.9 мы можем определить вероятность рассеяния p, при прохождении электроном через образец толщиной t

где (σtotal) из уравнения 2.8.
Хотя вычислительные ресурсы постоянно совершенствуются наши знания о значениях σ, λ, и θ неточны в лучшем случае, в частности, для 100-400 кэВ энергий пучков, используемых в ПЭМ. Мы можем объединить все наши знания о рассеянии, для предсказания путей в пучке электронов рассеивающихся в тонкой фольге, путем моделирования методом Монте Карло.
Рисунок 2.4 показывает, рассчитанные методом Монте-Карло пути электронов через тонкую фольгу из меди и золота.
Длина — свободный пробег — электрон
Cтраница 1
Длина свободного пробега электрона обратно пропорциональна вероятности рассеяния электр она внутри кристаллической решетки полупроводника. Мерой такой вероятности служит степень отступления от строгой периодичности идеальной кристаллической решетки.
[1]
Длина свободного пробега электронов, вычисленная из формул классической электронной теории, оказывается на несколько порядков больше межатомного расстояния, что противоречит основным представлениям теории.
[2]
Длина свободного пробега электронов весьма мала. Поэтому электроны под действием поляне успевают приобрести большой скорости; их средняя скорость упорядоченного ( создаваемого полем) движения и во много раз меньше средней скорости v их теплового движения.
[3]
Длина свободного пробега электронов в металле определяется волновыми свойствами электронов.
[4]
Длина свободного пробега электрона в пленке ограничивается не только ее поверхностью, но и структурными дефектами. На структуру пленки влияет температура подложки в момент осаждения, поэтому удельное сопротивление зависит от температуры подложки, уменьшаясь с возрастанием температуры. Снижение удельного сопротивления наблюдается у пленок, полученных на холодной подложке после прогрева в вакууме. Температура структурных превращений пленок близка к температуре рекристаллизации металла и существенно зависит от толщины пленок. Степень изменения удельного сопротивления после прогрева у тонких пленок более велика, чем у толстых.
[5]
Газокинетическая длина свободного пробега электрона Ае дает лишь приближенное представление о движении электронов в газе. Qe) оказывается зависящим также от скорости движения ( энергии) электронов. Здесь скорость электрона V3 см / сек связана с энергией электрона U3 эв соотношением v3 6 107 Уиз.
[7]
Если длина свободного пробега электронов превышает расстояние между электродами, то движение электронов можно рассматривать как свободное. Теплопередача сводится к переносу энергии электронами и к лучеиспусканию.
[8]
Понятие длина свободного пробега электронов и ее зависимость от кинетической энергии теряет смысл для таких ионных полупроводников, в которых длина пробега оказывается меньше межатомных расстояний. Длина волны электронов здесь превышает размеры рассеивающих центров, а неопределенность в значении кинетической энергии на порядок величины больше самой энергии.
[9]
Обычно длина свободного пробега электрона в полупроводнике значительно меньше толщины электронно-дырочного перехода. Если за время свободного пробега электроны успевают набрать достаточную энергию, то возникает ударная ионизация атомов электронами. Поскольку скорость электронов, определяющая их энергию, зависит от напряженности электрического поля: vn inE, для ударной ионизации необходима определенная величина этой напряженности.
[10]
Когда длина свободного пробега электрона начинает ограничиваться примесями и дефектами, она становится температурно независящей и сопротивление, которое и называется остаточным, становится практически постоянной величиной. В неупорядоченных сплавах даже при комнатной температуре сопротивление может обусловливаться главным образом неоднородностями.
[11]
Если длина свободного пробега электронов превышает расстояние между электродами, то движение электронов можно рассматривать как свободное. Теплопередача сводится к переносу энергии электронами и к лучеиспусканию.
[12]
Конечность длины свободного пробега электрона обусловлена неидеальностью решетки и взаимодействием электронов. Неидеальность же решетки, в свою очередь, связана с наличием примесей и искажений, а также с тепловыми колебаниями решетки. Таким образом, следует различать три основных механизма рассеяния электронов — рассеяние электронов примесными атомами, рассеяние электронов колебаниями решетки и рассеяние электронов электронами.
[13]
Вычисление длины свободного пробега электронов проводимости в металлах при комнатной температуре дает величину в несколько сотен ангстрем. Таким образом, в этом интервале толщин электроны проводимости в пленках будут чаще сталкиваться с поверхностью пленки, чем с другими центрами рассеяния, и рассеяние на поверхности становится важным механизмом для сопротивления. Так как этот механизм рассеяния не чувствителен к деформации, в целом чувствительность к деформации уменьшается. Если еще дальше уменьшать толщину пленки, пленка перестает быть сплошной, и общее сопротивление начинает определяться сопротивлением участков между отдельными островками.
[15]
Страницы:
1
2
3
4
Очевидно, что конкретный механизм рассеяния электронов играет для термоэлектричества важную роль. Можно, например, предположить, что электроны, имеющие большую скорость, должны рассеиваться атомами решетки под меньшими углами, чем электроны с меньшей скоростью. Другими словами, средняя длина свободного пробега электронов будет зависеть от их кинетической энергии. Это верно в целом, но конкретная взаимосвязь длины пробега и энергии сложна и сильно зависит от электронной структуры решетки. Сложность связи между длиной пробега и энергией электронов не дает возможности получить количественное описание термоэлектричества, хотя качественно картина явления проста. Другими словами, наших сведений о поверхности Ферми реального металла недостаточно для вычисления термо-э.д.с. Следует отметить, что для полупроводников ситуация проще, поскольку число электронов и дырок, участвующих в процессе проводимости, значительно меньше. В этом случае модель электронного газа, в которой частицы подчиняются статистике Максвелла — Больцмана, лучше отражает истинную природу явления. [c.268]
Полагаем, что движение электрона, как частицы с массой Ше и зарядом е, под действием поля Е и ускоряющей силы еЕ происходит в течение времени т = «к/, где v — средняя квадратичная скорость электрона (тепловая, так как скоростью дрейфа пренебрегаем из-за сравнительной малости), а «к — средняя длина свободного пробега электрона (пробег). Движение с ускорением еЕ/т за время т разгонит электрон до скорости дрейфа [c.33]
Средняя длина свободного пробега электрона в газе определяется выражением [c.111]
Значения средней длины свободного пробега электрона в воздухе (при 20°С) и в вакууме приведены ниже [c.111]
Заметим, что в реальной ситуации отношение Кэл/а оказывается величиной постоянной, не зависящей ни от сорта металла, ни от температуры, только при комнатных и более высоких температурах. В промежуточной области температур (между низкими и обычными) указанное отношение зависит от сорта металла й от температуры, поскольку теплопроводность в этой области меняется с температурой не так быстро, как это следует из закона Видемана — Франца, если определять теплопроводность металлов по их электропроводности. Это отклонение от закона Видел. на — Франца связано с тем, что средние длины свободного пробега электронов, соответствующие тепло- и электропроводности, вообще говоря, различны, а не одинаковы, как это предполагается в теории. Они с достаточно большой точностью равны только при высоких температурах. [c.195]
В отличие от диэлектриков, где длина свободного пробега фононов при низких температурах, в основном, определяется размерами образца, Б металлах длина свободного пробега электронов при этих температурах определяется дефектами и примесями. Это связано с тем, что энергия электронов (вблизи энергии Ферми), переносящих теплоту, слабо зависит от температуры [формула (6.57)]. Длина волны де Бройля Х=И/(mv ) таких электронов — порядка средних межатомных расстояний, поэтому электроны сильно рассеиваются на дефектах атомных размеров и средняя длина свободного пробега <Хэл> ограничена этими размерами. [c.196]
В собственном полупроводнике, где нет никаких примесей и дефектов, время релаксации определяется рассеянием носителей на фононах. При обсуждении закона Видемана — Франца мы отмечали (гл. 6), что средняя длина свободного пробега электрона обратно пропорциональна концентрации фононов [формула (6.103)], которая, в свою очередь, в области высоких температур пропорциональна температуре. Таким образом, [c.250]
Электрические свойства. По электропроводности аморфные металлы ближе к жидким металлам, чем к кристаллическим. Удельное сопротивление р аморфных металлических сплавов при комнатной температуре составляет (1—2) 10- Ом-см, что в 2—3 раза превышает р соответствующих кристаллических сплавов. Это связано с особенностями зонной структуры аморфных металлов. В кристаллических металлах длина свободного пробега электрона составляет примерно 50 периодов решетки даже при Т, близкой к температуре плавления. Отсутствие дальнего порядка в металлических стеклах обусловливает малую длину свободного пробега, соизмеримую с межатомным расстоянием. Следствием этого является повышенное удельное сопротивление и слабая зависимость его от температуры. [c.373]
Во-вторых, при помещении тонкого образца в магнитное попе наблюдается более сложное проявление масштабного эффекта, которое было уже упомянуто ранее. В этом случае в рассмотрение дополнительно вводится радиус R орбиты электрона в магнитном попе и задача сводится к исследованию геометрического (и потому классического) соотношения между В, I и а. При этом удается получить сведения не только относительно I, но также и относительно орбиты R, а следовательно, и об импульсе свободных электронов. В тех случаях, когда нет необходимости пользоваться чрезвычайно тонкими образцами металла и прилагать очень сильные магнитные поля, исследования масштабного эффекта следует производить при низких температурах, чтобы достигнуть возможно большей длины свободного пробега электронов. [c.204]
Согласно этой формуле, сопротивление тонкой проволоки не зависит от средней длины свободного пробега электронов в массивном образце ме-талла ). Подобным же образом при о// < 1, где о— глубина проникновения высокочастотного поля (угловой частоты ш), наблюдаемое сопротивление становится независимым от сопротивления массивного металла, измеренного при постоянном токе, в то время как по классической теории при высоких частотах оно должно быть пропорционально [c.209]
При деформациях этой поверхности заключенный в ней объем остается неизменным эти деформации имеют симметрию бриллюэновской зоны и направлены наружу вдоль тех направлений, по которым границы зоны ближе всего к центру зоны. В работе [70] предполагалось, что такие деформации уменьшают среднюю длину свободного пробега электрона при диффузии к противоположной точке поверхности и, следовательно, увеличивают горизонтальную диффу.зию по сравнению с вертикальным движением, вызывая тем самым отклонение /) > 1. [c.270]
Классическая теория не объясняет большой величины длины свободного пробега электронов в металлических кристаллах и не отвечает на вопрос почему электроны проводимости ведут себя подобно газу невзаимодействующих частиц Поскольку ионы расположены в правильной периодической решетке, то электронные волны, как и во всякой периодической структуре, распространяются свободно. Второй важный момент, а именно то, что электроны проводимости лишь редко испытывают рассеяние на других электронах (свободных), обусловлен действием принципа Паули. [c.104]
Таким образом, электрические свойства аморфных сплавов согласуются с представлениями о том, что из-за потери трансляционной симметрии в аморфных сплавах длина свободного пробега электронов становится существенно меньше, чем в кристаллических. В то же время проводимость остается металлической, что указывает по-прежнему на высокую плотность состояний электронов в окрестности уровня Ферми. [c.288]
Рассеяние на тепловых колебаниях решетки (на фононах). Подобно тому, как электромагнитное поле излучения можно трактовать как набор световых квантов — фотонов, так поле упругих колебаний, заполняющих кристалл, можно считать совокупностью квантов нормальных колебаний решетки — фононов. Средняя длина свободного пробега электронов должна, очевидно, быть обратно [c.60]
Электрическая прочность Е р газов сильно зависит от давления (рис.4.21). При высоких давлениях р увеличение Е р связано с уменьшением длины свободного пробега электронов, а при малых р — с уменьшением вероятности столкновений электронов с молекулами газа. [c.119]
При малых h электрическая прочность сильно увеличивается потому, что развитие процессов ионизации затрудняется из-за малой общей длины свободного пробега электронов. [c.174]
Температурный коэффициент удельного сопротивления металлов. Число носителей заряда (концентрация свободных электронов) в металлическом проводнике при повышении температуры практически остается неизменным. Однако вследствие усилений колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т. е. уменьшается средняя длина свободного пробега электрона X, уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рис. 7-2). Иными словами, температурный коэффициент (см. стр. 39) удельного сопротивления металлов (кельвин в минус первой степени) [c.192]
По Я и. Френкелю длина свободного пробега электронов об-ратна коэффициенту рассеяния электромагнитной волны 1=1/цр. [c.9]
Удобно пользоваться понятием длины свободного пробега электронов [c.182]
В области высоких температур основное значение имеет рассеяние электронов на тепловых колебаниях решетки — на фононах. Поэтому средняя длина свободного пробега электронов должна быть обратно пропорциональна концентрации фононного газа X оз ]/пф. Так как, согласно данным табл. 4.1, в области высоких температур Пф Ой Т, то X со 1/Т. Подставляя это в (7.12) и (7.14), получаем для невырожденного газа [c.184]
В области низких температур концентрация фононного газа согласно данным табл. 4.1 пропорциональна Р. Поэтому длина свободного пробега электронов, обусловленная рассеянием их на фо-нонах, должна быть обратно пропорциональна Т [c.187]
Однако это соотношение не учитывает следующего важного обстоятельства. При низких температурах средний импульс фононов оказывается настолько небольшим по сравнению с импульсом электронов проводимости, что для уничтожения движения электрона в данном направлении требуется не один, а v актов рассеяния его на фононах. Как показывает расчёт, v Т . Поэтому эффективная длина свободного пробега электрона на протяжении которой происходит хаотизация его движения, равна [c.187]
Длину свободного пробега электронов Я можно определить из выражения для подвижности и = qk/nin <С У >. При и = 10 mV(B- с) и 1Пп = т 1 л 6 10 м. Отсюда следует, что формулой (10.1) можно пользоваться для подсчета проводимости диэлектрических слоев толщиной от сотых долей микрометра до d L. [c.274]
Во многих случаях аморфные металлические сплавы упорядочиваются ферромагнитно, несмотря на то, что их кристаллические аналоги являются антиферромагнитными. Это свидетельствует о том, что при аморфизации структуры может измениться характер обменного взаимодействия. Выше отмечалось, что разупорядочива-ние атомной структуры приводит к уменьшению длины свободного пробега электронов проводимости, которая в аморфных металлах и сплавах может иметь порядок межатомного расстояния. Это означает, что значительно понижается вклад обменного взаимодействия через электроны проводимости. [c.374]
Зондгеймер считает, что по существу в проводниках наблюдается три широких класса явлений, в которых обнаруживается масштабный эффект. Во-первых, это наиболее простое проявление масштабного эффекта, заклю-чающ,ееся в возрастании удельного сопротивления образцов, представляющих собой очень тонкие проволочки или фольги (ленточки), по сравнению со значением, которое оно имеет в массивном образце. Такое увеличение возникает вследствие ограничения нормальной средней длины свободного пробега электронов благодаря рассеянию па границах образца и может быть использовано для определения отношения I к физическому размеру образца а. [c.204]
Интерпретация экспериментов по измерению сопротивления ) очень затруднительна по двум причинам. Первая из них связана с тем, что в сверхпроводящем состоянии проводимость обусловлена только нормальными электро 1амц, вследствие чего для вычисления о необходимо использовать двухжидкостную модель. Вторым источником трудностей является сложность теории проводимости даже для нормального состояния, что объясняется очень большой длиной свободного пробега электронов в нормальном состоянии по сравнению с глубиной скин-слоя. В результате для описания нормальной проводимости необходимо пользоваться более сложной теорией аномального скин-эффекта [178]. Таким образом, для объяснения рассмотренных экспериментов необходимо применить двухжидкостиую модель к усложненной теории проводимости. Поэтому мы можем рассчитывать лишь на качественное соответствие теории и опыта. В частности, нужно отметить, что наблюдаемая на опыте зависимость поверхностного сопротивления от частоты противоречит теории (см. гл. IX, п. 34). [c.649]
Экспериментальные доказательства необходимости упомянутой связи не очень многочисленны, но весьма убедительны. Во-первых, это—изменение глубины проникновения магнитного поля с концентрацией примесей индия (последняя изменяется от нуля до 3% см. гл. VIII). Наблюдалось уменьшение глубины проникновения почти в 2 раза, хотя в критической температуре не было заметно почти никакого изменения. По мнению Пиннарда, изменение глубины проникновения поля означает уменьшение длины свободного пробега электронов благодаря наличию примесей атомов индия и соответствующее уменьшение длины когерентности. Во-вторых, это—изменение глубины проникновения поля в монокристалле олова в зависимости от его ориентации ). Глубина проникновения имеет максимум, когда угол 6 между осью кристалла и осью четвертого порядка равен 60° и уменьшается для всех других углов (см. гл. VIИ). Это изменение не может быть объяснено предположением о тензорном характере параметра Л в уравнении Лондона, поскольку такое предполоягение приводило бы к монотонной зависимости от величины угла. Пиппард наблюдал соответствующее изменение в высокочастотном сопротивлении нормального олова, что опять не может быть объяснено простым учетом тензорного характера проводимости для объяснения приходится привлекать теорию аномального скин-эффекта. В последнем случае средняя длина свободного пробега электрона больше толщины скин-слоя, так что электрическое поле, действующее на электрон, существенно изменяется на протяжении длины свободного пробега. В-третьих, это—зависимость глубины проникновения поля от параметров металла данная зависимость будет рассмотрена позднее с позиции модифицированной теории Пиппарда (см. п. 26). [c.705]
Энергия оже-пика характеризует данный атом, поэтому анализ спектров оже-электронов позволяет получить информацию о составе приповерхностной области твердого тела, откуда происходит ЭОЭ. Энергия оже-электронов лежит в диапазоне 30—2000 эВ. Средняя длина свободного пробега электронов с такими же энергиями составляет 0,5—2 нм, так что спектры оже-электронов отражают свойства приповерхностного слоя толщиной до пяти монослоев. Амплитуда оже-пика пропорциональна концентрации ато.мов данного сорта на поверхности твердого тела и эффективности оже-переходов, которая характеризуется величиной, называемой оже-чувстви-тельностью. Она определяется числом вторичных оже-электронов с данной энергией, испущенных данным элементом, в расчете на число первичных электронов и зависит от энергии первичных электронов. Анализ спектров оже-электронов лежит в основе электронной оже-спектроскопии (ЭОС) — основного метода изучения состава поверхности твердых тел. [c.587]
При больших давлениях и соответственно повышенной плотности газа расстояние между отдельными молекулами становится меньше тем самым уменьшается длина свободного пробега электронов и, как следует из формулы (4-4), для того чтобы пробои произо-П-ел, должна быть увеличена напряженность поля. [c.63]
Теорию электрического пробоя можно применить к жидкостям, максимально очищенным от примеси. При высоких значениях напряженности электрического поля может происходить вырывануе электронов из металлических электродов и, как и в газах, разру.ие-пие молекул самой жидкости за счет ударов заряженными частицами. При этом повышенная электрическая прочность жидкого диэлектрика по сравнению с газообразным обусловлена значительно меньшей длиной свободного пробега электронов. Пробой жидкостей, содержащих газовые включения, объясняют местным перегревом жидкости (за счет энергии, выделяющейся в относительно легко ионизирующихся пузырьках газа), который приводит к образованию газового канала менаду электродами. Вода в виде отдельных мелких капелек, находящихся в трансформаторном масле, при нормальной темпера-Tj-pe значительно снижает (рис. 4-6). Под влиянием электрического поля сферические капельки воды —сильно дипольной жидкости — поляризуются, приобретают форму эллипсоидов и, притягиваясь между собой разноименными концами, создают между э/ектродами цепочки с повышенной проводимостью, по которым и происходит электрический пробой. [c.65]
Поэтому значение удельной проводимости у (или удельного сопротивления р) в основном зависит от средней длины свободного пробега электронов в данном проводнике X, которая, в свою очередь, олределяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой харак-т( ризуются наименьшими значениями удельного сопротивления поимеси, искажая решетку, приводят к увеличению р. К такому же выводу можно прийти, исходя из волновой природы электронов. Рассеяние электронных волн происходит на дефектах кристалличе-С1 ой решетки, которые соизмеримы с расстоянием около четверти [c.191]
Ряд исследований электросопротивления в зависимости от размера зерен для d < 1мкм проводился на образцах, полученных компактированием ультрадисперсных порошков, [5] и на электро-осажденных фольгах [271, 272]. В первом случае, однако, было трудно отделить влияние остаточной пористости на электросопротивление образца, а во втором случае на него влияли также внешние поверхности фольг из-за малой толщины последних, сравнимой с длиной свободного пробега электронов. [c.162]
Сравнение результатов, полученных с помощью расчетов в рамках данной модели, с экспериментальными результатами для случая Си показывает [273], что хорошее согласие между ними наблюдается при IR/ 1 — R) = 0,097мкм. В работе [275], используя данные [276] для скорости Ферми 1,57 х 10 см/с и времени релаксации 2,1 X 10 с при температуре 77К, вычислена длина свободного пробега электронов проводимости в Си I = 0,33 мкм. Исходя из этих результатов, коэффициент зеркального отражения электронов проводимости от границ зерен в Си, подвергнутой ИПД, оказался равным R = 0,23. Эта величина близка к вели- fnne 0,24, типичной для крупнокристаллической Си [274]. Следовательно, для довольно большой части электронов проводимости границы зерен являются непреодолимыми барьерами, и дальней-шее уменьшение размеров зерен в нанокристаллическую область [c.164]
Разряде накаленным катодом. Количество ионов, образующихся в камере, зависит от тока электронов с катода, давления газа в камере и напряжения на аноде. В напылительной установке, схема которой представлена на рис. 2.3, источником электронов является накаленный катод К. При давлении газа в камере выше 10 Па средняя длина свободного пробега электрона меньше 1 см. Поэтому если расстояние до анода значительно больше этой длины, то на своем пути до анода электрон успеет испытать большое число столкновений с атомами газа. Для то.то чтобы эти соударения приводили [c.64]
Если толщина пленки d порядка длины свободного пробега электрона в диэлектрике или меньше ее (d < X), то использовать понятие подвижности носителей заряда для расчета сопротивления такой пленки нельзя. В этом случае электроны металла, преодолевшие потенциальный барьер Фо и влетевшие в диэлектрическую пленку, будут попадать на второй контакт практически без столкновений (рис. 10.3, б). Такой механизм прохождения свободных зарядов через тонкую диэлектрическую пленку называют надбарьерной инжещией, или надбарьерной эмиссией. Воспользовавшись аналогией с термоэлектронной эмиссией в вакуум, можно определить плотности встречных электронных токов с металлических контактов по формуле Ричардсона — Дешмена [c.274]
Как уже указывалось, тонкопленочные структуры позволяют создавать приборы с разнообразными нелинейными ВАХ. В качестве примера рассмотрим пятислойную МДМДМ-структуру, показанную на рис. 10.10, а. В этой структуре первая диэлектрическая пленка между электродами Mi и Mi делается достаточно тонкой для обеспечения туннелирования сквозь нее фермневских электронов, инжектируемых из первого металла. Она играет роль эмиттерного перехода транзистора. Вторая диэлектрическая пленка берется значительно толще с тем, чтобы электроны могли проходить через нее только вследствие надбарьерной инжекции. При приложении к ней смещения и в отсутствие смещения на эмиттерной пленке ток между электродами М а Мз может быть поэтому весьма малым. Эта пленка играет роль коллекторного перехода. Ток через пленку можно увеличить, подав соответствующее смещение на эмиттерную пленку (рис. 10.10, б). Если толщина базы (металлической пленки М ) мала по сравнению с длиной свободного пробега электронов, инжектируемых в нее через эмиттерную пленку, то ток коллектора (пленки Дг) можно сделать почти равным току эмиттера, т. е. сделать коэффициент усиления по току в схеме с общей базой близким к 1. [c.284]