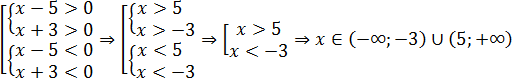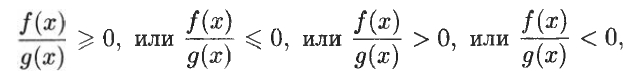§4. Рациональные неравенства. Метод интервалов.
В 9-м классе изучается метод интервалов прежде всего для многочленов. Он основан на том, что
а) двучлен `(x-a)` положителен при `x > a` и отрицателен при `x < a`, т. е. меняет знак при переходе через точку `a`,
б) квадрат двучлена `(x-a)^2` при переходе через точку `a` знак не меняет,
в) квадратный трёхчлен `x^2+px+q`, `p^2-4q < 0`, имеющий положительный коэффициент при `x^2` и отрицательный дискриминант, всегда положителен и может быть опущен при решении любого неравенства.
Заметим, что:
1) двучлен `(x-a)` в любой нечётной степени `(x-a)^(2n-1)`, n∈ℕ ninmathbb{N} ведёт себя так же, как и `(x-a)`,
2) двучлен `(x-a)` в любой чётной степени `(x-a)^(2n)`, n∈ℕ ninmathbb{N} ведёт себя так же, как и `(x-a)^2`,
Важно, что при переходе через точку `a`, может изменить знак только один множитель `(x-a)^(2k-1)`, а выражение `(x-b)^(2n-1)`, b≠a, bneq a, при переходе через `a` ни при каком `n` знак не меняет.
Прежде чем расставлять знаки, необходимо все многочлены записать правильно. Это значит, что во всех скобках коэффициенты при старшей степени переменной должны быть положительны, множители при произведениях в числителе и знаменателе тоже положительны – при больших `x` (когда `x` больше самого большого корня) многочлен всегда принимает положительные значения.
Итак, сформулируем
1. Проверяем, все ли множители записаны «правильно».
2. Находим корни числителя и знаменателя.
3. Представляем числитель и знаменатель в виде произведения неприводимых множителей, т. е. множителей вида `(x-a)^k` (все квадратные трёхчлены, имеющие отрицательный дискриминант, не записываем – их «опускаем»).
4. Наносим на числовую ось корни числителя (точками, если неравенство нестрогое, или «дырками», если неравенство строгое) и знаменателя (в любом неравенстве «дырками»).
5. Расставляем знаки дроби в промежутках между корнями, учитывая, что многочлен меняет знак при переходе через точку `a`, если в многочлене стоит `(x-a)^{2n-1}`, `ninN`
и не меняет знак, если в многочлене стоит `(x-a)^{2n}`, `ninN`.
6. Отмечаем прямоугольниками решение заданного неравенства и «снимаем» с рисунка ответ. При этом помним, что,
а) если неравенство строгое, то решением являются открытые промежутки;
б) если неравенство нестрогое, то к предыдущим решениям добавляются все «точки».
Когда говорим: Решим неравенство методом интервалов, – имеется в виду, что будут выполнены именно вышеприведённые действия.
Метод интервалов затем распространяется на рациональные функции.
Рациональной называется функция, которая может быть представлена в виде частного двух многочленов, т. е. в виде `{P(x)}/{Q(x)}`.
Например, функции `y=x-2`, `y={x^3-x+5}/{x+4}` — рациональные, а функция `y=sqrt(5x)` не является рациональной – она называется иррациональной.
Неравенства называются рациональными, если их правые и левые части являются рациональными функциями.
Рациональные неравенства чаще всего решаются сравнением с нулём, т. е. решаются неравенства вида `{P(x)}/{Q(x)}>0(<0)`.
Заметим, что дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель имеют одинаковые (противоположные) знаки, т. е.
`{P(x)}/{Q(x)}>0(<0)hArrP(x)Q(x)>0(<0)`,
поэтому метод интервалов применяется к дроби точно так же, как и к многочленам.
В школе принято писать для дроби ОДЗ: `Q(x)!=0`, но это является совершенно излишним. В самом алгоритме решения таких неравенств учитывается условие, что знаменатель не равен `0` – нули знаменателя отмечаются всегда кружочками («дырками»). Именно поэтому ОДЗ для рациональной дроби не пишут.
Некоторые учащиеся после нахождения ОДЗ даже «бросают» знаменатель. Они не понимают, что решение зависит не от того, равен или не равен `0` знаменатель, а от того, где знаменатель положителен, а где отрицателен.
При применении этого метода интервалов нет необходимости в рассмотрении «пробных» точек.
Найдите наименьшую длину промежутка, в котором расположены все решения неравенства 2-x54x+5≥0dfrac{displaystyledfrac{2-x}5}{4x+5}geq0.
Переписываем наше неравенство в правильном виде:
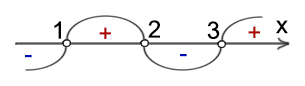
2-x54x+5≥0⇔x-2(x+54)≤0dfrac{displaystyledfrac{2-x}5}{4x+5}geq0Leftrightarrowdfrac{x-2}{(x+{displaystyledfrac54)}}leq0
и применяем метод интервалов — рис. 1.
| Рис. 1 |
C рисунка снимаем ответ.
`3,25`.
Заметим, что на нашей картинке нет никаких «змеек». Такой способ отмечать решение неравенства (который, с непривычки, некоторые отвергают, не попробовав) имеет преимущество, потому что он выделяет именно решение, а, кроме того, он даёт возможность «красиво» решать системы неравенств.
Решите систему неравенств
$$left{begin{array}{l}left(x-1right)left(x+dfrac14right)left(x+dfrac18right)geq0,\dfrac{left(x-2right)left(x-{displaystyledfrac{51}{50}}right)}{left(x+{displaystyledfrac3{16}}right)x}<0.end{array}right.$$
Здесь очень «плохие» пробные точки – дробные и близкие. Это сделано специально, чтобы привыкнуть их использовать.
Решаем сначала первое неравенство: наносим на числовую ось нули точками, т. к. неравенство нестрогое.
Теперь расставим знаки. Замечаем, что при больших `x` все множители положительны. При переходе через точку `x=1` функция меняет знак, т. к. `(x-1)` входит в нечётной (первой) степени. По этой же причине при переходе и через остальные точки функция опять меняет знак (рис. 2).
| Рис. 2 |
Теперь отметим «прямоугольниками» решение неравенства (рис. 3).
| Рис. 3 |
Теперь решаем второе: наносим на числовую ось нули и числителя, и знаменателя кружочками (дырками), т. к. неравенство строгое. Получаем рис. 4.
| Рис. 4 |
Теперь надо обе картинки поместить на одну ось. Надо ли соблюдать масштаб? А зачем? Не надо. Ведь нас интересует только взаимное расположение точек относительно друг друга, а расстояния между ними никакой роли не играют.
Теперь заштриховываем общие части прямоугольников – отлично виден ответ (рис. 5).
| Рис. 5 |
`x in(-3/16;-1/8]uu(51/50;2)`.
Найдите наименьшую длину промежутка, в котором расположены все решения неравенства
`(x-1)^2(x+1,5)^3(x-12)(x+2)^4(x-25)^8<=0`.
При решении неравенств, левая часть которых содержит чётные степени, можно поступать по-разному.
Первый способ
Левая часть уже записана правильно, корни видны сразу. Отмечаем их точками на числовой оси, а затем по вышеприведённым правилам расставляем знаки и отмечаем решение прямоугольниками – рис. 6.
| Рис. 6 |
С рисунка снимаем ответ, что `x in{-2;25}uu[-1,5;12]`. Отсюда следует, что наименьшая длина промежутка равна `25-(-2)=27`.
Второй способ
Можно заранее учесть, что бином `(x-a)^{2k}` принимает либо значение, равное `0`, либо положительно на всей числовой оси – поэтому можно записать в решение `x=a`, а бином «опустить», т. к. он не влияет на знак оставшегося выражения:
`(x-1)^2(x+1,5)^3(x-12)(x+2)^4(x-25)^8<=0 iff`
⇔x=1,x=-2,x=25,(x+1,5)(x-12)≤0⇔x∈-2;25∪-1,5;12.Leftrightarrowleft[begin{array}{l}begin{array}{c}x=1,\x=-2,\x=25,end{array}\(x+1,5)(x-12)leq0end{array}right.Leftrightarrow xinleft{-2;25right}cupleft[-1,5;12right].
`27`.
Решите неравенство `x<={8x-2}/{x+5}`.
`x<={8x-2}/{x-5}hArr{x^2-3x+2}/{x+5}<=0hArr{(x-1)(x-2)}/{x+5}<=0`
| Рис. 7 |
Из рис. 7 следует ответ
`(-oo;-5)uu[1;2]`.
Найти все пары целых чисел `x`, `y`, для которых верны неравенства
$$left{begin{array}{l}3y-2x<45,\x+y>24,\3x-y<3.end{array}right.$$
Запишем систему в стандартном виде (для сравнения с нулём)
$$left{begin{array}{l}3y-2x-45<0,\-x-y+24<0,\3x-y-3<0.end{array}right.$$
Заметим, что `y` входит в первое неравенство со знаком `« + »`, а во второе и третье со знаком `« – »`. Поэтому умножим сначала второе и третье неравенства на `3` (получились равносильные неравенства), а затем заменим второе и третье неравенства их суммами с первым – таким образом, мы исключим `y`. Итак,
$$left{begin{array}{l}3y-2x-45<0,\-x-y+24<0,\3x-y-3<0,end{array}right.Rightarrow$$
$$Rightarrowleft{begin{array}{l}3y-2x-45<0,\-3x-3y+72+3y-2x-45=-5x+27<0Leftrightarrow x>dfrac{27}5,\9x-3y-9+3y-2x-45=7x-54<0Leftrightarrow x<dfrac{54}7end{array}right.Rightarrow$$
(учтём, что мы ищем целые решения) ⇒x=6,7.Rightarrow x=left[begin{array}{l}6,\7.end{array}right.
Подставим последовательно найденные значения `x` в систему.
$$x=6Rightarrowleft{begin{array}{l}3y-57<0,\-y+18<0,\15-y<0end{array}right.Rightarrowvarnothing.$$
$$x=7Rightarrowleft{begin{array}{l}3y-59<0,\-y+17<0,Rightarrow y=19,\-y+18<0.end{array}right.$$
`(7,19)`.
Методом интервалов решают неравенства вида:
(х – х1)(х – х2)….(х – хn)>0 или (х – х1)(х – х2)….(х – хn)<0,
где х1, х2, …, хn – не равные друг другу числа, х – переменная. Также в неравенствах могут быть использованы знаки ≤ или ≥. Данный вид записи неравенства будем называть – стандартный.
Для решения данного вида неравенств используется свойство чередования знаков функции f(x)=(х – х1)(х – х2)….(х – хn), где числа х1, х2, …, хn называются нулями функции. Эти нули функции разбивают область определения (она представляет собой любое число, т.е. промежуток чисел от минус бесконечности до плюс бесконечности) на промежутки, в каждом из которых знак функции сохраняется, а при переходе через нуль ее знак изменяется. Данные промежутки называют интервалами, а решение неравенств данным способом – методом интервалов.
Для начала решения неравенство должно быть представлено в стандартном виде. Рассмотрим решение такого вида неравенств методом интервалов на примерах.
Пример №1. Решить неравенство:
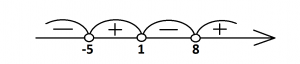
(х–1)(х+5)(х–8)>0
Найдем нули функции: для этого возьмем из каждой скобки данные числа с противоположными знаками, поэтому имеем х1=1, х2=–5, х3=8. Данные числа разбивают область определения на промежутки (−∞;−5);(−5;1);(1;8);(8;+∞). Удобно показать их на координатном луче, помня о том, что неравенство по условию строгое, значит, точки будут «выколотые»:
Теперь посмотрим, как расставить знаки в промежутках. Начнем справа, возьмем из этого промежутка любое число, например, 9 и подставим его в наше неравенство:
(9–1)(9+5)(9–8)=8×14×1>0,
то есть получили, что произведение – положительное число, поэтому ставим знак «плюс»; теперь берем число из промежутка (1;8), например, 5 и также подставим в неравенство для определения знака произведения:
(5–1)(5+5)(5–8)=4×10×(–3)<0
Значит, ставим в данном промежутке знак «минус». Также поступаем со следующим промежутком, возьмем число 0, подставим и получим, что произведение будет положительным, ставим знак «плюс». И аналогично ищем знак последнего промежутка, он будет «минус». Из рисунка видно, что знаки чередуются, поэтому надо запомнить, чтобы не проверять знак каждого промежутка, можно просто справа налево расставить знаки чередованием, начиная со знака «плюс». Для записи ответа возьмем промежутки, в которых стоит знак «плюс», так как в условии стоит знак «>».
Ответ: (−5;1)∪(8;+∞).
Пример №2. Решить неравенство:
х(х – 6)≤0
В данном случае мы видим, что есть отличие от неравенства стандартного вида. Но помним, что в случае сложения или вычитания переменной х и нуля мы получим переменную х, т.е. неравенство могло выглядеть так:
(х±0)(х – 6)≤0
Значит, одним из нулей функции будет число нуль. Итак, имеем нули функции 0 и 6. Ставим их на числовом луче, помня о том, что точки будут «приколотые», расставляем знаки путем чередования справа налево:
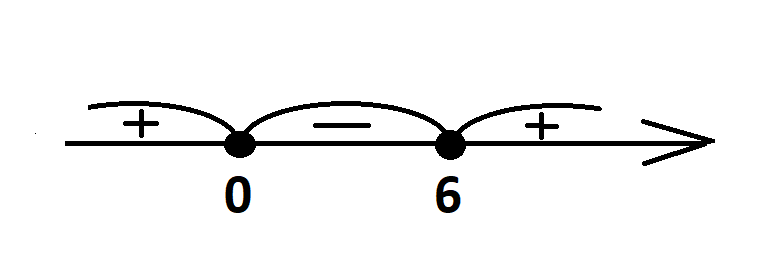
Ответ: [0; 6]
Пример №3. Решить неравенство:
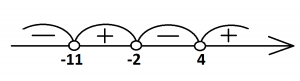
(х+11)(4 – х)(x+2)<0
В данном случаем мы видим отличие от записи неравенства стандартного вида во втором произведении, т.е. в (4 – х). Поэтому для начала надо привести неравенство к стандартному виду, для этого вынесем за скобки минус единицу –1(х+11)(х – 4)(x+2)<0, а теперь разделим обе части неравенства на эту минус 1, поменяв знак неравенства на противоположный:
(х+11)(х – 4)(x+2)>0
Именно это неравенство будем решать. Итак, нули функции – это –11, 4 и –2. Расставляем их на числовом луче и расставляем знаки путем чередования, получим:
Ищем промежутки, соответствующие неравенству стандартного вида, к которому мы привели, т.е. для (х+11)(х – 4)(x+2)>0.
Ответ: (–11; –2)∪(4;+∞)
Задание 13OM21R
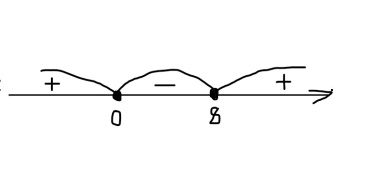
Укажите решение неравенства 8х – х2≥0
- [0; +∞)
- [8; +∞)
- [0; 8]
- (-∞;0]∪[8;+∞)
8х – х2≥0
Вынесем -х за скобки: -х(-8 + х) ≥0
Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
Теперь находим промежуток чисел, соответствующий неравенству х(х – 
В соответствии с его номером, это будет ответ под №3.
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 3.7k
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
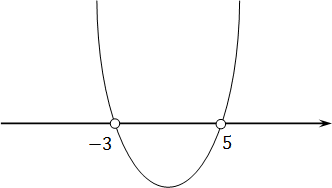
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств
- Тест по методу интервалов для строгих неравенств
- Сводный тест по задачам B12 (2 вариант)
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задачи B4: перевозка груза тремя фирмами
Решение неравенств является важной задачей в математике, которая находит применение в различных областях, от естественных наук до экономики и финансов. Неравенства могут быть сложными для решения, особенно если они содержат неизвестные в знаменателе. Один из методов решения неравенств — это метод интервалов, который позволяет определить интервалы значений, в которых искомые переменные удовлетворяют неравенству. В этой статье мы рассмотрим, как использовать метод интервалов для решения различных типов неравенств и как он может помочь вам решать математические задачи более эффективно.
Пусть у нас есть неравенство вида
где f(x) и g(x) — многочлены, которые уже разложены на простейшие множители, т.е. являются произведениями многочленов вида (x-a).
Рассмотрим решение неравенств методом интервалов на примерах.
Задача (Неравенство в стандартном виде)
Решите неравенство
(
x
−
4
)
2
(
x
−
8
)
3
(
x
+
2
)
(
x
−
3
)
(
x
+
5
)
4
≥
0
Решение:
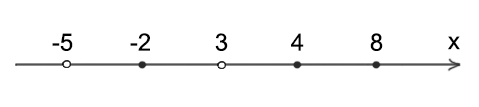
Отметим на числовой прямой точки, которые обращают в ноль и числитель, и знаменатель.
Т.к. знаменатель не может быть равен нулю, то те точки, которые обращают в ноль знаменатель рисуем «выколотые».
Т.к. неравенство нестрогое, то точки, которые обращают в ноль числитель, рисуются закрашенными. Если бы неравенство было бы строгим, точки, которые обращают в ноль числитель, следует так же сделать «выколотыми».
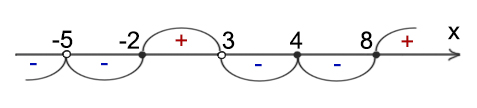
Далее, рисуем «змейку» справа налево. «Змейка» меняет знак на нечётной степени и сохраняет знак на чётной степени.
Если неравенство находится в стандартном виде, как в нашем случае, то «змейка» начинается с положительного знака. Обязательно должно быть (x-3), а не (2-x), именно x-8, а не 8-x и т.д. Этого всегда можно добиться, умножая неравенство на -1.
Нам нужно, чтобы дробь была ≥ 0. Можно написать уже ответ. Выбираем те интервалы, где положительный знак, а так же точки, которые обращают дробь в ноль.
x ∈ [-2; 3) ∪ {4} ∪ [8; +∞)
Важно не забыть точку 4.
Скобки будут квадратными, если точка закрашенная, и круглыми, если точка «выколотая».
Ответ: x ∈ [-2; 3) ∪ {4} ∪ [8; +∞)
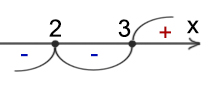
Задача (Без дроби)
Решите неравенство
(
x
−
1
)
(
x
−
2
)
(
x
−
3
)
>
0
Решение:
Когда нет дроби, решаем по тому же принцу, делая метод интервалов как бы только для знаменателя.
Ответ: x ∈ (1; 2) ∪ (3; +∞)
Задача (Приводим к стандартному виду)
Решите неравенство
(
3
−
x
)
(
2
−
x
)
2
≥
0
Решение:
Здесь видим, что неравенство не в стандартном виде, чтобы мы применили метод интервалов, описанный выше. Нужно привести его в стандартный вид.
Поменяем в первом выражении x и 3 местами, домножив неравенство на -1.
(
x
−
3
)
(
2
−
x
)
2
≤
0
Когда левая и правая часть неравенства умножается на отрицательное число, знак неравенства меняется на противоположный.
Слагаемые внутри скобок, которые находятся в чётной степени, можно менять и умножать на -1 не нужно.
(
x
−
3
)
(
x
−
2
)
2
≤
0
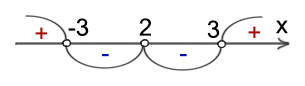
Теперь неравенство находится в стандартном виде, и его можно решить методом интервалов.
Теперь нам нужно выбрать интервалы с отрицательными знаками. Так же берём точку 2 и 3, где выражение обращается в ноль.
Ответ: x ∈ (-∞; 3]
Задача (Квадратный трёхчлен)
Решите неравенство
2
x
2
+
x
−
7
≥
0
Решение:
Здесь мы видим квадратный трёхчлен. Нам нужно привести неравенство к стандартному виду. Воспользуемся формулой разложения на множители квадратного трёхчлена.
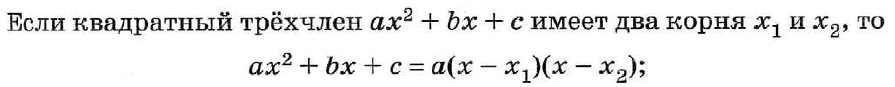
Найдём корни квадратного уравнения
2
x
2
+
x
−
7
=
0
x
1
=
−
1
−
57
4
x
2
=
−
1
+
57
4
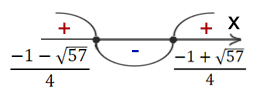
Тогда, получим неравенство в стандартном виде
(
x
+
1
+
57
4
)
(
x
+
1
−
57
4
)
≥
0
Ответ: x ∈ (-∞ ;
−
1
−
57
4
] ∪ [
−
1
+
57
4
; +∞)
Задача (Крепкий орешек)
Решите уравнение
x
x
+
3
+
2
x
−
2
<
5
x
(
x
+
3
)
(
x
−
2
)
Решение:
Перенесём всё в левую часть неравенства и просуммируем дроби.
x
2
−
5
x
+
6
(
x
+
3
)
(
x
−
2
)
<
0
Квадратный трёхчлен разложим на множители:
(
x
−
2
)
(
x
−
3
)
(
x
+
3
)
(
x
−
2
)
<
0
Такое неравенство можно заменить эквивалентным:
(
x
−
2
)
(
x
−
3
)
(
x
+
3
)
(
x
−
2
)
<
0
(
x
+
3
)
(
x
−
2
)
2
(
x
−
3
)
<
0
Ответ: x ∈ (-3; 2) ∪ (2; 3)
В заключение, можно отметить, что метод интервалов является эффективным инструментом для решения неравенств, особенно в тех случаях, когда выражение может быть представлено в виде множителей, а с другой стороны неравенство находится ноль. Этот метод может существенно ускорить процесс решения неравенств, сократить количество ошибок и упростить аналитические выкладки. Однако, следует помнить, что не все неравенства могут быть решены с помощью метода интервалов, и в некоторых случаях может потребоваться использование других методов.
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023