Задачи на движение протяженных тел и сложение скоростей
Это один из самых интересных типов текстовых задач на ЕГЭ по математике. Здесь и задачи на движение протяженных тел. И задачи, где два поезда движутся навстречу друг другу (по параллельным путям, конечно). И такие, где один поезд обгоняет другой.
Расскажем о секретах решения таких задач.
Что значит «движение протяженных тел»?
Если в условии задачи поезд проходит расстояние от Санкт-Петербурга до Москвы — длиной самого поезда можно пренебречь. Она намного меньше расстояния между городами. В физике говорят, что поезд в этом случае можно считать материальной точкой. Если же в задаче один поезд проходит мимо другого или поезд проходит через туннель — длину поезда также надо учитывать.
1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
36 секунд, за которые поезд проезжает мимо лесополосы, — это время от момента, когда голова поезда поравнялась с началом лесополосы, до момента, когда хвост поезда поравнялся с концом лесополосы. За это время поезд проезжает расстояние, равное сумме собственной длины и длины лесополосы.
Переведем 36 секунды в часы.
За это время поезд проехал
Ответ: 300
Задачи на встречное движение или обгон удобно решать в движущейся системе отсчета.
2. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина пассажирского поезда равна 400 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 38 секундам. Ответ дайте в метрах.
Решим задачу в системе отсчета, связанную с головой пассажирского поезда. Представим, что мы находимся в кабине машиниста неподвижного поезда, а мимо нас проносится скорый поезд. Скорость, с которой один поезд движется относительно другого, равна
Тогда 38 секунд, за которые движущийся поезд проезжает мимо неподвижного, — это время от момента, когда голова первого поезда поравнялась с хвостом второго, до момента, когда хвост первого поезда поравнялся с головой второго (смотри рисунки) За это время скорый поезд проезжает расстояние, равное сумме длин двух поездов.
Переведем 38 секунд в часы:
За это время поезд проехал
Ответ: 550
3. Два поезда движутся навстречу друг другу со скоростями 56 и 52 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 15 секунд. Найдите длину второго поезда. Ответ выразите в метрах.
Если пассажир находится в первом поезде, то в его системе отсчета второй поезд движется навстречу со скоростью, равной сумме скоростей поездов. Иначе она называется «скорость сближения», и она равна
Переведем эту скорость в метры/минуту.
Мы получили, что со скоростью 1800м/мин мимо пассажира первого поезда проходит весь второй поезд. По условию, это происходит за
Длина второго поезда равна
Ответ: 450 м.
4. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 140 метров, второй — длиной 60 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 800 метров. Через 15 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 1000 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Переведем минуты в часы:
Пусть и
— скорости первого и второго сухогрузов. Будем решать задачу в системе отсчета, связанной с первым сухогрузом. Представьте, что вы находитесь на нем и видите, как второй сухогруз догоняет и обгоняет ваш корабль со скоростью
Расстояние, пройденное вторым сухогрузом, — это сумма расстояний от носа второго сухогруза до кормы первого, длины первого сухогруза, расстояния от его носа первого до кормы второго и длины второго (см. рисунок).
Воспользуемся формулой:
км/ч
На 8 километров в час скорость второго сухогруза больше скорости первого.
Ответ: 8
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи на движение протяженных тел и сложение скоростей» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Как найти длину поезда зная скорость и время
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
1/60 * 60 = (x/1000)+0,4,
t = t1+t2 = s/20+s/480 = 5s/96,
Прототип задания B14 (Лысенко, 2013, №386)
Имеется кусок сплава меди с оловом общей массой 24 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
Прототип задания B14 (Лысенко, 2013, №387)
Два сосуда с раствором щёлочи разных концентраций (по объёму) содержат вместе 20 л раствора. Первый сосуд содержит 4 л щелочи, а второй — 6 л. Сколько процентов щёлочи содержит первый сосуд, если второй содержит щёлочи на 40% меньше первого?
Расчет длины поезда
Поезд — это сформированный и сцепленный состав, состоящий из группы вагонов, с одним или несколькими действующими локомотивами.
Формула длины поезда:
L — длина поезда в метрах;
Lл — длина локомотивов в метрах;
Lв — длина вагона в метрах;
Nв — количество вагонов;
Lз — запас по длине (обычно 10 метров).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета длины поезда по простой математической формуле в зависимости от длины локомотива, длины и количества вагонов, запаса по длине. С помощью этой программы вы в один клик сможете рассчитать длину поезда.
Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 6 секунд. Найдите длину поезда
Для решения данной задачи вспомним формулу вычисления расстояния. Расстояние равно произведению времени на скорость. s=v*t, где s — расстояние, v — скорость, t — время. Вычислим длину поезда, зная, что он двигался 6 секунд со скоростью 150 км/ч.
Переведём секунды в часы. 1 час = 3600 секунд. 6 секунд = 6/3600 = 1/600 часа.
s = 150 * 1/600 = 1/4 = 0,25 километра.
Переведём километры в метры.
1 километр = 1000 метров.
0,25 километра = 0,25 * 1000 = 250 метров.
Ответ: 250 метров.
Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 6 секунд.
Найдем длину поезда в метрах
Равномерное движение — это движение, при котором поезд за равные промежутки времени, проходит равные расстояния.
Так как, движение равномерное, то запишем формулу скорости движения поезда v = s/t, где:
- Скорость поезда равна v = 150 км/ч;
- время поезда t = 6 c;
- s — длина поезда.
Переведем скорость поезда в м/с.
Так как, в 1 км = 1 000 м, а в 1 ч = 3 600 с, тогда:
150 км/ч = 150 * км/ч = 150 * 1 000 м/3 600 с = 150 * 1 000/3 600 м/с = 150 * 10/36 м/с = 1 500/36 м/с;
Подставим известную скорость и время в формулу скорости движения автобуса. То есть получаем:
1 500/36 м/с = s/6 с;
1 500/36 м/с * с = s/6с * с;
Длина поезда измеряется в метрах.
Решим уравнение 1 500/36 = s/6
Приведем уравнение к линейному виду и получим:
Умножим уравнение на 36 и получим:
1500/36 * 36 — s/6 * 36 = 0;
1500/1 * 1 — s/1 * 6 = 0;
Уравнение является линейным, и записывается в виде a * x + b = 0, где a и b — любые числа. Если, а и b — любые числа, кроме 0, то корень находится по следующей формуле x = — b/a.
Отсюда получаем, что a = — 6, b = 1 500, значит, уравнение имеет один корень.
Сокращаем дробь 6 * 250/6 в числителе и знаменателе на число 6, тогда получим:
ell04ka
Мудрец
(13138)
12 лет назад
скорость * время = расстояние
расстояние меньше длины платформы на длину поезда
не забываем перевести к единым единицам измерения!
90 км/ч / 60 мин *0,5 мин = X км
X = 0,75 т. е. 750 м
значит поезд длиной 750-300 = 450 м
Травиата Кутуньо
Мудрец
(10306)
12 лет назад
Задачу необходимо решить, используя физические обозначения и формулы. Выразим скорость в м/с 90 км/ч = 90*1000м/3600с = 25м/с. Условия задачи: v = 25 м/с; l1 = 300м; t = 30с. Обозначим длину поезда l2 . Поезд начнет двигаться мимо платформы, когда локомотив будет проходить мимо переднего края платформы, и закончит свое движение тогда, когда последнй вагон пройдет мимо второго края платформы. При этом последнему вагону надо пройти путь, равный l1 + l2. Составим уравнение движения: vt = l1 + l2. Отсюда
l2 = vt — l1 Вычисления: l2 = 25м/с * 30с — 300м = 450 м. Ответ: l2 = 450 м.
Источник: Саабразила
Елизавета Дьяконова
Ученик
(245)
3 года назад
скорость * время = расстояние
расстояние меньше длины платформы на длину поезда
не забываем перевести к единым единицам измерения!
90 км/ч / 60 мин *0,5 мин = X км
X = 0,75 т. е. 750 м
значит поезд длиной 750-300 = 450 м
15
0
Решение задачи:
1.Определим скорость сближения поездов.
50 — 40 = 10 (км/час)
Следовательно, за 1 час пассажирский поезд сместится относительно товарного на 10 километров.
Тогда за 1 минуту произойдет смещение на 10 : 60 (км)
Соответственно, за 9 минут: 10/60 х 9 = 90/60 = 1.5 (км) = 1500 метров.
За 9 минут поезд прошел расстояние равное сумме длин двух поездов.
Следовательно, длина пассажирского поезда будет равна:
1500 — 1350 = 150 (м). Ответ: 150 метров длина пассажирского поезда.
2
0
Пассажирский поезд двигается относительно товарного со скоростью 50-40=10 км/ч.
Допустим, длина пассажирского поезда равна Х км., длина товарного поезда 1,35 км., 9 минут равно 0,15 часа. Тогда:
(Х+1,35)/10=0,15
Х+1,35=0,15*10=1,5
Х=1,5-1,35=0,15 км = 150 м.
Ответ: длина пассажирского поезда 150 м.
2
0
Для начала переведем все единицы измерения в единицы СИ.
50 км/ч = 13.(8) м/с
40 км/ч = 11.(1) м/с
Решим задачу в системе отсчета товарного поезда. С ее точки зрения пассажирский поезд едет со скоростью 10 км/ч = 2,(7) м/с
Возьмем за точку отсчета О край последнего вагона пассажирского поезда. Когда пассажирский поезд начал ехать мимо товарного О находилась на расстоянии Х=длине пассажирского поезда от края последнего вагона товарного поезда. За 9 минут (или 540 секунд) точка О переместилась в на Х+1350 метров.
Таким образом (Х+1350)/2.(7)=540
Х+1350=540*2.(7)=150<wbr />0
Х=1500-1350=150 метров длина пассажирского поезда.
Ответ: 150 метров.
2
0
Находим с какой скоростью двигался пассажирский поезд относительно товарного.
50 — 40 = 10 (км/ч) или 10 000 м/60 мин = 1000/6 м/мин.
Найдём насколько метров переместился пассажирский поезд относительно товарного за 9 минут.
1000/6 * 9 = 1500 (м).
Найдём длину пассажирского поезда:
1500 — 1350 = 150 (м)
Ответ: 150 метров длина пассажирского поезда.
Задачи на проценты решаем с помощью составления пропорций:
Допустим, вес Коли – Х кг.
63 кг – 100% (средний вес мальчиков)
Х кг – 90% (вес Коли)
Х=63*90/100= 56,7 (кг)
Ответ: Вес Коли равен 56 килограмм 700 грамм.
Находим стоимость билета для школьников:
230 * 50/100 = 115 (руб).
Находим стоимость проезда для 8 школьников:
115 * 8 = 920 (руб).
Находим стоимость проезда для 3 взрослых:
230 * 3 = 690 (руб).
Находим стоимость проезда 3 взрослых и 8 школьников:
690 + 920 = 1610 (руб).
Ответ: 1610 рублей стоит проезд 3 взрослых и 8 школьников.
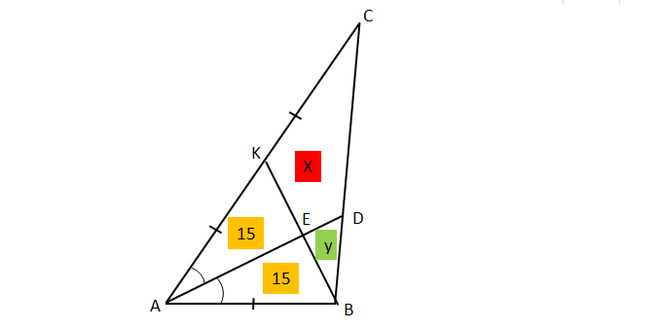
На рисунке, предоставленном автором вопроса, треугольник искаженный и не соответствует условию. По этой причине предлагаю свой вариант рисунка.
Биссектриса угла треугольника делит противоположную сторону на части пропорциональные к прилежащим к ней сторонам. Следовательно согласно условия АВ : АС = 1 :2. Тогда АК = АВ, а треугольник АКВ равносторонний и биссектриса АD делит его на равные части. В свою очередь медиана ВК делит треугольник АСВ на два равновеликих треугольника. Откуда площади треугольников АКЕ и АЕВ составляют по 15 кв. см.
Биссектриса треугольника делит так же площадь треугольника пропорционально прилежащим к ней сторонам. Тогда площади треугольников АDВ и АСD относятся друг к другу как 1 : 2.
На основании сказанного составим систему уравнений, обозначив неизвестные площади треугольников за х и у,
{х + у = 15
{15 + х = 2(15 + У).
Решая систему относительно х, получаем — площадь 4-угольника EDCK равна 25 кв. см.
То, что находится между модульными скобками |f(x)|, называется «подмодульным выражением». В простейшем случае это просто х, т.е. |x|, гораздо чаще более сложные, например |x-3|, иногда ещё более сложные, например |х^2-5x+6|. При решении нужно вычислить нули модуля, т.е. значения неизвестного, которые обращают подмодульное выражение в нуль. Так в первом случае один «нуль», и это значение х=0, во втором случае тоже один «нуль» х=3, в третьем случае — два «нуля» х=2 и х=3.
Процедура «избавления от модулей» называется «раскрытием модуля».
Эти «нули» разбивают всю числовую ось (от -∞ до +∞) на отдельные интервалы, например, в последнем случае на 3 интервала: (-∞; 2), (2;3), (3;+∞), в каждом из которых функция принимает свой вид. Если подмодульное выражение больше 0 или равно нулю, то при раскрытии модуля знаки подмодульного выражения сохраняются, а «раскрытие» сводится просто к удалению модульных скобок (при необходимости, замене их обычными скобками). Если подмодульное выражение меньше нуля, то при раскрытии модуля предварительно все знаки подмодульного выражения меняются на противоположные.
Ну, и после решения каждого из полученных уравнений (неравенств), обязательно из решений нужно выбрать только те, которые попадают в рассматриваемый интервал.
Такого рода задачи решаются по одному и тому же алгоритму. Скорость плавательного средства (в данном случае — баржи) обозначают какой-либо буквой, например, «v», а скорость течения реки другой буквой, например,»u». Тогда скорость плавсредства при движении по течению будет «v+u», а скорость плавсредства при движении против течения «v-u». Время движения плавсредства при движении по течению будет t1=S1/(v+u), а врем движения плавсредства при движении против течения будет t2=S2/(v-u). Очевидно, нет необходимости пояснять, что S1 и S2 расстояния, пройденные по течению и против течения, а t1 и t2 — соответственно времена, затраченные на эти движения. Ну и наконец можно составить уравнения по заданному про времена условию. В данном случае задано такое условие: t1+t2=4. Иногда в условии задается разность этих времён, например t2-t1.
И всё. Внимательно прочитав и поняв алгоритм, с задачами подобного типа справится даже первоклассник, который овладел такими понятиями, как скорость, быстрее, медленнее.
Нулевая точка отсчёта — это когда поезд поравняется с пешеходом. Пешеход за 18 секунд пройдёт… Какой же он пройдёт путь? Вычисляю:
18*6000/3600. Избавляюсь от нулей и 6 вычисляю:
18*1000/600 = 18*10/6 = 18*5/3 = 90/3 = 30 метров.
Поезд за 18 секунд проедет… Какой же он проедет путь? Вычисляю:
18*86000/3600. Избавляюсь от нулей и 2 вычисляю:
18*860/36 = 18*430/18 = 430 метров.
Поезд проехал 430 метров, но и пешеход не стоял, а прошёл 30 метров. Значит от длины поезда надо отнять расстояние пешехода. Вычисляю:
430 — 30 = 400 метров.
Мой ответ: длина поезда в метрах составляет 400 метров.
P.S. Все мои вычисления произведены без калькулятора.
Поезд, двигаясь равномерно со скоростью км/ч , проезжает мимо идущего в том же направлении параллельно путям со скоростью км/ч пешехода за секунд. Найдите длину поезда в метрах.
Решение задачи
В данном уроке показывается решение задачи на определение расстояния при известной скорости
и времени движения . Для начала рассматривается скорость поезда относительно пешехода, которая равняется разности скоростей поезда и пешехода. Проезжая мимо пешехода за время , поезд проходит расстояние, равное его длине. Следовательно, решение задачи сводится к нахождению данного расстояния. Так как по условию задачи длину поезда необходимо найти в метрах, скорость поезда из единицы измерения в км/ч переводится в м/с. Далее, подставив скорость и время движения поезда в формулу
, определяется искомая длина поезда.
В случае использования данного решения в качестве примера для решения типовых задач подготовка к ОГЭ станет более успешной и результативной.
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1. 26+4=30(км/ч) — скорость сближения поезда и пешехода, так как они движутся в разных направлениях.
2. 90/3600=1/40(ч) — время, за которое поезд проезжает мимо пешехода.
3. 30/40=0,75(км) — длина поезда в километрах.
4. 0,75·1000=750(м) — длина поезда в метрах.
Ответ: длина поезда 750 метров.
Поезд, двигаясь равномерно со скоростью 62 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 2 км/ч, за 33 секунды. Найдите длину поезда в метрах.
Решение:
1. 62-2=60(км/ч) — скорость сближения, так как пешеход и поезд движутся в одном направлении.
2. 33/3600=11/1200(ч) — время, за которое поезд проезжает мимо пешехода.
3. 60·11/1200=11/20(км) — длина поезда в километрах.
4. 11/20·1000=50·11=550(м) — длина поезда в метрах
Ответ: длина поезда 550 метров.
Задачи для самостоятельного решения:
1. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 8 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах.
Решение №1
Скорость поезда равна v = 80 км/ч; время (t) = 36 сек. Переведем в часы, получится 0.01 ч. (36:3600= 0.01). За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине. Длина поезда S = V(скорость поездка) • t(время); S = 80•0.01= 0.8(км) = 800м
Ответ: 800.
Центр «Снейл» 15 лет проводит массовые дистанционные образовательные конкурсы и олимпиады для детей. Это предметные и межпредметные интеллектуальные состязания среди школьников, специальные ЕГЭ-олимпиады, помогающие им готовиться к итоговой аттестации.
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1. 26+4=30(км/ч) — скорость сближения поезда и пешехода, так как они движутся в разных направлениях.
2. 90/3600=1/40(ч) — время, за которое поезд проезжает мимо пешехода.
3. 30/40=0,75(км) — длина поезда в километрах.
4. 0,75·1000=750(м) — длина поезда в метрах.
Ответ: длина поезда 750 метров.
Поезд, двигаясь равномерно со скоростью 62 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 2 км/ч, за 33 секунды. Найдите длину поезда в метрах.
Решение:
1. 62-2=60(км/ч) — скорость сближения, так как пешеход и поезд движутся в одном направлении.
2. 33/3600=11/1200(ч) — время, за которое поезд проезжает мимо пешехода.
3. 60·11/1200=11/20(км) — длина поезда в километрах.
4. 11/20·1000=50·11=550(м) — длина поезда в метрах
Ответ: длина поезда 550 метров.
Задачи для самостоятельного решения:
1. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 8 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах.