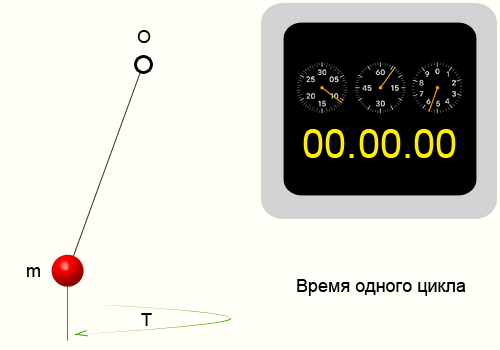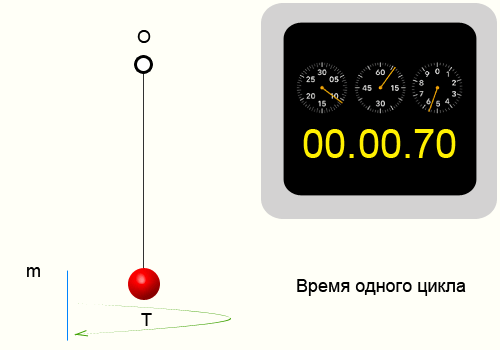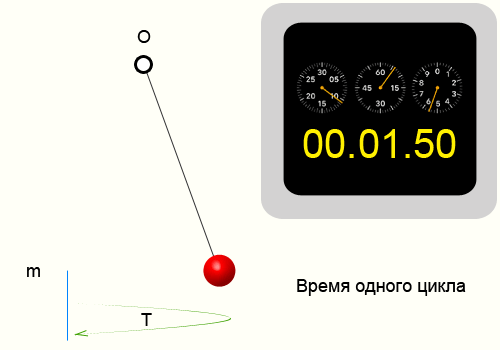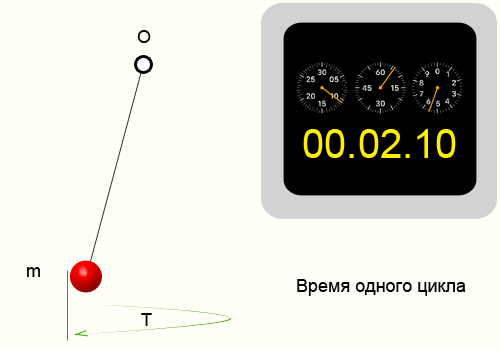
Расчет длины маятника
Маятник — это тело или система тел, подвешенная в поле тяжести и совершающая механические колебания.
Формула расчета длины маятника:
L = (T / 2π) 2 * g, где
L — длина маятника в метрах;
T — период колебаний в секундах;
g — ускорение свободного падения в м/с 2 .
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета длины маятника по простой математической формуле в зависимости от периода колебаний и ускорения свободного падения. С помощью этой программы вы в один клик сможете рассчитать длину маятника.
Расчет длины нити математического маятника
Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле , где — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет секунды.
Решение задачи
В данном уроке показано, как грамотно рассчитать длину нити математического маятника. По условию задана формула , с помощью которой приблизительно вычисляются колебания маятника. — это период колебания маятника, который известен по условию задачи ( секунды), а – это длина нити маятника, которую и необходимо рассчитать. Для решения задачи достаточно преобразовать формулу (представленную в виде алгебраического выражение) и подставить в нее известные данные. Для этого из формулы выражается переменная , в процессе этого выполняются операции упрощения выражения. Далее, для получения окончательного ответа, вместо переменной подставляется его числовое значение. Ответ представлен в виде десятичной дроби
При подготовке к ОГЭ можно успешно воспользоваться решением этой задачи, в частности при решении задач типа ОГЭ 20.
Как найти длину нити
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол появляется касательная составляющая силы тяжести (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
Если обозначить через линейное смещение маятника от положения равновесия по дуге окружности радиуса , то его угловое смещение будет равно . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:
Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению , а
Только в случае малых колебаний , когда приближенно можно заменить на математический маятник является гармоническим осциллятором , т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка ; при этом величина отличается от не более чем на . Колебания маятника при больших амплитудах не являются гармоническими.
Для малых колебаний математического маятника второй закон Ньютона записывается в виде
Таким образом, тангенциальное ускорение маятника пропорционально его смещению , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
Эта формула выражает собственную частоту малых колебаний математического маятника .
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс физического маятника находится ниже оси вращения на вертикали, проходящей через ось. При отклонении маятника на угол возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
Здесь – расстояние между осью вращения и центром масс .
Здесь – собственная частота малых колебаний физического маятника .
Более строгий вывод формул для и можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение есть вторая производная углового смещения по времени:
Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде
Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции можно выразить через момент инерции относительно оси, проходящей через центр масс маятника и параллельной оси вращения:
Окончательно для круговой частоты свободных колебаний физического маятника получается выражение:
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
1
габбас
[215K]
4 года назад
Если известен период колебаний математического маятника, то длину маятника можно подсчитать по известной формуле периода математического маятника Т=2*пи*корень квадратный из( L/g), где g=9,8 м/с2 — ускорение свободного падения на Земле (приблизительно). Оттуда длина маятника L = (Т^2*g)/(4*пи^2) = (1*9,8)/(4*3,14*3,14) = 9,8/39,48 = 0,248 м или примерно 25 см.
Ответ: 25 см.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Задания
Версия для печати и копирования в MS Word
Тип 12 № 311544
i
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле где
— длина нити (в метрах). Пользуясь данной формулой, найдите длину нити маятника, период колебаний которого составляет 7 с.
Спрятать решение
Решение.
Выразим длину маятника:
Подставляя, получаем:
Ответ: 12,25.
Аналоги к заданию № 46: 311544 337952 338064 … Все
Источник: ГИА-2012. Математика. Контрольная работа.(1 вар)
Спрятать решение
·
Прототип задания
·
Помощь
Как найти длину через период колебаний
- Как найти период и частоту колебаний
- Как найти резонансную частоту
- Как измерить частоту
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
— скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
— скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
— число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими. Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
Пример определения периода колебаний
Например возьмем кусочек пластилина и подвесим его на нитке. Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер. Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили. Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.