Условие
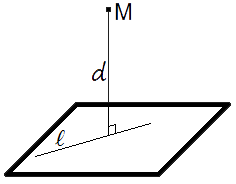
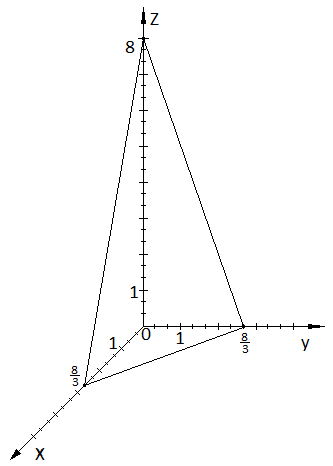
5.2.16. Найти длину перпендикуляра, опущенного из начала координат на плоскость 20х — 5y + 4z — 210 = 0 и угол, образованный этим перпендикуляром с осью Oz.
математика ВУЗ
5573
Решение
★
Пусть M(x_(o);y_(o);z_(o)) основание перпендикуляра.
vector{OM} коллинеарен вектору vector{n}
vector{OM}=(x_(o);y_(o);z_(o))
vector{n}=(20;-5;4)
Значит, координаты этих векторов пропорциональны
x_(o)/20=y_(o)/(-5)=z_(o)/4
или
x_(o)=20k
y_(o)=-5k
z_(o)=4k
k- коэффициент пропорциональности.
Точка M_(o) лежит на плоскости, значит ее координаты удовлетворяют соотношению
20x_(o)-5y_(o)+4z_(o)-210=0
20*20k-5*(-5k)+4*4k-210=0
441k=210
k=10/21
x_(o)=20k=200/21;
y_(o)=-5k=-50/21
z_(o)=4k=40/21
|OM_(o)|=sqrt((200/21)^2+(-50/21)^2+(40/21)^2)=
=sqrt(44100/441)=sqrt(100)=10
cosγ=z_(o)/|OM_(o)|=(40/21)/10=4/21
О т в е т. длина перпендикуляра равна 10; угол, образованный этим перпендикуляром и осью Оz равен arccos (4/21)
Все решения

Написать комментарий
Расстояние от точки до плоскости
Формула для вычисления расстояния от точки до плоскости
Если задано уравнение плоскости A x + B y + C z + D = 0 , то расстояние от точки M(M x , M y , M z ) до плоскости можно найти, используя следующую формулу:
| d = | |A·M x + B·M y + C·M z + D| |
| √ A 2 + B 2 + C 2 |
Примеры задач на вычисление расстояния от точки до плоскости
Решение. Подставим в формулу коэффициенты плоскости и координаты точки
d = |2·0 + 4·3 + (-4)·6 — 6| √ 4 + 16 + 16 = |0 + 12 — 24 — 6| √ 36 = |-18| 6 = 3
Ответ: расстояние от точки до плоскости равно 3.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы введем понятия расстояния от точки до плоскости, рассмотрим и докажем важнейшую теорему о трех перпендикулярах.
Вначале введем понятие перпендикуляра, наклонной и проекции и покажем построение отрезка, являющегося расстоянием между точкой и плоскостью, дадим строгое определение этого расстояния. Далее дадим определение расстояния между двумя параллельными плоскостями и покажем построение этого отрезка. Также дадим определение расстояния между прямой и параллельной ей плоскостью.
Далее дадим формулировку теоремы о трех перпендикулярах и докажем ее. Также сформулируем и докажем обратную теорему.
В конце урока решим несколько задач с использованием теоремы о трех перпендикулярах.
Прямая, перпендикулярная к плоскости.
Признак перпендикулярности прямой и плоскости.
Расстояние от точки до плоскости
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости
Определение . Прямой, перпендикулярной к плоскости , называют такую прямую, которая перпендикулярна к каждой прямой, лежащей на этой плоскости.
Признак перпендикулярности прямой и плоскости . Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в некоторой плоскости, то прямая перпендикулярна к этой плоскости.
Доказательство . Рассмотрим сначала следующий случай.
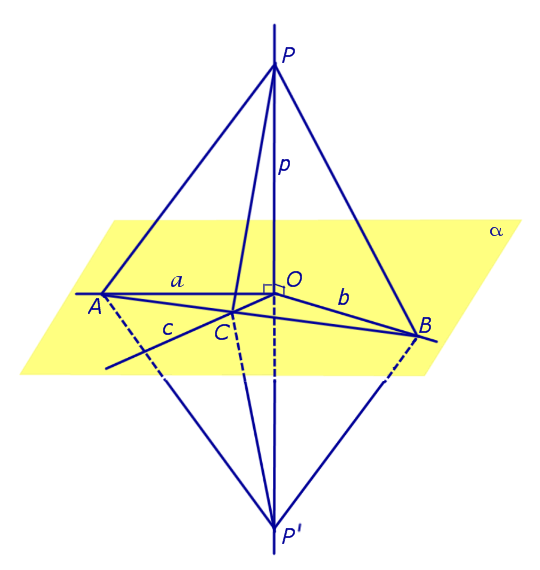
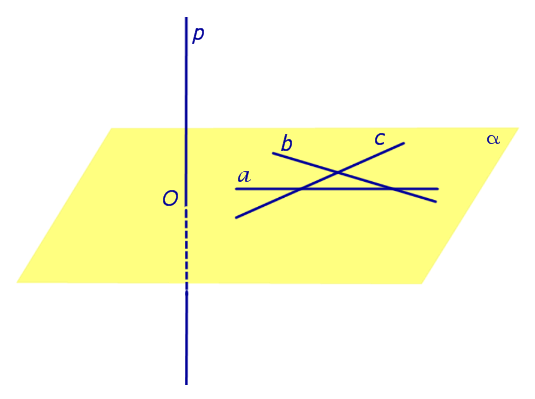
Предположим, что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α и проходящим через точку O . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей на плоскости α и проходящей через точку O .
С этой целью отметим на прямой a произвольную точку A , а на прямой b произвольную точку B (рис. 1).
Проведем прямую AB и обозначим буквой C точку пересечения прямых AB и c. Отметим на прямой p произвольную точку P и обозначим символом P’ точку, расположенную на прямой p так, чтобы точка O оказалась серединой отрезка PP’ . Поскольку прямые OA и OB являются серединными перпендикулярами к отрезку PP’ , то справедливы равенства
Из этих равенств, а также поскольку отрезок AB является общей стороной треугольников APB и AP’B , заключаем, что в силу признака равенства треугольников по трем сторонам трегольники APB и AP’B равны. Следовательно,
Отсюда в силу признака равенства треугольников по двум сторонам и углу между ними заключаем, что трегольник PBС равен треугольнику P’BС ( BP = BP’ , 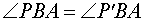
Таким образом, прямые PO и c перпендикулярны, что и требовалось доказать в рассматриваемом случае.
Теперь перейдем к общему случаю.
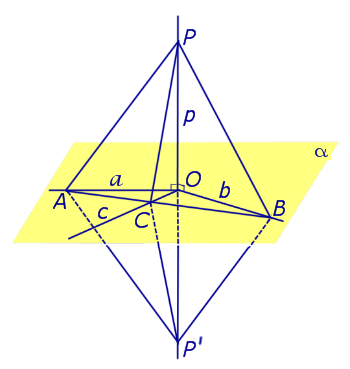
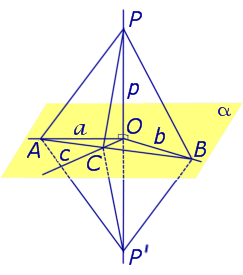
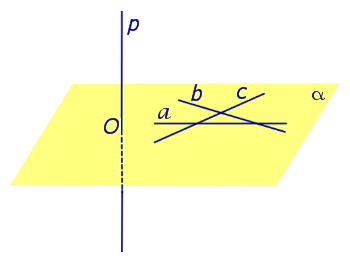
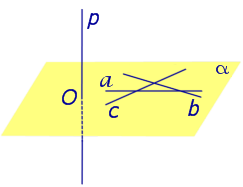
Предположим, что что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей плоскости α (рис. 2).
С этой целью проведем через точку O прямые a’ , b’ и c’ соответственно параллельные прямым параллельные прямым a , b и c .
По определению угла между скрещивающимися прямыми прямая будет перпендикулярна прямым a’ и b’ , проходящим через точку O, и мы оказываемся в условиях уже рассмотренного случая.
Доказательство признака перпендикулярности прямой и плоскости завершено.
Замечание . Прямую, перпендикулярную к плоскости, часто называют перпендикуляром к плоскости. Точку перечения прямой, перпендикулярной к плоскости, с самой плоскостью называют основанием перпендикуляра.
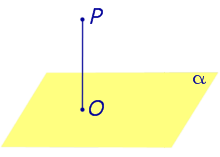
Так, например, на рисунке 1 точка O является основанием перпендикуляра, опущенного из точки P на плоскость α .
Свойства перпендикуляра к плоскости
Перечислим следующие свойства перпендикуляра к плоскости, доказательства которых мы оставляем читателю в качестве полезных упражнений.
| Рисунок | Свойство |
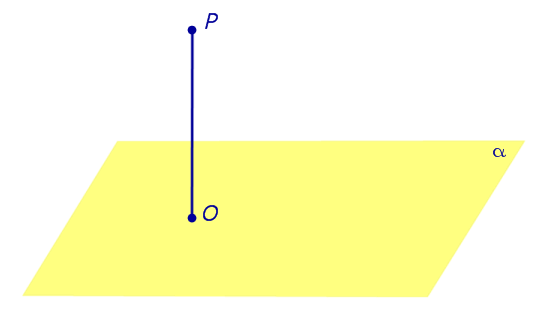 |
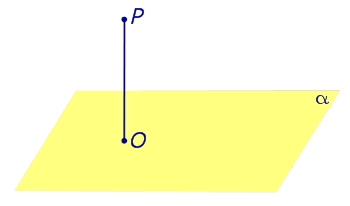
Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α. |
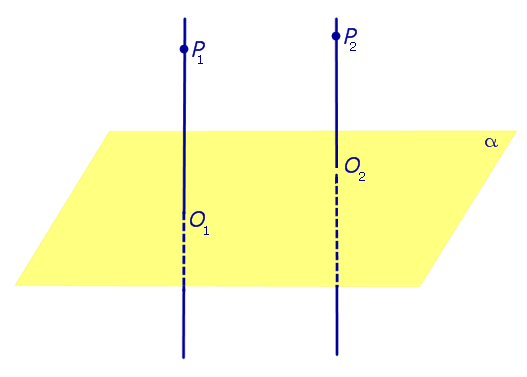 |
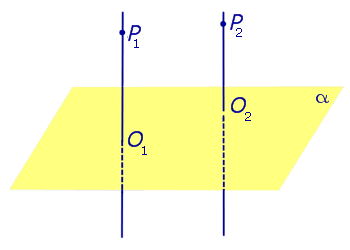
Два любых перпендикуляра к плоскости параллельны |
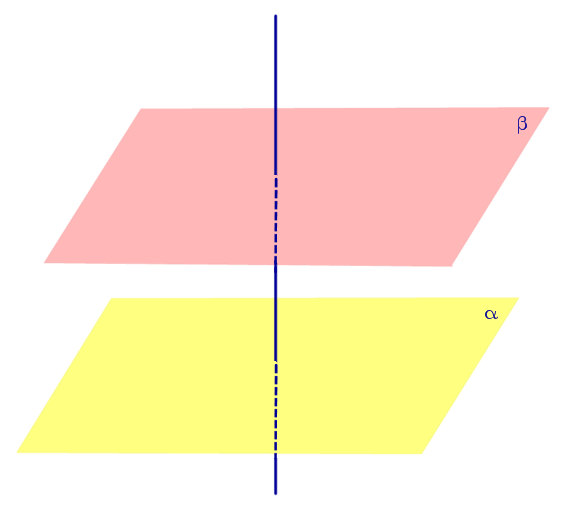 |
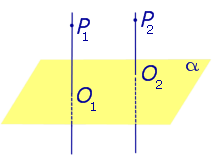
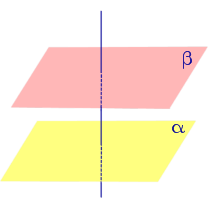
Плоскости, перпендикулярные к одной прямой, параллельны. |
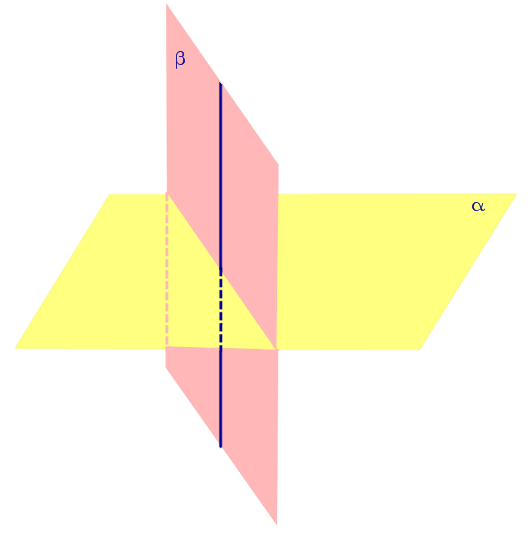 |
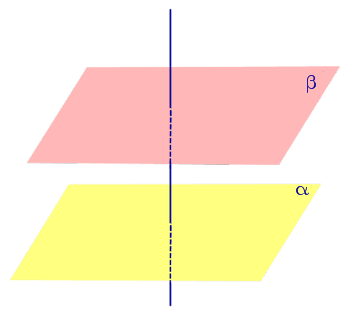
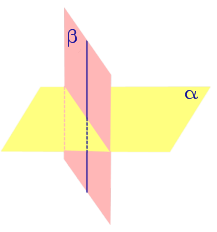
Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны. |
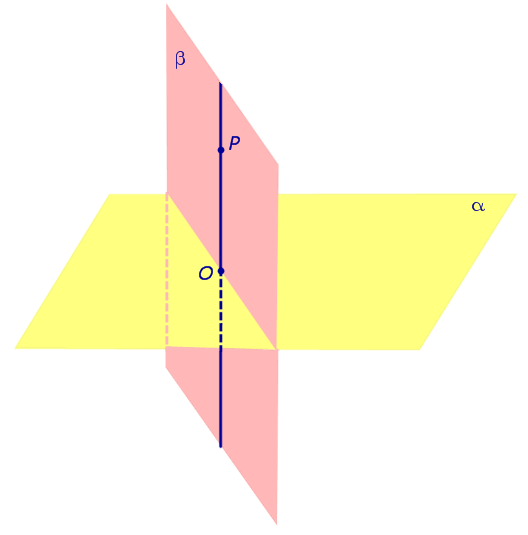 |
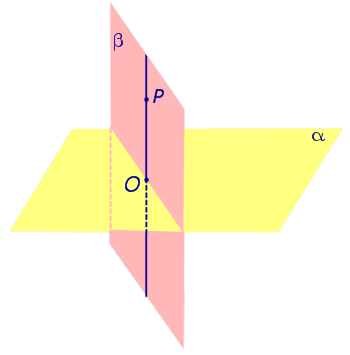
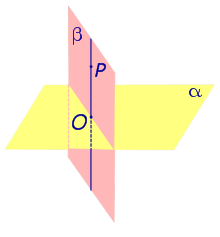
Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β. |
Свойство:
Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.
Свойство:
Два любых перпендикуляра к плоскости параллельны параллельны
Свойство:
Плоскости, перпендикулярные к одной прямой, параллельны.
Свойство:
Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.
Свойство:
Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.
36. Расстояние от точки до плоскости
Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.
Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:
A(x – x0) + B(y – y0) + C(z – z0) = 0.
Пример. Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и
Q(1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0.
Вектор нормали к плоскости 3х + 2у – z + 5 = 0 
Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и
В(3, 2, -1) перпендикулярно плоскости Х + У + 2Z – 3 = 0.
Искомое уравнение плоскости имеет вид: AX + BY + CZ + D = 0, вектор нормали к этой плоскости 


Таким образом, вектор нормали 
Итого, получаем уравнение плоскости: 11X — 7Y – 2Z – 21 = 0.
Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.
Находим координаты вектора нормали 
16 + 9 + 144 + D = 0
Итого, получаем искомое уравнение: 4X – 3Y + 12Z – 169 = 0
Пример. Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2; 1; 1),
1) Найти длину ребра А1А2.
2) Найти угол между ребрами А1А2 и А1А4.
3) Найти угол между ребром А1А4 и гранью А1А2А3.
Сначала найдем вектор нормали к грани А1А2А3 



Найдем угол между вектором нормали и вектором 

Искомый угол g между вектором и плоскостью будет равен g = 900 — b.
4) Найти площадь грани А1А2А3.
5) Найти объем пирамиды.

6) Найти уравнение плоскости А1А2А3.
Воспользуемся формулой уравнения плоскости, проходящей через три точки.
2x + 2y + 2z – 8 = 0
При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды.
Для запуска программы дважды щелкните на значке:
В открывшемся окне программы введите координаты вершин пирамиды и, нажимите Enter. Таким образом, поочередно могут быть получены все пункты решения.
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
http://interneturok.ru/lesson/geometry/10-klass/perpendikulyarnost-pryamyh-i-ploskostejb/rasstoyanie-ot-tochki-do-ploskosti-teorema-o-treh-perpendikulyarah
http://www.resolventa.ru/uslugi/uslugischoolvesh.htm
http://matica.org.ua/metodichki-i-knigi-po-matematike/kurs-vysshei-matematiki/36-rasstoianie-ot-tochki-do-ploskosti
На этой странице вы узнаете
- Как найти расстояние между мухой и столбом?
- Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
- Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?
Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее?
Расстояния между фигурами
Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое.
Таким образом, мы получаем расстояние между двумя точками.
Расстояние между точками — это длина отрезка, заключенного между ними.

Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров.
Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми.
Следовательно, мы пришли к выводу, что:
Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.
Иными словами, это отрезок, который мы прошли по асфальту.
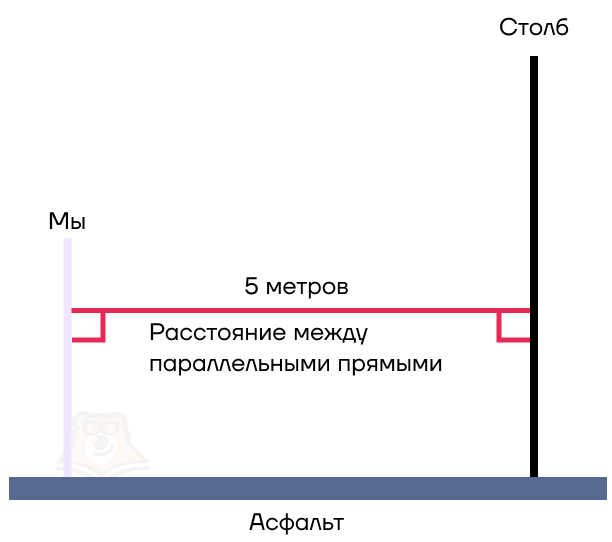
Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление.
Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.
Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.
Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
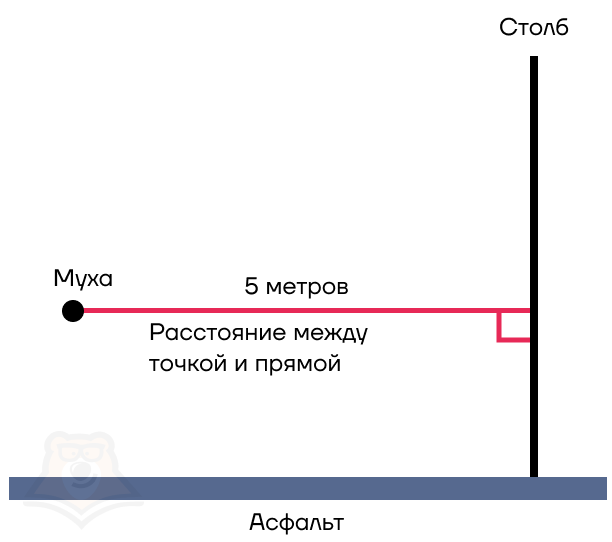
Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую.
Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?
Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке.
Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии. Прямые и плоскости в пространстве».
Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
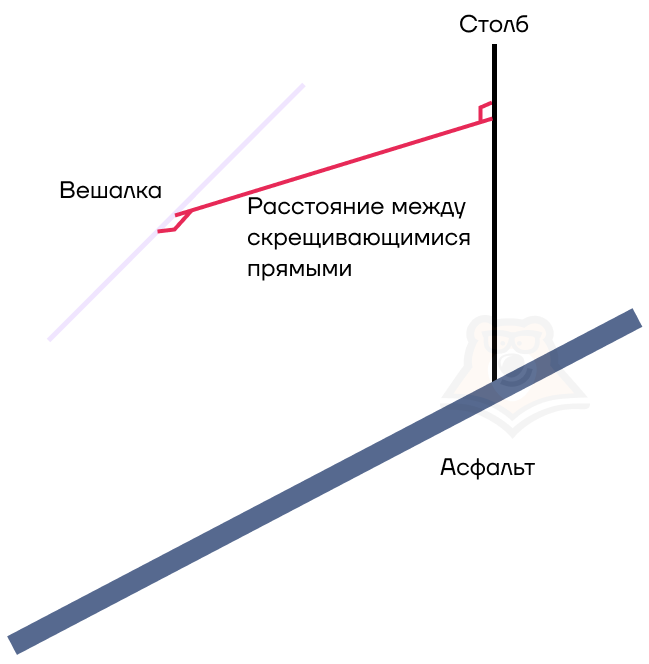
Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай.
В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола.
Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола.
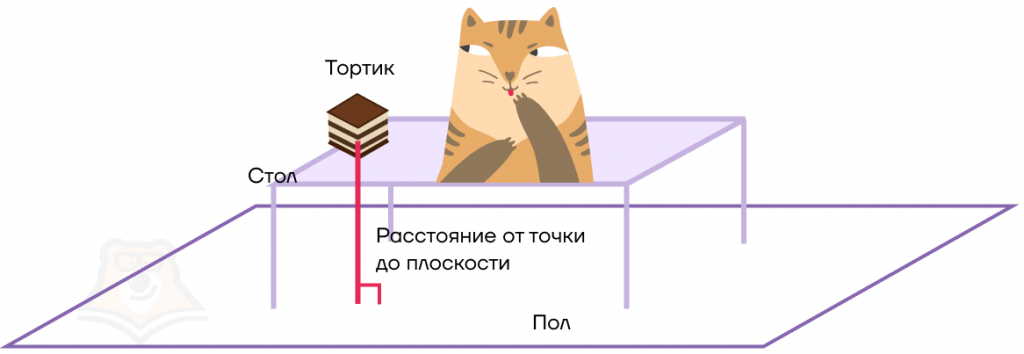
Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.
Расстояние от рулетика до пола можно было найти и другим способом, а именно найти расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу.
Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
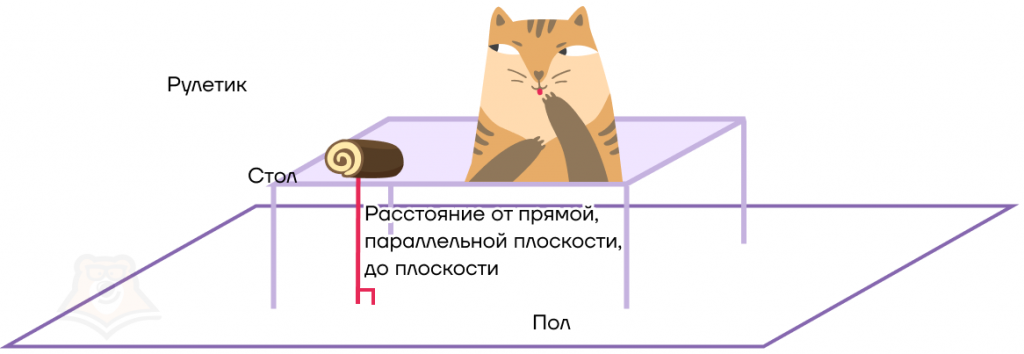
Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет.
Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола!
Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок.
Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике.
Теперь нам нужно найти расстояние между параллельными плоскостями.
Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
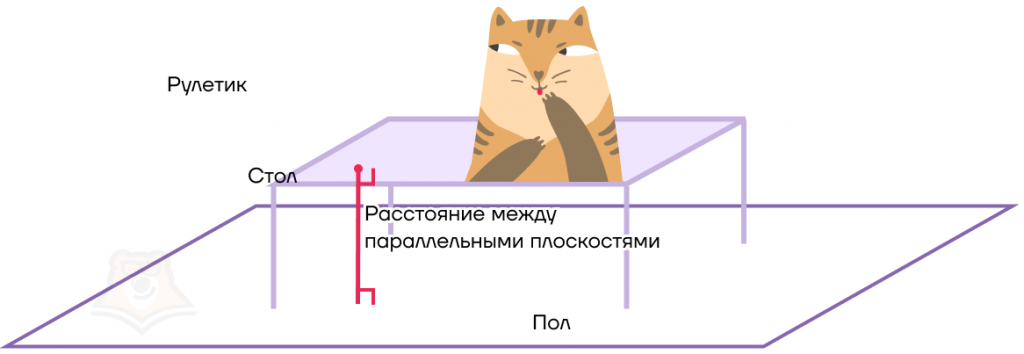
Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость.
Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами. Ничего сложного, верно?
При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.
Фактчек
- Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
- Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
- Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
Проверь себя
Задание 1.
Как найти расстояние между точкой и прямой?
- Найти длину любой линии от этой точки до прямой.
- Найти длину перпендикуляра, опущенного из этой точки на прямую.
- Невозможно найти расстояние между точкой и прямой.
- Ни один из вышеперечисленных вариантов.
Задание 2.
Как найти расстояние между скрещивающимися прямыми?
- Найти длину произвольной прямой между ними.
- Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
- Найти длину их общего перпендикуляра.
- Невозможно найти расстояние между скрещивающимися прямыми.
Задание 3.
Как найти расстояние от точки до плоскости?
- Найти длину перпендикуляра, опущенного из этой точки на плоскость.
- Найти длину произвольной линии, проведенной из точки к плоскости.
- Найти расстояние от точки до любой прямой, лежащей в плоскости.
- Невозможно найти расстояние между точкой и плоскостью.
Задание 4.
Как найти расстояние от прямой до плоскости?
- Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
- Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
- Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Невозможно найти расстояние между прямой и плоскостью.
Задание 5.
Как найти расстояние между параллельными плоскостями?
- Невозможно найти расстояние между параллельными плоскостями.
- Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
- Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
- Найти длину отрезка, соединяющего две произвольные прямые в плоскостях.
Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2
Министерство
образования и науки Российской Федерации
Калужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Московский
государственный технический университет
имени
Н.Э. Баумана»
кафедра
Высшая
математика
Учебное пособие по курсу аналитической геометрии «Решение типовых задач»
Составил:
Влайков Н.Д.
Рецензент:
к.ф.-м.н. Савотин А.И.
г.
Калуга, 2011 г.
Содержание.
-
Уравнение
прямой и плоскости в пространстве
стр. 2 -
Уравнения
кривых второго порядка
стр.7 -
Матричные
уравнения
стр. 8 -
Решение
СЛАУ
стр. 10 -
Задачи
для самостоятельного решения
стр. 14 -
Список
рекомендуемой литературы
стр. 16
-
Уравнение плоскости и прямой в пространстве.
Даны
координаты четырех точек в пространстве
.
Найти:
-
Уравнение
плоскости, проходящей через точки
.
-
Уравнение
и длину перпендикуляра, опущенного из
т.
на
плоскость, проходящую через точки
.
-
Расстояние
от т.
до прямой, проходящей через точки
.
-
Точку,
симметричную точке
,
относительно прямой, проходящей через
точки
.
-
Выполнить
чертеж.
Решение.
1.1.
Уравнение плоскости, проходящей через
три заданные точки,
,
имеет
вид:

Для наших точек:

Вычислим определитель:

уравнение искомой плоскости
.
1.2.
Составим уравнение перпендикуляра,
опущенного из т.
на
плоскость, проходящую через точки
.
Запишем это уравнение в каноническом
виде:
,
где
—
координаты точки, принадлежащей прямой,
а в знаменателях записаны соответствующие
координаты направляющего вектора
.
Координаты точки,
принадлежащей прямой, нам известны. В
качестве направляющего вектора, возьмем
нормальный вектор плоскости. Т.е.
.
Запишем
уравнение перпендикуляра:
.
Длина
перпендикуляра может быть найдена как
расстояние от т.
до плоскости
по формуле:
,
где
,
,
—
координаты нормального вектора плоскости,
а
— координаты точки
.
.
1.3. Расстояние от т. До прямой, проходящей через точки .
а)
Общий вид уравнения прямой проходящей
через две заданные точки
,
имеет
вид:
.
Для наших точек:
;
;
б)
Теперь найдем расстояние от точки
до
прямой
.
Для этого составим уравнение плоскости
,
проходящей через т.
,
перпендикулярно прямой
.
Уравнение плоскости, проходящей через
т.
,
с нормальным вектором
имеет вид:
.
Координаты
т.
известны,
а в качестве нормального вектора можно
выбрать направляющий вектор прямой
:
.
Подставим координаты в уравнение:
;
раскрыв скобки и приведя подобные
слагаемые получим уравнение плоскости
.
в)
Найдем координаты точки
—
точки пересечения прямой
и
плоскости
.
Точка
—
будет являться основанием перпендикуляра
опущенного из т.
на прямую
.
Т.к. т.
принадлежит и прямой и плоскости, ее
координаты должны удовлетворять двум
уравнениям, следовательно, координаты
можно найти, решив систему:

Для
этого перейдем к параметрическому
уравнению прямой
:
;

через
параметр
:

Подставим
в уравнение плоскости
и решим его:
;
.
Найдем
из системы:



Следовательно,
координаты т.
.
г)
Расстояние от т.
до прямой, проходящей через точки
можно найти как расстояние между точками
и
по формуле:
.
.
1.4.
Найдем координаты т.
,
симметричной точке
,
относительно прямой, проходящей через
точки
.
Координаты точки
можно найти из условия: т.
—
середина отрезка
(т.к. прямая
).
Координаты середины отрезка можно найти
по формулам:
,
,
.
Следовательно, координаты т.
можно
найти так:
,
,
.
Т.е.
,
,
.
.
1.5.
Построим несколько поясняющих чертежей:
1.5.1.
Построим
точки
.
Для примера построим т.
Рис
1.1 Точка
1.5.2.
На рис 1.2 построим плоскость
,
приведя общее уравнение к уравнению
плоскости в отрезках:
;
;
Рис
1.2 плоскость
.
1.5.3.
Изобразим прямую
:
Рис
1.3 прямая
1.5.4.
Построим точку
:
Рис
1.4 Точка
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти длину перпендикуляра
Строго говоря, перпендикуляром называют прямую, которая пересекает заданную линию под углом в 90°. Прямая бесконечна по определению, поэтому говорить о длине перпендикуляра неправильно. Говоря так, обычно имеют в виду расстояние между двумя точками, лежащими на перпендикуляре. Например, между заданной точкой и ее нормальной проекцией на плоскость или между точкой в пространстве и точкой пересечения перпендикуляра, опущенного из нее, с прямой линией.
Необходимость рассчитать длину перпендикуляра может возникнуть, если он опущен из точки с указанными в условиях координатами A(X₁;Y₁) на прямую, заданную уравнением a*X + b*Y + C = 0. В этом случае сначала подставьте координаты точки в уравнение прямой и рассчитайте абсолютное значение левой части тождества: |a*X₁ + b*Y₁ + C|. Например, при координатах точки A(15;-17) и уравнении прямой 3*X + 4*Y + 140 = 0 результатом этого шага должно стать число |3*15 + 4*(-17) + 140| = |45-61+140| = 124.
Рассчитайте нормирующий множитель. Это дробь, в числителе которой стоит единица, а в знаменателе — квадратный корень из суммы квадратов множителей по обеим координатным осям из уравнения прямой: 1/√(X²+Y²). Для использованного выше примера величина нормирующего множителя должна быть равна 1/√(3²+4²) = 1/√25 = 0,2.
Приведите уравнение прямой к нормальному виду — умножьте обе части равенства на нормирующий множитель. В общем виде результат должен выглядеть так: (a*X+b*Y+C)/√(X²+Y²) = 0. Левая часть этого уравнения и определяет длину перпендикуляра в общем виде: d = (a*X+b*Y+C)/√(X²+Y²). А в практических расчетах просто перемножьте полученное на первом шаге число и рассчитанный на втором шаге коэффициент. Для примера из первого шага ответом должно стать число 124*0,2=24,8 — такова длина перпендикулярного линии отрезка, соединяющего ее с заданной точкой.
Для нахождения длины перпендикуляра, опущенного из точки с известными трехмерными координатами A(X₁;Y₁;Z₁) на плоскость, заданную уравнением a*X + b*Y + c*Z + D = 0 используйте такую же последовательность операций. В этом случае под знак радикала в нормирующем множителе добавится третье слагаемое √(X²+Y²+Z²), как и в числитель дроби формулы, определяющей длину перпендикуляра в общем виде: d = (a*X+b*Y+c*Z+D)/√(X²+Y²+Z²).