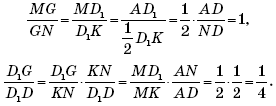Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Задания Д13 № 920
i
В правильной треугольной пирамиде SABC точка M − середина ребра AB, S − вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
Спрятать решение
Решение.
Найдем площадь грани SAB:
Отрезок SM является медианой равнобедренного треугольника SAB, проведённой к его основанию, а значит, SM является и его высотой. Тогда
Ответ: 10.
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
В данной задаче мы имеем правильную треугольную пирамиду SABC, где S — вершина, а точка N — середина ребра BC. Известно, что AB = 1 и площадь боковой поверхности равна 3. Нам нужно найти длину отрезка SN.
Поскольку треугольник ABC — прямоугольный, то мы можем воспользоваться теоремой Пифагора, чтобы найти длину грани AC. Из условия задачи мы знаем длину стороны AB, которая равна 1, и площадь боковой поверхности, которая равна 3. Зная формулу площади боковой поверхности, мы можем записать:
S = (1/2) * p * l,
где S — площадь боковой поверхности, p — периметр основания и l — длина боковой грани.
Для правильной треугольной пирамиды периметр основания равен 3, так как сторона треугольника ABC имеет длину 1. Таким образом, мы можем выразить длину боковой грани:
l = (2 * S) / p = (2 * 3) / 3 = 2.
Теперь мы можем найти длину грани AC, используя теорему Пифагора:
AC^2 = AB^2 + BC^2 = 1^2 + 2^2 = 5.
AC = sqrt(5).
Отрезок SN является медианой треугольника ABC, которая делит грань AC пополам. Таким образом, мы можем найти длину отрезка SN как половину длины грани AC:
SN = AC / 2 = sqrt(5) / 2.
Итак, мы получили ответ: длина отрезка SN равна sqrt(5) / 2.
Получи верный ответ на вопрос 🏆 «В правильной треугольной пирамиде SABC Q — середина ребра АВ, S — вершина. Известно, что SQ = 28, а площадь боковой поверхности равна 294. …» по предмету 📕 Геометрия, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Геометрия » В правильной треугольной пирамиде SABC Q — середина ребра АВ, S — вершина. Известно, что SQ = 28, а площадь боковой поверхности равна 294. Найдите длину отрезка BC.
Что проще? Разные подходы к решению стереометрических задач
В «Математике» 2009, № 6 были опубликованы две статьи,
посвященные векторно-координатному методу решения стереометрических задач [1,
2]. Мы приведем «чисто геометрические» решения всех 10 задач, разобранных в [1],
и обсудим плюсы и минусы двух подходов, а также рассмотрим некоторые
стереометрические задачи ЕГЭ. Нумерация задач сохранена.
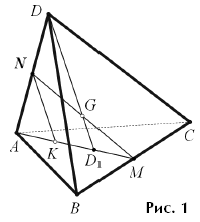
Задача 1. Отрезок, соединяющий вершину тетраэдра с
центроидом противолежащей грани, называется медианой этого тетраэдра; отрезок,
соединяющий середины противоположных ребер тетраэдра, называется его бимедианой.
Докажите:
а) что все медианы тетраэдра пересекаются в одной точке и эта
точка делит каждую из медиан в отношении 3 : 1, считая от вершины;
б) все бимедианы тетраэдра пересекаются в одной точке и
делятся ею пополам;
в) точка пересечения бимедиан тетраэдра совпадает с точкой
пересечения его медиан.
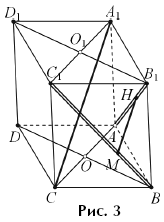
Решение. Рассмотрим произвольную медиану, например, DD1
и произвольную бимедиану, например, MN, где M — середина BC.
Они лежат в одной плоскости AMD, и потому пересекаются в некоторой точке
G. Зная отношения
AN : ND = 1 : 1 и AD1 : D1M
= 2 : 1,
легко найти, в каких отношениях отрезки MN и DD1
делят друг друга. Проще всего воспользоваться теоремой Менелая, из которой сразу
получим, что
MG = GN и DG = 3GD1.
Следовательно, все бимедианы имеют общую середину (G),
и эта точка делит любую медиану в отношении 3 : 1, считая от вершины тетраэдра,
что и требовалось доказать.
Если применение теоремы Менелая «недостаточно элементарно»,
нужные отношения можно найти, проведя, например, отрезок NK, параллельный
DD1 (рис. 1); тогда из теоремы Фалеса и подобия
соответствующих треугольников получим:
Задача 2.В параллелепипеде АВСDА1В1С1D1
точка М — середина диагонали А1С1
грани A1B1C1D1,
точка K — середина ребра ВВ1. Докажите, что прямые А1В1,
KМ и ВС1 параллельны некоторой плоскости.
Решение. Плоскость α = BC1D1 (рис. 2) содержит прямую BC1,
параллельна прямой A1B1 (так как C1D1
C
A1B1) и параллельна прямой MK (так
как MK C
BD1 как средняя линия треугольника BB1D1).
Поэтому все три рассматриваемые прямые параллельны любой плоскости, параллельной
α.
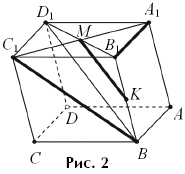
Задача 3. На диагоналях АВ1 и ВС1
граней AA1B1B и ВВ1С1С
параллелепипеда ABCDA1B1C1D1
взяты точки соответственно Н и M так, что отрезки НM и A1C
параллельны. Найдите отношение длин этих отрезков.
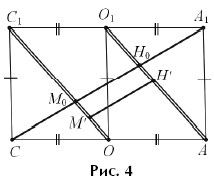
Решение. Нарисуем параллельную проекцию данной фигуры
(рис. 3) вдоль прямой BD; для определенности — на плоскость ACC1.
Получится рисунок 4: вся прямая BD проецируется в одну точку, а именно, в
точку O ее пересечения с AC, то есть в середину AC, и,
аналогично, прямая B1D1, параллельная BD,
перейдет в середину O1 отрезка A1C1.
Поскольку проекции AO1 и OC1 отрезков AB1
и BC1 параллельны, все отрезки MRHR
с концами на OC1 и AO1, параллельные A1C,
в том числе и проекция рассматриваемого отрезка MH, равны между собой.
Таким образом, они равны отрезку M0H0,
высекаемому прямыми AO1 и OC1
непосредственно на диагонали A1C (см. рис. 4; на самом
деле, этот отрезок как раз и будет проекцией отрезка MH, хотя это нам
сейчас и неважно). По теореме Фалеса CM0 = M0H0
= H0A1; следовательно, MH :
A1C = M0H0 : A1C
= 1 : 3.
В решении использовано то, что проекция отрезка MH —
это отрезок, параллельный A1C (или лежащий на прямой
A1C), и что эти отрезки пропорциональны своим проекциям;
эти факты следуют из известных основных свойств параллельной проекции.
Задача 4. В кубе ABCDA1B1C1D1,
ребро которого равно 6, найдите:
а) расстояние от вершины А1 до плоскости
ВС1D;
б) угол между диагональю ВА1 грани АА1В1В
и плоскостью ВС1D .
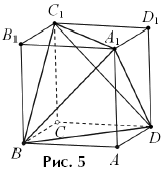
Решение. а) Рассмотрим тетраэдр A1BC1D
(рис. 5). Все его ребра — диагонали граней куба (они равны ), то есть этот
тетраэдр правильный. Расстояние от его вершины A1 до грани
BC1D есть его высота, и найти ее можно через объем.
Тетраэдр получается в результате отрезания от куба плоскостями его граней
четырех равных «прямоугольных» тетраэдров. Возьмем один из них, например,
ABDA1. Площадь его основания ABD вдвое меньше площади
грани куба, а высота равна высоте куба, поэтому его объем в 6 раз меньше объема
куба. Следовательно,
Статья опубликована при поддержке компании «Евина». Карнизы, фризы, кронштейны, пилястры, балясины, панно, порезки и другое. Гарантия качества, доступные цены, изготовление и реставрация лепнины. Узнать подробную информацию о компании, посмотреть каталог лепнины, цены и контакты Вы сможете
по ссылке — www.evina.ru.
Площадь S равностороннего треугольника BDC1
со стороной равна
Следовательно, искомое расстояние равно
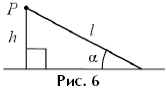
б) Если из точки P проведены к некоторой плоскости
наклонная длины l и перпендикуляр h (рис. 6), то угол
a между
наклонной и плоскостью можно найти по формуле В нашей задаче
и
Задача 5. Найдите расстояние между скрещивающимися
диагоналями АВ1 и ВС1 смежных граней АА1В1В
и ВВ1С1С куба ABCDA1B1C1D1,
если ребро этого куба равно 12.
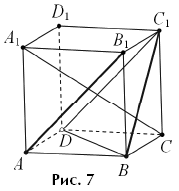
Решение. Поскольку AB1DC1,
плоскость BDC1 параллельна прямой AB1 (рис.
7). Следовательно, искомое расстояние равно расстоянию от любой точки прямой
AB1, например, от A, до указанной плоскости и найти его
можно через объем, как в задаче 4. С поправкой на другую длину ребра куба, мы,
фактически, уже вычислили и объем тетраэдра CBDC1 (он равен
объему ABDA1), и площадь грани BDC1.
Ответ:
Данную задачу можно было бы решить и с помощью задачи 3,
заметив, что диагональ A1C куба перпендикулярна и к
BC1, и к AB1 (это следует из теоремы о трех
перпендикулярах: например, проекция A1C на грань BCC1B1
есть диагональ B1C этой грани и перпендикулярна BC1,
значит, и A1C BC1). Таким образом, общий перпендикуляр прямых BC1
и AB1 есть отрезок с концами на этих прямых, параллельный A1C.
А в задаче 3 мы нашли, что он втрое короче A1C.=
Задача 6. Около правильной четырехугольной пирамиды,
каждое ребро которой равно 10, описан цилиндр так, что все вершины пирамиды
находятся на окружностях оснований цилиндра. Найдите объем и площадь боковой
поверхности цилиндра.
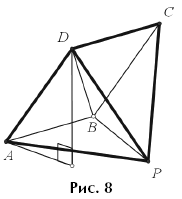
Решение этой задачи состоит из двух частей: сначала нужно
понять, как расположена данная пирамида PABCD внутри цилиндра и какие ее
параметры нужно найти, чтобы получить радиус основания и высоту цилиндра, а
затем все посчитать. Первая часть при любом подходе является «геометрической», а
во второй части центральный момент — вычисление высоты цилиндра, которая равна
расстоянию от плоскости боковой грани пирамиды (например, ABP; рис. 
противоположной стороны основания (CD), параллельной этой плоскости. То
есть нужно найти расстояние от вершины D (или C, или вообще любой
точки стороны) до плоскости ABP. В [1] это расстояние вычисляется
векторным методом, а мы, в качестве упражнения, предлагаем читателю найти его
через объем тетраэдра ABPD.
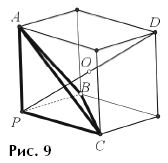
Задача 7. В треугольной пирамиде РАВС все плоские
углы при вершине Р прямые. Найдите площадь сферы, описанной около этой
пирамиды, если РА = 2, РВ = 3, РС = 4.
Решение. Достроим данную пирамиду до прямоугольного
параллелепипеда (рис. 9). Как известно, его диагонали равны и имеют общую
середину O. Точка O равноудалена от вершин параллелепипеда и,
следовательно, является центром его описанной сферы, которая, разумеется, будет
и описанной сферой пирамиды. Следовательно, радиус R сферы равен половине
диагонали d параллелепипеда, а ее площадь равна
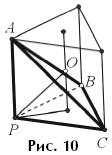
Задача 8. В
тетраэдре РАВС два плоских угла при вершине Р прямые, а величина
третьего плоского угла равна 60°.
Найдите радиус сферы, описанной около этой пирамиды, если РА = РВ = РС = 12.
В этом случае тетраэдр можно достроить до правильной призмы,
искомая сфера будет описана около этой призмы и ее центр будет серединой
отрезка, соединяющего центры оснований (рис. 10). Вычисление радиуса оставляем в
качестве упражнения.
Задачу 9 из [1] мы пропустим — это упрощенный вариант
задачи 7.
Задача 10. В трехгранном угле РАВС известны
величины плоских углов при вершине Р:
АРВ
= ВРС
= АРС
= 60°.
Сфера, центр которой удален от вершины Р на расстояние, равное касается
всех ребер этого угла. Найдите радиус данной сферы.
Решение. Рассматриваемый угол равен трехгранному углу
правильного тетраэдра. Поместим такой тетраэдр в куб, как это было сделано на
рисунке 5. Очевидно, что вписанная в куб сфера касается всех ребер тетраэдра, то
есть диагоналей граней куба (в их серединах). Ее центр находится в центре куба.
Если радиус сферы равен R, то ребро куба равно 2R, а расстояние от
его центра до вершины равно Поскольку оно равно
то
(Заметим, что решение этой
задачи занимает в [1] целую страницу!)
Разобранные примеры убеждают, что по части простоты
(краткости) и тем более изящности векторно-координатные решения не могут
тягаться с геометрическими. Достоинства векторно-координатного метода имеют
более прагматический характер. Во-первых, этот метод более «алгоритмичен»,
позволяет решать задачи «не думая», по шаблону. Во-вторых, он универсален —
предлагаемые алгоритмы решения применимы к любой геометрической конфигурации. И,
наконец, он практически не требует геометрических обоснований, которые все равно
почти никогда не бывают полными. Именно эти соображения выходят на первый план,
например, в условиях экзамена. Но нужно понимать, что они оборачиваются и тем,
что решения зачастую получаются громоздкими, с большим количеством вычислений,
которые оторваны от геометрического смысла, а значит, и с большей вероятностью
арифметических ошибок, которые трудно отследить. Кроме того, в школьном курсе
геометрии остались лишь только самые основные сведения о векторах и координатах
в пространстве, так что круг задач, в которых их целесообразно применять,
невелик. В первую очередь к таким задачам можно отнести задачи на углы между
скрещивающимися прямыми, в частности, на перпендикулярность. А в задачах на
нахождение расстояний удобнее использованный нами выше метод объемов, который не
уступает векторному методу в смысле «алгоритмичности», но, как правило, приводит
к более экономным вычислениям. Еще один полезный метод — метод проекций. Он был
использован в решении задачи 3, но применим и ко многим другим задачам типа
рассмотренных выше; подробнее см. [3].
Интересно посмотреть с этой точки зрения на стереометрические
задачи ЕГЭ. В [2] две такие задачи решены с применением координат на одном из
этапов решения. Вряд ли можно сказать, что это приносит особые дивиденды по
сравнению с «обычными» решениями, да и в целом анализ задач ЕГЭ показывает, что
они не очень «приспособлены» к векторно-координатному подходу. А вот хорошие
«геометрические» решения, использующие, как и многие из примеров выше, удачные
конкретные данные, встречаются. Такие решения иногда выглядят не совсем
«честными», но для экзаменационных задач они достаточно типичны — ведь задачи
составляются так, чтобы их можно было решить, да еще и чтобы ответ был хорошим.
Приведем пример из ЕГЭ 2008 г.
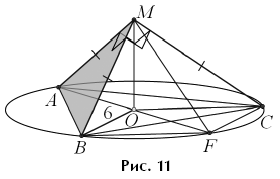
Задача 11. Дан конус с вершиной M, радиус
основания которого равен 6. На окружности его основания выбраны точки A,
B, C так, что углы BMA, AMC, CMB равны 90°
каждый. Точка F выбрана на дуге BC окружности основания конуса, не
содержащей точки A, так, что объем пирамиды MABFC наибольший.
Найдите расстояние от точки F до плоскости MAB.
Задача решается в несколько строк и практически без
вычислений. Ясно, что пирамида MABC правильная (рис. 11), а F —
середина дуги BC (кстати, последнее разрешалось не доказывать на
экзамене). Искомое расстояние hF — это высота пирамиды MABF,
опущенная на грань ABM.
Заметим, что высоту hC пирамиды MABC,
опущенную на ту же грань, легко найти — она совпадает с ребром CM и равна
Поэтому достаточно найти отношение hF :
hC, а оно равно отношению объемов пирамид. Имеем:
(мы учли, что пирамиды имеют общую высоту, проведенную из
вершины M; последнее равенство очевидно). Отсюда
Ответ:
Интересно, что аналогичные задачи из большинства других
вариантов этого же экзамена оказались значительно сложнее, что было явной
недоработкой составителей ЕГЭ. Предлагаем одну из этих задач в качестве
упражнения. Общий план ее решения такой же, как и в предыдущей задаче, но здесь
у нас нет такого подарка, как практически данная эталонная величина, с которой
можно сравнить искомое расстояние (длина ребра CM, равная расстоянию от
C до плоскости ABM). Поэтому приходится потрудиться. А при
вычислениях можно использовать и метод объемов, и проекцию.
Задача 12. Дан конус с вершиной M, радиус
основания которого равен В основание этого конуса вписан шестиугольник ABCDEF
так, что углы AMB, BMC, CMD, DME, EMF, FMA
равны a
каждый, причем На дуге BC окружности основания конуса, не содержащей
точки A, выбрана точка L так, что объем пирамиды MABLCDEF
наибольший. Найдите расстояние от точки L до плоскости ABM.
Литература
1. Потоскуев Е. Векторный метод решения
стереометрических задач // Математика, 2009, № 6, с. 27–34.
2. Фалин Г., Фалин А. Применение метода координат
для решения задач ЕГЭ по стереометрии // Математика, 2009, № 6, с. 24–26.
3. Дубровский В. Неожиданный ракурс // Квант, 1980, № 2, с. 46–50.
Дубровский В.
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023