Как найти длину наклонной прямоугольного треугольника

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Сторона треугольника через угол

Катет прямоугольного треугольника через угол и второй катет

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Прямоугольный треугольник — это треугольник у которого один из углов прямой (равен 90°). Стороны треугольника образующие прямой угол называются катетами треугольника. Сторона противоположная прямому углу называется гиппотенузой.

Радиан — это угол, соответствующий дуге, длина которой равна её радиусу. Своё название данная едииница измерения получила от слова радиус. Имеет обозначение: рад, международное: rad.

Радианы являются основной единицей используемой в вичислениях.

Градус — общепринятая единица измерения плоского угла, которая равняется dfrac<1> <90>части прямого угла или dfrac<1> <360>часть окружности. В отличии от радиан, градусы являются чисто символическими единицами измерения, так сказать «взятые с потолка» и не имеют в своём значении ни какого математического основания.

Причина выбора градуса в качестве единицы измерения углов неизвестна. В быту измерение углов в градусах выглядит удобнее и понятнее, но что касается математических вычислений, то здесь основными единицами являются радианы.

Формула нахождения стороны через угол

Посчитать длину одного из катетов треугольника можно через второй катет и угол противолежащий искомой стороне:

Свойства перпендикуляра и наклонной

Свойства перпендикуляра и наклонной вытекают из теоремы Пифагора и признаков равенства прямоугольных треугольников.

1) Любая наклонная больше перпендикуляра.

Дано: A∉a, AB — перпендикуляр,

Так как AB — перпендикуляр к прямой a, то треугольник ABC — прямоугольный.

По теореме Пифагора AC²=AB²+BC².

Так как BC>0, то и BC²>0.

Следовательно, AB²+BC²>AB². Отсюда, AC²>AB². Поскольку AC>0 и AB>0, то AC>AB.

Что и требовалось доказать.

2) Равные наклонные имеют равные проекции.

Дано: A∉a, AB — перпендикуляр,

AC и AD — наклонные,

BC и BD — их проекции,

Так как AB — перпендикуляр к прямой a, то треугольники ABC и ABD — прямоугольные.

1) AC=AD (по условию);

2) AB — общая сторона.

Следовательно, треугольники ABC и ABD равны (по катету и гипотенузе).

Из равенства треугольников следует равенство соответствующих сторон. Значит, BC=BD.

Что и требовалось доказать.

И обратно: если проекции наклонных равны, то и наклонные тоже равны.

Кроме того, из этого доказательства следует, что равные наклонные образуют равные углы с прямой a; углы между равными наклонными и перпендикуляром также равны.

3) Из двух наклонных больше та, у которой проекция больше.

Дано: A∉a, AB — перпендикуляр,

AC и AD — наклонные,

BC и BD — их проекции,

Так как AB — перпендикуляр к прямой a, то треугольники ABC и ABD — прямоугольные.

По теореме Пифагора AC²=AB²+BC² и AD²=AB²+BD².

Отсюда, AB²=AC²-BC² и AB²=AD²-BD².

Приравнивая правые части равенств, имеем: AC²-BC²=AD²-BD².

Так как BC>BD, то и BC²>BD².

Значит, и AC²>AD². А так как AC>0 и AD>0, то AC>AD.

Что и требовалось доказать.

И обратно: б о льшей наклонной соответствует б о льшая проекция.

Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Найти гипотенузу по катету и прилежащему к нему острому углу

Найти гипотенузу по катету и противолежащему к нему острому углу

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Найти катет по гипотенузе и прилежащему к нему острому углу

Найти катет по гипотенузе и противолежащему к нему острому углу

Найти катет по второму катету и прилежащему к нему острому углу

Найти катет по второму катету и противолежащему к нему острому углу

См. также

Примечание. Текст задачи взят с форума. Если Вы не нашли решения нужного типа задачи — пишите на форуме. Наверняка курс будет дополнен.

Задача.

Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .

Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.

Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора:
BC 2 + AC 2 = AB 2
и
BC 2 + CD 2 = BD 2

или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2

Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2

Подставим значения, которые известны по условию
AB 2 — 7 2 = BD 2 — 1
AB 2 — 49 = BD 2 — 1

Поскольку длины наклонных соотносятся как 1:2, обозначив длину BD как х (икс), получаем, что длина AB = 2x, откуда
4х 2 — 49 = х 2 — 1
3х 2 = 48
х 2 = 16
х = 4

Откуда длина второй наклонной равна 4 * 2 = 8 см

Ответ: 4 и 8 см.

Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.

Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .

Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора: BC 2 + AC 2 = AB 2

и
BC 2 + CD 2 = BD 2

или
BC 2 = AB 2 — AC 2
и
BC 2 = BD 2 — CD 2

Теперь, учитывая, что левые части обоих выражений равны, получаем
AB 2 — AC 2 = BD 2 — CD 2

Примем во внимание, что большая наклонная имеет большую проекцию.
Кроме того, поскольку одна наклонная на 26 см больше другой, то пусть BD = AB — 26.

Откуда AB = BD + 26

Подставим значения, которые известны по условию

(BD + 26) 2 — 40 2 = BD 2 — 12 2
BD 2 + 52BD + 676 — 1600 = BD 2 — 144
52BD = 780
BD = 15

Наклонная к прямой

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

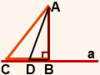
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

2 Comments

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.