Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Теория
(теоретические сведения см. также в уроке «Правильный тетраэдр»)
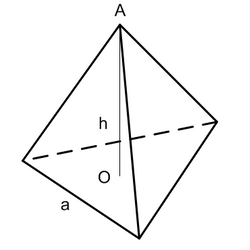
Правильный тетраэдр — это правильная треугольная пирамида у которой все грани являются равносторонними треугольниками.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
У тетраэдра 4 грани, 4 вершины и 6 ребер.
Основные формулы для правильного тетраэдра приведены в таблице.
Где:
S — Площадь поверхности правильного тетраэдра
V — объем
h — высота, опущенная на основание
r — радиус вписанной в тетраэдр окружности
R — радиус описанной окружности
a — длина ребра
Практические примеры
Задача.
Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3
Решение.
Поскольку все ребра треугольной пирамиды равны — она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a2√3 .
Тогда
S = 3√3
Ответ: 3√3
Задача.
Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды
Решение.
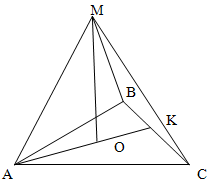
Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то
AO = R = √3 / 3 a
AO = 4√3 / 3
Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM
AO2 + OM2 = AM2
OM2 = AM2 — AO2
OM2 = 42 — ( 4√3 / 3 )2
OM2 = 16 — 16/3
OM = √(32/3)
OM = 4√2 / √3
Объем пирамиды найдем по формуле V = 1/3 Sh
При этом площадь основания найдем по формуле S = √3/4 a2
V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 )
V = 16√2 / 3
Ответ: 16√2 / 3 см
0
Площадь боковой поверхности правильной треугольной пирамиды |
Описание курса
| Пирамида и вписанный конус
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: длина медианы к стороне cd
|
|||
|
дан тетраэдр ABCD, нужно найти длину медианы к стороне СD мне нужно выполнить это задание, но пока не понимаю, медиана тетраэдра — это ведь отрезок, соединяющий вершину и центроид противолежащей грани, но у меня в задании сказоно найти медиану к стороне СD. Поясните, в чём тут подвох?
|
||
| Вернуться к началу |
|
||
|
arkadiikirsanov |
Заголовок сообщения: Re: длина медианы к стороне cd
|
|
vladislav1 писал(а): дан тетраэдр ABCD, нужно найти длину медианы к стороне СD мне нужно выполнить это задание, но пока не понимаю, медиана тетраэдра — это ведь отрезок, соединяющий вершину и центроид противолежащей грани, но у меня в задании сказоно найти медиану к стороне СD. Поясните, в чём тут подвох? Интересно, а из такого условия вообще длину какого-либо элемента тетраэдра можно найти?
|
|
| Вернуться к началу |
|
|
vladislav1 |
Заголовок сообщения: Re: длина медианы к стороне cd
|
|
само собой все координаты точек есть
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
В треугольнике АВС АВ= 10 см, ВС=4 см, AC = 8см. На стороне
в форуме Геометрия |
AllaL |
4 |
1077 |
25 фев 2017, 21:26 |
|
Равенство треугольников по двум углам и стороне
в форуме Геометрия |
Steys |
7 |
213 |
19 ноя 2020, 12:36 |
|
Построить треугольник по углу стороне и медиане
в форуме Геометрия |
immensity92 |
1 |
775 |
22 май 2016, 17:20 |
|
Найти точку, где биссектриса от А соответствует стороне ВС
в форуме Аналитическая геометрия и Векторная алгебра |
RedDragon |
1 |
267 |
14 дек 2016, 22:00 |
|
Найти сторону треугольника по медиане и стороне
в форуме Геометрия |
marie_t |
7 |
758 |
26 мар 2014, 13:44 |
|
Средняя линия треугольника по одной стороне и основанию
в форуме Геометрия |
Digenets |
1 |
231 |
27 сен 2018, 20:38 |
|
Отношение периметра описанного круга к стороне квадрата
в форуме Теория чисел |
HaI7I7y |
2 |
79 |
28 дек 2022, 18:27 |
|
Отношение периметра описанного круга к стороне идеального тр
в форуме Теория чисел |
HaI7I7y |
10 |
125 |
28 дек 2022, 17:18 |
|
Медианы в треугольнике
в форуме Геометрия |
alinamu |
2 |
235 |
27 фев 2019, 01:00 |
|
Нахождение медианы
в форуме Математическая статистика и Эконометрика |
matema+tika |
0 |
108 |
25 май 2022, 19:27 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 6 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы тетраэдра
Для расчёта всех основных параметров тетраэдра воспользуйтесь калькулятором.
Свойства тетраэдра
- Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед
- Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы — пополам
- Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер
Виды тетраэдров
-
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину - Равногранный тетраэдр — это такой тетраэдр, у которого все грани треугольники равны
- Ортоцентрический тетраэдр — это такой тетраэдр, у которого каждая высота, опущенная из вершины на противоположную грань, пересекается с остальными высотами в одной точке
- Прямоугольный тетраэдр — это такой тетраэдр, у которого каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине
-
Каркасный тетраэдр — это такой тетраэдр, который соответствует следующим условиям:
- есть сфера, которая касается каждого ребра
- суммы длин ребер, что скрещиваются равны
- суммы двугранных углов при противоположных ребрах равны
- окружности, которые вписаны в грани, попарно касаются
- каждый четырехугольник, образующийся на развертке тетраэдра — описанный
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке
- Инцентрический тетраэдр — это такой тетраэдр, у которого отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке
Формула высоты тетраэдра
$$
AO = {sqrt{2 over 3}} * a
$$
Формула объёма тетраэдра
$$
V = {sqrt{2} over 12} * a^3
$$
Основные формулы для правильного тетраэдра
-
Формула площади
$$
S = a^2 * sqrt{3}
$$ -
Радиус вписанной сферы, Rвпис
$$
R_{впис} = a * {sqrt{6} over 12}
$$ -
Радиус описанной сферы, Rопис
$$
R_{опис} = a * {sqrt{6} over 4}
$$







 , просто я не понял, что найти нужно
, просто я не понял, что найти нужно