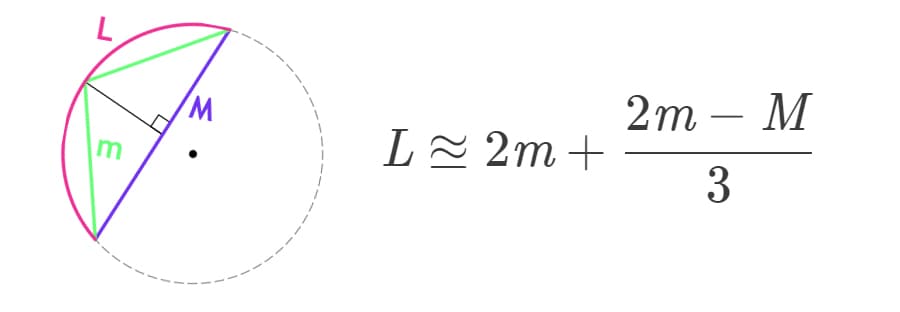{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности — важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
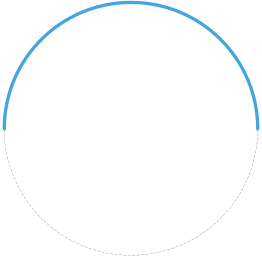
Если обобщить, то дуга окружности — это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность — это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r — радиус окружности.
-
Полуокружность — это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
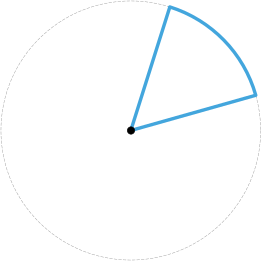
Сектор окружности — это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
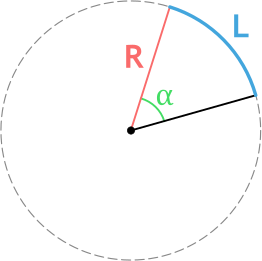
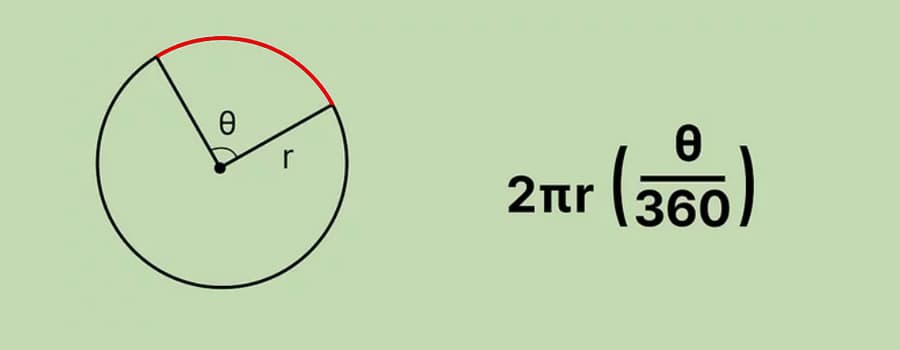
Формула длины дуги окружности через радиус и угол
{L = dfrac{pi R alpha}{180degree}}
R — радиус окружности
α — центральный угол (угол между радиусами) в градусах
{L = R alpha}
R — радиус окружности
α — центральный угол (угол между радиусами) в радианах
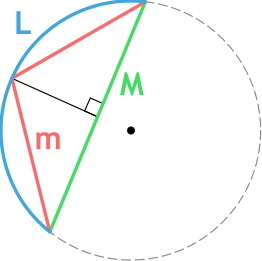
Формула длины дуги окружности по формуле Гюйгенса
{L approxeq 2m + dfrac{2m-M}{3}}
m — длина хорды m
M — длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак «равно или почти равно», который записывается так — «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое длина дуги?
Дуга — это часть окружности, ограниченная двумя точками на окружности.
Для вычисления длины дуги необходимо знать радиус окружности и центральный угол, охватывающий эту дугу.
Наш онлайн калькулятор длины дуги может вычислить длину дуги через угол в градусах и радианах.
Для вычисления длины дуги через центральный угол в градусах формула выглядит следующим образом:
L = r * θ * π / 180
где L — длина дуги, r — радиус окружности, θ — центральный угол в градусах, π — число Пи (3.14159…).
Для вычисления длины дуги через центральный угол в радианах формула выглядит следующим образом:
L = r * θ
где L — длина дуги, r — радиус окружности, θ — центральный угол в радианах.
Таким образом, чтобы использовать наш калькулятор для вычисления длины дуги через центральный угол в градусах, необходимо ввести радиус и угол в градусах, а для вычисления длины дуги через центральный угол в радианах — радиус и угол в радианах.
🔣 Формула Гюйгенса
Длину дуги можно найти, используя более редкую формула, в которой известны две хорды, как показано на рисунке выше. Это формула называется формулой Гюйгенса.
В формуле Гюйгенса используется знак «равно или почти равно» (≊), потому что вычисления с помощью этой формулы могут содержать погрешности. Эти погрешности обычно малы, но они существуют, и их нужно учитывать. Относительная погрешность формулы Гюйгенса составляет около 0,5% при угле дуги в 60°. Однако, при уменьшении угла дуги, погрешность также уменьшается. Например, при дуге в 45° относительная погрешность составит около 0,02%.
🌈 Пример использования калькулятора в повседневной жизни
Калькулятор для вычисления длины дуги может быть использован и в повседневной жизни в различных ситуациях:
Пример 1. При выборе размера ободной обрезиненной ленты для замены на велосипеде. Чтобы выбрать правильный размер ленты, необходимо знать длину окружности колеса. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину окружности колеса по его радиусу.
Пример 2. При планировании работы садовой или дачной зоны. Например, при расчете длины ленточного газона или длины обочин для дорожек. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить необходимую длину материала.
Пример 3. При выборе длины троса для подвешивания карниза или штор в доме. Чтобы подобрать правильную длину троса, необходимо знать длину окна и расстояние от карниза до пола. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину троса, необходимую для подвешивания карниза.
Помимо этого, калькулятор для вычисления длины дуги может быть использован для быстрого и удобного решения задач, связанных с геометрией, физикой и техническими науками. Например:
- Геометрия: в геометрии часто требуется вычислять длину дуги окружности для построения различных фигур и геометрических конструкций.
- Физика: в физике, например, длина дуги может быть использована для вычисления длины траектории движения тела по окружности.
- Технические науки: в инженерии и других технических науках, вычисление длины дуги может быть использовано для определения размеров и формы кривых поверхностей и для расчета траекторий движения механизмов и устройств.
Таким образом, калькулятор для вычисления длины дуги может быть полезным инструментом как в повседневной жизни, так и при решении задач, связанных с техническими науками.
🌀 Основные виды дуг
- Дуги окружности — это дуги, которые образуются на окружности. Они имеют равные начальный и конечный углы и могут быть выражены через радиус окружности и центральный угол, который они охватывают.
- Произвольные дуги — это дуги, которые не являются частью окружности и могут быть описаны любой кривой. Они могут быть параметризованы, то есть выражены через параметр, который изменяется от начального до конечного значения. (Примеры произвольных дуг включают дуги эллипсов, парабол, гипербол и других кривых, которые можно параметризовать).
- Круговые дуги — это дуги, которые образуются на круге. Они имеют равные начальный и конечный углы, как дуги окружности, но могут быть на любом расстоянии от центра круга.
- Сегменты — это дуги, которые являются частью окружности или круга и имеют начальный и конечный углы, которые не равны 360 градусам.
В зависимости от конкретного контекста могут быть и другие типы дуг, но основные типы — это дуги окружности и произвольные дуги.
В чем разница между градусом от радианом?
Градусы и радианы — это единицы измерения угла. Они могут использоваться для измерения углов различных фигур, таких как треугольники, прямоугольники, круги и другие.
Градус — это одна из самых распространенных единиц измерения угла. Он определяется как 1/360 часть полного угла, который составляет один оборот. Таким образом, полный угол равен 360 градусам.
Радиан — это другая единица измерения угла, которая используется в математике и физике. Радиан определяется как длина дуги, равной радиусу окружности, разделенная на радиус этой окружности. Таким образом, полный угол равен 2π радианам.
Отличие между градусами и радианами заключается в том, как они измеряют углы. Градусы измеряют углы в сотнях долей полного угла, а радианы измеряют углы в длинах дуг окружности.
В математике и физике часто используются радианы, так как они позволяют производить более точные вычисления.
❓ Вопросы и ответы
Некоторые из популярных вопросов и ответы на них по калькулятору длины дуги.
Что такое длина дуги?
Длина дуги — это длина части кривой линии, которая соединяет две заданные точки на кривой.
В каких областях применяется вычисление длины дуги?
Вычисление длины дуги находит применение в различных областях, таких как физика, инженерия, компьютерная графика, дизайн и другие. Например, при моделировании траекторий движения тел, в оптике для расчета оптических путей лучей, при создании графических объектов и многих других задачах.
Как перевести угол из градусов в радианы?
Для перевода угла из градусов в радианы используется следующая формула: θ (в радианах) = θ (в градусах) * π / 180, где π — число Пи (3.14159…).
Какой формат ввода углов используется в калькуляторе длины дуги?
Калькулятор длины дуги использует радианы и градусы для ввода углов.
Какой диапазон углов может быть введен в калькулятор длины дуги?
Углы могут быть введены в диапазоне от 0 до 2π (двух пи), что соответствует полной окружности.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Загрузить PDF
Загрузить PDF
Дуга – это некоторая часть окружности.[1]
Длина дуги равна расстоянию между двумя точками, которые лежат на окружности. Чтобы вычислить длину дуги, необходимо иметь некоторое представление о геометрии окружности. Так как дуга представляет собой часть окружности, нужно найти величину центрального угла (в градусах или радианах), а затем вычислить длину дуги.
-
1
Запишите формулу для вычисления длины дуги. Формула:
, где
– радиус окружности,
– центральный угол, измеренный в градусах.[2]
-
2
В формулу подставьте радиус окружности. Как правило, значение радиуса дается в задаче; в противном случае просто измерьте его. Значение радиуса подставляется вместо
.
- Например, если радиус окружности равен 10 см, формула запишется так:
.
- Например, если радиус окружности равен 10 см, формула запишется так:
-
3
В формулу подставьте центральный угол. Как правило, значение центрального угла дается в задаче; в противном случае просто измерьте его. В указанную формулу подставьте центральный угол, измеренный в градусах (а не в радианах). Значение центрального угла подставляется вместо
.
- Например, если центральный угол равен 135 градусов, формула запишется так:
.
- Например, если центральный угол равен 135 градусов, формула запишется так:
-
4
Радиус умножьте на
. Если нет калькулятора, воспользуйтесь следующим приблизительным значением:
. Перепишите формулу, подставив в нее полученное значение, которое равно длине окружности.[3]
-
5
Разделите центральный угол на 360. Так как в круге 360 градусов, это вычисление позволит определить, какую часть круга представляет сектор. Благодаря полученной информацию можно найти часть окружности, которую представляет дуга.
-
6
Перемножьте два числа. Получится длина дуги.
Реклама
-
1
Запишите формулу для вычисления длины дуги. Формула:
, где
– радиус окружности,
– центральный угол, измеренный в радианах.[4]
-
2
В формулу подставьте радиус окружности. Чтобы воспользоваться этим методом, нужно знать радиус. Значение радиуса подставляется вместо
.
- Например, если радиус окружности равен 10 см, формула запишется так:
.
- Например, если радиус окружности равен 10 см, формула запишется так:
-
3
В формулу подставьте центральный угол. В указанную формулу подставляйте центральный угол, измеренный в радианах. Если угол измеряется в градусах, этим методом пользоваться нельзя.
- Например, если центральный угол равен 2,36 радиан, формула запишется так:
.
- Например, если центральный угол равен 2,36 радиан, формула запишется так:
-
4
Умножьте радиус на центральный угол (измеренный в радианах). Получится длина дуги.
Реклама
Советы
- Если известен диаметр окружности, можно найти длину дуги. Приведенные выше формулы для вычисления длины дуги включают радиус окружности. Радиус равен половине диаметра, поэтому чтобы вычислить радиус, нужно просто разделить диаметр на 2.[5]
Например, диаметр окружности равен 14 см; чтобы найти радиус, разделите 14 на 2:.
Таким образом, радиус окружности равен 7 см.
Реклама
Об этой статье
Эту страницу просматривали 90 137 раз.
Была ли эта статья полезной?
Arc length is defined as the distance between the two points placed on the circumference of the circle and measured along the circumference. Arc length is the curved distance along the circumference of the circle. Length of the arc between two points is always greater than the chord between those two points.
What is Arc Length?
The arc length is defined as the circular distance between two points along the circumference of the circle. The length of the arc is directly dependent on the radius and central angle of the circle. The central angle is the angle subtended by the endpoints of the arc to the center of the circle. It is denoted by θ. It is measured both in degrees and radians. The figure given below shows the arc AB when the radius is r and the central angle is θ.
Arc Length Formula
Length of the arc is calculated using different formulas, the formula used is based on the central angle of the arc. Central angle is measured in degrees or radians, and accordingly, the length of an arc of the circle is calculated. For a circle, the formula for arc length formula is θ times the radius of the circle.
| Arc Length Formula (θ in degrees) | s = 2×π×r ×(θ/360°) |
| Arc Length Formula (θ in radians) | s = θ × r |
| Arc Length Formula (Integral Form) | s = ∫√(1 + (dy/dx)2dx |
There are different cases that are used accordingly to find the required Arc Length
Case 1: When Radius and Angle are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)… (1)
where
r is the radius of the circle
θ is the angle in degrees
L is the Arc lengthArc length when the angle is represented in radians
1 radian = π/180°
Substituting the value of radian in equation (1)
L = 2πr × (θ × / 360)
L = r θ…(2)
where,
r is the radius of the circle
θ is the angle in radians.
Case 2: When Area and Central Angle of the Arc are given
Formula to calculate the length of an arc is given by:
L = 2πr × (θ / 360)
where,
r is the radius of the circle
θ is the angle in degreesWe need to find the radius of the circle from the given area. After finding the radius, we will substitute the value of radius in the formula.
Area of the circle = πr2
Example: If area of the circle is 314 m2 and centeral angle of the arc is π radian find the length of the arc.
Sloution:
πr2 = 314 m2
r2 = 314/π (π = 3.14)
r2 = 314/3.14
r2 = 100
r = √100 = 10 m
Length of the arc with angle π radians will be:
L = r θ
L = 10 × π
L = 10 × 3.1415
L = 31.415 m
The value of r can be used in the same formula, as discussed above.
Case 3: Arc length In Integral Form
Arc length in integral form is given by:
L = ∫√(1 + (dy/dx)2)dx
where,
Y is the f(x) function
limit of integral is [a, b]
How to Find Arc Length?
Use the steps given below to find the Arc length of the given arc.
Step 1: Mark the central angle and length of the radius of the given arc.
Step 2: Use the formula as given above according to the value of the angle in degrees or radians accordingly.
Step 3: Simplify the above equation to get the required answer.
Also, Check
- Equation of a Circle
- Degrees To Radians
- Radians to Degrees
Solved Examples on Arc Length
Example 1: Find the length of the arc with a radius of 2m and angle π/2 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 2m and θ = π/2 radians
Length of arc = 2 × π/2
Length of arc = π
(π = 3.1415)
Length of arc = 3.1415 m
Thus, the length of the arc is 3.1415 m.
Example 2: Find the length of the arc of function f(x) = 8 between x =2 and x = 4.
Solution:
The formula to calculate the arc length for the function is given by:
L = ∫√(1 + (dy/dx)2)dx
The limit of integral is [a, b]
Substituting the values a = 2, b = 4, and y = 6 or dy/dx = 0 in the above formula,
L = ∫√(1 + (0)2)dx
L = ∫√1 dx
L = ∫1 dx
L = x
(Integral of 1 is x)
The limit of integral is [2, 4]
L = (4 – 2)
L = 2
Thus, the length of the arc of function f(x) = 8 between x = 2 and x = 4 is 2.
Example 3: Find the length of the arc with a radius of 5cm and an angle of 60°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 5cm and θ = 60°
Length of arc = 2πr × (60 / 360)
Length of arc = 2πr × 1/6
Length of arc = 2 × 3.1415 × 5/6
(π = 3.1415)
Length of arc = 5.235cm
Thus, the length of the arc is 5.235cm
Example 4: Find the length of the arc with a radius of 0.5m and an angle of π/4 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 0.5m and θ = π/4 radians
Length of arc = 0.5 × π/4
Length of arc = 0.392 m
(π = 3.1415)
Thus, the length of the arc is 0.392 m
Example 5: Find the length of the arc with a radius of 10cm and an angle of 135°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 10cm and θ = 135°
Length of arc = 2πr × (135/360)
Length of arc = (2 × 3.1415 × 10 × 135)/360°
(π = 3.1415)
Length of arc = 23.56cm
Thus, the length of the arc is 23.56cm.
Example 6: Find the length of the arc with a radius of 20mm and angle π/6 radians.
Solution:
The formula to calculate the length of the arc is given by:
L = r θ
Where,
L is the length of the arc
Given: r = 20mm and θ = π/6 radians
Length of arc = 20 × π/6
Length of arc = 10.47 mm
(π = 3.1415)
Thus, the length of the arc is 10.47 mm
Example 7: Find the length of the arc with a radius of 2 cm and an angle of 90°.
Solution:
The formula to calculate the length of the arc is given by:
L = 2πr × (θ / 360)
Where,
L is the length of the arc
Given: r = 2cm and θ = 90°
Length of arc = 2πr × (90 / 360)
Length of arc = 2πr × 1/4
Length of arc = 2 ×3.1415 × 2 × 1/4
(π = 3.1415)
Length of arc = 3.1415 cm
Thus, the length of the arc is 3.1415 cm.
FAQs on Arc Length
Question 1: What is the Arc Length of a Circle?
Answer:
Arc length of a circle is the length made by the arc which is measured along its circimference.
Question 2: Length of the arc is measured in which unit?
Answer:
Length of arc is of a circle is either measured in m or in cm.
Question 3: Does arc length is measured in radians?
Answer:
Angles are measured in radians and arc length is a measurement of distance, thus it cannot be measured in radians.
Question 4: How do you find the circumference if the arc length (l) and central angle (θ) are given?
Answer:
When arc length (l) and central angle (θ) is given then the circumference by the formula
Arc Length (L) / Circumference = θ/360º
Last Updated :
20 Jan, 2023
Like Article
Save Article
Как найти длину дуги окружности ?
r — радиус окружности
α — угол AOB, в градусах
Формула длины дуги ( L ):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Как найти дугу окружности зная другую дугу
Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула |
| Длина окружности |  |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Как найти длину дуги окружности ?
r — радиус окружности
α — угол AOB, в градусах
Формула длины дуги ( L ):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
http://mnogoformul.ru/dlina-dugi
http://b4.cooksy.ru/articles/kak-nayti-dugu-okruzhnosti-znaya-druguyu-dugu