Доверительный интервал для математического ожидания нормальной случайной
величины при неизвестной дисперсии
Пусть
, причем
и
неизвестны. Необходимо построить доверительный интервал,
накрывающий с надежностью
истинное значение параметра
.
Для этого из генеральной
совокупности СВ
извлекается
выборка объема
:
.
1) В качестве точечной
оценки математического ожидания
используется
выборочное среднее
, а в
качестве оценки дисперсии
–
исправленная выборочная дисперсия
которой соответствует стандартное отклонение
.
2) Для нахождения
доверительного интервала строится статистика
имеющая в этом случае распределение Стьюдента с
числом степеней свободы
независимо
от значений параметров
и
.
3) Задается требуемый
уровень значимости
.
4) Применяется следующая
формула расчета вероятности:
где
–
критическая точка распределения Стьюдента, которая находится по таблице критических точек распределения Стьюдента (односторонняя критическая область).
Тогда:
Это означает, что
интервал:
накрывает неизвестный
параметр
с
надежностью
Доверительный интервал для математического ожидания
нормальной случайной величины при известной дисперсии
Пусть количественный
признак
генеральной
совокупности имеет нормальное распределение
с
заданной дисперсией
и
неизвестным математическим ожиданием
. Построим
доверительный интервал для
.
1) Пусть для оценки
извлечена
выборка
объема
. Тогда
2) Составим случайную
величину:
Нетрудно показать, что случайная величина
имеет стандартизированное нормальное распределение, то есть:
3) Зададим уровень
значимости
.
4) Применяя формулу нахождения
вероятности отклонения нормальной величины от математического ожидания, имеем:
Это означает, что
доверительный интервал
накрывает неизвестный
параметр
с надежностью
. Точность оценки определяется величиной:
Число
определяется
по таблице значений функции Лапласа из равенства
Окончательно получаем:
Доверительный интервал для
дисперсии нормальной случайной величины при неизвестном математическом ожидании
Пусть
, причем
и
–
неизвестны. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется
исправленная выборочная дисперсия
:
которой соответствует стандартное отклонение
.
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
4) Тогда, используя таблицу критических точек хи-квадрат распределения, нетрудно указать критические
точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
дисперсии нормальной случайной величины при известном математическом ожидании
Пусть
, причем
–
известна, а
–
неизвестна. Пусть для оценки
извлечена выборка объема
:
.
1) В качестве точечной оценки дисперсии
используется выборочная дисперсия:
2) При нахождении
доверительного интервала для дисперсии в этом случае вводится статистика
имеющая
–
распределение с числом степеней свободы
независимо
от значения параметра
.
3) Задается требуемый
уровень значимости
.
4) Тогда, используя таблицу критических точек хи-квадрат распределения,
нетрудно указать критические точки
, для которых будет выполняться следующее
равенство:
Подставив вместо
соответствующее значение, получим:
Получаем доверительный
интервал для неизвестной дисперсии:
Доверительный интервал для
среднего квадратического отклонения
Извлекая квадратный корень:
Положив:
Получим следующий
доверительный интервал для среднего квадратического
отклонения:
Для отыскания
по заданным
и
пользуются специальными таблицами.
Для проверки на нормальность заданного распределения случайной величины можно использовать
правило трех сигм.
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.
Построить
доверительные интервалы для среднего и дисперсии с надежностью
Указание:
воспользоваться таблицами Стьюдента и хи-квадрат.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычисление средней и дисперсии
Вычислим среднее и
исправленную дисперсию
:
Нахождение доверительных интервалов для средней и дисперсии
Найдем доверительный интервал для оценки
неизвестного среднего. Он считается по формуле:
По таблице критических точек t-критерия Стьюдента, для уровня значимости
(односторонняя критическая область):
Искомый
доверительный интервал для среднего:
Найдем доверительный интервал для оценки дисперсии.
Он считается по формуле:
Для уровня значимости
и
получаем по таблице значений хи-квадрат:
Искомый доверительный интервал для дисперсии:
Ответ
Кроме этой задачи на другой странице сайта есть
пример расчета доверительного интервала математического ожидания и среднего квадратического отклонения для интервального вариационного ряда
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Для помощи во время экзамена/зачета в онлайн режиме необходимо договариваться заранее.
В пункте 3 был
рассмотрен вопрос об оценке неизвестного
параметра
распределения одним числом. Такую оценку
называют точечной. Однако часто требуется
найти не только приближенное значение
параметра, но и оценить его точность и
надежность. Для этого в математической
статистике пользуются доверительными
интервалами.
Пусть для параметра
из опыта получена несмещенная оценка
Зададимся вероятностьюp,
такой, что событие, происходящее с этой
вероятностью, можно было бы считать
практически достоверным (обычно эти
значения берут равными 0,9; 0,95; 0,99) и найдем
такое значение
для которого
(9.28)
или
Интервал
называютдоверительным
интервалом,
а p
– доверительной вероятностью; число
называютуровнем
значимости.
Границы интервала называют доверительными
границами.
Надо отметить, что
является случайным, так как случайно
его положение на оси абсцисс, определяемое
центромслучайна и его длина
так как величина
определяется из опытных данных. Таким
образом, величинуp
можно интерпретировать как вероятность,
с которой интервал
накроет истинные значения параметра
Кроме того,
можно считать множеством значений
параметрасовместимых с опытными данными и не
противоречащих им.
Пусть подтвердилась
гипотеза о нормальном законе распределения
случайной величины X.
Тогда доверительный интервал для
параметра
или, что то же самое, (см.(7.25), (9.6) и (9.15))
для математического ожидания имеет вид
(9.29)
где
–
оценка параметра;
–
несмещенное среднеквадратичное
отклонение;
n
– объем выборки;
–
коэффициент, который находят, пользуясь
табл.6 Приложения по выбранной доверительной
вероятностиp
и числу степеней свободы
Доверительный
интервал для дисперсии в указанной выше
ситуации имеет вид

где n
– объем выборки;
–
несмещенная оценка дисперсии (см.(9.8));
p
– доверительная вероятность;
–
значение, которое находят, пользуясь
табл.3 (или 3.а) Приложения по вероятностии числу степеней свободы, равным
–значение, которое
находят, пользуясь табл.3 или 3а Приложения
по вероятности
и числу степеней свободы
Пусть теперь
случайная величина X
имеет закон распределения, отличный от
нормального. Тогда доверительный
интервал для математического ожидания
приближенно имеет вид
(9.31)
где
–
оценка математического ожидания;p
– доверительная вероятность;
–среднее квадратическое
отклонение выборочного среднего,
(9.32)
–коэффициент,
который находят по табл.2 Приложения
как значение аргумента, при котором
функция Лапласа равна
Совершенно
аналогично может быть построен
доверительный интервал для дисперсии:
(9.33)
где
–
несмещенная оценка дисперсии (см.(9.8));–
коэффициент, который находят так же ,
как в формуле (9.31);–
среднее квадратическое отклонение
несмещенной выборочной дисперсии .
Для нахождения
можно воспользоваться тем, что
где
n
– объем выборки.
В этой формуле
неизвестную DX
можно заменить на приближенное значение
–
также можно заменить его оценкой:
Если нет оснований
считать, что закон распределения
случайной величины X
резко отличается от нормального, то
можно воспользоваться формулой
(9.34)
Кроме того, если
подтвердилась гипотеза о равномерном
законе распределения, то можно
воспользоваться формулой
(9.35)
Далее приведены
примеры, иллюстрирующие проверку
гипотезы о законе распределения и
построение доверительного интервала
для математического ожидания и дисперсии.
Пример
3. Получена
выборка из генеральной совокупности
-
42,54
48,56
62,55
69,26
52,12
56,16
61,17
58,97
64,45
56,28
66,28
58,07
65,04
62,72
63,96
56,72
64,96
55,80
48,31
35,84
49,90
45,53
48,26
46,24
63,18
44,89
57,23
68,22
54,04
73,46
53,91
46,38
71,06
49,27
40,48
69,86
75,85
51,32
42,93
55,00
72,77
61,13
60,40
63,71
38,82
61,02
75,92
53,44
76,33
35,26
38,88
70,45
53,61
65,08
51,59
53,07
51,41
62,40
50,81
65,11
51,99
63,58
61,00
51,38
61,38
54,90
58,05
48,70
66,70
43,37
53,52
45,04
55,81
55,99
60,60
57,75
48,89
58,00
50,22
54,84
58,84
61,38
46,34
43,26
64,91
32,68
53,00
46,72
52,72
63,82
48,88
52,70
52,21
72,72
53,24
52,72
45,23
49,79
43,43
68,50
По этой выборке
получаем вариационный ряд
-
32,68
43,43
48,31
50,81
53,00
55,00
58,05
61,38
63,96
69,26
35,26
44,89
48,56
51,32
53,07
55,80
58,07
61,38
64,91
69,86
35,84
45,04
48,70
51,38
53,24
55,81
58,84
62,40
64,96
70,45
38,82
45,23
48,88
51,41
53,44
55,99
58,97
62,45
65,04
71,06
38,88
45,53
48,89
51,99
53,52
56,16
60,40
62,55
65,08
72,72
40,48
46,24
49,27
52,12
53,61
56,28
60,60
62,72
65,11
72,77
42,54
46,24
49,79
52,21
53,61
56,72
61,00
63,18
66,28
73,46
42,93
46,38
49,90
52,70
54,04
57,23
61,02
63,58
66,70
75,85
43,26
46,72
50,22
52,72
54,84
57,75
61,13
63,71
68,22
75,92
43,37
48,26
50,59
52,72
54,90
58,00
61,17
63,82
68,50
76,33
Диапазон наблюденных
значений случайной величины X
укладывается в интервал (32;77). Разбиваем
интервал наблюдений значений случайной
величины на 9 разрядов с шагом
Дальнейшие шаги
рассмотрены ранее в пунктах 2-6. В
результате, после их выполнения, получаем
таблицу 5 и рис.5.
|
Таблица |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
13 |
16 |
22 |
15 |
16 |
6 |
6 |
|
2 |
|
0,03 |
0,03 |
0,13 |
0,16 |
0,22 |
0,15 |
0,16 |
0,06 |
0,06 |
|
3 |
|
0,006 |
0,006 |
0,026 |
0,032 |
0,044 |
0,030 |
0,032 |
0,012 |
0,012 |
|
4 |
|
34,5 |
39,5 |
44,5 |
49,5 |
54,5 |
59,5 |
64,5 |
69,5 |
74,5 |
|
5 |
|
-2,22 |
-1,70 |
-1,18 |
-0,66 |
-0,14 |
0,39 |
0,91 |
1,43 |
1,95 |
|
6 |
|
0,0339 |
0,0940 |
0,1989 |
0,3209 |
0,3961 |
0,3697 |
0,2637 |
0,1435 |
0,0596 |
|
7 |
|
0,004 |
0,010 |
0,021 |
0,033 |
0,041 |
0,039 |
0,028 |
0,015 |
0,006 |
|
8 |
|
0,020 |
0,050 |
0,105 |
0,165 |
0,205 |
0,195 |
0,140 |
0,075 |
0,030 |
|
9 |
|
2 |
5 |
10,5 |
16,5 |
20,5 |
19,5 |
14 |
7,5 |
3 |
|
10 |
|
-1 |
2,5 |
-0,5 |
1,5 |
-4,5 |
2 |
1,5 |
3 |
|
|
11 |
|
1 |
6,25 |
0,25 |
2,25 |
20,25 |
4 |
2,25 |
9 |
Комментарии к
табл.5.
Используя информацию
в строках 1-3, строим гистограмму, вид
которой позволяет выдвинуть гипотезу
о нормальном законе распределения
исследуемой случайной величины.
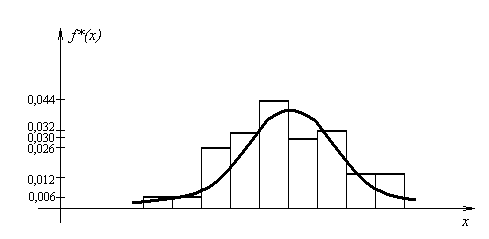
Рис.5. Гистограмма
и выравнивающая ее функция плотности
Результаты расчетов
в строках 4-7 дают возможность построить
ни гистограмме выравнивающую кривую
функции плотности. Отметим, что
предварительно, для вычислений значений
функции плотности, были найдены точечные
оценки математического ожидания
(см.(9.9)) и дисперсии (см.9.11)), что, согласно
(9.15), позволило получить и оценки
параметров
и
Для данного примера
имеем
В 8-й строке приведены
результаты вычислений по формуле (9.27).
В первом и во втором
разрядах оказалось менее 5 наблюдений,
поэтому объединим эти разряды в один.
По результатам
вычислений, приведенных в строках 9-11,
вычисляем по формуле (9.23) значение
Определим по
формуле (9.22) число степеней свободы —
параметр распределения
Учитывая, что число наложенных связей
для нормального распределения равно
3, а число разрядов уменьшилось на один,
то число степеней свободыВыберем уровень значимости
и по таблице 3 Приложения для
найдем
Так как наблюденное значение
оказалось меньше табличного значения,
то есть произошло событиевероятность которого равна 0,95, то можно
сделать вывод: выдвинутая гипотеза о
нормальном законе распределения не
противоречит опытным данным.
Построим доверительный
интервал для математического ожидания
по формуле (9.29). Зададимся доверительной
вероятностью
и, учитывая, что число степеней свободы
по табл.6 найдем
тогда
или
Построим доверительный
интервал для дисперсии по формуле
(9.30). Зададимся доверительной вероятностью
тогда
число степеней свободы
Тогда по таблице 3а находим
таким образом,
или
следовательно, истинное значение
случайной величиныX
находится в этом интервале с вероятностью
0,95.
Пример
4. В
механическом цехе с десятью станками
в течение определенного периода ежедневно
регистрировали количество выбывших их
строя станков, проведя 200 наблюдений.
Предполагается, что случайная величина
X
– число отказавших станков – удовлетворяет
распределению Пуассона, так как в
нормальных условиях производства отказ
станка можноь считать редким событием,
которое не зависит от отказа других
станков. Подтверждает ли выборка,
представленная в табл.6, эту гипотезу?
|
Таблица 6 |
||
|
Число отказов станков, |
Частота отказов, |
Относительная часота отказов, |
|
0 |
41 |
0,205 |
|
1 |
62 |
0,31 |
|
2 |
45 |
0,225 |
|
3 |
22 |
0,11 |
|
4 |
16 |
0,08 |
|
5 |
8 |
0,04 |
|
6 |
4 |
0,02 |
|
7 |
2 |
0,01 |
|
8 |
0 |
0 |
|
9 |
0 |
0 |
|
10 |
0 |
0 |
|
n=200 |
|
Чтобы использовать
критерий
надо по значениям выборки найти значение
параметраа
распределения
Пуассона и вычислить теоретические
частоты
Согласно (9.13), оценкойа
будет выборочное среднее
Для примера 4
вычисленное по формуле (9.9):
Вероятности
вычислены по формуле (9.21) с учетом того,
что
Все промежуточные
результаты для вычисления значения
представлены в табл.7.
|
Таблица |
|||||||
|
Число отказов станков |
Частота |
Относит. частота |
Вероятность |
Теорет. частота |
|
|
|
|
0 |
41 |
0,2050 |
0,1653 |
33,06 |
7,94 |
63,0436 |
1,91 |
|
1 |
62 |
0,3100 |
0,2975 |
59,5 |
2,5 |
6,25 |
0,11 |
|
2 |
45 |
0,225 |
0,2678 |
53,56 |
8,56 |
72,2736 |
1,37 |
|
3 |
22 |
0,1100 |
0,1607 |
32,14 |
10,14 |
102,8196 |
3,2 |
|
4 |
16 |
0,0800 |
0,0723 |
14,46 |
1,54 |
2,3716 |
0,16 |
|
5 6 7 8 9 10 |
|
0,0400 |
0,0260 |
|
6,72 |
45,1584 |
6,2 |
|
0,0200 |
0,0078 |
||||||
|
0,0100 |
0,0020 |
||||||
|
0 |
0,0005 |
||||||
|
0 |
0,0001 |
||||||
|
0 |
0,0000 |
||||||
|
200 |
1 |
1 |
200 |
|
В этом примере
объдинены последние 6 разрядов. Число
степеней свободы, с учетом (9.22),
так как по выбоке оценивался неизвестный
параметра.
Выбираем уровень значимости
Пользуясь табл. 3 Приложения по
и
находим
Так как
то гипотезу о распределении Пуассона
надо отвергнуть, следовательно, выборка
взята из генеральной совокупноти,
распределение которой не подчиняется
закону Пуассона.
На рис. 6 представлены
многоугольники распределения относительных
частот и вероятностей.
Р
Многоугольник распределения;

распределения
.
Построим доверительные
интервалы для MX
и DX.
С учетом формул (7.20) имеем:
Тогда по формуле (9.32) получаем
Возьмем доверительную вероятность
и по табл. 2 Приложения найдем значение
как значение аргумента, при котором
функция Лапласа равнатогда, используя формулу (9.31), получаем
доверительный интервал дляMX:
или
Для построения
доверительного интервала для дисперсии
по формуле (9.34) найдем
Тогда доверительный
интервал для дисперсии, найденный по
формуле (9.33), имеет вид
или
Пример
5. Имеем
результаты
наблюдений изучаемой случайной величиныX
-
0,03
0,11
0,64
0,35
0,13
0,01
0,27
0,01
0,22
0,92
0,01
0,64
0,77
0,92
0,48
0,03
0,04
0,25
0,39
0,97
0,06
0,19
0,47
0,32
0,48
0,11
0,11
0,19
0,80
0,26
0,12
0,11
0,20
0,98
0,56
0,08
0,01
0,57
0,47
0,84
0,05
0,49
0,12
0,14
0,36
0,19
0,06
0,37
0,09
0,98
0,07
0,09
0,07
0,07
0,34
0,02
0,04
0,68
0,27
0,53
0,01
0,23
0,84
0,21
0,63
0,55
0,05
0,36
0,15
0,84
0,18
0,01
0,66
0,74
0,36
0,08
0,22
0,57
0,35
0,12
0,21
0,52
0,25
0,03
0,11
0,78
0,07
0,34
0,93
0,04
0,14
0,02
0,12
0,35
0,50
0,24
0,03
0,70
0,68
0,21
Расположим эти
наблюдения не в порядке получения, а в
порядке их возрастания, получим
вариационный ряд.
-
0,01
0,03
0,07
0,11
0,18
0,23
0,35
0,48
0,63
0,80
0,01
0,03
0,07
0,11
0,19
0,24
0,35
0,48
0,64
0,84
0,01
0,04
0,07
0,12
0,19
0,25
0,35
0,49
0,64
0,84
0,01
0,04
0,08
0,12
0,19
0,25
0,36
0,50
0,66
0,84
0,01
0,04
0,08
0,12
0,20
0,26
0,36
0,52
0,68
0,92
0,01
0,05
0,09
0,12
0,21
0,27
0,36
0,53
0,68
0,92
0,02
0,05
0,09
0,13
0,21
0,27
0,37
0,55
0,70
0,93
0,02
0,06
0,11
0,14
0,21
0,32
0,39
0,56
0,74
0,97
0,03
0,06
0,11
0,14
0,22
0,34
0,47
0,57
0,77
0,98
0,03
0,07
0,11
0,15
0,22
0,34
0,47
0,57
0,78
0,98
Исходные данные
удобно разбить на 10 разрядов с шагом
Выполняя последовательно пункты этого
параграфа, получим таблицу 8.
|
Таблица |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
27 |
18 |
12 |
11 |
6 |
6 |
7 |
|
6 |
|
|
2 |
|
0,27 |
0,18 |
0,12 |
0,11 |
0,06 |
0,06 |
0,07 |
0,04 |
0,03 |
0,06 |
|
3 |
|
2,7 |
1,8 |
1,2 |
1,1 |
0,6 |
0,6 |
0,7 |
0,41 |
0,31 |
0,62 |
|
4 |
|
0,05 |
0,15 |
0,25 |
0,35 |
0,45 |
0,55 |
0,65 |
0,75 |
0,85 |
0,95 |
|
5 |
|
2,604 |
1,923 |
1,421 |
1,049 |
0,775 |
0,572 |
0,423 |
0,312 |
0,231 |
0,170 |
|
6 |
|
0,253 |
0,187 |
0,138 |
0,102 |
0,075 |
0,056 |
0,041 |
0,030 |
0,022 |
0,017 |
|
7 |
|
25,259 |
18,656 |
13,780 |
10,178 |
7,517 |
5,552 |
4,101 |
3,029 |
2,237 |
1,7 |
|
8 |
|
3,031 |
0,431 |
3,167 |
0,676 |
2,302 |
0,201 |
8,404 |
0,943 |
0,582 |
18,49 |
|
9 |
|
0,120 |
0,023 |
0,230 |
0,066 |
0,306 |
0,036 |
2,049 |
|
10,876 |
Пояснения к табл.8.
В-первых трех
строках последовательно определены
выборочные частоты
относительные частоты
и высоты
столбцов гистограммы по формулам (9.4),
(9.5) соответственно. По результатам
вычислений третьей строки построена
гистограмма, представленная на рис.7.
Рис.7. Гистограмма
и выравнивающая ее кривая функции
плотности
Исходя из вида
гистограммы, выдвигаем гипотезу о
показательном законе распределения,
функция плотности которого имеет вид
(7.21).
Найдем оценки MX
и DX
по формулам (9.9), (9.11) соответственно. Так
как
то
С учетом формулы
(7.22), имеем оценку параметра
закона распределения:
Значения функции плотности получаем
по формуле (7.21), заменяяего оценкой
и беря в качествеx
для i-го
разряда
Вероятности
находим по формуле (9.27). Вычисления,
выполненные в 7-й, 8-й и 9-й строках очевидны.
По формуле (9.23)
находим значение
а по формуле (9.22) определяем число
степеней свободыr
с учетом объединения разрядов и числа
параметров закона распределения,
оцениваемых по выборке:
Возьмем уровень значимости
по табл. 3 найдем критическое значение
а по формуле (9.22) определяем число
степеней свободыr
с учетом объединения разрядов и числа
параметров закона распределения,
оцениваемых по выборке:
Возьмем уровень значимости
по табл. 3 найдем критическое значение
Согласно (9.24), произошло событие,
вероятность которого равна 0,05, то есть
гипотеза о показательном распределении
противоречит опытным данным, а потому
должна быть отвергнута.
Найдем доверительные
интервалы для MX
и DX.
По формуле (9.32)
а по формуле (9.34)
Тогда для доверительной вероятности
найдем значение
по табл. 2 Приложения как значение
аргумента функции Лапласа, при котором
она равнаИ по формулам (9.31) и (9.33) получаем
соответственноили
и
или
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть X1,…,Xn – случайная выборка объёма n из нормально
распределённой генеральной совокупности N(m, σ). Рассмотрим варианты построения
доверительных интервалов для математического ожидания m и дисперсии σ2.
1.
Доверительный интервал для математического ожидания m
при известной дисперсии σ2.
В качестве центральной статистики выберем стандартизованное среднее
$U=frac{bar{X}-m}{{sigma }/{sqrt{n}};}sim{ }N(0,1)$. При таком выборе центральной статистики
доверительный интервал для математического ожидания на уровне значимости α имеет вид:
$left( bar{X}-frac{sigma }{sqrt{n}}{{u}_{1-alpha /2}};bar{X}+frac{sigma }{sqrt{n}}{{u}_{1-alpha /2}} right)$.
2.
Доверительный интервал для математического ожидания m
при неизвестной дисперсии σ2.
В качестве центральной статистики выберем стандартизованное среднее
$T=frac{bar{X}-m}{{S}/{sqrt{n}};}sim{ }T(n-1)$. Запишем тождество
(1*)
для статистики T:
$Pleft( {{t}_{alpha /2}}(n-1)<frac{bar{X}-m}{{S}/{sqrt{n}};}<{{t}_{1-alpha /2}}(n-1) right)=1-alpha $,
где ${{t}_{alpha /2}}(n-1)$ и ${{t}_{1-alpha /2}}(n-1)$ – квантили распределения Стьюдента с n–1
степенями свободы на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно m и учитывая симметричность
распределения Стьюдента, получим:
$Pleft( bar{X}-frac{S}{sqrt{n}}{{t}_{1-alpha /2}}(n-1)<m<bar{X}+frac{S}{sqrt{n}}{{t}_{1-alpha /2}}(n-1) right)=1-alpha $,
откуда следует, что интервал
$left( bar{X}-frac{S}{sqrt{n}}{{t}_{1-alpha /2}}(n-1);bar{X}+frac{S}{sqrt{n}}{{t}_{1-alpha /2}}(n-1) right)$
является доверительным для m на уровне значимости α.
3.
Доверительный интервал для дисперсии
σ2 при известном математическом ожидании m.
В качестве центральной статистики выберем статистику
$frac{n}{{{sigma }^{2}}}S_{0}^{2}sim{ }{{chi }^{2}}(n)$. Запишем тождество
(1*):
$Pleft( chi _{alpha /2}^{2}(n)<frac{n}{{{sigma }^{2}}}S_{0}^{2}<chi _{1-alpha /2}^{2}(n) right)=1-alpha $,
где $chi _{alpha /2}^{2}(n)$ и $chi _{1-alpha /2}^{2}(n)$ – квантили распределения хи-квадрат с n
степенями свободы на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно σ2, получим:
$Pleft( frac{nS_{0}^{2}}{chi _{1-alpha /2}^{2}(n)}<{{sigma }^{2}}<frac{nS_{0}^{2}}{chi _{alpha /2}^{2}(n)} right)=1-alpha $,
откуда следует, что интервал
$left( frac{nS_{0}^{2}}{chi _{1-alpha /2}^{2}(n)};frac{nS_{0}^{2}}{chi _{alpha /2}^{2}(n)} right)$
является доверительным для σ2 на уровне значимости α.
4.
Доверительный интервал для дисперсии
σ2 при неизвестном математическом ожидании m.
В качестве центральной статистики выберем статистику
$frac{n-1}{{{sigma }^{2}}}{{S}^{2}}sim{ }{{chi }^{2}}(n-1)$. Запишем тождество
(1*):
$Pleft( chi _{alpha /2}^{2}(n-1)<frac{n-1}{{{sigma }^{2}}}{{S}^{2}}<chi _{1-alpha /2}^{2}(n-1) right)=1-alpha $,
где $chi _{alpha /2}^{2}(n-1)$ и $chi _{1-alpha /2}^{2}(n-1)$ – квантили распределения хи-квадрат с n-1
степенями свободы на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно σ2, получим:
$Pleft( frac{(n-1)S_{{}}^{2}}{chi _{1-alpha /2}^{2}(n-1)}<{{sigma }^{2}}<frac{(n-1)S_{{}}^{2}}{chi _{alpha /2}^{2}(n-1)} right)=1-alpha$,
откуда следует, что интервал
$left( frac{(n-1)S_{{}}^{2}}{chi _{1-alpha /2}^{2}(n-1)};frac{(n-1)S_{{}}^{2}}{chi _{alpha /2}^{2}(n-1)} right)$
является доверительным для σ2 на уровне значимости α.
Рассмотрим теперь варианты построения доверительных интервалов, связанных с двумя выборками.
Пусть ${{X}_{11}},…,{{X}_{1,{{n}_{1}}}}$ и ${{X}_{21}},…,{{X}_{2,{{n}_{2}}}}$ – случайные выборки
объёмов n1 и n2 из нормально распределённых генеральных
совокупностей N(m1, σ1) и N(m2, σ2) соответственно.
5.
Доверительный интервал для разности математических ожиданий
m1 – m2
при известных дисперсиях $sigma _{1}^{2}$ и $sigma _{2}^{2}$.
В качестве центральной статистики выберем стандартизованную разность средних при известных дисперсиях:
$U=frac{({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-({{m}_{1}}-{{m}_{2}})}{sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma _{2}^{2}}{{{n}_{2}}}}}sim N(0,1)$.
Запишем тождество (1*):
$Pleft( {{u}_{alpha /2}}<frac{({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-({{m}_{1}}-{{m}_{2}})}{sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma_{2}^{2}}{{{n}_{2}}}}}<{{u}_{1-alpha /2}} right)=1-alpha $,
где ${{u}_{alpha /2}}$ и ${{u}_{1-alpha /2}}$ – квантили стандартизованного нормального распределения
на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно m1 – m2
и учитывая симметричность нормального распределения, получим:
$Pleft( ({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-{{u}_{1-alpha /2}}sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma_{2}^{2}}{{{n}_{2}}}}<{{m}_{1}}-{{m}_{2}}< right.$
$<left.({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})+{{u}_{1-alpha/2}}sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma _{2}^{2}}{{{n}_{2}}}} right)=1-alpha$,
откуда следует, что интервал
$left( ({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-{{u}_{1-alpha /2}}sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma_{2}^{2}}{{{n}_{2}}}};({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})+{{u}_{1-alpha /2}}sqrt{frac{sigma _{1}^{2}}{{{n}_{1}}}+frac{sigma _{2}^{2}}{{{n}_{2}}}}right)$
является доверительным для m1 – m2 на уровне значимости α.
6.
Доверительный интервал для разности математических ожиданий
m1 – m2
при неизвестных равных дисперсиях $sigma =sigma _{1}^{2}=sigma _{2}^{2}$.
В качестве центральной статистики выберем стандартизованную разность средних при неизвестных равных дисперсиях
$T=frac{({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-({{m}_{1}}-{{m}_{2}})}{Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}}}sim T({{n}_{1}}+{{n}_{2}}-2)$.
Запишем тождество (1*):
$Pleft( {{t}_{alpha /2}}({{n}_{1}}+{{n}_{2}}-2)<right.frac{({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-({{m}_{1}}-{{m}_{2}})}{Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}}}<$
$left.<{{t}_{1-alpha/2}}({{n}_{1}}+{{n}_{2}}-2) right)=1-alpha$,
где ${{t}_{alpha /2}}({{n}_{1}}+{{n}_{2}}-2)$ и ${{t}_{1-alpha /2}}({{n}_{1}}+{{n}_{2}}-2)$ – квантили распределения Стьюдента
с n1+n2–2 степенями свободы на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно m1 – m2 и
учитывая симметричность распределения Стьюдента, получим:
$Pleft( ({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-{{t}_{1-alpha/2}}({{n}_{1}}+{{n}_{2}}-2)Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}}<{{m}_{1}}-{{m}_{2}}< right.$
$left. <({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})+{{t}_{1-alpha /2}}({{n}_{1}}+{{n}_{2}}-2)Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}}right)=1-alpha$,
откуда следует, что интервал
$left( ({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})-{{t}_{1-alpha /2}}({{n}_{1}}+{{n}_{2}}-2)Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}} right.$;
$left. ({{{bar{X}}}_{1}}-{{{bar{X}}}_{2}})+{{t}_{1-alpha/2}}({{n}_{1}}+{{n}_{2}}-2)Ssqrt{frac{1}{{{n}_{1}}}+frac{1}{{{n}_{2}}}} right)$
является доверительным для m1 – m2 на уровне значимости α.
7.
Доверительный интервал для отношения дисперсий $sigma _{1}^{2}/sigma _{2}^{2}$ при известных математических ожиданиях
m1 и m2.
В качестве центральной статистики выберем статистику
${{F}_{0}}=frac{S_{01}^{2}/sigma _{1}^{2}}{S_{02}^{2}/sigma _{2}^{2}}sim F({{n}_{1}},{{n}_{2}})$.
Запишем тождество (1*):
$Pleft( {{f}_{alpha /2}}({{n}_{1}},{{n}_{2}})<frac{S_{01}^{2}/sigma _{1}^{2}}{S_{02}^{2}/sigma _{2}^{2}}<{{f}_{1-alpha/2}}({{n}_{1}},{{n}_{2}}) right)=1-alpha $,
где ${{f}_{alpha /2}}({{n}_{1}},{{n}_{2}})$ и ${{f}_{1-alpha /2}}({{n}_{1}},{{n}_{2}})$ – квантили распределения
Фишера с n1 и n2 степенями свободы в числителе и в знаменателе
на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно
$sigma _{1}^{2}/sigma _{2}^{2}$ и учитывая, что ${{f}_{alpha/2}}({{n}_{1}},{{n}_{2}})=frac{1}{{{f}_{1-alpha /2}}({{n}_{2}},{{n}_{1}})}$, получим:
$Pleft( frac{S_{01}^{2}}{S_{02}^{2}}f_{alpha /2}^{{}}({{n}_{2}},{{n}_{1}})<frac{sigma _{1}^{2}}{sigma_{2}^{2}}<frac{S_{01}^{2}}{S_{02}^{2}}f_{1-alpha /2}^{{}}({{n}_{2}},{{n}_{1}}) right)=1-alpha $,
откуда следует, что интервал
$left( frac{S_{01}^{2}}{S_{02}^{2}}f_{alpha /2}^{{}}({{n}_{2}},{{n}_{1}});frac{S_{01}^{2}}{S_{02}^{2}}f_{1-alpha /2}^{{}}({{n}_{2}},{{n}_{1}})right)$
является доверительным для $sigma _{1}^{2}/sigma _{2}^{2}$ на уровне значимости α.
8.
Доверительный интервал для отношения дисперсий $sigma _{1}^{2}/sigma _{2}^{2}$ при неизвестных математических ожиданиях
m1 и m2.
В качестве центральной статистики выберем статистику
${{F}_{0}}=frac{S_{1}^{2}/sigma _{1}^{2}}{S_{2}^{2}/sigma _{2}^{2}}sim F({{n}_{1}}-1,{{n}_{2}}-1)$.
Запишем тождество (1*):
$Pleft( {{f}_{alpha /2}}({{n}_{1}}-1,{{n}_{2}}-1)<frac{S_{1}^{2}/sigma _{1}^{2}}{S_{2}^{2}/sigma _{2}^{2}}<{{f}_{1-alpha/2}}({{n}_{1}}-1,{{n}_{2}}-1) right)=1-alpha $,
где ${{f}_{alpha /2}}({{n}_{1}}-1,{{n}_{2}}-1)$ и ${{f}_{1-alpha /2}}({{n}_{1}}-1,{{n}_{2}}-1)$ – квантили
распределения Фишера с n1–1 и n2–1 степенями свободы в числителе
и в знаменателе на уровнях α/2 и 1–α/2 соответственно.
Разрешая неравенство под знаком вероятности относительно
$sigma _{1}^{2}/sigma _{2}^{2}$ и учитывая, что ${{f}_{alpha/2}}({{n}_{1}},{{n}_{2}})=frac{1}{{{f}_{1-alpha /2}}({{n}_{2}},{{n}_{1}})}$, получим:
$Pleft( frac{S_{1}^{2}}{S_{2}^{2}}f_{alpha /2}^{{}}({{n}_{2}}-1,{{n}_{1}}-1)<frac{sigma _{1}^{2}}{sigma_{2}^{2}}<frac{S_{1}^{2}}{S_{2}^{2}}f_{1-alpha /2}^{{}}({{n}_{2}}-1,{{n}_{1}}-1) right)=1-alpha $,
откуда следует, что интервал
$left( frac{S_{1}^{2}}{S_{2}^{2}}f_{alpha /2}^{{}}({{n}_{2}}-1,{{n}_{1}}-1);frac{S_{1}^{2}}{S_{2}^{2}}f_{1-alpha /2}^{{}}({{n}_{2}}-1,{{n}_{1}}-1)right)$
является доверительным для $sigma _{1}^{2}/sigma _{2}^{2}$ на уровне значимости α.
Пример 1
Пример 2
Доверительные интервалы в случае нормальных выборок⚓︎
Warning
Формулы могут отображаться некорректно, как и само форматирование. Мне было влом делать нормально
Пусть случайная величина X имеет неизвестную характеристику {theta}
Это может быть, например, числовая характеристика случайной величины, параметр и т. д. Идея, лежащая в основе интервального оценивания характеристики {theta} состоит в том, что по результатам наблюдений {Х_1, X_2, Х_n} определяют две величины {underlinetheta} = {underlinetheta}. ({Х_1, X_2, … Х_n}) и {overlinetheta} = {overlinetheta} ({Х_1, X_2, … Х_n}) такие, что
где {γ} — наперед заданная вероятность. Величины {theta} и {overlinetheta} называют доверительными границами, а интервал ({underlinetheta}, {overlinetheta}) — доверительным интервалом для {theta}, соответствующим уровню надежности {γ}
Строить доверительный интервал можно исходя из точечной оценки. Пусть для {theta} известна точечная оценка {overlinetheta}. Подберем {varepsilon_γ} такое, чтобы выполнялось равенство
(13.1)
где {γ} — выбранная заранее вероятность. Тогда
и ({overlinetheta — varepsilon_γ, overlinetheta + varepsilon_γ}) можно рассматривать как доверительный интервал для {overlinetheta}. Так что задача состоит в том, чтобы по заданному {γ} выбрать соответствующее {varepsilon γ}
На основании (13.1) можно гарантировать, что с вероятностью {γ} значение точечной оценки отличается от неизвестного значения {theta} меньше, чем на {varepsilon γ}.
Вероятность {γ} обычно выбирают настолько близкой к единице, чтобы ее можно было считать вероятностью практически достоверного события
Тогда соответствующий доверительный интервал можно считать интервалом практически возможных значений {theta}, или интервалом значений {theta}, не противоречащих опытным данным
§ 13.1. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ⚓︎
Случай большой выборки⚓︎
Пусть закон распределения случайной величины X неизвестен.
Неизвестны также М(Х) и D(X), причем D(Х) < ∞. Над случайной величиной проделано n независимых наблюдений и получена выборка значений {Х_1, X_2, … Х_n}.
Если число наблюдений достаточно велико (хотя бы несколько десятков), то
(13.2)
где X — среднее арифметическое результатов наблюдений, а {t_γ} выбирается из таблицы функции Лапласа так, чтобы {2varphi_0(t_γ) = γ}. Возможен случай, когда дисперсия случайной величины известна, а неизвестно лишь математическое ожидание этой величины.
Такая ситуация возникает при измерении постоянной величины с прибором, который не имеет систематической ошибки.
Если дисперсия случайной ошибки прибора предварительно изучена и известна, то (13.2) можно рассматривать как доверительный интервал для истинного значения измеряемой величины. В самом деле, в результате измерения получается значение случайной величины {X = a + γ}, где {γ} — случайная ошибка.
По предположению {D(γ)} — известна, а {M(γ) = 0} ввиду отсутствия систематической ошибки. Тогда
{M(X) = M(a + γ) = a}
и {D(X) = D(a + γ) = D(а) + D(Y) = D(Y)}
Остается подставить найденные величины в (13.2)
Если вместе с {M(X)} неизвестна и {D(X)}, то из тех же опытных данных можно получить несмещенную и состоятельную оценку для дисперсии по формуле:
(13.3)
Тогда (13.2) имеет вид (13.4)
В выводе формулы (13.4) ключевую роль играет тот факт, что при большом числе независимых наблюдений среднее арифметическое их результатов имеет близкий к нормальному закон распределения
Формулу (13.4) можно использовать для любой случайной величины, лишь бы число наблюдений было достаточно велико (хотя бы несколько десятков)
Случай малой выборки⚓︎
При небольшом числе наблюдений для построения доверительного интервала необходима информация о типе закона распределения случайной величины. Рассмотрим практически важный случай, когда {X ~ N(m; σ^2)}
Если {σ^2} известно, а неизвестно лишь m, то при независимых наблюдениях можно воспользоваться свойством устойчивости нормального закона распределения
Согласно этому свойству сумма независимых случайных величин, подчиненных нормальному закону распределения, сама имеет нормальный закон распределения. Поэтому в названных условиях и при небольшом числе наблюдений можно утверждать, что X имеет близкий к нормальному закон распределения и использовать формулу (13.2)
Если дисперсия {σ^2} неизвестна, то при небольшом числе наблюдений ее оценка на основе опытных данных получается грубой и формула (13.4) не решает задачи построения доверительного интервала. Английский статистик Студент (У. Госсет) для {X ~ N(m; σ^2)} с неизвестными параметрами и {σ^2} в предположении независимости опытов изучил величину
где {s^2} — оценка дисперсии по формуле (13.3), а n — число наблюдений.
Оказалось, что распределение величины Т не зависит ни от X, ни от s, а зависит лишь от числа {n — 1}, которое принято называть числом степеней свободы. Студент нашел функцию плотности вероятности {f_n-1(t) = γ} и с ее помощью вычислил вероятности
{2varphi_0(t_γ) = γ}
(13.5)
которые свел в таблицу (см. приложение, табл. 3)
При заданном уровне надежности γ по таблице распределения студента для {n — 1} степени свободы можно найти соответствующее {t_У}. Подстановка этого {t_У} в (13.5) приводит к
или
(13.6)
Формула (13.6) по структуре похожа на формулу (13.4), но {t_У} в этих формулах определяется по разным таблицам.
ПРИМЕР 13.1⚓︎
{Х_1 = 592, Х_2 = 595, Х_3 = 594. Х_4 = 592, Х_5 = 593, Х_6 = 597, Х_7 = 595. Х_8 = 589, Х_9 = 590} Измерения сопротивления резистора дали следующие результаты (в омах): Известно, что ошибки измерения имеют нормальный закон распределения. Систематическая ошибка отсутствует. Построить доверительный интервал для истинного сопротивления резистора с надежностью 0,99 в предположении:
- Дисперсия ошибки измерения известна и равна 4
6) дисперсия ошибки измерения неизвестна
- В данной серии из девяти наблюдений
Если дисперсия ошибки измерения известна, то можно воспользоваться формулой (13.2). Для этого из таблицы функции Лапласа (см. приложение, табл. 2) находим, что {2varphi_theta(2.58) = 0.99}. Т. е. уровню надежности 0,99 соответствует значение {t_У = 2,58}. Тогда по формуле (13.2)
593 - 2,58 * 2/√9 < М(Х) < 593 + 2,58 * 2/√9 или {591,28 < М(Х) < 594,72} с вероятностью 0,99
В случае неизвестной дисперсии ее можно оценить на основе тех же опытных данных:
{s = sqrt{6,5} ≈ 2,55}
По таблице распределения студента (см. приложение, табл. 3) для n - 1 = 9 - 1 = 8 степеней свободы и заданной вероятности γ = 0,99 находим tУ = 3,355. Тогда по формуле (13.6)
или {590,15 < М(X) < 595,85} с вероятностью 0,99
ПРИМЕР 13.2⚓︎
В таблице приведены сгруппированные данные измерений роста у 50 наугад выбранных студентов:
Оценить средний рост и дисперсию роста студентов. Построить доверительный интервал для среднего роста студентов с надежностью 0,9
- Так как данные сгруппированы, то в качестве представителя каждого интервала можно взять середину этого интервала
Тогда:

{2varphi_theta(1.65) = 0.9}, то по формуле (13.4) имеем
или {176,86 < М(Х) < 179,14} с вероятностью 0,9
ПРИМЕР 13.3⚓︎
По результатам девяти измерений емкости конденсатора получена оценка X = 20 мкФ Среднеквадратическая ошибка измерения известна и равна 0,04 мкФ. Построить доверительный интервал для емкости конденсатора с надежностью 0,95.
- В предположении, что ошибки измерения имеют нормальный закон распределения можно воспользоваться формулой
(13.2). Так как {2varphi_theta(1,96) = 0,95}. то20 - 1,96 * 0,04 / 3 < M (X) < 20 + 1 > 1,96 * 0,04 / 3или19,974 < М(Х) < 20,026с вероятностью0,95
§ 13.2. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ⚓︎
ВЕРОЯТНОСТИ СОБЫТИЯ⚓︎
Пусть вероятность Р(А) = р неизвестна. Проделаем n независимых опытов и определим k/n — частоту события в данной серии опытов. Если n достаточно велико, то вероятность и частота события связаны соотношением:
(13.7)
К сожалению, в формуле (13.7) доверительные границы для вероятности р выражаются через саму эту неизвестную вероятность. Это затруднение можно обойти заметив, что pq <= 1/4. Тогда (13.7) можно записать в виде
(13.8)
Оценка pq величиной 1/4 приемлема, если есть уверенность, что неизвестная вероятность p близка к 1/2. Но при значениях р близких к нулю или единице такая оценка слишком груба. Например, при р = 0,1 получаем всего лишь pq = 0,1 * 0,9 = 0,09 вместо 0,25. Можно точный доверительный интервал заменить приближенным, если учесть, что при большом числе опытов k/n ≈ p в силу закона больших чисел:
(13.9)
ПРИМЕР 13.4⚓︎
Для обследования большой партии изделий (несколько тысяч штук) наугад выбрано 160 изделий. Среди них оказалось 56 изделий низкого сорта. Оценить долю изделий низкого сорта в этой партии с надежностью 0,95.
- Так как партия изделий крупная, то для упрощения можно считать, что по мере выбора изделий состав партии заметно не изменяется и вероятность выбрать наугад изделие низкого сорта равна доле низкосортных изделий в этой партии. Тогда задача сводится к построению доверительного интервала для вероятности выбора из этой партии изделия низкого сорта. Частота изделий низкого сорта в выборке {frac{k}{n} = frac{56}{160} = 0.35}. Из таблицы функции
Лапласаследует, что {2varphi_theta(1.96) = 0.95}. Поэтому
или 0,27 < р < 0,42. Итак, по данной выборке можно с вероятностью 0,95 утверждать, что во всей партии содержится от 27% до 42% изделий низкого сорта
ПРИМЕР 13.5⚓︎
Было проведено 400 испытаний механизма катапультирования. В этих испытаниях не зарегистрировано ни одного отказа. С надежностью 0,95 оценить вероятность отказа механизма катапультирования
- В данной серии испытаний частота появления отказа
к/400 = 0. Поэтому непосредственно использовать формулу(13.9)нельзя. Заметим, чтоp * q <= 1/4, так какр + q = 1. Функция Лапласа {2varphi_theta(x)} строго возрастает
Поэтому меньшему значению аргумента соответствует меньшее значение функции. В расчете на худший вариант можно воспользоваться формулой (13.8). По таблице функции Лапласа находим, что {2varphi_theta(x)(1.96) = 0.95}. Поэтому tγ = 1,65 и 0 < р < 1,65 * 1/2√400 = 0,041
Доверительный интервал (0; 0,041) построен в расчете на худший вариант, когда вероятность события близка к 1/2. Но большое число опытов (n = 400) и нулевая частота события в них позволяют с уверенностью утверждать, что вероятность события близка к нулю. Если несколько ухудшить статистику испытаний и посчитать что один отказ все-таки наблюдался, то p * q ≈ 1/40 * 399/400 = 0,0025. Тогда по формуле (13.9) получаем приближенный доверительный интервал
или 0 < р < 0,0066. Это приближенный доверительный интервал, но он определенно более точен, чем грубая оценка по формуле (13.8)
ПРИМЕР 13.6⚓︎
Сколько независимых наблюдений нужно проделать, чтобы с вероятностью 0,95 можно было построить доверительный интервал для вероятности события шириной не более 0,2?
- По таблице функции Лапласа
(см. приложение, табл. 2)находим, что {2varphi_theta(x)(1.96) = 0.95}. Вероятность события неизвестна. Так какpq <= 1/4, то и k/n (1 - k/n) <= 1/4. Доверительный интервал располагается симметрично относительно частоты события, поэтому в формуле(13.9)
Откуда {sqrt{n} = frac{1.96}{0.2} = 9.8}. Следовательно, т = 96,04. Т. е. т > 96
Последнее обновление: 2021-06-17
Созданный: 2021-06-17