Чтобы понять, что такое дирекционный угол, представим на карте линию (отрезок) с начальной точкой А и конечной точкой В.
Теперь проведем из начала отрезка (точки А) луч, параллельный осевому меридиану зоны и направленный на север. И будем поворачивать этот
луч вокруг точки А по часовой стрелке до тех пор, пока он не пересечется с точкой В. Угол, на который мы повернули луч,
и будет называться дирекционным углом линии АВ.
Калькулятор угла по координатам
С помощью этого калькулятора Вы сможете производить расчет дирекционных углов линий на основе заданных координат точки стояния (А) и точки
ориентирования (В), а также рассчитывать расстояние между этими точками.
Калькулятор координат по углу и расстоянию
Этот калькулятор поможет Вам рассчитать координаты конечной точки пути на основе координат начальной точки, дирекционного угла и расстояния между точками.
Угол можно указывать как в десятичных градусах (226,27303°), так и в градусах — минутах — секундах (226° 16′ 22″).
Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Решение обратной геодезической задачи онлайн
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB
Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.
Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.
Сначала находим приращения координат:
ΔX = XB – XA ;
ΔY = YB – YA .
Величину угла rAB определяем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
Положение
какого-либо объекта на местности чаще
всего определяют и указывают в полярных
координатах, то есть углом между начальным
(заданным) направлением и направлением
на объект и расстоянием до объекта. В
качестве начального выбирают направление
географического (геодезического,
астрономического) меридиана, магнитного
меридиана или вертикальной линии
координатной сетки карты. За начальное
может быть принято и направление на
какой-нибудь удаленный ориентир. В
зависимости от того, какое направление
принято за начальное, различают
географический (геодезический,
астрономический) азимут А, магнитный
азимут Ам, дирекционный угол.
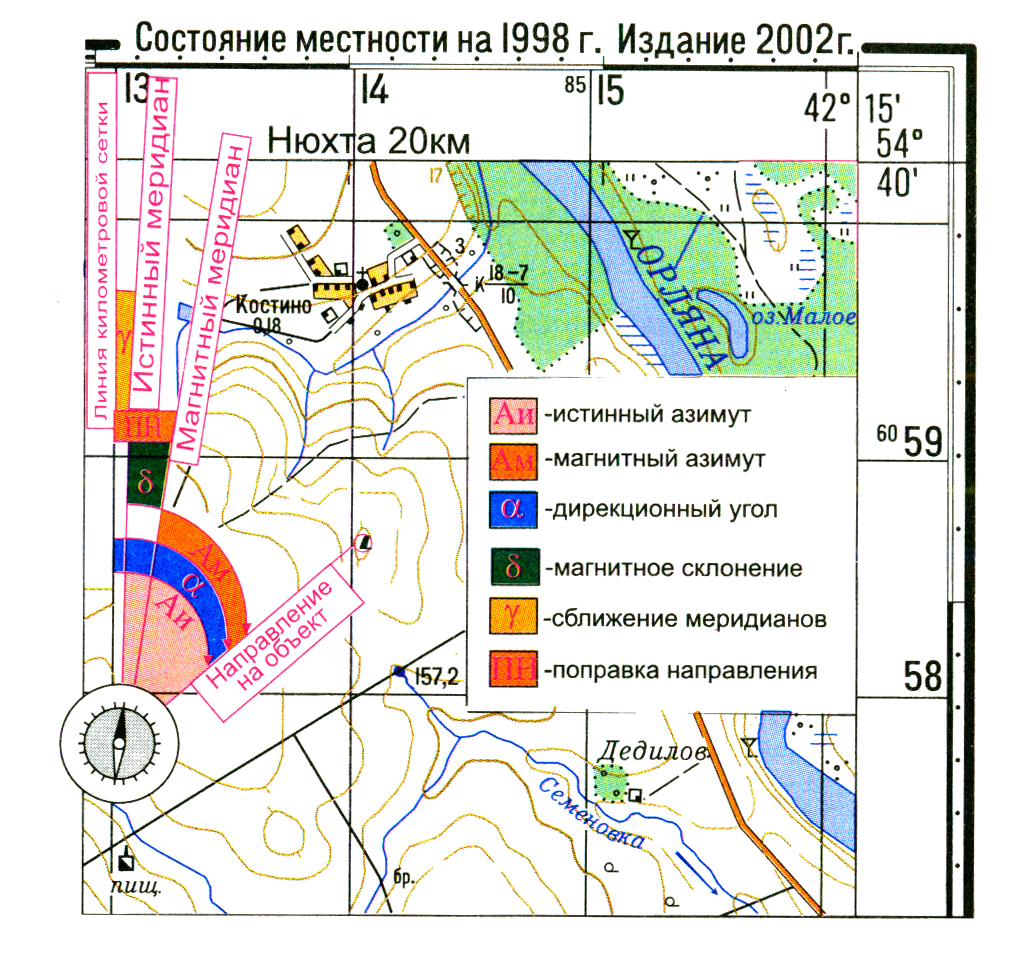
Взаимозависимость
между магнитным азимутом, дирекционным
углом и геодезическим (истинным) азимутом
показана на рис. 24.
Магнитный
азимут Ам
– горизонтальный угол, отсчитываемый
от северного направления магнитного
меридиана по ходу часовой стрелки до
направления на предмет.
Дирекционный
угол α –
угол между северным направлением
вертикальной линии координатной сетки
карты и направлением на местный предмет
(ориентир), отсчитанный по ходу часовой
стрелки.
Геодезический
(истинный) азимут Аи
– угол между северным направлением
геодезического (истинного) меридиана
(боковой стороной рамки карты или линии,
параллельной ей) и направлением на
предмет, отсчитанный по ходу часовой
стрелки. Направлению
геодезического меридиана на топографической
карте соответствуют боковые стороны
ее рамки, а также прямые линии, которые
можно пронести между одноименными
минутными делениями долгот.
Магнитный,
геодезический азимут, как и дирекционный
угол, могут иметь значения от 0° до 360°.
Рис.
24. Взаимозависимость между магнитным
азимутом,
дирекционным
углом и геодезическим азимутом
Сближение
меридианов γ
– угол между северным направлением
геодезического меридиана и вертикальной
линией координатной сетки. Сближение
меридианов отсчитывается от северного
направления геодезического меридиана
по ходу или против хода часовой стрелки
до северного направления вертикальной
линии сетки. Для точек, расположенных
восточнее геодезического меридиана,
значение сближения положительное, а
для точек, расположенных западнее, –
отрицательное. На топографических
картах Республики Беларусь значение
сближения меридианов не превышает ±3°.
Сущность сближения меридианов приведена
на рис. 25.
Рис.
25. Сущность сближения меридианов
Величина
сближения меридианов, указанная на
топографической карте в левом нижнем
углу, относится к центру листа карты.
Магнитное
склонение δ
– угол между северным направлением
геодезического меридиана и направлением
магнитного меридиана (магнитной стрелки).
Если северный конец магнитной стрелки
отклоняется от геодезического меридиана
на восток, магнитное склонение считается
положительным, а на запад – отрицательным.
Поправка
направления (ПН) –
угол между направлением вертикальной
линии координатной сетки и магнитным
меридианом. Она равна алгебраической
разности магнитного склонения и сближения
меридианов:
ПН
= (±δ)
– (±γ).
Данные
о магнитном склонении, сближении
меридианов и значение поправки направления
помещаются под южной стороной рамки
каждого листа топографической карты
крупного масштаба. Переход от измеренных
на карте дирекционных углов и геодезических
азимутов к магнитным азимутам выполняется
по формулам
Ам
= α – (±ПН);
Ам
= А – (±δ).
Измерение
по карте дирекционных углов.
Дирекционные углы направлений на местные
предметы (ориентиры) измеряют по карте
транспортиром, артиллерийским кругом
и хордоугломером.
Транспортиром
дирекционный угол на карте измеряют в
такой последовательности:
ориентир,
на который измеряют дирекционный угол,
соединяют прямой линией с точкой стояния
так, чтобы эта прямая была больше радиуса
транспортира и пересекла хотя бы одну
вертикальную линию координатной сетки;
совмещают
центр транспортира с точкой пересечения,
как показано на рис. 26, и отсчитывают по
транспортиру значение дирекционного
угла.

Рис.
26.
Измерение дирекционных углов по карте
транспортиром
В
нашем примере дирекционный угол с
исходной точки на яму равен 65°, а
дирекционный угол с исходной точки на
мост – 274°.
Артиллерийский
круг
представляет собой целлулоидную
пластину, по внешнему срезу которой
нанесена шкала в делениях угломера.
Цена одного деления равна 0-10. Большие
деления, соответствующие 1-00, оцифрованы
от 0 до 60; при этом ряд красных цифр
нанесен в возрастающем порядке по ходу
часовой стрелки, а ряд черных цифр –
против хода часовой стрелки.
При
измерении дирекционного угла артиллерийский
круг устанавливают на карте так, чтобы
его центр совпал с точкой пересечения
линии определяемого направления и
вертикальной линии координатной сетки,
а нулевой штрих – с северным направлением
этой линии. Затем снимают отсчет по
красной шкале круга против линии
определяемого направления.
Измерение
угла с помощью хордоугломера выполняют
в таком порядке. Через главные точки
условных знаков исходного пункта и
местного предмета, на который определяется
дирекционный угол, проводят на карте
тонкую прямую линию длиной не менее
15см. Из точки пересечения этой линии с
вертикальной линией координатной сетки
карты циркулем-измерителем делают
засечки на линиях, образовавших острый
угол, радиусом, равным расстоянию на
хордоугломере от 0 до 10 больших делений.
Затем измеряют хорду – расстояние между
отметками. Не изменяя раствора
циркуля-измерителя, левую его иглу
передвигают по крайней левой вертикальной
линии шкалы хордоугломера до тех пор,
пока правая игла не совпадет с каким-либо
пересечением наклонной и горизонтальной
линий. Левая и правая иглы циркуля-измерителя
должны быть всегда на одной и той же
горизонтальной линии. В таком положении
игл снимают отсчет по хордоугломеру.
Если
угол меньше 15-00 (90°), то по верхней шкале
хордоугломера отсчитывают большие
деления и десятки малых делений угломера,
а по левой вертикальной шкале – единицы
делений угломера.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скачать с Depositfiles
2.5 Вычисление дирекционных углов замкнутого теодолитного хода
Дирекционный угол начальной стороны выбирают из табл.2. Дирекционные углы последующих сторон полигона вычисляют по формуле
(7)
В этой формуле исправленный угол тот, который заключен, между предыдущей и последующей сторонами полигона. Например, для второй стороны полигона, т.е. стороны (II-III) дирекционный угол вычисляется по формуле
Знак «минус» перед третьим членом в первой части формулы берут в том случае, когда сумма двух первых членов превышает 180°.
Если же сумма двух первых членов настолько велика, что после вычитания из нее 180° значение дирекционного угла какой-нибудь стороны полигона окажется больше чем 360°, то в этомслучае следует еще вычесть 360°. Это и будет искомое значение дирекционного угла.
Тан, пользуясь приведенной выше формулой, последовательно переходя от одной стороны к другой, т.е. от предыдущей к последующей, вычисляют дирекционные углы всех сторон полигона.
Вычислив дирекционные углы всех сторон полигона, производят контроль вычислений. Для этого необходимо продолжить вычисления, используя исправленное значение последнего измеренного угла полигона, чтобы получить вторично значение дирекционного угла начальной стороны.
Вычисления считаются безошибочными, если полученное путем вычислений значение дирекционного угла начальной стороны полигона будет в точности (до I») равно заданной величине.Эту величину следует записать в графу «Дирекционные углы» в конце всех вычислений.
2.6 Вычисления приращений координат точек замкнутого хода
Формулы, по которым определяются приращения координат, следующие:
(8)
где и
— приращения координат;
— горизонтальное приложение длины линии;
— дирекционный угол стороны полигона.
Пример
Значения приращений координат в теодолитном ходе вычисляет с округлением до сотых долей метра.
2.7. Вычисление невязок в приращениях координат и их распределение
В замкнутом теодолитной ходе невязки в приращениях координат определяют по формулам:
(9)
где и
— алгебраические суммы приращений координат по координатным осям, соответственно X и Y.
Прежде чем распределить полученные невязки, необходимо убедиться в их допустимости, судя не по каждой отдельной невязке или
, а по невязке в периметре полигона.
Абсолютная линейная невязка в периметре полигона вычисляется по формуле:
(10)
Невязка в полигоне зависит главным образом от периметра полигона. Чем больше периметр, тем большую невязку следует в нем ожидать. Поэтому и допустимость невязки определяют в зависимости от периметра полигона. Невязка в периметре теодолитного полигона
при благоприятных условиях измерения линий считается допустимой,
если она не превышает 1/2000 периметра Р, т.е.
Отношение к периметру хода Р, т.е.
называется относительной невязкой в периметре хода.
Если полученные невязки окажутся больше допустимых, то следует прежде всего проверить правильность вычисления. При отсутствия ошибок в вычислениях следует перемерить в первую очередь длины тех сторон дирекционные углы которых близки к дирекционному углу вычисленному по формуле
Если невязка в периметре оказалась допустимой (табл.6), то невязки по осям координат
и
распределяют с обратным знаком на все приращения (по соответствующей оси) пропорционально длинам сторон полигона.
Поправки в приращения координат вычисляют по формулам:
(11)
……………….……………….
Для упрощения вычислений поправок в приращения координат периметр и длины сторон полигона рекомендуется выражать в сотнях метров. Поправки в приращения вычисляются с точностью до сантиметра.
Пример:
Р=789м=7,9 сотни метров (табл.6)
Сумма поправок должна быть равна невязке с обратным знаком. Если сумма поправок вследствие приближенных вычислений не равна невязке, то некоторые из поправок следует исправить так, чтобы эта сумма равнялась невязке с обратным знаком, т.е.
В том случае, когда невязка в приращениях по какой-либо оси мала» невязку распределяют по I см только на несколько приращений, подученных по наиболее длинным сторонам полигона.
Поправки в приращения координат с их знаком подписывают «над» или «под» вычисленными знаками приращений. Затем производят алгебраическое сложение значений приращений координат. Величины исправленных приращений заносят в графы 9 и 10 табл. 6
Контролем вычислений исправленных приращений служит точное совпадение алгебраической суммы их по каждой из осей в отдельности о теоретической величиной, т.е. эти суммы должны быть равны нулю.
2.8 Вычисление координат вершин полигона
Координаты начальной точки полигона приведены в табл. 1.Координата X иди У последующей вершины полигона равна координате предыдущей вершины плюс (алгебраически) соответствующее исправленное приращение со своим знаком.
………………………
Контролем вычислений координат вершин замкнутого полигона является получение координат первой вершины полигона, которые должны быть равны значениям заданных координат этой вершины. Вычисленные значения координат вершин полигона записывают на самой н… стороне в соответствующих графах ведомости.
Скачать с Depositfiles