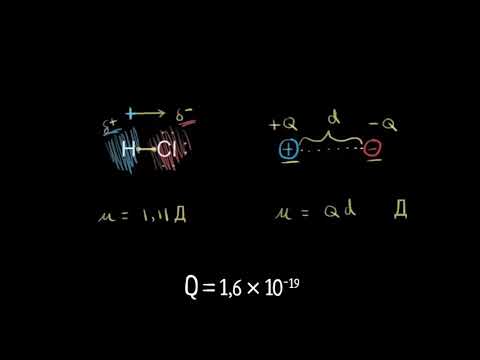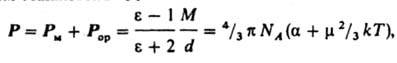Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Основные положения метода
Обозначения, используемые в методе Гиллеспи
Алгоритм определения строения молекул по методу Гиллеспи
Геометрия молекул неорганических и органических веществ
Дипольный момент молекулы
Примеры определения строения молекул по методу Гиллеспи
Задачи для самостоятельного решения
Основные положения метода
- Все электроны, образующие химические связи атомов, считаются равноценными независимо от их типа (s, p, d, f).
- Атомный остов, содержащий ядро и внутренние электронные оболочки, не оказывает влияние на расположение валентных электронов.
- Электронные пары располагаются в пространстве таким образом, чтобы отталкивание между ними было минимальным (две электронные пары располагаются линейно, три образуют правильный треугольник, четыре располагаются тетраэдрически и т.д.).
- Строение молекулы определяется расположением в пространстве связывающих электронных пар.
- Орбиталь кратной связи считается единичной, независимо от того, содержит она одну или две π-связи. В то же время электронные пары двойной и тройной связи занимают в пространстве несколько больше места, чем электронная пара одинарной связи.
- Неподелённая электронная пара в пространстве занимает больше места, чем связывающая электронная пара.
Обозначения, используемые в методе Гиллеспи
При рассмотрении геометрической формы молекулы методом Гиллеспи её формула записывается в виде AХnEm , где:
А – центральный атом;
X – лиганд, с которым центральный атом образует химическую связь, то есть даёт связывающие электронные пары;
Е – неподелённая электронная пара;
n, m – соответственно число связывающих и неподелённых электронных пар.
Алгоритм определения строения молекул по методу Гиллеспи
Для того, чтобы определить строение молекулы методом Гиллеспи, предлагается следующий порядок действий.
- На основании формулы молекулы определяется число лигандов n, с которыми центральный атом образует связь и записывается формула AХnEm с указанием значения n.
- Находится общее число связывающих и неподелённых электронных пар (n + m) по формуле:
(n + m) = 1/2 (Nц + Nл – z ) – π (1)
где:
Nц – число электронов центрального атома на его внешнем электронном слое,
Nл – число электронов лигандов, участвующих в образовании связей с центральным атомом,
π – число π-связей в молекуле,
z – заряд иона (в случае определения строения молекулярного аниона).
- Определяется пространственное расположение всех электронных пар (связывающих и неподелённых).
- Находится число неподелённых электронных пар m и уточняется формула молекулы AХnEm (указывается значение m).
- Устанавливается геометрия молекулы.
В табл. 1. обобщаются возможные варианты использования метода Гиллеспи для определения строения различных молекул.
Таблица 1. Геометрия молекул неорганических и органических веществ.
| № | Тип молекулы | Примеры | Общее число связывающих и неподелённых электронных пар | Пространственное расположение электронных пар | Число связывающих электронных пар | Геометрия молекулы |
| 1 | AX2E0 | BeCl2, CO2 | 2 | линейное | 2 | линейная |
| 2 | AX3E0 | BF3, SO3 | 3 | правильный треугольник | 3 | правильный треугольник |
| 3 | AX2E1 | SnCl2 SO2 | 3 | правильный треугольник | 2 | угловая |
| 4 | AX4E0 | CH4, CCl4 | 4 | тетраэдр | 4 | тетраэдр |
| 5 | AX3E1 | NH3, PH3 | 4 | тетраэдр | 3 | треугольная пирамида |
| 6 | AX2E2 | H2O | 4 | тетраэдр | 2 | угловая |
| 7 | AX5E0 | PCl5 | 5 | тригональная бипирамида | 5 | тригональная бипирамида |
| 8 | AX4E1 | SF4 | 5 | тригональная бипирамида | 4 | “качели” |
| 9 | AX3E2 | ClF3 | 5 | тригональная бипирамида | 3 | “Т-образная” |
| 10 | AX2E3 | XeF2 | 5 | тригональная бипирамида | 2 | линейная |
| 11 | AX6E0 | SF6 | 6 | октаэдр | 6 | октаэдр |
| 12 | AX5E1 | ICl5 | 6 | октаэдр | 5 | квадратная пирамида |
| 13 | AX4E2 | XeF4 | 6 | октаэдр | 4 | плоская |
| 14 | A+X4E0 | NH4+ | 4 | тетраэдр | 4 | тетраэдр |
| 15 | AX42-E0 | SO42- | 4 | тетраэдр | 4 | тетраэдр |
| 16 | AX32-E1 | SO32- | 4 | тетраэдр | 3 | треугольная пирамида |
| 17 | A— X6E0 | PCl6— | 6 | октаэдр | 6 | октаэдр |
| 18 | AX’1X»2E0 | COCl2 | 3 | правильный треугольник | 3 | правильный треугольник |
Дипольный момент молекулы
Мера полярности связи – её дипольный момент (μ) – определяется произведением:
μ = ql
где q – эффективный заряд, l – длина диполя (расстояние между двумя равными по величине и противоположными по знаку зарядами +q и –q).
Дипольный момент – это векторная величина. Понятия “дипольный момент связи” и “дипольный момент молекулы” совпадают только для двухатомных молекул. Дипольный момент сложной молекулы равен векторной сумме дипольных моментов всех связей. Дипольный момент многоатомной молекулы зависит не только от полярности отдельных связей в молекуле, но и от геометрической формы молекулы.
Например, в линейной молекуле СО2 каждая из связей С–О полярна, а молекула в целом неполярна ( μ(СО2)=0), так как дипольные моменты связей компенсируют друг друга (рис. 1). В угловой молекуле Н2О связи расположены под углом 104,5o и векторная сумма дипольных моментов двух связей выражается диагональю параллелограмма (рис. 1). Если μ≠0, то молекула полярна.

Рис. 1. Дипольные моменты молекул СО2 и Н2О
Примеры определения строения молекул по методу Гиллеспи
Пример 1. Молекула BF3.
- Формула молекулы AX3Em.
- Атом бора даёт три электрона на образование σ-связей и каждый из трех атомов фтора дают по одному электрону; π-связи в молекуле отсутствуют. Общее число образующих σ-связи электронных пар:
n + m = (3 + 3)/2 = 3 .
- Расположение электронных пар в пространстве – правильный треугольник.
- Число неподелённых электронных пар m = 3 – 3 = 0. Формула молекулы AX3E0.
- Строение молекулы – правильный треугольник. Все валентные электроны атома бора идут на образование-связей с тремя атомами фтора. Неподелённых электронных пар у атома бора нет.
Пример 2. Молекула SnCl2 .
- Формула молекулы AX2Em.
- Общее число электронных пар в валентной оболочке атома олова:
n + m = (4 + 2)/2 = 3
(у олова на внешнем слое четыре электрона и два электрона дают атомы хлора; π-связи в молекуле отсутствуют).
- Расположение электронных пар в пространстве – правильный треугольник.
- Число неподелённых электронных пар m = 3 – 2 = 1. Формула молекулы AX2E1.
- Строение молекулы – нелинейная (угловая).
Пример 3. Молекула XeF4.
- Формула молекулы AX4Em.
- Общее число электронных пар в валентной оболочке атома ксенона:
n + m = (8 + 4)/2 = 6
(у атома Хе восемь электронов на внешнем электронном слое и два электрона дают атомы F; π-связи в молекуле отсутствуют).
- Расположение электронных пар в пространстве – октаэдр.
- Число неподелённых электронных пар m = 6–2 = 2. Формула молекулы AX4E2.
- Строение молекулы – квадрат.
Пример 4. Молекула SO2.
- Формула молекулы AX2Em. Молекула содержит две π-связи.
- Общее число электронных пар в валентной оболочке атома серы
n + m = (6 + 4)/2 – 2 = 3
(у атома серы на внешнем электронном слое шесть электронов, четыре электрона дают два атома кислорода; в молекуле две π-связи которые вычитаются при определении n+m).
- Расположение электронных пар в пространстве – правильный треугольник.
- Число неподелённых электронных пар m = 3 – 2 =1. Формула молекулы AX2E1.
- Строение молекулы – нелинейная (угловая).
Атом серы имеет шесть валентных электронов. Из них четыре идут на образование π- и σ-связей с двумя атомами кислорода (О= S= O). В результате, у атома серы остается одна неподелённая пара электронов.
Пример 5. Молекулярный ион СO32- .
- Формула иона AX3Em. Ион содержит одну π-связь.
- Общее число электронных пар в валентной оболочке атома углерода n + m = (4 + 6 – 2)/2 – 1 = 3 (к четырём электронам атома углерода прибавляем шесть электронов атома кислорода и вычитаем два электрона атома кислорода – заряд карбонат-иона; из полученной величины вычитаем также число π-связей).
- Расположение электронных пар в пространстве – плоский треугольник.
- Число неподелённых электронных пар m = 3 – 3 =0. Формула карбонат-иона AX3E0.
Строение карбонат-иона – плоский треугольник.
Задачи для самостоятельного решения
1. Из приведенных молекул полярными являются:
| 1) N2 | 2) NH3 | 3) XeF2 |
| 4) BF3 | 5) CO | 6) PCl5 |
2. Неполярными молекулами с полярными связями являются:
| 1) BeCl2 | 2) SnCl2 | 3) H2S |
| 4) SO3 | 5) SO2 | 6) O2 |
3. Определите по методу Гиллеспи геометрическую форму молекул: H2S, BCl3, XeF2.
4. Определите по методу Гиллеспи геометрическую форму молекулы SO3.
5. Определите по методу Гиллеспи геометрическую форму иона NO2—.
6.Определите по методу Гиллеспи геометрическую форму молекулы SOCl2.
7. Определите по методу Гиллеспи геометрическую форму молекулы SO2Cl2.
8.Определите по методу Гиллеспи геометрическую форму иона SO42- .
9. Определите по методу Гиллеспи геометрическую форму иона PCl6—.
10. Установите последовательность увеличения полярности двухатомных молекул:
1) HI; 2) HBr; 3)HF; 4) HCl; 5) Cl2.
Связь,
образованная электронами, принадлежащими
обоим атомам, называется ковалентной.
Ковалентная неполярная возможна лишь
между одинаковыми атомами.
АВ
: А+
↔ В—
(электростатическое притяжение). Это
ионная связь. Строго говоря, соединения
с чисто ионной связью нет. Самый частый
тип связи – полярная ковалентная. В
этом случае общая электронная пара
смещена к одному из атомов в соответствии
с их электроотрицательностью. ЭО – это
суммарная хар-ка способности атома
отдавать и присоединять электроны. ЭО
сами по себе не очень важны, важны ΔЭО.
Чем больше ΔЭО,
тем полярнее (ионнее) связь.
Смещение
электронной плотности при образовании
полярной ков. связи можно учесть, приписав
атомам эффективные
заряды в единицах заряда электрона
(δ,+δ,
-δ).
Это условные величины, т.к. электрон
нельзя “разделить” между атомами.
Эффективные заряды определяют
экспериментально и они позволяют
представить полярную ковалентную связь
комбинацией “чисто” ковалентной и
“чисто” ионной связей.
Если
связь “чисто” ковалентная, то δ=0,
если ионная, то δ
= ±1 (однократная), δ=±2
(двухкратная связь) и т.п.
А
для полярной ковалентной связи –
промежуточные значения.
пример
Н+0,2∙∙∙Cl-0,2
0,8*0+0,2*1 (80% ковалентной связи и 20% ионной).
Так даже у CsF
δ=
±0,99, значит «чисто» ионных соединений
нет!
Дипольный
момент связи (μ)
А∙∙∙В равен произведению эффективного
заряда на расстояние между ядрами
атомов: μ=δ∙d.
Дипольный момент молекулы равен векторной
сумме дипольных моментов связей с учетом
неподеленных электронных пар. Единица
μ
– один Дебай (1Д), 1Д=3,3∙10-30Кл*м.
Обычно
μ
трудно предсказать, т.к. δ
и d
изменяются противоположно. Например:
HF;
HCl;
HBr:
падение δ
(μ
падает); CsF;
CsCl;
CsBr:
рост d
(μ
растет).
Что
важно – чем симметричнее молекула, тем
меньше ее μ,
например симметричные молекулы (CO2;
BCl3;
CCl4;
PCl5;
SF6)
неполярны и имеют μ=0.
Вопрос 19) Основные положения метода молекулярных орбиталей (мо лкао). Объясните парамагнитные св-ва … и найдите кратность связи в … и …
Основные
положения метода МО:
1)
При соединении двух атомов в молекулу
возможны два состояния – две МО: с более
низкой энергией (Есвяз)
и более высокой энергией (Еразр).
Переход электрона на первую орбиталь
ведёт к образованию связи, а на вторую
– не даёт. Если атомная орбиталь
“переселяется”
в молекулу без изменений энергии, она
наз. несвязывающей.
2)
Метод МО учитывает вклад в хим. связь
отдельных е.
3)
В первом приближении один электрон на
разрыхляющей орбитали сводит на нет
действие одного связывающего электрона.
Отсюда кратность связи равна полуразности
числа связывающих и разрыхляющих
электронов.
Вопрос 20) Основные положения метода валентных связей при описании химической связи в комплексных соединениях. Рассмотрите на примерах … и …
Согласно
представлениям метода ВС хим. связь в
компл. соед. носит донор-акцепторный
характер. Свободные пары е, которыми
обладают лиганды, заполняют пустые
орбитали центрального иона. Эти орбитали
объединяют в гибридные комбинации в
зависимости от координационного числа
(к.ч).
Компл.
соед. с к.ч., равным двум, описываются с
позиции sp-гибридизации.
Компл.
соед. с к.ч., равным трём, обычно описываются
исходя из sp2-гибрид.
Компл.
соед. с к.ч., равным четырём, возможны
два варианта. Есв
– энергия образования связи; Епары
– энергия образования электронной пары
из неспаренных е. Если Есв
< Епары,
то спиновое состояние центрального
иона в компл. останется тем же, связь в
компл. анионе характеризует sp3-гибрид.,
компл. ион имеет тетраэдрическое строение
и характеризуется высоким спином. Если
Есв
>
Епары,
то происходит обр. пары, хим. связь в
этом компл. описываем с позиций
dsp2-гибрид,
квадратное строение и характеризуется
низким спином.
Компл.
соед. с к.ч., равным пяти: dsp3-гибрид.
Компл.
соед. с к.ч., равным шести: ….
Соседние файлы в предмете Неорганическая химия
- #
- #
- #
- #
наталия Богдановна врецена
Эксперт по предмету «Химия»
Задать вопрос автору статьи
Процесс возникновения диполя
В процессе образования ковалентной полярной связи один из атомов сильнее притягивает к себе электроны, в результате чего общая электронная пара смещается к его ядру. Возникает ковалентная полярная связь. Способность атома притягивать электроны является критерием его электроотрицательности (ЭО). Чем выше электроотрицательность у атома, тем больше вероятность смещения электронной пары в сторону ядра данного атома. Разность ЭО атомов характеризует полярность связи.
В результате смещения электронной пары к ядру одного из атомов, повышается плотность отрицательного заряда у данного атома и он получает эффективный заряд атома $delta ^-$. У другого атома увеличивается плотность положительного заряда $delta ^+$. Возникает диполь — электрически нейтральная система с двумя одинаковыми по величине, но разными по знаку зарядами, находящимися на определенном расстоянии (длина диполя $l_д$) друг от друга.
Постоянный дипольный момент
Мерой полярности является дипольный момент $mu $. Его величина равна произведению эффективного заряда $delta $ на длину диполя $l_д$:
Единица измерения постоянного дипольного момента — кулон на метр ($Кл cdot м$), или внесистемная единица измерения — дебай $D$, равная $3,34 cdot 10-30 Кл cdot м$.
Пример 1
Предположим, что в молекуле фтороводорода $HF$ — ионная связь. То есть на атомах водорода и фтора сосредоточены заряды $+1$ и $-1$, соответственно. Заряды ионов кратны заряду электрона, равному $1,60 cdot 10^{-19}$ Кл. Расстояние между зарядами составляет $9,17cdot 10^{-11}$ м. Постоянный дипольный момент, исходя из этих данных, равен:
$mu = q cdot r =1,60 cdot 10^{-19} Кл cdot 9,17 cdot 10^{-11} м = 1,47 cdot 10{-29} Кл cdot м$.
В дебаях дипольный момент равен:
$mu = frac{1,47 cdot 10^{-29} Кл cdot м}{3,34 cdot 10^{-30} Кл cdot м cdot D^{-1}} = 4,40 D$.
Величина $mu = 4,40 D$ характеризует дипольный момент молекулы $HF$ при условии, что химическая связь в ней полностью ионная. В действительности же $mu = 1,83 D$. Сопоставляя эти величины, можно вычислить «долю ионности связи» (частичный ионный характер связи) в молекуле $HF$.
Ионный характер связи = $frac{1,83 D cdot 100}{4,40 D} = 41,6%$
С увеличением разности электроотрицательности постоянный момент диполя растет.
Дипольный момент является векторной величиной. Направление диполя условно принимают от отрицательного полюса к положительному.
«Постоянный дипольный момент» 👇
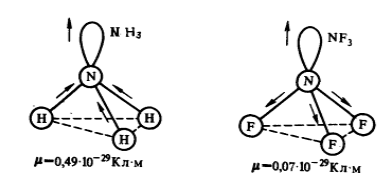
Пример 2
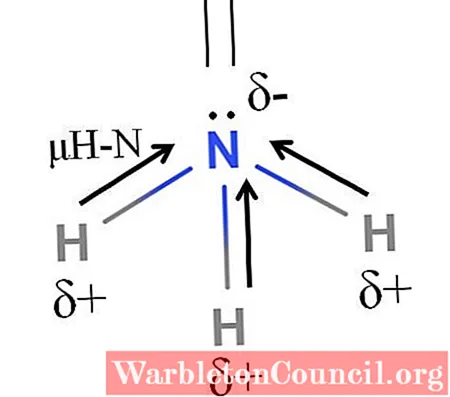
У молекул аммиака $NH_3$ и фторида азота $NF_3$ одинаковая тригонально — пирамидальная форма (Рис. 1). Полярность связей $N-H$ и $N-F$ тоже примерно одинакова. Однако дипольный момент аммиака равен $0,49 cdot 10^{-29} Кл cdot м$, а фторида азота — $0,07 cdot 10^{-29} Кл cdot м$. Такая разница объясняется тем, что в молекуле аммиака направление дипольного момента связывающей $N-H$ и несвязывающей электронной пары совпадает и при векторном сложении обусловливает больший электрический момент диполя. В молекуле фторида азота дипольные моменты связей $N-F$ и электронной пары направлены в противоположные стороны. Если их сложить, то происходит частичная компенсация.
Рисунок 1. Направления дипольных моментов и электронных пар в молекулах аммиака $NH_3$ и фторида азота $NF_3$
Для многоатомных молекул необходимо различать дипольный момент отдельных связей и молекулы в целом. Если в молекуле присутствует несколько связей, то их электрические моменты (векторы) складываются по правилу параллелограмма. Результирующий дипольный момент будет отличаться от электрических дипольных моментов отдельных связей. Если молекула высокосимметрична, то дипольный момент может быть равен нулю, в то время как отдельные связи обладают высокой полярностью.
Пример 3
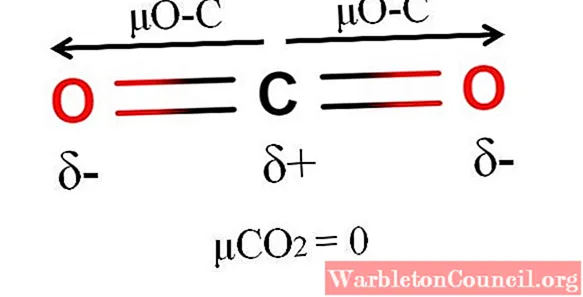
Молекула диоксида углерода линейной формы неполярна ($mu = 0$), в то время как каждая связь $C=O$ имеет значительный дипольный момент ($mu = 8,9 cdot 10^{-29} Кл cdot м$). Это происходит в результате того, что равные по величине постоянные дипольные моменты связей направлены навстречу друг другу.
Чем более полярна молекула и значительнее смещены общие электронные пары к одному из атомов, тем больше значение постоянного дипольного момента.
Методы определения постоянного дипольного момента
Как правило, методы определения электрических дипольных моментов основаны на нахождении ориентационного эффекта полярных молекул в приложенном электрическом поле.
-
Методы микроволновой спектроскопии. Основаны на эффектах расщепления и сдвига спектральных линий в электрическом поле. Позволяет наиболее точно определить значение величины и направление вектора постоянного дипольного момента. К этим методам относят: метод Штарка, резонансный микроволновой метод, молекулярных пучков и др.
-
Методы, основанные на измерении диэлектрической проницаемости $varepsilon$ вещества.
При разных температурах измеряется диэлектрическая проницаемость веществ. Если вещество поместить в электрическое поле, создаваемое конденсатором, то емкость конденсатора возрастет в ? раз, то есть
где $c_0$ и $c$ — емкость конденсатора в вакууме и в среде вещества.
Энергия электрического поля в конденсаторе равна:
где $U$ — энергия электрического поля в конденсаторе;
$c$ — емкость конденсатора в среде вещества;
$V$ — напряжение на обкладках конденсатора.
В среде вещества конденсатор имеет больший запас энергии, чем в вакууме. Это объясняется тем, что под действием электрического поля происходит ориентация диполей и деформация молекул вещества.
Постоянный дипольный момент находят с помощью уравнения Ланженева — Дебая, которое связывает температурную зависимость диэлектрической проницаемости и дипольный момент:
где $M$ — относительная молекулярная масса вещества;
$rho $ — плотность;
$N_a$- число Авогадро;
$k$ — постоянная Больцмана, равная $frac{R}{N_a}$;
$R$- универсальная газовая постоянная;
$alpha $ — деформационная поляризуемость.
Измерив $varepsilon$ при двух температурах при помощи уравнения Ланжевена — Дебая можно определить деформационную поляризуемость и постоянный дипольный момент.
Зная значение дипольного момента, можно указать характер химической связи (ковалентная полярная или неполярная, ионная) и судить о геометрической структуре молекулы.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание
- Как рассчитывается дипольный момент?
- Примеры
- вода
- Метанол
- Аммиак
- Этанол
- Углекислый газ
- Метан
- Ссылки
В дипольный момент это химическое свойство, которое указывает, как неоднородно электрические заряды распределяются в молекуле. Выражается в единицах Дебая, 3,33 · 10-30 C · m, а обычно их значения находятся в диапазоне от 0 до 11 D.
Высокополярные соединения обычно имеют большие дипольные моменты; а неполярные — малые дипольные моменты. Чем более поляризованы электрические заряды в молекуле, тем больше ее дипольный момент; то есть должна быть область, богатая электронами, δ-, и другая, бедная электронами, δ +.
Дипольный момент μ является векторной величиной, поэтому на него влияют углы связей и, в целом, молекулярная структура.
Когда молекула линейна, ее можно сравнить с двухцветным ластиком. Его отрицательный конец δ- будет соответствовать красному цвету; в то время как положительное, δ +, будет синим цветом. По мере увеличения величин отрицательных зарядов на δ-полюсе и расстояния, отделяющего его от δ +, дипольный момент увеличивается.
С химической точки зрения это означает, что чем больше разница в электроотрицательности между двумя атомами и чем больше расстояние, которое их разделяет, тем больше дипольный момент между ними.
Как рассчитывается дипольный момент?
Считается ковалентной связью между двумя атомами, A и B:
А-Б
Расстояние между положительным и отрицательным частичными зарядами уже определяется длиной их связи:
Кδ+-Bδ-
Поскольку протоны и электроны имеют одинаковую величину электрического заряда, но с противоположными знаками, 1,6 · 10-19C, это то, что принимается во внимание при оценке дипольного момента между A и B с использованием следующего уравнения:
μ = δ·d
Где μ — дипольный момент, δ — заряд электрона без знака минус, а d длина ссылки, выраженная в метрах. Например, если предположить, что d имеет значение 2 Å (1 10-10м) дипольный момент μA-B будет:
мкА-В = (1,6 · 10-19С) · (2 · 10-10м)
= 3,2·10-29См
Но поскольку это значение очень мало, используется единица Дебая:
μ = (3,2·10-29См) (1 Д / 3,33 10-30 См)
= 9.60 Д
Это значение μA-B может привести к предположению, что связь A-B является более ионной, чем ковалентной.
Примеры
вода
Чтобы вычислить дипольный момент молекулы, все дипольные моменты их соответствующих связей должны быть добавлены векторно, учитывая валентные углы и небольшую тригонометрию. Это в самом начале.
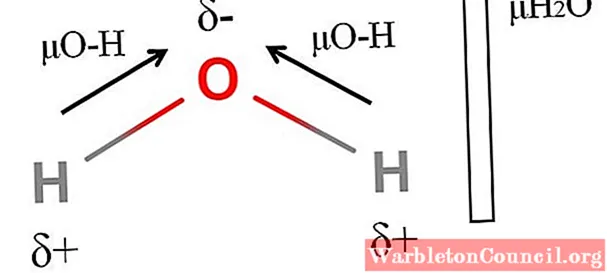
Вода имеет один из самых больших дипольных моментов, который можно ожидать для ковалентного соединения. На верхнем изображении мы видим, что атомы водорода имеют положительный частичный заряд, δ +, а кислород несет отрицательный частичный заряд, δ-. Связь O-H достаточно полярна (1,5D), и их две в молекуле H2ИЛИ.
Обычно рисуется вектор, направленный от наименее электроотрицательного атома (H) к наиболее электроотрицательному (O). Хотя они не нарисованы, на атоме кислорода есть две пары неподеленных электронов, которые еще больше «концентрируют» отрицательную область.
Из-за угловой геометрии H2Или дипольные моменты складываются в направлении атома кислорода. Обратите внимание, что сумма двух μO-H даст 3D (1,5 + 1,5); но это не так. Дипольный момент воды имеет экспериментальное значение 1,85D. Здесь показан эффект угла около 105 ° между связями H-O-H.
Метанол
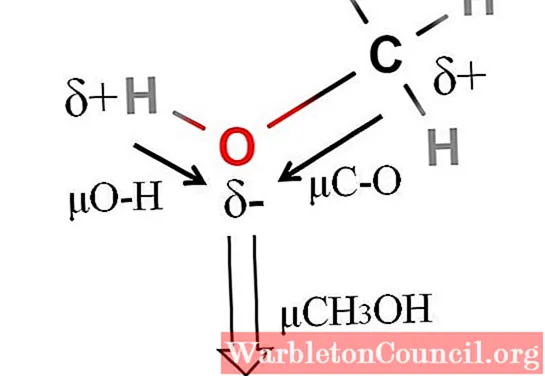
Дипольный момент метанола составляет 1,69 D. Это меньше, чем у воды. Следовательно, атомные массы не имеют большого влияния на дипольный момент; но их атомные радиусы равны. В случае метанола мы не можем утверждать, что его связь H-O имеет μ, равную 1,5D; так как в CH3ОН и Н2ИЛИ.
Вот почему вам нужно будет измерить длину связи H-O в метаноле, чтобы рассчитать μO-H. Что можно сказать, так это то, что μO-H больше, чем μC-O, поскольку разница электроотрицательностей между углеродом и кислородом меньше, чем между водородом и кислородом.
Метанол указан как один из самых полярных растворителей, которые можно найти вместе с водой и аммиаком.
Аммиак
Связи H-N довольно полярны, поэтому азот из-за своей более высокой электроотрицательности притягивает электроны к себе (верхнее изображение). В дополнение к этому у нас есть неподеленная пара электронов, которые вносят свои отрицательные заряды в δ-область. Следовательно, на атоме азота аммиака преобладают электрические заряды.
Аммиак имеет дипольный момент 1,42D, меньше, чем у метанола. Если бы и аммиак, и метанол можно было превратить в ластики, было бы видно, что ластик из метанола имеет более определенные полюса по сравнению с ластиком из аммиака.
Этанол
В случае этанола CH3CH2ОН, его дипольный момент очень близок к дипольному моменту метанола, но, как правило, имеет более низкие значения. Поскольку в области δ + становится больше атомов углерода, атом кислорода, представляющий δ-, начинает терять часть своей «относительной отрицательной интенсивности».
Углекислый газ
Углекислый газ имеет две полярные связи C = O с соответствующими дипольными моментами μO-C. Однако, как видно на изображении выше, линейная геометрия CO2 Это заставляет два μO-C векторно компенсировать друг друга, даже когда углерод имеет положительный частичный заряд, а атомы кислорода имеют отрицательный частичный заряд.
По этой причине диоксид углерода является неполярной молекулой, поскольку μCO2 имеет значение 0D.
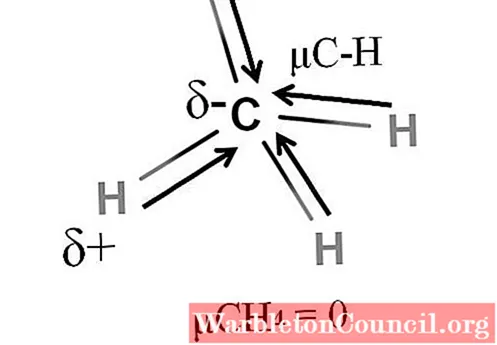
Метан
И метан, и углекислый газ имеют нечто общее: это высокосимметричные молекулы. В общем, чем симметричнее молекула, тем меньше ее дипольный момент.
Если мы увидим молекулу CH4, его связи C-H полярны, а электроны направлены к атому углерода, потому что он немного более электроотрицателен. Можно было бы подумать, что углерод должен быть сильно отрицательной δ-областью; как ластик с темно-красным центром и голубоватыми концами.
Однако, разделив CH4 в середине мы получили бы две половинки H-C-H, одну слева, а другую справа, аналогичные молекуле H2О. Таким образом, дипольный момент, возникающий в результате сложения этих двух мкС-Н, компенсируется дипольным моментом другой половины. Следовательно, μCH4 имеет значение 0D.
Ссылки
- Уиттен, Дэвис, Пек и Стэнли. (2008). Химия. (8-е изд.). CENGAGE Обучение.
- Уолтер Дж. Мур. (1963). Физическая химия. В химической кинетике. Четвертое издание, Longmans.
- Ира Н. Левин. (2009). Основы физико-химии. Издание шестое, стр. 479-540. Мак Гроу Хилл.
- Хельменстин, Энн Мари, доктор философии (29 января 2020 г.). Определение дипольного момента. Получено с: thinkco.com
- Блабер Майк. (29 сентября 2019 г.). Дипольные моменты. Химия LibreTexts. Получено с: chem.libretexts.org
- ЛаРита Уильямс. (2020). Дипольный момент: определение, уравнения и примеры. Исследование. Получено с: study.com
- Википедия. (2020). Дипольный момент связи. Получено с: en.wikipedia.org
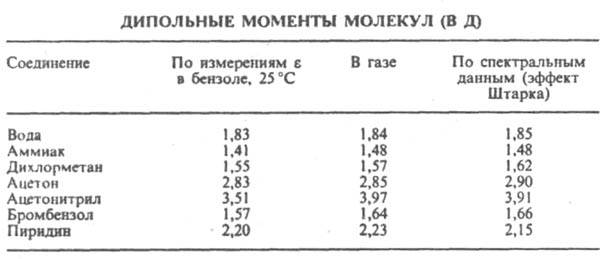
ДИПОЛЬНЫЙ МОМЕНТ
ДИПОЛЬНЫЙ МОМЕНТ электрический, векторная величина, характеризующая асимметрию распределения положит. и отрицат. зарядов в электрически нейтральной системе. Два одинаковых по величине заряда +q и —q образуют электрич. диполь с дипольным моментом m = q l, где l — расстояние между зарядами. Для системы из n зарядов qi радиусы-векторы к-рых ri, 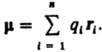
центры положит. зарядов qА совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом
случае дипольный момент 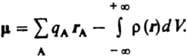
от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе дипольному моменту молекулы иногда приписывают противоположное направление. Часто вводят представление о дипольных моментах отдельных хим. связей, векторная сумма к-рых дает дипольный момент молекулы. При этом дипольный момент связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда.
Дипольный момент хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий дипольный момент существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный дипольный момент молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО2 и
CCl4). Если же дипольный момент молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н2О полярна; суммирование дипольных моментов двух полярных связей ОН также дает отличный от нуля дипольный момент, направленный по биссектрисе валентного угла НОН.
Порядок величины дипольного момента молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим. связи (порядка 10—10 м), т. е. составляет 10—29 Кл.м. В справочной литературе дипольные моменты молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл.м.
Спектроскопич. методы определения дипольных моментов молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие дипольный момент со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины дипольного момента (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора дипольного момента. Важно, что точность определения дипольного момента почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых дипольных моментов ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, дипольный момент пропана равен 0,085 b 0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов.
Направление вектора дипольного момента молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка.
Др. группа методов определения дипольного момента основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены дипольные моменты молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине дипольного момента основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний дипольный момент единицы объема) складывается из наведенной, или индуцированной, поляризации Рм и ориентационной поляризации Рор и связана с m ур-нием Ланжевена — Дебая:
где М — мол. масса, d — плотность, a — поляризуемость молекулы, NA — число Авогадро, k — постоянная Больцмана, Т — абс. т-ра. Измерения диэлектрич. проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. При наиб. распространенном варианте метода — измерениях в разбавл. р-рах неполярных р-рителей — предполагается аддитивность поляризаций растворенного в-ва и р-рителя.
Сопоставление дипольных моментов полярных молекул нек-рых орг. соед., полученных разными методами, показано в таблице.
Важнейшая область применения данных о дипольных моментах молекул -структурные исследования, установление конформации молекул, конформационного и изомерного состава в-ва, его зависимости от т-ры. Величины дипольных моментов молекул позволяют судить о распределении электронной плотности в молекулах и зависимости этого распределения от характера отдельных
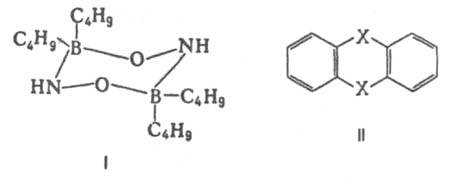
заместителей. В общем случае структурная интерпретация дипольных моментов требует сравнения эксперим. величин со значениями, полученными квантовомех. расчетом либо при помощи аддитивной векторной схемы с использованием дипольных моментов отдельных связей и атомных групп. Последние находят либо по интенсивностям колебат. полос поглощения, либо путем векторного разложения дипольных моментов нек-рых симметричных молекул. Расчеты с использованием векторной аддитивной схемы могут учитывать разл. проявления стереохим. нежесткости, напр., затрудненное или своб. внутр. вращение молекулы. Высокосимметричные мол. структуры, обладающие центром инверсии, двумя взаимно перпендикулярными осями вращения или осями, перпендикулярными плоскости симметрии, не должны иметь дипольных моментов. По наличию или отсутствию дипольного момента молекулы можно в отдельных случаях выбрать для нее ту или иную структуру без к.-л. теоретич. расчетов. Так, равенство нулю эксперим. дипольного момента димера аминооксидибутилборана (ф-ла I) служит доказательством того, что он существует в виде устойчивой кресловидной конформации, обладающей центром инверсии. Наоборот, наличие дипольного момента у тиантрена (ф-ла II, X = S) и селенантрена (II, X = Se), равных 1,57 Д и 1,41 Д соотв., исключает для них центросимметричную структуру, в частности плоскую.
===
Исп. литература для статьи «ДИПОЛЬНЫЙ МОМЕНТ»: Минкин В. И., Осипов О. А., Жданов Ю. А., Дипольные моменты в органической химии. Л., 1968; Осипов О. А., Минкин В. И., Гарновский А. Д., Справочник по дипольным моментам, 3 изд.. М., 1971; Exner О., Dipole moments in organic chemistry, Stuttg., 1975. В. И. Muнкин.
Страница «ДИПОЛЬНЫЙ МОМЕНТ» подготовлена по материалам химической энциклопедии.