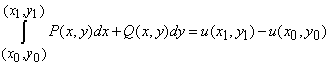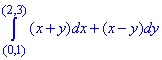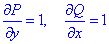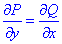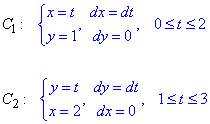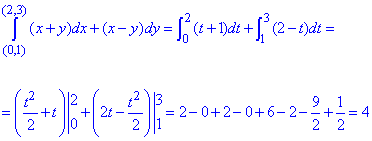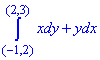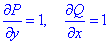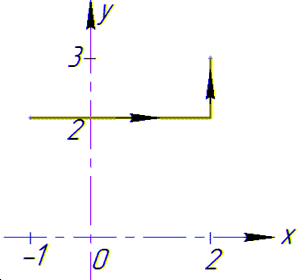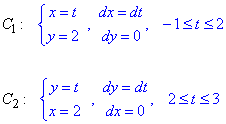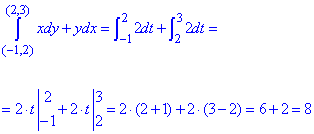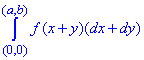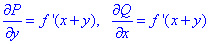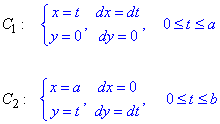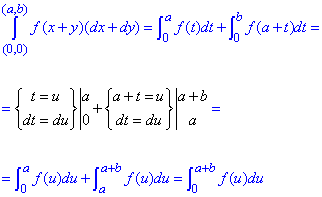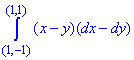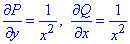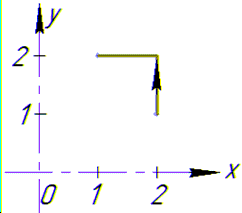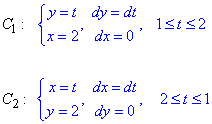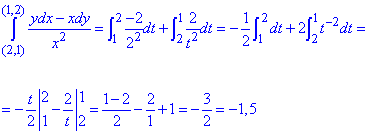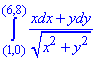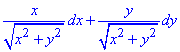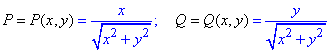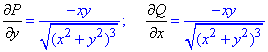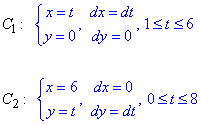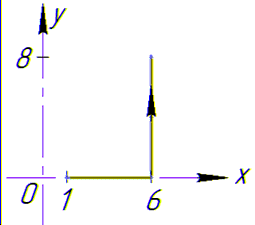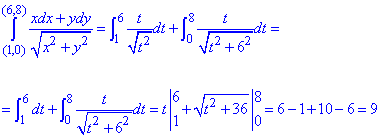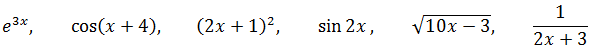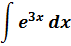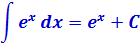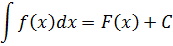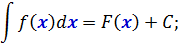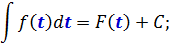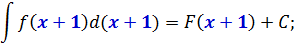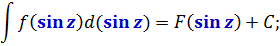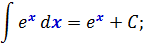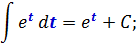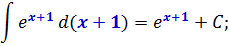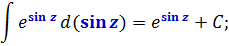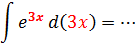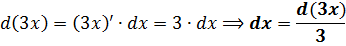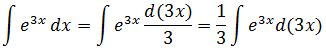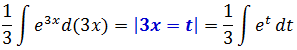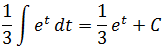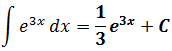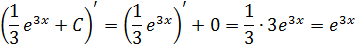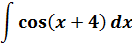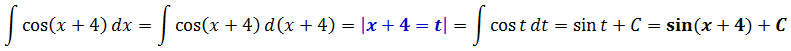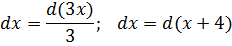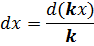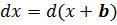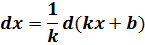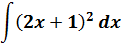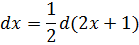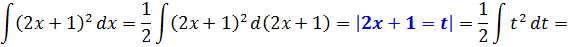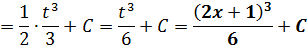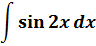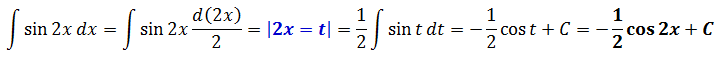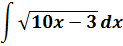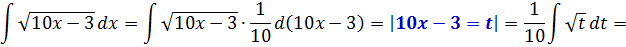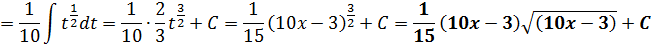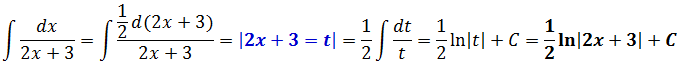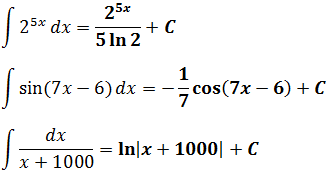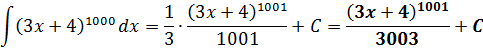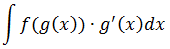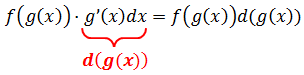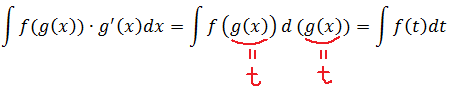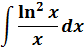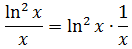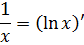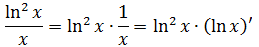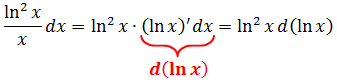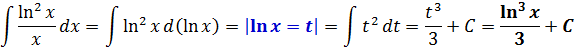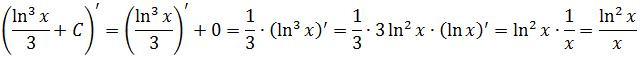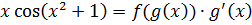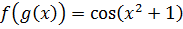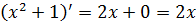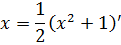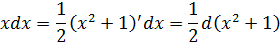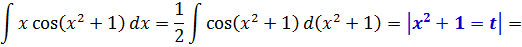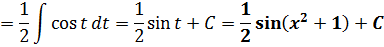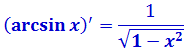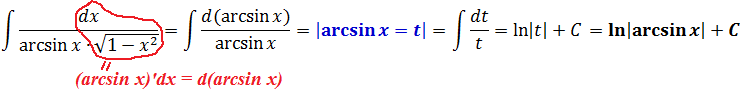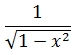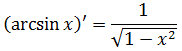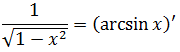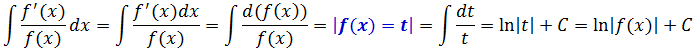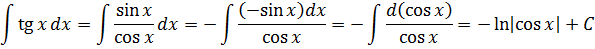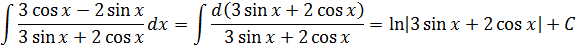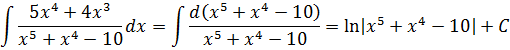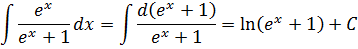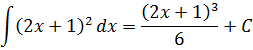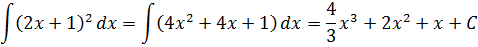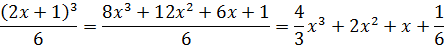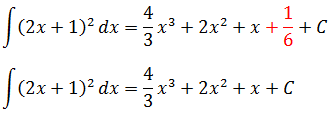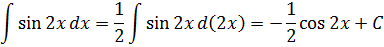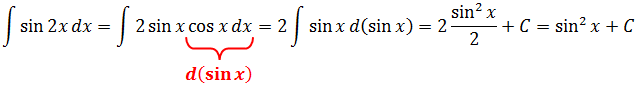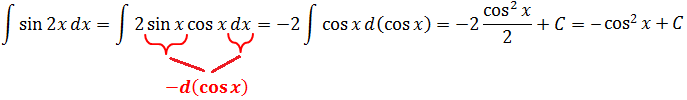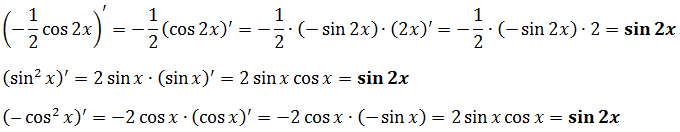Одно из самых значимых понятий в математике — интеграл. Термин часто можно встретить при решении задач по математике и физике. С помощью интеграла существенно упрощается поиск площади под кривой, пройденного пути объекта, движущегося неравномерно, массы неоднородного тела, функции по производной.
Что такое интеграл — понятие и определение
Интеграл представляет собой аналог суммы для бесконечного числа бесконечно малых слагаемых.
Интеграл является эффективным инструментом для решения задач из математического анализа. Слово «интеграл» происходит от латинского «integer», то есть «целый». Впервые это понятие ввел Иоганн Бернулли.
Разобраться в определении интеграла можно, если рассмотреть понятный график функции:
Исходя из графика, можно сделать вывод, что интегралом является сумма малых частей, которые составляют в целом рассматриваемый объект. Компоненты складываются в какую-то геометрическую фигуру. При сложении этих частей можно определить, какова ее площадь. Таким образом, пояснение для интеграла заключается в следующем: интеграл является площадью какой-то фигуры, расположенной под линией функции.
Данное понятие относится к определенному интегралу. Он определен на отрезке между точками а и b. В верхней части в качестве ограничения выступает некоторый график функции, как представлено на рисунке:
Математическая запись интеграла:
(int_{a}^{b}{f(x)dx})
где f(x) является той самой функцией, график которой ограничивает фигуру в верхней части;
a и b представляют собой пределы;
x соответствует направлению, вдоль которого построены столбцы на графике.
Процесс интегрирования является обратным дифференцированию. В том случае, когда требуется определить минимальный промежуток заданной функции, целесообразно взять от нее производную. Это объясняется тем, что производная или дифференциал являются быстрым методом поиска части чего-либо. Можно наглядно определить с помощью рисунка, что минимальная фигура, которая является частью целого, при таком числе составляющих компонентов не повторяет форму кривой функции. Таким образом, требуется уменьшить габариты таких частей, чтобы они максимально точно совпадали с графиком. Площадь наименьшего компонента фигуры будет стремиться к нулевому значению. Точность повышается с уменьшением размеров рассматриваемой части. Площадь геометрической фигуры состоит из суммы таких частей, которые стремятся к нулю. Записать это можно с помощью уравнения:
(P=lim_{Delta x_{i}rightarrow 0}sum{y_{i}Delta x_{i}})
Подробно полученное выражение можно рассмотреть на графике:
Площадь малой части фигуры определяется так же, как площадь прямоугольника. Значение Y нужно помножить на значение ΔХ. Так как фигура представляет собой совокупность малых частей, то их требуется сложить. Следует учитывать, что каждый компонент фигуры ΔХ стремится к нулевому значению. Поэтому формула, которая представлена выше, включает это условие и позволяет определить результат максимально точно.
Если обозначить количество частей ΔХ, стремящихся к бесконечности, то можно определить, что существует предел интегральной суммы, которая состоит из таких компонентов, стремящихся к нулю и к бесконечности по числу таких частей. Таким образом, правая граница фигуры, изображенной на графике, является пределом. В этом выражается геометрический смысл определенного интеграла.
Физический смысл интеграла состоит в том, что это сумма бесконечно малых величин на бесконечно большом интервале. Исходя из этого, можно определить любую величину, которая изменяется, согласно функции. К примеру, рассчитать общий путь по закону изменения скорости. Необходимость в интеграле возникла, когда потребовалось рассчитать площади каких-либо фигур и объем любых тел, выбранных произвольно.
В том случае, когда расчеты подразумевают наличие постоянной характеристики, к примеру, скорости, найти путь можно с помощью произведения этой постоянной скорости и времени. Этот же момент можно проверить при вычислении интеграла от такой функции и записи уравнения прямой. Но скорость в процессе движения может меняться. Данное изменение можно представить в виде зависимости. Тогда следует вписать граничные условия, например, в случае пути — это время, в интеграл скорости по времени. Полученное выражение будет равно площади трапеции, которая расположена под функцией скорости, что является физическим смыслом определенного интеграла.
Свойства, которыми обладает определенный интеграл:
- Когда функции f и g интегрируются на интервале [a, b], то для любых чисел (alpha) и (beta (alpha in R, beta in R)) функция (varphi(x) = alpha f(x) + beta g(x)) также интегрируема на отрезке [a, b]. Справедливо равенство: (intlimits_a^b (alpha f(x) + beta g(x)) dx = alpha intlimits_a^b f(x) dx + beta intlimits_a^b g(x) dx.label{ref1})
- Если функции f и g интегрируемы на отрезке [a, b], то функция (varphi(x) = f(x)g(x)) также интегрируема на этом отрезке.
- В том случае, когда функция f(x) интегрируема на отрезке (Delta = [a, b]) она интегрируема на любом отрезке (Delta_{1} subset Delta.)
- При функции f(x), интегрируемой на отрезке [a, b] и a < c < b, будет работать формула: (intlimits_a^b f(x) dx = intlimits_a^c f(x) dx + intlimits_c^b f(x) dx)
- При функции f, интегрируемой на отрезке [a, b] и если (c_{1}, c_{2}, c_{3}) являются любыми точками данного интервала, то (intlimits_{c_{1}}^{c_{3}} f(x) dx = intlimits_{c_{1}}^{c_{2}} f(x) dx + intlimits_{c_{2}}^{c_{3}} f(x) dx)
Термин «неопределенный интеграл» применим в ситуациях, когда требует найти площадь криволинейной трапеции, путь в соответствии с известной скоростью тела, которое движется неравномерно, и для решения других подобных задач.
Свойства, которыми характеризуется неопределенный интеграл:
- Константу можно выносить за знак интеграла: (int kf(x) dx = kint f(x) dx)
- Интеграл разности или суммы функций соответствует разности или сумме интегралов от этих функций: (int ( f(x) pm g(x) ) dx = int f(x) dx pm int g(x) dx)
- Производная интеграла определяется как выражение, находящееся под знаком интеграла: (bigg (int f(x) dx bigg )’ = f(x))
- Интеграл от производной функции равен сумме этой функции и постоянной: (int F'(x) dx = F(x) + C)
- Интеграл дифференциала функции равен сумме этой функции и постоянной интегрирования: (int df(x) dx = f(x) + C)
Таблица интегралов для студентов
Такие формулы позволяют упростить решение многих задач. Основные интегралы:
(int 0dx=C)
(int dx=int 1dx=x+C)
(int x^n dx = frac{x^{n+1}}{n+1}+C)
(int frac{dx}{x}=ln |x|+C)
(int a^x dx = frac{a^x}{ln a} + C)
(int e^x dx = e^x + C)
(int sin x dx = -cos x + C)
(int cos x dx = sin x+C)
(int frac{dx}{sin^2 x}=-ctgx + C)
(int frac{dx}{cos^2 x}=tgx+C)
(int frac{dx}{sqrt{a^2-x^2}}=arcsin frac{x}{a}+C)
(int frac{dx}{a^2+x^2}=frac{1}{a}arctgfrac{x}{a}+C)
(int frac{dx}{a^2-x^2}=frac{1}{2a} ln|frac{a+x}{a-x}|+C)
(int frac{dx}{sqrt{x^2pm a^2}}=ln|x+sqrt{x^2pm a^2}|)
Методы решения интегралов
Данные методики позволяют преобразовать сложные уравнения в простые формы, решения которых можно найти в таблице. Также к преобразованным выражениям можно применять свойства интегралов.
Непосредственное интегрирование
Данный метод целесообразно применять, когда в интеграле имеются табличные простейшие функции, либо функции, которые можно представит в таком виде по результатам элементарных действий. К примеру, когда требуется вынести константу за знак интеграла, разбить интеграл на слагаемые в виде интегралов, чтобы в подынтегральном выражении присутствовала готовая функция для интегрирования. Можно привести простой пример:
Необходимо определить интеграл непосредственным интегрированием:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx)
Исходя из свойства суммы интегралов, получим:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = int x^3 dx + int frac{3 dx}{2sqrt{x}} + int frac{2 dx}{x})
Первый интеграл записан в табличном виде. В таком случае можно воспользоваться непосредственным интегрированием:
(int x^3 dx = frac{x^{3+1}}{3+1} = frac{x^4}{4} + C)
Второй интеграл обладает константой, которую допустимо вынести за знак. Затем интеграл будет преобразован в табличную форму:
(int frac{3dx}{2sqrt{x}} = 3 int frac{dx}{2sqrt{x}} = 3 sqrt{x} + C)
В третьем интеграле можно вынести константу. Далее необходимо воспользоваться методом непосредственного интегрирования:
(int frac{2dx}{x} = 2int frac{dx}{x} = 2 ln x + C)
Полученные выражения необходимо представить в виде одной записи:
(int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x + C)
Ответ: (int bigg ( x^3 + frac{3}{2sqrt{x}} + frac{2}{x} bigg ) dx = frac{x^4}{4} + 3sqrt{x} + 2ln x+ C)
Метод подведения под знак дифференциала
Решить некоторые типы интегралов можно с помощью этого способа. Он заключается в вынесении под знак интеграла. Таким образом получается интеграл табличной формы. Формула имеет следующий вид:
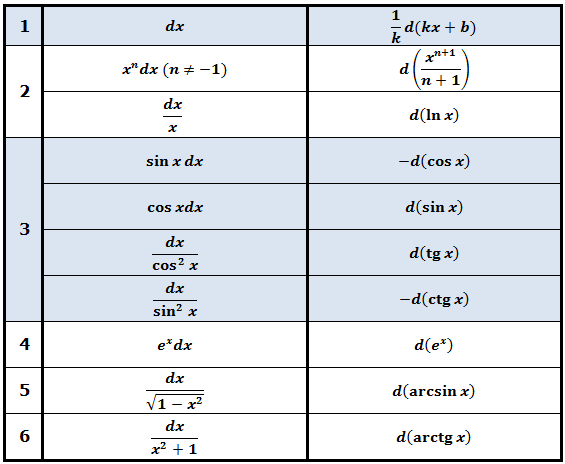
(f'(x) dx = d( f(x) ))
В том случае, когда подынтегральная функция содержит произведение пары функций, одна из которых представляет собой дифференциал другой, нужно внести под знак дифференциала нужную функцию. Данное действие можно записать таким образом:
(int f(varphi(x)) varphi'(x) dx = int f(varphi(x)) d(varphi(x))=int f(u) du)
(u=varphi(x))
Воспользоваться способом подведения основных функций можно при знании таблицы производных и интегрирования. Из них следуют следующие уравнения:
(dx = d(x+c) )
(c=const)
(-sin x dx=d(cos x))
(dx=frac{1}{a} d(ax))
(cos x dx = d(sin x))
(xdx=frac{1}{2} d(x^2+a) )
(frac{dx}{x} = d(ln x))
(-frac{dx}{x^2}= d(frac{1}{x}))
(frac{dx}{cos^2 x} = d(tg x))
(int f(kx+b)dx = frac{1}{k} int f(kx+b)d(kx+b) = frac{1}{k} F(kx+b) + C)
В качестве примера можно решить задачу на нахождение интеграла, обладающего таким видом:
(int sin x cos x dx)
В этом случае допустимо заносить под знак дифференциала любую из указанных функций. Целесообразно занести (cos x) из-за удобства смены знаков. Применяя формулы, получим:
(int sin x cos xdx = int sin x d(sin x) = frac{1}{2} sin^2 x + C)
Ответ: (int sin x cos x dx = frac{1}{2} sin^2 x + C)
Метод интегрирования по частям
Данная методика применима, когда требуется решить интегралы от произведения двух простейших функций. Одна из них достаточно просто дифференцируется, а вторая — интегрируется. В данном случае справедлива методика для неопределенных и определенных интегралов. Неопределенный интеграл характеризуется уравнением:
(int udv = uv — int vdu)
Определенный интеграл соответствует формуле:
(int limits_{a}^{b} udv = uv bigg |_{a}^{b} — int limits_{a}^{b} vdu)
В качестве примера можно определить интеграл:
(int xe^xdx)
Заметим, что в состав подынтегральной функции входит пара функций. Одна из них путем дифференцирования преобразуется в единицу, а вторая достаточно просто интегрируется. Поэтому в данном случае справедлив метод интегрирования по частям. Можно предположить, что:
(u = x rightarrow du=dx)
(dv = e^x dx rightarrow v=e^x)
Далее необходимо подставить полученные значения в первую формулу интегрирования:
(int xe^x dx = xe^x — int e^x dx = xe^x — e^x + C)
Ответ: (int xe^x dx = xe^x — e^x + C)
Метод замены переменной или метод подстановки
Этот способ нахождения интегралов применим в задачах, где одна функция — это производная второй функции. Допустим, что интеграл записан так:
(int f(x) dx)
Можно заменить (x=phi(t)). При этом функция (phi(t)) является дифференцируемой, поэтому можно найти (dx = phi'(t) dt.)
Далее следует подставить (begin{vmatrix} x = phi(t) \ dx = phi'(t) dt end{vmatrix}) в интеграл. Таким образом:
(int f(x) dx = int f(phi(t)) cdot phi'(t) dt)
Полученное выражение является формулой замены переменной в неопределенном интеграле.
При условиях задачи, которая содержит интеграл (int f(phi(x)) cdot phi'(x) dx), целесообразно заменить переменную на новую:
(t = phi(x))
(dt = phi'(t) dt)
Таким образом, интеграл преобразуется в форму, которую легко рассчитать с помощью основных методов интегрирования:
(int f(phi(x)) cdot phi'(x) dx = int f(t)dt)
Следует помнить, что по итогам расчетов требуется вернуть замененную переменную назад к x.
Например, можно рассмотреть задачу, по условиям которой необходимо вычислить неопределенный интеграл с помощью замены переменной:
(int e^{3x} dx)
Замена переменной будет выполнена следующим образом:
(t = 3x)
(dt = 3dx)
Таким образом:
(int e^{3x} dx = int e^t frac{dt}{3} = frac{1}{3} int e^t dt =frac{1}{3} e^t + C = frac{1}{3} e^{3x} + C)
Ответ: (int e^{3x} dx = frac{1}{3} e^{3x} + C)
Примеры решения
Задача 1
Требуется рассчитать определенный интеграл:
(int_0^1 frac{x}{x^4+1} dx)
Решение
Требуется заменить (t = x^2)
Таким образом, (dt = 2xdx)
Далее необходимо пересчитать пределы интегрирования для переменной t. Для этого нужно подставить 0 и 1 в замену (t = x^2)
В данной задаче они остались прежними. После манипуляций с подстановками получим:
(int_0^1 frac{x}{x^4+1}dx = int_0^1 frac{1}{2} frac{dt}{t^2+1})
Можно найти интеграл по таблице:
(int_0^1 frac{1}{2} frac{dt}{t^2+1}=frac{1}{2} arctg t bigg |_0^1)
Используя формулу Ньютона-Лейбница, запишем решение:
(frac{1}{2} arctg t bigg |_0^1 =frac{1}{2} arctg 1 — frac{1}{2} arctg 0 = frac{1}{2} cdot frac{pi}{4} = frac{pi}{8})
Ответ: (int_0^1 frac{x}{x^4+1} dx = frac{pi}{8})
Задача 2
Необходимо решить определенный интеграл:
(int_0^pi (x+5)sin x dx)
Решение
Можно заметить произведение двух функций, которое находится под интегралом. В этом случае целесообразно воспользоваться методом интегрирования по частям:
(int udv = uv — int vdu)
(int_0^pi (x+5) sin x dx = begin{vmatrix} u = x+5 & du = dx \ dv = sin x dx & v = -cos x end{vmatrix})
Нужно подставить в уравнение интегрирования по частям рассчитанные данные из вертикальных скобок:
(-(x+5)cos x bigg |_0^pi + int_0^pi cos x dx)
С помощью формулы Ньютона-Лейбница для вычисления определенного интеграла запишем ответ:
(-(x+5)cos x bigg |_0^pi + int_0^pi cos x dx = -(pi+5) cdot (-1) + 5 + sin x bigg |_0^pi = pi + 10 + sin pi — sin 0 = pi + 10)
Ответ: (int_0^pi (x+5)sin x dx = pi + 10)
Задача 3
Требуется найти определенны интеграл, записанный в виде:
(int_0^2 (x^3 + 2x + 2) dx)
Решение
Используя способ разложения интеграла на простейшие, после получения промежуточного результата необходимо интегрировать каждый интеграл индивидуально:
(int_0^2 (x^3+2x+2) dx = int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx)
В случае первых двух интегралов целесообразно воспользоваться правилом:
(x^p = frac{x^{p+1}}{p+1})
Третий интеграл содержит константу. Таким образом:
(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )
Далее следует подставить пределы интегрирования в каждую функцию и записать ответ:
(int_0^2 x^3dx + 2int_0^2 xdx + 2int_0^2 dx = frac{x^4}{4} bigg |_0^2 + 2 frac{x^2}{2} bigg |_0^2 + 2x bigg |_0^2 = frac{x^4}{4} bigg |_0^2 + x^2 bigg |_0^2 + 2x bigg |_0^2 )
Ответ: (int_0^2 (x^3 + 2x + 2) dx = 12)
Задача 4
Необходимо найти решение интеграла:
(int 3cos x dx)
Решение
Требуется вынести константу по первому свойству за знак интеграла и записать ответ:
(int 3cos x dx = 3 int cos x dx = 3 sin x + C)
Ответ: (int 3cos x dx = 3 sin x + C)
Задача 5
Необходимо определить интеграл:
(int (e^x + sin x) dx)
Решение
Исходя из первого свойства неопределенного интеграла, интеграл суммы равен сумме интегралов:
(int (e^x + sin x) dx = int e^x dx + int sin x dx = e^x — cos x)
Ответ: (int (e^x + sin x) dx = e^x — cos x)
Задача 6
Требуется определить производную от интеграла:
( int ln x dx)
Решение
Согласно третьему свойству неопределенного интеграла, производная неопределенного интеграла определяется, как подынтегральная функция:
(bigg (int ln x dx bigg )’ = ln x)
Ответ: (bigg (int ln x dx bigg )’ = ln x)
Задача 7
Требуется доказать следующее выражение:
( int (x^2+x)’ = x^2+x+C)
Решение
В первую очередь необходимо определить производную подынтегральной функции:
( (x^2+x)’ = (x^2)’ + (x)’ = 2x + 1)
Исходя из первого и второго свойства неопределенного интеграла, получим ответ:
(int (2x+1) dx = int 2x dx + int 1 dx = 2 int x dx + int 1 dx =2 cdot frac{x^2}{2} + x + C = x^2 + x + C)
Ответ: выражение доказано.
Благодаря теоретическим знаниям и практическим навыкам решения задач с интегралами, можно с легкостью осваивать самые сложные темы по физике и математическому анализу. Главное — уметь пользоваться таблицей с основными формулами и свойствами определенного и неопределенного интегралов. Если в процессе изучения материала возникают трудности, то в любое время можно открыть сервис Феникс.Хелп.
В настоящей статье научимся вычислять криволинейный интеграл от полного дифференциала.
Схема решения:
- сначала нужно убедиться, что подынтегральная функция является полным дифференциалом
- дальше найти интеграл между заданными точками.
Формула Ньютона-Лейбница для криволинейного интеграла от полного дифференциала
Криволинейный интеграл имеет одно полезное для вычислений свойство, он не зависит от формы кривой, по которой интегрируем.
Поэтому вместо интегрировать по прямой между двумя точками строят ломаную параллельно осям координат и интегрируют по ней.
За счет этого один из дифференциалов в интеграле превращается в нуль, таким образом упрощаются вычисления.
Детальнее алгоритм проверки подынтегрального выражения на полный дифференциал и вычисление криволинейных интегралов приведены в следующих 6 примерах.
Пример 1 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл int[(x+y)dx+(x-y)dy]
Решение: Подынтегральные функции являются первобытными для полного дифференциала
(x+y)dx+(x-y)dy.
Выпишем P=P(x, y)=x+y, Q=Q(x, y)=x-y.
но найдем частичные производные первого порядка функций P(x, y) и Q(x, y):
Сравнением убеждаемся, что частичные производные равны
поэтому подынтегральное выражение (x+y)dx+(x-y)dy является полным дифференциалом.
Криволинейный интеграл от точки (0,1) к точке (2,3) будем вычислять вдоль прямых y=1 и x=2.
Так верно выполнять, поскольку на каждом интервале один из дифференциалов равен нулю, следовательно, интеграл упрощается.
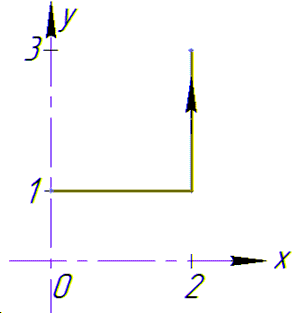
Вычислим заданный криволинейный интеграл:
Пример 2 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
Решение: Имеем подынтегральное выражение:
xdy+ydx.
Выпишем значение при дифференциалах
P=P(x, y)=y, Q=Q(x, y)=x.
Найдем частичные производные первого порядка функций P, Q:
Сравнением значений убеждаемся, что подынтегральное выражение является полным дифференциалом.
Заданный криволинейный интеграл от точки (- 1,2) к точке (2,3) будем вычислять вдоль прямых y=2 и x=2.
На графике направление и контур интегрирования имеют вид
Выпишем как буду изменяться координаты и дифференциалы на каждом интервале
Найдем криволинейный интеграл через сумму двух:
Пример 3 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
где f(u) непрерывная функция.
Решение: Выписываем подынтегральное выражение:
f(x+y)(dx+dy)=f(x+y)dx+f(x+y)dy.
Отсюда P=P(x, y)=f(x+y), Q=Q(x, y)=f(x+y).
Поскольку P, Q симметрично содержат переменные, то их частичные производные
равны, а это значит что подынтегральное выражение является полным дифференциалом.
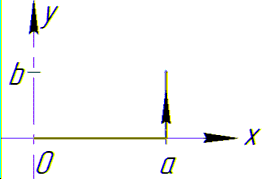
Криволинейный интеграл от точки (0,0) к точке (a, b) будем вычислять вдоль прямых y=0 и x=a.
Выпишем пределы интеграла и дифференциалы
Криволинейный интеграл упрощаем с помощью замены переменных:
здесь f(u) заданная непрерывная функция.
Пример 4 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
Пример 5 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
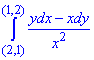
вдоль путей, которые не пересекают ось Oy.
Решение: Имеем подынтегральное выражение:
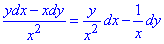
Отсюда P=P(x, y)=y/x2, Q=Q(x, y)=-1/x.
Вычислим частичные производные функций P(x, y), Q(x, y):
они равны между собой, поэтому подынтегральное выражение является полным дифференциалом.
Криволинейный интеграл от точки (2,1) к точке (1,2) будем вычислять вдоль прямых x=2 и y=2.
Запишем диапазон изменения пределов интеграла и дифференциалы
Вычислим заданный криволинейный интеграл:
Пример 6 Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл
вдоль кривых, что не проходят через начала координат.
Решение: Подынтегральное выражение разобьем на сумму двух:
Выписываем производные при дифференциалах
Найдем частичные производные первого порядка функций P, Q:
Сравнением значений делаем вывод что имеем полный дифференциал под интегралом.
Заданный криволинейный интеграл от точки (1,0) к точке (6,8) будем вычислять вдоль прямых y=0 и x=6, то есть на двух интервалах
В декартовой плоскости контур интегрирования имеет вид
Криволинейный интеграл равен 9
Приведенных примеров на вычисление криволинейного интеграла от полного дифференциала вполне достаточно, чтобы выучить алгоритм проверки подынтегральной функции на полный дифференциал.
Разбивать участок между точками на промежутки параллельные осям тоже не трудно.
Интегрировать Вы должны уметь хорошо прежде чем браться за подобные примеры.
Если имеете трудности в интегрировании обращайтесь к нам за помощью, думаю, договоримся!
Итак, продолжаем наше знакомство с основными приёмами интегрирования. В прошлый раз мы научились с вами пользоваться таблицей интегралов и рассмотрели самые простые примеры интегрирования самых простых функций. Теперь настала пора двигаться дальше и понемногу расширять наши возможности.
Итак, метод подведения функции под знак дифференциала — в чём его суть? Вообще говоря, данный метод не является самостоятельным методом интегрирования. Это, скорее, частный случай более общего и мощного метода — метода замены переменной. Или метода подстановки. Почему? А потому, что сам процесс интегрирования подведением под дифференциал всё равно сопровождается последующим введением новой переменной. Звучит пока малопонятно, но на примерах всё куда яснее будет.
Что нам потребуется в сегодняшнем материале:
1) Правило раскрытия дифференциала любой функции f(x). Именно само правило. Строгое определение, что же такое дифференциал, нам здесь не нужно. А правило — вот:
d(f(x)) = f’(x)dx
Всё просто, как в сказке: считаем производную функции f’(x) и помножаем её на dx (дифференциал аргумента).
2) Таблица производных. Да-да! Я серьёзно. 
3) Таблица интегралов. Ну, логично. Раз уж мы здесь вовсю интегрируем.) Это тема прошлых двух уроков.
4) Правило дифференцирования сложной функции.
Вот, собственно, и всё.
Когда чаще всего применяется данный метод? Чаще всего он применяется в двух типовых ситуациях:
Случай 1 — Сложная функция от линейного аргумента
Подынтегральная функция имеет вид:
f(kx+b)
В аргументе — линейная конструкция kx+b. Или, по-другому, под интегралом стоит какая-то сложная функция от линейного аргумента kx+b.
Например:
И тому подобные функции. Интегралы от таких функций очень легко сводятся к табличным и берутся в уме буквально через пару-тройку успешно решённых примеров. И мы порешаем.)
Случай 2 — Сложная функция от произвольного аргумента
В данном случае подынтегральная функция представляет собой произведение:
f(g(x))·g’(x)
Иными словами, под интегралом тусуется произведение некой сложной функции f(g(x)) и производной от её внутреннего аргумента g’(x). Или интеграл легко сводится к такому виду. Это более сложный случай. О нём — во второй части урока.
Чтобы не томить народ долгими ожиданиями и разглагольствованиями, сразу приступаем к примерам на случай 1. Будем интегрировать те функции, что я выписал выше. По порядочку.
Как подвести под дифференциал линейную функцию?
И сразу пример в студию.)
Пример 1
Лезем в таблицу интегралов и находим похожую формулу (это 4-я группа):
Всё бы хорошо, но… есть проблемка. В таблице интегралов в показателе экспоненты ex стоит просто икс. У нас же в показателе тусуется 3х. Три икс. Не катит… Не годится табличная формула для прямого применения: тройка всё испортила. Доцент! А, доцент! Что делать-то будем? (с)
Чтобы справиться с этим примером, нам придётся «подогнать» данный интеграл под табличную формулу. И сейчас я подробно покажу, как именно происходит подгонка. Для этого давайте-ка вернёмся в самое начала раздела и вспомним самую общую запись неопределённого интеграла. В общем виде. Вот она:
Надеюсь, подробная расшифровка всех значков и буковок в этой записи уже не требуется? Кому всё-таки непонятно, читаем самую первую статью: Что такое первообразная и неопределённый интеграл.
Так вот. Весь фокус состоит в том, что эта самая общая запись неопределённого интеграла будет справедлива не только для переменной икс, но и для любой другой буквы — y, z, t или даже целого сложного выражения. Какого хотим. Важно, чтобы соблюдалось одно единственное требование: в скобочках подынтегральной функции f(…), первообразной функции F(…) и под дифференциалом d(…) стояли одинаковые выражения. Во всех трёх местах! Это важно.
Например:
И так далее.) Какая бы буковка и какое бы сложное выражение ни стояли в этих трёх местах, табличная формула интегрирования всё равно сработает! И это неудивительно: любое сложное выражение мы имеем полное право обозначить одной буквой. И работать целиком со всей конструкцией как с одной буквой. А таблице по барабану, какая там буква стоит — икс, игрек, зэт, тэ… Для неё все буквы равноправны.) Поэтому сама конструкция во всех скобочках может при этом быть совершенно любой. Лишь бы одной и той же. )
Поэтому, для нашей конкретной табличной формулы ∫exdx = ex + C, мы можем записать:
И так далее. Стоять в этих трёх местах может какой угодно монстр. В общем, идея ясна, я надеюсь.)
А теперь порассуждаем. Для того чтобы в нашем примере у нас появилось право воспользоваться таблицей, нам надо добиться того, чтобы под интегралом образовалась вот такая конструкция:
И в показателе и под дифференциалом должно стоять выражение 3х. А теперь посмотрим ещё раз на наш пример:
С показателем и так всё как надо, там у нас 3х. По условию.) А вот под дифференциалом пока что стоит просто х. Непорядок! Как же нам из dx сделать d(3x)?
Для достижения этой благородной цели нам надо как-то связать между собой два дифференциала — новый d(3х) и старый dx. В данном случае это очень легко сделать. Если, конечно, знать, как раскрывается дифференциал.)
Получим:
Отлично! Значит, связь между старым и новым дифференциалами будет вот такой:
dx = d(3x)/3.
Что? Не помните, как раскрывать дифференциал? Это вопрос к первому семестру. К дифференциальному исчислению.)
А теперь что делаем? Правильно! Подставляем вместо старого дифференциала dx новое выражение d(3x)/3 в наш пример. Тройка в знаменателе нам уже не помеха: мы её того… наружу. За знак интеграла.)
Что получим:
Вот и отлично. В показателе экспоненты и под дифференциалом образовалось совершенно одинаковое выражение 3х. Чего мы, как раз, так усиленно добивались.) И с выражением 3х теперь можно работать целиком, как с одной новой буквой. Пусть t, например. Тогда после замены выражения 3x на t наш интеграл станет выглядеть вот так:
А новый интеграл по переменной t — уже так нужный нам табличный! И теперь можно с чистой совестью воспользоваться табличной формулой и твёрдой рукой записать:
Но расслабляться рано. Это пока ещё не ответ: нам икс нужен, а не t. Осталось лишь вспомнить, что t = 3x и выполнить обратную замену. И теперь наш ответ полностью готов! Вот он:
Вот всё и получилось.) Ну что, проверим? А вдруг, напортачили где-то? Дифференцируем результат:
Нет. Всё гуд.)
Пример 2
В таблице интегралов функции cos(x+4) нету. Есть просто косинус икс. Но! Если мы как-то организуем выражение х+4 и под дифференциалом d(x+4), то выйдем на табличный интеграл:
∫cos x dx = sin x + C
Итак, связываем наш требуемый новый дифференциал d(x+4) со старым dx:
d(x+4) = (х+4)’·dx = 1·dx = dx
Ух ты, как хорошо! Оказывается, наш новый дифференциал d(x+4) это то же самое, что и просто dx! И безо всяких дополнительных коэффициентов. Халява сплошная!)
Да.) Так и есть. Смело заменяем dx на d(x+4), работаем со скобкой (x+4) как с новой буквой и с чистой совестью пользуемся таблицей.
В этот раз решение запишу чуть компактнее:
Проверяем результат интегрирования обратным дифференцированием:
(sin(x+4)+C)’ = (sin(x+4))’ + C’ = cos(x+4)∙(x+4)’+0 = cos(x+4)∙1 = cos(x+4)
Всё в шоколаде.)
Ну как, хлопотно? Согласен, хлопотно. Каждый раз выписывать дифференциалы, связывать один с другим, выражать старый дифференциал через новый… Не отчаивайтесь! Есть хорошая новость! Так обычно и не делают. Я так подробно расписал решение чисто для понимания сути алгоритма. На практике же поступают гораздо проще. Давайте ещё разок выпишем наши связи между старыми и новыми дифференциалами из обоих примеров:
Что можно заметить из этих записей? Два очень важных факта!
Запоминаем:
1) Любой ненулевой числовой коэффициент k (k≠0) можно внести под дифференциал, для компенсации разделив полученный результат на этот коэффициент:
2) Любое постоянное слагаемое b можно внести под дифференциал без последствий:
Строго доказывать данные факты не буду. Ибо просто это. Из примеров и так всё понятно, надеюсь.) Если хотите строгости — ради бога. Упрощайте правые части обоих равенств, раскрывая дифференциалы. И там и там получите просто dx.
Данные два факта можно легко объединить в один, более универсальный.
Любую линейную конструкцию kx+b можно внести под дифференциал dx по правилу:
Подобная процедура носит название подведение функции под знак дифференциала. В данном случае под дифференциал подводится линейная конструкция kx+b. Мы искусственно превращаем неудобный нам дифференциал dx в удобный d(kx+b).
И зачем нам такие ужасающие возможности — спросите вы? Просто так — незачем. Но зато с помощью такого искусного манёвра очень многие нетабличные интегралы теперь будут щёлкаться буквально в уме. Как орешки.)
Смотрите!
Пример 3
Этот пример будем сводить к табличному интегралу от степенной функции:
Для этого подведём под дифференциал нашу линейную конструкцию 2х+1, стоящую под квадратом. То есть, вместо dx пишем d(2x+1). Так нам надо. Но математике надо, чтобы от наших действий суть примера не изменилась! Поэтому идём на компромисс и, согласно нашему правилу, домножаем дополнительно всю конструкцию на коэффициент 1/2 (у нас k = 2, поэтому 1/k = 1/2).
Вот так:
И теперь считаем:
Готово дело.) А вот тут у некоторых читателей может возникнуть вопрос. Очень хороший вопрос, между прочим!
Мы ведь могли и не подводить выражение 2х+1 под дифференциал, не вводить никакую новую переменную, а просто взять и тупо возвести скобки в квадрат по школьной формуле квадрата суммы
(2х+1)2 = 4х2+4х+1,
после чего почленно (в уме!) проинтегрировать каждое слагаемое. Можно так делать? Конечно! А почему — нет? Попробуйте! И сравните полученные результаты. Будет вам там сюрприз! Подробности — в конце урока.
А мы пока движемся дальше. Оставшиеся примеры распишу уже без особых комментариев… Подводим линейный аргумент kx+b под дифференциал, а образовавшийся коэффициент 1/k выносим за знак интеграла. И срабатываем по таблице. Окончательные ответы выделены жирным шрифтом.
Пример 4
Легко!
Пример 5
Без проблем!
И, наконец, последний пример.
Пример 6
И тут всё проще простого!
Ну как? Понравилось? И теперь такие примеры вы можете щёлкать в уме! Заманчивая возможность, правда?) Более того, сами подобные интегралы частенько бывают отдельными слагаемыми в более накрученных примерах.
Кстати сказать, после определённого навыка работы с таблицей первообразных, со временем полностью отпадает необходимость вводить новую промежуточную переменную t. За ненадобностью.
Например, очень скоро, вы сразу в уме на подобные примеры будете давать готовый ответ:
И так далее…
И даже в один присест расправляться с монстрами типа:
А вы попробуйте вычислить данный интеграл «в лоб», через возведение в 1000-ю степень по формуле бинома Ньютона! Придётся почленно интегрировать 1001 слагаемое, да… А вот с помощью подведения под дифференциал — в одну строчку!
Так, ну хорошо! С линейной функцией всё предельно ясно. Как именно подводить её под дифференциал — тоже. И тут я слышу закономерный вопрос: а только ли линейную функцию можно подвести под дифференциал?
Разумеется, нет! Любую функцию f(x) можно подвести под дифференциал! Ту, которая удобна в конкретном примере. А уж какая там удобна — от конкретного примера зависит, да… Просто на примере линейной функции очень просто демонстрировать саму процедуру подведения. На пальцах, что называется.) А теперь мы плавненько подходим к более общему случаю 2.
Как подвести под дифференциал любую произвольную функцию?
Речь пойдёт о случае, когда подынтегральная функция имеет вот такой вид:
f(g(x))·g’(x).
Или, что то же самое, подынтегральное выражение имеет вид:
f(g(x))·g’(x)dx
Ничего особенного. Просто dx приписал.)
Одним словом, речь пойдёт об интегралах вида:
Не пугаемся всяких штрихов и скобочек! Сейчас всё куда яснее станет.)
В чём здесь суть. Из исходной подынтегральной функции можно выделить сложный аргумент g(x) и его производную g’(x). Но не просто выделить, а расписать именно в виде произведения некой сложной функции f(g(x)) от этого самого аргумента на его производную g’(x). Что и выражается записью:
f(g(x))·g’(x)
Перефразируем теперь всё в терминах дифференциала: подынтегральное выражение можно представить в виде произведения некой сложной функции f(g(x)) и дифференциала её аргумента g’(x)dx.
Разбираемся дальше. Мы с вами знаем (надеюсь), что g’(x)dx = d(g(x)). Прямо по смыслу дифференциала.)
И тогда, стало быть, всё наше подынтегральное выражение можно расписать вот так:
Говоря по-русски, мы вносим промежуточную функцию g(x) под знак дифференциала. Было dx, а стало d(g(x)). И зачем нам эти метаморфозы? А затем, что, если сейчас ввести новую переменную t = g(x), то наш интеграл существенно упростится:
И, если новый интеграл по новой переменной t вдруг (!) окажется табличным, то всё в шоколаде. Празднуем победу! )
«Многа букафф», да. Но на примерах сейчас всё куда понятнее будет. Итак, вторая часть пьесы!
Пример 7
Это классика жанра. Под интегралом дробь. Напрямую таблицей не воспользуешься, никакими школьными формулами ничего не преобразуешь. Только подведение под дифференциал и спасает, да.) Для этого распишем нашу подынтегральную дробь в виде произведения. Хотя бы вот такого:
А теперь разбираемся. С логарифмом в квадрате всё ясно. Он и в Африке логарифм… А что такое 1/x? Вспоминаем нашу незабвенную таблицу производных… Да! Это производная логарифма!
Вставляем теперь в подынтегральную функцию вместо 1/х выражение (ln x)’:
Вот мы и представили исходную подынтегральную функцию в нужном нам виде f(g(x))·g’(x). Превратили её в произведение некой функции от логарифма f(ln x) и производной от этого самого логарифма (ln x)’. А именно — в произведение ln2x и (ln x)’.
А теперь давайте подробно расшифруем, какие же именно действия у нас скрываются за каждой буковкой.
Ну, с функцией g(x) всё ясно. Это логарифм: g(x) = ln x.
А что же скрывается под буквой f? Не всех осеняет сразу… А под буквой f у нас скрывается действие — возведение в квадрат:
Вот и вся расшифровка.)
А всё подынтегральное выражение можно теперь переписать вот так:
И какую же функцию мы внесли под дифференциал в данном примере? В данном примере мы внесли под дифференциал логарифмическую функцию ln x!
А дальше всё очевидно. Заменяем теперь наш логарифм новой буквой t, вставляем в пример и получаем вместо ужасной дроби безобидный табличный интеграл от… степенной функции!
Готово дело.) Для того чтобы убедиться в правильности результата, всегда можно (и нужно) продифференцировать ответ:
Ура! Всё ОК.)
А теперь обратите внимание, как именно мы дифференцируем окончательный ответ всех примеров этого урока. Неужели до сих пор не уловили закономерность? Да! Как сложную функцию! Оно и естественно: дифференцирование сложной функции и подведение функции под знак дифференциала — это два взаимно обратных действия.
Это был довольно несложный пример. Чтобы разобраться, что к чему. Теперь пример посолиднее.)
Пример 8
Опять же, впрямую ничего не решается. Попробуем метод подведения под дифференциал с последующей заменой. Вопрос — что подводить и заменять будем? А вот тут уже задачка.)
Нам надо попробовать подынтегральную функцию x·cos(x2+1) как-то представить в виде произведения функции от чего-то на производную этого самого чего-то:
Ну, произведение у нас и так уже есть — икса и косинуса.) Чутьё подсказывает, что функцией g(x), которую мы и будем подводить под дифференциал, будет выражение x2+1, которое сидит внутри косинуса. Прямо таки напрашивается:
Всё чётко. Внутренняя функция g — это x2+1, а внешняя f — это косинус.
Хорошо. А теперь давайте проверим, не связан ли как-то оставшийся множитель x с производной выражения x2+1, которое мы выбрали в качестве кандидата на подведение под венец дифференциал.
Дифференцируем:
Да! Связь налицо! Если 2x = (x2+1)’, то для одинарного икса мы можем записать:
Или, в виде дифференциалов:
Всё. Кроме x2+1, никаких других выражений с иксом у нас больше нигде в примере нет. Ни в подынтегральной функции, ни под знаком дифференциала. Чего мы и добивались.
Переписываем теперь наш пример с учётом этого факта, заменяем выражение x2+1 новой буквой и — вперёд! Правда, это… Коэффициент 1/2 ещё вылез… Не беда, мы его наружу, наружу!
Вот и всё. Как мы видим, в предыдущем примере под дифференциал вносилась логарифмическая функция, а здесь — квадратичная.
Рассмотрим теперь более экзотический пример.
Пример 9
На вид ужас-ужас! Однако, горевать рано. Самое время вспомнить нашу горячо любимую таблицу производных.) А чуть конкретнее — производную арксинуса.
Вот она:
Тогда, если подвести этот самый арксинус под дифференциал, то этот злой пример решается в одну строчку:
И все дела!
А теперь, давайте на данном примере проанализируем весь наш увлекательный процесс подведения функции арксинус под дифференциал. Что нам пришлось сделать, чтобы успешно справиться с этой задачей? Нам пришлось опознать в выражении
производную другого выражения — арксинуса! Иными словами, сначала вспомнить (по таблице производных), что
и затем сработать справа налево. Вот так:
А вот это уже посложнее, чем простое дифференцирование, согласитесь! Точно так же, как и, например, извлекать квадратный корень сложнее, чем возводить в квадрат.) Нам приходится подбирать нужную функцию. По таблице производных.
Поэтому, помимо прямого дифференцирования, в интегрировании нам ещё надо будет постоянно проводить обратную операцию — распознавать в функциях производные других функций. Здесь чёткого алгоритма нет. Тут практика рулит.) Рецепт здесь один — решать примеры! Как можно больше. Прорешаете хотя бы 20-30 примеров — и такие замены вы будете замечать и проделывать достаточно быстро и легко. На автомате, я бы даже сказал. И обязательно надо знать таблицу производных! Наизусть.)
Я даже не поленюсь и самые популярные конструкции сведу в отдельную таблицу дифференциалов.
Этой небольшой сводной таблички уже вполне достаточно, чтобы успешно расправляться с большей частью примеров, решаемых методом подведения функции под знак дифференциала! Имеет смысл разобраться.
Скажу отдельно, что конструкция dx/x и соответствующий ей табличный интеграл ln|x| — одни из самых популярных в интегрировании!
К этой табличной формуле с логарифмом сводятся все интегралы от дробей, числитель которых является производной знаменателя. Смотрите сами:
Например, даже безо всякой замены, по этому правилу можно в одну строчку проинтегрировать тангенс, к примеру. Кто-то тут как-то спрашивал про тангенс? Пожалуйста!
И даже такие гиганты тоже интегрируются в одну строчку!
Забавно, правда?
Возможно, у особо глазастых возник вопрос, почему в первых трёх случаях я под логарифмом написал модуль, а в последнем случае — не написал?
Ответ: выражение ex+1, стоящее под логарифмом в последнем примере, положительно при любом действительном x. Поэтому логарифм от выражения ex+1 всегда определён, и в данном случае вместо модуля можно использовать обычные скобки.
А зачем вообще под логарифмом в табличном интеграле стоит модуль? Ведь, в таблице производных у логарифма никакого модуля нету и при дифференцировании мы спокойненько пишем:
(ln x)’ = 1/х
А при интегрировании функции 1/x ещё и модуль зачем-то пишем…
На этот вопрос отвечу позже. В уроках, посвящённых определённому интегралу. Связан этот модуль с областью определения первообразной.
Заметьте: мы, как фокусники в цирке, по правде говоря, просто осуществляем какой-то набор махинаций с функциями, превращая их друг в друга по некой табличке. А с областью определения пока что вообще никак не паримся. И, по правде говоря, зря. Ведь мы работаем всё-таки с функциями! А область определения — важнейшая часть любой функции, между прочим! В том числе и тех функций, с которыми мы здесь работаем — подынтегральной f(x) и первообразной F(x). Так что про область определения мы ещё вспомним. В специальном уроке.) Терпение, друзья!
Вот мы и рассмотрели с вами типовые примеры интегралов, решаемых подведением функции под знак дифференциала.) Сложно? Поначалу — да. Но после определённой тренировки и выработки навыка такие интегралы вам будут казаться одними из самых простых!
А теперь — обещанный сюрприз!
Давайте вновь вернёмся к примеру №3. Там, подводя выражение 2х+1 под дифференциал, мы получили вот такой ответ:
Это правильный ответ. Продифференцируйте на бумажке, как сложную функцию, и убедитесь сами.
А теперь рассмотрим другой способ решения этого же примера. Не будем ничего подводить под дифференциал, а просто тупо раскроем квадрат суммы и почленно проинтегрируем каждое слагаемое. Имеем полное право!
Получим:
И это тоже правильный ответ!
Вопрос: первый и второй ответы к одному и тому же интегралу – одинаковы или различны?
Ведь, по логике, ответы к одному и тому же примеру, полученные двумя разными способами, должны совпадать, не так ли? Сейчас узнаем! Преобразуем первый результат, раскрыв куб суммы по формуле сокращённого умножения (a+b)3 = a3+3a2b+3ab2+b3.
Что получим:
А теперь сравниваем оба результата:
И… что-то тут не так! Откуда же в первом результате взялась «лишняя» дробь 1/6? Получается, что к одному и тому же интегралу получены два разных ответа!
Парадокс? Мистика?
Спокойствие! Разгадка тайны кроется в определении неопределённого интеграла. Вспоминаем самый первый урок по интегрированию. Там зачем-то приведена оч-чень важная фраза: две первообразные одной и той же функции F1(x) и F2(x) отличаются друг от друга на константу.
А теперь вновь всматриваемся в наши результаты. И… видим, что в нашем случае так и есть: полученные двумя разными путями ответы как раз и отличаются на константу. На одну шестую.
F1(x) — F2(x) = 1/6
Вот и весь секрет. Так что никакого противоречия нет.
Дальше — больше! Посмотрим теперь на интеграл из примера №4:
А его вообще можно взять аж… тремя различными способами! Не верите? Смотрите cами!
Способ №1. Синус двойного угла не трогаем, а просто подводим аргумент 2x под дифференциал (как, собственно, уже делали в процессе разбора):
Способ №2. Раскрываем синус двойного угла, под дифференциал подводим sin x:
Способ №3. Снова раскрываем синус двойного угла, но под дифференциал подводим cos x:
А теперь дифференцируем все три ответа и удивляемся дальше:
Чудеса, да и только! Получилось три разных ответа! Причём в этот раз даже внешне не похожих друг на друга. А производная — одна и та же! Неужели дело опять в интегральной константе, и каждая из трёх функций отличается от другой на константу? Да! Как это ни странно, но это именно так.) А вы поисследуйте эти три функции самостоятельно! Не сочтите за труд. Преобразуйте каждую функцию к одному виду — либо к sin2x, либо к cos2x. И да помогут вам школьные формулы тригонометрии!
К чему я рассмотрел эти сюрпризы и вообще затеял все эти светские беседы про интегральную константу?
А дело вот в чём. Как вы видите, даже небольшое различие в интегральной константе способно, в принципе, сильно изменить внешний вид ответа, да… Но фишка в том, что от этого ответ не перестаёт быть правильным! И, если в сборнике задач вы, вдруг, увидите ответ, не совпадающий с вашим, то огорчаться рано. Ибо этот факт вовсе не означает, что ваш ответ неверен! Возможно, что вы просто пришли к ответу иным путём, чем предполагал автор примера. Так бывает.) А убедиться в правильности ответа всегда поможет самая надёжная проверка, основанная на определении неопределённого интеграла. Какая? Правильно! Дифференцирование окончательного ответа! Получили подынтегральную функцию — значит, всё ОК.
Ну как, прочувствовали теперь, насколько важен значок dx под интегралом? Во многих примерах только он и спасает, да. Мощная штука! Так что теперь не пренебрегаем им!
А теперь — тренируемся! Поскольку тема не самая простая, то и примеров для тренировки в этот раз будет больше обычного.
Методом подведения функции под знак дифференциала найти неопределённые интегралы:
Ответов в этот раз давать не буду. Так будет неинтересно. Не ленитесь дифференцировать результат! Получили подынтегральную функцию — ОК. Нет — ищите, где накосячили. Все примеры очень простые и решаются в одну (максимум две) строчки. Кому позарез нужны ответы, все примеры взяты из сборника задач по матанализу Г.Н. Бермана. Скачивайте, ищите свой пример, сверяйтесь. Успехов!