Главная › ЕГЭ. Стереометрия
В правильной четырехугольной пирамиде найти диагональ основания
Автор: Ирина Гайкова
Комментариев нет
477
Telegram
VK
OK
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SD = 10, SO = 6. Найдите длину отрезка AС.
Интересная статья? Поделитесь ею пожалуйста с другими:
Хотите обучаться математике индивидуально?
Запишитесь на консультацию.
Мы храним ваши данные в тайне
Похожие записи:
-
Найдите площадь боковой поверхности правильной шестиугольной призмы
-
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9.
-
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4.
Оставьте свой комментарий:
- на Блоге
- в Вконтакте
- в Фейсбук










Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя *
Email *
Вебсайт
Получать новые комментарии по электронной почте. Вы можете подписаться без комментирования.
Нажимая на кнопку «Отправить комментарий», я соглашаюсь с политикой обработки персональных данных
Определение
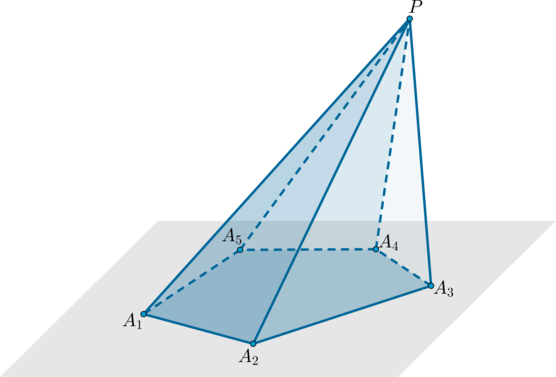
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.
1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).
Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).
2) Докажем, что из ((b)) следует ((c)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).
3) Докажем, что из ((c)) следует ((a)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).
4) Докажем, что из ((b)) следует ((d)).
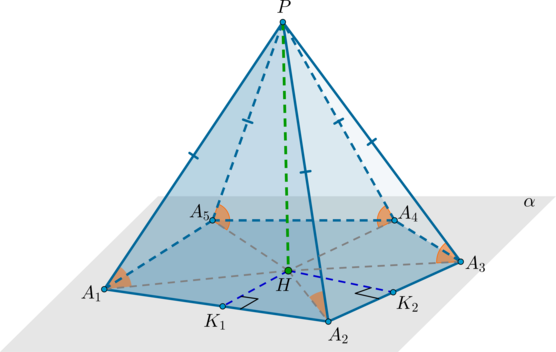
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.
5) Докажем, что из ((d)) следует ((b)).
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
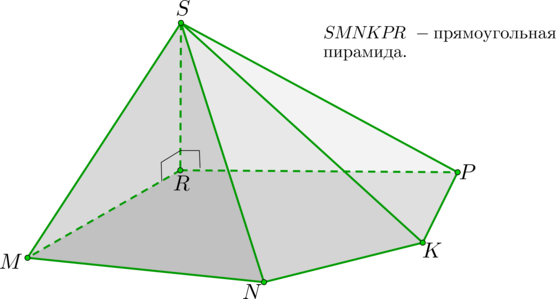
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.
3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
[{Large{text{Объем и площадь поверхности пирамиды}}}]
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),
2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).
3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).
4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
[{Large{text{Усеченная пирамида}}}]
Определение
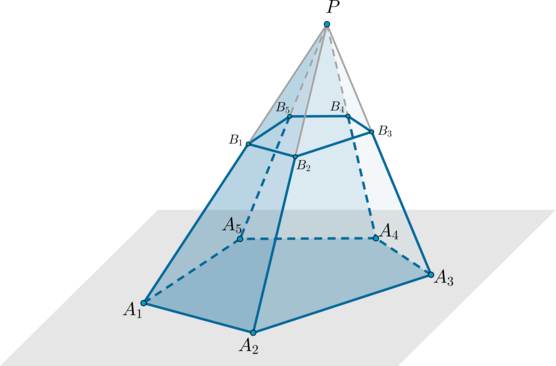
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).
Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача.
Диагональ основания правильной четырехугольной пирамиды равна 4 см, а боковая грань образует с основанием угол 60 градусов. найдите объем пирамиды.
Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
Ответ: 8√6 / 3 см3.
Задача.
Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны
α. Найти площадь полной поверхности пирамиды.
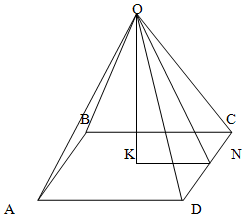
Решение.
Поскольку пирамида правильная, то ее высота проецируется в центр основания.
Значит KN = a/2
Соответственно, треугольник OKN — прямоугольный. Значит
ON = KN / cos α = a / 2cos α
Поскольку пирамида правильная, то треугольник DOC — равнобедренный. Значит его площадь равна
Sт = DC * ON / 2
Sт = ( a * a / 2cos
α) / 2 = a2 / 4cos α
Откуда площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней
Sб = 4a2 / 4cos
α
Sб = a2 / cos α
Откуда площадь полной поверхности равна
Sп = a2 / cos
α + a2 = a2 ( 1 + 1 / cos α )
Ответ: площадь полной поверхности правильной четырехугольной пирамиды равна a2 ( 1 + 1 / cos α )
0
Правильная пирамида с четырехугольником в основании |
Описание курса
| Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
План урока:
Понятие пирамиды
Правильная пирамида
Усеченная пирамида
Типичные задачи на пирамиды
Понятие пирамиды
Построим на некоторой плос-ти α произвольный многоугольник А1А2…Аn. Далее отметим в пространстве точку Р, не принадлежащую плос-ти α. Соединив точку Р с вершинами многоуг-ка получим многогранник, который именуется пирамидой (в различной литературе может использоваться сокращение пирам-а).
Та единственная точка Р, не находящаяся в одной плос-ти со всеми остальными вершинами, именуется вершиной пирам-ы. Многоугольник, образованный остальными вершинами – это основание пирамиды.
Основанием пирам-ы может быть многоугольник с любым количеством сторон. Если в основании лежит, например, пятиугольник, то и пирам-у называют пятиугольной. Если же в основании находится десятиугольник, то это будет уже десятиугольная пирам-а. В общем случае пирам-у, у которой в основании располагается n-угольник, именуется n-угольной. Ясно, что треугольная пирам-а и тетраэдр – это по сути одна и та же фигура.
Все грани пирам-ы, за исключением ее основания, именуются боковыми гранями. Понятно, что каждая боковая грань – это треугольник. Ребра пирамиды, выходящие из ее вершины, именуются боковыми ребрами пирамиды.
Посчитаем количество ребер, вершин и граней пирам-ы. Если она n-угольная, то у неё (n + 1) вершин (n точек в основании и ещё одна точка, не лежащая в основании). Также у нее (n + 1) граней, из них одна – это основание, а остальные n – боковые грани пирамиды (по одной на каждую сторону n-угольника). Наконец, у пирам-ы n ребер находятся в плос-ти основания, а ещё n ребер являются боковыми. Итого имеем 2n ребер. Теперь можно убедиться, что теорема Эйлера для пирам-ы выполняется:
Из вершины пирам-ы можно опустить перпендикуляр на плос-ть основания. Он будет именоваться высотой пирамиды.
Как и в случае с призмой, можно подсчитать площадь боковой поверхности призмы, которую обозначают как Sбок. Если же к ней ещё добавить и площадь основания (Sосн), то в сумме получится уже площадь полной поверхности призмы (Sполн). Эту связь между величинами можно представить в виде формулы:
Правильная пирамида
Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:
1) в их основании находится правильный многоугольник;
2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.
Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.
Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:
Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.
Построим из О радиусы ОА1, ОА2, ОА3,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА1, ∆РОА2, ∆РОА3… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА1, ОА2, ОА3… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА1, РА2, РА3…, также одинаковы, ч. т. д.
Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА1, РА2, РА2… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А1, А2, А3… Получатся прямоугольные ∆РОА1, ∆РОА2, ∆РОА3… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА1, ОА2, ОА3… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА1, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.
Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.
Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.
Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.
Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:
Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:
Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:
Усечённая пирамида
Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА1, РА2, РА3… в точках В1, В2, В3… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.
У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.
Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:
Нам надо доказать, что А1А2В2В1 – это трапеция. Действительно, прямые А1А2 и В1В2 не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А1А2||В1B2. Две другие стороны грани, А1В1 и А2В2, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А1А2В2В1 будет трапецией, ведь у него две стороны параллельны, а две другие – нет.
Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:
Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А1А2А3…An и В1В2В3…Bn:
Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:
Мы уже знаем, что грани А1А2В2В1 и А2А3В3В2 – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.
Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А1А2А3 = ∠В1В2В3. Действительно, мы знаем, что А1А2||В1В2 и А2А3||B2B3, и потому стороны углов ∠А1А2А3 = ∠В1В2В3 оказываются сонаправленными лучами.
Так как в нижнем многоуг-ке А1А2А3…An все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В1В2В3…Bn также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.
Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА1А2А3…Рn была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В1В2В3…Вn– правильный многоуг-к. Отрезки РА1, РА2, РА3… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А1В1, А2В2, А3В3 одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ1, РВ2, РВ3… Значит, в пирам-е РВ1В2В3…Вn в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.
Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:
Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:
Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:
Типичные задачи на пирамиды
Рассмотрим несколько задач, в которых фигурируют пирам-ы. Перед просмотром решения попытайтесь решить их самостоятельно.
Задание. Существует ли пирамида, у которой ровно 999 ребер?
Решение. Если в основании пирам-ы находится n-угольник, то у нее 2n ребер. Так как n– целое число, то 2n будет уже четным числом. То есть количество ребер у любой пирам-ы всегда четно. Поэтому не существует пирам-ы с 999 ребрами, ведь 999 – нечетное число.
Задание. Верно ли, что всякий правильный тетраэдр одновременно является и правильной пирам-ой? И наоборот, является ли каждая правильная треугольная пирам-а правильным тетраэдром?
Решение. Напомним, что правильный тетраэдр – это тетраэдр, у которого все ребра одинаковы. Если одну из вершин тетраэдра принять за вершину пирам-ы, то получится, что в ее основании равносторонний треугольник, который, как мы знаем, является правильным многоуг-ком. Также окажется, что все боковые ребра пирам-ы также одинаковы. Это значит, что она – правильная.
Теперь посмотрим на произвольную правильную треугольную пирам-у. Будет ли она обязательно правильным тетраэдром? Нет, ведь ее боковые ребра могут отличаться по длине от ребер, находящихся в основании. Например, в основании может находиться равносторонний треуг-к со стороной 5 см, а боковое ребро правильной пирамиды может иметь длину 10 см. Таким образом, можно считать правильный тетраэдр лишь частным случаем правильной пирам-ы.
Задание. В основании пирам-ы находится ромб со стороной 5 см.Одна из его диагоналей имеет длину 8 см. Высота пирам-ы имеет длину 7 см и проходит через точку, в которой пересекаются диагонали ромба. Вычислите длину боковых ребер.
Решение.
Обозначим ромб в основании как АВСD, а вершину пирам-ы буквой Р. Пусть диагонали пересекаются в точке О, тогда РО – высота. Также пусть диагональ АС равна 8 см. По свойству ромба О будет серединой диагоналей, поэтому
Отрезок OD будет иметь ту же длину 3 см, ведь О – середина BD.
Так как высота РО перпендикулярна всем прямым в плос-ти основания, то ∆АОР, ∆ВОР, ∆СОР, ∆DOP – прямоугольные, и боковые ребра пирам-ы будут гипотенузами этих треугольников. Вычислим АР по теореме Пифагора:
Задание. В основании пирам-ы лежит квадрат, а одно из ее боковых ребер перпендикулярно основанию. Одна из боковых граней образует с плос-тью основания угол в 45°. Длина длиннейшего ребра пирам-ы составляет 12 см. Определите высоту пирам-ы и площадь ее боковой поверхности.
Решение.
Обозначим квадрат, находящийся в основании, как АВСD, а вершину пирам-ы как Р. Пусть ребро PD перпендикулярно основанию. Тогда PD⊥AD и PD⊥CD. Ясно, что PD как раз и является искомой нами высотой пирам-ы.
Теперь надо понять, какие углы в пирам-е составляют 45° и какое ребро равно 12 см. Грани ADP и СDP проходят через перпендикуляр PDк основанию, а потому они перпендикулярны основанию. Значит, угол в 45° с основанием образует либо грань АВР, либо грань СВР.
Заметим, что АВ⊥AD (это смежные стороны квадрата), а AD – это проекция ребра АР на основание. Тогда по теореме о трех перпендикулярах АВ⊥АР. Аналогично из того факта, что ВС⊥СD, вытекает, что ВС⊥СР. Также заметим, что ∆ADP и ∆СDP прямоугольные, имеют общий катет PD и одинаковые катеты AD и CD (это стороны квадрата). Значит, это равные треугольники, и
∠PAD = ∠PCD
Грань АВР пересекается c основанием по прямой АВ, причем AD⊥АВ и АР⊥АВ. Значит, ∠РАD – это угол между гранью АВР и основанием. Аналогично и ∠РСD является углом между гранью СВР и основанием. Но эти углы одинаковы. Значит, каждый из этих углов будет равен 45°, иначе в пирам-е не останется угла между плос-тями, который мог бы составлять 45°.
Ясно, что ребро АР длиннее ребра РD, ведь в прямоугольном ∆ADP АР – это гипотенуза, а РD катет (гипотенуза всегда длиннее катета). Теперь заметим, что ∆РАВ и ∆РСВ – также прямоугольные, ведь АВ⊥АР и ВС⊥СР. Но в них гипотенузой является уже РВ, то есть РВ длиннее АВ, ВС, АР и РС. Так как отрезки AD и AC равны АВ как стороны квадрата, получаем, что именно ребро РВ – длиннейшее в пирам-е, то есть его длина составляет 12 см.
В прямоугольном ∆ADP∠PAD = 45°. Это значит, что ∆ADP является прямоугольным и равнобедренным, то есть AD = PD. Обозначим искомую нами длину РD как x. Теперь проведем диагональ BD:
Её длину можно вычислить из ∆ADB:
Итак, высоту нашли, теперь нужно рассчитать боковую площадь. Но для этого предварительно найдем АР из ∆АРD:
Такую же длину имеет и РС, ведь ∆АРD и ∆СРD равны.
Мы уже выяснили, что каждая боковая грань – прямоугольный треугольник. Зная длины катетов, легко найдем площадь каждой грани:
Задание. В правильной шестиугольной пирам-е ребро при основании равно 3 см. Высота этой пирам-ы составляет 4 см. Вычислите длину апофемы этой пирам-ы, а также угол, который ее боковые грани образуют с основанием.
Решение.
Основание пирам-ы обозначим как АВСDEF, а вершину как Р. Пусть РО – высота, тогда О – центр описанной окружности. Напомним, что у правильного шестиугольника радиус описанной окружности совпадает с длиной его стороны, то есть
Теперь надо найти угол между гранью АВР и основанием. Они пересекаются по прямой АВ. РН⊥АВ, ведь РН – апофема. ОН – это проекция РН на основание. Так как АВ⊥РН, то по обратной теореме о трех перпендикулярах и ОН⊥АВ. Значит, ∠ОНР и является искомым углом между гранью АВР и основанием. Для его вычисления применим тригонометрию к ∆ОНР:
Задание. В правильной шестиугольной пирам-е все ребра имеют длину, равную единице. Найдите угол между прямыми АР и BD:
Решение. Для нахождения угла между АР и BD, у которых нет общей точки, можно вычислить угол между прямыми, которые будут им параллельны. Легко заметить, что АЕ||BD. Докажем это, рассмотрев основание пирам-ы:
Каждый угол правильного шестиугольника составляет 120°. В частности, это относится к ∠F и ∠С. ∆АFЕ – равнобедренный, ведь его стороны FE и AF одинаковы. Тогда и углы при основании будут одинаковыми. Найдем их:
Аналогично можно определить, что все углы четырехугольника АВDE прямые, то он представляет собой прямоугольник. Его противоположные стороны параллельны, в частности, АЕ||BD. Это означает, что искомый нами угол – это ∠РАЕ:
Для его вычисления необходимо вычислить длины сторон ∆РАЕ. Ребра РА и РЕ по условию равны единице. Длину ЕА найдем из ∆FAE, применив теорему косинусов:
Задание. В правильной шестиугольной пирам-е боковые ребра имеют длину 2, а ребра в основании равны 1. Вычислите угол между плос-тями РFA и PDE:
Решение. Сначала надо найти прямую, по которой эти две грани пересекаются. Мы видим одну их общую точку – Р. Продолжим ребра FA и ED до тех пор, пока они не пересекутся в некоторой точке К. Эта точка K также будет общей для плос-тей, проходящих через грани PFA и РЕD. Значит, они пересекаются по прямой РК:
Найдем углы в ∆КЕF, помня при этом, что все в шестиугольнике АВСDEF составляют по 120°:
Получили, что все углы в ∆КЕF составляют по 60°, то есть он равносторонний, и поэтому стороны KE и KF одинаковы. Но также одинаковы и грани FA и DE. Отсюда получаем и равенство отрезков АК и DK:
Теперь сравним ∆АРК и ∆KPD. КР – их общая сторона, АР = РD как боковые ребра правильной пирам-ы, и АК = DK. Получается, что эти треугольники равны.
Далее в ∆АРК опустим высоту АН. Из равенства ∆АРК и ∆KPD вытекает, что и HD будет высотой в ∆PHD, ведь в равных треугольниках высоты должны делить равные стороны в одном и том же отношении. Тогда по определению двугранного угла ∠AHD и будет искомым углом между гранями, ведь KP – линия их пересечения, АН⊥KP и DH⊥KP.
∆AKP – равнобедренный, ведь отрезки АК и АР оказались одинаковыми. Значит, АН не только высота, но и медиана. Поэтому
Отрезок AD окажется диаметром окружности, описанной около шестиугольника. Мы знаем, что радиус такой окружности равен длине стороны шестиугольника, то есть единице. Тогда диаметр будет вдвое больше:
Сегодня мы познакомились с ещё одним видом многогранника –пирамидой. Они нередко встречаются в задачах ЕГЭ, посвященных стереометрии. Особо часто используются правильные пирамиды, поэтому важно помнить их основные свойства.