Посчитать диагональ прямоугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Посчитать диагональ прямоугольника
Чтобы посчитать диагональ прямоугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Чему равна диагональ прямоугольника если сторона
a = ,
а сторона
b = ?
Ответ: d =
0
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
d = √a2 + b2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
d = √102 + 52 = √100 + 25 ≈ 11.18 см
См. также
Загрузить PDF
Загрузить PDF
Диагональ — это отрезок, который соединяет две противолежащие вершины прямоугольника.[1]
В прямоугольнике две равные диагонали.[2]
Если известны стороны прямоугольника, диагональ можно найти по теореме Пифагора, потому что диагональ делит прямоугольник на два прямоугольных треугольника. Если стороны не даны, но известны другие величины, например, площадь и периметр или отношение сторон, можно найти стороны прямоугольника, а затем по теореме Пифагора вычислить диагональ.
-
1
-
2
-
3
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
4
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[5]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
-
1
Запишите формулу для вычисления площади прямоугольника. Формула:
, где
— площадь прямоугольника,
— длина прямоугольника,
— ширина прямоугольника.[6]
(На рисунке вместо S использовано обозначение А.) -
2
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула запишется так:
-
3
Перепишите формулу так, чтобы обособить
. Для этого разделите обе стороны уравнения на
. Затем полученное выражение нужно подставить в формулу для вычисления периметра.
-
4
Запишите формулу для вычисления периметра прямоугольника. Формула:
, где
— длина прямоугольника,
— ширина прямоугольника.[7]
-
5
В формулу подставьте значение периметра прямоугольника. Это значение подставляется вместо
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
.
- Например, если периметр прямоугольника равен 24 сантиметра, формула запишется так:
-
6
Разделите обе стороны уравнения на 2. Вы получите сумму сторон прямоугольника, а именно
.
-
7
В формулу подставьте выражение для вычисления
. Это выражение, полученное при обособлении
.
-
8
Избавьтесь от дроби. Для этого обе части уравнения умножьте на
.
-
9
Приравняйте уравнение к 0. Для этого из обеих сторон уравнения вычтите член с переменной первого порядка.
-
10
Упорядочьте члены уравнения. Первым членом будет член с переменной второго порядка, затем член с переменной первого порядка, а затем свободный член. При этом не забудьте про знаки («плюс» и «минус»), которые стоят перед членами. Обратите внимание, что уравнение запишется в виде квадратного уравнения.
-
11
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
12
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (это корни уравнения), которые в случае прямоугольника являются его длиной и шириной.
-
13
-
14
-
15
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
16
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[10]
Вы найдете, то есть гипотенузу треугольника, а значит, и диагональ прямоугольника.
Реклама
-
1
-
2
-
3
В формулу подставьте значение площади прямоугольника. Это значение подставляется вместо
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
.
- Например, если площадь прямоугольника равна 35 квадратных сантиметров, формула примет вид:
-
4
В формулу подставьте выражение, характеризующее отношение сторон. В случае прямоугольника можно подставить выражение для вычисления
или
.
-
5
Запишите квадратное уравнение. Для этого раскройте скобки и приравняйте уравнение к нулю.
-
6
Разложите квадратное уравнение на множители. Чтобы получить подробные инструкции, прочитайте эту статью.
-
7
Найдите
. Для этого приравняйте каждый множитель к нулю и вычислите
. Вы получите два значения (так называемые корни уравнения).
-
8
Подставьте найденное значение ширины (или длины) в уравнение, характеризующее отношение сторон. Так можно найти другую сторону прямоугольника.
-
9
-
10
-
11
Длину и ширину возведите в квадрат, а затем сложите полученные результаты. Помните, что при возведении числа в квадрат оно умножается на себя.
-
12
Извлеките квадратный корень из обеих сторон уравнения. Воспользуйтесь калькулятором, чтобы быстро извлечь квадратный корень. Также можно воспользоваться онлайн-калькулятором.[16]
Вы найдете, то есть гипотенузу треугольника, а значит и диагональ прямоугольника.
Реклама
Об этой статье
Эту страницу просматривали 557 545 раз.
Была ли эта статья полезной?
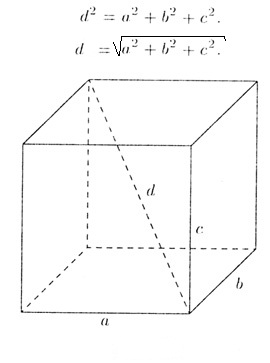
Прямая призма, основанием которой является прямоугольник, называется прямоугольным параллелепипедом.
Длины трёх рёбер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
Например, три измерения — это длины трёх рёбер
DA,DC,DD1
.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
,
где (a, b, c) — измерения прямоугольного параллелепипеда, т. е. его длина, ширина и высота.
На рисунке:
DB12=DA2+DC2+DD12
.
Обрати внимание!
У прямоугольного параллелепипеда все диагонали равны:
Пример:
формула диагоналей куба.
Так как у куба все измерения равны, обозначаем их за (a), тогда
Упрощаем и получаем формулу диагонали куба:
Укажите размеры:
Диагональ =
Решение:
Ссылка на страницу с результатом:
# Теория
Прямоугольник — это четырёхугольник у которого все углы прямые (по 90 градусов).
Диагональ прямоугольника — это прямая линия соединяющая противоположные углы. Диагонали прямоугольника обладают следующими свойствами:
- Диагонали прямоугольника равны.
- Диагональ делит прямоугольник на два равных прямоугольных треугольника и является их гипотенузой.
Формула диагонали прямоугольника
Так как диагональ делит прямоугольник на два одинаковых труегольника и является их гипотенузой, то длина и ширина прямоугольника будут катетами образованного треугольника. Поэтому для расчёта диагонали мы применяем теорему Пифагора:
Квадрат гипотенузы равен сумме квадратов катетов: c² = a² + b²
Отсюда, формула для расчётадиагонали прямоугольника выглядит следующим образом:
a
b
d
d = sqrt{a^2 + b^2}
- d — диагональ прямоугольника
- a — длина прямоугольника
- b — ширина прямоугольника
Похожие калькуляторы:
Войдите чтобы писать комментарии
Как найти диагональ прямоугольного параллелепипеда
Прямоугольный параллелепипед — это разновидность многогранника, состоящая из 6 граней, каждая из которых является прямоугольником. В свою очередь, диагональ — это отрезок, который соединяет противоположные вершины параллелограмма. Его длину можно найти двумя методами.
Вам понадобится
- Знание длины всех сторон параллелограмма.
Инструкция
Метод 1. Дан прямоугольный параллелепипед со сторонами a, b, c и диагональю d. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов трех его сторон. Отсюда следует, что сама длина диагонали может быть рассчитана с помощью извлечения квадрата из данной суммы (рис.1).
Метод 2. Допустим, что прямоугольный параллелепипед является кубом. Куб — это такой прямоугольный параллелепипед, у которого каждая грань представлена квадратом. Следовательно, все его стороны равны. Тогда формула для расчеты длины его диагонали будет выражена так:
d = a*√3
Источники:
- формула диагонали прямоугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.











































