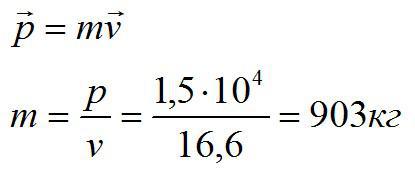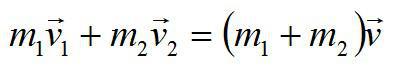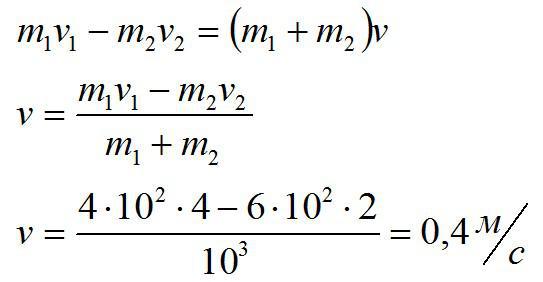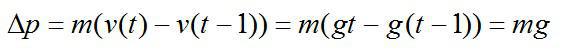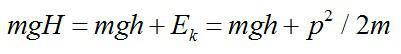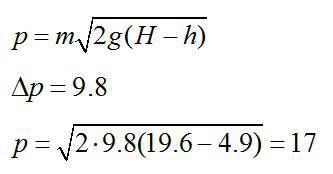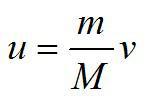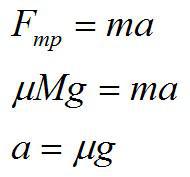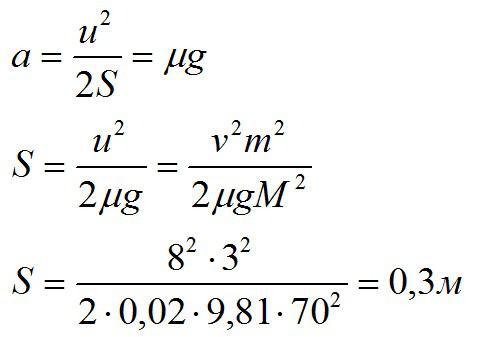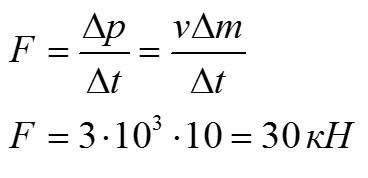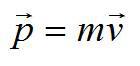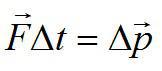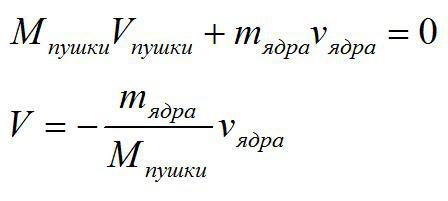Сегодня в рубрике «Физика для чайников» занимаемся решением и разбором задач на закон сохранения импульса. И не говорите, что вы этого не ждали.
Полезные лайфхаки и новости для студентов – ежедневно на нашем телеграм-канале. Подписывайтесь!
Задачи на закон сохранения импульса с решением
Задача №1 на нахождение импульса
Условие
Небольшой автомобиль движется со скоростью 60 км/ч, его импульс равен 1,5*10^4 кг*м/с. Какова масса автомобиля?
Решение
По формуле для импульса найдем:
Ответ: 903 кг.
Задача №2 на закон сохранения импульса
Условие
Дрезина массой 400 кг движется со скоростью 4 м/с, а навстречу ей со скоростью 2 м/с едет дрезина массой 60 кг. После неупругого соударения дрезины движутся вместе. В каком направлении и с какой скоростью будут двигаться дрезины?
Решение
Общий импульс системы до и после соударения должен остаться неизменным:
Запишем закон сохранения импульса в проекции на горизонтальную ось:
Движение будет происходить в сторону первой дрезины. Именно она изначальна имела больший импульс.
Ответ: 0,4 м/с.
Задача №3 на нахождение импульса
Условие
Тело массой m=1 кг упало с высоты H=19,6 м. Определить изменение импульса тела за последнюю секунду движения и импульс тела на высоте h=4,9 м.
Решение
Изменение импульса тела за последнюю секунду движения равно:
Импульс тела на заданной высоте найдем по закону сохранения энергии, который имеет вид для двух состояний:
Отсюда получим:
Ответ: Изменение импульса равно 9,8 кг*мс2; р=17 кг*мс2.
Задача №4 на применение закона сохранения импульса и второго закона Ньютона
Условие
Хоккеист массой М = 70 кг стоит на льду и бросает в горизонтальном направлении шайбу массой m = 3 кг со скоростью v = 8 м/с относительно льда. На какое расстояние S откатится при этом конькобежец, если коэффициент трения равен 0,02.
Решение
По закону сохранения импульса найдем скорость u, с которой хоккеист откатиться назад:
По второму закону Ньютона для хоккеиста:
С другой стороны:
Ответ: 0,3 м.
Задача №5 на реактивное движение
Условие
Реактивный двигатель каждую секунду выбрасывает 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты. Какую силу тяги он развивает?
Решение
Запишем второй закон Ньютона в импульсной форме и найдем силу, которая действует на выбрасываемые продукты сгорания топлива:
По третьему закону Ньютона сила тяги будет равна найденной силе.
Ответ: 30 кН.
Вопросы на закон сохранения импульса
Вопрос 1. Что такое замкнутая система?
Ответ. Замкнутая система – такая система, на которую не действуют внешние силы со стороны других тел.
Вопрос 2. Что такое импульс силы?
Ответ. Импульс силы – физическая величина, равная произведению силы на время ее действия.
Вопрос 3. Как направлен импульс тела?
Ответ. Направление импульса совпадает с направлением вектора скорости тела.
Вопрос 4. Что такое реактивное движение?
Ответ. Реактивное движение – движение, основанное на принципе отдачи. По аналогии с системой «пушка-ядро», систему «ракета-выхлопные газы» также можно считать замкнутой.
Вопрос 5. Два тела разной массы движутся с одинаковой скоростью. Импульс какого тела больше?
Ответ. Тело с большей массой обладает большим импульсом.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Импульс и закон сохранения импульса
Что такое импульс в механике
Импульс, или количество движения – векторная физическая величина, равная произведению массы тела на его скорость.
Обозначается латинской буквой p и измеряется в килограммах на метр в секунду.
Второй закон Ньютона с применением импульса можно записать следующим образом:
Здесь дельта p – изменение импульса тела за время дельта t под действием равнодействующей силы F.
Закон сохранения импульса
Этот фундаментальный закон природы и гласит:
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Закон сохранения импульса является следствием второго и третьего законов Ньютона.
Более подробную теорию по этой и другим темам вы найдете в нашем справочнике.
Пример действия закона сохранения импульса
Представим себе пушку, которая стреляет ядрами. Систему «пушка-ядро» можно считать замкнутой. При стрельбе из пушки действует закон сохранения импульса. Ядро летит в одну сторону, а пушка под действием отдачи откатывается назад. При этом скорость, приобретенная пушкой, зависит от соотношения масс орудие/ядро и скорости ядра.
Знак минус указывает на то, что пушка и ядро движутся в разные стороны.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.2k
Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса
Классическое определение импульса тела
Определение
Векторную величину ($overline{p}$), служащую мерой механического движения равную произведению массы ($m$) этой точки на скорость ($overline{v}$) ее перемещения:
[overline{p}=moverline{v}left(1right)]
называют импульсом материальной точки.
Вектор импульса имеет такое же направление как вектор скорости, так как масса является положительной величиной.
В Международной системе единиц (СИ) единицей измерения импульса считают килограмм — метр в секунду ($frac{кгcdot м}{с}$):
[left[pright]=left[mright]left[vright]=кгcdot frac{м}{с}.]
Определение
Импульсом тела называют импульс системы материальных точек, которые составляют данное тело:
[overline{p}=sumlimits^N_{i=1}{m_i{overline{v}}_ileft(2right),}]
где $m_i$ — масса элемента тела (материальной тоски системы); ${overline{v}}_i$ — скорость данного элемента тела; $N$ — число материальных точек. Суммирование импульсов точек проводят с учетом их направлений.
Импульс и уравнение движения
Если на тело действуют другие тела, то мерой этого воздействия можно считать величину $frac{doverline{p}}{dt}$. Эта производная зависит от положения материальной точки по отношению к окружающим телам, иногда даже от ее скорости: $frac{doverline{p}}{dt}(overline{r},overline{v}{rm )}$. Такой функцией является сила ($overline{F}$($overline{r},overline{v}$)). Второй закон Ньютона в данной трактовке записывают как:
[overline{F}=frac{doverline{p}}{dt}left(3right),]
где $overline{F}$ — можно считать векторной суммой всех внешних сил, которые действуют на тело.
Содержание второго закона Ньютона заключается в том, что сила зависит только от координат и скорости материальной точки. Уравнение (3) называют уравнением движения материальной точки. Конкретное содержание этот закон Ньютона получает, когда определена функция $overline{F}$($overline{r},overline{v}$). К установлению вида этой функции сводится основная задача механики для каждого конкретного случая.
Из формулы (3) получим, что:
[Delta overline{p}=intlimits^{t_2}_{t_1}{overline{F}dt}left(4right),]
$Delta overline{p}$ — изменение импульса тела.
Если сила, действующая на материальную точку постоянна, то второй закон Ньютона можно представить в форме:
[overline{F}Delta t=Delta overline{p}left(5right).]
Формула (5) означает, что изменение импульса материальной тела прямо пропорционально силе, которая на нее воздействует и сонаправлено с этой силой. Величину $overline{F}Delta t$ называют импульсом силы. Из уравнения (5) следует, что равные изменения импульса точки могут быть получены в результате действия большой по модулю силы за маленький промежуток времени или воздействуя на точку небольшой силой длительное время.
Закон сохранения импульса
Если на тело не действуют внешние силы ($overline{F}=0$) или их действие взаимно компенсируется, то из уравнения движения (3), мы видим, что:
[frac{doverline{p}}{dt}=0to overline{p}=constleft(6right).]
Для системы тел закон сохранения импульса тоже выполняется, только формулу (6) следует читать так: векторная сумма импульсов всех тел изолированной системы не изменяется при любых взаимодействиях, которые происходят внутри рассматриваемой системы. Это не значит, что какие — то тела системы не могут изменять свой импульс, но суммарный импульс системы остается неизменным.
Для материальной точки закон сохранения импульса закон сохранения импульса означает, что при отсутствии внешних сил, она перемещается прямолинейно и равномерно. Для системы материальных точек в нерелятивистском случае закон говорит о том, что центр масс системы движется равномерно и прямолинейно.
Закон сохранения импульса выполняется и в релятивистском случае и нерелятивистском. Но в релятивистском случае нельзя говорить о равномерном и прямолинейном движении центра масс, так как в этом случае центра масс не существует. Но существует система центра масс, в которой закон сохранения импульса сводится к равенству $overline{p}=0$, и это означает, что данная система при любых процессах внутри нее остается системой центра масс.
Примеры задач на импульс тела и закон сохранения импульса
Пример 1
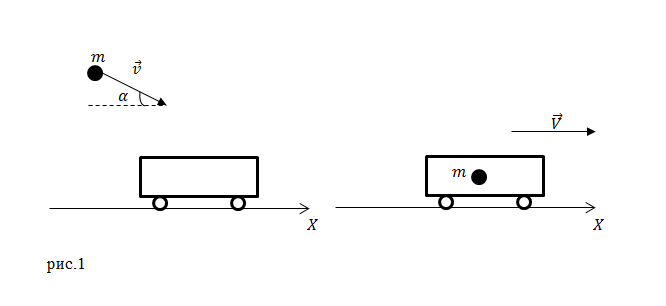
Задание. Контейнер с песком массой $M$ стоит на рельсах на горизонтальном участке дороги. В песок падает тело массой $m,$ и остается в нем. С какой скоростью станет двигаться контейнер, если в момент попадания скорость тела была равна $v$, ее направление было сверху вниз под углом $alpha $ к горизонту (рис.1)? Силу трения не учитывать.
Решение. Задачу будем решать на основе закона сохранения импульса, так как в отсутствии сил трения систему из двух тел (контейнер — тело) можно считать изолированной. Тогда закон сохранения импульса запишем в виде:
[sum{{overline{p}}_1=sum{{overline{p}}_2}left(1.1right),}]
где ${overline{p}}_1$ — импульс системы до попадания тела в песок контейнера. Этот импульс будет равен импульсу движущегося тела, так как скорость контейнера равна нулю:
[{overline{p}}_1=moverline{v }left(1.2right).]
Импульс системы после того, как тело застряло в песке, равен:
[{overline{p}}_2=left(m+Mright)overline{V}left(1.3right).]
Согласно закону сохранения импульса имеем:
[moverline{v }=left(m+Mright)overline{V}left(1.4right).]
Запишем проекцию уравнения (1.4) на ось X, имеем:
[mv{cos alpha =left(m+Mright)Vleft(1.5right). }]
Из уравнения (1.5) выразим искомую скорость:
[V=frac{mv {rm cos}alpha }{m+M}.]
Ответ. $V=frac{mv {rm cos}alpha }{m+M}$
Пример 2
Задание. Каково приращение импульса тела ($Delta overline{p}$) за время полета $tau $, которое бросили под углом к горизонту с начальной скоростью ${overline{v}}_0$? Сопротивление воздуха не учитывать.
Решение. Изменение импульса будем искать, используя формулу:
[Delta overline{p}=intlimits^{tau }_0{overline{F}dt}left(2.1right),]
где $tau $ — время полета тела. Тело при заданных условиях движется в поле тяжести Земли:
[overline{F}=moverline{g }left(2.2right).]
Из (2.2) очевидно, что сила не изменяется при движении тела. Подставим (2.2) в интеграл, получим:
[Delta overline{p}=intlimits^{tau }_0{moverline{g }dt}=moverline{g }tau .]
Ответ. $Delta overline{p}=moverline{g }tau $
Читать дальше: колебательное движение.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Реактивное
движение.
-
Импульс тела.
-
Импульс силы.
-
Связь между
приращением импульса материальной
точки и импульсом силы (закон изменения
импульса). -
Механическая
система. -
Внутренние силы.
-
Внешние силы.
-
Импульс механической
системы. -
Замкнутая
механическая система. -
Закон сохранения
импульса. -
Реактивное
движение.
11. К.Э.Циолковский
основатель.
1.Импульс
тела ( количество движения) – векторная
физическая величина равная произведению
массы тела на его скорость:
.
Импульс измеряется
в
.
2. Импульс
силы – векторная
физическая величина равная произведению
силы на время её действия:
.
3. Связь
между приращением импульса материальной
точки и импульсом силы ( Закон
изменения импульса).
Пусть
на материальную точку массы m
в течение
интервала времени
действует постоянная сила
,
сообщая ей ускорение:
Умножая обе части
этого равенства на m,
получим
Здесь
,
— импульс точки в начальный момент
времени
,
импульс
точки в момент времени t
.
Таким
образом, получаем, что изменение импульса
точки в единицу времени равно силе,
вызывающей
это изменение
.
Из этого равенства
получим
т.е. изменение
импульса точки равно импульсу силы,
действующей на точку (обобщенное
выражение
второго закона Ньютона.
Последние два
равенства представляют собой два
выражения закона изменения импульса.
4.Механическая
система –
совокупность взаимодействующих
материальных точек (тел). Примером
механической системы является Солнечная
система.
5. Внутренние
силы – силы,
с которыми материальные точки системы
взаимодействуют между собой.
6. Внешние
силы – силы,
с которыми материальные точки системы
взаимодействуют с посторонними телами,
не входящими в данную систему.
7. Импульс
механической системы
– геометрическая сумма импульсов тел,
входящих в данную систему:
.
По третьему закону
Ньютона все внутренние силы механической
системы попарно равны по модулю и
противонаправлены. Поэтому равнодействующая
всех внутренних сил равна нулю. Это
значит, что внутренние силы не могут
изменить положение центра масс системы,
скорость, а следовательно и импульс
механической системы.
8. Замкнутая
система – механическая
система, на которую не действуют внешние
силы. Механическая система может
считаться замкнутой и в том случае,
когда равнодействующая всех внешних
сил равна нулю,
Система может быть
замкнутой вдоль какой-либо оси, если
сумма проекций всех внешних сил на эту
ось равна нулю.
9. Закон
сохранения импульса.
Геометрическая сумма импульсов тел
замкнутой системы остаётся постоянной
при любых взаимодействиях тел системы
между собой:
.
Покажем выполнение
закона сохранения импульса на примере
упругого столкновения двух шаров, массы
которых
и
.
Эти шары представляют пример замкнутой
системы, т.к. отсутствуют вешние силы.
Пусть
и
— импульсы шаров до удара,
и
—
импульсы шаров после удара.
Введём обозначения:
—
продолжительность удара,
— сила, с которой первый шар действует
на второй,
—
сила, с которой второй шар действует на
первый.
По третьему закону
Ньютона, силы с которыми действуют шары
друг на друга равны по модулю и
противонаправлены:
.
Умножая обе части
этого равенства на
получим
,
т.е. импульсы сил,
с которыми шары действуют друг на друга
равны по модулю и противонаправлены.
Это в свою очередь означает, что равны
по модулю и противоположно направлены
изменения импульсов шаров
.
Отсюда получаем
,
Или
.
Итак, векторная
сумма импульсов двух шаров до столкновения
равна векторной сумме этих шаров после
столкновения.
Если же удар
неупругий, то после столкновения тела
продолжают движение как одно целое со
скоростью
.
Поэтому согласно закону сохранения
импульса запишем
.
При решении задач
на закон сохранения импульса удобно
пользоваться правилом сложения векторов
(правилом параллелограмма). Покажем
это на примерах.
П
усть
тело массы
,
двигаясь со скоростью
,
сталкивается с покоящимся телом массы
.
Удар предполагаем упругий и не прямой,
т.е. после удара тела разлетаются под
некоторым углом, имея импульсы
и
.
По закону сохранения импульса векторная
сумма импульсов тел после удара равна
векторной сумме импульсов до удара.
Учитывая, что до столкновения второе
тело находилось в состоянии покоя, и
его импульс был равен нулю, запишем
.
Это значит, что
импульс
равен диагонали параллелограмма,
построенного на векторах
и
(Рис.48).
Здесь
импульсы тел до столкновения (до
взаимодействия) ,
и
— импульсы тел до взаимодействия.
П
усть
тело массы m,
двигаясь со скоростью
в некоторый момент времени распадается
на два осколка с массами
,
которые разлетаются под некоторым
углом, имея импульсы
и
.
По закону сохранения импульса векторная
сумма импульсов осколков равна импульсу
тела до распада, т. е.
Здесь
импульс
тела до распада равный диагонали
параллелограмма, построенного на
векторах
(Рис.49).
10. Реактивное
движение –
движение
механической системы,
возникающее при отбрасывании
внутренними
силами какой-либо её части с некоторой
скоростью.
В качестве примера
реактивного движения рассмотрим
выстрел из пушки. Пусть ствол пушки
установлен горизонтально. Пушка и снаряд
– замкнутая система. До выстрела пушка
и снаряд находились в состоянии покоя,
и их суммарный импульс был равен нулю.
Положим
и
,
и
— массы и скорости снаряда и пушки
соответственно (Рис.50).
Согласно закону
сохранения импульса суммарный импульс
пушки и снаряда после выстрела останется
равным нулю
.
Отсюда получим
скорость пушки после выстрела
.
Следовательно при
выстреле пушка получает скорость в
противоположном направлении, т.е.
возникает отдача
Примером реактивного
движения является движение ракеты. В
простейшем случае ракета – есть цилиндр,
закрытый с одной стороны и заполненный
порохом (Рис.51). До воспламенения пороха
суммарный импульс пороха и ракеты равен
нулю. Когда порох горит, продукты сгорания
выбрасываются из сопла ракеты с большой
скоростью
,
а ракета приобретает скорость в
противоположном направлении. Пусть
и
— массы пороха и ракеты,
—
скорость, которую приобретает ракета
после полного выгорания пороха. По
закону сохранения импульса запишем
.
Отсюда получим
модуль скорости ракеты после выгорания
пороха
.
1
1.
К.Э.Циолковский
основатель современной космонавтики
теоретически
доказал возможность запуска искусственного
спутника Земли и межпланетных полетов.
К.Э.Циолковский
является автором проекта реактивного
двигателя на жидком топливе (жидкостного
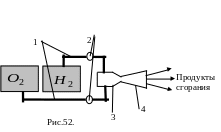
реактивного двигателя – ЖРД) (Рис.52).
Топливо – жидкий
водород
,
окислитель – жидкий кислород
по трубам – 1, с помощью турбин – 2
поступает в камеру сгорания – 3 , где
происходит сгорание водорода и продукты
сгорания с большой скоростью выбрасываются
из сопла – 4 , создавая реактивную силу
тяги.
Этот двигатель
удобен тем, что его можно в случае
необходимости включить или выключить,
меняя обороты турбин , регулировать
силу тяги. Реактивный двигатель на
твёрдом топливе (РДТТ) работает до
полного выгорания твёрдого топлива.
Для увеличения скорости и дальности
полета К.Э.Циолковский предложил идею
многоступенчатых ракет.
К.Э.Циолковский
получил уравнение движения тела
переменной массы, которое стало
теоретической основой движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Импульс. Закон сохранения импульса
Необходимо запомнить
ВАЖНО!
Импульс тела (материальной точки) – это векторная величина, равная произведению массы тела на скорость тела: $overrightarrow{p} = m overrightarrow{nu}$.
Направление импульса тела всегда совпадает с направлением скорости, т.к. $m > 0$: $overrightarrow{p} uparrow uparrow overrightarrow{nu}$.
Единица измерения импульса : $[p] = frac{кг cdot м}{с}$.
Импульс силы − произведение силы на время её действия: $overrightarrow{F} Delta t$.
Направления $Delta overrightarrow{p}$ и $overrightarrow{F}$ совпадают, т.к. $Delta t > 0$.
2-й закон Ньютона в импульсной форме: изменение импульса тела (материальной точки) равно импульсу силы, действующей на него: $Delta overrightarrow{p} = overrightarrow{F} Delta t$.
Импульс тела равен сумме импульсов отдельных элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы:
$overrightarrow{p} = overrightarrow{p_1} + overrightarrow{p_2} + …$.
Силы, с которыми взаимодействуют между собой тела системы, называют внутренними, а силы, создаваемые телами, не принадлежащими к данной системе, – внешними.
Систему, на которую не действуют внешние силы, или векторная сумма внешних сил равна нулю, называют замкнутой.
Абсолютно неупругий удар – столкновение тел, в результате которого они соединяются вместе и движутся дальше как одно целое.
Абсолютно упругий удар – столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса:
Векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется при любых взаимодействиях между телами системы: $sum overrightarrow{p} = const$.