Количество теплоты
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: количество теплоты, удельная теплоёмкость вещества, уравнение теплового баланса.
Как мы знаем, одним из способов изменения внутренней энергии является теплопередача (теплообмен). Предположим, что тело участвует в теплообмене с другими телами, и при этом не совершается механическая работа — ни самим телом, ни другими телами над этим телом.
Если в процессе теплообмена внутренняя энергия тела изменилась на величину , то говорят, что тело получило соответствующее количество теплоты:
.
Если при этом величина отрицательна, т.е. тело отдавало энергию, то говорят также, что тело отдавало тепло. Например, вместо формально верной, но несколько нелепой фразы «тело получило —5 Дж тепла» мы скажем: «тело отдало 5 Дж тепла».
Удельная теплоёмкость вещества
Предположим, что в процессе теплообмена агрегатное состояние вещества тела не изменяется (не происходит плавление, кристаллизация, парообразование или конденсация). Начальную температуру тела обозначим , конечную температуру —
.
Опыт показывает, что количество теплоты, полученное телом, прямо пропорционально массе тела и разности конечной и начальной температур:
Коэффициент пропорциональности c называется удельной теплоёмкостью вещества тела. Удельная теплоёмкость не зависит от формы и размеров тела. Удельные теплоёмкости различных веществ можно найти в таблицах.
Введя обозначение , получим также:
Чтобы понять физический смысл удельной теплоёмкости, выразим её из последней формулы:
Мы видим, что удельная теплоёмкость численно равна количеству теплоты, которое необходимо для нагревания 1кг данного вещества на (или, что то же самое, на
). Измеряется удельная теплоёмкость в Дж/(кг·
C) или в Дж/(кг·K).
Чем больше удельная теплоёмкость вещества, тем большее количество теплоты требуется для нагревания тела данной массы на заданное количество градусов.
В задачах часто фигурируют вода и лёд. Их удельные теплоёмкости желательно помнить.
Вода: Дж/(кг·
C).
Лёд: Дж/(кг·
C).
Произведение удельной теплоёмкости вещества на массу тела называется теплоёмкостью тела и обозначается :
Соответственно, для количества теплоты имеем:
Уравнение теплового баланса
Рассмотрим два тела (обозначим их 1 и 2), которые образуют замкнутую систему. Это означает, что данные тела могут обмениваться энергией только друг с другом, но не с другими телами. Считаем также, что механическая работа не совершается — внутренняя энергия тел меняется только в процессе теплообмена.
Имеется фундаментальный закон природы, подтверждаемый всевозможными экспериментами — закон сохранения энергии. Он гласит, что полная энергия замкнутой системы тел не меняется со временем.
В данном случае закон сохранения энергии утверждает, что внутренняя энергия нашей системы будет оставаться одной и той же: . Если изменение внутренней энергии первого тела равно
, а изменение внутренней энергии второго тела равно
, то суммарное изменение внутренней энергии будет равно нулю:
Но — количество теплоты, полученное первым телом в процессе теплообмена; аналогично
— количество теплоты, полученное вторым телом в процессе теплообмена. Стало быть,
(1)
Попросту говоря, сколько джоулей тепла отдало одно тело, ровно столько же джоулей получило второе тело. Так как система замкнута, ни один джоуль наружу не вышел. Соотношение (1) называется уравнением теплового баланса. В общем случае, когда тел образуют замкнутую систему и обмениваются энергией только с помощью теплопередачи, из закона сохранения энергии с помощью тех же рассуждений получаем общее уравнение теплового баланса:
(2)
В качестве простого примера применения уравнения теплового баланса рассмотрим следующую задачу.
Смешали г воды при температуре
и
г воды при температуре
. Найти установившуюся температуру смеси.
Обозначим искомую установившуюся температуру через . Запишем уравнение теплового баланса (1):
где — удельная теплоёмкость воды. Раскрываем скобки и находим:
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Количество теплоты» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Удельная теплоёмкость — это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.
Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.
Содержание:
- Формула
- Инструкция по расчёту параметра
- Расчёт
- Как рассчитать теплоемкость продуктов питания
- Полезные советы
- Видео
Формула
Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.
Формула для расчёта удельной теплоёмкости имеет следующий вид:
- с = Q/(m*∆T)
Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:
ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.
ΔT можно рассчитать по формуле:
ΔT = t2–t1, где
- t1 – первичная температура;
- t2 – конечная температура после изменения.
m – масса вещества используемого при нагреве (гр).
Q – количество теплоты (Дж/J)
На основании Цр можно вывести и другие уравнения:
- Q = m*цp*ΔT – количество теплоты ;
- m = Q/цр*(t2 — t1) – массы вещества;
- t1 = t2–(Q/цp*m) – первичной температуры;
- t2 = t1+(Q/цp*m) – конечной температуры.
Инструкция по расчёту параметра
Рассчитать с вещества достаточно просто и чтобы это сделать нужно, выполнить следующие шаги:
- Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
- Выписать исходные данные.
- Подставить их в формулу.
- Провести расчёт и получим результат.
В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.
Согласно инструкции приведённой выше производим следующие действия:
Выписываем исходные данные:
- Q = 35 тыс. Дж;
- m = 480 г;
- ΔT = t2–t1 =250–15 = 235 ºC.
Берём формулу, подставляем значения и решаем:
с=Q/(m*∆T)=35тыс.Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.
Расчёт
Выполним расчёт CP воды и олова при следующих условиях:
- m = 500 грамм;
- t1 =24ºC и t2 = 80ºC – для воды;
- t1 =20ºC и t2 =180ºC – для олова;
- Q = 28 тыс. Дж.
Для начала определяем ΔT для воды и олова соответственно:
- ΔТв = t2–t1 = 80–24 = 56ºC
- ΔТо = t2–t1 = 180–20 =160ºC
Затем находим удельную теплоёмкость:
- с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
- с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.
Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.
Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.
Как рассчитать теплоемкость продуктов питания
При расчёте емкости питания уравнение примет следующий вид:
с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908 *a), где:
- w – количество воды в продукте;
- p – количество белков в продукте;
- f – процентное содержание жиров;
- c – процентное содержание углеводов;
- a – процентное содержание неорганических компонентов.
Определим теплоемкость плавленого сливочного сыра Viola. Для этого выписываем нужные значения из состава продукта (масса 140 грамм):
- вода – 35 г;
- белки – 12,9 г;
- жиры – 25,8 г;
- углеводы – 6,96 г;
- неорганические компоненты – 21 г.
Затем находим с:
- с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.
Полезные советы
Всегда помните, что:
- процесс нагревания металла проходит быстрее, чем у воды, так как он обладает CP в 2,5 раза меньше;
- по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
- в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
- при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.
Видео
Разобраться в этой теме вам поможет видео урок.
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем,
что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом
случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система
микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии,
которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой).
Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание,
что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом.
Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$delta Q=c m d T=nu c_{mu} d T(2)$$
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{mu}=c cdot mu$ — молярная теплоемкость,
$mu$ – молярная масса вещества,
$nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты
($Delta Q$), которое получает тело при увеличении его температуры на величину
$Delta t = t_2 — t_1$ можно вычислить как:
$$Delta Q=c m Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности
($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты,
которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты
($delta Q$) равное:
$$delta Q=lambda d m$$
где $lambda$ – удельная теплота плавления, dm – элемент массы тела.
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура
одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 —
количество теплоты части воды температурой t1 и массой m1;
Q2=cm2t2— количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$
begin{array}{l}
mathrm{cmt}=mathrm{cm}_{1} t_{1}+mathrm{~cm}_{2} t_{2} rightarrow mathrm{mt}=mathrm{m}_{1} t_{1}+mathrm{~m}_{2} t_{2} rightarrow \
rightarrow rho mathrm{Vt}=rho V_{1} t_{1}+rho mathrm{V}_{2} t_{2} rightarrow mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2)
end{array}
$$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1.3)
$$$
Так, мы получаем систему уравнений:
$$
left{begin{array}{c}
V t=V_{1} t_{1}+V_{2} t_{2} \
V=V_{1}+V_{2}
end{array}right.
$$
Решив ее получим:
$$
begin{array}{l}
V_{1}=frac{left(t_{2}-tright)}{t_{2}-t_{1}} V \
V_{2}=frac{left(t-t_{1}right)}{t_{2}-t_{1}} V
end{array}
$$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$
begin{array}{l}
V_{1}=frac{(60-40)}{60-10} 200=80 text { (л) } \
V_{2}=frac{(40-10)}{60-10} 200=120 text { (л) }
end{array}
$$
Ответ. V1=80 л, V2=120 л.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
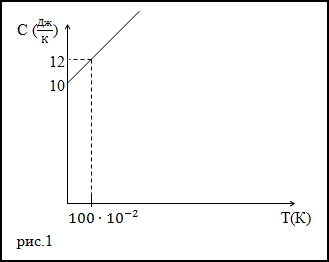
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в
рассматриваемом интервале $T_{1} leq T leq T_{2}$ .
Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:
$C(T)=10+2 cdot 10^{-2} T$ (Дж/К)
Основой для решения задачи послужит формула для количества теплоты в виде:
$$delta Q=C d T(2.2)$$
Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:
$$
begin{array}{c}
Delta Q=int_{300}^{400}left(10+2 cdot 10^{-2} Tright) d T=left.left(10 cdot T+10^{-2} T^{2}right)right|_{300} ^{400}= \
=left(10 cdot 400+10^{-2} cdot(400)^{2}right)-left(10 cdot 300+10^{-2} cdot(300)^{2}right)=1700left(mathrm{~A}^{*}right)
end{array}
$$
Ответ. $Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.
Теплоёмкость
Теплоёмкость — количество теплоты, поглощаемой (выделяемой) телом в процессе нагревания (остывания) на 1 кельвин.
Более точно, теплоёмкость — физическая величина, определяемая как отношение количества теплоты δ Q {displaystyle delta Q} , поглощаемой/выделяемой термодинамической системой при бесконечно малом изменении её температуры T {displaystyle T} , к величине этого изменения d T {displaystyle mathrm {d} T} [1][2][3][4][5]:
C = δ Q d T . {displaystyle C={delta Q over mathrm {d} T}.}
Малое количество теплоты обозначнётся δ Q {displaystyle delta Q} (а не d Q {displaystyle mathrm {d} Q} ), чтобы подчеркнуть, что это не дифференциал параметра состояния (в отличие, например, от d T {displaystyle mathrm {d} T} ) а функция процесса.
Поэтому и теплоёмкость — это характеристика процесса перехода между двумя состояниями термодинамической системы[6], которая зависит и от пути процесса (например, от проведения его при постоянном объёме или постоянном давлении)[7][8], и от способа нагревания/охлаждения (квазистатического или нестатического)[7][9].
Неоднозначность в определении теплоёмкости[10] на практике устранят тем, что выбирают и фиксируют путь квазистатического процесса (обычно оговаривается, что процесс происходит при постоянном давлении, равным атмосферному).
При однозначном выборе процесса теплоёмкость становится параметром состояния[11][12] и теплофизическим свойством вещества, образующего термодинамическую систему[13].
Удельная, молярная и объёмная теплоёмкости[ | ]
Основные статьи: Удельная теплоёмкость, Молярная теплоёмкость, Объёмная теплоёмкость
Очевидно, что чем больше масса тела, тем больше требуется теплоты для его нагревания, и теплоёмкость тела пропорциональна количеству вещества, содержащегося в нём. Количество вещества может характеризоваться массой или количеством молей. Поэтому удобно пользоваться понятиями удельной теплоёмкости (теплоёмкости единицы массы тела):
c = C m {displaystyle c={C over m}}
и молярной теплоёмкости (теплоёмкости одного моля вещества):
C μ = C ν , {displaystyle C_{mu }={C over u },}
где ν = m μ {displaystyle u ={m over mu }} — количество вещества в теле; m {displaystyle m} — масса тела; μ {displaystyle mu } — молярная масса. Молярная и удельная теплоёмкости связаны соотношением C μ = c μ {displaystyle C_{mu }=cmu } [14][15].
Объёмная теплоёмкость (теплоёмкость единицы объёма тела):
C ′ = C V . {displaystyle C’={C over V}.}
Теплоёмкость для различных процессов и состояний вещества[ | ]
Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).
Теплоёмкость идеального газа[ | ]
Основная статья: Теплоёмкость идеального газа
Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.
Молярная теплоёмкость при постоянном объёме:
C V = d U d T = i 2 R , {displaystyle C_{V}={dU over dT}={frac {i}{2}}R,}
где R {displaystyle R} ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная, i {displaystyle i} — число степеней свободы молекулы[14][15].
Молярная теплоёмкость при постоянном давлении связана с C V {displaystyle C_{V}} соотношением Майера:
C P = C V + R = i + 2 2 R . {displaystyle C_{P}=C_{V}+R={{i+2} over 2}R.}
Теплоёмкость кристаллов[ | ]
Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела
Существует несколько теорий теплоёмкости твердого тела:
Примечания[ | ]
- ↑ Теплоёмкость. БРЭ, 2016.
- ↑ Булидорова Г. В. и др., Физическая химия, кн. 1, 2016, с. 41.
- ↑ Артемов А. В., Физическая химия, 2013, с. 14.
- ↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 20.
- ↑ Сивухин Д. В.
, Термодинамика и молекулярная физика, 2006, с. 65.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2006, с. 66.
- ↑ 12Лифшиц Е. М., Теплоёмкость, 1992.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 94.
- ↑ Лифшиц Е. М.
, Теплоёмкость, 1976.
- ↑ Базаров И. П., Термодинамика, 2010, с. 39.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 115.
- ↑ Кубо Р., Термодинамика, 1970, с. 22.
- ↑ Беляев Н. М., Термодинамика, 1987, с. 5.
- ↑ 12Никеров. В. А. Физика: учебник и практикум для академического бакалавриата. — Юрайт, 2015. — С. 127—129. — 415 с. — ISBN 978-5-9916-4820-2.
- ↑ 12Ильин В. А. Физика: учебник и практикум для прикладного бакалавриата.
— Юрайт, 2016. — С. 142—143. — 399 с. — ISBN 978-5-9916-6343-4.
Литература[ | ]
- Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
- Булидорова Г. В., Галяметдинов Ю. Г., Ярошевская Х. М., Барабанов В. П. Физическая химия. Книга 1. Основы химической термодинамики. Фазовые равновесия. — М.: КДУ; Университетская книга, 2016. — 516 с. — ISBN 978-5-91304-600-0.
- Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Лифшиц Е. М. Теплоёмкость // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 77–78.
- Лифшиц Е. М. Теплоёмкость // Большая советская энциклопедия / Ред. А. М. Прохоров. — 3-е издание. — М.: Большая Советская Энциклопедия, 1976. — Т. 25. — С. 451.
- Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2006. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
- Теплоемкость // Большая российская энциклопедия. — М.: Большая российская энциклопедия, 2016. — Т. 32. — С. 54.
Удельная теплоёмкость
удельная теплоёмкость, удельная теплоёмкость 8 класс
Уде́льная теплоёмкость — отношение теплоёмкости к массе, теплоёмкость единичной массы вещества (разная для различных веществ); физическая величина, численно равная количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу.
В Международной системе единиц (СИ) удельная теплоёмкость измеряется в джоулях на килограмм на кельвин, Дж/(кг·К). Иногда используются и внесистемные единицы: калория/(кг·К) и т.д.
Удельная теплоёмкость обычно обозначается буквами c или С, часто с индексами.
На значение удельной теплоёмкости влияет температура вещества и другие термодинамические параметры. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C.
Кроме того, удельная теплоёмкость зависит от того, каким образом позволено изменяться термодинамическим параметрам вещества (давлению, объёму и т. д.
); например, удельная теплоёмкость при постоянном давлении (CP) и при постоянном объёме (CV), вообще говоря, различны.
Формула расчёта удельной теплоёмкости: где c — удельная теплоёмкость, Q — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), m — масса нагреваемого (охлаждающегося) вещества, ΔT — разность конечной и начальной температур вещества. Удельная теплоёмкость может зависеть (и в принципе, строго говоря, всегда — более или менее сильно — зависит) от температуры, поэтому более корректной является следующая формула с малыми (формально бесконечно малыми) и :
- 1 Значения удельной теплоёмкости некоторых веществ
- 2 См. также
- 3 Примечания
- 4 Литература
- 5 Ссылки
Значения удельной теплоёмкости некоторых веществ
Таблица I: Стандартные значения удельной теплоёмкости
| воздух (сухой) | газ | 1,005 |
| воздух (100 % влажность) | газ | 1,0301 |
| алюминий | твёрдое тело | 0,903 |
| бериллий | твёрдое тело | 1,8245 |
| латунь | твёрдое тело | 0,377 |
| олово | твёрдое тело | 0,218 |
| медь | твёрдое тело | 0,385 |
| молибден | твёрдое тело | 0,250 |
| сталь | твёрдое тело | 0,462 |
| алмаз | твёрдое тело | 0,502 |
| этанол | жидкость | 2,460 |
| золото | твёрдое тело | 0,129 |
| графит | твёрдое тело | 0,720 |
| гелий | газ | 5,190 |
| водород | газ | 14,300 |
| железо | твёрдое тело | 0,444 |
| свинец | твёрдое тело | 0,130 |
| чугун | твёрдое тело | 0,540 |
| вольфрам | твёрдое тело | 0,134 |
| литий | твёрдое тело | 3,582 |
| ртуть | жидкость | 0,139 |
| азот | газ | 1,042 |
| нефтяные масла | жидкость | 1,67 — 2,01 |
| кислород | газ | 0,920 |
| кварцевое стекло | твёрдое тело | 0,703 |
| вода 373 К (100 °C) | газ | 2,020 |
| вода | жидкость | 4,187 |
| лёд | твёрдое тело | 2,060 |
| сусло пивное | жидкость | 3,927 |
ВеществоАгрегатное состояниеУдельнаятеплоёмкость,кДж/(кг·K)Значения приведены для стандартных условий, если это не оговорено особо.
Таблица II: Значения удельной теплоёмкости для некоторых строительных материалов
| асфальт | 0,92 |
| полнотелый кирпич | 0,84 |
| силикатный кирпич | 1,00 |
| бетон | 0,88 |
| кронглас (стекло) | 0,67 |
| флинт (стекло) | 0,503 |
| оконное стекло | 0,84 |
| гранит | 0,790 |
| талькохлорит | 0,98 |
| гипс | 1,09 |
| мрамор, слюда | 0,880 |
| песок | 0,835 |
| сталь | 0,47 |
| почва | 0,80 |
| древесина | 1,7 |
ВеществоУдельнаятеплоёмкостькДж/(кг·K)
См. также
- Теплоёмкость
- Объёмная теплоёмкость
- Молярная теплоёмкость
- Скрытая теплота
- Теплоёмкость идеального газа
- Удельная теплота парообразования и конденсации
- Удельная теплота плавления
Примечания
- ↑ Для неоднородного (по химическому составу) образца удельная теплоемкость является дифференциальной характеристикой , меняющейся от точки к точке.
Зависит она в принципе и от температуры (хотя во многих случаях изменяется достаточно слабо при достаточно больших изменениях температуры), при этом строго говоря определяется — вслед за теплоёмкостью — как дифференциальная величина и по температурной оси, т.е.
строго говоря следует рассматривать изменение температуры в определении удельной теплоёмкости не на один градус (тем более не на какую-то более крупную единицу температуры), а на малое с соответствующим количеством переданной теплоты . (См. далее основной текст).
- ↑ Кельвины (К) здесь можно заменять на градусы Цельсия (°C), поскольку эти температурные шкалы (абсолютная и шкала Цельсия) отличаются друг от друга лишь начальной точкой, но не величиной единицы измерения.
Ссылки
- Таблицы физических величин. Справочник, под ред. И. К. Кикоина, М., 1976.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика.
- E. М. Лифшиц Теплоёмкость // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: «Советская энциклопедия», 1998. — Т. 2.
Теплоемкость материалов — таблица
В строительстве очень важной характеристикой является теплоемкость строительных материалов.
От нее зависят теплоизоляционные характеристики стен постройки, а соответственно, и возможность комфортного пребывания внутри здания.
Прежде, чем приступить к ознакомлению с теплоизоляционными характеристиками отдельных строительных материалов, необходимо понять, что собой представляет теплоемкость и как она определяется.
Удельная теплоемкость материалов
Теплоемкость – это физическая величина, описывающая способность того или иного материала накапливать в себе температуру от нагретой окружающей среды.
Количественно удельная теплоемкость равна количеству энергии, измеряемой в Дж, необходимой для того, чтобы нагреть тело массой 1 кг на 1 градус.
Ниже представлена таблица удельной теплоемкости наиболее распространенных в строительстве материалов.
Для того, чтобы рассчитать теплоемкость того или иного материала, необходимо обладать такими данными, как:
- вид и объем нагреваемого материала (V);
- показатель удельной теплоемкости этого материала (Суд);
- удельный вес (mуд);
- начальную и конечную температуры материала.
Теплоемкость строительных материалов
Теплоемкость материалов, таблица по которой приведена выше, зависит от плотности и коэффициента теплопроводности материала.
А коэффициент теплопроводности, в свою очередь, зависит от крупности и замкнутости пор. Мелкопористый материал, имеющий замкнутую систему пор, обладает большей теплоизоляцией и, соответственно, меньшей теплопроводностью, нежели крупнопористый.
Это очень легко проследить на примере наиболее распространенных в строительстве материалов. На рисунке, представленном ниже, показано каким образом влияет коэффициент теплопроводности и толщина материала на теплозащитные качества наружных ограждений.
Из рисунка видно, что строительные материалы с меньшей плотностью обладают меньшим коэффициентом теплопроводности.
Однако так бывает не всегда. Например, существуют волокнистые виды теплоизоляции, для которых действует противоположная закономерность: чем меньше плотность материала, тем выше будет коэффициент теплопроводности.
Поэтому нельзя доверять исключительно показателю относительной плотности материала, а стоит учитывать и другие его характеристики.
Сравнительная характеристика теплоемкости основных строительных материалов
Для того, чтобы сравнить теплоемкость наиболее популярных строительных материалов, таких дерево, кирпич и бетон, необходимо рассчитать величину теплоемкости для каждого из них.
В первую очередь нужно определиться с удельной массой дерева, кирпича и бетона. Известно, что 1 м3 дерева весит 500 кг, кирпича – 1700 кг, а бетона – 2300 кг. Если мы берем стенку, толщина которой составляет 35 см, то путем нехитрых расчетов получим, что удельная масса 1 кв.
м дерева составит 175 кг, кирпича – 595 кг, а бетона – 805 кг.
Далее выберем значение температуры, при которой будет происходить накопление тепловой энергии в стенах. Например, это будет происходить в жаркий летний день с температурой воздуха 270С.
Для выбранных условий рассчитываем теплоемкость выбранных материалов:
- Стена из дерева: С=СудхmудхΔТ; Сдер=2,3х175х27=10867,5 (кДж);
- Стена из бетона: С=СудхmудхΔТ; Сбет=0,84х805х27= 18257,4 (кДж);
- Стена из кирпича: С=СудхmудхΔТ; Скирп=0,88х595х27= 14137,2 (кДж).
Из произведенных расчетов видно, что при одинаковой толщине стены наибольшим показателем теплоемкости обладает бетон, а наименьшим – дерево. О чем это говорит? Это говорит о том, что в жаркий летний день максимальное количество тепла будет накапливаться в доме, выполненном из бетона, а наименьшее – из дерева.
Этим объясняет тот факт, что в деревянном доме в жаркую погоду прохладно, а в холодную погоду тепло. Кирпич и бетон легко накапливают в себе достаточно большое количество тепла из окружающей среды, но так же легко и расстаются с ним.
Теплоемкость и теплопроводность материалов
Теплопроводность – это физическая величина материалов, описывающая способность проникновения температуры с одной поверхности стены на другую.
Для создания комфортных условий в помещении необходимо, чтобы стены обладали высоким показателем теплоемкости и низким коэффициентом теплопроводности. В этом случае стены дома будут в состоянии накапливать тепловую энергию окружающей среды, но при этом препятствовать проникновению теплового излучения внутрь помещения.
Теплопроводность и теплоемкость материалов
статьи
- 1 Теплопроводность
- 2 Теплоемкость
- 3 Тепловое расширение
Теплопроводность – способность материала проводить тепловой поток через свою толщину при наличии разности температур на поверхностях, ограничивающих материал. Показателем теплопроводности является коэффициент теплопроводности λ. Иногда теплопроводность выражают величиной, обратной λ,— термическим сопротивлением (R = 1 / λ).
Коэффициент теплопроводности зависит от природы материала, его строения, пористости и влажности. Материал кристаллического строения обычно более теплопроводен по сравнению с материалом аморфного строения.
Коэффициент теплопроводности слоистых (слоистые пластики) и волокнистых (древесина) материалов существенно зависит от направления теплового потока по отношению к слоям или волокнам.
Так, у древесины вдоль волокон он примерно вдвое больше, чем поперек.
Величина λ тем больше, чем крупнее поры в материалах. Коэффициент снижается с уменьшением средней плотности однородных материалов, причем наименьшую теплопроводность имеют материалы с развитой пористостью и небольшой влажностью.
При увлажнений материала теплопроводность его увеличивается, так как коэффициент теплопроводности воды примерно в 25 раз больше, чем воздуха.
Ниже приводятся коэффициенты теплопроводности различных материалов, Вт / (м · °С); для сравнения даются значения λ воды и воздуха:
медь……………………. 403,00
сталь……………………. 58,00
гранит……………………. 2,92
бетон тяжелый…………. 1,28—1,55
кирпич глиняный………. 0,70—0,85
туф……………………….. 0,35—0,45
сосна:
вдоль волокон 0,30
поперек волокон 0,17
минеральная вата 0,06—0,09
бетон теплоизоляционный . .0,03—0,08
вода… … 0,599
воздух 0,023
Теплопроводность имеет практическое значение при выборе материалов для наружных стен, перекрытий и покрытий зданий, изоляции теплосетей, холодильников, котлов и т. п.
Теплоемкость
Теплоемкость – свойство материала поглощать тепло при нагревании и отдавать при охлаждении. Отношение теплоемкости к единице количества материала (по массе или объему) называется удельной теплоемкостью, которая численно равна количеству тепла (в Дж), необходимому для нагревания I кг материала на I °С. Удельная теплоемкость, кДж / (кг -°С), приведенных ниже материалов составляет:
медь 0,38
сталь 0,46—0,48
алюминиевые сплавы 0,90
природные каменные материалы 0,75—0,93
бетон тяжелый 0,80—0,92
кирпич 0,74
сосна . . 2,51
Теплоемкость учитывают при определении теплоустойчивости наружных ограждений отапливаемых зданий (требуются материалы с наиболее высокой удельной теплоемкостью), при расчете подогрева составляющих бетона и раствора, также мастик для работ в зимнее время и т. п.
Тепловое расширение
Тепловое расширение – свойство материала изменять объем и размеры при нагревании. Количественно характеризуется коэффициентами объемного и линейного расширения.
Коэффициент объемного расширения равен относительному увеличению объема материала, а коэффициент линейного расширения – относительному увеличению его длины при нагревании на 1 °С.
Жесткое соединение нескольких материалов с разными коэффициентами теплового расширения может вызвать в конструктивном элементе значительные по величине напряжения, которые приведут к его короблению и растрескиванию. При большом изменении размеров материала из-за колебаний температуры может произойти его разрушение.
Огнестойкость – способность материала противостоять действию огня и высоких температур во время пожара. По степени огнестойкости все материалы делят на несгораемые, трудносгораемые и сгораемые.
Под действием огня или высокой температуры материалы ведут себя по-разному: несгораемые (природные каменные материалы, бетон, кирпич, сталь и т. п.
) не воспламеняются, не тлеют и не обугливаются; трудносгораемые (фибролит, асфальтовый бетон, древесина, пропитанная огнезащитными составами) с трудом воспламеняются, тлеют или обугливаются в присутствии источника огня; сгораемые (незащищенная древесина, войлок, рубероид, большинство полимерных материалов) воспламеняются и продолжают гореть после удаления источника огня.
Причем из числа несгораемых одни материалы (кирпич глиняный, черепица, большинство бетонов) практически не деформируются и не растрескиваются, другие – значительно деформируются (сталь), а некоторые разрушаются (гранит, мрамор, известняк).
При оценке огнестойкости материалов необходимо также учитывать совместное действие высокой температуры, воды и других жидкостей, используемых при тушении пожара, а также химических веществ и газов, выделяющихся из некоторых материалов (особенно полимерных).
Огнеупорность – свойство материала выдерживать, не расплавляясь и не деформируясь, длительное воздействие высоких температур.
По степени огнеупорности материалы подразделяют на огнеупорные, тугоплавкие и легкоплавкие: огнеупорные (например, шамотный кирпич) выдерживают продолжительное воздействие температуры свыше 1580 °C (используют для внутренней облицовки промышленных печей), тугоплавкие (гжельский кирпич) выдерживают температуру 1350—1580 °С, легкоплавкие (кирпич глиняный обыкновенный) противостоят температуре ниже 1350 °С.
Электропроводность – способность материала проводить электрический ток. Она зависит от обратного электропроводности свойства – электрического сопротивления. Очевидно, что чем меньше удельное электрическое сопротивление материала, тем лучше он проводит электрический ток.
В зависимости от этого показателя все материалы подразделяют на проводники, полупроводники и изоляторы. К проводникам относятся серебро, медь и ее сплавы, алюминий, сталь. Хорошими изоляторами являются резина, асбест, фарфор, стекло, пластические массы.
Полупроводники (кремний, мышьяк и др.) занимают промежуточное положение между проводниками и изоляторами; в обычных условиях они слабо проводят электрический ток.
Полупроводники широко применяются в различных отраслях народного хозяйства, в частности для регулирования силы тока и напряжения, преобразования одного вида энергии в другой.
Электропроводность и соответственно электрическое сопротивление материалов учитывают при оценке качества и выборе шнуров, проводов, кабелей, электроустановочных и других изделий.
Цвет материалов – это определенное зрительное ощущение, вызываемое в результате воздействия на глаз потоков электромагнитного излучения в диапазоне видимой части спектра. В общем случае цвет материала связан с его окраской, свойствами поверхности и оптическими свойствами источников света. Цвет играет большую роль при выборе облицовочных и отделочных материалов.
Структура – строение материала, определенное сочетание его составных частей. В структуре материалов различают структуру горной породы, структуру металла и др.
Фактура (от латинского фактура – обработка, строение) – видимое строение поверхности материала. Различают две группы фактур: рельефные (с разной высотой и разнообразным характером рельефа) и гладкие (от зеркально-блестящих до шероховато-ровных).
Цвет, структура и фактура различных материалов более подробно рассмотрены при их характеристике в соответствующих главах книги.
Теплоемкость – это… Чему равна теплоемкость? Таблица теплоемкости
Теплоемкость – это способность поглощать некоторые объемы тепла во время нагревания или отдавать при охлаждении. Теплоемкость тела – это отношение бесконечно малого числа теплоты, что получает тело, к соответствующему приросту его температурных показателей. Величина измеряется в Дж/К. На практике применяют немного другую величину – удельную теплоемкость.
Определение
Что означает удельная теплоемкость? Это величина, относящаяся к единичному количеству вещества. Соответственно, численность вещества можно измерить в кубометрах, килограммах или даже в молях.
От чего это зависит? В физике теплоемкость зависит напрямую от того, к какой количественной единице она относиться, а значит, различают молярную, массовую и объемную теплоемкость.
В строительной сфере вы не будете встречаться с молярными измерениями, но с другими – сплошь и рядом.
Что влияет на удельную теплоемкость?
Что такое теплоемкость, вы знаете, но вот какие значения влияют на показатель, еще не ясно. На значение удельной теплоемкости напрямую воздействуют несколько компонентов: температура вещества, давление и иные термодинамические характеристики.
Во время роста температуры продукции его удельная теплоемкость растет, однако определенные вещества отличаются совершенно нелинейной кривой в этой зависимости.
Например, с возрастанием температурных показателей с нуля до тридцати семи градусов удельная теплоемкость воды начинает понижаться, а если предел будет находиться между тридцатью семью и ста градусами, то показатель, наоборот, возрастет.
Стоит отметить, что параметр зависит еще и от того, каким образом разрешается изменяться термодинамическим характеристикам продукции (давлению, объему и так далее). Например, удельная теплоемкость при стабильном давлении и при стабильном объеме будут отличаться.
Как рассчитать параметр?
Вас интересует, чему равна теплоемкость? Формула расчета следующая: С=Q/(m·ΔT). Что это за значения такие? Q – это количество теплоты, что получает продукция при нагреве (или же выделяемое продукцией во время охлаждения). m — масса продукции, а ΔT — разность окончательной и начальной температур продукции. Ниже приведена таблица теплоемкости некоторых материалов.
Что можно сказать о вычислении теплоемкости?
Вычислить теплоемкость – это задача не из самых простых, особенно если применять исключительно термодинамические методы, точнее это невозможно сделать. Потому физики используют методы статистической физики или же знания микроструктуры продукции.
Как произвести вычисления для газа? Теплоемкость газа рассчитывается из вычисления средней энергии теплового движения отдельно взятых молекул в веществе.
Движения молекул могут быть поступательного и вращательного типа, а внутри молекулы может быть целый атом или колебание атомов.
Классическая статистика говорит, что на каждую степень свободы вращательных и поступательных движений приходится в мольной теплоемкости газа величина, что равняется R/2, а на каждую колебательную степень свободы значение равняется R. Это правило еще именуют законом равнораспределения.
При этом частичка одноатомного газа отличается всего тремя поступательными степенями свободы, а потому его теплоемкость должна приравниваться к 3R/2, что отлично согласуется с опытом.
Каждая молекула двухатомного газа отличается тремя поступательными, двумя вращательными и одной колебательной степенями свободы, а значит, закон равнораспределения будет равняться 7R/2, а опыт показал, что теплоемкость моля двухатомного газа при обычной температуре составляет 5R/2.
Почему оказалось такое расхождение теории? Все связано с тем, что при установлении теплоемкости потребуется учитывать разные квантовые эффекты, другими словами, пользоваться квантовой статистикой. Как видите, теплоемкость – это довольно-таки сложное понятие.
Квантовая механика говорит, что любая система частичек, что совершают колебания или же вращения, в том числе и молекула газа, может иметь определенные дискретные значения энергии. Если же энергия теплового движения в установленной системе недостаточна для возбуждения колебаний необходимой частоты, то данные колебания не вносят вклада в теплоемкость системы.
В твердых телах тепловое движение атомов являет собой слабые колебания поблизости определенных положений равновесия, это касается узлов кристаллической решетки.
Атом обладает тремя колебательными степенями свободы и по закону мольная теплоемкость твердого тела приравнивается к 3nR, где n– количество имеющихся атомов в молекуле. На практике это значение является пределом, к которому стремится теплоемкость тела при высоких температурных показателях.
Значение достигается при обычных температурных изменениях у многих элементов, это касается металлов, а также простых соединений. Также определяется теплоемкость свинца и других веществ.
Что можно сказать о низких температурах?
Мы уже знаем, что такое теплоемкость, но если говорить о низких температурах, то как значение будет рассчитываться тогда? Если речь идет о низких температурных показателях, то теплоемкость твердого тела тогда оказывается пропорциональной T 3 или же так называемый закон теплоемкости Дебая.
Главный критерий, позволяющий отличить высокие показатели температуры от низких, является обычное сравнение их с характерным для определенного вещества параметром – это может быть характеристическая или температура Дебая qD.
Представленная величина устанавливается спектром колебания атомов в продукции и существенно зависит от кристаллической структуры.
У металлов определенный вклад в теплоемкость дают электроны проводимости. Данная часть теплоемкости высчитывается с помощью статистики Ферми-Дирака, в которой учитываются электроны.
Электронная теплоемкость металла пропорциональная обычной теплоемкости, представляет собой сравнительно небольшую величину, а вклад в теплоемкость металла она вносит только при температурных показателях, близких к абсолютному нулю.
Тогда решеточная теплоемкость становится очень маленькой, и ею можно пренебречь.
Массовая теплоемкость
Массовая удельная теплоемкость – это количество теплоты, что требуется поднести к единице массы вещества, дабы нагреть продукт на единицу температуры. Обозначается данная величина буквой С и измеряется она в джоулях, поделенных на килограмм на кельвин – Дж/(кг·К). Это все, что касается теплоемкости массовой.
Что такое объемная теплоемкость?
Объемная теплоемкость – это определенное количество теплоты, что требуется подвести к единице объема продукции, дабы нагреть ее на единицу температуры. Измеряется данный показатель в джоулях, поделенных на кубический метр на кельвин или Дж/(м³·К). Во многих строительных справочниках рассматривают именно массовую удельную теплоемкость в работе.
Применение на практике теплоемкости в строительной сфере
Многие теплоемкие материалы применяют активно при строительстве теплоустойчивых стен. Это крайне важно для домов, отличающихся периодическим отоплением. Например, печным.
Теплоемкие изделия и стены, возведенные из них, отлично аккумулируют тепло, запасают его в отопительные периоды времени и поэтапно отдают тепло после выключения системы, позволяя таким образом поддерживать приемлемую температуру на протяжении суток.
Итак, чем больше будет запасено тепла в конструкции, тем комфортней и стабильней будет температура в комнатах.
Стоит отметить, что обычный кирпич и бетон, применяемые в домостроении, обладают значительно меньшей теплоемкостью, чем пенополистирол. Если брать эковату, то она в три раза более теплоемкая, нежели бетон.
Следует отметить, что в формуле расчета теплоемкости совершенно не зря присутствует масса.
Благодаря большой огромная массе бетона или кирпича в сравнении с эковатой позволяет в каменных стенах конструкций аккумулировать огромные объемы тепла и сглаживать все суточные температурные колебания.
Только малая масса утеплителя во всех каркасных домах, несмотря на хорошую теплоемкость, является самой слабой зоной у всех каркасных технологий. Чтобы решить данную проблему, во всех домах монтируют внушительные теплоаккумуляторы. Что это такое? Это конструктивные детали, отличающиеся большой массой при достаточно хорошем показателе теплоемкости.
Примеры теплоаккумуляторов в жизни
Что это может быть? К примеру, какие-то внутренние кирпичные стены, большая печь или камин, стяжки из бетона.
Мебель в любом доме или квартире является отличным теплоаккумулятором, ведь фанера, ДСП и дерево фактически в три раза больше могут запасаться теплом лишь на килограмм веса, нежели пресловутый кирпич.
Есть ли недостатки в теплоаккумуляторах? Конечно, главный минус данного подхода состоит в том, что теплоаккумулятор требуется проектировать еще на стадии создания макета каркасного дома. Все из-за того, что он отличается большим весом, и это потребуется учесть при создании фундамента, а после еще представить, как данный объект будет интегрирован в интерьер.
Стоит сказать, что учитывать придется не только массу, потребуется оценивать в работе обе характеристики: массу и теплоемкость.
К примеру, если применять золото с невероятным весом в двадцать тонн на кубометр в качестве теплоаккумулятора, то продукция будет функционировать как нужно лишь на двадцать три процента лучше, нежели бетонный куб, вес которого составляет две с половиной тонны.
Какое вещество больше всего подходит для теплоаккумулятора?
Наилучшим продуктом для теплоаккумулятора является совсем не бетон и кирпич! Неплохо с этой задачей справляется медь, бронза и железо, но они очень тяжелые.
Как ни странно, но лучший теплоаккумулятор – вода! Жидкость имеет внушительную теплоемкость, самую большую среди доступных нам веществ.
Больше теплоемкость только у газов гелия (5190 Дж/(кг·К) и водорода (14300 Дж/(кг·К), но их проблематично применять на практике. При желании и необходимости смотрите таблицу теплоемкости нужных вам веществ.
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.