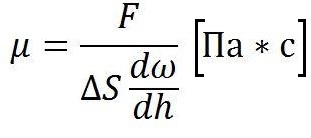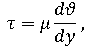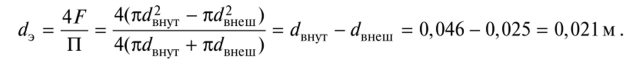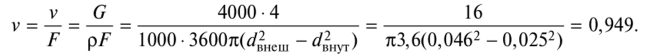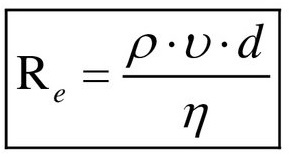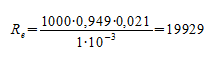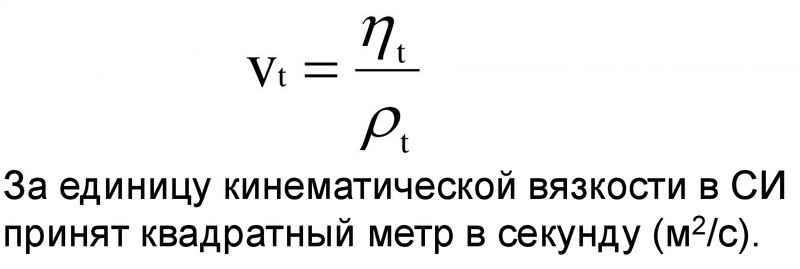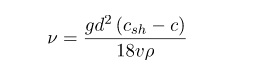Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
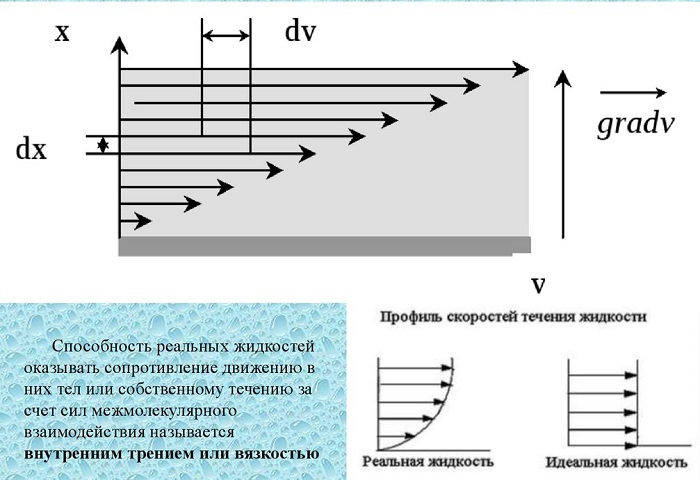
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ — показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
Коэффициент динамической вязкости газа
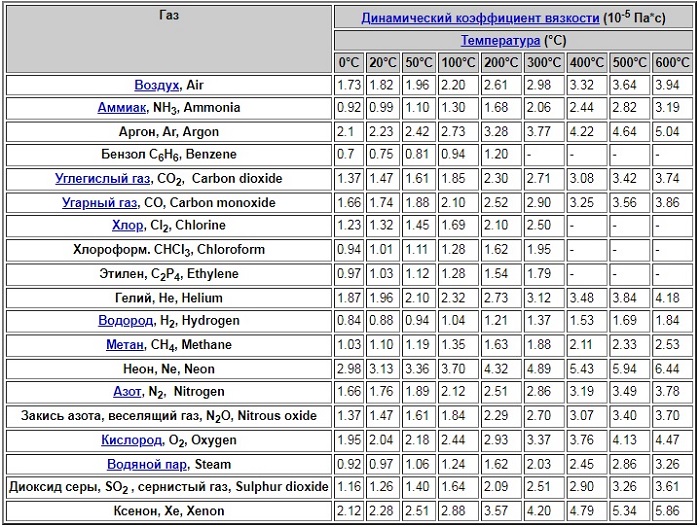
Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:
Коэффициент вязкости жидкостей
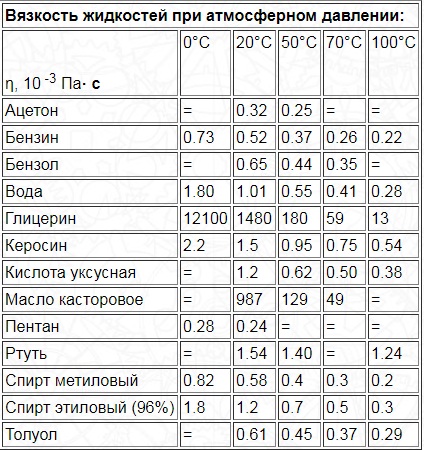
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
Связь коэффициента вязкости с числами Рейнольдса и силой трения
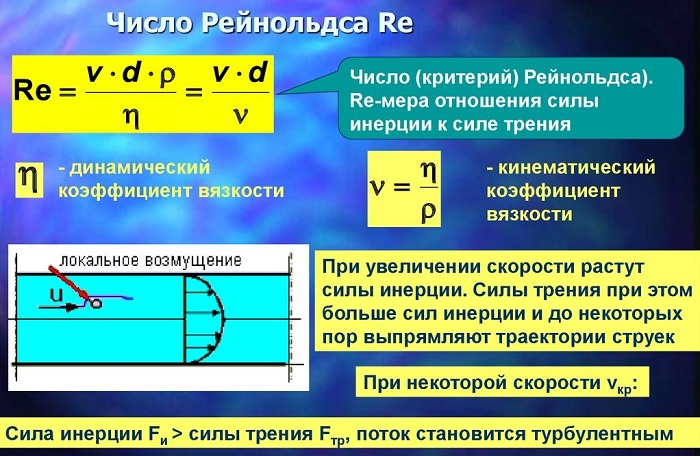
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
6
ЛАБОРАТОРНАЯ
РАБОТА № 17
ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ВЯЗКОСТИ
ЖИДКОСТИ
МЕТОДОМ СТОКСА
Оборудование:
стеклянный цилиндр с жидкостью,
измерительный микроскоп, секундомер,
шарики из свинца.
Краткая теория
Реальная жидкость,
в отличие от идеальной, обладает вязкостью
(внутренним трением), обусловленной
сцеплением между молекулами. Если в
движущейся жидкости различные слои
имеют различную скорость, то между
слоями действуют силы внутреннего
трения.
Опыт
показал, что сила внутреннего трения
пропорциональна площади S
соприкосновения слоев жидкости и
градиенту скорости
(градиентом скорости называется изменение
скорости на единице длины в направлении
перпендикулярном скорости).
Сила
внутреннего трения выражается формулой
(законом) Ньютона:
F
=
S, (1)
где
— коэффициент пропорциональности,
называемый коэффициентом внутреннего
трения (коэффициентом вязкости жидкости).
Физический
смысл коэффициента вязкости состоит в
том, что он численно равен силе внутреннего
трения, действующей на 1 м2
площади соприкосновения параллельно
движущихся слоев жидкости и температуры.
Вязкость
жидкости с повышением температуры
уменьшается, так как при этом увеличивается
среднее расстояние между молекулами
и, следовательно, уменьшается сцепление
между ними. Коэффициент вязкости
определяется различными методами.
Цель
данной работы – определение коэффициента
вязкости методом Стокса.
Рассмотрим
падение тела внутри покоящейся жидкости.
При соприкосновении твердого тела с
жидкостью к поверхности тела прилипают
молекулы жидкости, образуя мономолекулярный
слой жидкости, обволакивающей тело.
Прилегающий к телу мономолекулярный
слой жидкости движется вместе с телом
со скоростью движения тела. Он увлекает
соседние частицы жидкости. Эти частицы
увлекают более удаленные частицы в
результате действия сил сцепления между
ними. Удаленные от тела частицы жидкости
движутся медленнее, более близкие к
телу – быстрее. В этих условиях между
частицами, движущимися с разными
скоростями, действуют силы внутреннего
трения. Силы внутреннего трения,
действующие со стороны удаленных частиц
на прилегающие к телу частицы, тормозят
движение тела, являясь силами сопротивления.
Они направлены в сторону, противоположную
перемещению тела.
Опыты
показывают, что сила сопротивления
зависит от скорости движения тела, от
геометрической формы тела и вязкости
среды. Силу сопротивления среды можно
наиболее просто определить для тела
сферической формы (шарика) движущегося
под действием силы тяжести в покоящейся
жидкости.
Теоретические
расчеты, выполненные Стоксом, приводят
к выражению (закон Стокса)
F=3dv, (2)
где: d
– диаметр шарика;
v
– скорость движения шарика;
— коэффициент вязкости.
На шарик
массой m и диаметром d,
падающий со скоростью v
в жидкости с коэффициентом вязкости ,
действуют три силы: сила тяжести F1,
выталкивающая сила FА,
и сила сопротивления F
жидкости (рис. 1). Так как силы F1
и FА постоянны, а
сила F возрастает с
увеличением скорости движения шарика,
то с некоторого момента времени эти
силы уравновесят друг друга:
F1
= FA +
F (3)
Т
шарик будет двигаться равномерно.
Учитывая,
что по закону Ньютона
F1
= mg
=
d31g
, (4)
а по
закону Архимеда
FA
=
d32
g, (5)
где: 1
– плотность шарика;
2
– плотность жидкости;
g
– ускорение свободного падения.
Имеем
—
расчетная формула (6)
т.к.
,
то равенство (1.6) примет вид
(7)
где: l
–путь, пройденный шариком в жидкости
за время t.
Таким
образом, наблюдая за равномерным
движением шарика в жидкости по формуле
(7) можно определить ее коэффициент
вязкости.
Если
обозначить
,
то расчетная формула примет вид
(7а)
Описание аппаратуры
и метод измерений
Прибор
состоит из стеклянного цилиндра,
наполненного исследуемой жидкостью.
На внешней поверхности цилиндра имеются
две метки m и n,
расположенные на расстоянии l
друг от друга. Метки представляют собой
проволочные кольца. Верхнее кольцо
должно быть на 5 – 8 см ниже уровня
жидкости (рис. 2).
Д
шариков измеряются на микроскопе,
снабженном окулярным микрометром.
Окулярный микрометр представляет собой
тонкую стеклянную пластинку с нанесенной
на нее шкалой. Эта пластинка установлена
в фокальной плоскости окуляра микроскопа.
При рассмотрении шарика в микроскоп, в
поле зрения окуляра одновременно видны
изображения шарика и шкалы окулярного
микрометра. Цена деления окулярного
микрометра указана на микроскопе ( в
нашем случае она равна 0,05 мм). Время
падения шарика измеряют секундомером.
Рис. 2
Измерения.
-
С помощью микроскопа
измерить диаметр шарика (свинцовая
дробь). Для опыта надо взять пять
шариков, диаметр каждого измерить один
раз. Для измерения шарик кладут в круглое
отверстие в основании микроскопа и
сфокусировав микроскоп производят
отсчет делений окулярного микрометра.
Фокусировка микрометра производится
в таком порядке:
-
вращая окуляр,
добиться отчетливого изображения шкалы
окулярного микрометра, -
не нарушая
фокусировки окуляра, перемещая тубус
вверх и вниз специальным кольцом на
микроскопе, добиться отчетливого
изображения шарика, -
поместив шарик в
центре поля зрения микроскопа, по
середине шкалы (рис. 3) определить его
диаметр, как разность отсчетов по шкале
микрометра с левого и правого боков
шарика.
d = 2,75 – 2,15 = 0,6 мм
Рис. 3
-
Измерив, диаметр
шарика, опускают его в сосуд с жидкостью
как можно ближе к оси цилиндра. В момент
прохождения шарика через верхнюю метку,
пускают секундомер. В момент прохождения
шарика через нижнюю метку, секундомер
останавливается. Определяют время
движения шарика t для
всех пяти шариков. -
По меткам на
цилиндре и миллиметровой шкале определить
l – путь шарика. -
Результаты измерений
и вычислений занести в таблицу 1.
Таблица 1
|
№ |
Путь шарика |
Время t |
Диаметр d |
Плотность шарика 1 |
Плотность 2 |
Коэффициент вязкости i |
i |
i2 |
|
1. 2. 3. 4. 5. |
Вычисления
-
Вычислить для
каждого измерения коэффициент вязкости
по формуле (7) в системе СИ
_ -
Вычислить среднее
арифметическое значение
. -
Вычислить абсолютные
ошибки отдельных измерений по формуле
(8)
4. Вычислить
стандартное отклонение:
(9)
где n – число измерений.
5.По
заданной надежности W =
0,95 и числу измерений n из
таблицы найти значение коэффициента
Стьюдента и
вычислить абсолютную ошибку результата
по формуле:
(10)
соответственно
округлив ее. Округлить среднее значение
на порядок округленной ошибки (10).
-
Вычислить
относительную ошибку
(11)
где:
— вычислена по формуле (4.3) и округлена
—
тоже округлена
7.
Записать результат:
Пас
Контрольные
вопросы
-
Чем обусловлены
силы внутреннего трения в жидкостях? -
От чего зависят
силы внутреннего трения? -
Напишите уравнение
силы внутреннего трения и поясните
физический смысл величин
и . -
Напишите формулу
Стокса и поясните, при каких условиях
можно по ней вычислить силу внутреннего
трения? -
Какие силы действуют
на шарик в жидкости? -
Какое условие
установившегося (равномерного) движения
шарика в жидкости? -
Как будет зависеть
вязкость жидкости от изменения
температуры? -
Из формулы (1)
определите вязкость в системе СИ. -
Выведите расчетную
формулу (7).
Литература
-
Грабовский Р.И.
Курс физики. М.: Высшая школа, 1980 -
Зисман Г.А., Тодес
О.М. Курс общей физики. М.: Наука, 1972-74,
т.1 -
Савельев И.В. Курс
общей физики. М.: Наука, 1977-79, т.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
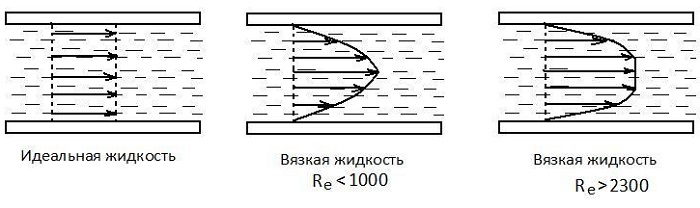
Вязкость жидкости

Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.
Содержание
- Физический смысл вязкости
- Вязкость кинематическая, динамическая и абсолютная
- Коэффициент вязкости жидкости
- Методы измерения вязкости. Метод Стокса.
- Видео по теме вязкости
Физический смысл вязкости
Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример. Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ1
Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ1.
Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.
Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде
где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения
μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.
Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.
Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу
Вязкость кинематическая, динамическая и абсолютная
Теперь определимся с различными понятиям вязкости:
Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па·с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.
Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.
Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.
Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести
Абсолютная вязкость получается при умножении кинематической вязкости на плотность. В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.
Коэффициент вязкости жидкости
В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости
ν = μ / ρ
где ρ – плотность жидкости.
Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.
В физической системе единиц кинематическая вязкость имеет единицу измерения см2/с и называется Стоксом(Ст).
Вязкость некоторых жидкостей
| Жидкость | t, °С | ν, Ст |
| Вода | 0 | 0,0178 |
| Вода | 20 | 0,0101 |
| Вода | 100 | 0,0028 |
| Бензин | 18 | 0,0065 |
| Спирт винный | 18 | 0,0133 |
| Керосин | 18 | 0,0250 |
| Глицерин | 20 | 8,7 |
| Ртуть | 0 | 0,00125 |
Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью
ξ = 1/μ
Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры. Для различных жидкостей зависимость вязкости от температуры получается различной.
Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.
Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.
Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.
Методы измерения вязкости. Метод Стокса.

Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.
Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.
Существует следующие методы определения вязкости жидкости.
Капиллярный метод.
Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.
Метод по Гессе.
Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.
Ротационный метод.
Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого. В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.
Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.
Метод Стокса

Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.
Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.
Видео по теме вязкости
Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.
Вместе со статьей «Вязкость жидкости» смотрят:

Гидравлические машины это? Описание и принцип работы.

Турбулентный режим движения жидкости

Уравнение неразрывности струи и потока жидкости.
Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ — показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
The resistance to motion that most fluids provide is referred to as “viscosity.” When there is relative motion between layers of fluid, viscosity develops. It precisely measures the resistance to flow caused by internal friction between fluid layers as they pass through one another during fluid flow. Viscosity may also be defined as a measure of a fluid’s thickness or barrier to passing items through it.
Because of its strong intermolecular interactions, a fluid with a high viscosity resists motion by creating a lot of internal friction, which prevents layers from moving past one another. A fluid with low viscosity, on the other hand, flows easily because its molecular composition causes very little friction when it is in motion. Gases have viscosity as well, although it’s less noticeable in everyday life.
What is Viscosity?
The viscosity of a fluid is a measurement of its resistance to flow. The ratio of shearing stress to velocity gradient in a fluid is used to calculate viscosity.
- Viscosity is measured in Poiseuille, a SI unit of measurement (PI).
- The newton-second per square meter— (N s m-2) and the pascal-second are the other units (Pa s.)
- [ML-1T-1] is the dimensional formula for viscosity.
The viscosity of liquids reduces fast as the temperature rises, but the viscosity of gases rises as the temperature rises. As a result, liquids flow more freely when heated, and gases flow more slowly. Viscosity is also an intensive property since it does not vary when the amount of matter changes.
Formula for the Coefficient of Viscosity
η = F . dx / A . dv
where,
- η is the coefficient of viscosity,
- dv/dx is the velocity gradient between two layers of liquid,
- F is the viscous force, and
- A is the surface area.
Types of Viscosity
There are two types of viscosity of a fluid:
- Dynamic Viscosity (Absolute Viscosity): This type of viscosity is used to measure the fluid’s resistance to flow when a force is applied to it. The term for this is Dynamic Viscosity.
- Kinematic Viscosity: This type of viscosity is used to measure the fluid’s resistive flow under gravity’s weight. Kinematic viscosity is the name given to this measure of fluid viscosity.
Many people misunderstand the two viscosity measurements and believe they are one and the same. In actuality, they are rather different from one another. Kinematic viscosity is more beneficial than absolute or dynamic viscosity in a few instances.
Dynamic Viscosity
Dynamic viscosity is a method of measuring a fluid’s resistance to flow when an external force is applied.
Dynamic viscosity
The viscosity of a fluid is a crucial attribute to know in order to understand its behavior. Also, when it comes into touch with solid limits, how it will move. The viscosity of a fluid is a measurement of its resistance to progressive deformation under tensile or shear stress. The intermolecular friction that occurs when layers of fluids attempt to glide over each other can cause shear stress in the fluid.
A rotational viscometer is a useful tool for determining dynamic viscosity. The probe in the liquid sample will be rotated by these instruments. The force, or torque, required to turn the probe is used to determine viscosity.
Formula for Dynamic Viscosity
Dynamic Viscosity Formula for the fluid will specify its internal resistance to the flow due to a certain shearing force. This is a type of tangential force that occurs when two horizontal planes contact. During the analysis of liquid behavior and fluid motion near solid boundaries, viscosity is an essential fluid characteristic.
As a result, dynamic viscosity is the force required by a fluid to overcome internal molecular friction and allow it to flow. So, dynamic viscosity may be defined as the tangential force per unit area necessary to move a fluid in one horizontal plane relative to another plane at a velocity of unit value while the fluid’s molecules remain a unit distance apart.
The tangential force required to shift one horizontal plane of a fluid relative to another is known as dynamic viscosity. As a result, we may write it as:
Dynamic viscosity = Shearing stress / Shearing rate change
or
η = T/γ
where,
- η is the Dynamic Viscosity,
- T is the shearing stress, and
- γ is the shear rate.
The SI unit for Dynamic Viscosity is Pa.s or Ns/m2
Sample Problems
Problem 1: Shearing stress of 0.76 N per m2 in a fluid with a shear rate of 0.5 per second. Which of these fluids does it match to based on its dynamic viscosity? (Water dynamic viscosity = 1 Pa s, Air dynamic viscosity = 0.018 Pa s and Mercury dynamic viscosity = 1.526 Pa s)
Solution:
Given,
T = 0.76 N per m2
γ = 0.5 per second
So the formula is,
η = T / γ
= 0.76 / 0.5
= 1.52 Pa s
As a result, it is obvious that Mercury fluid will be compatible with this fluid.
Problem 2: With a shear rate of 0.35 s-1 and dynamic viscosity of 0.018 Pa s, what pressure is required to move a plane of fluid?
Solution:
Given,
Shear rate = 0.35 s-1
Dynamic viscosity = 0.018 Pa s
From the dynamic velocity formula,
T = η × γ
Substituting the values,
T = (0.018 × 0.35)
T = 0.0063 Pa
= 0.0063 Pa
Problem 3: A 2.5 × 10-4 m2 metal plate is placed over a 0.25 × 10-3m thick layer of castor oil. Calculate the coefficient of viscosity of castor oil if a force of 2.5 N is required to move the plate at a velocity of 3 × 10-2m s-1.
Solution:
Given:
A = 2.5 × 10-4 m2,
dx = 0.25×10-3m,
dv = 3×10-2 m s-1
F = 2.5 N
Formula is,
η = F.dx / A .dv
Substitute the values in the formula,
η = (2.5)(0.25 × 10-3) / (2.5 × 10-4)(3 × 10-2)
= 0.083 × 103 Nm-2s
Problem 4: Water is flowing slowly on a horizontal plane, with a viscosity coefficient of 0.01 poise and a 100 cm2 surface area. What external force is necessary to keep the flow’s velocity gradient at 1 s-1?
Solution:
Given,
dv/dx = 1s-1.
A = 100 cm2 = 10-2 m2.
η = 0.01 poise = 0.001 kg/ms.
From the formula:
F = -η A (dv/dx)
Substitute the given values in the above, to calculate F,
F = 0.001 × 10-2 × 1
= 10-5 N
Problem 5: 0.04 N/m2 is found to be the shear stress at a point in a liquid. At this point, the velocity gradient is 0.22 s-1. What would the viscosity be?
Solution:
Given,
F/A = 0.04 N/m2 ( shear stress)
dv/dx = 0.22 s-1
Formula for the viscous force is:
F = -ηA (dv/dx)
By Rearranging the formula:
η = (F/A) / (dv/dx)
Substitute the values to calculate η,
η = 0.04 N/m2 / 0.22 s-1
= 0.181 N s/m2
Last Updated :
04 Apr, 2022
Like Article
Save Article