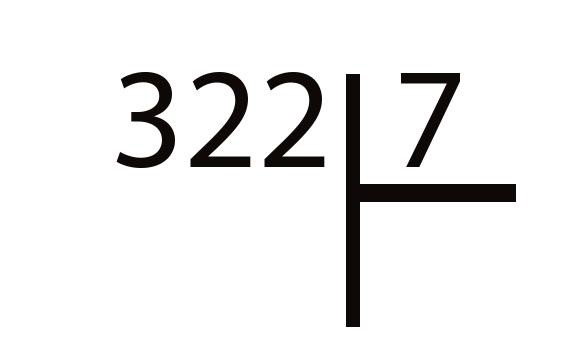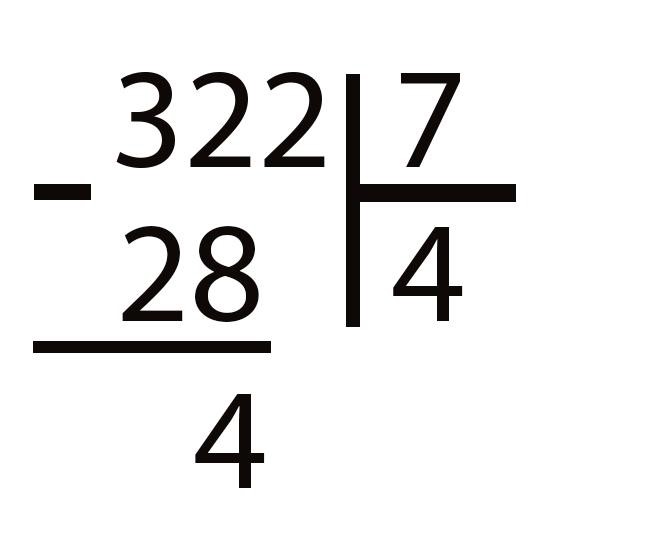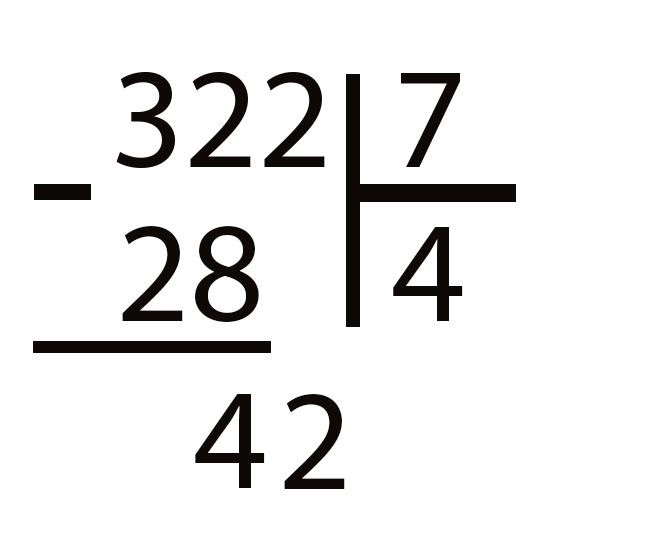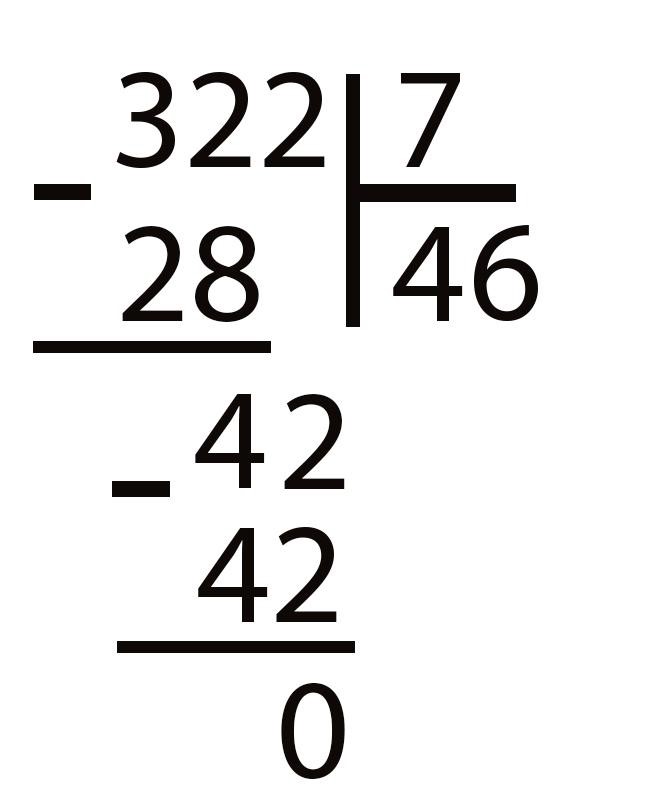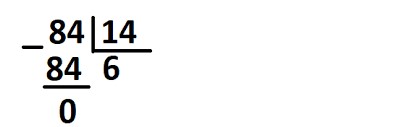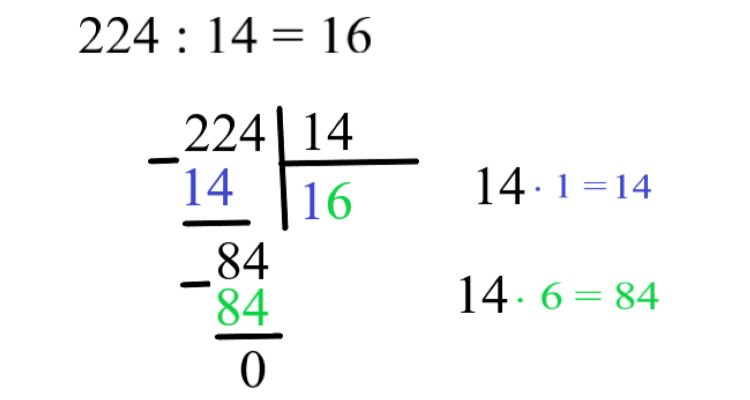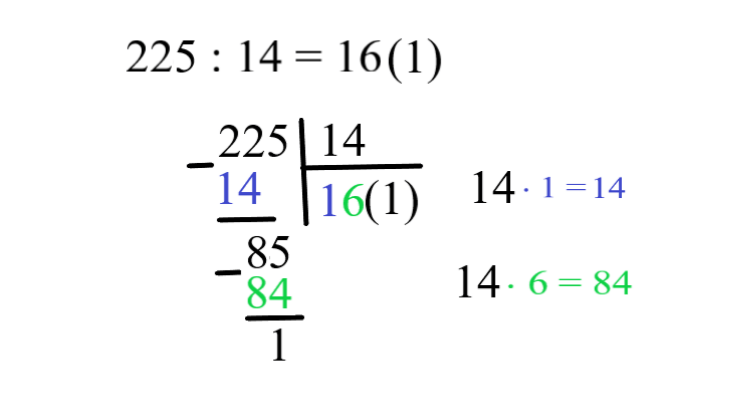Деление столбиком используют, когда нужно разделить простые или сложные многозначные числа. Оно помогает найти ответ за счёт разбивания решения на ряд более простых шагов. В статье объясним на примерах, как делить в столбик и дадим пошаговый алгоритм.
Какие арифметические действия используют при делении в столбик
При знакомстве с делением в столбик у школьника могут возникнуть трудности и недопонимания. Отчасти потому, что при сложении в столбик мы только складываем, а при вычитании только вычитаем. Когда же мы делим в столбик, то по очереди выполняем: деление, умножение и вычитание. Кроме того, нужно знать таблицу умножения, уметь делить с остатком и аккуратно писать цифры, каждую в своей клетке, чтобы не ошибиться в расчётах.
Термины «делимое», «делитель», «частное», «неполное делимое»
Делить в столбик двузначные числа на однозначное
Разделим 86 на 2
1. Для начала определим первое неполное делимое и узнаем, сколько будет цифр в частном. 8 можем разделить на 2, значит, 8 — первое неполное делимое, в частном будет первая цифра. После 8 есть ещё одна цифра, значит, и в частном будет ещё одна цифра — всего две цифры.
2. Разделим первое неполное делимое 8 на делитель 2, получим первую цифру частного — 4.
3. Умножим делитель 2 на цифру частного 4, получим ответ — 8. Этот результат записываем под первым неполным делимым.
4. Находим остаток 8 — 8 = 0. Остаток 0 меньше делителя 2, значит, продолжаем вычисления. Остаток 0 можно не писать.
5. Сносим (переписываем) цифру 6 — это новое неполное делимое.
6. Делим неполное делимое 6 на делитель 2, получаем — 3. Результат записываем в частное.
7. Умножаем делитель 2 на новую цифру частного 3, получаем 6. Результат записываем под вторым неполным делимым.
8. Записываем последний остаток 0. Больше мы не можем снести ни одной цифры, значит, неполных делимых не осталось. Деление в столбик закончено.
Делить в столбик трёхзначное число на однозначное
Разделим 486 на 3
1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.
2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.
3. Далее умножим делитель на полученную цифру частного: 3 · 1 = 3. Запишем 3 под первым неполным делителем.
4. Теперь нужно найти остаток при помощи вычитания.
5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.
6. Разделим 18 на 3 и получим вторую цифру частного — 6.
7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.
8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.
9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.
Пример деления с нулём в частном, или сколько раз можно сносить цифру делимого, чтобы получить одно новое неполное делимое
Разделим 816 на 8
1. Первое неполное делимое 8, а за ним ещё две цифры. Значит, в частном будет 3 цифры.
2. Разделим первое неполное делимое 8 на делитель 4 и запишем в частное ответ — 2.
3. Умножим делитель 4 на цифру частного 2, получим 8. Запишем число под первым неполным делимым.
4. Сносим цифру 1 — это новое неполное делимое. Остаток 0 не пишем.
5. Вспомним деление с остатком и разделим 1 на 4. В результате получим 0, остаток — 1. Цифру 0 записываем в частное.
6. Умножим делитель 4 на цифру частного 0, результат 0 запишем под вторым неполным делимым. Остаток 1.
7. Сносим 6 и получаем новое неполное делимое 16. Делим 16 на 4, получаем цифру частного 4.
8. Умножаем делитель 4 на цифру частного 4 и пишем результат под неполным делимым.
9. Записываем последний остаток 0 — деление выполнено.
Как можно сократить запись деления
Когда мы получили неполное делимое 1, которое меньше делителя 4, сносим вторую цифру делимого, чтобы новое неполное делимое было больше делителя. А в частное ставим 0. И далее выполняем деление в установленном порядке.
В этом примере мы дважды сносили цифру делимого, чтобы получить неполное делимое, которое больше делителя.
Надеемся, что теперь у вашего ребёнка не возникнет трудностей с делением в столбик. А если вдруг они есть, наши репетиторы с удовольствием готовы вам помочь!
Влюбляем в обучение на уроках в онлайн-школе Тетрика
Оставьте заявку и получите бесплатный вводный урок
Прием деления столбиком
Когда мы говорим о делении, то подразумеваем, что надо нечто целое поделить на несколько одинаковых частей. Допустим, мы хотим поделить торт на восемь человек поровну. Для этого надо порезать торт так, чтобы все восемь кусков оказались одинакового размера.
Источник: paulinecakeclub.ru
Сначала мы режем торт пополам (делим на 2 одинаковые части). После этого каждую половинку режем еще раз пополам (получаем 4 одинаковых куска). И, наконец, делим на 2 одинаковые части каждую четвертинку. В результате получаем 8 одинаковых кусков торта.
Так знание математической операции «деление» помогло нам не обидеть никого из гостей. В повседневной жизни вам придется часто сталкиваться с делением. Например, вы всемером заказали две пиццы, и надо их стоимость поделить на всех.
Мы подскажем, как легко и просто сделать это без помощи взрослых и разных умных гаджетов. Разберемся с операцией деления на примерах для учащихся начальной школы — учеников третьего и четвертого классов. Покажем, как делить числа состоящие из двух или трех знаков.
Как делить «с остатком»
При делении большого числа на маленькое не всегда получается сделать это так, чтобы не было остатка. При этом остаток, получившийся в результате деления, не может быть равен делителю или больше него. Он всегда меньше.
Допустим, мы хотим поделить 18 конфет поровну на 2-х человек. Понятно, что каждому достанется по 9 конфет (18 : 2 = 9). Это пример деления без остатка.
Если же мы захотим поделить 18 конфет на 4-х человек, то каждый получит по 4 конфеты (4 × 4 = 16). И у нас останется еще 2 конфеты — это и будет остаток.
2 < 4. Остаток не превышает делитель и не равен ему — значит, мы поделили конфеты правильно.
18 : 4 = 4 (2). Ответ: 4 и остаток 2.
Что было бы, если бы мы решили дать каждому из четверых человек по 3 конфеты, а не по 4? 4 × 3 = 12. Тогда у нас бы осталось еще 6 конфет (18 − 12 = 6).
Но 6 > 4. Получилось бы, что наш остаток превышает делитель — значит, мы поделили бы неправильно.
Разберем еще два примера.
- Разделим 22 на 5. Какое число меньше, чем 22, и при этом делится на 5 без остатка? Это числа 5, 10, 15, 20. Нам нужно выбрать из них самое большое — число 20. Если его поделим на 5, то получим 4. Делаем проверку: 5 × 4 = 20, 22 − 20 = 2. Ответ: 4 и остаток 2. Принято записывать так: 22 : 5 = 4 (2).
- Разделим 39 на 6. Самое большое число, кратное 6 и при этом меньше, чем 39 — это 36. 36 : 6 = 6, 39 – 36 = 3. Разделив 39 на 6, мы получим 6 и в остатке будет 3. Запишем решение в виде: 39 : 6 = 6 (3).
Что значит «делить столбиком»
Если вы умеете делить одно число на другое в уме, это замечательно. Но когда числа большие, даже взрослые могут затрудниться это сделать. Чтобы не запутаться при делении больших чисел, математики придумали способ деления столбиком с помощью бумаги и ручки или карандаша.
Мы познакомим вас с алгоритмом деления в столбик. Он очень простой и легко запоминается. После небольшой тренировки вы без затруднения сможете решать похожие примеры самостоятельно.
Делим трехзначное число на однозначное
Давайте разберем, как делить в столбик многозначное число на простом примере: в качестве делимого возьмем трехзначное число 322, а в качестве делителя — однозначное число 7. Необходимо найти частное.
322 : 7 = ?
Приступаем к алгоритму. Каждое действие обозначим отдельными шагами — этапами.
Этап 1. Делимое 322 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель. Должно получиться как на картинке внизу.
Этап 2. Внимательно изучаем делимое: из скольких сотен, десятков и единиц оно состоит. Нам надо найти число, которое называется «неполным делимым». Оно может оказаться равным делителю или быть больше него.
Число сотен в нашем примере равно 3. Его нельзя поделить на 7, так как 3 < 7. Значит, его мы отбрасываем.
Число десятков у нас — 32. При этом 32 > 7. Значит, оно и будет нашим искомым «неполным делимым».
Делим 32 на 7. Поделить без остатка не получится. Делитель 7 целиком входит 4 раза в делимое 32. Значит, мы нашли неполное частное 4: 7 × 4 = 28, но при этом получили и в остатке 4: 32 − 28 = 4.
Вот как это будет выглядеть в вашей тетради.
Если бы в качестве неполного частного мы взяли число 5, то нам пришлось бы от 32 отнимать 7 × 5 = 35. Мы не можем отнять 35 от 32, так как вычитаемое не может быть больше уменьшаемого.
Если бы мы рассматривали как неполное частное число 3, то при вычитании мы получили бы в остатке число большее, чем делитель: 7 × 3 = 21, 32 − 21 = 11, 11 > 7. Это решение также было бы ошибочным. Остаток не может быть больше делителя.
Этап 3.
Припишем к полученному остатку с правой стороны следующую цифру делимого. В математике принято обозначать это действие словами «снести двойку». У нас получилось число 42, которое нам нужно продолжить делить на наше делимое 7.
Этап 4. Пробуем получившееся число 42 поделить на 7. Вспоминаем таблицу умножения: 7 × 6 = 42. Значит, 42 делится на 7 без остатка. Пишем рядом с неполным частным 4 (справа от него) цифру 6. Получаем полное частное в виде числа 46.
Пишем внизу: 42 − 42 = 0. Это означает, что число 322 поделилось на 7 нацело, без остатка.
Источник: googleusercontent.com
Ответ: 322 : 7 = 46
Если в результате деления большего числа на меньшее вместо нуля в остатке вы получите какое-то другое число (меньшее, чем делитель), значит оно делится не нацело, а с остатком. И получившееся вместо нуля число и будет этим остатком.
В конце статьи вы найдете задания с ответами, потренировавшись на которых вы легко сможете перейти к следующему уровню.
Делим трехзначное число на двузначное
Если вы достаточно натренировались в делении на однозначные числа, то пора переходить к двузначным, взятым в качестве делителя.
Сначала потренируемся: научимся делить двузначное числа на аналогичное. Попробуем поделить 84 на 14.
84 : 14 = ?
Этап 1. Запишем делимое 84 слева, потом знак уголка, затем справа от него — делитель 14.
Этап 2. Анализируем наше делимое: 8 на 14 поделить нельзя. Будем действовать методом подбора. Найдем, на какое число надо умножить 14, чтобы в результате получилось 84.
14 × ? = 84
Этап 3. По очереди перебираем возможные варианты ответа:
- 14 × 2 = 28;
- 14 × 3 = 42:
- 14 × 4 = 56;
- 14 × 5 = 70;
- 14 × 6 = 84.
Последний вариант нас устраивает.
Запишем цифру 6 в качестве частного под знаком уголка с правой стороны:
Источник: gstatic.com
Ответ: 84 : 14 = 6.
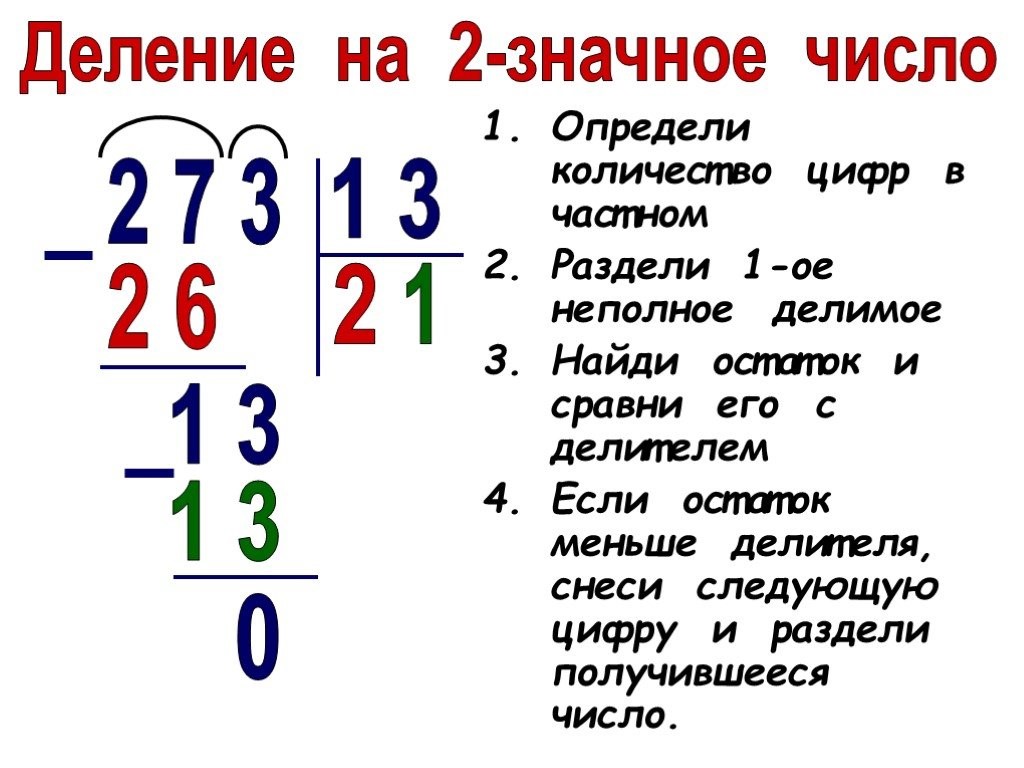
Теперь рассмотрим более сложный пример: попробуем разделить трехзначное число 273 на число 13, которое является двузначным.
Итак, наше делимое — 273, делитель — 13. Необходимо найти частное.
273 : 13 = ?
Этап 1. Делимое 273 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель.
Этап 2. Анализируем наше делимое, как и в предыдущем случае, слева направо. Число 2 на 13 не делится. А вот число 27 нам подходит: 27 > 13. Значит, оно и будет нашим искомым «неполным делимым».
Делим 27 на 13. Поделить без остатка мы не можем. Делитель 13 дважды укладывается целиком в делимое 27. Таким образом, мы нашли неполное частное 2: 13 × 2 = 26, но при этом получаем в остатке единицу: 27 − 26 = 1. Остаток не превышает делитель и не равен ему (1 < 13), значит все в порядке.
Этап 3. Приписываем к полученной единице справа следующую цифру делимого. В нашем случае это цифра 3. Говоря другими словами, «сносим тройку». В результате нас получилось число 13.
Этап 4. Теперь для нас не представляет никакого труда разделить 13 на 13. Любое число делится само на себя без остатка: 13 : 13 = 1. Записываем с правой стороны от неполного частного 2 цифру 1. Получаем полное частное — число 21.
Дописываем наш столбик в самом низу: 13 − 13 = 0. Таким образом, число 273 поделилось на 13 нацело, без остатка.
Возьмем другой пример:
Попробуем поделить трехзначное число 410 на двузначное 82.
410 : 82 = ?
Этап 1. Запишем делимое 410 слева, потом знак уголка, затем справа от него — делитель 82.
Этап 2. Анализируем наше делимое: 4 на 82 поделить невозможно, но и 41 тоже меньше, чем наш делитель 82. Получается, что способ деления столбиком здесь не подходит. Придется действовать методом подбора.
Этап 3. По очереди перебираем возможные варианты ответа:
- 82 × 2 = 164;
- 82 × 3 = 246:
- 82 × 4 = 328;
- 82 × 5 = 410.
Мы нашли искомое частное путем подбора. Ответ: 410 : 82 = 5.
Делим число столбиком с остатком
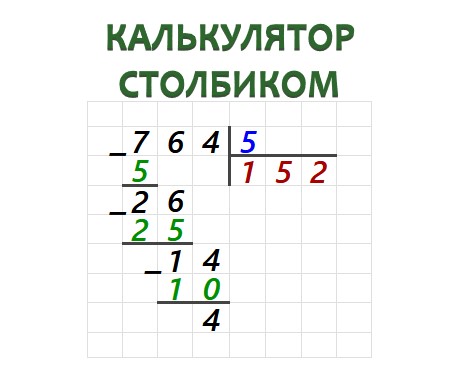
Возьмем трехзначное число 764 и вместе попробуем поделить его на однозначное число 5.
Делимое — 764, делитель — 5. Наша задача — найти частное и проверить, что будет в остатке.
764 : 5 = ?
Действуем по отработанному алгоритму.
Этап 1. Слева записываем делимое 764, рядом с ним рисуем знак уголка, после которого чуть правее записываем делитель 5.
Источник: findhow.org
Этап 2. Анализируем делимое 764 в уже известной нам последовательности. Число сотен 7 больше, чем наш делитель 5. Значит, 7 — наше начальное «неполное делимое».
Делим 7 на 5. Получаем неполное частное 1 и остаток, равный «двойке»: 7 − 5 = 2. Остаток не больше делителя (2 < 5), как и должно быть.
Этап 3. Приписываем к полученной двойке справа следующую цифру делимого. В данном примере это цифра 6. Получаем число 26.
Этап 4. Проделываем всю процедуру еще раз. Ищем самое большее из чисел, делящихся на 5, но при этом меньше, чем 26. Таким числом будет 25 — наш делитель 5 укладывается в него целиком ровно 5 раз: 5 × 5 = 25. Записываем пятерку справа от единицы. 26 − 25 = 1. Все верно — остаток 1 меньше, чем делитель 5.
Этап 5. К полученной в качестве остатка единице сносим четверку — крайнюю из цифер делимого. Получаем число 14, которое надо продолжить делить на 5.
Этап 6. Ближайшее к 14 число, чуть меньше его и делящееся на 5 — это 10. Делим 10 на 5 и получаем 2. Проверяем: 5 × 2 = 10. Двойку приписываем справа в окошке для частного. 14 − 10 = 4. Делаем проверку: остаток 4 < 5. У нас не осталось больше неиспользованных цифр в делимом. Значит, 4 — это конечный искомый остаток. А в окошке для частного — окончательный ответ, искомое частное.
Ответ: 764 : 5 = 152 (4)
Теперь разберем пример деления с остатком трехзначного числа на двузначное.
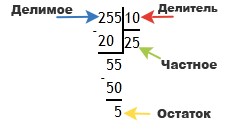
В качестве делимого возьмем 255, в качестве делителя — 10. Найдем частное вместе с остатком.
255 : 10 = ?
Этап 1. Пишем привычным образом делимое 255 и после знака уголка справа записываем делитель 10.
Этап 2. Рассмотрим делимое 255. Число 2 не подходит по определению (нам нужно число, состоящее не менее чем из двух знаков). Следующее число 25 больше, чем наш делитель 10. Следовательно, оно нам подходит.
Делим 25 на 10. Ближайшее кратное к 10 число — 20. Оно дважды содержит число 10. Таким образом, кроме неполного частного 2 мы получили остаток, равный пяти: 25 − 20 = 5. Остаток не превышает делитель (5 < 10), все верно.
Источник: binary2hex.ru
Этап 3. Сносим вниз к полученной пятерке справа цифру 5, стоящую самой последней в делимом. Мы получили число 55, которое надо разделить на 10.
Этап 4. Продолжаем деление. Наибольшее число, кратное 10, и при этом меньше, чем 55 — это число 50. Наш делитель 10 входит в него 5 раз: 10 × 5 = 50. Записываем пятерку справа от двойки в окошке для записи частного. Проверяем: 55 − 50 = 5. Значит, остаток мы нашли правильно (5 < 10). А число 25 будет искомым частным.
Ответ: 255 : 10 = 25 (5)
Упражнения для самостоятельного деления в столбик
Чтобы убедиться в том, правильно ли вы усвоили материал, стоит немного поупражняться. Попробуйте решить столбиком примеры, приведенные ниже, а потом сверьтесь с нашими ответами.
Начните с легкого (1) уровня:
- 32 : 4 = ?
- 65 : 5 = ?
- 54 : 9 = ?
- 72 : 6 = ?
- 81 : 3 = ?
Решили? Тогда переходите к среднему (2) уровню сложности:
- 192 : 12 = ?
- 245 : 5 = ?
- 221 : 13 = ?
- 432 : 9 = ?
- 928 : 8 = ?
Если вы и с этим успешно справились, попробуйте более сложный (3) уровень, где в качестве делимого выступают четырехзначные числа.
- 7485 : 3 = ?
- 3105 : 23 = ?
- 5538 : 26 = ?
- 6344 : 61 = ?
- 1423 : 25 = ?
Самые отважные могут попробовать свои силы в делении столбиком пятизначного числа (уровень *)
- 48633 : 39 = ?
Ответы:
- примеры 1 уровня: 8; 13; 6; 12; 27;
- примеры 2 уровня: 16; 49; 17; 48; 116.
Посмотреть процесс решения примеров более сложного уровня вы можете на иллюстрации, нажав на ссылку:
- 7485 : 3 = 2495;
- 3105 : 23 = 135;
- 5538 : 26 = 213;
- 6344 : 61 = 104;
- 1423 : 25 = 56 (23);
- 48633 : 39 = 1247.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Сегодня мы рассмотрим деление в столбик — объяснение (3 класс).
Бывают небольшие числа, и с ними можно работать в уме. Бывают очень большие числа, для таких чисел люди нашли разные способы умножения и деления. Есть умножение в столбик. Это замечательно, там сразу видно что куда необходимо переносить и куда добавлять. Конечно, если аккуратно записывать. Но если есть умножение в столбик, тогда должно быть и деление в столбик.
Люди нашли удобный способ представления деления больших чисел, чтобы ничего не забыть.
Пример:
Это удобно, но почему так?
Сегодня в этом разбираются Бом, Бим и ребята.
Деление — это действие обратное умножению
Деление двух чисел — это действие обратное к умножению. Используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
Деление в столбик — объяснение (3 класс)
Деление в столбик — это удобный способ представления деления одного числа на другое.
Сегодня ребята пришли раньше на представление и пошли осматривать цирк. По дороге им встретился Бим, который вез тележку с тремя коробками.
— Здравствуйте, ребята! — обрадовался. Бим. — Пойдемте за кулисы, поможете мне и Бому!
Бим и ребята пошли к Бому. В трех коробках находились бананы: в первой большой коробке лежали два больших пакета, в каждом большом пакете лежало по 100 бананов. Во второй, средней коробке, лежали два средних пакета; и здесь в каждом среднем пакете лежало по 10 бананов. В третьей маленькой коробке лежало четыре банана.
— Давайте посчитаем сколько всего бананов получается, — предложил Бим. — В большом пакете 100 бананов. Всего 2 больших пакета. В двух больших пакетах будет:
2 х 100 = 200 бананов.
Всего в большой коробке лежит 200 бананов. Теперь считаем сколько бананов в средней коробке: два пакета по 10 бананов,
2 х 10 = 20 бананов.
В маленькой коробке 4 банана. Получается, что во всех трех коробках будет:
200 + 20 + 4 = 224 банана.
Мне буфетчица сказала, что надо поделить эти бананы на 14 представлений и дать тебе, Бом, для твоих подопечных. Вот, что я придумал. Давайте все бананы высыплем в одну коробку и будем раскладывать по одному банану на 14 подносов пока все бананы не закончатся.
Бим начал высыпать все бананы в маленькую коробку.
— Здесь, конечно, бананов немного, а если бы бананов была тонна, то ты тоже по одному банану раскладывал бы? — поинтересовался Бом. — Очень легко запутаться. Давай придумаем другой способ.
— Ребята, — обратился Бом к школьникам, — помогите Биму все бананы сложить на место. В большой коробке должно быть два больших пакета по 100 бананов, всего в большой коробке будет 200 бананов. В средней коробке два средних пакета по 10 бананов в каждом пакете, всего в средней коробке будет 20 бананов. В маленькой коробке будет четыре банана.
И давай, Бим, договоримся, что в большой коробке будут лежать только большие пакеты по 100 бананов, в средней только средние пакеты по 10 бананов, в маленькой коробке только оставшиеся бананы без никаких пакетиков.
Ребята быстро помогли Бому и Биму.
— Вот теперь всё на месте, — подытожил Бом. — Давайте теперь будем делить так, чтобы бананов хватило на 14 представлений. В большой коробке два больших пакета, два на 14 не делится. А что, если мы бананы переложим из большой коробки в среднюю? Но для этого нужно достать каждый большой пакет и выложить из него бананы по 10 штук в средние пакети, и тогда мы можем бананы из большой коробки переложить в среднюю коробку.
Бом достал большой пакет из большой коробки. Ребята переложили бананы в средние пакеты и начали считать:
— Из одного большого пакета получается 10 средних пакетов по 10 бананов.
— У нас два больших пакета, значит из двух больших пакетов у нас получается 20 средних пакетов по 10 бананов, продолжил Бом. — Мы все средние пакеты помещаем в среднюю коробку.
Ого! В средней коробке уже 22 средних пакета. Такое количество уже делится на 14, это у нас неполное деление с остатком. Получается, на каждое представление будет по одному среднему пакету.
Бом взял 14 подносов и разложил по 1 среднему пакетику на каждый поднос:
— У нас было 22 средних пакетика, 14 мы разложили по местам, остаток 8 средних пакетиков в средней коробке и 4 банана в маленькой. Восемь на четырнадцать не делится. Но если мы оставшиеся в средней коробке бананы в восьми средних пакетах высыплем в маленькую коробочку, то получится в маленькой коробочке 84 банана:
8 х 10 + 4 = 84.
84 банана делятся на 14, получается по 6 бананов, то есть мы на каждый поднос должны добавить еще по 6 бананов. У нас всего 14 подносов, и на каждом подносе лежит одинаковое количество бананов. Значит мы поделили поровну все бананы, которые у нас были. На каждом подносе 1 средний пакет и 6 бананов. Выходит, что всего на каждом подносе по 16 бананов.
— Неужели всякий раз придется по разным пакетикам раскладывать, чтобы правильно поделить? — озадаченно спросил Бим.
— Совсем не обязательно, — ответил Коля. — Люди вместо коробок и пакетиков договорились, как будет называться каждая из цифр в числе. Цифра, которая стоит в числе самой правой, называется разрядом единиц. У нас в маленькой коробке 4 банана, значит число единиц — 4.
— Следующая цифра, которая находится левее разряда единиц называется разрядом десятков, — продолжила Оля. — У нас в средней коробке 2 пакета, значит число десятков равно 2. И мы знаем, что 2 десятка — это 20, и у нас в средней коробке как раз 2 пакетика по 10 бананов, всего 20 бананов.
— Следующая цифра, которая находится левее разряда десятков называется разрядом сотен. У нас это самая большая коробка, в ней два больших пакета, значит число бананов 200, — закончил Вася. — И мы знаем, что 2 сотни — это число 200.
— А какие еще числа могут стоять … в разрядах? — поинтересовался Бим.
— Число в каждом из разрядов может быть любой цифрой от 0 до 9, — ответил Биму Коля. — Еще левее от разряда сотен стоит разряд тысяч. У нас нет еще большей коробки, в которой лежали бы пакеты с количеством бананов по 1000 в каждом, поэтому мы ничего не пишем.
— Мы разложили бананы, у нас общее число бананов 224: 4 банана в маленькой коробке, 2 средних пакета по 10 бананов в средней коробке, — всего 20, и 2 больших пакета из 100 бананов в большой коробке, — подытожил Бом. — Число единиц у нас 4, число десятков 2, число сотен 2. Записываем: 4 стоит справа, левее стоит число десятков 2, еще левее число сотен 2. Теперь это число 224 будем делить на 14.
— Давайте теперь запишем деление 224 на 14 в столбик, — предложил Коля. — Делимое у нас 224, делитель 14. Смотрим: первая цифра слева 2 (число сотен) на 14 не делится, значит надо к ней справа приписать следующую за “2” цифру 2. Читаем число, которое получилось — 22. Число 22 уже делится на 14. Число 14 помещается в числе 22 по одному (1) разу, вот это число “1” и записываем в ответ для частного первым, потом надо из 22 вычесть 14 х 1:
22
—
14
____
8
Мы при делении 22 на 14 находим неполное частное 1 и остаток 8. Неполное частное записываем в частное результата, остаток пишем как при обычном вычитании чисел в столбик.
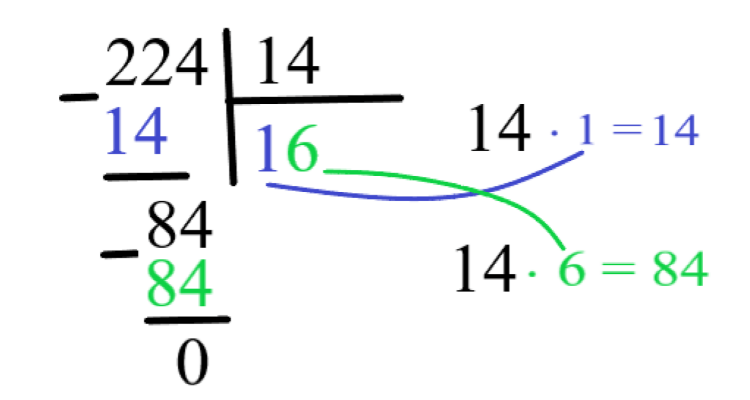
Теперь смотрим, есть ли еще цифры справа, в делимом 224. Да такая цифра есть, после 22 стоит цифра 4, мы её записываем справа от остатка 8. Эта четверка будет стоять на том же месте в строке, где стоит 4 в числе 224, но только ниже возле “8”. У нас внизу получается число “84”. Смотрим, делится ли оно на делитель “14”. Делится. В результате деления 84 на 14 получаем “6”, его записываем справа от “1” в частном. А внизу после того, как умножим 14 х 6 = 84 мы пишем опять обыкновенное вычитание в столбик:
84
—
84
___
0
Ура! Еще и остаток в конце равен 0. В числе 224 нет справа больше цифр, сносить на более нижние строки нечего. Значит, мы закончили деление. Частное — 16.
— Смотрите, получилось такое же число, как и количество бананов на каждом подносе, — обрадовалась Оля.
— Проверка, что деление выполнено правильно, делается также как и для обычного деления: частное умножается на делитель, должно получиться делимое, — добавил Вася.
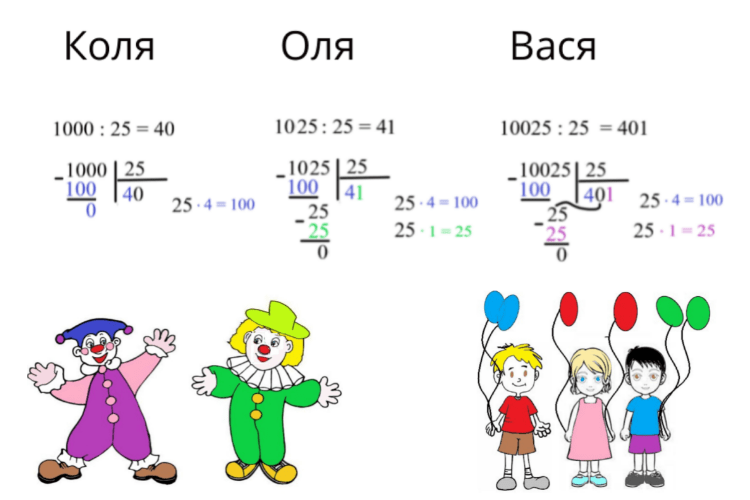
— Сейчас каждый из нас еще по одному примеру деления в столбик запишет, — продолжил Коля.
Коля 1000 : 25 = 40. Оля 1025 : 25 = 41. Вася 10025 : 25 =401.
— Жалко, что у нас нет бананов в остатке, я бы его съел, огорчился Бим.
— Делаем вывод, — продолжил Коля. — Все деление в столбик состоит из неполных делений чисел, пока в числе не окончатся все разряды, но если после того, как мы снесли последний разряд (число единиц) остался остаток, то все деление у нас неполное, и результат будет состоять из частного-результата и остатка-результата. Если в конце деления остаток 0, то так и говорят, что делимое делится на делитель без остатка.
Можно и так определить деление в столбик, — подытожил Бом:
Деление в столбик — это ряд неполных делений чисел (неполных делимых), составленных из остатков от деления и цифр делимого, на делитель. В результате деления в столбик должны быть использованы все цифры делимого.
Вначале в делимом выделяем первое неполное делимое из цифр делимого, начиная с левой цифры делимого, пока неполное делимое не будет делиться не делитель. Частное от неполного деления записываем первой цифрой в частном.
К остатку от неполного деления сносим следующие цифры из делимого, пока новое неполное делимое не будет делится на делитель. При этом, если после снесенной цифры, неполное делимое не делится на делитель, то в частное ставится справа 0. После деления нового неполного делителя на делимое неполное частное записывается справа от уже найденных цифр частного, а к полученному неполному остатку опять сносятся последующие цифры из делимого. Действия повторяются, пока не будут снесены все цифры делимого.
Деление в столбик с остатком: объяснение (3 класс)
Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик.
— Получается, — подхватил Вася, — что при делении в столбик тоже может быть неполное деление, когда есть остаток в самом конце деления. И результат тогда пишут, как при обычном неполном делении: частное-результат или как обычно говорят “частное”, а в конце в скобочке пишут остаток.
Пример:
— Спасибо ребята, что помогли нам сегодня разобраться с делением в столбик, — поблагодарил зрителей Бом. — Вот вам 315 конфет. Поделите в столбик 315 на 15 и разложите по 15 конфет в каждый кулечек. Три пакетика заберите себе, а остальные я раздам другим ребятам. Сколько всего получится пакетиков и сколько пакетиков мне останется раздать ребятам пусть посчитают ребята, которые научились делению в столбик.
— Подсказка. В ответе должен быть 21 кулечек, три из которых получили Коля, Оля и Вася, — добавил Бим. — Теперь напишите, пожалуйста, вопросы и ответы для ребят с Бомом, а я побежал одеваться, мой выход в самом начале представления, а выход Бома с обезьянками будет позже.
Бим убежал.
— До начала представления еще есть время, — посмотрел на часы Бом. — Ребята, давайте запишем вопросы:
- Что такое деление?
- Деление в столбик — это …
- Деление в столбик с остатком — это …
И как обычно, ответы:
- Деление двух чисел — это действие обратное к умножению, используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
- Деление в столбик — это удобный способ представления обыкновенного деления. Деление — это действие обратное к умножению.
- Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик
— Спасибо, ребята! — обрадовался Бом. — Вы очень помогли нам с Бимом. А теперь бегите на представление.
Заключение
Сегодня мы постарались в игровой форме рассмотреть тему: «Деление в столбик — объяснение (3 класс)». Надеемся, что ребята выучат деление в столбик и оно им еще не один раз пригодится.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются. По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Деление в столбик с остатком

4.6
Средняя оценка: 4.6
Всего получено оценок: 259.
4.6
Средняя оценка: 4.6
Всего получено оценок: 259.
Деление – это естественная часть реальной жизни. Без деления не обойтись обычной торговой сделке в продуктовом магазине и программистам в их работе. Но реальный мир не совершенен, поэтому далеко не всегда удается нацело разделить число, именно о таких случаях сегодня пойдет речь.
Деление
Что такое деление? Деление – это процедура, обратная умножению. Деление показывает, сколько раз в делимом повторяется число делителя. Если мы 30 поделим на 6, то узнаем, что для получения числа 30 пришлось 5 раз сложить число 6. Или же число 6 умножить на 5.
Деление с остатком
Деление с остатком подразумевает, что нацело число поделить не удалось и осталась какая-то часть, которая меньше делителя и которую разделить нельзя.
Где это может пригодиться в реальной жизни? Представим себе вполне реальную ситуацию: мы покупаем в магазине конфеты батончики по 38 рублей. Всего у нас 200 рублей, сколько сдачи нам должны дать?
Очевидно, что ровное количество конфет купить не получится, поскольку 200 на 38 нацело не поделится, но и конфету пилить в магазине не будут. Значит, остаток от 200 нам должны будут вернуть в виде сдачи.
$200:38=5 (ост.10)$ – именно 10 рублей остатка и будут сдачей, которую нам должны вернуть.
Долгое время только такие вычисления и производились, до тех пор, пока не возникла надобность в точных расчетах. Тогда на смену делению с остатком пришли десятичные дроби.
Деление в столбик
Но случаются ситуации, когда числа значительно больше, и в уме такие операции выполнить не получится. В этом случае пригодится деление в столбик с остатком. Запись в столбик предполагает запись делимого, вертикальную черту, которая делится пополам горизонтальной чертой, уходящей вправо. Над чертой записывается делитель, а под чертой пишется результат.
Приведем пример деления большого числа с остатком.
Для этого решим задачу.
Геннадий готовится к дальнему походу. В качестве съестного припаса он решил накупить тушенки. Бюджет, отведенный на эту статью, составляет 13800 рублей. Банка тушенки, подходящей под запросы Геннадия стоит 47 рублей. Сколько банок сможет купить Геннадий?
- Поделим 13800 на 47. При делении столбиком сначала выделяется число из первых чисел делимого значения, которое можно поделить на делитель. В нашем случае делитель это 47. Первые цифры это 1,3,8. Числа, которые мы можем использовать это 1,13,138, 1380 и 13800. Очевидно, что первым значением из ряда чисел, которое поделиться на 47 будет 138.
- Ближайшее число к 138, которое делиться на 47 – это 94=47*2. Следующее после 94 это 141, которое нам не подходит, так как оно больше 138. Записываем под горизонтальным числом 2, а под значением 138 записываем 94, так чтобы цифра 9 оказалась под 3, а 4 под 8. Вычитаем из 138 число 94 столбиком и записываем ниже 94 результат: 44. Сверху после 138 осталось два 0. Один из них сносится вниз и приписывается к 44. Получаем число 440.
- По тому же принципу подбираем число, которое можно поделить на 47 наиболее близкое к 440. Это 423=47*4. Также записываем рядом с 2 под чертой 4, а ниже 440 подписываем 423 и вычитаем столбиком. Осталось 17
- Сносим последний 0. Получается число 170. Ближайшее из делимых на 47: 141=47*3
Записываем рядом с 2 и 4 цифру 3, а под 170 подписываем 141.
$$170-141=29$$
Это число поделить на 47 не получится, значит именно столько и останется у Геннадия после посещения супермаркета.
$$13800:47=293 (ост.29)$$
Для проверки результатов деления столбиком с остатком, нужно результат умножить на делитель, а после прибавить остаток. Если получившееся число равняется делимому, то все выполнено верно.
$$293*47=13771$$
$$13771+29=13800$$
Что мы узнали?
Мы узнали, как производится процедура деления в столбик с остатком. Разобрались, в каких случаях стоит использовать эту процедуру, и привели пример.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Шварева Наталья
4/5
-
Ольга Тимохина
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 259.
А какая ваша оценка?