Как найти дефицит графа

From Wikipedia, the free encyclopedia

Deficiency is a concept in graph theory that is used to refine various theorems related to perfect matching in graphs, such as Hall’s marriage theorem. This was first studied by Øystein Ore.^[1][2]: 17 A related property is surplus.

Definition of deficiency[edit]

Let G = (V, E) be a graph, and let U be an independent set of vertices, that is, U is a subset of V in which no two vertices are connected by an edge. Let N_G(U) denotes the set of neighbors of U, which is formed by all vertices from ‘V’ that are connected by an edge to one or more vertices of U. The deficiency of the set U is defined by:

Suppose G is a bipartite graph, with bipartition V = X ∪ Y. The deficiency of G with respect to one of its parts (say X), is the maximum deficiency of a subset of X:

Sometimes this quantity is called the critical difference of G.^[3]

Note that def_G of the empty subset is 0, so def(G;X) ≥ 0.

Deficiency and matchings[edit]

If def(G;X) = 0, it means that for all subsets U of X, |N_G(U)| ≥ |U|. Hence, by Hall’s marriage theorem, G admits a perfect matching.

In contrast, if def(G;X) > 0, it means that for some subsets U of X, |N_G(U)| < |U|. Hence, by the same theorem, G does not admit a perfect matching. Moreover, using the notion of deficiency, it is possible to state a quantitative version of Hall’s theorem:

Theorem — Every bipartite graph G = (X+Y, E) admits a matching in which at most def(G;X) vertices of X are unmatched.

Proof. Let d = def(G;X). This means that, for every subset U of X, |N_G(U)| ≥ |U|-d. Add d dummy vertices to Y, and connect every dummy vertex to all vertices of X. After the addition, for every subset U of X, |N_G(U)| ≥ |U|. By Hall’s marriage theorem, the new graph admits a matching in which all vertices of X are matched. Now, restore the original graph by removing the d dummy vertices; this leaves at most d vertices of X unmatched.

This theorem can be equivalently stated as:^[2]: 17

where ν(G) is the size of a maximum matching in G (called the matching number of G).

Properties of the deficiency function[edit]

In a bipartite graph G = (X+Y, E), the deficiency function is a supermodular set function: for every two subsets X₁, X₂ of X:^{[2]: Lem.1.3.2}

A tight subset is a subset of X whose deficiency equals the deficiency of the entire graph (i.e., equals the maximum). The intersection and union of tight sets are tight; this follows from properties of upper-bounded supermodular set functions.^{[2]: Lem.1.3.3}

In a non-bipartite graph, the deficiency function is, in general, not supermodular.

Strong Hall property[edit]

A graph G has the Hall property if Hall’s marriage theorem holds for that graph, namely, if G has either a perfect matching or a vertex set with a positive deficiency. A graph has the strong Hall property if def(G) = |V| — 2 ν(G). Obviously, the strong Hall property implies the Hall property. Bipartite graphs have both of these properties, however there are classes of non-bipartite graphs that have these properties.

In particular, a graph has the strong Hall property if-and-only-if it is stable — its maximum matching size equals its maximum fractional matching size.^[3]

Surplus[edit]

The surplus of a subset U of V is defined by:

sur_G(U) := |N_G(U)| − |U| = −def_G(U)

The surplus of a graph G w.r.t. a subset X is defined by the minimum surplus of non-empty subsets of X:^[2]: 19

sur(G;X) := min [U a non-empty subset of X] sur_G(U)

Note the restriction to non-empty subsets: without it, the surplus of all graphs would always be 0. Note also that:

def(G;X) = max[0, −sur(G; X)]

In a bipartite graph G = (X+Y, E), the surplus function is a submodular set function: for every two subsets X₁, X₂ of X:

A surplus-tight subset is a subset of X whose surplus equals the surplus of the entire graph (i.e., equals the minimum). The intersection and union of tight sets with non-empty intersection are tight; this follows from properties of lower-bounded submodular set functions.^{[2]: Lem.1.3.5}

For a bipartite graph G with def(G;X) = 0, the number sur(G;X) is the largest integer s satisfying the following property for every vertex x in X: if we add s new vertices to X and connect them to the vertices in N_G(x), the resulting graph has a non-negative surplus.^{[2]: Thm.1.3.6}

If G is a bipartite graph with a positive surplus, such that deleting any edge from G decreases sur(G;X), then every vertex in X has degree sur(G;X) + 1.^[4]

A bipartite graph has a positive surplus (w.r.t. X) if-and-only-if it contains a forest F such that every vertex in X has degree 2 in F.^{[2]: Thm.1.3.8}

Graphs with a positive surplus play an important role in the theory of graph structures; see the Gallai–Edmonds decomposition.

In a non-bipartite graph, the surplus function is, in general, not submodular.

References[edit]

Дефицит — это концепция в теории графов, которая используется для уточнения различных связанных теорем на идеальное соответствие в графах, например, теорема Холла о браке. Впервые он был изучен Øystein Ore. Связанное свойство: излишек .

Содержание

• 1 Определение дефицита
• 2 Дефицит и соответствие
• 3 Свойства функции дефицита
• 4 Свойство Стронга Холла
• 5 Излишек
• 6 Ссылки

Определение дефекта

Пусть G = (V, E) — граф, и пусть U — независимое множество вершин — подмножество V, в котором нет двух вершины соединены ребром. Обозначим N G (U) множество соседей U — подмножество V, которое содержит все вершины, соединенные ребром с одной или несколькими вершинами U. Недостаток множества U определяется следующим образом:

def G (U): = | U | — | N G (U) |

Предположим, что G — двудольный граф с двудольным графом V = X u Y. дефект графа G относительно в одну из его частей (скажем, X), является максимальным недостатком подмножества X:

def (G; X): = max [U подмножество X] def G (U)

Иногда эту величину называют критической разностью числа G.

Обратите внимание, что def G пустого подмножества равно 0, поэтому def (G; X) ≥ 0.

Недостаток и соответствие

Если def (G; X) = 0, это означает, что для всех подмножеств U из X, | N G (U) | ≥ | U |. Следовательно, согласно теореме Холла о браке, G допускает совершенное соответствие.

Напротив, если def (G; X)>0, это означает, что для некоторых подмножеств U из X, | N G (U) | < |U|. Hence, by the same theorem, G does not admit a идеальное соответствие. Более того, используя понятие дефекта, можно сформулировать количественную версию теоремы Холла:

Каждый двудольный граф G = (X + Y, E) допускает паросочетание, в котором не более def (G; X) вершин графа X не имеют себе равных.

Доказательство. Пусть d = def (G; X). Это означает, что для каждого подмножества U в X, | N G (U) | ≥ | U | -d. Добавьте фиктивные вершины в Y и соедините каждую фиктивную вершину со всеми вершинами X. После добавления для каждого подмножества U в X, | N G (U) | ≥ | U |. По теореме Холла о браке новый граф допускает сопоставление, в котором сопоставляются все вершины X. Теперь восстановите исходный граф, удалив фиктивные вершины; это оставляет не более d вершин X несовпадающими. Другие способы сформулировать эту теорему:

ν (G) = | X | — def ⁡ (G; X) { displaystyle nu (G) = | X | — operatorname {def} (G; X)}

где ν (G) — размер максимального соответствия в G ( также называется совпадающим числом G).

Свойства функции дефицита

В двудольном графе G = (X + Y, E) функция дефицита является функцией супермодульного множества : для каждых двух подмножеств X 1, X 2 из X:

def G ⁡ (X 1 ∪ X 2) + def G ⁡ (X 1 ∩ X 2) ≥ def G ⁡ (X 1) + def G ⁡ (X 2) { displaystyle operatorname {def} _ {G} (X_ {1} cup X_ {2}) + operatorname {def} _ {G} (X_ {1} cap X_ {2}) geq operatorname {def} _ {G} (X_ {1}) + operatorname {def} _ {G} (X_ {2})}

A плотно subset — это подмножество X, недостаток которого равен недостатку всего графа (то есть равен максимуму). Пересечение и объединение тесных множеств плотно; это следует из свойств ограниченных сверху функций супермодулярного множества.

В недвудольном графе функция дефекта, как правило, не является супермодулярной.

Сильное свойство Холла

Граф G обладает свойством Холла, если для этого графа выполняется теорема Холла о браке, а именно, если G имеет либо идеальное соответствие, либо множество вершин с положительным недостатком. Граф обладает сильным свойством Холла, если def (G) = | V | — 2 ν (G). Очевидно, что сильное свойство Холла влечет за собой свойство Холла. Двудольные графы обладают обоими этими свойствами, однако существуют классы недвудольных графов, которые обладают этими свойствами.

В частности, граф имеет сильное свойство Холла, если и только если он стабильный — его максимальный размер сопоставления равен его максимальному размеру дробного сопоставления.

Излишек

Излишек подмножества U из V определяется следующим образом:

sur G (U): = | N G (U) | — | U | = — def G (U)

Избыток графа G относительно подмножество X определяется минимальным избытком непустых подмножеств X:

sur (G; X): = min [U непустое подмножество X] sur G (U)

Обратите внимание на ограничение на непустые подмножества: без него избыток всех графов всегда был бы 0. Отметим также, что:

def (G; X) = max [0, — sur (G; X) ]

В двудольном графе G = (X + Y, E) функция прибавки — это функция субмодульного множества : для каждых двух подмножеств X 1, X 2 из X:

sur G ⁡ (X 1 ∪ X 2) + sur G ⁡ (X 1 ∩ X 2) ≤ sur G ⁡ (X 1) + sur G ⁡ (X 2) { displaystyle operatorname {sur} _ {G} (X_ {1} cup X_ {2}) + operatorname {sur} _ {G} (X_ {1} cap X_ {2}) leq operatorname {sur} _ {G} (X_ {1}) + operatorname {sur} _ {G} (X_ {2})}

A ограниченное сальдо подмножество — это подмножество X, избыток которого равен избытку всего график (т.е. равен минимуму). Пересечение и объединение плотных множеств с непустым пересечением являются плотными; это следует из свойств ограниченных снизу функций субмодулярного множества.

Для двудольного графа G с def (G; X) = 0 число sur (G; X) является наибольшим целым числом s, удовлетворяющим следующему свойству для каждой вершины x в X: если мы добавим s новых вершин к X и соединим их с вершинами в N G (x), полученный граф будет иметь неотрицательный избыток.

Если G — двудольный граф с положительным избытком, такой, что удаление любого ребра из G уменьшает sur (G; X), то каждая вершина в X имеет степень sur (G; X) +1.

Двудольный граф имеет положительный избыток (относительно X) тогда и только тогда, когда он содержит лес F такой, что каждая вершина в X имеет степень 2 в F.

Графы с положительным избытком играют важную роль в теория графовых структур; см. разложение Галлаи – Эдмондса.

В недвудольном графе функция прибавки, как правило, не является субмодулярной.

Ссылки

Для начала докажем, что .

1. Покажем, что  :

   Пусть . Тогда существует максимальное паросочетание графа , не покрывающее . Поскольку любое максимальное паросочетание графа покрывает , то и более того, если, для некоторой вершины , , то — максимальное паросочетание графа , не покрывающее . Таким образом, .

2. покажем, что :

Предположим, что существует максимальное паросочетание графа , не покрывающее вершину . Пусть — смежная с вершина, а — максимальное паросочетание графа , не покрывающее . Так как , максимальное паросочетание покрывает вершину . Рассмотрим граф — очевидно, он является объединением нескольких путей и чётных циклов. Пусть — компонента связности графа , содержащая . Так как (степень вершины), то — путь с началом в вершине . В пути чередуются рёбра из и , причём начинается путь ребром из . Так как , то вершина a либо не принадлежит пути , либо является её концом (в этом случае последнее ребро пути принадлежит паросочетанию ). Рассмотрим несколько случаев:

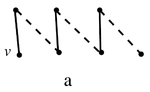
a. Путь кончается ребром из (см. рисунок)
Рассмотрим паросочетание (симметрическая разность
и . то есть, рёбра, входящие ровно в одно из двух множеств).
Очевидно, — максимальное паросочетание графа , не покрывающее , поэтому , противоречие.

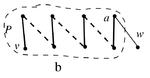
b. Путь кончается ребром из , вершина — конец пути . (см.рисунок)
Рассмотрим паросочетание . Тогда — максимальное паросочетание графа , не покрывающее , поэтому , противоречие.

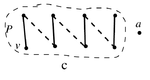
c. Путь кончается ребром из (см. рисунок)
Рассмотрим паросочетание . Тогда , причём . Противоречие с максимальностью паросочетания .

Таким образом, наше предположение невозможно и .
А значит, .

Так как , то все вершины, которые были соседями , таковыми и остались. Однако, по условию , значит .

Так же заметим, что

Наконец, так как , то все максимальные паросочетания в включали . Следовательно, . Заметим, что, взяв любое максимальное паросочетания в и удалив ребро инцидентное , мы получим паросочетание , которое на 1 меньше исходного, при этом . В свою очередь, это самое большое паросочетание, которое мы могли теоретически получить в . Следовательно,

1. Максимальное паросочетание в двудольном графе.

Паросочетанием
называется множество ребер (дуг), не
имеющих общих вершин. Паросочетание с
наибольшим числом ребер называется
максимальным паросочетанием.

Вершина называется
насыщенной в паросочетании М,
если она
является концевой для некоторого ребра,
входящего в М.
Полным
паросочетанием

X
с Y
в двудольном
графе G
= (X
U
Y,E)
называется
такое паросочетание,

что все вершины
из X
являются
насыщенными. Если |X|
= |Y|
, то полное паросочетание называется
совершенным.

Пусть S
– произволное
подмножество X,
а ГS
— подмножество вершин

Y,
смежных с вершинами S.

Полное паросочетание
X
с Y
в двудольном
графе G
= (X
U
Y,E)
существует

тогда и только
тогда, когда |S|

|ГS|
для любого
S

X
(теорема
Холла).

Дефицитом
двудольного графа G
называется
величина

σ (G)
= max
{|S|
|ГS|
}

S

X

Поскольку не
исключается случай S
= 0, то σ (G)
≥ 0.

Основной результат,
касающийся паросочетаний в двудольных
графах,

Заключается в
том, что в максимальное число ребер в
паросочетании

равно |X|
— σ (G)
(теорема
Кенига –Оре) [5].

Заметим, что
полное паросочетание X
с Y
существует
тогда и только тогда,

когда дефицит
двудольного графа равен нулю.

В качестве
примера рассмотрим двудольные графы,
представленные на

рис. 14 и 15.

Не трудно
проверить, что дефицит графа на рис. 14
равен 1, так как существует единственная
положительная разность

|{ x₁,
x_2, x₃
}| — |Г{ x₁,
x_2, x₃
}| = |{ x₁,
x_2, x₃
}| — |{ y₁,
y₂ }| = 1

Граф, представленный
на рис. 15, отличается от графа на рис. 14

наличием pебра
(x₃, y₄).
Дефицит графа на рис. 15 равен 0.
Следовательно, существует полное
паросочетание X с
Y, например,

M
= {(x₁,
y₁),
(x₂,
y₂),
(x₃,
y₄),
(x₄,
y₃)}.

X
Y
X Y

○ y₁
○
y₁

x₁
○
x₁ ○

○ y₂
○
y₂

x₂
○
x₂ ○

○ y₃
○
y₃

x₃
○
x₃
○

○ y₄
○
y₄

x₄
○
x₄
○

○ y₅
○
y₅

Рис. 14
Рис. 15

Приведем
формулировку теоремы Холла в терминах
теории

трансверсалей.

Пусть P
— непустое
множество, а S
= { S_1,
S_2,…,
S_k}
– семейство

Непустых подмножеств
множества P,
причем
допускается, что S_i
= S_J

при i≠j
. Системой
различных представителей или трансверсалью
семейства

S называется
множество k
различных
элементов множества P
, по одному

из каждого S_i.

Например, если
P={1,2,3,4,5,6},
S₁={1,3,4},
S₂={1,3,4},
S₃={1,2,5},
S₄={3,6},

то
T
={1,3,2,6}
множества
S_1,
S_2,
S_3,S₄.

С другой стороны,
если S₅={3,6},
S₆={4},
то для семейства S_1,
S_2,
S_3,S_4
,S_5,S₆

трансверсаль не
существует.

Задача нахождения
трансверсали может быть сведена к задаче
построения полного паросочетания в
двудольном графе G
= (X
U
Y,E),
построенном
следующим образом.

Поставим во
взаимно однозначное соответствие
элементы множества вершин двудольного
графа X
элементам
семейства S
(x_i
↔S_i),
а элементам множества Y
– элементы множества P
(p_i
↔y_i).
Ребро (x_i
,y_j)

E
тогда и только тогда, когда p_i
S_i.

Нетрудно
заметить, что необходимые и достаточные
условия существования трансверсали
эквивалентны условиям существования
полного паросочетания X
с
Y
. Таким образом , для существования
трансверсали семейства подмножеств

S
множества P
необходимо
и достаточно чтобы объединение
произвольных k

подмножеств из S
содержало
не менее k
элементов из P.

Пример 6.
Построим двудольные графы для двух
рассмотренных ранее случаев. На рис.16
приведен граф, когда P={1,2,3,4,5,6},
S
={S_1,
S_2,
S_3,S₄
}, а
на

рис.17
– для
случая,
когда
S
={S_1,
S_2,
S_3,S_4
,S_5,S₆}

○ y₁
(p₁)
x₁
○ ○ y₁

(

S₁)
x₁
○

○ y₂
(p₂)
x₂
○ ○ y₂

(

S₂)
x₂
○

○ y₃
(p₃)
x₃
○ ○ y₃

(
S₃)
x₃
○

○ y₄
(p₄)
x₄
○ ○ y₄

(
S₄)
x₄
○

○ y₅
(p₅)
x ₅
○ ○ y₅

○ y₆
(p₆)
x ₆
○ ○ y₆

Рис. 16
Рис. 17

В первом случае
выполняется условие теоремы Холла, а
во втором –

условие нарушается:
|{ x₁,
x₂, x₄,
x₅, x₆
}| > |{ y₁,
y₃, y₄,
y₆ }|, а
также объединение пяти подмножеств S_1,
S_2, S_4
, S_5, S₆
содержит только четыре

элемента p₁,
p₃, p₄,
p₆.
Следовательно, трансверсаль существует
только в первом случае.

Рассмотрим
алгоритм нахождения максимального
паросочетания в двудольном графе G
= (X U
Y,E)
[6]. Построим транспортную сеть, в

качестве вершин
которой возьмем элементы множеств X
и Y , добавив к ним

исток s
и сток t. Соединим
s с каждой вершиной
x_j
X
дугой (s,
x_j
) с пропускной способностью, равной
1, а каждую вершину y_j
Y
с t дугой
(y_j
,t) с пропускной
способностью, также равной 1, а каждую
вершину x_j
X
с y_j
Y

дугой (x_j
,y_j),
если y_j

Гx_j
, с пропускной способностью, равной
∞ . На рис.19

изображена
транспортная сеть, соответствующая
двудольному графу на рис.18.

Нетрудно заметить,
что число ребер в максимальном
паросочетании равно величине максимального
потока в построенной таким образом
транспортной сети. Используя алгоритм
Эдмондса-Карпа, можно найти максимальное
паросочетание за о(m²n)
шагов, где m — число
дуг, n — число вершин
в построенной транспортной сети. Однако
особый вид этой сети позволяет построить
более эффективный алгоритм, который
рассматривается ниже и носит название
алгоритма Хопкрофта-Карпа.

x₁
∞
y₁

x₁
○ ○ y₁ ○
○ 1

1
x₂ ∞
∞ y₂

x₂
○ ○ y₂
1 ○
○ 1

1
x₃
∞ y₃
1

x₃
○ ○ y₃
○ ○
○ ○

1
x₄
∞ y₄
1

x₄
○ ○ y₄ ○
○

1
x₅
∞ y₅
1

x
₅ ○ ○ y₅ ○
○

Рис. 18
Рис. 19

Пусть M
– паросочетание в графе G
= (X U
Y,E).
Добавляющим путем P
по отношению к M
называется такой путь между ненасыщенными
вершинами

x_j
X
и
y_j
Y
, ребра
которого поочередно входят в E
M
и M.
Если найдется добавляющий путь
P,
то
можно
построить паросочетание
M’
= (MP)
U
(PM),

которое имеет на
одно ребро больше, чем паросочетание
M.
Выбрав
ненасыщенную вершину в X
, можно
строить дерево с чередующимися ребрами

до тех пор, пока
не найдется P
— добавляющий
путь. Если не удается построить

дерево с корневой
вершиной u
, один из путей в котором является P
– добавляющим, то это соответствует
нарушению условия теоремы Холла.

Пример 7.
Пусть необходимо построить совершенное
паросочетание в графе

на рис.20. Начальное
паросочетание M
= {(x₂
,y₁),
(x₃
,y₂)}

x₁
○ ○ y₁ x₁

○

x₂
○ ○ y₂
y₁
y₂

○ ○

x₃
○ ○ y₃

M

x₂
○ ○ x₃

x₄
○ ○ y₄

y₃
○

x
₅ ○ ○ y₅

Рис.20
Рис.21

x₁
○ ○ y₁
○ x₄

x₂
○ ○ y₂

○ y₃

x₃
○ ○ y₃

○ x₂

y₁
y₂

x₄
○ ○ y₄
○
○

x
₅ ○ ○
y₅
x₁
○
○ x₃

Рис.22
Рис.23

Выбираем вершину
x₁,
которая в паросочетании M
ненасыщена, и пытаемся построить P
– добавляющий путь с начальной вершиной
x₁
. На рис.21
ребра начального паросочетания M
изображены непрерывными линиями.
Построение дерева с чередующимися
ребрами заканчивается при построении

P
– добавляющуго пути {
x₁,
y₁,
x₂,
y₃}.
Новое паросочетание M’
= {(x₁
,y₁),

(x₂
,y₃),
(x₃
,y₂)}
на рис.22 содержит на одно ребро больше,
чем паросочетание M.

Теперь
выбираем вершину x₄
и строим дерево с чередующимися ребрами
до тех пор, пока это возможно. Построение
дерева заканчивается на этапе, изображенном
на рис.23. При этом не удается построить
P
– добавляющий путь. Вершины {x₁,
x₂,
x₃,
x₄}
и {y₁,
y₂,
y₃},
включенные в дерево, образуют подмножества
S
и ГS,
на которых нарушается условие теоремы
Холла. Таким образом, граф на рис.20 не
имеет совершенного паросочетания.

Доказано [7], что
число фаз алгоритма Хопкрофта-Карпа не
превышает 2√s
+1,

где s
– наибольшая мощность паросочетания
в графе. Под фазой алгоритма понимается
построение добавляющего пути P
и увеличение паросочетания

M’ =
(MP) U (PM).

Оценим сложность
алгоритма Хопкрофта-Карпа. Каждая фаза
алгоритма имеет сложность о(n²),
которая определяется мощностью входных
данных. Умножая на число фаз, окончательно
получим вычислительную сложность
алгоритма — о(n^5/2)
, где n
— число вершин двудольного графа.

Рассмотрим один
из вариантов задачи о назначении. Пусть
имеется n
рабочих {x₁,
x₂,
…,
x_n}
и n
видов работ
{y₁,
y₂,
…,y_n},
причем каждый рабочий может выполнять
любой вид работы. Каждому назначению
сопоставим число, которое оценивает
эффективность работы рабочего x_i
при выполнении задания y_j
. Требуется назначить рабочих на различные
работы по одному таким образом, чтобы
максимизировать общую эффективность.

Построим двудольный
граф G
= (X
U
Y,E)
, в котором X
— множество вершин, представляющих
рабочих, Y
— множество вершин, представляющих
работы, причем для всех x_i
и y_j
существует ребро (x_i
, y_j).
Припишем каждому ребру (x_i
, y_j)
вес w_i,j
= w(x_i
, y_j),
который показывает эффективность
выполнения работы y_j
рабочим x_i
. Тогда задача об оптимальном значении
соответствует

задаче определения
в таком взвешенном графе совершенного
паросочентания с максимальным весом.
Такое паросочетание называется
оптимальным. Рассмотрим
алгоритм сложности о(n⁴),
предложенный Каном и Мункресом [2] для
решения задачи об оптимальном назначении.

Допустимой
вершинной разметкой называется функция
f,
определенная на множестве X
U
Y
и удовлетворяющая условию f
(x)+
f
(y)
≥ w(x,
y).
Нетрудно

заметить, что
допустимая вершинная разметка всегда
существует, независимо

от веса ребер. Для
этого достаточно положить

f
(x)
= max {
w(x,
y)
},
x X

y
Y

f
(y)
= 0 , y Y

Обозначим через
E_f
подмножество ребер графа, для которых
выполняется условие f
(x)+ f
(y) = w(x,
y). Обозначим через
G_f
подграф, включающий те и только те
ребра, которые принадлежат E_f.

Работа алгоритма
начинается с произвольной допустимой
вершинной разметки f.
Затем строится подграф равенств G_f
и находится максимальное паросочетание
M в G_f.
Если подграф G_f
имеет совершенное паросочетание,
то оно и является оптимальным. Если G_f
не имеет совершенного паросочетания,
то строится новая допустимая вершинная
разметка и новый подграф равенств, в
котором строится максимальное
паросочетание. Для построения максимального
паросочетания используется ранее
рассмотренный алгоритм. В этом алгоритме,
если совершенного паросочетания
построить не удается, то имеем дерево
с чередующимися ребрами, в котором не
существует добавляющего пути и для
некоторого S 
X выполняется
неравенство |S| >|ГS|.
Новая допустима вершинная разметка
вычисляется следующим образом:

f
(z) — d_f
, z
S

f’
(z) =
f (z) +
d_f ,
z ГS

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)