В жизни мы встречаем газообразное состояние вещества, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (он занимает весь предоставленный ему объем), состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояния точно три?
На самом деле, есть еще четвертое — плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Давление газа
Мы только что выяснили, что молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, на каждый квадратный сантиметр за 1 с молекулами воздуха наносится столько ударов, что их количество выражается двадцати трехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул о стенки сосуда приводит к значительному давлению. Это как если бы один комар толкал машину, то она бы и не сдвинулась с места, а вот пару сотен миллионов комаров вполне себе способны эту машину сдвинуть.
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает: давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление
p = F/S
p — давление [Па]
F — сила [Н]
S — площадь [м^2]
То есть, если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы они толкали грузовой автомобиль (просто потому что легковая меньше грузовика).
Из формулы давления следует, что давление на легковой автомобиль будет больше из-за меньшей площади.
Давайте рассмотрим аналогичный пример с двумя сосудами разной площади.
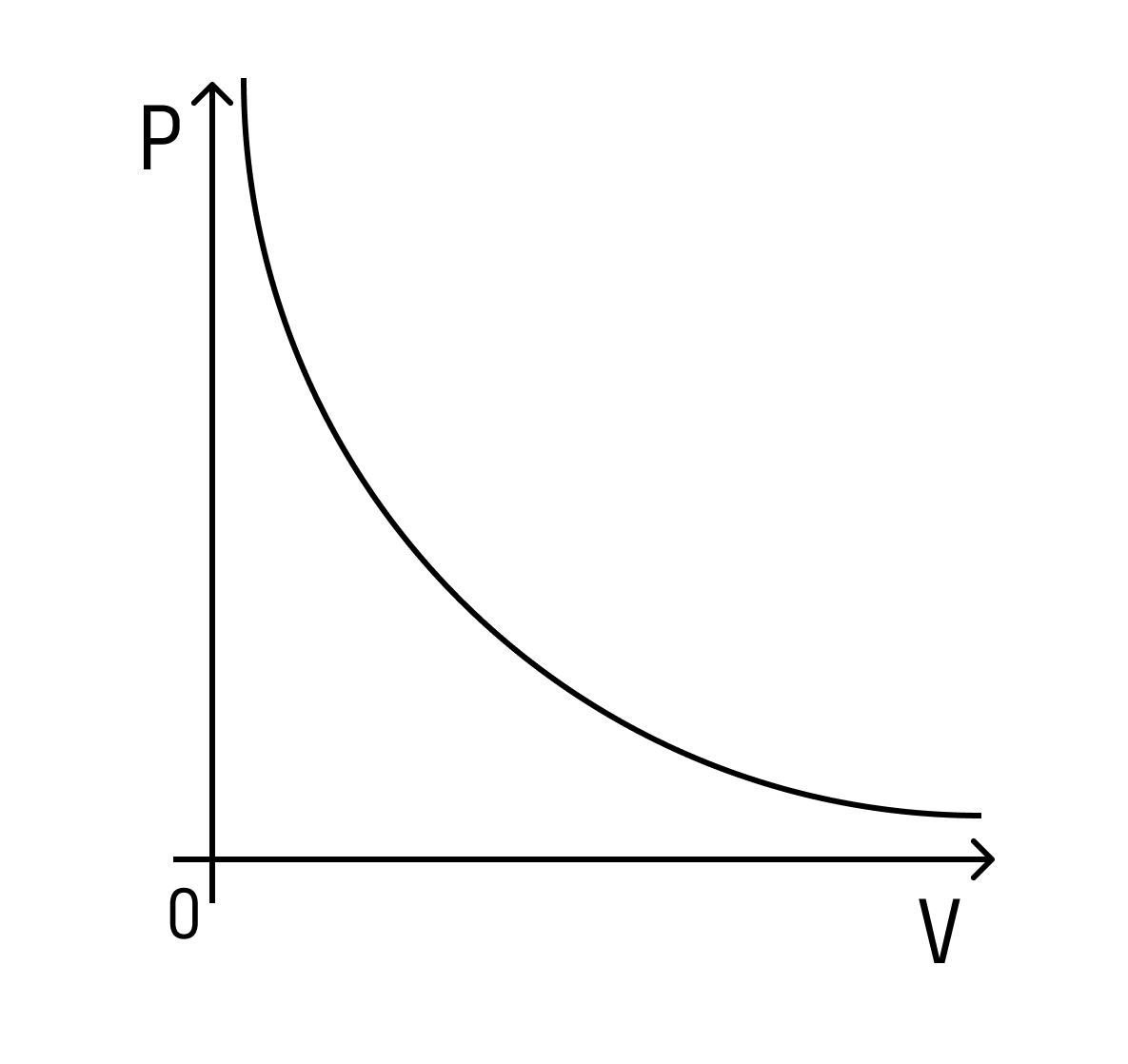
Давление в левом сосуде будет больше, чем во втором, по аналогичной схеме — потому что площадь меньше. Но если площадь основания меньше, то и объем меньше. Это значит, что давление будет зависеть от объема следующим образом: чем больше объем, тем меньше давление — и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Такая зависимость называется законом Бойля-Мариотта.
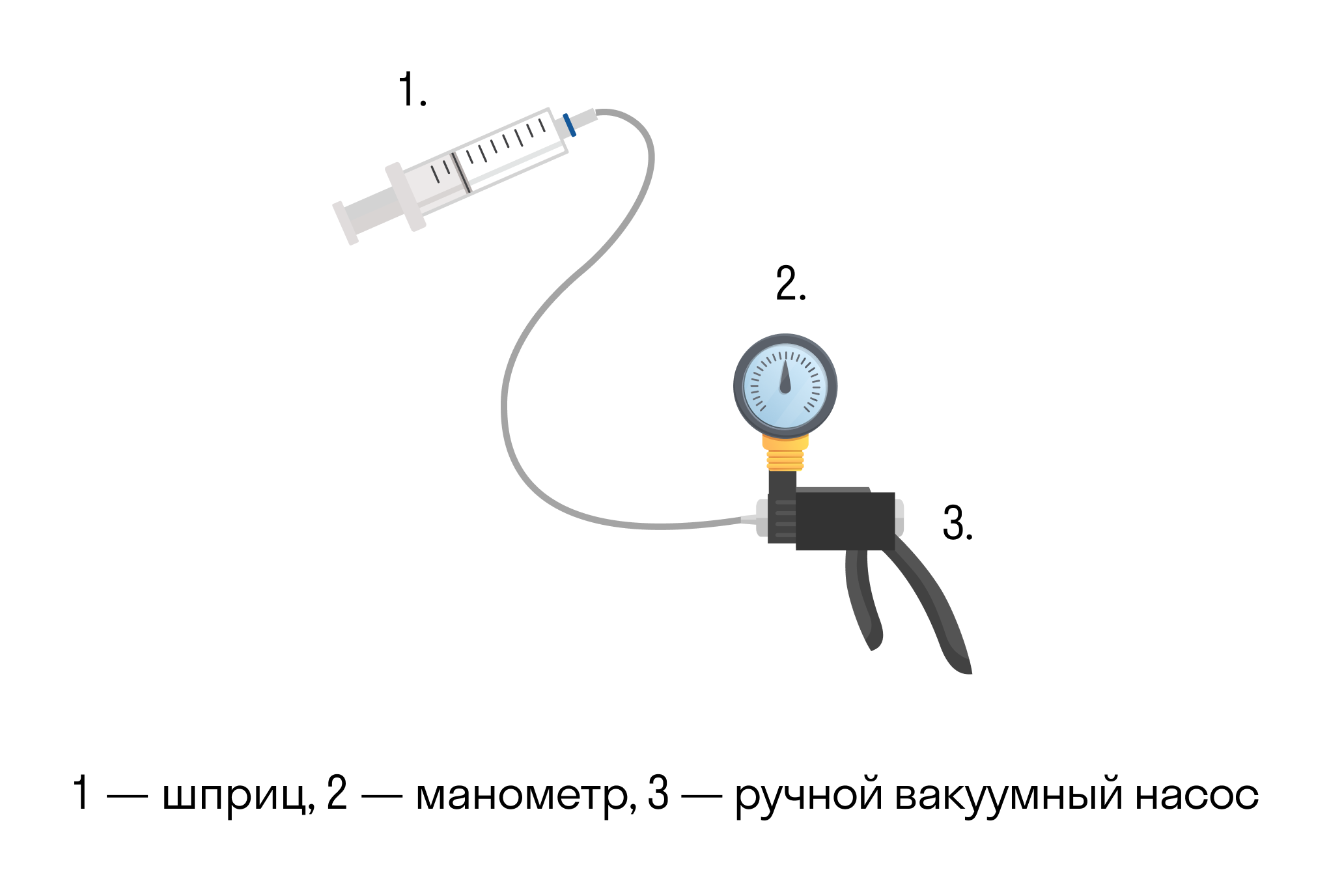
Она экспериментально проверяется с помощью такой установки.
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в Жаком Шарлем.
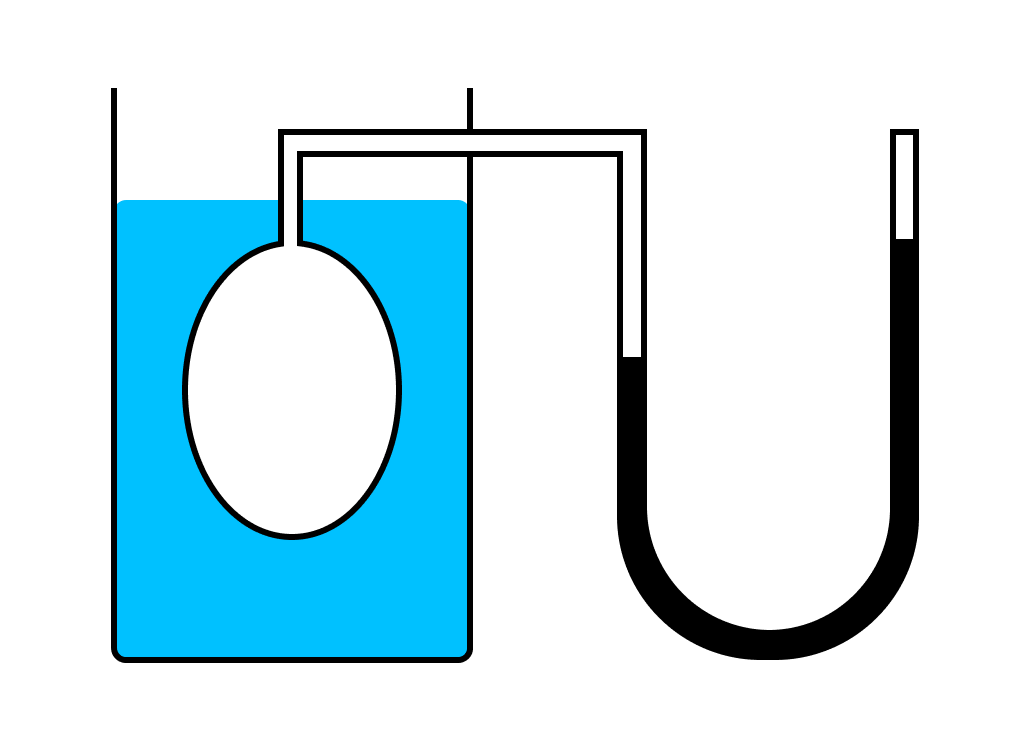
Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке.
Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру, а соответствующее давление — по манометру.
Этот эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейно:
Эта зависимость называется законом Шарля.
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить — их помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или любым способом пытаться сделать в них отверстие, даже после использования.
Загрузить PDF
Загрузить PDF
В химии «парциальным давлением» называют давление, которое оказывает отдельно взятый компонент из газовой смеси внешней среды, например, на колбу, баллон или границу атмосферы. Вы можете подсчитать давление каждого газа, если знаете его количество, какой объем он занимает и какова его температура. Затем вы можете сложить парциальные давления и найти общее парциальное давление смеси газов, или найдите вначале общее давление, а затем — парциальное.
-
1
Примите каждый газ как «идеальный». В химии «идеальный газ» — тот, который взаимодействует с другими веществами, не вступая с ними в соединение. Отдельные молекулы могут сталкиваться друг с другом и отталкиваться, как шары для бильярда, не деформируясь при этом.[1]
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.[2]
- Давление может быть указано в нескольких различных единицах. Одна из них, Паскаль (Па), определяется как сила в 1 ньютон, приложенная к площади в 1 квадратный метр. Другой вариант представления давления — в атмосферах (атм). Эта единица определяется как давление земной атмосферы на уровне моря. Давление в 1 атмосферу равно 101,325 Па.[3]
- Температура идеального газа возрастает при увеличении его объема и снижается при уменьшении объема. Это отношение называют законом Чарльза, по имени Жака Чарльза. Математическая запись закона: k = V / T, где k — константа соотношения между объемом и температурой, V вновь представляет объем газа, а T — его температуру.[4]
[5]
- Температура газов в этих уравнениях приведена в градусах Кельвина, ее можно найти, прибавив 273 к числу градусов Цельсия в температуре газа.
- Эти два отношения можно объединить в одно уравнение: k = PV / T, которое также можно записать как PV = kT.
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.[2]
-
2
Определите количество газов. У газов есть и масса, и объем. Объем обычно измеряют в литрах (л), но есть два варианта подсчета массы.
- Обычно массу измеряют в граммах или, если она достаточно велика, в килограммах.
- Поскольку газы обычно весят очень мало, их масса также вычисляется в отдельной единице измерения, называемой молекулярной массой, или молярной массой. Молярная масса определяется как сумма атомарных весов всех атомов в газообразном веществе, каждый атом сравнивается с массой карбона (12)[6]
- Поскольку атомы и молекулы слишком малы, чтобы работать с ними непосредственно, количество газа определяется в молях. Количество молей в данном газе можно найти, разделив массу на молярную массу, значение отмечается буквой n.
- Мы можем заменить постоянную k константу в уравнении газа числом n, количеством молей (mol), и ввести новую константу R. Тогда уравнение будет записано в виде nR = PV/T или PV = nRT.[7]
- Значение R зависит от единиц, в которых измеряются давление газа, объемы и температура. Для объема в литрах, температуры в Кельвинах и давления в атмосферах, значение равно 0,0821 л атм/K мол. Это можно записать в виде 0,0821 л атм K-1 мол -1, чтобы избежать использования разделительной черты при указании единиц измерения.[8]
-
3
Понимание закона Дальтона о парциальном давлении. Закон, открытый химиком и физиком Джоном Дальтоном, который первым предположил, что химические элементы состоят из отдельных атомов,[9]
гласит: общее давление смеси газов равняется сумме давлений каждого газа в смеси.- Закон Дальтона можно записать в таком виде: Pобщее = P1 + P2 + P3 … с таким количеством слагаемых после знака равенства, каково количество газов в смеси.
- Уравнение закона Дальтона можно расширить при работе с газами, чье индивидуальное давление неизвестно, но для которых известны температура и объем. Парциальное давление газа — такое же, как и для равного объема газа, полностью занимающего отведенный объем.
- Для каждого парциального давления мы можем переписать уравнение идеального газа. Вместо PV = nRT мы может оставить только P в левой части перед знаком равенства. Чтобы сделать это, обе части уравнения нужно разделить на V: PV/V = nRT/V. Две V слева сокращаются, остается P = nRT/V.
- Затем для каждого P справа мы можем выполнить замену, вписав уравнение парциального давления: Pобщее =(nRT/V) 1 + (nRT/V) 2 + (nRT/V) 3 …
Реклама
-
1
Определите уравнение парциального давления для газов, с которыми вы работаете. Для вычислительных целей возьмем пример: в колбе объемом 2 литра содержится 2 газа, нитроген (N2), оксиген (O2) и карбон диоксид, углекислый газ (CO2). Каждого газа — по 10 г, температура каждого газа в колбе равна 37 градусам Цельсия. Нужно найти парциальное давление каждого газа и общее давление смеси газов на емкость.
- Наше уравнение парциального давления будет выглядеть следующим образом: Ptotal = Pнитроген + Pоксиген + Pкарбон диоксид.
- Поскольку мы пытаемся найти давление, которое оказывает каждый из газов, знаем объем и температуру и можем найти количество молей каждого газа, основываясь на массе вещества, мы можем переписать уравнение в следующей форме: Pобщее =(nRT/V) нитроген + (nRT/V) оксиген + (nRT/V) карбон диоксид
-
2
Переведите температуру в градусы Кельвина. Температура по Цельсию равна 37 градусам, потому мы добавим 273 к 37 и получим 310 градусов K.
-
3
Найдите количество молей каждого газа в образце. Число молей газа равно массе газа, деленной на его молярную массу,[10]
которая, как уже говорилось, равна сумме весов всех атомов в составе.- Для нашего первого газа, нитрогена (N2), каждый атом обладает атомарной массой 14. Поскольку нитроген содержит два атома (состоит из двухатомных молекул), мы должны умножить 14 на 2, чтобы найти молярную массу нитрогена, она равна 28. Затем мы делим массу в граммах, 10 г, на 28, чтобы получить количество молей, которое приблизительно равно 0,4 моль.
- У второго газа, оксигена (O2), масса каждого атома равна 16. Оксиген также двухатомный газ, потому мы умножаем 16 на 2 и получаем молярную массу, равную 32. Разделив 10 г на 32, мы получим примерно 0,3 моль оксигена в составе образца смеси газов.
- Третий газ, карбон диоксид (CO2), состоит из 3 атомов: одного атома карбона с атомарной массой 12 и двух атомов оксигена, каждый с атомарной массой 16. Мы складываем все три веса: 12 + 16 + 16 = 44 составляет молярную массу. Разделив 10 г на 44, мы получим примерно 0,2 моля карбон диоксида.
-
4
Подставьте значения для молей, объема и температуры. Наше уравнение будет выглядеть так: Pобщее =(0,4 * R * 310/2) нитроген + (0,3 *R * 310/2) оксиген + (0,2 * R *310/2) карбон диоксид.
- Для простоты мы оставили текущие значения единиц измерения. Эти единицы уйдут после математических вычислений, и останутся только те, которые участвуют в определении давления.
-
5
Подставьте значение константы R. Мы будем указывать парциальное и общее давление в атмосферах, потому используем значение R, равное 0,0821 л атм/K моль. Подстановка этого значения в уравнение дает нам Pобщее =(0,4 * 0,0821 * 310/2) нитроген + (0,3 *0,0821 * 310/2) оксиген + (0,2 * 0,0821 * 310/2) карбон диоксид.
-
6
Подсчитайте парциальное давление каждого газа. Сейчас все значения на месте, пора перейти к математическим вычислениям.
- Чтобы найти парциальное давление нитрогена, умножим 0,4 моль на нашу константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,4 * 0,0821 * 310/2 = 5,09 атм, приблизительно.
- Для получения парциального давления оксигена умножим 0,3 моль на константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,3 *0,0821 * 310/2 = 3,82 атм, приблизительно.
- Чтобы найти парциальное давление карбон диоксида, умножаем 0,2 моль на константу 0,0821 и температуру 310 градусов K, затем делим на 2 литра: 0,2 * 0,0821 * 310/2 = 2,54 атм, приблизительно.
- Теперь сложим полученные значения давлений и найдем общее давление: Pобщее = 5,09 + 3,82 + 2,54, или 11,45 атм, приблизительно.
Реклама
-
1
Определите парциальное давление, как и раньше. Вновь, возьмем в пример колбу на 2 литра с тремя газами: нитрогеном (N2), оксигеном (O2) и карбон диоксидом (CO2). У нас по 10 г каждого газа, температура каждого газа в колбе равна 37 °C.
- Температура по Кельвину будет такой же, 310 градусов, как и раньше, у нас будет примерно 0,4 моль нитрогена, 0,3 моль оксигена и 0,2 моль карбон диоксида.
- Мы также будем указывать давление в атмосферах, потому будем использовать значение 0,0821 л атм/K моль для константы R.
- Таким образом, наше уравнение парциального давления на текущий момент выглядит так же, как раньше: Pобщее =(0,4 * 0,0821 * 310/2) нитроген + (0,3 *0,0821 * 310/2) оксиген + (0,2 * 0,0821 * 310/2) карбон диоксид.
-
2
Сложите количество молей каждого газа в образце, чтобы найти общее количество молей в смеси газов. Поскольку объем и температура одинаковы для всех газов, не говоря о том, что каждая молярная масса умножается на одну и ту же константу, мы можем использовать распределительное свойство умножения и переписать уравнение в следующем виде: Pобщее = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
- Складываем 0,4 + 0,3 + 0,2 = 0,9 моль смеси газов. Это упростит наше выражение до Pобщее = 0,9 * 0,0821 * 310/2.
-
3
Найдите общее давление смеси газов. Умножаем 0,9 * 0,0821 * 310/2 = 11,45 моль, приблизительно.
-
4
Найдите пропорцию каждого газа в смеси. Для этого разделите количество молей каждого газа на общее количество молей в смеси.
- У нас 0,4 моль нитрогена, потому 0,4/0,9 = 0,44 (44 процента) в образце, приблизительно.
- У нас 0,3 моль оксигена, потому 0,3/0,9 = 0,33 (33 процента) в образце, приблизительно.
- У нас 0,2 моль карбон диоксида, потому 0,2/0,9 = 0,22 (22 процента) в образце, приблизительно.
- Хотя в вычислениях выше сумма приблизительных значений в процентах дает всего 0,99, точные значения являются периодическими, так что сумма на самом деле будет равна повторяющимся девяткам после запятой. По определению это то же самое, что 1 или 100 процентов.
-
5
Умножим пропорциональное количество каждого газа на общее давление, чтобы найти парциальное давление.
- Умножаем 0,44 * 11,45 = 5,04 атм, приблизительно.
- Умножаем 0,33 * 11,45 = 3,78 атм, приблизительно.
- Умножаем 0,22 * 11,45 = 2,52 атм, приблизительно.
Реклама
Советы
- Вы заметите небольшую разницу в значениях при вычислении сначала парциального давления, а затем общего, и при подсчете вначале общего, а затем парциального давления. Помните, что приведенные значения даны приблизительно, поскольку они округлены до 1 или 2 знаков после запятой для простоты подсчетов и понимания. Если вы выполняете вычисления самостоятельно без округления, вы заметите или меньшую разницу между значениями или не заметите ее вовсе.
Реклама
Предупреждения
- Знание парциального давления газов может стать вопросом жизни и смерти для дайверов. Слишком низкое парциальное давление кислорода может привести к бессознательному состоянию или смерти, но слишком высокое парциальное давление азота или кислорода также может привести к отравлению.[11]
[12]
Реклама
Вам потребуются
- Калькулятор
- Справочник атомарных весов / молярных масс
Об этой статье
Эту страницу просматривали 82 671 раз.
Была ли эта статья полезной?


Разбор задач из учебника 7 класса
Авторы
Исаченкова Л. А., Лещинский Ю. Д.
Издательство
Народная асвета
Отличный помощник для учеников 7 класса, которые только начинают изучать физику. Главная задача данного сайта: помочь добросовестным ученикам понять ход решения и научиться решать аналогичного рода задачи на занятиях и дома. Все задачи разобраны исключительно в образовательных целях. Автор данного сайта категорически не приветствует списывание. По вопросу репетиторства обращаться по контактам, которые можете найти в разделе «О себе».
Краткое условие задачи №4
Определите давление газа в колбе, если в манометре использована ртуть. Какие значения давления можно измерять этим манометром?

Решение задач предоставлено исключительно в образовательных целях. Все решения защищены авторским правом и принадлежат лидеру данного сайта. Любое копирование данных с данного ресурса без согласия автора — это нарушение закона об авторском праве и смежных правах, которое
ведет к административной и уголовной ответственности
Лучше чем решеба в миллион раз!
Самый крутой ГДЗ по физике. Браво!
Лучший решебник по физике из существующих! В разы лучше чем resheba.top
Моя дочь занималась физикой в период с сентября по май, целью было повысить уровень знаний. Преподаватель пунктуальный и ответственный, хорошо и понятно объясняет, всегда есть наглядный материал для демонстрации лабораторых работ. Помог разобраться с решением задач. Обучение проходило онлайн. Ребенок остался доволен — повысились знания и успеваемость. Рекомендую
Квалифицированный педагог, легко нашел общий язык с подростком. Обьясняет доступно. Сыну нравится заниматься. Оценки стали лучше.
Очень понравился. Сильный преподаватель, быстро нашёл подход к ребёнку, доступно объяснял материал.За год подготовил нас к сдаче ЦТ по физике. Спасибо огромное. Мы рады,что вы с нами работали.
Плюсы: Тактичный, обязательный, современный преподаватель, который может найти подход к ребенку, общается с ним на равных и может вызвать интерес к предмету
Минусы: Не заметили
Описание: О работе репетитора в первую очередь можно судить по успехам ребенка. Мой ребенок стала чувствовать себя в разы увереннее в решении задач по физике и в целом очень повысилось понимание предмета
Дмитрий замечательный специалист. Очень ответственно относится к проведению занятий, даёт много материала в доступной форме. Быстро нашел общий язык с ребенком. Благодаря занятиям с Дмитрием, сын не только повысил свой уровень знаний и школьные отметки, но и физика стала одним из любимых предметов.Очень рекомендую занятия с данным специалистом.
Я сама по образованию педагог, и хочу отметить, что Дмитрий проявил себя как очень ответственный, конструктивно настроенный, эмпатийный профессионал своего дела, который умеет заинтересовать своим предметом и привить интерес. Благодаря занятиям с ним моя дочь выбрала для себя направление профиля «физ.-мат.» в старшей школе. Спасибо!
Плюсы: Пунктуальность, доступная и современная подача материала
Минусы: Нет
Описание: У подростка улучшилась успеваемость по физике, занятиями очень доволен. Однозначно рекомендую!
Выражаю благодарность Дмитрию за его работу. Очень ответственный человек и грамотный преподаватель. Его занятия в онлайн формате организованы и проходят на высоком уровне.
Занятия на 10+, у ребёнка проснулся интерес к физике, школьный балл с 6 поднялся до 9 за одну четверть.
Репетитор понравился. Проводил занятия с подростком и сумел привить интерес к предмету. Материал воспринимается легко, имеются конспекты с основными формулами по всем темам. Много наглядных материалов для лучшего понимания темы. Довольны результатами! Рекомендуем!
Хороший репетитор, доступно изгалагает материал, всегда пунктуален во времени проведения занятий, ребёнку нравиться с ним заниматься и есть результат в повышении уровня знаний. Мы довольны выбором данного репетитора. Рекомендуем.
Самый качественный сайт о физике!
Спасибо вам за качественную работу! Все четко. Отдельно респект за простую навигацию по сайту.
Лучший решебник по физике из существующих! В разы лучше чем resheba.top
решеба физика
физика решебник
решебник по физике
решебник физика
физика гдз
гдз физика
физика
сайт решений задач по физике
решить физику онлайн бесплатно
решить физику онлайн
физика задачи
по физике
учебные материалы по физике
учебники физики
решеба по физике
resheba top
megaresheba
Superresheba
ГДЗ путин
ГДЗ
формулы физика цт
все формулы по физике для цт
формулы по физике для цт
формулы для цт по физике
основные формулы физики
физика формулы
формулы из физики
физика основные формулы
все формулы по физике 7-11 класс
формулы по физике 7-11 класс
формулы по физике с 7 по 11 класс
все формулы по физике 7-11 класс скачать бесплатно
формулы по физике скачать
все формулы по физике скачать
физика основные понятия
дрт 2022 физика
репетиционное тестирование по физике 2014
физика тесты
физика цт задания
физик формулы
формулы по физике
потиху готовлюсь к цт, сайт очень помогает!
Огромное спасибо за Ваш труд. Очень нужное и полезное подспорье, когда закончил школу более 25 лет тому назад.
физику с вашим сайтом
теперь щелкаю как орешки))))
Есть вопросы?
Готовы ответить=)



Полезное

Механика. Кинематика и динамика
Методы физических исследований

Механика. Кинематика и динамика
Измерение расстояний и времени

Механика. Кинематика и динамика
Кинематика прямолинейного движения

Механика. Кинематика и динамика
Относительность движения

Механика. Кинематика и динамика
Первый закон Ньютона

Механика. Кинематика и динамика
Второй закон Ньютона

Механика. Кинематика и динамика
Третий закон Ньютона

Механика. Кинематика и динамика
Упругие деформации. Вес и невесомость

Механика. Кинематика и динамика
Сила всемирного тяготения

Механика. Кинематика и динамика
Сила трения

Механика. Кинематика и динамика
Исскуственные спутники Земли

Механика. Кинематика и динамика
Динамика вращательного движения

Законы сохранения в механике. Механические колебания и волны
Статика

Законы сохранения в механике. Механические колебания и волны
Закон сохранения импульса

Законы сохранения в механике. Механические колебания и волны
Закон сохранения момента импульса

Законы сохранения в механике. Механические колебания и волны
Закон сохранения эннергии в механике

Законы сохранения в механике. Механические колебания и волны
Закон Бернулли

Законы сохранения в механике. Механические колебания и волны
Механические колебания

Законы сохранения в механике. Механические колебания и волны
Механические волны

Законы сохранения в механике. Механические колебания и волны
Звуковые волны

Электромагнитные колебания и волны
Электромагнитные колебания

Электромагнитные колебания и волны
Переменный ток

Электромагнитные колебания и волны
Закон Ома для цепи переменного тока

Электромагнитные колебания и волны
Электромагнитные волны

Электромагнитные колебания и волны
Излучение электромагнитных волн

Электромагнитные колебания и волны
Радио и телевидение

Электростатика. Законы постоянного тока
Электрические заряды

Электростатика. Законы постоянного тока
Потенциал. Разность потенциалов

Электростатика. Законы постоянного тока
Диэлектрики в электрическом поле

Электростатика. Законы постоянного тока
Электроемкость

Электростатика. Законы постоянного тока
Постоянный электрический ток

Электростатика. Законы постоянного тока
Магнитное поле тока

Электростатика. Законы постоянного тока
Движение заряженнных частиц

Электростатика. Законы постоянного тока
Электромагнитная индукция

Электростатика. Законы постоянного тока
Магнетики

Электростатика. Законы постоянного тока
Электрические генераторы и двигатели

Электростатика. Законы постоянного тока
Трехфазная система токов

Электростатика. Законы постоянного тока
Электроизмерительные приборы

Электрический ток в различных средах
Электрический ток в металлах

Электрический ток в различных средах
Проводимость полупроводников

Электрический ток в различных средах
p-n переход

Электрический ток в различных средах
Транзистор

Электрический ток в различных средах
Электронно-лучевая трубка

Электрический ток в различных средах
Электрический ток в газах

Электрический ток в различных средах
Тлеющий разряд

Электрический ток в различных средах
Электрический ток в электролитах

Оптика и специальная теория относительности
Законы распространения света

Оптика и специальная теория относительности
Скорость света

Оптика и специальная теория относительности
Дисперсия света

Оптика и специальная теория относительности
Рентгеновское излучения

Оптика и специальная теория относительности
Применение электромагнитных волн

Оптика и специальная теория относительности
Интерференция света

Оптика и специальная теория относительности
Дифракция света

Оптика и специальная теория относительности
Линзы

Оптика и специальная теория относительности
Оптические приборы

Оптика и специальная теория относительности
Глаз

Оптика и специальная теория относительности
Эксперименнтальные основы СТО

Оптика и специальная теория относительности
Энергия и импульс в СТО

Оптика и специальная теория относительности
Законы сохранения в СТО

Оптика и специальная теория относительности
Масса и энергия частиц в СТО

Молекулярная физика
Дискретное строение вещества

Молекулярная физика
Взаимодействие частиц вещества

Молекулярная физика
Количество вещества

Молекулярная физика
Температура

Молекулярная физика
Давление газа

Молекулярная физика
Уравнение состояния идеального газа

Молекулярная физика
Теплоемкость

Молекулярная физика
Кристаллы

Молекулярная физика
Модели кристаллических решеток

Молекулярная физика
Ионный проектор

Термодинамика
Внутренняя энергия

Термодинамика
Работа газа

Термодинамика
Законы термодинамики

Термодинамика
Паровая машина Ползунова

Термодинамика
Паровая турбина

Термодинамика
Четырехактный двигатель внутреннего сгорания

Термодинамика
Газотурбинный двигатель

Термодинамика
Компрессионный холодильник

Термодинамика
Ракетные двигатели

Термодинамика
Энергетика и энергетические ресурсы

Квантовая физика
Открытие электрона

Квантовая физика
Фотоэффект

Квантовая физика
Спектры

Квантовая физика
Планнетарная модель атома

Квантовая физика
Модель атома водорода по Бору

Квантовая физика
Опыты Франка и Герца

Квантовая физика
Корпускулярно-волновой дуализм

Квантовая физика
Соотношение неопределенностей

Квантовая физика
Лазеры

Квантовая физика
Частицы и античастицы

Физика атомного ядра
Атомное ядро

Физика атомного ядра
Ядерные реакции

Физика атомного ядра
Радиоактивность

Физика атомного ядра
Свойства ионизирующих излучений

Физика атомного ядра
Методы регистрации частиц

Физика атомного ядра
Дозиметрия

Физика атомнного ядра
Допустимые и опасные дозы облучения

Физика атомного ядра
Ядерная энннергетика

Физика атомного ядра
Фундаментальные взаимодействия

Физика атомного ядра
Эволюция вселенной
Давление газа это физическая величина, которая зависит от нескольких факторов: температура, объем и атмосферного давления.
Давление = (число столкновений / секунда)(1/площадь)(импульс / столкновение)
Закон Авогадро позволяет идентифицировать молекулы, присутствующие в газе. На основании этого закона можно объяснить также, почему объемы реагирующих газов находятся в таком же простом отношении, что и числа молей в уравнениях реакций.
Что такое давление газа
Давление — важная характеристика газа. Поэтому возможность объяснения природы давления газа на основании кинетической теории является большим успехом.
Измерение давления газа
Газ оказывает равномерное давление на все стенки сосуда, в который он заключен. Стандартным методом измерения давления является определение высоты столба ртути, уравновешивающего давление газа.
Прибор для измерения давления воздуха показан на рис. , А; он называется барометром. Мы можем сделать барометр сами. Для этого надо наполнить длинную трубку, запаянную с одного конца, ртутью и затем опустить ее открытым концом в сосуд, также наполненный ртутью.
Ртуть из трубки будет стекать в сосуд до тех пор, пока давление столба ртутив трубке не сравняется с давлением воздуха. В приведенном примере давление воздуха равно 755 миллиметрам ртутного столба (755 мм рт ст.).
Эта цифра выражает высоту столба ртути. (Заметим, что в верхней части трубки находятся только пары ртути. При комнатной температуре давление этих паров невелико — приблизительно 10-3 мм рт. ст.
Измерение давления газа барометром
Давление данного газа можно измерить с помощью прибора, аналогичного барометру; он называется манометром. На рис. , Б и В по казаны манометры двух типов. На рис. , Б изображен U-образный манометр с закрытым концом, в котором давление столба ртути уравновешивается давлением газа, находящегося в колбе.
Давление газа в данном случае равно 105 мм рт. ст. Так же, как и в барометре, в верхней части правого колена трубки находятся лишь пары ртути.
Прибор, показанный на рис., В, отличается от этого манометра тем, что в нем правое колено трубки открыто. В манометре такого типа атмосферное давление направлено на столб ртути в правом колене.
Таким образом, давление в колбе и давление столба ртути суммарно точно равны атмосферному давлению. В приведенном примере давление газа составляет 755—650 = 105 мм рт. ст.; при измерении с помощью манометра с закрытым концом было получено такое же давление.
Нормальные условия температуры и давления. В химических опытах часто надо знать два важнейших условия — температуру и давление. Поэтому во время опыта химики обычно измеряют температуру и давление и поддерживают их на определенном уровне.
Кроме того, многие экспериментальные данные полезно привести к общепринятым нормальным условиям температуры и давления. Это облегчает сравнение различных результатов, полученных разными химическими лабораториями.
Температуру 0°С легко достичь и поддерживать с помощью бани с тающим льдом. Большинство термометров калибруется по этой температуре, что в свою очередь облегчает измерения. Температура, которую легко поддерживать и измерять, является хорошим стандартом температуры.
Давление воздуха в различные дни и в разных местах неодинаково. Тем не менее давление воздуха всегда близко к 760 мм рт. ст. Поэтому атмосферное давление является удобным, хотя и приблизительным, нормальным давлением.
Однако для многих целей это давление недостаточно постоянно. По международному соглашению, нормальным давлением для газов является давление столба ртути высотой 760 мм. Это нормальное давление часто записывают просто как одну атмосферу (1 атм).
Нормальная температура и давлением
Таким образом, химики приняли температуру 0° С и давление 1 атм в качестве удобных нормальных условий. Эти условия — температура 0° С и давление 760 мм рт. ст. — называются нормальными температурой и давлением.
Нормальное давление определяется по показаниям стандартного барометра. В стандартном барометре принимается во внимание то, что гравитационное притяжение ртути Землей мало изменяется в зависимости от места и что при нагревании ртуть расширяется и становится менее плотной.
Так, столб ртути в барометре при 20° С на несколько миллиметров выше, чем при 0° С. В стандартном барометре ртуть находится при 0° С. По опубликованным таблицам можно рассчитать, насколько различаются показания обычного и стандартного барометров.
Поправка редко превышает 1—2 мм рт. ст. и часто пренебрежимо мала по сравнению с другими возможными ошибками. Если другие ваши измерения недостаточно точны, не следует вносить поправку в показания обычного барометра.
Причина возникновения давления газа
Газ оказывает давление в результате столкновения его частиц со стенками сосуда. Такая модель давления газа составляет часть кинетической теории. Каждый раз, когда молекула газа сталкивается со стенкой (или с поверхностью ртути), она оказывает на стенку небольшое давление, подобно тому как давит на стену брошенный в нее мяч.
Действующая на единицу поверхности сила, называемая давлением, прямо пропорциональна числу молекул, сталкивающихся с единицей площади поверхности.
Если в данном объеме содержится вдвое больше молекул, то число столкновений на единицу поверхности также увеличится вдвое и, следовательно, давление возрастет в 2 раза по сравнению с первоначальным.
Именно этим объясняется увеличение давления в автомобильной шине, когда в нее накачивается воздух. Если объем и температура шины не изменяются, то давление возрастает прямо пропорционально числу молей накачиваемого воздуха.
Упражнение для самообразования
Сосуд определенного объема содержит 2 моля газа при комнатной температуре. Давление в сосуде — 4 атм. В сосуд вводят еще 3 моля газа при той же температуре.
На основании приведенных выше рассуждений покажите, что теперь давление равно 10 атм.
Парциальное давление
Парциальное давление — это такое давление, которое оказывал бы газ, если бы в сосуде находился он один.
На рисунке изображены три колбы емкостью 1 л при 25° С. В первой колбе содержится 0,0050 моля воздуха. Манометр показывает, что давление равно 93 мм рт. ст.
Во второй колбе находится 0,0011 моля паров воды. Давление в этой колбе равно 20 мм рт. ст. В третьей колбе содержится смесь 0,0050 моля воздуха и 0,0011 моля паров воды.
Третий манометр показывает, что давление в этой колбе равно 113 мм рт. ст.
Этот опыт показывает, что давление смеси газов точно равно сумме давления воздуха и давления паров воды:
113 мм рт. ст. = 93 мм рт. ст. + 20 мм рт. ст. (4)
Общее давление можно рассматривать как сумму давлений, создаваемых каждым компонентом смеси.
Давление, оказываемое каждым газом газовой смеси, называется парциальным давлением этого газа.
В примере, приведенном на рис. 2 -3, общее давление в третьей колбе равно 113 мм рт. ст. Парциальное давление паров воды равно 20 мм рт. ст., парциальное давление воздуха — 93 мм рт. ст.
Упражнение для самообразования
Предположим, что в 0,0050 моля воздуха содержится 0,0040 моля азота N2 и 0,0010 моля кислорода О2. Каково парциальное давление кислорода в первой колбе, показанной на рис. 2-3? Каково парциальное давление кислорода в третьей колбе?
Результаты опыта, иллюстрированного рис. 2-3, легко объяснить с помощью кинетической теории газов.
Молекулы газа находятся на таком большом расстоянии друг от друга, что каждая из них ведет себя независимо, внося свою долю в общее давление в результате столкновений со стенками сосуда Молекулы воды в третьей колбе редко сталкиваются друг с другом или с молекулами воздуха.
Поэтому они оказывают точно такое же давление, как и во второй колбе, — давление, которое существовало бы в третьей колбе в отсутствие воздуха.
Давление, создаваемое 0,0011 моля паров воды, будет равно 20 мм рт. ст. независимо от того, имеется ли в колбе воздух. 0,0050 моля воздуха создают давление 93 мм рт, ст. независимо от того, имеются ли в колбе пары воды.
Сумма парциальных давлений 93 и 20 мм рт. ст. определяет общее давление в колбе.
Температура и кинетическая энергия
Если кинетическая теория применима к газам, то можно ожидать, что давление зависит не только от числа молей в единице объема. Например, масса молекул и скорость их движения также имеют большое значение.
Как известно, волейбольный мяч ударяется в руку игрока с большей силой, чем мяч для настольного тенниса, летящий с той же скоростью. Быстро летящий мяч ударяет сильнее, чем мяч, летящий медленно.
Для того чтобы выяснить, какое значение в кинетической теории имеют масса и скорость молекул, рассмотрим понятие о температуре.
Чтобы измерить температуру газа, мы погружаем в него термометр. Если термометр холоднее, чем система, то определенное количество тепла передается термометру до тех пор, пока газ и термометр не будут иметь одинаковую температуру.
При этом термометр показывает числовое значение температуры. Если термометр нагрет сильнее, чем газ, то определенное количество тепла передается от него системе Если же передачи тепла не происходит, то говорят, что термометр находится в тепловом равновесии с газом.
Типы термометров
Существует несколько типов термометров. В термометрах можно использовать любое вещество, которое обладает легко измеряемым свойством, чувствительным к изменению температуры. Действие обычного ртутного термометра основано на том, что при повышении температуры жидкость расширяется.
Объем твердых веществ и газов также изменяется в зависимости от температуры. Поэтому и эти вещества можно использовать в термометрах. Если газ поддерживать при постоянном объеме, то с увеличением температуры возрастает давление.
Такой метод наиболее часто используется для измерения температуры: объем газа поддерживают постоянным, при этом давление изменяется в зависимости от температуры.
Измерение температуры газа термометром
Измерим температуру газа А, приведя его в контакт с газом Б (наш термометр). Если эти два газа в начальный момент имеют различные температуры, то произойдет передача тепла.
Тепло от более нагретого газа будет передаваться менее нагретому. Когда передача тепла прекратится, газы достигнут теплового равновесия. Теперь оба газа имеют одинаковую температуру.
То, что при этом происходит, можно представить с помощью кинетической теории газов. Предположим, что температура газа А выше, чем газа Б. Мы объясняем тем, что молекулы газа А обладают большей энергией движения по сравнению с энергией движения молекул газа Б — молекулы газа А имеют более высокую кинетическую энергию (в среднем).
Когда газы соприкасаются, быстро движущиеся молекулы газа А при соударении могут передавать кинетическую энергию медленно движущимся молекулам Б. В результате этого переноса кинетической энергии от газа А к газу Б повышается температура газа Б и понижается температура газа А.
Когда переход кинетической энергии от одного газа к другому в результате теплового контакта между молекулами газов А и Б заканчивается, эти газы находятся в тепловом равновесии; они имеют одинаковую температуру.
Таким образом, теплообмен между двумя газами мы представляем как переход кинетической энергии. Этот процесс длится до тех пор, пока молекулы обоих газов не приобретут одинаковую среднюю кинетическую энергию.
Результатом этого является достижение обоими газами одинаковой температуры. Это и есть основная предпосылка кинетической теории: если газы находятся при одной и той же температуре, их молекулы имеют одинаковую среднюю кинетическую энергию.
Абсолютная температура
(В этих опытах давление сохранялось постоянным.) Эти соотношения выводятся на основании простого опыта. В узкую стеклянную трубку длиной 0,5 м, запаянную с одного конца, помещают каплю ртути.
Эта капля удерживается воздухом на некоторой высоте. Поскольку трубка имеет равномерное сечение, мы можем принять высоту слоя воздуха до капли ртути за меру его объема.
Ртутная пробка может перемещаться вверх или вниз, благодаря чему в трубке сохраняется постоянное давление.
Мы можем поместить трубку в ледяную воду (0° С) и измерить относительный объем воздуха. Если трубку перенести в кипящую воду (100° С при 1 атм), то относительный объем увеличится.
По результатам этих измерений и результатам аналогичных измерений, полученным для других температур, можно составить приведенную ниже таблицу 1.
|
Таблица 1 |
|
|
Температура, °С |
Относительный объем (измеренный по высоте слоя воздуха) |
|
200 |
1,73 |
|
100 |
1,37 |
|
50 |
1,18 |
|
0 |
1,00 |
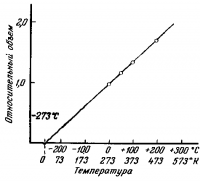
Если мы отложим значения относительного объема на оси ординат (вертикальная ось), а температуру на оси абсцисс (горизонтальная ось), то получим график, изображенный на рис. 3.
Через экспериментальные точки проходит прямая линия. Если продолжить прямую линию вверх, то можно видеть, что объем воздуха при 273° С вдвое больше, чем при 0° С.
Если продолжить эту линию вниз, то получается, что объем становится равным нулю при.—273°С. Изменение объема при изменении температуры на 1°С составляет 1/273 объема при 0° С. В действительности все газы сжижаются еще до того, как их температура достигнет —273° С.
Если газ нагревать или охлаждать при постоянном объеме, то его давление тоже изменяется на 1/273 давления при 0° С. Давление газа становится равным нулю при —273° С. Согласно кинетической теории, при этой температуре движение молекул прекращается. Кинетическая энергия становится равной нулю.
Абсолютная шкала температур
Абсолютная шкала температур обладает тем преимуществом, что ее нуль соответствует —273° С. В то время как «нуль» стоградусной шкалы выбран произвольно (температура плавления льда), нулевая точка абсолютной шкалы имеет определенный смысл в кинетической теории.
Если мы выражаем температуры в абсолютных градусах, то при этом объем определенного количества газа (при постоянном давлении) прямо пропорционален температуре.
В соответствии с кинетической теорией кинетическая энергия молекул прямо пропорциональна абсолютной температуре. По этой причине мы часто выражаем температуру по абсолютной шкале.
Эта шкала температур, имеющая такую же единицу измерения (градус), что и стоградусная шкала, называется шкалой Кельвина.
Температура по этой шкале выражается в градусах Кельвина (° К). На рис. 4-5 приведены значения температуры, выраженные в градусах Кельвина и по стоградусной шкале — в градусах Цельсия.
Все числовые значения по шкале Кельвина на 273 градуса выше, чем соответствующие температуры, выраженные в градусах Цельсия.
Упражнение для самообразования
а) Выразите следующие температуры в градусах Кельвина:
Температура кипения воды 100°С Температура замерзания ртути 38,9°С Температура кипения жидкого, азота —196°С
б) Выразите следующие температуры в градусах Цельсия:
Температура плавления свинца 600 °К Комнатная температура 298 °К Температура кипения жидкого гелия 4°К.
2) При реакции 2,0 • 10-3 моля металлического магния Mg с соляной кислотой НСl выделяется газообразный водород, который при 25° С и давлении 1 атм занимает объем 49,0 мл.
а) При реакции 1 моля магния с соляной кислотой выделяется 1 моль водорода. Вычислите объем 1 моля водорода при 25° С (298° К) и давлении 1 атм.
б) Вычислите объем 1 моля водорода при 0° С (273° К) и давлении 1 атм.
Как указывалось выше, при температуре 0° К всякое движение молекул прекращается. Кинетическая энергия становится равной нулю.
При температурах, близких к 0° К, наблюдаются очень интересные явления (например, сверхпроводимость многих металлов и сверхтекучесть жидкого гелия). В связи с этим ученые весьма заинтересованы в достижении температур, как можно более близких к абсолютному нулю.
Для охлаждения очень часто используют жидкий водород (кипящий при 20° К) и жидкий гелий (кипящий при 4° К). При пониженном давлении гелий кипит при еще более низкой температуре, и это обеспечивает достижение температур, близких к 1° К.
Разработаны другие более сложные методы, с помощью которых может быть достигнута температура до 0,001° К. Однако в этих условиях термометрия становится такой же трудной, как и сам метод достижения низких температур.
Закон Авогадро и кинетическая теория
Кинетическая теория основана на предположении, что если два газа находятся при одной и той же температуре, то молекулы этих газов имеют одинаковую среднюю кинетическую энергию.
То, что с помощью этой теории можно объяснить закон Авогадро, является одним из наиболее важных ее успехов.
Мы можем представить закон Авогадро в такой форме: если два газа при одной и той же температуре имеют одинаковое число частиц в данном объеме, то они должны оказывать одинаковое давление. Масса молекулы, а также скорость ее движения должны влиять на давление.
Если молекулы двух газов имеют различные массы, то у них должны быть и разные скорости, чтобы кинетическая энергия оставалась постоянной. Более легкие молекулы должны двигаться быстрее, поэтому они будут сталкиваться со стенками сосуда за 1 сек большее число раз.
Более частые столкновения се стенками сосуда молекул с меньшей массой как раз и компенсируют более слабый «удар» этих молекул при каждом столкновении.
Все это очень хорошо согласуется с законом Авогадро: два газа, занимающие одинаковый объем и находящиеся при одной и той же температуре, оказывают на стенки сосуда одинаковое давление, несмотря на то что массы их молекул различны.
Объяснение закона Авогадро
Закон Авогадро легко можно доказать. Кинетическая энергия движущейся частицы выражается уравнением
КЭ = 1/2 mυ2 (5)
где т — масса частицы; υ — скорость движения частицы. Таким образом, для газов А и Б с одинаковой температурой мы имеем
(КЭ)А = (КЭ)Б (6)
или
mАυ2А=тБυ2Б (7)
Теперь предположим, что мы поместили п молекул в кубический сосуд со стороной d. Давление определяется числом столкновений молекул со стенками в 1 сек на 1 см2, умноженным на импульс, передаваемый за одно столкновение:
Давление = (число столкновений / секунда)(1/площадь)(импульс / столкновение)
Импульс зависит от массы и скорости частицы. Частица приближается к стенке с импульсом mv и после удара отскакивает от нее с тем же по величине импульсом, но с противоположным знаком. Поэтому импульс, переданный стенке, равен
Импульс = 2mυ (9)
С другой стороны, число столкновений со стенкой в 1 сек зависит от размеров сосуда и скорости частицы (так как молекула отскакивает от одной стенки к другой и обратно). Мы можем предположить, что треть молекул движется взад и вперед в данном направлении между двумя противоположными стенками.
Поэтому если в сосуде находится п молекул, то п/3 молекул ударяются в эти две стенки. Столкновение с одной из стенок происходит тогда, когда молекула пройдет расстояние между стенками d и обратно, т. е. общий путь равен 2d.
Число столкновений/секунда = число частиц в обоих направлениях/время за которое проходит путь 2d
Число столкновений/секунда = (n/3)/(2d/υ) = (n/3)(υ/2d) = nυ/6d (10)
Комбинируя уравнение находим, что
Давление = (Число столкновений/секунда)(1/Площадь)(Импульс/столкновение) = (1nυ/6d)(1/d2)2mυ = 1/3(n/d3)(mυ2) (11)
Применив уравнение к каждому из двух газов получим
PA = 1/3(nA/d3)(mAυ2A) (12)
PБ = 1/3(nБ/d3)(mБυ2Б) (13)
Если газы имеют одинаковое давление (РА= РБ), мы можем приравнять уравнения (12) и (13):
1/3(nA/d3)(mAυ2A) = PБ = 1/3(nБ/d3)(mБυ2Б) (14)
Если температура обоих газов одинакова, то справедливо уравнение (7). Тогда уравнение (14) принимает вид
nA/d3 = nБd3
Таким образом, мы видим, что при одинаковых температуре и давлении два газа имеют равное число молекул в единице объема. А это и есть закон Авогадро.
Идеальный газ
Это газ, который ведет себя так, как будто между его молекулами не существует никакого взаимодействия, называется идеальным газом.
Экспериментальные данные о давлении и объеме для кислорода, аммиака и хлористого водорода. В каждом случае в пределах ошибки опыта наблюдается определенная закономерность: PV = const.
Многочисленные опыты подтвердили, что большинство газов подчиняется этой простой закономерности. Из этого общего правила есть и исключения, как и в случае других научных утверждений.
Любое правило выводится на основании ряда измерений, каждое из которых допускает некоторую неточность, поэтому постоянство PV установлено только в определенных пределах ошибки. Более того, существуют пределы давления, в которых можно изучать поведение газов.
Пример идеального газа
Например, рассмотрим данные для 17,0 г аммиака при 0° С, . По этим данным PV = 24,5, но для этой величины должны быть учтены ошибки измерения и пределы применимости этих данных. В этом случае ошибка равна ±0,7, а пределы давления составляют 0,2—2 атм.
На основании этих данных можно сделать вывод, что произведение объема и давления — постоянная величина, выраженная четырьмя цифрами: PV = 24,50. Однако нельзя сказать с полной уверенностью, что это произведение будет постоянным за пределами 0,2—2 атм, установленными для давления.
Напомним, что правило справедливо лишь в тех пределах, в которых проводились опыты. Если требуется более высокая точность измерений давления и объема при более высоком давлении, то необходимо проводить дополнительные опыты. В приведены результаты таких более точных измерений давления и объема.
Наиболее поразительным в табл. 2 является значительное отклонение от PV = 24,5, наблюдаемое при давлении выше 9,800 атм. Соотношение PV = const больше не соблюдается. Это показывает, насколько осторожно нужно производить экстраполяцию полученных данных за установленные пределы.
Даже при более низком давлении, чем давление, при котором происходит конденсация, произведение давления и объема не совсем постоянно.
Проводя измерения с достаточной тщательностью и точностью, мы убеждаемся, что произведение PV для аммиака при 25° С не является постоянным. Оно изменяется от 24,45 при 0,1000 атм до 23,10 при 9,800 атм, когда уже начинается конденсация.
Подобные измерения с 28,0 г окиси углерода при 0° С показывают, что произведение PV равно 22,410 при 0,2500 апгм, но при давлении 4,000 атм это произведение становится равным 22,308. Такой тип отклонения от постоянной величины является общим для всех газов.
В результате тщательных измерений установлено, что ни для одного газа не соблюдается идеально соотношение PV = const при всех давлениях. С другой стороны, все газы подчиняются этому правилу приблизительно, и соответствие улучшается при уменьшении давления.
Таким образом, мы нашли, что при понижении давления каждый газ приближается к идеальному газу, для которого PV = const.
Объяснение образования идеального газа
Для отклонения от правила имеется разумное объяснение. Кинетическая теория, «объясняющая» поведение газа, основана на предположении, что между частицами газа не существует взаимодействия. Но реальные молекулы взаимодействуют друг с другом!
Конденсация любого газа при охлаждении показывает, что между частицами действуют силы притяжения. Эти силы не имеют существенного значения, когда молекулы находятся далеко друг от друга (т. е. при низких давлениях), но они становятся заметными при более высоких давлениях.
Теперь мы убедились, что кинетическая теория справедлива для «идеализированного» газа, т. е. для газа, в котором отсутствует взаимодействие между молекулами.
Каждый реальный газ приближается к такому идеальному поведению при достаточно низком давлении. В этих условиях молекулы в среднем настолько удалены друг от друга, что силы притяжения незначительны.
Давление и объем аммиака
Результаты точных измерений давления и объема для 17.0 г аммиака при 25°С Таблица 2
| Давление, атм | Объем, л | PV |
| 0,1000 | 244,5 | 24,45 |
| 0,2000 | 122,2 | 24,44 |
| 0,4000 | 61,02 | 24,41 |
| 0,8000 | 30,44 | 24,35 |
| 2,000 | 12,17 | 24,34 |
| 4,000 | 5,975 | 23,90 |
| 8,000 | 2,925 | 23,40 |
| 9,800 | 2,360 | 23,10а |
| 9,800 | 0,020 | 0,20б |
| 20,00 | 0,020 | 0,40в |
| 50,00 | 0,020 | 1,0в |
а Начинается конденсация.
б Газа не остается, только жидкость.
в Жидкость.
Молярные объемы газов
Молярные объемы некоторых газов при температуре 0°С и давлении 1 атм Таблица 3
| Газ | Формула | Молекулярный вес, г | Молярный объем, л |
| Водород | Н2 | 2,0160 | 22,430 |
| Гелий | Не | 4,003 | 22,426 |
| («Идеальный» газ) | — | — | (22,414) |
| Азот | N2 | 28,016 | 22,402 |
| Окись углерода | СО | 28,011 | 22,402 |
| Кислород | О2 | 32,000 | 22,393 |
| Метан | CH4 | 16,043 | 22,360 |
| Двуокись углерода | СО2 | 44,011 | 22,262 |
| Хлористый водород | HCl | 36,465 | 22,248 |
| Аммиак | NH3 | 17,032 | 22,094 |
| Хлор | Сl2 | 70,914 | 22,063 |
| Двуокись серы | SO2 | 64,066 | 21,888 |
Закон Авогадро согласуется с кинетической теорией. Следовательно, идеальный газ подчиняется закону Авогадро. При 0° С и давлении 1 апгм 1 моль (6,02•1023 молекул) идеального газа занимает объем 22,414 л.
Насколько близко реальные газы приближаются к идеальному газу при 0° С и 1 атм, показывают измерения молярного объема — объема, занимаемого 1 молем этого газа. В табл. 3 приведены молярные объемы некоторых газов.
Реальные газы при 0° С и 1 атм близки к идеальному газу (до трех значащих цифр). Каждый газ становится идеальным при уменьшении давления до нуля.
Давление газа вывод
Закономерности, наблюдаемые в поведении газов, в значительной мере помогают понять структуру вещества. Одной из наиболее важных закономерностей является гипотеза Авогадро: одинаковые объемы газов содержат равное число частиц (при одинаковых температуре и давлении).
Эта зависимость используется при определении молекулярных формул веществ, которые необходимо знать для того, чтобы понять природу химической связи.
Согласно кинетической теории, если два газа находятся при одинаковой температуре, то молекулы этих газов обладают одинаковой средней кинетической энергией.
При изменении температуры газа при постоянном давлении объем прямо пропорционален температуре, если температура выражена в градусах абсолютной шкалы.
Температура плавления льда (0° С) по этой шкале (называемой шкалой Кельвина) равна 273° К. Температура кипения воды при 1 атм (100° С) равна 373° К- Предполагается, что при температуре, равной нулю по шкале Кельвина, прекращается всякое движение молекул.
Все эти данные подтверждают в справедливость атомно-молекулярной теории и способствуют ее дальнейшему развитию.
Предположения, принятые при рассмотрении газов, применимы также и в случае конденсированных фаз — жидкостей и твердых веществ.
Вопросы и задачи для самообразования
1. Сколько молекул содержится в молярном объеме газа при 100° С? При 0°С?
2. Определите молярный объем воды в каждом из следующих случаев:
а) Твердое вещество, 0° С; плотность льда 0,915 г/см3.
б) Жидкость, 0° С; плотность воды (жидкость, 0°С) 1,000 г/см3.
в) Газ, 100° С; плотность паров воды (100° С, 1 атм) 5,88•10-4 г/см3.
3. Каков молекулярный вес газа, если при 0° С и 1 атм 1,00 л газа весит 2,00 г?
4. При реакции двуокиси серы с кислородом образуется трехокись серы:
2SO2 (г) + O2 (г) →2SO3 (г)
5. Стеклянная колба после удаления из нее воздуха весит 108,11 г. Наполненная кислородом при комнатной температуре и давлении 1 атм колба весит 109,56 г. Если эту колбу наполнить вулканическим газом при таких же условиях, то она будет весить 111,01 г. Какая из указанных формул для вулканического газа соответствует приведенным данным:
(CO2, OCS, Si2H6, SO2) (NF3, SO3, S8, CO2 + Kr).
6. Сжатый газообразный кислород находится в стальном баллоне емкостью 40 л при давлении 130 атм.
а) Сколько молей кислорода содержится в полном баллоне?
б) Сколько это составляет килограммов?
В огнетушителе емкостью 3 л находится 4,4 кг двуокиси углерода. Какой объем будет занимать это количество газа при нормальных условиях?
8. Для наполнения метеорологических зондов часто применяют водород, полученный при реакции гидрида кальция СаН2 с водой. При этом образуются гидроокись кальция и газообразный водород.
а) Напишите уравнение реакции и определите, сколько молей СаН2 потребуется для наполнения водородом зонда емкостью 250 л при нормальных условиях температуры и давления.
б) Сколько расходуется воды для получения такого количества водорода?
Содержание:
- Свойства газов
- Давление газов
- Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
- Зависимость между плотностью газа и его давлением
- Зависимость объёма газа от температуры. Закон Гей-Люссака
- Зависимость давления газа от температуры. Закон Шарля
- Абсолютная шкала температур
- Зависимость между объёмом, давлением и температурой газа
- Физическая сущность понятия абсолютного нуля
- Изменение температуры газа при быстром расширении и сжатии
- Применение сжатых газов
Газ — это одно из трёх основных агрегатных состояний вещества, характеризующееся очень слабыми связями между составляющими его частицами (молекулами, атомами или ионами), а также их большой подвижностью. Частицы газа почти свободно и хаотически движутся в промежутках между столкновениями, во время которых происходит резкое изменение характера их движения.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Свойства газов
Главные свойства газов – это подвижность и хаотичное движение частиц, направление которых меняется при столкновении. Газ – одно из 4 агрегатных состояний веществ, которые на сегодняшний день известны науке.
Давление газов
Всякий газ производит давление на оболочку, внутри которой он находится.
Давление, производимое газом на стенки сосуда, объясняется ударами движущихся молекул.
При ударе о стенку молекулы газа отдают ей определённое количество движения; стенка испытывает при этом действие некоторой силы.
Удар каждой отдельной молекулы о стенку сосуда производит очень небольшое действие. Но молекул газа очень много, удары о стенки сосуда происходят беспрерывно, поэтому в результате получается значительное давление.
Хаотичность движения молекул приводит к тому, что давление газа одинаково во всех направлениях.
При нагревании давление газа увеличивается. Так как при этом число молекул газа не изменяется, то увеличение давления можно объяснить только тем, что удары молекул о стенки заключающего газ сосуда делаются при нагревании чаще и что каждый удар становится сильнее. Удары же могут стать чаще и сильнее, если увеличивается скорость движения молекул. Это подтверждается, как мы видели (гл. V), многочисленными опытами.
Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
Состояние газа определяется его объёмом, давлением и температурой. С изменением этих величин меняется и состояние газа. Мы будем рассматривать последовательно процессы, при которых одна из величин, характеризующих состояние газа, постоянна, а две другие меняются.
Изучим сначала такой процесс, при котором давление и объём газа изменяются, а температура остаётся постоянной. Такой процесс называется изотермическим 1.
1 От греч. слов: изос — равный, термос — тёплый.
Итак, рассмотрим, как изменяется давление данной массы газа при изменении его объёма, если температура газа не меняется.
Опыты, устанавливающие эту зависимость, можно произвести на приборе, три положения которого изображены на рисунке 134.
Рис. 134. Прибор для установления зависимости между объёмом и давлением газа (в трёх положениях).
В этом приборе стеклянная трубка А соединяется резиновой трубкой с другой стеклянной трубкой В. Трубка А вверху снабжена краном 
Откроем кран 
Поднимем теперь трубку В вверх на столько, чтобы объём воздуха в трубке А уменьшился вдвое (положение II). Уровень ртути в трубке В при этом значительно поднимется над уровнем в трубке А.
Рассмотрим теперь, чему будет равно давление воздуха в трубке А. Это давление уравновешивает атмосферное давление и давление всего столба ртути в трубке В, стоящего выше уровня n1 высота этого столба n1n оказывается равной 76 см. Таким образом, давление воздуха в трубке А уравновешивает не одну, как в первом случае, а две атмосферы (р2 = 2 am).
Значит, с уменьшением объёма данной массы газа в два раза давление его увеличивается в два раза. Если уменьшить объём газа в 1,5; 2,5; 3 раза, то соответственно в 1,5; 2,5; 3 раза увеличится его давление.
Опустим теперь трубку В так, чтобы масса воздуха в трубке А заняла вдвое больший объём (положение III). Уровень ртути в трубке А при этом понизится. Атмосферное давление теперь уравновешивает давление воздуха в трубке А и давление столба ртути от уровня n в трубке А до уровня в трубке В. Измерения показывают, что высота этого столба ртути равна 38 см. Давление, производимое воздухом в трубке А, найдём, вычтя из атмосферного давления давление столба ртути: р3 = 76 см—38 см = 38 см; следовательно, р3 = 0,5 am.
Итак, при увеличении объёма газа в два раза его давление уменьшается в два раза.
Перемещая трубку В в различные положения и отсчитывая каждый раз объём и давление воздуха в трубке А, найдём, что при уменьшении объёма исследуемой массы воздуха в некоторое число раз давление его увеличивается во столько же раз. Температура воздуха при всех опытах остаётся постоянной.
Опыты, проведённые с другими газами, дали те же результаты.
Изучая на опыте зависимость давления газа от его объёма, английский учёный Бойль (1627—1691) и французский учёный Мариотт (1620—1684) независимо один от другого открыли следующий закон.
Давление данной массы газа при неизменной температуре обратно пропорционально объёму газа.
Этот закон называется законом Бойля — Мариотта.
Выразим закон Бойля — Мариотта математически. Пусть температура некоторой массы газа постоянная и пусть:
V1 — объём газа при давлении р1,
V2 » » » » р2.
Согласно закону Бойля — Мариотта можно написать:
Из этой формулы следует, что:
Полученное равенство можно рассматривать как новое выражение закона Бойля — Мариотта.
Произведение объёма данной массы газа на его давление при неизменной температуре есть величина постоянная.
Изобразим графически изотермическое изменение состояния газа. Для этого по оси абсцисс будем откладывать значения объёмов газа, а по оси ординат соответствующие им значения давлений. Выберем масштаб так, чтобы начальные значения объёма и давления были равны 1. Тогда начальное состояние газа будет изображено точкой А (рис. 135). Если давление увеличится вдвое, объём уменьшится в два раза, состояние газа изобразится на графике точкой В. При уменьшении первоначального давления вдвое объём удвоится, получим точку С. Беря далее давления в три, четыре и т. д. раза больше или меньше начального, а объёмы соответственно в три, четыре и т. д. раза меньше или больше, получим ряд точек, изображающих различные состояния одной и той же массы газа при одинаковой температуре.
Рис. 135. График изотермического процесса.
Проведя через эти точки линию, получим кривую, которая называется изотермой.
Тщательными исследованиями установлено, что для реально существующих газов закон Бойля — Мариотта имеет лишь приближённое значение. Так, например, если произведение pV при 1 am равно единице, то при 2 am оно имеет следующие значения:
для воздуха ………………………0,99977
» водорода …………………….. 1,00026
» окиси углерода………………….. 0,99974
» двуокиси углерода………………… 0,99720
При очень больших давлениях (в сотни и тысячи атмосфер) закон Бойля — Мариотта становится совершенно неприменимым; в таких случаях зависимость между объёмом и давлением газа выражается более сложными уравнениями.
Зависимость между плотностью газа и его давлением
Плотность газа численно равна массе, заключённой в единице объёма.
Масса газа не меняется при его сжатии или расширении, но объём меняется; следовательно, меняется и плотность газа.
Пусть при постоянной температуре: D1 — плотность газа при объёме V1 и давлении p1 , a D2 — плотность газа при объёме V2 и давлении p2.
Если масса газа равна m, то можно написать:
откуда:
Но 
При постоянной температуре плотность газа прямо пропорциональна его давлению.
Нетрудно понять справедливость этого вывода, исходя из молекулярно-кинетической теории. В самом деле, давление газа обусловлено ударами его молекул. Если объём газа уменьшится вдвое, то в новом объёме , плотность газа станет вдвое больше. Вдвое увеличится и число ударов молекул о стенки, т. е. давление газа возрастёт в два раза.
Зависимость объёма газа от температуры. Закон Гей-Люссака
Как и все тела, газы при нагревании расширяются, причём весьма заметно даже при незначительном нагревании. Это легко обнаружить на следующем простом опыте (рис. 136).
Рис. 136. Установка для наблюдения расширения газа при нагревании.
Колба А соединяется с расположенной горизонтально трубкой CD, которая укреплена вдоль шкалы. Внутри этой трубки находится небольшой столбик ртути. Достаточно к колбе прикоснуться рукой, как столбик ртути в трубке CD начнёт двигаться.
При охлаждении колбы столбик ртути перемещается влево, а при нагревании — вправо; следовательно, газ при охлаждении сжимается, а при нагревании расширяется. Зная объём колбы и диаметр трубки, можно измерить увеличение объёма газа.
Постепенно нагревая газ в колбе, можно установить, что при постоянном давлении изменение объёма данной массы газа пропорционально изменению температуры. Поэтому тепловое расширение газа, так же как и других тел, можно охарактеризовать при помощи коэффициента объёмного расширения.
Пусть при температуре 0°С объём газа равен V0 , а при температуре t объём Vt. Увеличение объёма, приходящееся на каждую единицу объёма, взятого при 0°С, при нагревании на один градус будет равно:
откуда: 
Величина 
Жозеф Луи Гей-Люссак (1778—1850)— один из выдающихся французских химиков и физиков. Он открыл ряд важных химических и физических законов, из которых в физике широко известен закон одинакового расширения газов и паров при одинаковом повышении температуры.
Французский учёный Гей-Люссак, исследуя на опыте тепловое расширение газов, открыл, что, коэффициент объёмного расширения у всех газов при постоянном давлении одинаков и численно равен
В этом отношении расширение газов при нагревании отличается от расширения твёрдых и жидких тел, где, как мы видели (см. § 81 и 82), коэффициент объёмного расширения зависит от химического состава тел.
Положим в формуле (1):
получим: 

Этот закон получил название закона Гей-Люссака. Процессы, подобные рассмотренному, протекающие при постоянном давлении, называются изобарными1.
1 От греч. слов: изос — равный, барос — тяжесть, вес.
Формула (1) показывает, что объём газа при температуре t° равен произведению его объёма, взятого при 0°С, на двучлен объёмного расширения
Пример. 1. Объём некоторой массы газа при 0°С равен 10 л. Найти объём его при t=273°С, если давление постоянно.
По условиям задачи нам известен объём газа при 0°С, т. е. V0 = 10 л; подставляя числовые данные задачи в формулу 
Пример 2. При температуре 273°С объём некоторой массы газа равен 10 л. Чему будет равняться объём этого газа при температуре 546°С, если давление постоянно?
Нам известен объём газа при температуре 273°С; чтобы определить объём этого газа при t2 = 546°С, надо предварительно найти его объём при 0°.
Этот объём найдётся из равенства:
откуда:
Найдём теперь объём газа при 546°:
Зависимость давления газа от температуры. Закон Шарля
Нагревая газ в закрытом цилиндре, например в папиновом котле (рис. 136а), можно по манометру заметить, что давление газа увеличивается. Следя по термометру за повышением температуры, легко установить, что при постоянном объёме давление газа возрастает пропорционально повышению температуры.
Рис. 136а. При нагревании газа в закрытом цилиндре давление его повышается.
Аналогично тому, как для характеристики теплового расширения газов мы ввели коэффициент объёмного расширения, введём величину, характеризующую изменение давления газа при изменении его температуры.
Обозначим буквой р0 давление газа при 0°С, a pt — давление при t°. Увеличение давления, приходящееся на каждую единицу начального давления при нагревании на 1°С, будет равно:

Величина 
Измерения показывают, что величина термического коэффициента давления для всех
газов одинакова и равна
Определяя из формулы (1) величину pt получим:

Положим в формуле (2) 
Отсюда следует, что давление данной массы газа при нагревании на 1° при постоянном объеме увеличивается на 
Этот закон называется законом Шарля, по имени французского учёного, открывшего его в 1787 г.
Из закона Шарля следует, что термический коэффициент давления газа 

Пусть некоторая масса газа заключена в цилиндре под поршнем (рис. 137, а) и пусть температура её в этом начальном состоянии равна 0°, объём V0 и давление р0. Закрепим поршень АВ и нагреем газ до температуры t° (рис. 137, б); тогда давление газа увеличится и станет равным рt объём же его останется прежним.
По закону Шарля:
Будем теперь газ нагревать от 0 до t° (рис. 137, в), предоставив поршню свободно перемещаться. Давление газа останется таким же, каким было в начальном его состоянии, т. е. р0 , объём же увеличится до Vt. По закону Гей-Люссака:
Рис. 137.
а) начальное состояние газа: 0°, V0, р0;
б) состояние газа, определяемое величинами:
в) состояние газа, определяемое величинами:
Итак, имеем: при температуре t° объём данной массы газа V0 и давление 

После упрощения этого выражения получаем равенство:
Выразим сначала в виде таблицы, а потом графически зависимость давления газа от температуры. Для этого воспользуемся уравнением:
Рис. 138. График изменения давления газа от температуры.
Отложим по оси абсцисс в некотором условном масштабе температуры газа, а по оси ординат соответствующие этим температурам давления, взятые из написанной выше таблицы.
Соединяя на графике отмеченные точки, получим прямую LM (рис. 138), представляющую собой график зависимости давления газа от температуры при постоянном объёме.
Процесс изменения состояния газа, происходящий при неизменном объёме газа, называется изохорным 1 процессом, а линия LM, изображающая изменение давления газа при постоянном объеме в зависимости от температуры, называется изохорой.
1 От греч. слов: изос — разный, хорема — вместимость.
Пример 1. Давление газа при 0°С равно 780 мм рт. ст. Определить давление этого газа при температуре 273°С.
По формуле 
Пример 2. Чему будет равно давление газа при температуре 546°, если давление его при температуре 273° равно 780 мм рт. cm.?
В этой задаче прежде всего надо определить давление газа при 0°С. По формуле 
Теперь можно определить давление газа при t = 546°:
Законы Гей-Люссака и Шарля так же, как и закон Бойля — Мариотта, лишь приближённо отражают свойства газов. Это можно видеть хотя бы. из того факта, что для разных газов величины 


Точные измерения показывают, что для каждого данного газа значения 

Абсолютная шкала температур
Вернёмся ещё раз к графику изменения давления газа с температурой (рис. 138).
Продолжим прямую LM на этом графике до пересечения её с горизонтальной осью, по которой откладываются температуры газа, она пересечёт эту ось в точке K. Отрезок ОК будет изображать на этом графике такую температуру газа, при которой давление его равно нулю. Чему равна эта температура?
Обратимся к уравнению 
Так как давление газа при 0°С не равно нулю 
откуда: 
Итак, давление газа равняется нулю при температуре —273°С.
Вильям Томсон (Кельвин) (1824— 1907) — выдающийся английский физик. Ему принадлежат важные открытия в области теории электричества и теплоты и изобретения, из которых наиболее значительным было усовершенствование телеграфной связи. Он ввёл в физику понятие об абсолютной температуре. Его именем названы градусы шкалы абсолютных температур — градусы Кельвина.
Английский учёный Вильям Томсон (Кельвин) предложил такую шкалу температур, при которой за нуль градусов принята температура — 273°. Эта шкала получила название абсолютной шкалы температур, или шкалы Кельвина, а нуль градусов этой шкалы, равный — 273°, называется абсолютным нулём температур.
В шкале Кельвина величина градуса та же, что и в стоградусной шкале.
Будем обозначать температуру по шкале Кельвина буквой Т.
При нормальном атмосферном давлении температура таяния льда по шкале Кельвина Т0 = 273°, температура же кипения воды T = 373°.
Всякая другая температура t° стоградусной шкалы связана с абсолютной температурой Т соотношениями:
Зависимость между объёмом, давлением и температурой газа
Объединённый закон газового состояния. Мы рассмотрели процессы, в которых одна из трёх величин, характеризующих состояние газа (объём, давление и температура), не меняется.
Вы видели, что если не меняется температура, то давление и объём газа связаны друг с другом законом Бойля —- Мариотта. При постоянном давлении объём газа изменяется с изменением температуры по закону Гей-Люссака, и, наконец, при постоянном объёме давление газа меняется с изменением температуры по закону Шарля.
Однако в природе часто имеют место процессы, когда одновременно меняются все три величины, характеризующие состояние газа. Установим теперь, какая связь существует между объёмом, давлением и температурой.
Пусть для двух каких-либо произвольных состояний некоторой массы газа эти величины будут:
Из этих состояний изменением величин р, V или t газ можно перевести в любые другие состояния. Будем, например, сохраняя постоянным давление, переводить газ из состояний 1) и 2) в состояния, при которых температура газа будет равна 0°С.
По закону Гей-Люссака объём газа V1 после уменьшения температуры от до 0° будет равен 
Новые состояния газа выразятся так:
В обоих этих состояниях температура газа одинакова, поэтому на основании закона Бойля — Мариотта можно написать:

Так как величины р, V, t, характеризующие состояние рассматриваемого газа и обозначенные индексами 1 и 2, выбраны были нами произвольно, то равенство (1) справедливо для любых состояний этого газа. Поэтому можно утверждать, что:

Для данной массы газа произведение давления газа на его объём, делённое на двучлен объёмного расширения, есть величина постоянная.
Выведенная нами зависимость между объёмом, давлением и температурой газа называется объединённым законом газового состояния, а равенство (1) или (2) — уравнением состояния газа.
Уравнение состояния газа можно упростить, введя в него вместо температуры t по стоградусной шкале температуру Т по абсолютной шкале температур. Для этого преобразуем уравнение:
Введя в него значение 
что после сокращения на 273 даст:
Но 

Это означает, что для данной массы газа произведение давления на объём, делённое на абсолютную температуру, постоянно при всех температурах:
В частности, если при температуре Т = 273° объём газа равен V0 и давление его р0 , то можно написать:
Физическая сущность понятия абсолютного нуля
Мы уже отмечали, что реальные газы лишь приближённо следуют законам Гей-Люссака, Шарля и Бойля — Мариотта. Однако можно представить себе газ, для которого эти законы выполнялись бы в точности. Молекулы такого газа можно представить себе в виде упругих шариков исчезающе малого объёма, взаимодействие между которыми осуществляется только через их столкновения друг с другом. В физике такой газ принято называть идеальным газом.
Из уравнения 
Опыт показывает, что при малых давлениях свойства реальных газов очень близки к свойствам идеального газа. Следовательно, при приближении к температуре абсолютного нуля должно прекратиться тепловое движение молекул и реального газа. Этот вывод относится не только к газам, но и к твёрдым и жидким телам.
Физикой установлено, что такое состояние вещества недостижимо, но к нему можно подойти очень близко. В настоящее время достигнута температура, которая выше абсолютного нуля всего на несколько стотысячных долей градуса.
Изменение температуры газа при быстром расширении и сжатии
Опыты показывают, что при быстром сжатии температура газа повышается, а при быстром расширении понижается.
Увеличение температуры газа при сжатии можно показать на следующем простом опыте. Возьмём толстостенный цилиндрический стеклянный сосуд, внутри которого может двигаться поршень (рис. 139). При быстром сжатии воздух в сосуде сильно нагревается, и легко воспламеняющееся вещество (например, ватка, смоченная эфиром), положенное на дно сосуда, вспыхивает. Такого рода явление используется, например, в двигателях внутреннего сгорания —дизелях: при сжатии воздуха в цилиндре двигателя горючая смесь, введённая в цилиндр, нагревается до температуры воспламенения (работа двигателя описана в § 131).
Рис. 139. При быстром сжатии воздух в цилиндре сильно нагревается и легко воспламеняющееся вещество вспыхивает.
При быстром же расширении газа температура его понижается. Это можно наблюдать на следующем опыте. Будем накачивать воздух в прочную закрытую пробкой стеклянную банку, содержащую пары воды. При достижении определённого давления пробка выскочит; при этом воздух, расширяясь, совершит работу и охладится, вследствие чего водяной пар превратится в туман (рис. 140).
Рис. 140. Сжатый в сосуде воздух, выбрасывая пробку, расширяется. Совершая при этом работу, он охлаждается, вследствие чего водяной пар в сосуде превращается в туман.
Понижение температуры при быстром расширении газа используется для получения сжиженных газов; об этом будет рассказано в § 122.
Изменение температуры тела, как было установлено в § 71, связано с изменением внутренней энергии тела. Так как при быстром сжатии температура газа повышается, то внутренняя энергия его при этом увеличивается. Увеличение внутренней энергии газа происходит в результате работы, совершённой при его сжатии. Расширяясь же, газ совершает работу; при этом внутренняя энергия его уменьшается, и если расширение происходит быстро, то температура газа, как мы видели в наших опытах, понижается.
Процесс, происходящий в теле без теплообмена с окружающими его другими телами, называется адиабатным процессом.
Все быстро протекающие процессы практически могут считаться адиабатными.
Применение сжатых газов
Многие сжатые газы в настоящее время находят широкое применение в технике.
Сжатый воздух, например, применяется в работе различных пневматических инструментов: отбойных молотков, заклёпочных молотков, в разбрызгивателях краски и др.
На рисунке 141 показана схема устройства отбойного молотка. Сжатый воздух подаётся в молоток по шлангу М. Золотники Z, аналогичные применяемым в паровых машинах, направляют его поочерёдно то в заднюю, то в переднюю часть цилиндра. Поэтому воздух давит на поршень Р то с одной, то с другой стороны, что вызывает быстрое возвратно-поступательное движение поршня и пики молотка В. Последняя наносит быстро следующие друг за другом удары, внедряется в уголь и откалывает куски его от массива.
Рис. 141. Схема устройства отбойного молотка.
Существуют также пескоструйные аппараты, которые дают сильную струю воздуха, смешанную с песком. Эти аппараты применяются, например, для очистки стен. Сейчас нередко можно видеть работу специальных аппаратов, применяемых для окраски стен, где краска распыляется сжатым воздухом. Сжатым воздухом открываются двери вагонов метро и троллейбусов. Сжатый воздух используется в работе тормозов на транспорте. Схематическое устройство одного из видов пневматического тормоза железнодорожного вагона изображено на рисунке 142.
Компрессор подаёт воздух по магистрали в стальной резервуар А. Поршень В тормозного цилиндра оказывается под одинаковым давлением справа и слева; поэтому соединённая с ним тормозная колодка D отжата от колеса. Если открыть тормозной кран М, то находящийся в магистрали под давлением воздух устремится в атмосферу; клапан К захлопнется, и, таким образом, стальной резервуар изолируется от магистрали. Теперь давление на поршень В справа станет больше, чем давление слева, вследствие чего тормозная колодка прижмётся к ободу колеса. Если теперь кран М закрыть и снова подать в магистраль сжатый воздух, то восстановится первоначальное положение.
Рис. 142. Схема устройства железнодорожного пневматического тормоза.
В технике применяется не только сжатый воздух, но и некоторые другие газы, так, например, водород, ацетилен и кислород применяются при газовой сварке; аммиак используется в холодильном деле. Чтобы газы было удобно перевозить, их помещают в прочные стальные баллоны, накачивая до давления 60—200 am.
Рис. 142а. Внешний вид мощного компрессора.
Сжатие газов осуществляется с помощью мощных нагнетательных насосов — компрессоров.
На рисунке 143, а, б дана схема работы компрессора.
Компрессор состоит из цилиндра с поршнем и двумя клапанами; один из них входной, другой выходной. При движении поршня вниз (рис. 143, б) открывается входной клапан и в цилиндр поступает воздух из помещения; при движении поршня вверх (рис. 143, а) входной клапан закрывается, вошедший воздух сжимается поршнем и через выходной клапан поступает в стальной баллон для хранения сжатого газа.
Существуют так называемые многоступенчатые компрессоры, в которых газ последовательно
сжимается в трёх или четырёх цилиндрах. Такие компрессоры позволяют получить газ, сжатый до давления в тысячи атмосфер. На рисунке 142а изображён внешний вид одного из типов многоступенчатых компрессоров.
Рис. 143, а, б. Схема работы компрессора.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно — кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома