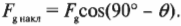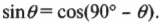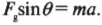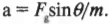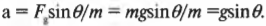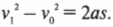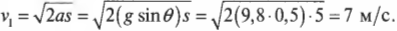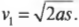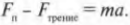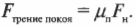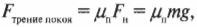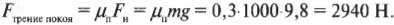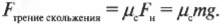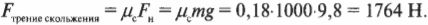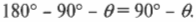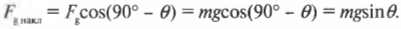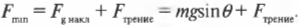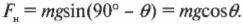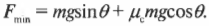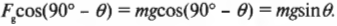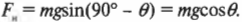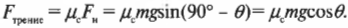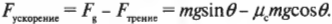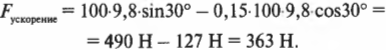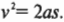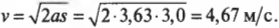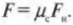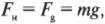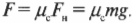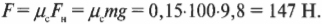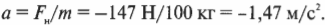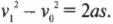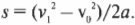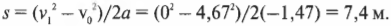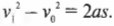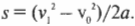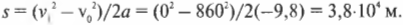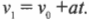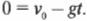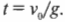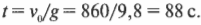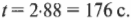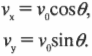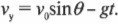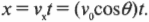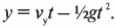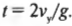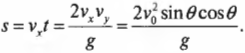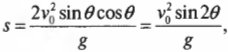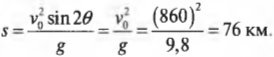Как найти дальность полета ядра - Avtoru.top - решение различных проблем

В этой главе…

Постигаем гравитацию
Изучаем влияние наклона плоскости
Учитываем силы трения
Измеряем дальность полета под действием силы тяжести

Сила гравитационного притяжения — вот основная тема этой главы. В главе 5 было показано, что для ее преодоления требуется применять силу. В этой главе будет представлены способы влияния гравитационного притяжения и трения на движение объектов по наклонным плоскостям. Кроме того, будет показано, как гравитация влияет на траекторию полета объекта.

Содержание

Разбираемся с гравитацией
Движемся по наклонной плоскости
- Вычисляем углы
  - Ищем компоненту вектора силы Fg вдоль наклонной плоскости
  - Вычисляем скорость вдоль наклонной плоскости
- Разбираемся с ускорением
Преодолеваем трение
- Вычисляем силу трения и нормальную силу
- Разбираемся с коэффициентом трения
- Знакомимся со статическим и кинетическим трением
  - Изучаем статическое трение
  - Поддерживаем движение вопреки трению скольжения
- Тянем груз в гору и боремся с трением
  - Вычисляем компоненту силы тяжести
  - Определяем силу трения
  - Вычисляем путь скольжения холодильника до полной остановки
    - Вычисляем ускорение скольжения
    - Вычисляем путь скольжения по полу
Как гравитация влияет на свободное падение объектов
- Стреляем вверх: максимальная высота
- Время подъема ядра
- Общее время полета
- Стреляем под углом
  - Разбиваем движение ядра на компоненты
  - Определяем максимальную дальность полета ядра

Разбираемся с гравитацией

На поверхности Земли сила гравитационного притяжения ( mathbf{F_g} ) (или сила тяжести) постоянна и равна ( mmathbf{g} ), где ( m ) — это масса объекта, a ( mathbf{g} ) — ускорение свободного падения под действием силы тяжести, равное 9,8 м/с².

Ускорение — это вектор, а значит, он имеет величину, направление и точку приложения (подробнее об этом см. главу 4). Уравнение ( mathbf{F_g}=mmathbf{g} ) интересно тем, что ускорение свободного падения объекта ( g ) не зависит от массы объекта.

Поскольку ускорение свободного падения не зависит от массы объекта, то более тяжелый объект падает нисколько не быстрее, чем более легкий объект. Сила тяжести сообщает свободно падающим телам одинаковое направленное вниз ускорение ( mathbf{a} ) (на поверхности Земли равное ( mathbf{g} )), независимо от их массы.

Сказанное выше относится к объектам вблизи поверхности Земли, а в главе 7 рассматриваются другие ситуации вдали от Земли (например, на орбите Луны), где сила тяжести и ускорение свободного падения имеют другие значения. Чем дальше вы находитесь от центра Земли, тем меньше сила тяжести и ускорение свободного падения. В примерах этой главы ускорение свободного падения направлено вниз. Но это не значит, что оно влияет только на движение предметов вертикально вниз. Здесь рассматриваются также примеры движения объектов под углом к вертикали.

Движемся по наклонной плоскости

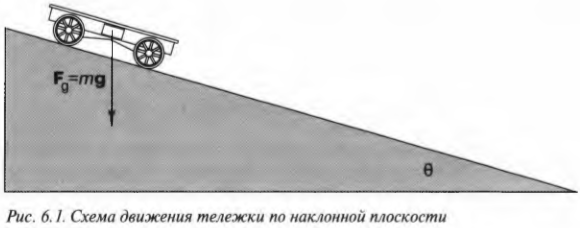
В курсе физики часто упоминаются наклонные плоскости и рассматривается движение объектов по ним. Взгляните на рис. 6.1. На нем показана тележка, которая скатывается по наклонной плоскости. Тележка движется не строго вертикально, а вдоль плоскости, наклоненной под углом ( theta ) к горизонтали.

Допустим, что угол ( theta ) = 30°, а длина наклонной плоскости равна 5 метрам. До какой скорости разгонится тележка в конце наклонной плоскости? Сила тяжести сообщит тележке ускорение, но учтите, что вдоль наклонной плоскости ускорение будет отличаться от ускорения свободного падения. Дело в том, что разгон вдоль наклонной плоскости будет выполнять только компонента силы тяжести вдоль этой наклонной плоскости.

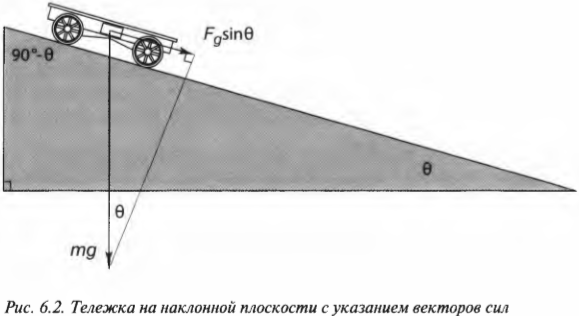
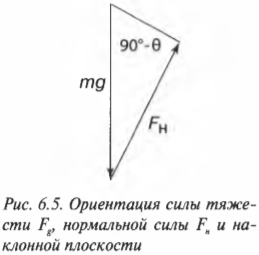
Чему равна компонента силы тяжести, действующей вдоль наклонной плоскости, если на тележку действует направленная вертикально сила тяжести ( mathbf{F_g} )? Взгляните на рис. 6.2, на котором показаны упомянутые выше угол ( theta ) и вектор силы ( mathbf{F_g} ) (подробнее о векторах см. главу 4). Для определения компоненты силы тяжести, действующей вдоль наклонной плоскости, нужно определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью. Для этого потребуются элементарные сведения из геометрии (подробности см. в главе 2), а именно то, что сумма углов треугольника равна 180°. Угол между вектором силы ( mathbf{F_g} ) и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием равен ( theta ). Поэтому, глядя на рис. 6.2 , можно легко определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью: 180°-90°-( theta ) или 90°-( theta ).

Вычисляем углы

Преподаватели физики используют особый способ вычисления углов между векторами и наклонными плоскостями. Однако читателям книги можно раскрыть этот “секрет” определения угла ( theta ). Для начала обратите внимание на то, что если ( theta ) стремится к 0°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 90°. И наоборот, если ( theta ) стремится к 90°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 0°. На основании этого простого наблюдения можно предположить, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Как видите, для определения взаимосвязи между углами бывает полезно попробовать поменять значения некоторых углов от 0° до 90°.

Ищем компоненту вектора силы F_g вдоль наклонной плоскости

Итак, зададимся вопросом: чему равна компонента вектора силы ( mathbf{F_g} ) вдоль наклонной плоскости? Теперь мы знаем, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Значит, компонента вектора силы вдоль наклонной плоскости ( F_{g,накл} ) равна:

Если вы добросовестно учили тригонометрию, то вам наверняка должно быть известно (а если нет, то обратитесь к главе 2), что:

(Часто это знать совсем не обязательно, и может сгодиться предыдущее уравнение.)

Следовательно:

Полученное выражение можно легко проверить следующим образом. Когда ( theta ) стремится к 0°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к 0, поскольку наклонная плоскость стремится к горизонтальному положению. А когда ( theta ) стремится к 90°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к ( F_g ) поскольку наклонная плоскость стремится к вертикальному положению. Итак, если вдоль наклонной плоскости на тележку с массой 800 кг действует сила ( F_gsintheta ), то каким будет ускорение тележки? Это легко определить по известной формуле:

Следовательно:

Задача упрощается, если вспомнить, что ( F_g=mg ) и тогда:

Итак, теперь нам известно, что ускорение тележки вдоль наклонной плоскости равно ( a=gsintheta ). Это соотношение справедливо для любого объекта, ускоряющегося под действием силы тяжести, если не учитывать силы трения.

Вычисляем скорость вдоль наклонной плоскости

Логично было бы поинтересоваться: а какова скорость тележки в конце наклонной плоскости? Для этого нам потребуется следующее уравнение, которое было выведено в главе 3:

Поскольку начальная скорость ( v_0 ) = 0, а длина наклонной плоскости ( s ) = 5 м, то получим:

Итак, скорость тележки в конце наклонной плоскости ( v_1 ) = 7 метров в секунду. Хотя это не такая уж и большая скорость для автомобиля, но все же не рекомендуется проводить такие эксперименты в домашних условиях. Имейте в виду, что на самом деле скорость будет несколько ниже, поскольку часть энергии расходуется на вращение колес, движение других частей автомобиля, трение и т.д.

Разбираемся с ускорением

Блиц-вопрос: а какую скорость в конце наклонной плоскости приобретет кубик льда при скольжении без трения? Ответ: он будет иметь такую же скорость, что и тележка в предыдущем примере, т.е. 7 м/с. Ускорение любого объекта, движущегося без трения вдоль наклонной плоскости под углом ( theta ), равно ( gsintheta ). Как видите, имеет значение не масса объекта, а компонента ускорения свободного падения вдоль наклонной плоскости. Если нам известно ускорение движения кубика льда и пройденное расстояние ( s ), то получим значение скорости по известной формуле:

Итак, масса не входит в формулу для определения конечной скорости.

Преодолеваем трение

Трудно представить себе повседневную жизнь без трения. Без трения автомобили не могли бы ездить, люди — ходить, а руки — брать любые предметы. Трение создает проблемы, но без него жизнь была бы просто невозможной.

Трение возникает из-за взаимодействия между поверхностными неровностями. Поверхность состоит из множества микроскопических выступов и впадин. При соединении двух поверхностей эти выступы одной поверхности и впадины другой поверхности сцепляются и препятствуют свободному проскальзыванию.

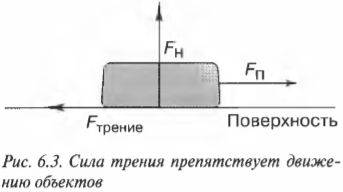
Допустим, что ваши сбережения хранятся в виде огромного золотого слитка, который показан на рис. 6.3, и некий злоумышленник задумал украсть его, но не может нести такой огромный слиток в руках, а может только тащить его волоком. Этот воришка стремится приложить силу к слитку, чтобы ускорить его и сбежать от преследующей его полиции. Однако благодаря силе трения вор не сможет развить большого ускорения.

Определим количественно влияние силы трения на движение объектов. Результирующая сила на слиток и создаваемое ею ускорение определяется как разность приложенной силы ( F_п ) и силы трения ( F_{трение} ) вдоль оси X:

Эта формула выглядит очень просто, но как определить силу трения? Как будет показано ниже, она зависит от нормальной силы.

Вычисляем силу трения и нормальную силу

Сила трения ( F_{трение} ) всегда противодействует приложенной силе, которая вызывает движение. Причем сила трения пропорциональна приложенной силе.

Как показано на рис. 6.3, слиток золота давит на горизонтальную поверхность с силой, равной весу слитка, ( mg ). А поверхность с той же силой действует на слиток. Эту силу называют нормальной силой (или силой нормального давления), ( F_н ).(Нормальной называется компонента силы со стороны поверхности, направленная по нормали к поверхности, т.е. перпендикулярно к поверхности.) Нормальная сила по величине не всегда совпадает с силой тяжести, поскольку нормальная сила всегда перпендикулярна поверхности, по которой движется объект. Иначе говоря, нормальная сила — это сила взаимодействия поверхностей разных объектов, и чем она больше, тем сильнее трение.

В примере на рис. 6.3 слиток скользит вдоль горизонтальной поверхности, поэтому нормальная сила равна весу объекта, т.е. ( F_н=mg ) Итак, у нас есть нормальная сила, которая равна силе давления слитка на горизонтальную поверхность. Для чего она нам нужна? Для определения силы трения.

Разбираемся с коэффициентом трения

Сила трения определяется характеристиками поверхностей соприкасающихся материалов. Как физики теоретически описывают их? Никак. У физиков есть множество общих уравнений, которые предсказывают общее поведение объектов, например ( sum!F=ma ) (см. главу 5). Однако у физиков нет полного теоретического понимания механизмов взаимодействия поверхностей материалов. Поэтому поверхностные характеристики материалов известны, в основном, из опыта.

А из опыта известно, что нормальная сила непосредственно связана с силой трения. Оказывается, что с большой точностью эти две силы пропорциональны друг другу и их можно связать с помощью константы ( mu ) следующим образом:

Согласно этому уравнению, чтобы определить силу трения, нужно умножить нормальную силу на некую постоянную величину, т.е. константу ( mu ). Такая константа называется коэффициентом трения, и именно она характеризует свойства сцепления шероховатостей данных поверхностей.

Величина коэффициента трения находится в диапазоне от 0 до 1. Значение 0 возможно только в идеализированном случае, когда трение отсутствует вообще. А значение 1 соответствует случаю, когда сила трения максимальна и равна нормальной силе. Это значит, что максимальная сила трения для автомобиля не может превышать его веса.

Обратите внимание, что уравнение ( F_{трение}=mu F_н ) не является соотношением между векторами, поскольку эти векторы направлены в разные стороны. Например, на рис. 6.3 они перпендикулярны друг другу. Действительно, нормальная сила ( mathbf{F_н} ) всегда перпендикулярна поверхности, а сила трения ( mathbf{F_{трение}} ) — параллельна. Эти направления определяются их природой: нормальная сила ( mathbf{F_н} ) определяет степень сжатия поверхностей, а сила трения ( mathbf{F_{трение}} ) — степень противодействия скольжению вдоль поверхностей.

Сила трения не зависит от площади соприкосновения двух поверхностей. Это значит, что слиток с той же массой, но вдвое длиннее и вдвое ниже исходного будет испытывать точно такую же силу трения при скольжении по поверхности. При этом увеличивается вдвое площадь соприкосновения, но уменьшается вдвое давление, т.е. величина силы, которая приходится на единицу площади.

Итак, мы получили предварительные сведения и готовы вычислить силу трения? Не так быстро. Оказывается, что коэффициент трения бывает двух типов.

Знакомимся со статическим и кинетическим трением

Два разных коэффициента трения соответствуют двум разным типам трения: статическому трению (или трению покоя) и кинетическому трению (или трению скольжения).

Дело в том, что эти типы трения соответствуют двум разным физическим процессам. Если две поверхности не движутся относительно друг друга, то на микроскопическом уровне они взаимодействуют более интенсивно, и этот случай называется трением покоя. А когда поверхности уже скользят относительно друг друга, то микроскопические неровности не успевают вступить в интенсивное взаимодействие, и этот случай называется трением скольжения. На практике это значит, что для каждого из этих двух типов трения используются свои коэффициенты трения: коэффициент трения покоя ( mu_п ) и коэффициент скольжения ( mu_с ).

Изучаем статическое трение

Трение покоя сильнее трения скольжения, т.е. коэффициент трения покоя ( mu_п ) больше коэффициента трения скольжения ( mu_с ). Это можно упрощенно объяснить следующим образом. В состоянии покоя соприкасающиеся поверхности интенсивно взаимодействуют на микроскопическом уровне, а при скольжении поверхности успевают вступить в интенсивное взаимодействие только на более крупном макроскопическом уровне.

Трение покоя возникает тогда, когда нужно привести в движение покоящийся объект. Именно такую силу трения нужно преодолеть для начала скольжения объекта.

Предположим, что в примере на рис. 6.3 коэффициент трения покоя между слитком и поверхностью равен 0,3, а масса слитка равна 1000 кг (очень приличный слиток). Какую силу должен приложить воришка, чтобы сдвинуть слиток? Из предыдущих разделов нам уже известно, что:

Поскольку поверхность горизонтальна, то нормальная сила направлена противоположно силе тяжести слитка и имеет ту же величину:

где ( m ) — масса слитка, a ( g ) — ускорение свободного падения, вызванное силой притяжения со стороны Земли. Подставляя численные значения, получим:

Итак, воришке потребуется приложить силу 2940 Н, чтобы сдвинуть с места неподвижный слиток. Довольно большая сила! А какая сила потребуется ему, чтобы поддерживать скольжение слитка? Для ответа на этот вопрос нужно рассмотреть трение скольжения.

Поддерживаем движение вопреки трению скольжения

Сила трения скольжения, возникающая из-за скольжения двух соприкасающихся поверхностей, не так велика, как сила трения покоя. Но это совсем не значит, что коэффициент трения скольжения можно легко вычислить теоретически, даже если нам известен коэффициент трения покоя. Оба коэффициента трения приходится определять из опыта.

Именно из опыта известно, что трение покоя больше трения скольжения. Представьте себе, что вы разгружаете неподвижный ящик на наклонной плоскости, но он вдруг начинает скользить вниз. Достаточно заблокировать его движение ногой и с большой вероятностью ящик останется в состоянии покоя, если аккуратно убрать ногу. Именно так, в состоянии покоя, проявляется трение покоя, а в процессе движения ящика — трение скольжения.

Пусть слиток на рис. 6.3 имеет массу 1000 кг, а коэффициент трения скольжения ( mu_c ) равен 0,18. Какую силу должен приложить воришка, чтобы сдвинуть с места неподвижный слиток? Для ответа на этот вопрос нужно воспользоваться следующей формулой:

Подставляя численные значения, получим:

Воришке потребуется приложить силу 1764 Н, чтобы поддерживать скольжение слитка. Не такая уж и маленькая сила, если, конечно, воришке не помогают его верные друзья. Однако это не так уж и легко, и полиция быстро сможет догнать этого воришку. Зная законы физики, полицейские вряд ли захотят прилагать лишние усилия: “Слиток-то мы нашли, а вот домой тащите его сами”.

Тянем груз в гору и боремся с трением

В предыдущих примерах со слитком описывалось трение на горизонтальной поверхности. А как определить силу сопротивления со стороны трения на наклонной плоскости?

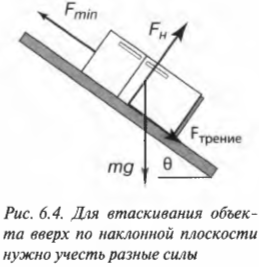
Допустим, что, собираясь на рыбалку, вы решили захватить с собой холодильник массой 100 кг. Единственный способ погрузить его в багажник автомобиля — это втащить холодильник по наклонной плоскости, как показано на рис. 6.4. Пусть наклонная плоскость расположена под углом 30°, коэффициент трения покоя равен 0,2, а коэффициент трения скольжения — 0,15. Хорошая новость заключается в том, что вам помогают два друга, а плохая — в том, что каждый из вас способен приложить силу не более 350 Н.

Ваши друзья растеряны? “Не стоит беспокоиться, немного физики — и все будет в порядке”, — можете ответить им вы, доставая калькулятор. Итак, нам нужно вычислить минимальную силу, которую нужно приложить, чтобы втащить холодильник вверх по наклонной плоскости в багажник автомобиля вопреки силе трения и силе тяжести.

Вычисляем компоненту силы тяжести

Для этого нужно внимательно изучить схему на рис. 6.4. Сила тяжести действует на холодильник и направлена вертикально вниз. Сумма углов треугольника, образованного вектором силы тяжести, наклонной плоскостью и ее основанием, равна 180°. Угол между вектором силы тяжести и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием — ( theta ). Поэтому угол между наклонной плоскостью и вектором силы тяжести равен:

Компонента силы тяжести, действующая вдоль наклонной плоскости, равна:

Таким образом, минимальная сила, с которой нужно толкать холодильник вверх по наклонной плоскости, равна сумме силы трения, ( F_{трение} ), и этой компоненты ( F_{g,накл} ), т.е.:

Определяем силу трения

Следующий вопрос: чему равна сила трения, ( F_{трение} )? Какой коэффициент трения нужно использовать для ее определения: покоя или скольжения? Поскольку коэффициент трения покоя больше коэффициента трения скольжения, то для оценки минимально необходимой силы имеет смысл учесть коэффициент трения покоя. Ведь после того как холодильник удастся сдвинуть с места, для скольжения придется прикладывать меньшую силу. Итак, с учетом коэффициента трения покоя, получим для силы трения

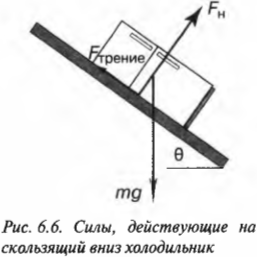
Для определения этой силы трения нам потребуется вычислить нормальную силу, ( F_н ) (более подробно эта сила описывается выше в этой главе). Она равна компоненте силы тяжести, которая направлена перпендикулярно (т.е. по нормали, откуда и происходит ее название) к наклонной плоскости. Как мы уже выяснили, угол между наклонной плоскостью и вектором силы тяжести равен 90°-( theta )(рис. 6.5).

С помощью тригонометрических соотношений (см. главу 2) получим:

Чтобы проверить справедливость этого выражения, попробуйте устремить угол ( theta ) к нулю, при котором нормальная сила ( F_н ) становится равной ( mg ), что и следовало ожидать. Теперь получаем:

После подстановки численных значений получим:

Итак, три человека должны приложить минимально необходимую силу 660 Н, т.е. по 220 Н каждый, что меньше максимально возможной силы 350 Н. С радостным призывом “Приступим!” вы приступаете к работе, втаскиваете холодильник на самый верх наклонной плоскости. Допустим, что из-за несогласованности действий кто-то из вас перестал прикладывать силу. Как результат, холодильник после непродолжительной остановки неожиданно заскользил вниз, а после достижения основания продолжил движение по полу до полной остановки.

Вычисляем путь скольжения холодильника до полной остановки

Допустим, что наклонная плоскость и пол имеют одинаковые коэффициенты трения скольжения. Каким будет путь скольжения холодильника до полной остановки? Пусть сначала холодильник скользит из состояния покоя до основания наклонной плоскости длиной 3 м, как показано на рис. 6.6. Во время такого скольжения холодильник разгоняется и вполне может столкнуться с автомобилем на расстоянии 7,5 м. О, Боже! Неужели они столкнутся? Нужно немедленно достать калькулятор и приступить к расчетам.

Вычисляем ускорение скольжения

При скольжении вниз действующие на холодильник силы направлены иначе, чем при скольжении вверх. Теперь вы и ваши друзья уже не прилагают свои силы, а холодильник скользит только под действием компоненты силы тяжести, направленной вдоль наклонной плоскости. А ей противодействует лишь сила трения. Чему же равна результирующая сумма этих сил? Из предыдущих разделов уже известно, что компонента силы тяжести вдоль наклонной плоскости равна:

А нормальная сила равна:

Это значит, что сила трения скольжения равна:

Результирующая сила, которая действует на холодильник в направлении движения и определяет его ускорение, равна:

Обратите внимание на то, что сила трения, ( F_{трение} ), имеет отрицательный знак, т.е. она направлена противоположно компоненте силы тяжести вдоль наклонной плоскости, которая приводит в движение холодильник. После подстановки численных значений получим:

Поскольку масса холодильника равна 100 кг, то он скользит с ускорением 363 Н/100 кг = 3,63 м/с² вдоль наклонной плоскости длиной 3 м. Для вычисления конечной скорости холодильника, ( v ), в конце наклонной плоскости нужно использовать следующую известную нам формулу:

После извлечения квадратного корня и подстановки численных значений получим:

Такой будет скорость холодильника в конце наклонной плоскости.

Вычисляем путь скольжения по полу

Как на основе данных, полученных в предыдущем разделе, определить путь скольжения холодильника по полу? Столкнется ли холодильник с автомобилем?

Итак, нам известно, что холодильник начинает движение по полу со скоростью 4,67 м/с. Вопрос: какое расстояние он пройдет до полной остановки? Теперь в горизонтальном направлении на него действует только сила трения, а компонента силы тяжести по горизонтали равна нулю. Поэтому холодильник постепенно замедляется и рано или поздно остановится. Но уцелеет ли при этом стоящий поодаль автомобиль? Как обычно, сначала вычисляем суммарную силу ( F ), действующую на холодильник в направлении движения и определяющую его ускорение. В данном случае она равна силе трения:

Поскольку холодильник движется вдоль горизонтальной поверхности, то нормальная сила ( F_н ) равна силе тяжести ( F_g ), действующей на холодильник:

т.е. суммарная сила равна:

После подстановки численных значений получим:

Именно такая сила сопротивления действует на холодильник и… терроризирует всю округу! Итак, насколько длинным будет тормозной путь холодильника? Подставим численные значения и получим:

Здесь отрицательный знак обозначает замедление холодильника (см. главу 2).

По формуле:

найдем тормозной путь холодильника:

Поскольку конечная скорость ( v_1 ), равна 0, то эта формула упрощается и принимает вид:

Вот это да! Холодильник проедет расстояние 7,4 м и остановится всего в 10 см от автомобиля, который находится на расстоянии 7,5 м от основания наклонной плоскости. Можно расслабиться и понаблюдать за вашими друзьями, которые охвачены паникой и с ужасом в глазах ожидают столкновения холодильника и автомобиля.

Как гравитация влияет на свободное падение объектов

В главе 7 сила гравитационного притяжения (или сила тяжести) описывается в космическом масштабе, а здесь она рассматривается только вблизи поверхности Земли. В физике часто встречаются задачи с учетом силы тяжести. Этот раздел посвящен тому, как сила тяжести влияет на свободное падение объектов, и его следует рассматривать, как переходный между материалом предыдущей главы и материалом главы 7.

Стреляем вверх: максимальная высота

Зная ускорение свободного падения и начальную скорость объекта, можно легко вычислить дальность его полета. Эти знания могут пригодиться при подготовке праздничных фейерверков!

Предположим невероятное: на день рождения друзья подарили вам пушку, способную разгонять ядро весом 10 кг до начальной скорости 860 м/с. С изумлением рассматривая ее, гости начали спорить: а на какую максимальную высоту эта пушка способна выстрелить? Поскольку вы уже владеете всеми необходимыми знаниями, то можете быстро дать ответ на этот вопрос.

Нам известна начальная скорость ядра, ( v_0 ), и ускорение свободного падения ( g ) под действием силы тяжести. Как определить максимальную высоту подъема ядра? В точке максимального подъема ядра его скорость будет равна нулю, а затем оно начнет обратное движение вниз. Следовательно, для вычисления максимальной высоты подъема ядра, ( s ), можно использовать следующую формулу, в которой конечная скорость ( v_1 ) равна нулю:

Отсюда получим:

Подставляя численные значения для начальной скорости ( v_0 ) = 860 м/с², ускорения свободного падения под действием силы тяжести ( g ) = —9,8 м/с² (минус обозначает направление ускорения, противоположное направлению перемещения), получим:

Ого! Ядро улетит на высоту 38 км. Совсем неплохо для пушки, подаренной на день рождения. Интересно, а сколько же времени придется его ждать обратно?

Время подъема ядра

Итак, сколько времени потребуется для того, чтобы ядро поднялось на максимальную высоту? В примере из главы 4, где мяч для игры в гольф падал с вершины обрыва, для вычисления дальности его полета использовалось следующее уравнение:

Однако это уравнение представляет собой всего один из многих возможных вариантов поиска ответа на заданный вопрос.

Нам известно, что в точке максимального подъема скорость ядра равна 0. Поэтому для определения времени полета до максимальной высоты можно использовать следующее уравнение:

Поскольку ( v_1 ) = 0 и ( a ) = ( -g ), то:

Иначе говоря, получим:

После подстановки численных значений получим:

Итак, ядру потребуется 88 с, чтобы достичь максимальной высоты. А каково общее время полета?

Общее время полета

Сколько времени потребуется ядру, чтобы достичь максимальной высоты 38 км и вернуться обратно к пушке, если на подъем ему потребовалось 88 с? Общее время полета вычислить очень просто, поскольку обратный путь вниз симметричен прямому пути вверх. Это значит, что скорость ядра в каждой точке обратного пути вниз равна по величине и имеет противоположное направление по сравнению с прямым путем вверх. Поэтому время падения равно времени подъема и общее время полета равно удвоенному времени подъема:

Итак, общее время полета равно 176 с, или 2 минуты и 56 секунд.

Стреляем под углом

В предыдущих разделах пушка стреляла вертикально вверх. Попробуем теперь поразить цель, стреляя ядром из пушки под углом, как показано на рис. 6.7.

Разбиваем движение ядра на компоненты

Как характеризовать движение ядра при стрельбе под углом? Поскольку любое движение всегда можно разбить на компоненты по осям X и Y, а в данном примере сила притяжения действует только вдоль оси Y, то задача упрощается. Разобьем начальную скорость на компоненты (подробнее об этом рассказывается в главе 4):

Эти компоненты независимы, а сила притяжения действует только в направлении оси Y. Это значит, что компонента ( v_x ) остается постоянной, а меняется только компонента ( v_y ):

Теперь легко определить координаты ядра в любой момент. Например, координата ядра по оси X выражается формулой:

Поскольку сила тяжести влияет на движение ядра по вертикали, то координата ядра по оси Y выражается формулой:

Из предыдущего раздела нам уже известно, что общее время полета ядра по вертикали равно:

Теперь, зная время, можно легко определить дальность полета ядра по оси X:

Итак, для вычисления дальности полета ядра по горизонтали нужно знать начальную скорость ядра, ( v_0 ), и угол, ( theta ), под которым сделан выстрел.

Определяем максимальную дальность полета ядра

При каком угле выстрела ( theta ) ядро улетит на максимальное расстояние по горизонтали? Из тригонометрии известно, что ( 2sinthetacostheta=sin2theta ).

Тогда:

и расстояние ( s ) будет максимальным при максимальном значении ( sin2theta=1 ), т.е. при ( theta ) = 45°.

В таком случае:

Совсем неплохо для пушки, подаренной на день рождения!

Глава 6. Запрягаемся в упряжку: наклонные плоскости и трение

3 (59.02%) 41 votes

Источник

Обучение технике толкания ядра

Введение

Возрастающий уровень требований к системе подготовки спортивного резерва предполагает повышение её эффективности с первых этапов многолетнего спортивного пути использования. Одним из важных разделов этого процесса является выполнение требований принципиальных установок юношеского спорта:

целевая направленность системы управления подготовкой юных спортсменов по отношению к высшему спортивному мастерству;

перспективное опережение формирования технического мастерства.

Формированию технического мастерства спортсмена, специалистами спорта всегда уделялось большое внимание. Однако обучению рациональной техники толкания ядра юных легкоатлетов посвящено незначительное количество работ .

Это определило выбор темы курсовой работы.

Целью курсовой работы является расширение и углубление теоретических знаний по методике обучения технике толкания ядра.

Для достижения поставленной цели необходимо решить следующие задачи:

Изучить основы современной техники толкания ядра.

Определить основные задачи в методике обучения техники.

Выявить основные средства обучения.

При написании курсовой работы были использованы следующие методы:

Анализ научно-методической литературы.

Беседа с тренером.

1. Основы современной техники толкания ядра

Спортивная техника в настоящее время рассматривается большинством специалистов как специальная система движений, соответствующая особенностям данного вида спорта и направленная на достижение высоких спортивных результатов .

Достижение спортивных результатов в толкании ядра связано с конкретной целью — как можно дальше толкнуть ядро . Это зависит от многих факторов и в первую очередь от уровня технической подготовленности спортсмена .

В структуре технической подготовленности спортсмена выделяют базовые и дополнительные движения и действия . К базовым, относятся движения и действия составляющих основу техники толкания ядра, без которых невозможно эффективное осуществление соревновательной борьбы с соблюдением существующих правил. Дополнительные движения и действия — это второстепенные, элементы отдельных движений, которые характерны для конкретных спортсменов и связанные с их индивидуальными особенностями.

С точки зрения механики, теоретическая дальность полета ядра рассчитывается по следующей формуле :

S — спортивный результат (м);

v — скорость вылета ядра (м/сек);

α. — угол вылета ядра (градусы);

q — ускорение силы тяжести (м/сек)

Как видно из формулы, спортивный результат зависит в основном от трех составляющих: скорость, угол вылета и ускорение силы тяжести. Ускорение силы тяжести величина постоянная и равна 9,81 м/сек. Изменить её невозможно. Угол вылета ядра влияет на дальность его полета. Оптимальный угол вылета ядра находится в пределах 38-41 . Изменение угла вылета в зоне оптимальных величин в пределах 1-3 незначительное влияние на результат . Наибольшее влияние на спортивный результат имеет скорость вылета ядра. Она зависит от пола, возраста, квалификации и физической подготовленности спортсмена, а также от веса самого ядра.

1.1 Траектория движения ядра

На верхней части рисунка 1.1., представлена схема пути движения ядра при сообщении ему скорости разгона . На участке пути А-Б осуществляется предварительный разгон. На участке Б-В выполняется финальный разгон снаряда, скорость его продвижения увеличивается в несколько раз. В точке В ядро покидает руку метателя. Далее движение ядра продолжается по траектории В-Г.

Эффективная техника толкания позволяет спортсмену направить все свои усилия так, чтобы на пути А-Б разогнать и сообщить снаряду оптимальную скорость движения, соответствующую уровню подготовленности спортсмена. На отрезке Б-В ядро разгоняется за кратчайший промежуток времени, достигая максимальной скорости в точке В. Оптимальная траектория полета ядра может быть получена, если его движение, начиная с середины пути Б1-В, будет происходить под определенным углом к горизонту. На пути В-Г скорость движения ядра не увеличивается.

Рис. 1.1. Система связей основных характеристик элементов движений при сообщении скорости ядру (условные обозначения в тексте)

Теоретически считается, что на дальность полета ядра также влияет сопротивление воздушной среды. Однако, эти воздействие ничтожно мало, поэтому в спортивной практике оно не учитывается. Установлено, что дальность полета ядра увеличивается от высоты, на которой снаряд покидает руку метателя . Поскольку высота точки вылета для каждого спортсмена индивидуальна, и увеличить её невозможно, то и этот фактор в спортивной практике не учитывается .

Таким образом, ядро разгоняется сначала на более длинном пути с меньшей силой. Затем на более коротком пути, но с проявлением большей силы.

1.2 Скорость движения ядра

Среди перечисленных параметров начальная скорость вылета, наиболее изменяемая. В таблице 1.1. представлены данные о дальности полёта ядра в зависимости от угла и скорости вылета.

Обучение технике толкания ядра

Введение

перспективное опережение формирования технического мастерства.

Это определило выбор темы курсовой работы.

Для достижения поставленной цели необходимо решить следующие задачи:

Изучить основы современной техники толкания ядра.

Определить основные задачи в методике обучения техники.

Выявить основные средства обучения.

При написании курсовой работы были использованы следующие методы:

Анализ научно-методической литературы.

Беседа с тренером.

1. Основы современной техники толкания ядра

С точки зрения механики, теоретическая дальность полета ядра рассчитывается по следующей формуле :

S — спортивный результат (м);

v — скорость вылета ядра (м/сек);

Угол вылета ядра (градусы);

q — ускорение силы тяжести (м/сек)

Как видно из формулы, спортивный результат зависит в основном от трех составляющих: скорость, угол вылета и ускорение силы тяжести. Ускорение силы тяжести величина постоянная и равна 9,81 м/сек. Изменить её невозможно. Угол вылета ядра влияет на дальность его полета. Оптимальный угол вылета ядра находится в пределах 38-41º . Изменение угла вылета в зоне оптимальных величин в пределах 1-3° незначительное влияние на результат . Наибольшее влияние на спортивный результат имеет скорость вылета ядра. Она зависит от пола, возраста, квалификации и физической подготовленности спортсмена, а также от веса самого ядра.

1.1 Траектория движения ядра

На верхней части рисунка 1.1., представлена схема пути движения ядра при сообщении ему скорости разгона . На участке пути А-Б осуществляется предварительный разгон. На участке Б-В выполняется финальный разгон снаряда, скорость его продвижения увеличивается в несколько раз. В точке «В» ядро покидает руку метателя. Далее движение ядра продолжается по траектории В-Г.

1.2 Скорость движения ядра

Расчёты, проведённые рядом авторов , показали, что скорость вылета ядра 10 м/сек соответствует результату — 12 м, а скорость 15 м/сек — результату около 25 м, т.е. увеличение скорости в 1,5 раза приводит к увеличению результата в 2,08 раза.

В свою очередь, скорость вылета ядра зависит от величины силы, длины пути воздействия силы и времени её приложения . Скорость ядру сообщается на различных по длине отрезках пути, расположенных последовательно друг за другом. Вначале в процессе скачка и достигает 2-3 м/с, — это предварительная скорость. Затем в финальном усилии — заключительная скорость, возрастающая примерно в 4-5 раз по сравнению с предварительной скоростью.

Таблица 1.1. Дальность полёта ядра в зависимости от угла и скорости вылета

Угол вылета (в градусах)Скорость вылета (м/сек)111212,51313,514Дальность полёта (м)3814,1416,7417,9719,2620,6021,943914,4316,7818,0219,3220,6622,034014,4416,8018,0519,3520,7022,084114,4416,8118,0719,3720,7322,12

Для увеличения скорости движения снаряда крайне важно, чтобы на всем пути воздействия на него, усилия спортсмена возрастали. Это достигается за счет определенно-последовательного сокращения мышц. Пример последовательности включения определенных мышечных групп в работу можно увидеть на рисунке 1.2. На нём схематично представлено тело метателя: нижнее звено (1) — ноги, среднее звено (2) — туловище, верхнее звено (3) — верхний плечевой пояс, рука. Набрав скорость в скачке, спортсмен, при постановке левой ноги в упор, под действием инерции массы тела и работы правой ноги, перемещает туловище и руку с ядром вперед-вверх. Закончив движение до вертикали, нижнее звено (1) затормаживается. Под действием инерции и усилий мышц,

Рис. 1.2. Схема последовательного включения мышечных групп спортсмена в финальном усилии при толкании ядра

туловище движется также до вертикали и затормаживает своё движение (2). Далее, под действием инерции масс руки с ядром и усилий мышц плечевого пояса, а также руки, ядро движется до вертикали (3), где под действием инерции, в верхней точке покидает руку толкателя.

Таким образом, последовательное включение в работу отдельных звеньев тела спортсмена, способствует возрастанию скорости ядра. Происходит это за счет переноса количества движения с нижних звеньев на верхние . Предварительная скорость, сообщается снаряду за счет работы мышц ног и туловища, а заключительная, за счет включения мышц плечевого пояса и руки .

Улучшение спортивных результатов в метаниях связано с постоянным совершенствованием ритма движений. Ритм — это комплексная характеристика, отражающая определённое соотношение между отдельными частями, периодами, фазами, элементами какого-либо физического упражнения по усилиям во времени и пространстве .

В толкании ядра совершенствованием ритма движений выражается в повышении скорости движения спортсмена уже с фазы предварительного разгона (V1д) до его вылета (V80) . В нижней части рис. 1.1., представлена система связей основных элементов движений при толкании ядра. Большая скорость движения в этой фазе способствует, в свою очередь, увеличению обгона снаряда (О2) и пути финального разгона (Ф3), что в тоже время приводит к сокращению времени финального разгона (Т4). Иными словами, большая скорость предварительного разгона активизирует финальную фазу в метаниях.

Сокращение времени финального разгона связано с увеличением усилий, условно обозначенных как вращательное — F5 (туловище и толкающая рука) и разгибательное — F6 (ноги и туловище). Если общая сила движения ног и туловища, при их разгибании, является ведущей в создании угла вылета ядра (?7), то общая сила вращательного движения туловища и толкающей руки является ведущей в создании скорости вылета снаряда (V80).

Повышение скорости вылета ядра обеспечивает увеличение дальности его полёта и улучшение спортивных результатов S9.

1.3 Анализ техники

Технику толкания ядра для удобства рассмотрения можно разделить на фазы в соответствии с их задачами :

) держание снаряда;

) подготовка к разгону и разгон скачком;

) подготовка к финальному усилию (перекат);

) финальное усилие;

) вылет и снаряда.

Держание снаряда. Задача этой фазы — держать ядро так, чтобы выполнить толкание свободно, с оптимальной амплитудой движения. Правильное держание должно способствовать передаче метателем силы снаряду для движения его в нужном направлении по оптимальной траектории, а также выпуску его с наибольшей скоростью. С целью увеличения амплитуды движений в скачке и увеличения пути приложенной силы в заключительной фазе ядро удерживается кистью так, чтобы он был ближе к концам пальцев.

Перед скачком метатель становится у задней по направлению толкания части круга. Перед толканием ядро должно лежать на пальцах. Указательный, средний и безымянный пальцы несколько раздвигают. Большим пальцем и мизинцем ядро удерживают от скатывания.

В исходном положении, когда спортсмен стоит в круге спиной к направлению толкания, ядро держится у шеи, а локоть отводится от туловища вперед вправо. Возможны некоторые различия, зависящие от соотношения длины плеча и предплечья, от силы мышц и исходного положения. Держать ядро на весу не разрешается правилами соревнования.

Подготовка к разгону и разгон скачком. Основная задача этой фазы — выполнить оптимальные двигательные действия, способствующие достижению контролируемой скорость в предварительном разгоне ядра.

Большое значение в толкании ядра приобретает исходное стартовое положение спортсмена. Оно должно обеспечивать удлинение пути при наращивании скорости движения снаряда. Предварительный разгон включает совместный разгон и обгон нижних звеньев тела и завершается занятием исходной позиции перед финальным разгоном. Предварительный разгон в толкании ядра осуществляется при одноопорном и безопорном положении. К концу предварительного разгона, дальнейшее создание поступательной скорости достигается обгоном нижними звеньями тела верхних. Обгон осуществляется как в прямолинейном движении (точка опоры — стопа правой ноги находится впереди проекции снаряда), так и в криволинейном (ось таза опережает ось плеча и руки с ядром). Обгон, выполненный быстро и свободно, создает благоприятную исходную позицию для проведения финального разгона (усилия) снаряда.

Разгону предшествует выполнение метателем в исходном положении различных движений, которые способствуют эффективному выполнению последующих движений. В толкании ядра разгон выполняется в одном случае поступательным движением — в форме скачка, а в другом, вращательно-поступательным — в форме одного поворота.

При разбеге метатель может придать ускорение снаряду только при опоре ногами о грунт. Причем в двухопорном положении, спортсмен воздействует на ядро с наибольшей силой, чем в одноопорном положении, и придает ему большее ускорение. Поэтому метатель должен сократить время пребывания в одноопорном и особенно в безопорном положении до минимума .

Скачок выполняется из положения, стоя спиной к направлению толкания. Правая нога ставится вплотную к обручу, левая нога отставляется назад на носок или ставится рядом. Взгляд направлен сторону, противоположную толканию. Левая рука свободно вытянута вперед-вверх.

Подготавливаясь к скачку, толкатель поднимается на носок правой ноги и, переносит на него тяжесть тела. Одновременно он отводит левую ногу назад-вверх. После этого, наклоняясь вперед, приседает на правой ноге и опускает левую согнутую ногу вниз, подводя её к правой. Вслед за этим делает быстрый мах левой ногой назад, сопровождаемый отталкиванием правой ногой. При взмахе левой ногой вес толкателя находится на правой ноге. По мере отведения левой ноги назад он перемещается в том же направлении, сохраняя опору на правой ноге. Разведение бедер достигает максимума (120° и более) .

Оттолкнувшись правой ногой, спортсмен, подтягивает голень к себе. Заканчивается скачок постановкой правой ноги на опору.

Подготовка к финальному усилию (перекат). Задача этой фазы — принять рациональное положение для наращивания скорости при выполнении финального усилия.

При минимальной потере линейной скорости движения ядра, ускоренным движением ног и таза, создаётся предварительное натяжение мышц всего тела. Предварительно растянутые мышцы при последующем сокращении проявляют большую силу тяги .Это натяжение достигается поворотом туловища вправо, с оптимальным наклоном в обратную сторону направления толкания, а также сгибанием ног до оптимальных пределов. Для увеличения приложения усилий к ядру имеет и ширина расстановки ног. Ширина их расстановки зависит от индивидуальных особенностей толкателя . В целом же подготовка к финальному усилию является пассивной, ибо начинается после скачка, с момента постановки правой ноги на грунт и заканчивается при постановки левой ноги.

Правая нога, после скачка, ставится на носок. Исходное направление стопы при этом сохраняется, или она поворачивается слегка внутрь. После постановки правой ноги спортсмен проходит промежуточное положение, характеризующееся оптимальным наклоном туловища в направлении, противоположном толканию. Веса тела спортсмена на правой согнутой ноге.

Левая нога быстро ставится у сегмента слева от диаметра круга. Такое направление стопы сохраняется до окончания толчка . С постановкой левой ноги происходит так называемый обгон верхних звеньев тела спортсмена нижними — «скручивание» туловища, в процессе которого растягиваются мышцы, активно участвующие в последующей работе. Принимается наиболее выгодное положение для финального усилия, и создаются лучшие условия для слитного перехода предварительного в финальный разгон.

Финальное усилие. Задача этой фазы метания — вытолкнуть ядро с максимальной скоростью, под оптимальным углом вылета.

Финальный разгон, или финальное усилие спортсмена, является решающим в достижении максимальной скорости вылета снаряда в нужном направлении. При благоприятной исходной позиции для проведения финального усилия обеспечивается растягивание и напряжение мышц ног, туловища, плечевого пояса и метающей руки. В этих условиях возрастает сила сокращения мышц, которые выполняют разгибательное и вращательное движение с сообщением скорости и выталкиванием ядра.

Таким образом, в процессе толкания ядра, скорость ему сообщается в определенной последовательности: сначала телу метателя и снаряду; в начальной фазе финала — верхним частям тела и снаряду; в заключительной фазе финала — только снаряду и руке. При этом имеет место использование принципа «хлыста»: торможение нижележащих звеньев тела способствует передаче их количества движения (импульс тела) вышележащим звеньям волнообразно, с увеличением скорости движения последних, так как движущаяся масса уменьшается от всего тела до руки со снарядом (рис. 1.2). Эта задача выполняется за счёт согласованной работы мышц ног. Как только метатель примет двухопорное положение после скачка, мышцы ног, сокращаясь, поднимают туловище. Одновременно происходит выведение таза вперед. Выпрямление ног и выведение таза вперед необходимы для того, чтобы мышцы туловища остались растянутыми, а выпрямленная левая нога послужила упором для прекращения движения звена.

Выпрямленные ноги метателя являются твердой опорой, необходимой для сокращения мышц туловища. Только после полного сокращения мышц туловища включаются в работу мышцы верхнего плечевого пояса и руки.

Особое значение в финальном усилии приобретает последовательное сокращение мышц. Установлено, что, если соблюдается поочередное сокращение мышц, т.е. сила последующей мышечной группы включается в тот момент, когда сила предыдущей равна нулю, достигается наибольшая скорость движения снаряда .

Вылет снаряда. Во всех метаниях, кроме толкания ядра, сила воздействия на снаряд не влияет на угол вылета. А при толкании ядра, чем меньше сила воздействия на снаряд, тем больше угол вылета, и наоборот.

Активное финальное усилие выполняется в двухопорном положении. Левая нога, упруго поставленная на грунт с началом финального усилия, несколько сгибается под давлением движущейся массы тела и вслед за этим быстро выпрямляется. Давлением правой ноги при упоре левой метатель выводит таз, продвигая его несколько вперед-вверх. После этого, спортсмен быстро выпрямляет туловище, поворачивая его и плечевой пояс влево, опережая этим выпрямление руки в локтевом суставе. Правое плечо в заключительный момент толкания обычно выше левого.

Разгибание руки при выталкивании ядра опережает выведение локтя вперед. Это движение способствует заключительному подхлестывающему усилию метателя кистью и пальцами для сообщения снаряду ускорения.

После скачка и постановки левой ноги, левая рука активно отводится через сторону назад. Этим метатель создает нужное натяжение мышц, помогает выпрямить туловище при финальном усилии и уравновесить тело.

К моменту вылета ядра правая рука и левая нога находятся на одной вертикальной плоскости, расположенной по направлению полета ядра.

После вылета ядра, следует смена ног прыжком. Это затормаживает движение тела вперед и выход спортсмена за пределы круга.

Таким образом, базовой основой техники толкания ядра является: держание снаряда, подготовка к разгону и разгон (скачком), подготовка к финальному усилию (перекат) и финальное усилие.

2. Обучение технике

Обучать технике толкания ядра можно всех занимающихся, независимо от их физической подготовленности. На первых занятиях, особенно для лиц, слабо подготовленных физически, применяются более легкие ядра: весом 2-3 кг для женщин и 4-5 кг для мужчин Желательно, чтобы число ядер соответствовало количеству занимающихся.

Площадка для занятий толканием ядра с начинающими должна представлять собой ровное место с плотным грунтом и кругами для толкания. Чтобы предупредить несчастные случаи, занимающихся размещают на одной стороне площадки на расстоянии 3-4 м друг от друга. Снаряд толкают только в одну сторону. Выходить за снарядом разрешается после того, как все выполнят упражнение.

2.1 Этапы обучения спортивной технике

Процесс обучения спортивной технике подразделяют на ряд этапов. Большинство исследователей проблемы обучения в спорте выделяют три этапа:

) ознакомления с изучаемым спортивным упражнением или его отдельными подсистемами;

) овладения техникой предмета обучения;

) совершенствования в его выполнении.

В большинстве случаев обучению спортивной технике предшествует этап подготовки, задачи которого:

определить способности занимающихся к данному виду спорта;

сформировать активно положительное отношение к занятиям;

обеспечить физическую подготовленность — основание для овладения техникой данного спортивного упражнения;

способствовать развитию координации движений.

Средства решения задач для данного этапа — разнообразные двигательные действия, не всегда сходные по структуре с избранным видом спорта.

На первом этапе, который продолжается от одного до нескольких занятий, главная задача — сформировать целостное представление о технике данного спортивного упражнения, характерном для него ритме.

Второй этап длится от нескольких недель до года и более. Его основные задачи:

) создать четкие представления о кинематических, динамических и в особенности ритмических параметрах изучаемого движения;

) овладеть спортивной техникой в такой мере, чтобы быть способным выполнять изучаемые действия в целом, но в упрощенных условиях;

) способствовать развитию двигательных способностей, проявляющихся в изучаемом спортивном упражнении;

К третьему этапу обучения следует переходить, когда спортсмен станет способен сохранять стабильную технику спортивного упражнения, выполняя его с вариативными усилиями в оптимальных условиях.

Основные задачи третьего этапа, который продолжается так долго, как долго спортсмен стремится повысить (или сохранить) достигнутые им результаты:

) совершенствовать требуемую структуру и ритм движений, характерный для данного спортивного упражнения при выполнении его с максимальными усилиями в вариативных условиях;

) способствовать стабилизации спортивной техники.

Этапы обучения повторяются в учебно-тренировочном процессе спортсменов любой квалификации несколько раз. Как только поставлена задача, добиться большего совершенства в выполнении спортивного упражнения, внести какой-либо новый элемент в технику или изменить ранее усвоенное действие, тренер и спортсмен, возвращаются к решению задач, характерных для первых этапов обучения, а иногда и к этапу подготовки .

2.2 Последовательность обучения спортивной технике

Соблюдение рациональной последовательности обучения спортивной технике основывается на признании системности как основополагающего условия успешной деятельности в любой области . Оно обязывает тренера найти порядок в овладении спортсменом отдельными двигательными действиями, которые составляют основу техники и подобрать для обучения соответствующие упражнения.

Исходным положением, для установления последовательности обучения технике спортивных упражнений, является выделение частей, фаз или элементов от правильности которых в большей мере зависит эффективность изучаемого действия . Эти части, фазы или элементы называются основными движениями.

Определение структурной (биомеханической) основы двигательного действия — начало для установления рациональной последовательности обучения спортивной технике . Из содержания первой главы становится понятно, что основной в достижении спортивного результата в толкании ядра является фаза финального усилия. Однако по последовательности двигательных действий эта фаза является заключительной.

В соответствии с местом нахождения основы движения в общей цепи двигательного действия выделяют три варианта последовательного обучения технике спортивных упражнений (табл. 2.1.) . В одном из них основная часть находится в начале (Н), в другом — средине (С), в третьем — конце (К). Если основная часть находится в начале, ее осваивают первой; затем изучают среднюю часть; к ней присоединяют уже освоенную начальную часть; вслед за тем изучают технику заключительной части; к ней присоединяется освоенная средняя часть; наконец, осваивают и закрепляют технику упражнения в целом. То же относится к обучению отдельным частям и фазам упражнения. Следовательно, каждый из вариантов последовательного обучения состоит из шести вспомогательных этапов («шагов»).

Таблица 2.1. Варианты последовательности обучения спортивной технике

ВариантПоследовательность шагов в обучении1234561НСНСКСКНСК2СННСКСКНСК3КССКННСНСК

Этот распространяется и на те случаи, когда основная часть или фаза техники спортивного упражнения находится в середине или в конце, и тогда вначале осваивают соответственно среднюю или конечную часть или фазу.

Таким образом, обучение спортивной технике ведется не обязательно в порядке развертывания двигательного действия (от начала — к концу) н не от простого к сложному, а, как правило, наоборот — от трудного к легкому.

2.3 Методика обучения

Ниже приведена общепринятая методика обучения толканию ядра с основными задачами, средствами и методическими указаниями к обучению.

Задача 1. Ознакомить с техникой толкания ядра с разбега скачком.

Средства: 1. Ознакомление со снарядом, местом занятия и правилами выполнения толкания на соревнованиях. 2. Объяснение и показ толкания со скачка из крута. 3. Демонстрация наглядных пособий.

Задача 2. Научить держать и выталкивать ядро.

Средства: 1. Показ и проверка правильности держания ядра 2. Имитация выталкивания ядра. 3. Толкание ядра вверх, затем вперед-вверх.

Надо следить за тем, чтобы начинающие не держали ядро на концах пальцев во избежание травмы. Толкать ядро в этих упражнениях нужно из положения, стоя полуоборотом к направлению толкания ноги на ширине плеч, без глубокого приседа.

Основное внимание обращать на правильное выпрямление руки с ядром, при котором предплечье должно следовать за ядром. При выведении вперёд локтя ядро скатывается с пальцев, что может привести к травме. Выпрямляя руку надо поворачивать плечевой пояс. Толчки ядра чередуются с имитацией выталкивания.

Выталкивание ядра выполняется после предварительного небольшого сгибания ног, которые выпрямляются затем одновременно с разгибанием толкающей руки.

Задача 3. Научить финальному усилию.

Средства: 1. Толкание ядра с места из исходного положения, стоя боком к направлению толкания. 2. То же, из исходного положения, стоя спиной к направлению толкания. 3. То же, из положения, стоя на правой ноге с постановкой левой ноги на грунт. 4. Имитация толкания из названных ниже походных положений без ядра и с ядром.

Методические указания. При толкании с места изучаются те движения и усилия, которые должны следовать после скачка.

Толкание ядра с места сначала выполняется стоя боком в сторону толкания, но обязательно после предварительного поворота плечевого пояса направо. Ноги при этом слегка согнуты, правая стопа располагается сначала почти под прямым углом к направлению толкания. Это — переходное упражнение к толканию из положения, стоя спиной к направлению толкания.

При толкании обязательно добиваться активной работы ног в сочетании с полным поворотом плечевого пояса. Следует помнить о характерных ошибках новичков при выполнении финального усилия: преждевременном повороте головы и плечевого пояса налево, несогласованных движениях плечевого пояса и руки с ядром и наклоне тела влево или вперед.

По мере овладения толканием ядра с места из промежуточного положения, стоя боком надо переходить к толканию из положения, стоя спиной к направлению толкания. Исходное положение постепенно изменяется, прежде всего за счет все большего «скручивания» туловища направо.

Затем изучается толкание ядра из того же положения (стоя на правой ноге спиной к направлению толкания) с отведением и постановкой левой ноги назад. Подготовка к толканию (замах) заключается в наклоне туловища вперед со сгибанием правой ноги в колене с переносом веса тела на переднюю часть стопы и отведением левой ноги назад.

Для контроля направления вылета ядра, полезно толкать его через предметы, расположенные вверху (планка или веревочка на высоких стойках), или по направлению более удаленных других ориентиров.

Чтобы создать у занимающихся представление о правильном сочетании движений отдельных частей тела, полезно имитировать финальное усилие без ядра и с легким ядром, а при замахе делать движения («скручивание»), обратные выталкиванию ядра, — «обратный ход».

Для совершенствования навыков владения телом и снарядом при толкании (использование массы тела, эластичности мышц, силы ног, ускорения), могут применяться дополнительные упражнения. Они связаны с толканием и бросанием ядер, набивных мячей, камней разного веса; с активным вращательным движением плечевого пояса; толкание двумя руками и одной от груди вперед; бросание двумя руками снизу вверх и назад через голову; бросание ядра из-за головы вперед. Эти упражнения способствуют также развитию силы и координации соответствующих групп мышц техникой толкания.

Задача 4. Научить скачкообразному разбегу.

Средства: 1. Скачки на правой ноге без ядра, стоя спиной к направлению толкания в наклоне вперед с отведенной назад левой ногой. 2. Подготовительные движения перед скачком. 3. То же с последующим скачком.

Методические указания. Обучать скачку можно параллельно с решением предыдущих задач. Чтобы занимающийся лучше ощутил правильные движения в скачке, их следует делать с помощью партнера. Партнер (лучше, если это будет обучающий) придерживает отведенную назад левую ногу толкателя у подъема и легко тянет его за ногу, направляя скачок по горизонтали. Обучающийся делает скачки на правой ноге, используя силу тяги партнера и обращая внимание на полное разведение бедер и быстрое подтягивание голени. Скачки выполняются непрерывно сериями по 3-5 раз. Наряду с этим следует уделять внимание обучению маху левой ногой назад и выполнению низкого скачка на правой ноге с быстрым подтягиванием голени.

адача 5. Научить технике толкания ядра со скачка.

Средства: 1. Скачки с ядром. 2. Толкание со скачка облегченного и нормального ядра. 3. Толкание ядра со скачка из круга с соблюдением правил соревнований.

Методические указания. На каждом занятии начинающие должны толкать ядро с места в соответствии с задачей 3 и изучать скачок. Сначала делается короткий скачок (40-50 см), так как в этом случае можно толкнуть ядро более согласованно со скачком.

Нужно, чтобы во время скачка занимающиеся стремились сохранять наклон туловища, выполняли скачок согласованно с финальным усилием, а финальное усилие — с ярко выраженным ускорением. Прерывистость движения после скачка обычно вызывается высоким и далеким скачком с последующим опусканием туловища после приземления. Не меньшее значение может иметь и неправильное стремление метателя начать финальное усилие лишь после того, как будет занято прочное двух опорное положение. Это происходит у занимающихся непроизвольно, по ассоциации с толканием с места из исходного положения стоя прочно на двух ногах.

Задача 6. Совершенствовать технику в толкания ядра.

Средства: 1. Толкание ядер различного веса из круга. 2. Упражнения, перечисленные ранее (3, 4, 5-я задачи). 3. Толкание ядра на результат.

Методические указания. При овладении основами техники толкания ядра со скачка следует исправлять ошибки и пробовать изучать детали техники, которые не удавались ранее. Эти детали, обычно связаны со стремлением, выполнить скачок и финальное усилие слитно и с большой скоростью, для увеличения и полета снаряд.

Особое внимание приходится обращать на активную, согласованную работу ног, туловища и рук в финальном усилии и на выполнение толкания ядра в целом в нужном ритме. Надо стремиться изыскивать и другие средства, позволяющие толкать ядро с наибольшим ускорением.

При изучении новых элементов техники толкания ядра и для выполнения движений с большой скоростью полезно применять облегченные ядра.

Толкание более тяжелых ядер применяется для того, чтобы закрепить у занимающихся навык в работе большой мощности и затем использовать этот навык при толкании ядра нормального веса. Безусловно, толкание ядер разного веса способствует и развитию силы соответствующих групп мышц и быстроты движений.

Как правило, обучение основам спортивной техники достигается с наибольшим трудом. Следовательно, обучение в спорте ведется не от простого к сложному и не от легкого к трудному, а, как правило, наоборот.

Для достижения совершенства в выполнении изучаемого действия больше времени и внимания следует уделять найденным в нем двигательным основам.

Заключение

В результате выполненной работы получены следующие выводы.

Основой современной техники толкания ядра является: держание снаряда, разгон, группировка, финальное усилие и выпуск.

Процесс обучения технике толкания ядра делится на три этапа: ознакомления; овладения; совершенствования.

Основной задачей в методике обучения толкания ядра является — обучение финалу.

Основными средствами обучения являются соревновательное и специально-подготовительные упражнения.

Список источников

1. Алабин В.Г., Алабин А.В., Бизин В.П. Многолетняя тренировка юных спортсменов. — Харьков: Основа, 1993. — 224 с.

Боген М.М. Обучение двигательным действиям. М.: Физкультура и спорт, 1985. — 192 с.

Донской Д.Д., Зациорский В.М. Биомеханика. — М.: Физкультура и спорт, 1979. — 264 с.

Григалка О..Я. Толкание ядра. — М.: Физкультура и спорт, 1970. — 72 с.

Иванченко Е.И. Теория и практика спорта. — Мн.: Четыре четверти, 1997. — Часть 2. — 180 с.

Книга тренера по лёгкой атлетике. — Изд. 3-е, пераб. / Под ред. Л.С. Хоменкова. — М.: Физкультура и спорт, 1987. — 399 с.

Ланка Я.Е., Шалманов А.А. Биомеханика толкания ядра. — М.: Физкультура и спорт, 1982. — 72 с.

Лёгкая атлетика за рубежом / Под ред. Е.Н. Кайтмазовой. М.: Физкультура и спорт, 1974. — 430 с.

Легкая атлетика: учебник для ин-тов физ. культуры / Под общ. ред Н.Г. Озолина, В.И. Воронкина, Ю.Н. Примакова. — Изд. 4-е, доп., перераб. — М.: Физкультура и спорт, 1989. — 671 с.

Матвеев Л.П. Основы спортивной тренировки. М.: Физкультура и спорт, 1977. — 271 с.

Методика обучения легкоатлетическим упражнениям: Учеб. пособие для ин-тов физ. культуры и фак-ов физ. воспитания / Под общ. ред. М.П. Кривоносова, Т.П. Юшкевича. — Мн.: Вышейшая школа, 1986. — 312 с.

Озолин Н.Г. Современная система спортивной тренировки. — М.: Физкультура и спорт, 1970. — 480 с.

Озолин Н.Г. Молодому коллеге. — М.: Физкультура и спорт, 1988. — 288 с.

Озолин Н.Г. Настольная книга тренера: Наука побеждать. — М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2002. — 864 с.

Основы лёгкой атлетики / Сост. А.Ф. Бойко. М.: Физкультура и спорт, 1976. — 200 с.

Основы управления подготовкой юных спортсменов / Под общей ред. М.Я. Набатниковой. — М.: Физкультура и спорт, 1982. -280 с.

Платонов В.Н. Теория и методика спортивной тренировки. — К.: Вища школа, 1984. — 352 с.

Платонов В.Н. Общая теория подготовки спортсменов в олимпийском спорте. — К.: Олимпийская литература, 1997. — 584 с.

Попов В.Б., Суслов Ф.П., Ливадо Е.А. Юный легкоатлет. — М.: Физкультура и спорт, 1984. — 224 с.

Попов В.Б., Суслов Ф.П. Германов Г.Н. Легкая атлетика для юношества: — Москва-Воронеж, 1999. — 220 с.

Система подготовки спортивного резерва / Под общ. ред. В.Г. Никитушкина. — М.: МГФСО, 1993. — 320 с.

Совершенствование технического мастерства спортсменов / Под общ. ред. В.М. Дьячкова. М.: Физкультура и спорт, 1972. — 231 с.

ядро толкание спортивный техника

Заказ работы

Наши специалисты помогут написать работу с обязательной проверкой на уникальность в системе «Антиплагиат»
Отправь заявку
с требованиями прямо сейчас, чтобы узнать стоимость и возможность написания.

Основной целью спортивных метаний является дальность полёта снаряда, однако падение снаряда должно быть в зоне, установленной правилами соревнований.

Все метания подчинены общим закономерностям механики.

Легкоатлетические метания являются ациклическими упражнениями. В зависимости от веса и формы снаряда применяются различные способы метаний. Движения метателей имеют одну цель — сообщить снаряду наибольшую скорость вылета, ибо дальность полёта снаряда зависит от начальной скорости его вылета, угла вылета, сопротивления воздушной среды. Дальность полёта определяется по формуле

Где V
—
начальная скорость полёта снаряда;  — угол вылета; g
— ускорение силы тяжести.

Из этой формулы видно, что увеличение дальности полёта снаряда в наибольшей степени зависит от повышения начальной скорости полёта и увеличения угла вылета (так как ускорение свободного падения — величина постоянная). Однако лишь увеличение начальной скорости будет способствовать увеличению спортивных результатов. Увеличение же угла вылета имеет предел, равный 45, дальнейшее повышение этого угла не приводит к увеличению дальности полёта снаряда.

Скорость снаряду сообщается на различных по длине отрезках пути, расположенных пространственно отдельно один от другого.

Вначале скорость сообщается снаряду в процессе разбега (копьё — 7,8 м/с), скачка (ядро — 2 — 3 м/с, диск — 7 — 8 м/с) или нескольких поворотов (молот 20 — 23 м/сек) — это предварительная скорость
.

Затем скорость сообщается снаряду в финальном усилии — заключительная скорость.
Она возрастает по сравнению с предварительной скоростью при метании копья и толкании ядра примерно в 4 — 5 раз, при метании диска — в 2 раза, а при метании молота предварительная скорость значительно больше окончательной (соотношение примерно 5: 1).

Предварительная скорость сообщается снаряду за счёт работы мышц ног и туловища, а заключительная — за счёт включения мышц плечевого пояса и руки (копьё, ядро, диск).

Таким образом, снаряд разгоняется сначала на более длинном пути меньшей по величине силой, а затем на более коротком пути с большей силой.

Скорость вылета снаряда зависит от силы, приложенной к снаряду, длины пути воздействия силы на снаряд и времени приложения силы. Эту зависимость можно выразить формулой

Где V
—
скорость
вылета снаряда; F
—
сила, прикладываемая к снаряду; l
—
длина пути воздействия силы; t
—
время приложения силы.

Если рассматривать как градиент силы (скорость её нарастания), то можно сказать, что дальность полёта снаряда зависит от градиента силы и длины пути приложения усилий к снаряду. Если градиент силы измерять скоростно-силовым индексом, а длину пути приложения усилий к снаряду брать как степень технического мастерства, то в конечном итоге мы приходим к выводу, что результат в спортивном метании находится в прямой зависимости от скоростно-силовой подготовки и технического мастерства.

Для увеличения скорости движения снаряда крайне важно, чтобы на всём пути усилия возрастали. Это достигается путём последовательного подключения всё более мелких мышц.

Рис. 9. Схема последовательного включения мышечных групп метателя в работу финального усилия при метании копья:

1 —
ноги; 2 —
туловище; 3 —
плечо; 4 —
предплечье

Пример последовательности включения определённых мышечных групп в работу можно увидеть на рис. 9, где изображено финальное усилие в метании копья.

На отрезке 1  4 — многозвенное строение тела метателя. Набрав скорость в разбеге, копьеметатель при постановке левой ноги в упор под действием инерции массы тела и работы правой ноги ускоренно перемещает туловище и руку с копьём (сектор а
). Закончив движение до вертикали, нижнее звено останавливается. Под действием инерции и усилий мышц туловище движется до вертикали (сектор б
). Далее под действием инерции и усилий мышц плечевого пояса плечо движется до вертикали (сектор в).
И, наконец, под действием инерции массы предплечья, массы копья и мышц предплечья (сектор г)
копьё в верхней точке по касательной покидает руку метателя.

Угол вылета снаряда существенно влияет на дальность полёта и зависит от начальной скорости вылета, высоты выпуска снаряда над землёй, аэродинамических свойств снаряда (для диска и копья), состояния атмосферы (направления ветра), скорости разбега (для копья и ядра).

Оптимальный угол вылета для всех снарядов меньше 45. Для результатов уровня  разряда и выше оптимальный угол вылета снаряда находится в пределах (при отсутствии ветра): в толкании ядра — 38 — 41; в метании копья — 24 — 30; в метании диска у женщин — 33 — 35; у мужчин — 36 — 39; в метании молота — 44.

Во всех видах метаний, кроме диска, с увеличением скорости разбега угол вылета незначительно повышается (в метании диска понижается).

На дальность полёта снаряда влияет сопротивление среды. При метании молота, гранаты и толкании ядра эти воздействия ничтожно малы, поэтому в спортивной практике они не учитываются. При метании копья и диска воздушная среда оказывает положительное влияние, так как она создаёт подъёмную силу.

На дальность полёта оказывает влияние и высота точки вылета снаряда. Поскольку высоту точки вылета для каждого спортсмена увеличить невозможно, то этот фактор не рассматриваем.

Технику спортивных метаний для удобства изучения можно разделить на части в соответствии с их задачами:

держание снаряда;
подготовка к разбегу и разбег;
подготовка к финальному усилию;
финальное усилие;
вылет и полёт снаряда.

Держание снаряда.
Задача этой части — держать снаряд так, чтобы выполнить метание свободно, с оптимальной амплитудой движения. Правильное держание должно способствовать передаче метателем снаряду силы для движения его по наибольшему пути в нужном направлении, а также выбрасыванию снаряда с наибольшей скоростью. С целью увеличения пути приложения силы в заключительной фазе снаряд удерживается кистью так, чтобы он был ближе к концам пальцев.

Подготовка к разбегу и разбег.
Основная задача этой части — сообщение системе «метатель — снаряд» оптимальной начальной скорости.

Разбегу предшествует выполнение метателем в исходном положении различных движений, которые совершаются предварительным раскачиванием тела и размахиванием отдельных звеньев тела, а также снаряда. Главная задача этих движений: сосредоточить внимание на выполнении метания в целом; подготовить рациональное исходное положение; привести мышцы в растянутое состояние; сообщить снаряду начальную скорость.

Энергия, приобретённая метателем при вращении, находится в прямой зависимости от величины угловой скорости массы тела и радиуса его вращения.

При разбеге в форме поворота метатель может придать ускорение снаряду только при опоре ногами о грунт. Причём в двухопорном положении спортсмен воздействует на снаряд с большей, чем в одноопорном положении, силой и придаёт ему большее ускорение.

В метаниях при любой форме разбега увеличение скорости выше оптимальной, когда теряется контроль за движениями, является отрицательным моментом. Однако метатель должен повышать оптимальную для себя скорость разбега.

Подготовка к финальному усилию.
Задача этой части — при минимальной потере линейной скорости движения снаряда ускоренным движением отдельных частей тела растянуть мышцы всех звеньев тела так, чтобы создать условия для их последовательного сокращения. Нужно прийти в такое положение, чтобы снаряд оказался на возможно большем расстоянии от предполагаемой точки вылета (рис. 10 — 18). Это положение достигается с помощью оптимального наклона, поворота или скручивания туловища в сторону, обратную направлению метания, а также сгибания ног до оптимальных пределов и расстановки ног на необходимую ширину.

Ширина расстановки ног для каждого метателя определяется опытным путём.

Рис. 18. Положение в момент вылета копья

Рис.10. Положение перед толчком ядра

Рис. 13 Положение перед выталкиванием ядра

Рис. 12. Положение перед броском копья
В процессе подготовки к финальному усилию возможно также незначительное увеличение скорости движения снаряда (не всей системы «метатель — снаряд») или за счёт группировки спортсмена (метание диска), или за счёт уменьшения наклона туловища (толкание ядра). В целом же

Рис.14. Положение перед выбрасыванием диска

Рис. 15. Положение перед выбрасыванием копья

Рис. 11. Положение перед броском диска

Рис. 16. Положение в момент вылета ядра

Рис. 17. Положение в момент вылета диска

подготовка к финальному усилию является пассивной, ибо в этот момент из-за отсутствия ускорения происходит снижение скорости движения системы «метатель — снаряд».

Финальное усилие.
Задача этой части метания — сообщение снаряду максимальной скорости вылета под оптимальным углом при правильном его расположении в пространстве. Эта задача выполняется за счёт быстрого, строго последовательного сокращения мышц, прежде всего мышц ног.

Как только метатель занял двухопорное положение после разбега, мышцы ног, сокращаясь, поднимают туловище. Одновременно происходит выведение таза вперёд. Выпрямление ног и выведение таза вперёд необходимы для того, чтобы мышцы туловища остались растянутыми, а выпрямленная левая нога послужила упором для прекращения движения звена.

Особое значение в финальном усилии имеет последовательное сокращение мышц. Установлено, что если соблюдается очерёдность сокращения мышц, т.е. сила последующей мышцы включается в тот момент, когда сила предыдущей равна нулю, достигается наивысшая скорость движения снаряда.

Вылет и полёт снаряда.
На дальность полёта снарядов, обладающих аэродинамическими свойствами (диск, копьё), кроме высоты вылета, скорости стартового разгона силы воздействия на снаряд, начальной скорости вылета влияет состояние атмосферной среды (встречный или попутный ветер).

Аэродинамические свойства диска в 4,5 раза лучше чем у копья. В полёте диск и копьё вращаются. Копьё вращается вокруг горизонтальной оси, диск — вертикальной. При полёте диска возникает гироскопический момент, в результате чего его положение в воздухе стабилизируется.

Рис. 19. Схема возникновения подъёмной силы у летящего диска:

 —
прямой удар; 
—
косой удар с нормальным положением диска; 
—
косой удар с повышенным углом атаки
В метании копья снаряд совершает до 25 оборотов, что недостаточно для возникновения гироскопического момента, но большая скорость вращения всё же стабилизирует в какой-то мере положение копья.

В метании копья и диска подъёмная сила превышает лобовое сопротивление, увеличивая тем самым дальность полёта

При метании копья оптимальный угол атаки находится в пределе 2 — 10.

На дальность полёта диска и копья влияет угол атаки. Полёт диска происходит с разными углами атаки. Первое время диск летит с выгодными углами атаки и воздушная среда в большей степени способствует увеличению дальности полёта. Затем, по мере увеличения углов атаки, воздушная среда всё меньше и меньше способствует полёту диска, и, наконец, при углах атаки больших, примерно 42, воздух начинает тормозить скорость полёта диска и уменьшает его дальность.

Таким образом, полёт диска можно разделить на две зоны: 1-я — удлиняющая полёт и 2-я — укорачивающая (рис. 20).

Способ выброса диска с отрицательным углом атаки более предпочтителен по сравнению со способом метания в ребро, так как позволяет увеличить дальность метания и уменьшить потери в результатах при ошибках в углах. Угол вылета диска при попутном ветре надо повышать до 44. При этом угол атаки становится положительным, и метателю целесообразнее выбрасывать диск, направляя свои усилия в ребро. При встречном ветре диск целесообразно выбрасывать под углом 27

При метании «женского» диска в условиях встречного ветра требуется большее снижение угла вылета (до 23), чем при метании «мужского».

При метании копья с увеличением дальности метания углы вылета повышаются примерно с 37 (результат 67 м) до 39 (результат 92 м).

Рис. 20. Полёт диска в воздухе

Во всех метаниях, кроме толкания ядра, сила воздействия на снаряд не влияет на угол вылета. А при толкании ядра чем меньше сила воздействия на снаряд, тем больше угол вылета, и наоборот. Техника сильнейших мастеров.ppt

Основная цель метателей — толкнуть снаряд на возможно большее расстояние, соблюдая определенные правила, ограничивающие действия спортсменов.

Толкание ядра в основном осуществляется спиной в сторону метания, где прямолинейность разбега (скачка) сочетается с поворачивающим движением тела в момент выбрасывания снаряда. В последнее время при толкании ядра применяется разбег в виде поворота, где одновременно сочетаются поступательные и вращательные движения (с одним поворотом).

Все метания подчинены общим законам механики. На любой снаряд, бросаемый под углом к горизонту, действуют одни и те же факторы, определяющие дальность его полета. Исходя из законов механики, дальность полета снаряда равна: ,

где V о — начальная скорость вылета снаряда; ? — угол вылета снаряда;

g — ускорение свободного падения.

Это уравнение, однако, не учитывает воздействия атмосферной среды и того факта, что снаряд покидает руку метателя на некоторой высоте вылета (h о).

Рис. Система полета снаряда: S — длина полета по горизонтали; V 0 — начальная скорость вылета; — угол вылета; H — высота взлета; h o — начальная высота вылета; Z — угол местности

Высота начальной точки вылета (h o) зависит от роста метателя, длины его рук, техники. Чем выше высота начальной точки вылета, тем лучше. Но поскольку, высоту начальной точки вылета увеличить для одного и того же спортсмена практически невозможно, поэтому рассчитывать на рост результата за счет этого не приходится.

Вышеприведенную формулу можно использовать для определения дальности полета снаряда, но всегда следует учитывать и другие параметры. Итак, в целом, на результат в метании легкоатлетических снарядов влияют следующие факторы:

а) начальная скорость вылета снаряда (V о);

б) угол вылета снаряда (),

в) воздействие атмосферной среды (сопротивление воздуха, сила и направление ветра);

г) высота выпуска снаряда над землей (h o);

д) аэродинамические свойства снаряда;

е) угол атаки снаряда ().

Все факторы определяют в каждом конкретном случае эффективность метаний, но при этом значение каждого из параметров далеко не равноценно. В практике наибольшее значение имеют — начальная скорость, угол вылета и воздействие атмосферной среды. Их анализ необходим, прежде всего, для правильной оценки всех движений метателя, совершающего бросок снаряда.

Основным фактором увеличения дальности полета снаряда во всех метаниях является начальная скорость.

Теоретически нет никаких ограничений для увеличения начальной скорости. В формуле начальная скорость возведена в квадрат (V 0 2), поэтому если скорость возрастает в два раза, то дальность полета, при прочих равных условиях, увеличивается в 4 раза, при увеличении в 3 раза — в 9 раз и т.д. Например, скорости вылета ядра 10 м/с соответствует результат 12 м, а скорости 15 м/с — около 25 м, т.е. увеличение скорости в 1,5 раза приводит к увеличению результата в 2,25 раза.

В метаниях скорость вылета снаряда создается в итоге использования быстроты: ядро соревнования спортсмен снаряд

Предварительного размахивания;

Предварительного перемещения («метатель + снаряд» в разбеге);

Заключительного, финального усилия метателя в момент самого броска.

При этом степень сообщения скорости в разбеге и финальном движении для разгона снаряда в различных видах метания разная. Так, скорость стартового разгона в толкании ядра составляет 15-20, а остальная скорость сообщается снаряду в финальном усилии.

Как видно, в толкании ядра больше значение для разгона снаряда имеет финальное движение. Характерно, что у спортсменов высокого класса более равномерно увеличивается скорость снаряда от старта до вылета. Значительные колебания скорости видны и наблюдаются, как правило, у спортсменов младших спортивных разрядов. Спортсменов высокого класса отличает больший прирост скорости снаряда в финальном усилии.

Начальная скорость вылета снаряда является результатом суммирования скоростей отдельных звеньев тела — ног, туловища, рук. При этом, что особенно важно, происходит последовательный разгон звеньев снизу вверх, т.е. каждое последующее звено начинает движение, когда скорость предыдущего достигает максимума. Начальная скорость сообщается снаряду за счет работы мышц ног и туловища, а заключительная — включения мышц плечевого пояса и руки.

Кроме этого скорость вылета снаряда зависит от величины силы, приложенной к снаряду, и времени воздействия этой силы на него. Если исходить из второго закона Ньютона (V=Ft/m), то получится, что скорость прямо пропорциональна силе и времени ее приложения (масса снаряда — величина постоянная). Значит, чем большей силой мы будем воздействовать на снаряд и чем продолжительнее будет это воздействие, тем с большей скоростью снаряд покинет руку метателя. Если длину пути приложения на снаряд брать как степень технического мастерства спортсмена, то в конечном итоге мы приходим к выводу, что начальная скорость снаряда (и результат в спортивном метании) находится в прямой зависимости от специальной силовой подготовленности и технического мастерства метателя.

Важно подчеркнуть, что для обеспечения воздействия на движущийся с относительно большой скоростью снаряд мышцы метателя должны быть не только сильными, но и быстрыми. Причем спортсмен в процессе всего метания должен сообщать скорость не одному снаряду, а всему телу и снаряду, то есть системе «метатель + снаряд». Лишь во второй половине финального усилия ускоряется только один снаряд.

Следующим фактором, от которого в значительной мере зависит дальность полета, является угол вылета снаряда.

Углом вылета ()называется угол, построенный в точке вылета снаряда и заключенный между горизонтальной линией и вектором скорости снаряда (касательной к началу траектории полета). Как известно, если снаряд бросить в безвоздушном пространстве под углом 45 к горизонту, то он пролетит наибольшее расстояние. Но на практике оптимальные углы вылета различных снарядов оказываются меньше. Во-первых, это обусловливается тем, что спортивный снаряд выпускается в среднем на высоте от 160 до 220 см. Наличие разницы уровней вылета и приземления снаряда (так называемый угол местности) является первой причиной уменьшения теоретического угла выпуска. Во-вторых, метание под меньшим углом позволяет увеличить путь воздействия на снаряд и, в-третьих, строение мышечной системы спортсмена способствует большему приложению усилий при более низком угле вылета. Во всех видах метаний, кроме метания диска, с увеличением скорости разбега угол вылета незначительно повышается (в метании диска понижается).

Таким образом, угол вылета зависит от высоты выпуска снаряда над землей, состояния атмосферы (направление ветра), скорости разбега.

В спортивных метаниях надо использовать так называемые оптимальные углы вылета снарядов. В данном случае под оптимальным углом понимают наиболее выгодный угол для дальности полета снаряда.

После того, как снаряд покинул руку метателя, на него сразу же начинают действовать две силы воздушной среды:

1) сила сопротивления (или лобового сопротивления);

2) подъемная сила.

Сила сопротивления направлена против скорости снаряда и тем самым уменьшает дальность его полета. Она, в основном, зависит от площади поперечного сечения снаряда и от квадрата скорости его движения.

Подъемная сила- это сила, которая удерживает снаряд в полете, противодействуя силе тяжести. Если снаряд движется так, что потоки воздуха его обтекают равномерно как сверху, так и снизу, то на него не будет действовать подъемная сила.

При полете такого тяжелого снаряда, как ядро, действие этих сил практически незначительно и фактически не влияет на их полет в воздухе.

Все существующие метания являются целостными ациклическими упражнениями.

Текущая страница: 5 (всего у книги 13 страниц) [доступный отрывок для чтения: 9 страниц]

4.3. Основы техники легкоатлетических метаний

В легкой атлетике имеются 5 видов метаний – ядра, диска, копья, молота и гранаты.

Основная цель метателей – бросить (метнуть, толкнуть) снаряд на возможно большее расстояние, соблюдая определенные правила, ограничивающие действия спортсменов. Метания построены на трех основных способах бросания снарядов: 1) через плечо (копье, граната); 2) с боку (диск, молот); 3) от плеча (ядро). Эти способы определяют форму разбега и финального усилия в метании.

Метание копья и гранаты выполняется с прямолинейной формой разбега – лицом вперед. Толкание ядра в основном осуществляется спиной в сторону метания, где прямолинейность разбега (скачка) сочетается с поворачивающим движением тела в момент выбрасывания снаряда. Наконец, при метании диска, молота, а в последнее время и ядра, применяется разбег в виде поворота, где одновременно сочетаются поступательные и вращательные движения (с одним поворотом в диске, ядре и 3–4 поворотами в молоте). Несмотря на различную форму и вес снаряда, на разные условия и способы выполнения метаний, имеется много закономерностей, обусловливающих рациональную технику метаний.

1. Какие факторы влияют на дальность полета легкоатлетических снарядов?

Все метания подчинены общим законам механики. На любой снаряд, бросаемый под углом к горизонту, действуют одни и те же факторы, определяющие дальность его полета. Исходя из законов механики, дальность полета снаряда равна:

где V
о – начальная скорость вылета снаряда; α
– угол вылета снаряда; g
– ускорение свободного падения.

Высота начальной точки вылета (h
о) зависит от роста метателя, длины его рук, техники. Чем выше высота начальной точки вылета, тем лучше. Но поскольку высоту начальной точки вылета увеличить для одного и того же спортсмена практически невозможно, рассчитывать на рост результата за счет этого не приходится.

Рис. 9. Система полета снаряда: S – длина полета по горизонтали;V о – начальная скорость вылета; α – угол вылета; H – высота взлета; h о – начальная высота вылета; z – угол местности

Вышеприведенную формулу можно использовать для определения дальности полета снаряда, но всегда следует учитывать и другие параметры. Итак, в целом на результат в метании легкоатлетических снарядов влияют следующие факторы
(рис. 9):

а) начальная скорость вылета снаряда (V

о
);

б) угол вылета снаряда (α),

в) воздействие атмосферной среды (сопротивление воздуха, сила и направление ветра);

г) высота выпуска снаряда над землей (h
о
);

д) аэродинамические свойства снаряда;

е) угол атаки снаряда (β).

Все факторы определяют в каждом конкретном случае эффективность метаний, но при этом значение каждого из параметров далеко не равноценно. В практике наибольшее значение имеют – начальная скорость, угол вылета и воздействие атмосферной среды. Их анализ необходим прежде всего для правильной оценки всех движений метателя, совершающего бросок снаряда. Рассмотрим подробнее каждый из основных факторов, влияющих на дальность полета снаряда.

2. Как влияет начальная скорость вылета снаряда на дальность его полета?

Рассматривая составные величины указанной выше формулы, становится очевидным, что основным фактором увеличения дальности полета снаряда во всех метаниях является начальная скорость.

Теоретически нет никаких ограничений для увеличения начальной скорости. В формуле начальная скорость возведена в квадрат (V
о 2), поэтому если скорость возрастает в два раза, то дальность полета, при прочих равных условиях, увеличивается в 4 раза, при увеличении в 3 раза – в 9 раз и т. д. Например, скорости вылета ядра 10 м/с соответствует результат 12 м, а скорости 15 м/с – около 25 м, т. е. увеличение скорости в 1,5 раза приводит к увеличению результата в 2,25 раза.

В метаниях скорость вылета снаряда создается в итоге использования быстроты:

– предварительного размахивания;

– предварительного перемещения («метатель + снаряд» в разбеге);

– заключительного, финального усилия метателя в момент самого броска.

При этом степень сообщения скорости в разбеге и финальном движении для разгона снаряда в различных видах метания разная. Так, скорость стартового разгона в толкании ядра составляет 15–20 %, метании копья – 15–22 %, метании диска – 40–45 %, метании молота – 80–85 %, а остальная скорость сообщается снаряду в финальном усилии.

Как видно, в толкании ядра и метании копья большее значение для разгона снаряда имеет финальное движение, в метании диска эти части техники метания имеют примерно равное значение, а в метании молота предварительная скорость значительно больше окончательной. Характерно, что у спортсменов высокого класса более равномерно увеличивается скорость снаряда от старта до вылета. Значительные колебания скорости видны и наблюдаются, как правило, у спортсменов младших спортивных разрядов. Спортсменов высокого класса отличает больший прирост скорости снаряда в финальном усилии.

Начальная скорость вылета снаряда является результатом суммирования скоростей отдельных звеньев тела – ног, туловища, рук. При этом, что особенно важно, происходит последовательный разгон звеньев снизу вверх, т. е. каждое последующее звено начинает движение, когда скорость предыдущего достигает максимума.

Начальная скорость сообщается снаряду за счет работы мышц ног и туловища, а заключительная – включения мышц плечевого пояса и руки (копье, ядро, диск, граната).

Кроме этого, скорость вылета снаряда зависит от величины силы, приложенной к снаряду, и времени воздействия этой силы на него.
Если исходить из второго закона Ньютона (V
= Ft
/m
), то получится, что скорость прямо пропорциональна силе и времени ее приложения (масса снаряда – величина постоянная). Значит, чем большей силой мы будем воздействовать на снаряд и чем продолжительнее будет это воздействие, тем с большей скоростью снаряд покинет руку метателя.
Если длину пути приложения на снаряд брать как степень технического мастерства спортсмена, то в конечном счете мы приходим к выводу, что начальная скорость снаряда (и результат в спортивном метании) находится в прямой зависимости от специальной силовой подготовленности и технического мастерства метателя.

Следует отметить еще два условия, влияющие на увеличение начальной скорости в метаниях с вращением (диск, молот). Большую роль для создания начальной скорости полета снаряда здесь играет величина угловой скорости и радиус вращения, то есть расстояние от оси вращения до центра тяжести снаряда.

На величину радиуса влияет длина руки метателя (при метании диска), длина снаряда и расположение центра тяжести в самом снаряде (при метании молота). Чем больше радиус вращения при данной угловой скорости, тем выше начальная скорость полета и лучше результат метания.

3. Как влияет угол вылета снаряда на спортивный результат?

Следующим фактором, от которого в значительной мере зависит дальность полета, является угол вылета снаряда.

Углом вылета

(α) называется угол, построенный в точке вылета снаряда и заключенный между горизонтальной линией и вектором скорости диска (касательной к началу траектории полета).
Как известно, если снаряд бросить в безвоздушном пространстве под углом 45° к горизонту, то он пролетит наибольшее расстояние. Но на практике оптимальные углы вылета различных снарядов оказываются меньше. Во-первых
, это обусловливается тем, что спортивный снаряд выпускается в среднем на высоте от 160 до 220 см. Наличие разницы уровней вылета и приземления снаряда (так называемый
угол местности

) является первой причиной уменьшения теоретического угла выпуска.

Во-вторых
, метание под меньшим углом позволяет увеличить путь воздействия на снаряд и, в-третьих
, строение мышечной системы спортсмена способствует большему приложению усилий при более низком угле вылета. Во всех видах метаний, кроме метания диска, с увеличением скорости разбега угол вылета незначительно повышается (в метании диска понижается). Кроме этого, в планирующих снарядах (диск, копье) на изменение угла вылета влияет еще направление и величина ветра.

Таким образом, угол вылета зависит от высоты выпуска снаряда над землей, аэродинамических свойств снаряда (для диска и копья), состояния атмосферы (направление ветра), скорости разбега.

– при метании копья: 30–35
º; – при метании диска: 36–38
º; – при толкании ядра: 38–41
º; – при метании молота и гранаты: 42–44
º.

4. В чем заключается воздействие атмосферной среды на дальность полета снаряда?

После того как снаряд покинул руку метателя, на него сразу же начинают действовать две силы воздушной среды: 1) сила сопротивления (или лобового сопротивления); 2) подъемная сила.

Сила сопротивления

направлена против скорости снаряда и тем самым уменьшает дальность его полета. Она в основном зависит от площади поперечного сечения снаряда и от квадрата скорости его движения.

Подъемная сила – это сила, которая удерживает снаряд в полете, противодействуя силе тяжести. Если снаряд движется так, что потоки воздуха его обтекают равномерно как сверху, так и снизу, то на него не будет действовать подъемная сила. Если же направление скорости не совпадает с направлением продольной оси снаряда (плоскости диска), то потоки воздуха сверху и снизу будут неодинаковы. При этом сверху частицы воздуха будут обтекать снаряд быстрее и в то же время проходить большее расстояние, чем снизу, а, следовательно, давление воздуха на снаряд будет меньше, чем давление снизу. В результате разности давлений сверху и снизу возникает подъемная сила.

Существенно помнить, что подъемная сила не обязательно направлена вверх, ее направление может быть различным. Это зависит от положения снаряда и направления воздушного потока относительно его. В тех случаях, когда подъемная сила направлена вверх и уравновешивает вес снаряда, он начинает планировать. Планирование копья и диска существенно повышает результаты в метаниях.

При полете таких тяжелых снарядов, как ядро и молот, действие этих сил практически незначительно и фактически не влияет на их полет в воздухе. Иначе с так называемыми планирующими снарядами, как диск и копье, которым в полете оказывает существенное сопротивление атмосферная среда (плотность воздуха, сила и направление ветра). Важную роль при метании планирующих снарядов играет
угол атаки

, который образуется продольной осью (плоскостью) снаряда и направлением набегающего потока воздуха. Он может быть положительным, равным нулю или отрицательным.
Если поток воздуха набегает на нижнюю поверхность диска и копья, то угол атаки положительный, если на верхнюю – отрицательный.

Рис. 10. Силы, действующие на планирующий снаряд в полете: g – сила тяжести; X – сила сопротивления среды; Y – подъемная сила; α – угол вылета; β – угол атаки; V – скорость вылета

Как видно из рис. 10, на снаряд действуют сила тяжести (g
), сила сопротивления среды (Х
), подъемная сила (Y
). Фиксируются углы вылета (α) и атаки (β).

В метании диска лучше, если значение угла атаки вначале будет равно углу вылета. Иными словами, метатель должен стремиться направить усилия точно в плоскость снаряда. В этом случае диск в полете не будет совершать поперечных движений. Метатели копья стремятся, чтобы угол атаки был близок к нулю («попасть точно в копье»). При полете мяча, ядра и молота угла атаки нет.

Следует иметь в виду, что с увеличением угла атаки (β) увеличивается как подъемная сила, так и лобовое сопротивление воздушной среды, но при этом прирост подъемной силы будет идти гораздо быстрее, чем прирост лобового сопротивления. Впоследствии лобовое сопротивление продолжает возрастать, а подъемная сила начинает уменьшаться, и когда плоскость снаряда станет перпендикулярной направлению скорости, подъемная сила станет равной нулю. Следовательно, на траектории есть участки, где подъемная сила больше лобового сопротивления, и участок, где лобовое сопротивление превышает подъемную силу. Отсюда и вытекает необходимость найти оптимальные углы выпуска и атаки, при которых подъемная сила на большом участке траектории полета превышала бы лобовое сопротивление, а значит, и снаряд мог бы пролететь большее расстояние.

Большое влияние на полет планирующих снарядов оказывает направление движения воздуха. При метании диска и копья против встречного ветра возрастает сила лобового сопротивления воздуха и пропорционально увеличивается подъемная сила. Так создается аэродинамический прирост дальности полета снаряда. При метаниях против ветра для лучшего использования подъемной силы несколько уменьшают угол вылета снарядов по мере увеличения скорости ветра
. Расчеты показывают, что встречный ветер порядка 5 м/с, например, увеличивает дальность полета диска на 10 %, а попутный снижает на 2,5 %.

Интересно, что аэродинамические свойства женского диска выше, чем мужского. При одной и той же начальной скорости женский диск летит дольше, чем мужской. Причем при сильном встречном ветре это преимущество еще более возрастает. При попутном ветре скорость его совпадает с направлением полета снаряда и происходит уменьшение аэродинамической силы. Но поскольку при этом уменьшается и сила лобового сопротивления, то это обстоятельство нужно уметь использовать для увеличения дальности броска. Это достигается путем увеличения угла вылета.

Самым неудобным для копья и диска является действие бокового ветра, который нарушает основные законы планирования снарядов в полете.

5. Охарактеризуйте основные части легкоатлетических метаний

Все существующие метания являются целостными ациклическими упражнениями.

Однако для удобства анализа техники каждое метание условно состоит из шести взаимосвязанных частей:

I – держание снаряда;

II – подготовка к разбегу и разбег (поворот, скачок);

III – подготовка к финальному усилию («обгон» снаряда);

IV – финальное движение (усилие);

V – торможение и сохранение равновесия после выпуска снаряда;

VI – вылет и полет снаряда.

I. Держание снаряда

Задача

этой части – держать снаряд так, чтобы выполнить метание свободно, с оптимальной амплитудой движения, обеспечив наиболее эффективное приложение своих сил.
Правильное держание снаряда зависит от его формы, веса, способа метания и позволяет наиболее полно использовать длину и силу конечностей, по возможности расслаблять мышцы метающей руки до финального усилия и сохранять контроль за движениями спортсмена. Все это способствует передаче силы метателя на снаряд в нужном направлении и по наибольшему пути, что и обеспечивает высокую начальную скорость вылета снаряда.

При метании диска и молота, с точки зрения биомеханики, нужно держать снаряд так, чтобы его центр был подальше удален от оси вращения спортсмена. Тем самым увеличивается радиус вращения, а значит, повышается начальная скорость вылета.

II. Подготовка к разбегу и разбег

Основная
задача

этой части – создать предварительную (оптимальную) скорость движения метателя со снарядом и обеспечить благоприятные условия для финального усилия.
Во время разбега метатель составляет как бы единую систему со снарядом, где приобретенное им ускорение передается снаряду. Разбег выполняется в виде ускоренного бега (метание гранаты и копья), скачка (толкание ядра) и поворота (метание диска и молота, а также в последнее время – толкания ядра).

Разбегу в некоторых метаниях предшествует выполнение спортсменом предварительных движений. В толкании ядра – это замах (наклон тела) и группировка, в метании диска – размахивания, в метании молота – предварительные размахивания. Только в метании гранаты и копья спортсмен из исходного положения сразу начинает разбег.

Главная задача предварительных движений – сосредоточить внимание на выполнении метания в целом, занять рациональное исходное положение, создать наиболее выгодные условия для максимальной работы мышц в последующих движениях. В метании молота эти движения (вращения молота) позволяют к тому же придать снаряду значительную скорость до начала поворотов.

При выполнении разбега в форме одного (диск) или нескольких поворотов (3–4 в молоте) возникает значительная центробежная сила (при метании молота на 75 м она равна 300 кг), которая затрудняет движения метателя. Спортсмен обязан не только противостоять возрастающей центробежной силе, т. е. обеспечить устойчивое положение тела, но и завершить технически правильный мощный выпуск снаряда.

В разбеге (в форме поворотов или скачка) метатель может придать скорость системе «метатель + снаряд» только при опоре ногами на грунт, так как в двухопорном положении он может действовать на снаряд с наибольшей, чем при одноопорном положении, силой и, следовательно, придать снаряду большую скорость.
При этом время пребывания в безопорном положении, в течение которого метатель не в состоянии увеличить скорость, следует свести к минимуму.

Предварительные движения (разбег, скачок и повороты) не выполняются на слишком высокой скорости. Эта скорость в различных метаниях должна быть оптимальной, при которой спортсмен в состоянии контролировать свои действия для создания благоприятных условий при выполнении финального движения.
Скорости движения метателя и снаряда должны соответствовать техническим, скоростным и силовым возможностям метателя.

Независимо от движений и усилий метателя более совершенной техникой метания следует считать такую, когда скорость движения снаряда обязательно должна возрастать к концу метания. Скорость разбега всегда должна подбираться со строгим учетом возможностей метателя, позволяя полноценно «передать» приобретенную метателем во время разбега «энергию» снаряду. Наибольшая скорость перемещения снаряда создается в метании молота, где шар в конце 3–4 поворота достигает скорости 23–24 м/с, проходя путь 60–70 м. При метании диска снаряд развивает скорость 10–12 м/с, проходя за время поворота путь 12–15 м. При метании копья скорость перемещения снаряда и метателя достигает 6–8 м/с. Самый медленный разбег при толкании ядра – около 3 м/с.

Переход от разбега к броску в метаниях – наиболее трудный компонент техники, и он оказывается тем сложнее, чем больше скорость движения метателя в разбеге (особенно в копье, молоте, диске).

О роли разбега в метаниях говорят такие факты: при толкании ядра разница в дальности между броском с места и с разбега составляет в среднем 1,5–2 м, при метании диска – 7–10 м, при метании копья – 20–25 м. Эти данные могут служить критерием эффективности разбега.

III. Подготовка к финальному усилию («обгон» снаряда)

Во второй части разбега, разогнав снаряд до определенной горизонтальной скорости, метатель готовится к финальному усилию. Эта подготовка не есть простой переход от разбега к выпуску снаряда, а довольно сложное перераспределение усилий отдельных мышечных групп, и чем большая скорость движений, тем труднее его выполнить. Задача

этой части – при минимальной потере линейной скорости движения снаряда ускоренным движением отдельных частей тела растянуть мышцы всех звеньев тела так, чтобы создать условия для их последовательного сокращения.

При подготовке к финальному усилию метатель должен сделать следующее:

б) в конце разбега (поворота) обогнать снаряд;

в) понизить общий центр масс тела для лучшего использования силы ног при броске;

г) обеспечить правильное устойчивое исходное положение перед финальным усилием.

Остановимся более подробно на этих действиях метателя.

В разных метаниях подобные действия происходят различно, однако во всех случаях большое значение отводится созданию предпосылок для увеличения скорости к концу метания.

Если метатель не может удержать достаточную горизонтальную скорость, то разбег (поворот) теряет свой смысл и даже мешает.

Обгоном снаряда

называют действия метателя в процессе разбега, когда нижняя часть тела спортсмена (ноги, таз) обгоняет верхнюю (туловище, руки) и снаряд.
Иными словами, обгон снаряда осуществляется путем увеличения скорости нижней части тела метателя относительно верхней части. При этом обгон снаряда происходит не только в передне-заднем направлении, но и путем скручивания туловища в поясничной области в сторону, обратную направлению метания. Обгоняя снаряд, спортсмен увеличивает воздействие на него в финальном усилии.

В процессе подготовки к финальному усилию метатель за счет более широкой расстановки и сгибания ног понижает общий центр масс тел. Это делается для того, чтобы увеличить вертикальную скорость вылета снаряда. Метатель должен стремиться к тому, чтобы как можно ниже сместить ОЦМТ и этим увеличить путь подъема его в финальном усилии.
При этом, чем ниже смещен ОЦМТ, тем больше времени требуется для его подъема. Вот почему, в зависимости от своих силовых и скоростных качеств, каждый метатель определяет для себя оптимальное понижение ОЦМТ.

Исходное положение метателя перед финальным усилием во всех видах метаний имеет общие черты. Оно характеризуется следующими моментами: ноги широко расставлены; тяжесть тела перенесена на правую ногу; рука со снарядом находится как можно дальше от предполагаемой точки вылета снаряда; мышцы ног, таза, туловища и плечевого пояса растянуты.

Все эти действия метателя перед финальным усилием выполняются с целью обеспечения оптимальных условий для увеличения пути и силы воздействия на снаряд, а также максимального использования энергии, приобретенной метателем в разбеге. Эта часть метания исключительно важна и технически трудна.

IV. Финальное усилие (движение)

Финальное усилие является самой важной и ответственной частью техники метания. Сильное, мощное финальное усилие может быть выполнено лишь тогда, когда атлет правильно и в необходимом ритме исполнил все предшествующие ему движения.

Задача

этой части метания – сообщение снаряду максимальной скорости вылета под оптимальным углом при правильном расположении его в пространстве.
Финальное усилие во многом зависит от устойчивости положения метателя, длины пути воздействия на снаряд и времени этого воздействия. Во всех метаниях переход к развитию мощного финального усилия начинается с постановки впереди стоящей левой ноги на опору.

При этом спортсмен должен по возможности ускорить приход в двухопорное положение. В финальном усилии происходит резкое торможение скорости продвижения нижней части тела метателя ногами. Вследствие этого потенциальная энергия, приобретенная при разбеге, переходит от ног к туловищу, ускоряя его движение вместе с метающей рукой. Количество движений, накопленное телом метателя в разбеге, от нижних конечностей передается к верхним и затем к снаряду.

При этом основные мышечные группы, участвующие в финальном усилии, включаются в работу последовательно, причем перед сокращением мышцы предварительно растягиваются. Последними включаются в работу мышцы дистальных звеньев – кисти метающей руки и стопы ноги.

Благодаря растягиванию и сокращению мышц во время финального усилия метатель добивается к моменту выбрасывания снаряда предельно высокой скорости разгибания верхних конечностей. Характерны в этом отношении движения метателя копья, когда он во время финального усилия занимает положение, напоминающее по своей форме положение «натянутого лука».
И чем больше будет лук натянут, тем лучше, тем мощнее будет хлёст туловищем, тем эффективнее будет выбрасывающее движение рукой. Это положение сходно с промежуточными положениями и при других метаниях.

Исследованиями установлено, что путь приложения усилий в финальной стадии метания при толкании ядра равен примерно 2 м, метании копья и диска – 3 м, молота – 7 м. Скорость движения ядра при этом возрастает на 12 м/с, копья – на 30 м/с, диска – на 16 м/с и молота – на 4 м/с.

Следует отметить, что определенной границы между разбегом, подготовкой к финальному усилию и самим финальным усилием не существует.
Ошибкой является наличие паузы или сохранение определенного положения вместо стремительного перехода к броску. При этом финальное усилие является своеобразным мерилом техники метания в целом, а об эффективности его можно судить по устойчивости положения спортсмена после выпуска снаряда.

Таким образом, развитие скорости движения снаряда условно осуществляется в три стадии: на первой (при стартовом разгоне) скорость сообщается всей системе «метатель – снаряд»; на второй стадии (начало финального движения) в результате торможения ногами довольно резко возрастает скорость поступательного движения верхней части тела метателя; на третьей стадии (заключительная часть финального движения) все направлено главным образом на проявление максимальных усилий и их приложение к снаряду с целью придания ему наибольшей скорости вылета.

V. Торможение и сохранение равновесия после выпуска снаряда

Главная
задача

этой фазы заключается в погашении всей скорости перемещения тела после броска, не нарушая правила соревнований.
Удержание равновесия ОЦМТ метателем после выпуска снаряда прямо на дальность полета не влияет. Но если спортсмен потеряет равновесие и не удержится в кругу или переступит через планку, бросок не засчитывается. Метателю необходимо много времени уделять и этому элементу техники.

В зависимости от вида метаний торможение может быть выполнено различными способами.

В толкании ядра, метании диска, копья и гранаты торможение проводится прыжком или переступанием со сменой ног, когда правая нога является своеобразным «тормозом», гасящим поступательную скорость метателя.
Иногда при метании копья, мяча или гранаты выполняется несколько подскоков на правой (левой) ноге. Важно, чтобы нога ставилась впереди проекции ОЦМТ метателя для более эффективного снижения и погашения горизонтальной скорости.

В метании молота торможение выполняется в виде вращения – пируэта на левой ноге с переносом правой ноги вокруг левой и последующей ее постановкой в круг.

VI. Вылет и полет снаряда

Траектория полета любого спортивного снаряда начинается в точке вылета снаряда (то есть в точке, поднятой над землей на определенную высоту), а заканчивается на плоскости сектора, который находится на одной горизонтальной линии с местом опоры метателя. Чем выше точка вылета, тем дальше, при прочих равных условиях (сопротивление воздушной среды, угол вылета, начальная скорость), будет лететь снаряд. Поэтому метатели высокого роста имеют определенные преимущества перед низкорослыми спортсменами, так как у них траектория полета выпущенного снаряда имеет возможность заканчиваться дальше ввиду большей разности в уровнях точки вылета и точки приземления
. Большая длина полета снаряда, таким образом, может быть достигнута за счет так называемого угла местности. Угол местности

(Z

) образуется горизонталью и линией, соединяющей точку приземления с точкой вылета снаряда
(см. рис. 8). Величина этого угла находится в прямой зависимости от высоты (h
о) точки вылета снаряда и в обратной зависимости от дальности полета снаряда. Самый большой угол местности при толкании ядра (около 8º), при метании диска, копья, молота и гранаты угол местности незначителен, всего 2–3º.

При различных видах метаний точки вылета, естественно, различны. При метании копья, гранаты, толкании ядра точки вылета находятся на высоте, равной росту тела + длина вытянутой под оптимальным углом руки.

В других метаниях точки вылета находятся:

– на уровне плечевого сустава (диск);

– несколько выше плечевого сустава (при метании молота).

Для создания устойчивого положения в полете диску и копью при выпуске придается также вращательное движение, и поэтому снаряд сохраняет заданное положение оси вращения до самого падения. Вращение снаряда в полете несколько уменьшает сопротивление воздуха и, следовательно, увеличивает дальность полета. Однако вращение копья и диска происходит вокруг разных осей: копье вращается вокруг горизонтальной оси, диск – вокруг вертикальной.
Вследствие этого при полете диска возникает гироскопический эффект (подобный тому, который позволяет не падать вращающемуся волчку), и положение диска в воздухе стабилизируется. При полете копья возникает опрокидывающий момент, стремящийся «вернуть» копье.

Что касается других факторов, влияющих на положение легкоатлетических снарядов в полете, то это описано в разделе, посвященном воздействию атмосферной среды на дальность полета снарядов.

Источник

In projectile motion, you need to concern yourself with the two components of displacement:

$$x=x_0 + v_x t + frac{1}{2}a_x t^2$$
$$y=y_0 + v_y t + frac{1}{2}a_y t^2$$

If we place the cannon at the origin, then $(x_0,y_0) = (0,0)$. Furthermore, there is no acceleration in the $x$ direction if we neglect things like air resistance. Then $a_x = 0$. The acceleration in the $y$ direction is due to gravity $a_y = -g$.

$$x=v_x t$$
$$y=v_y t — frac{1}{2}g t^2$$

We need to find the range. That is, we need to find the displacement in $x$ that occurs when the cannonball hits the ground, or when $y=0$.

$$x=v_x t$$
$$0=v_y t — frac{1}{2}g t^2$$

The velocity can be broken up into components with trigonometry.

$$v_x = 800cos60^circ m/s$$
$$v_y = 800sin60^circ m/s$$

Using this information, solve for $t$ when the cannonball hits the ground. Then use that time to calculate displacement in $x$.

Источник

Тело,брошенное под углом к горизонту .

(y=y_0+v_{0}sin ; (alpha)cdot t -dfrac{gt^2}{2} )

(x=x_0+v_{0}cos ; (alpha)cdot t )

(alpha ) -угол, под которым брошено тело

(v_{0}) — начальная скорость тела

Задача 1. (;;;;;;;;;; kornev-school.ru )

Тело брошено с поверхности земли под углом ( alpha=30^0 ) к горизонту, со скоростью (v_0=10 м/с ).

Какое время тело будет находиться в полете?
(g=10м/с^2 . )