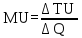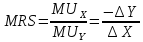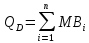Список формул микроэкономики
Микроэкономика — это исследование экономики, в котором оценивается, анализируется и изучается деятельность фирм и отдельных лиц по достижению устойчивых результатов с использованием ограниченных ресурсов. Он также исследует, как один человек или фирма взаимодействует с другим человеком или фирмой. Широкая цель микроэкономики состоит в том, чтобы определить и исследовать рыночные цены на предлагаемые товары и услуги и насколько хорошо ограниченные ресурсы используются для предоставления товаров и услуг.
Оглавление
- Список формул микроэкономики
- #1 – Общий доход
- #2 – Предельный доход
- №3 – Средний доход
- # 4 — Общие затраты
- # 5 — Предельные затраты
- # 6 — Средняя общая стоимость
- #7 – Средние постоянные затраты
- #8 – Средние переменные затраты
- # 9 — Прибыль, полученная фирмой
- Примеры
- Пример №1
- Пример #2
- Пример №3
- Рекомендуемые статьи
Ниже перечислены следующие микроэкономические формулы, которые помогают понять положение экономики:
Sr NoФормула НазваниеФормула1Общий доходЦена x количество в спросе2Предельный доходИзменения в общем заработанном доходе/изменения в количестве проданных товаров3Средний доходОбщий доход или доход, полученный бизнесом/общее количество4Общие затратыОбщие затраты, понесенные на фиксированной основе + общие затраты, которые меняются в зависимости от произведенного количества5Предельные затратыИзменения на уровне общих затрат/изменений уровня произведенного количества6Средние затратыОбщие затраты/общее количество7Средние фиксированныеобщие постоянные затраты/общее количество8Средние переменныеОбщие переменные затраты/общее количество9Прибыль Полученнаяобщая выручка – общие затраты10Прибыль полученнаяПредельная выручка – предельные затраты
#1 – Общий доход
Это ситуация, когда спрос оценивается с точки зрения ценовой эластичности. Он выражается как произведение общей цены и количества в спросе. Количество в спросеВеличина спроса — это количество конкретного товара по определенной цене. Он меняется с изменением цены и не зависит от рыночного равновесия. Подробнее. Если цены высоки, это приведет к неэластичному спросу, что приведет к увеличению доходов. И наоборот, спрос эластичен, когда цены высоки, а объемы малы.
Математически это можно проиллюстрировать следующим образом:
Общий доход = цена x объем спроса
#2 – Предельный доход
Предельный доходПредельный доходФормула предельного дохода вычисляет изменение общего дохода при увеличении количества проданных товаров и единиц». Значение обозначает полученный предельный доход. Предельный доход = изменение общего дохода/изменение количества проданных товаров. общий доход изменяется в зависимости от изменения количества проданного товара в розницу. Предельный доход — это дополнительный доход, полученный за дополнительное проданное количество. Математически это можно проиллюстрировать следующим образом:
Предельный доход = изменения в общем заработанном доходе / изменения в объеме сделок
№3 – Средний доход
Выручка может быть описана как выручка, полученная фирмой после продажи готовой продукции своим потребителям. Средняя выручка – это отношение общей выручки к общему количеству проданных товаров. Математически это можно проиллюстрировать следующим образом:
Средний доход = общий доход или доход, полученный бизнесом / общее количество
# 4 — Общие затраты
В разделе «Экономика» «Экономика» — это область социальных наук, изучающая производство, распределение и потребление ограниченных ресурсов в обществе. Более подробная информация: общая стоимость определяется как сумма фиксированных затрат. любым уменьшением или увеличением количества произведенных или проданных единиц в краткосрочной перспективе. Это вид затрат, не зависящий от хозяйственной деятельности. Читать далее и переменные затраты. Переменные затраты — это затраты, которые имеют тенденцию меняться в зависимости от количества товаров, продаваемых организацией. Постоянные затраты — это тип затрат, которые остаются одинаковыми на всех уровнях количества, продаваемого бизнесом.
Математически это можно проиллюстрировать следующим образом:
Общие затраты = общие затраты, понесенные на фиксированной основе + общие затраты, которые меняются в зависимости от произведенного количества.
# 5 — Предельные затраты
Формула предельных издержекФормула предельных издержекФормула предельных издержек помогает рассчитать величину увеличения или уменьшения общих производственных затрат компании в течение рассматриваемого периода при изменении объема производства на одну дополнительную единицу. Он рассчитывается путем деления изменения затрат на изменение количества. Он определяется как повышение или ухудшение общих затрат, которые несет бизнес. В то же время он готовит готовую продукцию, готовую к продаже. Графически предельные издержки изображаются в виде U-образной кривой, на которой первоначально издержки растут, а по мере роста производства цены снижаются. Математически это можно проиллюстрировать следующим образом:
Предельные затраты = изменения уровня общих затрат / изменения уровня произведенного количества.
# 6 — Средняя общая стоимость
Средняя общая стоимостьСредняя общая стоимостьСтоимость единицы произведенного количества рассчитывается по формуле средней общей стоимости. Он рассчитывается путем деления общей производственной себестоимости на общее количество произведенных единиц. Подробнее — это общие затраты, понесенные бизнесом, связанным с производством и производством, на количество изделий, произведенных компанией. В таком соотношении определите общие затраты и общее количество, чтобы получить средние общие затраты. Математически это можно проиллюстрировать следующим образом:
Средние затраты = общие затраты / общее количество
#7 – Средние постоянные затраты
Средняя фиксированная стоимостьСредняя фиксированная стоимостьСредняя фиксированная стоимость относится к фиксированным производственным затратам компании на единицу произведенной продукции. Постоянные затраты — это затраты, которые не зависят от количества продукции, произведенной компанией, и не зависят от количества товаров или услуг, произведенных бизнесом. количество изделий, произведенных предприятием. В таком отношении определите общие постоянные затраты и общее количество, чтобы получить средние общие постоянные затраты. Математически это можно проиллюстрировать следующим образом:
Средние постоянные затраты = общие постоянные затраты / общее количество
#8 – Средние переменные затраты
Средняя переменная стоимостьСредняя переменная стоимостьСредняя переменная стоимость относится к стоимости, которая напрямую зависит от объема производства каждой единицы товаров или услуг. Он оценивается путем деления общих переменных затрат, понесенных в течение периода, на количество произведенных единиц. Подробнее — это общие переменные затраты. единиц и помогает проанализировать общую стоимость и рентабельность компании. Формула общих переменных затрат = количество произведенных единиц x переменные затраты на единицу. Подробнее, понесенные компанией, занимающейся производством и производством, к количеству товаров, произведенных бизнесом. В таком отношении определите общие переменные затраты и общее количество, чтобы получить средние общие переменные затраты. Математически это можно проиллюстрировать следующим образом:
Средние переменные затраты = общие переменные затраты / общее количество
# 9 — Прибыль, полученная фирмой
В микроэкономике прибыльПрибыльПрибыль относится к доходам, которые человек или бизнес забирают домой после оплаты всех затрат. В экономике этот термин ассоциируется с денежной прибылью. Читать далее можно вычислить, используя несколько соотношений. Во-первых, его можно рассчитать как разницу между общими доходами и затратами. Его можно рассчитать как разницу в предельной выручке и предельных издержках. Формула предельных издержек помогает рассчитать величину увеличения или уменьшения общих производственных затрат компании в течение рассматриваемого периода при изменении объема производства на одну дополнительную единицу. Он рассчитывается путем деления изменения затрат на изменение количества. Подробнее. Всякий раз, когда прибыль меньше средних переменных издержек, бизнес больше не может поддерживать себя и должен быть закрыт. Математически это можно проиллюстрировать следующим образом:
Полученная прибыль = общий доход – общие затраты
Дополнительно это можно проиллюстрировать следующим образом:
Полученная прибыль = предельный доход – предельные затраты.
Когда предельный доход превышает предельные издержки, организация или фирма должны производить больше товаров, чтобы повысить свою прибыльность. Точно так же, когда предельный доход становится ниже предельных издержек, организации или фирме следует создавать меньше товаров, чтобы снизить издержки.
Примеры
Давайте рассмотрим несколько простых и продвинутых примеров формулы микроэкономики, чтобы лучше понять ее.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы Excel для микроэкономики здесь – Формула микроэкономики Шаблон Excel
Пример №1
Возьмем пример малого бизнеса. Он продает готовую продукцию по 100 долларов за единицу. Обычно он производит 100 единиц в год. Каждая единица несет затраты в размере 80 долларов США на разработку готовой продукции. Помогите руководству определить прибыль, полученную малым бизнесом.
Решение
Используйте приведенные ниже данные:
Расчет общего дохода:
- =100$*100
- Общий доход = 10 000 долларов США.
Расчет общих затрат:
- =80$*100
- Общие затраты = 8000 долларов США.
Расчет полученной прибыли:
- = 10 000–8 000 долларов США
- Полученная прибыль = 2000 долларов США
Следовательно, бизнес получил прибыль в размере 2000 долларов США при производстве и продаже 100 единиц.
Пример #2
Возьмем пример решений для процессов знаний. Бизнес сосредоточен на разработке хорошего контента для обслуживания веб-сайтов своих клиентов. Стоимость программного обеспечения ежегодно составляет 1000 долларов США в год. Компания взимает со своих клиентов 50 долларов за каждую отправленную и принятую статью. Ежегодно бизнес поставляет своим клиентам около 100 артикулов. Помогите руководству определить прибыль, полученную от разработки и предоставления услуг.
Решение
Используйте приведенные ниже данные:
Расчет общего дохода:
- =$50*100
- Общий доход = $5000
Расчет полученной прибыли:
- = 5000 долларов – 1 000 долларов США
- Полученная прибыль = 4000 долларов США
Таким образом, предприятие получило прибыль в размере 4000 долларов США от производства и продажи 100 изделий при годовых затратах в размере 1000 долларов США.
Пример №3
Возьмем пример компании Uber. Компания является популярной организацией, которая предлагает услуги агрегатора такси для ежедневных пассажиров и пассажиров. Бизнес разработал динамический механизм, изучающий спрос на такси с поставкой кабин с пассажирами.
Они также изучают уровни цен, на которых происходит взаимодействие между пассажирами и водителями такси. Например, выяснилось, что потребительский спрос был относительно неэластичным, когда стоимость проезда удвоилась в два раза. Далее система проанализировала случаи, когда водитель принимал заказ Uber и отклонял его. Он широко изучал факторы, связанные со временем, ценой, спросом и предложением.
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле микроэкономики. Мы обсудили микроэкономические расчеты, примеры и загружаемый шаблон Excel. Вы можете узнать больше из следующих статей: –
- Определение микро-крышки
- Микроэкономика Значение
- Микроэкономика против макроэкономики
- Прикладная экономика Значение
- Формулы экономики
Список обозначений и сокращений
|
Р |
– цена |
|
PL |
– цена |
|
PK |
– цена |
|
PZ |
– цена |
|
Q |
– объём |
|
Д |
– спрос, |
|
S |
– предложение, |
|
I |
– доход |
|
ТР |
– совокупный |
|
АР |
– средний |
|
МР |
– предельный |
|
МU |
– предельная |
|
TU |
– совокупная |
|
МRS |
– предельная |
|
МRTS |
– предельная |
|
TR |
– совокупный |
|
AR |
– средний |
|
МR |
– предельный |
|
ТС |
– совокупные |
|
ТFC |
– совокупные |
|
TVC |
– совокупные |
|
ATC |
– средние |
|
AFC |
– средние |
|
AVC |
– средние |
|
МС |
– предельные |
|
L |
– количество |
|
W |
– ставка |
|
К |
– количество |
|
i |
– ставка |
|
r |
– реальная |
|
π |
– ожидаемый |
|
R |
– доход |
|
П1 |
– прибыль |
|
П |
– совокупная |
|
|
– изменение, |
|
|
– коэффициент |
|
MRP |
– предельная |
|
MRC |
– предельные |
|
PV |
– |
|
NPV |
– чистая |
|
PC |
– частные |
|
EC |
– внешние |
|
SC |
– общественные |
|
MPC |
– предельные |
|
MEC |
– предельные |
|
MSC |
– предельные |
|
PB |
– частные |
|
EB |
– внешние |
|
SB |
– общественные |
|
MPB |
– предельные |
|
MEB |
– предельные |
|
MSB |
– предельные |
|
Е(х) |
– |
|
σ2 |
– дисперсия, |
|
σ |
– стандартное |
|
πi |
– вероятность |
Основные формулы для решения задач
Тема
2
I = px
X + pY
Y
Темы
3 – 6
TR
= р Q
TС
= АТС Q
П = TR
– TC
TC = TFC +
TVC
ATC = AFC +
AVC
МR
= МС
Тема 7
ТVCL
= W L
MRPL
=
MPL
p =
MRCL
=
MRPL
=
MRCL

Тема 8
NPV = – I
+ PV
Пэк
= TR – TCэк
TCэк
= TCвнешние
+
TCвнутренние
Пбух
= TR
– TCвнешние
Пнорм
= TCвнутренние
Пэк
= Пбух
– Пнорм
Тема 9
i = r + π
Тема 10
Тема
11
MPC = ∆PC
/ ∆Q
MEC = ∆EC
/ ∆Q
MSC = ∆SC
/ ∆Q
MSC = MPC +
MEC
MPB = ∆PB
/ ∆Q
MEB = ∆EB
/ ∆Q
MSB = ∆SB
/ ∆Q
MSB = MPB +
MEB
Тема
12
Тема
13
СПИСОК ЛИТЕРАТУРЫ
ПО МИКРОЭКОНОМИКЕ
Основная
-
Микроэкономика
: практический подход / под ред. А. Г.
Грязновой, А. Ю. Юданова. – 4-е изд. –
Москва, 2008. – 704 с. -
Базылев,
Н. И. Микроэкономика / Н. И. Базылев. –
Минск, 2007. – 288 с. -
Зороастрова,
И. В. Микроэкономический анализ : задачи
и ситуации / И. В. Зороастрова, Н. М.
Розанова. – Ростов н/Д, 2007. – 293 с. -
Микроэкономика
/ А. В. Бондарь [и др.] ; под ред. А. В.
Бондаря, В. А. Воробьева. – Минск, 2009. –
415 с. -
Экономическая
теория . В 2-х ч. Ч. 1 / под ред. И. В. Новиковой,
Ю. М. Ясинского. – Минск, 2009. – 261 с. -
Авраменко,
А. И. Экономическая теория : практикум
/ А. И. Авраменко, Ю. Р. Тихонов, А. Я.
Коховец ; под ред. А. И. Авраменко. –
Минск, 2008. – 480 с. -
Ивашковский,
С. Н. Микроэкономика : учебник / С. Н.
Ивашковский. – Москва, 2001. – 415 с.
Дополнительная
-
Микроэкономика
: учебное пособие / под ред. М. И.
Плотницкого. – Минск, 2002. – 426 с. -
Тарануха,
Ю. В. Микроэкономика / Ю. В. Тарануха, Д.
Н. Земляков ; под общ. ред. А. В. Сидоровича.
– Москва, 2002. – 304 с. -
Гребенников,
П. И. Микроэкономика : учебник / П. И.
Гребенников, А. И. Чеусский, Л. С. Тарасевич.
– Москва, 2008. – 374 с. -
Плотницкий,
М. И. Микро- и макроэкономика : учебное
пособие / под ред. М. И. Плотницкого. –
Минск, 2004. – 185 с. -
Головачев,
А. С. Экономическая теория. Общие основы
: курс лекций / А. С. Головачев, И. В.
Головачева, Э. А. Лутохина. – 4-е изд. –
Минск, 2005. – 240 с. -
Современная
политическая экономия : учебное пособие
/ Т. И. Адамович, С. А. Бородич, П. С.
Лемещенко ; под общ. ред. П. С. Лемещенко.
– Минск, 2005. -
Мэнкью,
Н. Г. Принципы экономикс / Н. Г. Мэнкью.
– 2-е изд. – СПб, 2003. – 496 с. -
Пиндайк,
Р. Микроэкономика / Р. Пиндайк, Д.
Рубинфелльд. – СПб, 2002. – 606 с. -
Макконелл,
К. Экономикс : принципы, проблемы и
политика : учебник / К. Макконелл, С. Брю.
– 14-е изд. – Москва, 2003. – 970 с.
ВОПРОСЫ
К ЭКЗАМЕНУ ПО МИКРОЭКОНОМИКЕ
1.
Предмет микроэкономики и границы
микроэкономической теории.
2.
Методы микроэкономического анализа.
Предельный и функциональный анализ.
3.
Проблема оценки общей полезности в
кардинализме и ординализме.
4.
Аксиомы ординализма. Кривые безразличия.
5.
Бюджетные ограничения покупателя.
Равновесие
потребителя.
6.
Кривые «доход-потребление» и
«цена-потребление».
7.
Типы конкуренции и основные рыночные
структуры.
8.
Совершенная конкуренция, её основные
признаки.
9.
Равновесие конкурентной фирмы в
краткосрочном периоде.
10.
Равновесие конкурентного производителя
в долгосрочном периоде.
11.
Совершенная конкуренция и эффективность.
12.
Основные черты чистой монополии. Виды
монополии.
13.
Определение цены и объема производства
в условиях чистой монополии.
14.
Экономические последствия монополии.
Регулируемая монополия.
15.
Чистая монополия и эффективность.
16.
Основные черты монополистической
конкуренции.
17.
Равновесие фирмы в кратко- и долгосрочном
периодах при моно-полистической
конкуренции.
18.
Монополистическая конкуренция и
эффективность.
19.
Основные признаки олигополии.
20.
Типология моделей олигополии.
21.
Модель с ломаной кривой спроса.
22.
Олигополия и эффективность.
23.
Показатели монопольной власти.
Антимонопольное законодательство.
24.
Спрос на ресурсы: общий подход. Предельная
доходность ресурса. Предельные издержки
ресурса.
25.
Модель конкурентного рынка труда.
26.
Рынок труда в условиях несовершенной
конкуренции.
27.
Номинальная и реальная заработная
платы. Формы и системы заработной платы.
28.
Особенности функционирования рынка
труда в РБ.
29.
Рынок капитала и его структура. Рынок
капитальных благ.
30.
Рынок ссудного капитала и ссудный
процент. Номинальная и реальная ставка
процента.
31.
Дисконтирование будущих доходов.
Критерий чистой дисконтированной
стоимости.
32.
Рынок ценных бумаг. Цены и доходы на
рынке ценных бумаг.
33.
Предпринимательская способность и
экономическая прибыль. Функции и
источники экономической прибыли.
34.
Земля как фактор производства.
Ограниченность земли.
35.
Земельная рента и определение её размера.
Рента и арендная плата. Цена земли.
36.
Дифференциальная рента по плодородию
и местоположению.
37.
Формирование рынка земли в РБ.
38.
Частичное и общее равновесие. Взаимосвязи
на рынках продуктов и ресурсов.
39.
Общее экономическое равновесие и
общественное благосостояние.
40.
Фиаско рынка и необходимость
микроэкономического регулирования.
41.
Общественные и частные, положительные
и отрицательные внешние эффекты.
42.
Интернализация внешних эффектов. Теорема
Коуза.
43.
Регулирование внешних эффектов.
Использование теории внешних эффектов
в экономической практике.
44.
Выбор в условиях неопределенности.
Понятие асимметричной информации.
45.
Рынки с асимметричной информацией. Виды
рыночных сигналов.
46.
Моральный риск. Проблема «принципал-агент».
Гарантии и поручительства.
47.
Чистые частные и чистые общественные
блага. Свойства общественных благ.
48.
Особенности спроса на общественные
блага.
49.
Роль государства в обеспечении предложения
общественных благ.
50.
Методология анализа общественного
выбора. Политика как обмен.
51.
Политико-экономический цикл.
52.
Проблема эффективности государственного
вмешательства в экономику.
53.
Эффективность обмена. Кривая потребительских
возможностей.
54.
Эффективность производства. Кривая
производственных возможностей.
132
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Основные обозначения и формулы по
экономике:
I. Обозначения
1.
P — цена
2. Q —
количество
3. D –
спрос
4. S —
предложение
5.
QD – величина спроса
6.
QS – величина предложения
7.
Qдеф – дефицит (объем дефицита)
8.
Qпродаж – объём продаж
9.
QИЗБ – объём избытка (излишки)
10. EDP–
коэффициент эластичности спроса по цене
11.
ESP– коэффициент эластичности предложения по цене
12. I –
доход
13.
EDI— коэффициент эластичности спроса по доходу
14.
EDC— коэффициент перекрестной эластичности спроса
15. TR –
совокупный доход (выручка продавца)
16. TC –
общие затраты
17.
Pr – прибыль
18. PD –
цена спроса
19.
PS– цена предложения
20. PE–
равновесная цена
II. Формулы:
1.
y= k*x+b – уравнение описывающее функцию
спроса
2.
QD= k*P+b – функция
спроса
3.
EDP= Δ QD (%)/ΔP (%) –
коэффициент эластичности спроса по цене
4.
EDP= (Q2 –Q1): (Q2 + Q1)/
(P2 –P1): (P2 + P1) –
формула средней точки, где P1 – цена товара до изменения, P2 –
цена товара после изменения, Q1 – величина спроса
до изменения цены, Q2 – величина спроса после изменения цены;
5.
EDI= (Q2 –Q1): (Q2 + Q1)/
(I2 –I1): (I2 + I1) –
формула коэффициента эластичности спроса, где I1 – величина
дохода до изменения, I2 – величина дохода после
изменения, Q1 – величина спроса до изменения
дохода, Q2 – величина спроса после изменения дохода;
6.
EDС = (Q2 –Q1): (Q2 + Q1)/
(P2 –P1): (P2 + P1) –
формула средней точки, где P1 – цена второго товара до
изменения, P2 – цена второго товара после изменения, Q1 –
величина спроса первого товара до изменения цены, Q2 –
величина спроса первого товара после изменения цены;
7.
TR = P*Q – формула расчета выручки
продавца
8.
Pr= TR – TС – формула
расчета прибыли;
9.
QD= k*P+b – функция
предложения;
10. ESP=
(QS2 –QS1): (QS2 + QS1)/
(P2 –P1): (P2 + P1) –
формула коэффициента предложения, где P1 – цена товара до
изменения, P2 – цена товара после изменения, QS1 –
величина предложения до изменения цены, QS2 – величина
предложения после изменения цены;
11.
Qдеф = QD— QS–
формула для определения объема дефицита;
12. Qдеф = QS — QD–
формула для определения объема излиш
Формула
расчёта необходимого для обращения количества денег:
1)
КД — масса денег;
Ецт — сумма цен товаров;
К — товары, проданные в кредит;
СП — срочные платежи;
ВП — взаимопогашаемые платежи (бартерные сделки);
СО — скорость оборота денежной единицы (в год).
2)
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Уравнение обмена:
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Это уравнение показывает, что совокупные расходы в денежном выражении
равны стоимости всех товаров и услуг, произведенных экономикой. Формула для нахождения реального дохода:
ИПЦ — индекс потребительских цен. Формула для нахождения покупательной
способности денег:
Iпcд — покупательная способность денег;
Iц — индекс цен. Формула для нахождения индекса
потребительских цен:
Формула для расчёта стоимости
потребительской корзины:

P 1 — цена первого товара;
Р 2 — цена второго товара;
Р n — цена n-го товара;
Q 1 — количество первого товара;
Q 2 — количество второго товара;
Q n — количество n-го товара. Формула для расчёта темпа инфляции:
В зависимости от темпа инфляции различают несколько ее видов:
1.Мягкая (ползучая), когда цены растут в пределах 1—3% в год.
2.Умеренная — при росте цен до 10% в год.
3.Галопирующая — при росте цен от 20 до 200% в год.
4.Гиперинфляция, когда цены растут катастрофически — более чем 200% в
год. Формула для расчёта простого процента:
P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях. Формула для расчёта сложного процента:
P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях;
N — сколько раз начисляется в году. Формула для расчёта сложного процента начисляемого за несколько
лет:
P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях. Формула для расчёта смешанного процента за дробное колличество лет:
P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях;
n — число дней. Формула для расчёта банковских резервов:
S — норма обязательных резервов в процентах;
R — общая сумма резервов;
Д — величина депозитов на счету КБ. Формула расчёта уровня безработицы:
Формула расчёта уровня занятости:
Формула расчёта перекрёстной ценовой
эластичности:

Формула расчёта амортизации:
1)
2)
Формула расчёта личного дохода домохозяйств:
Формула расчёта ВНП по доходам:

Формула расчёта ЧНП:
Формула расчёта средних общих издержек:
1)
2)
Формула расчёта общих издержек:
Формула расчёта средних постоянных издержек:


1)
2)
Формула расчёта бухгалтерской прибыли:
Формула расчёта экономической прибыли:
1)
2)
Формула расчёта рентабельности продукции:



Формула расчёта величины циклической безработицы:
Формула расчёта величины естественной безработицы:
Формула расчёта производительности труда:
Формула расчёта дуговой эластичности по доходу:
<=»»
form=»»>
Коэффициент Джини
Самое краткое определение коэффициента Джини –коэффициент концентрации
богатства. Чем он выше – тем выше и
неравенство. Более полное
определение – мера
неравенства распределения доходов. Еще более полное определение – коэффициент
девиации экономики от абсолютного равенства в распределении доходов.
Коэффициент выводится из кривой Лоренца и представляет
собой отношение площади между этой кривой и линией абсолютного равенства к
общей площади под линией абсолютного равенства. Линия абсолютного равенства –
биссектриса между осями «доля домохозяйств» и «доля
доходов». Коэффициентможет быть рассчитан и по точной формуле.
Максимальное значение коэффициента равно единице и это –абсолютное неравенство.
Минимальное равно нулю и это абсолютное равенство
В силу социально-политической
значимости получаемых на основе коэффициента оценок, он активно рассчитывается,
дискутируется и используется для разного уровня выводов. Одна из наиболее
активных сфер использования – сравнительный межстрановой и временной анализ.
Например, коэффициент Джини
для России в 1991 году был
равен 0,24, в 2008 году 0,42. В так называемых «образцовых»
европейских и особенно североевропейских странах он находится в диапазоне от
0,2 до 0,3.
Но вряд ли уместны прямые
заключения из сравнения коэффициента по странам и по времени. У него есть ограничения, переходящие в
недостатки, что объясняется двумя обстоятельствами. Во-первых,
относительным характером этого показателя. Во-вторых, его диапазонной
асимметричностью: одно распределение может быть более равным, чем другое в
одном диапазоне, и менее равным в другом при одном том же значении коэффициента
для обоих распределений. Поэтому прямые выводы из сравнения коэффициента в
разных странах и во временной динамике могут привести к ошибочным оценкам.
Коэффициент назван в честь его автора – итальянца Коррадо Джини (Corradо Gini), преподавателя статистики,
социологии и демографии в университете Рима. Коэффициент был предложен им в 1912 году, поэтому у коэффициента
намечается знаменательная дата — 100 лет практического использования
Рассчитать коэффициент
Джини.
Рассчитать коэффициент
Джини:Всего население 1млн100тыс человек.
15%-богатые семьи месячный доход 200 тыс.
35%-средний класс месячный доход 30 тыс.
50%-бедные месячный доход 10 тыс.
Рассчитаем долю доходов бедных
семей.
Доход всех семей: 1.1млн*(0.15*200тыс+0.35*30тыс+0.5*10тыс)=1.1млн*(45.5тыс).
Значит доля доходов бедных семей =(1.1млн*(0.5*10тыс)/(1.1млн*(45.5тыс)=0.11.
Таким же образом находим долю доходов среднего класса в общих доходах ( равна
0.23).
Значит доля доходов бедных и среднего класса в общих доходах = 0.34.
Индекс Джини я рассчитывал как отношение площади фигуры(S), заключенной между
кривой абсолютного равенства и кривой Лоренца, к площади фигуры, заключенной
между кривой абсолютного равенства и кривой абсолютного неравенства(Sан=0.5)
S=0.5-S1-S2-S3-S4-S5
S1,S2,S3,S4,S5 можно легко найти по имеющимся данным,
а значит можно найти и индекс Джини.
Как найти данные
S1,S2,S3,S4,S5,чему они равны?И что делать дальше,как найти именно коэффициент
Джини?
·
S1,S3,S5 — это прямоугольные треугольники, их площадь находится
как половина произведения катетов
S2,S4 — это прямоугольники, их площадь — это произведение сторон
G = =
= 0.5865
·
Некое общество состоит из двух социальных групп, внутри каждой
из которых доход распределен равномерно. Известно, что среднедушевой доход в
первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц,
а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц.
Определите значение коэффициента Джини для этого общества.
·
·
Решение
и ответ
·
Обозначим
количество членов более бедной социальной группы за , более богатой —
за , а доходы
групп соответственно за и
. Тогда:

Кривая Лоренца будет иметь следующий вид:
·
·
Построив
ее, легко посчитать коэффициент Джини:
.
·
Ответ:
·
.
Четырехмерный коктейль
Для приготовления одной порции
коктейля «Неустойчивое равновесие» — фирменного коктейля бара
«Economics» — требуется 1 единица ингредиента A, 2 единицы
ингредиента B, 3 единицы ингредиента C и 4 единицы ингредиента D (названия
ингредиентов являются коммерческой тайной и не разглашаются). Однако владелец
бара, знаменитый бармен и экономист Сэм Полуэльсон, обладает лишь ограниченными
ресурсами для закупки дорогих ингредиентов. Так, на имеющиеся у него денежные
средства он может купить либо 100 единиц ингредиента A, либо 200 единиц
ингредиента B, либо 300 единиц ингредиента C, либо 400 единиц ингредиента D в
день.
Какое максимальное число порций фирменного коктейля сможет приготовить Сэм за
день?
Мне первым в голову пришло вообще
другое решение-логическое
Заметим тот факт,что для покупки любого ингредиента(А,B,C,D) на 1 порцию
коктейля нам надо потратить 1/100 всех денег,то-есть на 1 коктейль мы тратим
1/25 всех денег,поэтому всего можем сделать 25 коктейлей
·
Задача
на коэффициент Джини.
Всех жителей некоторой общины
можно условно разделить на три равные группы по численности: бедные, средние,
богатые. Доход Бедной группы составляет 20% от общего дохода всех жителей
данной общины. Доход средней группы составляет 30%. Рассчитайте коэффициент
Джини ().
В общине решили ввести налог на доходы богатой части общества в размере 30% от
их дохода. Полученная сумма налога распределяется следующим образом: две трети
полученной суммы идет бедным, одна треть — средней группе. Рассчитайте новое
значение коэффициенты Джини().
Решение: После введения налога
доход «богатых» составит: от
общего дохода всех жителей, то есть распределиться между оставшимися группами общего дохода, следовательно доходы
«бедных» составят: ;
доходы «средних» составят ,
что равно доходам «богатых», то есть теперь общество делиться на 2
группы: «бедные» ( населения
и от общего дохода) и
«средние-богатые»( населения и
от общего дохода).
Коэффициент Джини можно рассчитать, используя лемму о ломаной кривой Лоренца ,
имеющей два линейных участка (доказательство леммы в задаче, которая называется
«В некоторой стране», введите в поиске по сайту, ссылку вставить не
получилось), отсюда
Вычислите
коэффициент Джини, примерно отражающий общемировое неравенство доходов, если
ВВП развивающихся стран, в которых проживает 80 % населения Земли, в сумме
составляют только 20 % общемирового продукта (заметим, что это соотношение
держится уже много лет по данным Всемирного банка).
Решение и ответ
j=1-(0,8+(0,2+1))*0.2=1-2*0.2=0.6
Ответ:
0,6
В некоторой стране
В некоторой стране общество состоит
из двух неравных по численности и уровню доходов групп: богатых и бедных.
Допустим, бедные получают 40% совокупного дохода. Значение коэффициента Джини
составляет 0,3. Рассчитайте долю бедных и долю богатых от общей численности
населен
, где
-доля беднейшего
населения, — доля
дохода беднейшего населения. Теперь для полноправного использования выведем эту
формулу:
Ну или можно просто стандартно
рассчитать коэффициент Джини, что в конечном итоге даст аналогичный результат
результат))
·
Сложение
кривых Лоренца
В двух странах с одинаковым ВВП
на душу населения коэффициенты Джини отличаются на единицу. Государство с менее
равномерным распределением доходов – тоталитарное и милитаризованное – решило
развязать войну со своим более демократичным соседом. Однако, несмотря на
значительные расходы (на кампанию было потрачено около ВВП), агрессор потерпел явную неудачу.
В ходе кровопролитных боев погибло населения
нападающей страны. Для сравнения, демократическое государство потратило на
оборону только ВВП, пожертвовав жизнями
населения. В итоге страны решили
заключить мирный договор и образовать союзное государство. Оказалось, что
коэффициент Джини в объединенном государстве равен . Каков был бы
коэффициент Джини, если бы страны решили объединиться до войны?
Решение и ответ
Коэффициенты Джини отличаются на один из них равен
(в демократической стране), а другой –
(в тоталитарной).
Обозначим демократическую страну «D», а тоталитарную – «T», – ВВП,
– численность населения, момент до
войны – «0», момент после войны – «1».
Тогда
;
.
;
.
Отсюда
;
.
Но в силу равенства ВВП на душу населения до войны .
Значит,.
Обозначим .
Тогда .
Поймем, как будет выглядеть кривая Лоренца объединенного государства. Самые
бедные в новом государстве – это жители бывшего тоталитарного государства,
имеющие нулевые доходы. Их доля в населении нового государства равна , поэтому на
отрезке кривая
Лоренца нового государства будет совпадать с осью абсцисс. «Средний класс» в
новом государстве будут составлять бывшие жители демократического государства.
Вместе с бедными они будут составлять почти все население нового государства, а
суммарная доля доходов этих групп населения в общем ВВП равна . Кроме
того, внутри среднего класса распределение доходов абсолютно равномерно,
поэтому следующий участок общей кривой Лоренца будет отрезком прямой с концами
в точках и
. И, наконец, соединяя точку
с точкой
, получаем
отрезок общей кривой Лоренца, «ответственный» за богатых, то есть за ту самую
крайне малочисленную группу населения тоталитарной страны, располагавшую всем
ее ВВП. В итоге общая кривая Лоренца имеет вид:
Тогда коэффициент Джини равен .
Учитывая то, что , имеем:
Значит, .
Получается, что до войны страны имели одинаковый ВВП и одинаковую численность
населения!
Если бы страны объединились до войны, то общая кривая Лоренца имела бы
качественно такой же вид, как и в случае объединения после войны. Следуя
описанной выше логике построения этой кривой, нетрудно установить, что
совокупная кривая Лоренца до войны проходила бы через точки , и совокупный
коэффициент Джини был бы равен .
Ответ:
.
Неравенство
среднедушевых доходов
Некое общество состоит из двух
социальных групп, внутри каждой из которых доход распределен равномерно.
Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в
месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход
составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для
этого общества.
Решение и
ответ
Обозначим количество членов более
бедной социальной группы за , более богатой — за
, а доходы групп соответственно за
и
. Тогда:

Кривая Лоренца будет иметь следующий вид:
Построив ее, легко посчитать
коэффициент Джини:
.
Ответ:
.
$«Три
поросенка и Серый волк»$
Жили-были на свете три
брата-поросенка: Ниф-Ниф, Нуф-Нуф и Наф-Наф. Все одинакового роста,
кругленькие, розовые, с одинаковыми веселыми хвостиками. Вот только навыки их
различались. За лето Ниф-Ниф мог построить три дома из соломы или два дома из
камня. Нуф-Нуф, более тщательный и аккуратный, мог построить за лето целых пять
соломенных домиков. И по лесу ходили слухи, что как-то, поспорив с братьями, он
смог за лето построить 2 домика из соломы и три дома из камня. Но самым
трудолюбивым из поросят был Наф-Наф: в июне он мог построить 2 соломенных
домика, в июльский зной его производительность снижалась, и его хватало лишь на
то, чтобы целиком построить один домик из соломы и начать еще один. Зато в
августе Наф-Наф работал, не покладая рук – не только мог доделать начатое в
июле, но и построить 4 новых соломенных домика. А каменщиком Наф-Наф был еще
более искусным: на каждый дом из камня он тратил на 40% времени меньше, чем на
соломенный.
Построенные домики поросята продавали жителям соседнего леса, которым покупка
домика из соломы обходилась в 10 монет, а домика из камня – в 15 монет.
Однажды, нежась в лужице, братья договорились, что будут заниматься
строительством вместе, создав девелоперскую компанию «ХрякДомСтрой».
— Но мы же всего лишь поросята, — сказал Наф-Наф, самый разумный из них, – нам
нужен бухгалтер, который будет учитывать все наши операции и составлять баланс.
— А давайте позовем Серого волка, — предложил Нуф-Нуф, — ведь после той
истории, сделавшей нас знаменитыми, он изменился, тоже работать хочет. Видимо
не зря мы его проучили!
Поросята согласились с предложением брата, но решили устроить волку экзамен,
чтобы проверить, не собирается ли он снова попытаться «надуть» их. Вот какие
задания были предложены Серому волку на экзамене:
1. Покажи, какими являются возможности каждого из братьев-поросят, если они
будут работать поодиночке. (5 баллов)
2. На стене одного из домов проиллюстрируй возможности строительства домиков,
которыми будет обладать компания «ХрякДомСтрой». (6 баллов)
3. Если надо будет построить несколько соломенных, и несколько каменных домов,
какие именно дома должен строить каждый из братьев? (5 баллов)
4. Скажи, какие домики стоит строить, чтобы «ХрякДомСтрой» смог получить
максимальный доход от их продажи жителям леса, если солома, необходимая для
постройки одного дома, обходится в 3 монеты, а камни – в 10 монет (10 баллов).
Серый волк решил задачки, но теперь перед поросятами встала новая проблема: как
проверить ответы волка? За верными ответами они обратились к нам. А мы – к вам.
1) Ниф-ниф :
Нуф-нуф :
Наф-наф :
3)Ниф-ниф строит соломенные
Нуф-нуфу всеравно какие
Наф-наф строит Каменные
4) Ниф-нифу и нуф-нуфу строить только соломенные а Наф-нафу строить Каменные
Прибыль получилась
А в чем проблема-то?
1) У Ниф-Нифа есть две крайние
точки на КПВ, у Нуф-Нуфа есть крайняя точка по оси соломы и точка (2;3) (если
строить КПВ в осях (соломенные домики;каменные домики)), у Наф-Нафа две крайние
точки 8 и по оси ординат и абсцисс
соответственно. Если чуть подробнее с Наф-Нафом, то у нас есть крайняя точка 8,
также известно, что на каменные домики тратится на 40% меньше, то есть 60%,
значит другая крайняя точка:
2) Здесь просто смотрите у кого меньшая альтернативная стоимость в производстве
какого-либо вида домиков, потом начинаете строить общую КПВ, начиная с
наименьшей а.с.
3) Опять же все сводится к альтернативной стоимости
4) Проверяете «краевые» точки суммарной КПВ, то есть 2 точки излома и
две крайние точки. Если более обоснованно, то тут вроде надо записать, что и пусть эта прямая «ездит»
по суммарной КПВ до тех пор, пока не будет
максимально.
Кстати, в задачнике Акимова есть очень похожие задачи на эту тему,просто там
вместо прибыли, надо было максимизировать выручку.
Задача
про зайцев
В темно-синем лесу, где трепещут
осины, компания «Зайцы Ltd.» является монополистом на рынке трын-травы и имеет
функцию издержек . Ежемесячно проводятся торги, каждый месяц
функция спроса на трын-траву одинакова и задается уравнением . Дед
Мазай, представляющий в лесу государство, собирается вмешаться в
ценообразование. Он хочет добиться снижения цены до определенного уровня , но, чтобы
вмешательство не казалось резким, Мазай будет проводить свою политику в три
этапа:
1.
Установит потолок цены на уровне ,
который выше , но при котором «Зайцы Ltd.» будут производить столько же,
сколько производили бы при .
2.
Снизит потолок до такого уровня ,
при котором оптимальный выпуск «Зайцев Ltd.» максимален.
3.
Наконец, снизит потолок до уровня .
Когда Дед Мазай спросил «Зайцев
Ltd.», выгодно ли им косить трын-траву при цене или лучше уйти с рынка, они ответили
своей знаменитой фразой: «А нам всё равно!».
1.
Какую прибыль получили бы «Зайцы Ltd.», если бы не было Деда
Мазая?
2.
Найдите цены, которые установятся на рынке после каждого этапа
вмешательства. Какую прибыль будут получать «Зайцы Ltd.» при каждой из этих
цен?
3.
Прокомментируйте действия Деда Мазая с точки зрения
общественного благосостояния.
Решение и ответ
Найдем прибыль «Зайцев Ltd.» до
государственного вмешательства:
|
|
Рассмотрим механизм выбора монополистом
объема производства при установке потолка цены . Новая
кривая спроса будет иметь два участка: ниже уровня она останется прежней, а на уровне
станет совершенно неэластичной. Исходя
из этого, левее
будет горизонтальной на уровне
, а правее
останется прежней (жирная линия на рисунке 1).
При каждом значении «Зайцы Ltd.» определяют уровень
выпуска, при котором пересекает
новую .
,
значит, речь идет о долгосрочном периоде. Поскольку при цене фирме безразлично, уйти из отрасли или
остаться, эта цена равна минимуму средних издержек (она получает нулевую
экономическую прибыль при оптимальном выпуске). Очевидно, что оптимальный объем
выпуска в этом случае лежит на горизонтальном участке кривой .
|
|
Какую цену может установить Дед Мазай, чтобы
объем производства тоже был равен 5? Такую, чтобы величина спроса при этой цене
была равна 5.
Осталось найти . Максимальный из
оптимальных объемов производства достигается при установке потолка на уровне
пересечения и
кривой спроса. (Кстати, именно такая цена и такой объем производства сложились
бы на рынке, если бы он был совершенно конкурентен.) Если потолок будет выше
или ниже этого уровня, «Зайцам Ltd.» будет выгодно снизить выпуск.
|
|
Говоря о последствиях действий
Деда Мазая для общества, можно заметить, что установка цен и
целесообразна, так
как снижает уровень цены и увеличивает объем продаж (при ситуация сходна с совершенной
конкуренцией), а снижение цены до вызывает появление
потерь общества от ценового регулирования и появления дефицита трын-травы на
рынке.
Примечание:
Подробно и с картинками поведение
монополиста в условиях ценового регулирования описано в известном учебнике
Роберта Пиндайка и Даниэля Рубинфельда в главе «Рыночная власть: монополия и
монопсония».
Сто фирм в условиях совершенной конкуренции имеют следующую зависимость общих издержек от объёма выпуска:
| Объём выпуска фирмы | 800 | 900 | 1000 | 1100 |
| Общие издержки фирмы, тыс. р. | 40 | 45,5 | 51,6 | 58,2 |
Шкала рыночного спроса показана в следующей таблице:
| Величина рыночного спроса | 80 000 | 90 000 | 100 000 | 110 000 |
| Цена, р. | 70 | 65 | 61 | 58 |
а) Определите рыночную цену.
б) Является ли производство прибыльным? Какую экономическую прибыль (убыток) получает одна фирма?
Решение:
а) В условиях совершенной конкуренции ни одна фирма не может повлиять на цену. Цена складываются под влиянием отраслевого спроса и отраслевого предложения. Найдём рыночное равновесие, при котором Qd = Qотр.
Рассчитаем объём выпуска всей отрасли, Qотр. = N * Qi, а также предельные издержки фирмы.
Для расчёта предельных издержек фирмы воспользуемся формулой:
МС = ΔTC / ΔQ,
где
ΔTC — прирост общих издержек,
ΔQ — прирост объёма выпуска.
Предельные затраты девятисотой единицы будут равны:
МС(900) = (45500 — 40000) / (900 — 800) = 55 и т. д.
Сведём исходные данные и результаты вычислений в одну таблицу.
| Объём выпуска фирмы, Qi | Общие издержки фирмы, TC, р. | Объём выпуска отрасли, Qотр. | Предельные издержки, МСi, р. | Величина рыночного спроса, Qd | Цена, Ррын р. |
| 800 | 40 000 | 80 000 | — | 80 000 | 70 |
| 900 | 45 500 | 90 000 | 55 | 90 000 | 65 |
| 1000 | 51 600 | 100 000 | 61 | 100 000 | 61 |
| 1100 | 58 200 | 110 000 | 66 | 110 000 | 58 |
Целью всех фирм является максимизация прибыли. Условие максимизации прибыли: MR = MC.
В условиях совершенной конкуренции Р = MR. Следовательно, условие максимизации прибыли для совершенного конкурента: P = MC.
Из таблицы видно, что равновесие на рынке, при котором Qd = Qотр наступает при цене равной P = MC = 61 р. При чём при такой цене каждая фирма произведёт 1000 единиц продукции.
б) Оптимальный объём выпуска, при котором прибыль будет максимальна равен 1000 единиц.
Найдём прибыль при Q = 1000 по формуле:
П(1000) = TR — TC = PQ — TC = 61*1000 — 51 600 = 9 400
Производство является прибыльным. Прибыль каждой фирмы равна 9400.
Условие задачи взято из: Мицкевич А.А.
Сборник заданий по экономике : Для учащихся 9—11 классов: В 3-х книгах .- Ч. 1: Задачник по микроэкономике .- 3-е изд., переработанное .- М. : Вита-Пресс, 2001.- 462 с.