Центробежный момент инерции уголка
мм4
Центробежный
момент инерции всего сечения относительно
осей ZcYc:
Iyczc=(300669+(-10)∙(-99)∙1390)+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)
Iyczc=
19761573
мм4
Для
проверки правильности выбора знака
угла
следует разбить уголок на два прямоугольника
(рис.3) пересчитать и сравнить их
расхождение в центробежном моменте
инерции. Если расхождение велико это
означает, что угол выбран не с тем знаком.
рис.3
Центробежный
момент для всего сечения с уголком,
разделенным на два простых прямоугольника
равен:
F1x=560
мм2
– площадь поперечного сечения
F1xx=880
мм2
– площадь поперечного сечения
a1x=8.4
мм – координата от оси Zc1x
до Zс
b1x=-131
мм – координата от оси Yc1x
до Yс
a1xx=-76
мм – координата от оси Zc1xx
до Zс
b1xx=-22.5
мм – координата от оси Yc1xx
до Yс
Iyczc=(Iyc1zc1+((a1x∙
b1x∙F1x)+(a1xx∙
b1xx∙F1xx)))+(Iyc2zc2+a2∙
b2∙F2)+(
Iyc3zc3+a3∙
b3∙F3)
Iyczc=(0+((8.4)∙(-131)∙560)+((-76)∙(-22.5)∙880))+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)
Iyczc=19785224
мм4
Как видно из расчетов центробежные
моменты инерции вычисленные разными
способами расходятся в значениях не
более чем на 0.12%. Это означает, что знак
угла α выбран правильно.
3. Нахождение положения главных осей и моментов инерции:
Угол
наклона главных осей инерции, проходящих
через центр тяжести составного сечения,
к центральным осям инерции ZcYcопределим по формуле:
Так
как угол >0, то
откладываем его по осиZпротив
движения часовой стрелки.
Определение
величин главных моментов инерции Iuи Ivсечения:
Верхние знаки следует брать при Izc
> Iyc , а нижниеIzc < Iyc
=69204276мм4
=29060227 мм4
Проверка
IU + IV = Izc
+ Iyc
69204276+29060227 = 52648839+4561566498264503=98264503
Главная
центральная ось Uполучается на
чертеже поворотом осиZcпротив часовой стрелки, так как>0
и осьUбудет являться осью относительно
которой момент инерции будет максимальным.
Раздел II
ЦЕНТРАЛЬНОЕ
РАСТЯЖЕНИЕ (СЖАТИЕ ) СТЕРЖНЕЙ .
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ.
Основные понятия и зависимости.
Центральным
растяжением (сжатием)
называется такой вид деформации, при
котором в поперечных сечениях стержня
возникает только нормальная (продольная)
сила N
остальные силовые факторы равны нулю.
В дальнейшем центральное растяжение
(сжатие) коротко называется просто
растяжением (сжатием). Нормальная
(продольная) сила
в поперечном сечении представляет собой
равнодействующую нормальных внутренних
сил распределенных по площади поперечного
сечения и связана с нормальными
напряжениямив этом сечении зависимостью:
.
Принято считатьположительной
нормальную силу, вызывающую растяжение,
отрицательной нормальную силу, вызывающую
сжатие.
Нормальные силы в поперечных сечениях
определяют методом сечений. Считается
что при растяжении (сжатии) справедлива
гипотеза плоских сечений (гипотеза
Бернулли) следовательно, нормальные
напряжения в поперечных сечениях стержня
распределены равномерно и
,
где—
площадь поперечного сечения. Положительным
считается растягивающее нормальное
напряжение. Согласно гипотезе плоских
сечений материал стержня при растяжении
(сжатии) находится в линейном напряженном
состоянии. На основании закона Гука
относительное удлинение бесконечно
малого участка стержня:,
где модуль продольной упругости
материала (модуль Юнга). Полное удлинение
стержня в общем случае, когда нормальная
сила и площадь поперечного сечения
меняются по длине: ,
где —
длина стержня. В частном случае, когда
нормальная сила и площадь по длине
постоянны: .
Для ступенчатого стержня полное
удлинение вычисляется как сумма удлинений
его участков: ,
где
соответственно длина, площадь поперечного
сечения, нормальная сила на i
— том участке.
Растяжение
(сжатие) сопровождается изменением
поперечных размеров стержня. Между
относительной поперечной —
и относительной продольной —
деформациями при растяжении (сжатии)
существует связь ,
где
— коэффициент Пуассона (коэффициент
поперечной деформации) является
константой материала. Знак «-» в уравнении
отражает тот факт, что
и
всегда имеют противоположные знаки.
Условия
прочности
для стержней работающих на растяжение
сжатие записываются для опасных сечений
стержня, в которых действуют наибольшие
по величине растягивающие и сжимающие
напряжения. В случае, когда материал
стержня имеет одинаковую прочность на
растяжение и сжатие достаточно одного
условия прочности
,
где допускаемое напряжение для материала
стержня. Если материал стержня имеет
разную прочность при растяжении и сжатии
необходимо выполнение одновременно
двух условий прочности:,
,
где,
—
допускаемые напряжения для материала
стержня соответственно на растяжение
и сжатие.
Статически
неопределимыми системами
называются такие системы, в которых
количество неизвестных сил (реакций,
внутренних силовых факторов) превышает
число уравнений равновесия. Степенью
статической неопределимости n
называется разность между r
— количеством неизвестных и u
— числом уравнений статики: .
В статически неопределимых задачах не
удается определить силовые факторы из
условий равновесия и прежде чем решать
задачи прочности и жесткости необходимо
раскрыть статическую неопределимость.
Общий принцип
раскрытия статической неопределимости
заключается в том, что в дополнении к
имеющимся уравнениям равновесия всегда
можно составить n
условий совместности деформаций
(совместности перемещений). Условия
совместности деформаций (перемещений)
связывают между собой деформации
отдельных элементов системы или
перемещения ее точек. Затем в условиях
совместности деформации (или перемещения)
выражаются через внутренние усилия,
которые в свою очередь могут быть
выражены методом сечений через внешние
силы. После решения условий совместности
вместе с уравнениями равновесия
относительно неизвестных усилий,
статическая неопределимость будет
раскрыта.
Для
реальных стержней на основании принципа
Сен-Венана гипотеза плоских сечений
справедлива лишь вдали от мест приложения
внешних сосредоточенных нагрузок и
мест изменения размеров и формы
поперечного сечения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
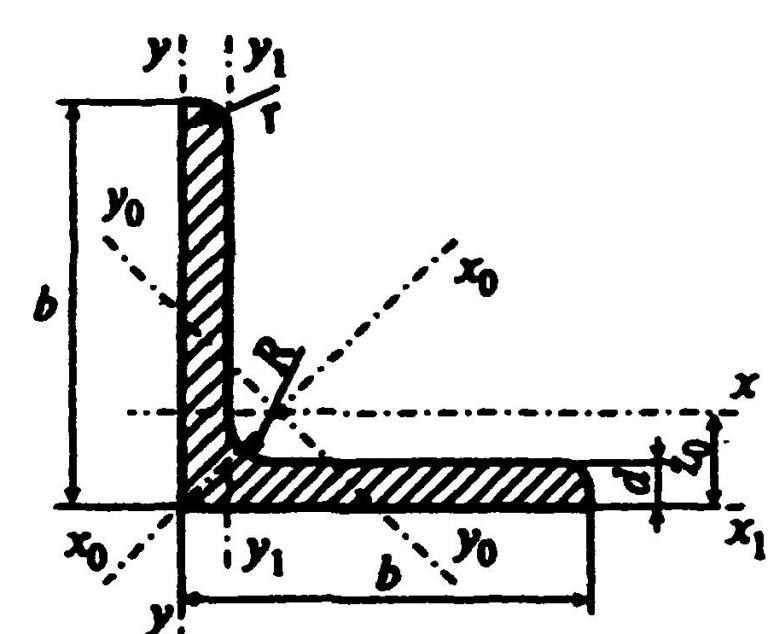
Решение задач по сопромату. Сортамент фасонных профилей: уголок
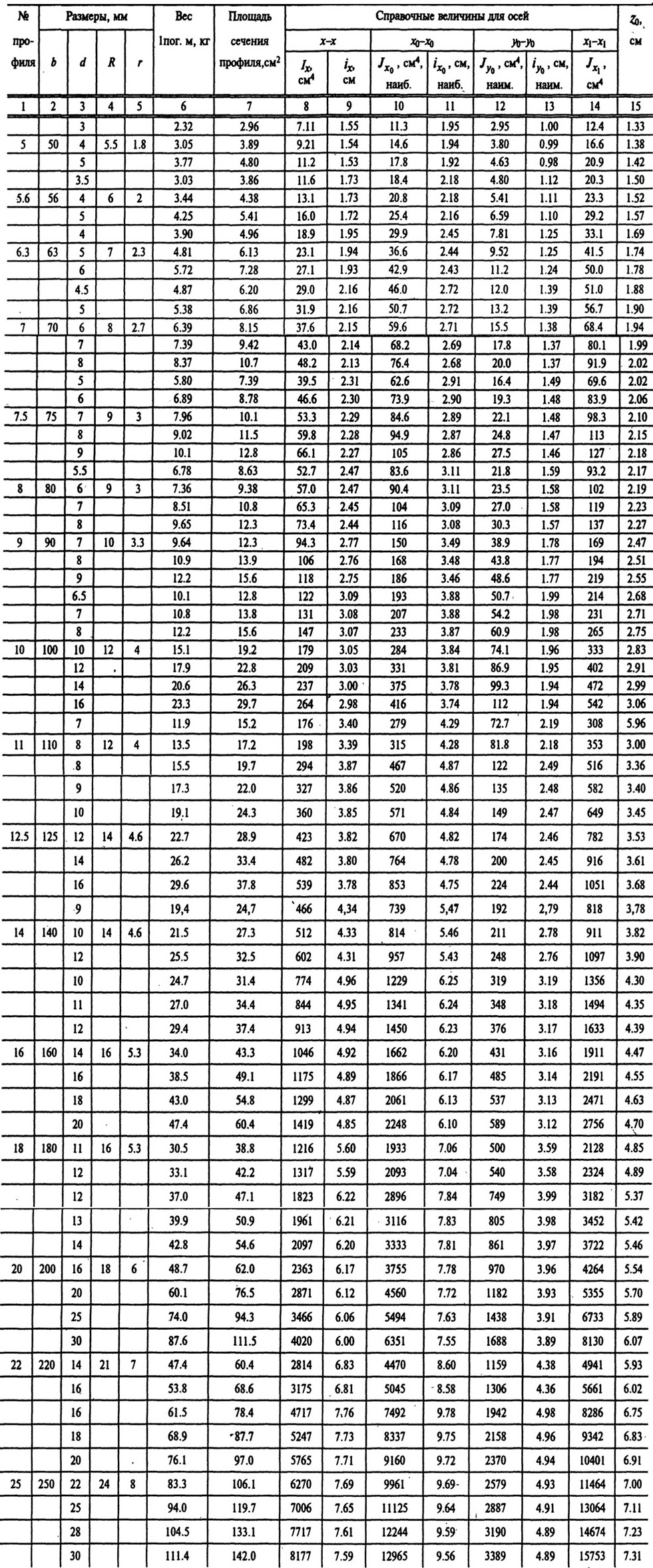
Сортамент уголков / Угольники равнобокие. Сталь прокатная (по ГОСТ 8509-57)
В результате расчетов на прочность и жесткость необходимо принять решение о выборе профиля – номера уголка.
Таблица параметров уголков применяются при решении задач на внецентренное сжатие, определении геометрических характеристик и решении множества других практических задач, где необходимо выбрать уголок, параметры которого удовлетворяют условиям прочности и жесткости. Сортамент уголков разнообразен (в 2-3 раза больше вариантов, чем у швеллеров и двутавров), поэтому принять конструкторское решение будет не так сложно. Всегда нужно стараться подобрать как можно меньший номер уголка, чтобы уменьшить массу и размеры, но при этом оговоренные условия должны соблюдаться. Если характеристики уголка уступают расчетным меньше, чем на 5% (например, осевой момент инерции относительно одной из главных центральных осей), то принимают соответствующий номер уголка, если больше 5%, то принимают следующий за ним номер уголка.
На чертеже уголка (изображение выше) показаны основные геометрические размеры, которые отражены в таблице сортамента уголков. Кроме геометрических параметров сортамент уголков содержит:
геометрические характеристики:
- осевые моменты инерции уголка относительно горизонтальных и вертикальных осей
- проходящих через центр тяжести
- совпадающих с контуром профиля
- радиус инерции уголка относительно главных центральных осей
- вес погонного метра уголка
- площадь сечения профиля уголка
Подсказка: Центробежный момент инерции уголка равен 0 относительно главных центральных осей (которые на чертеже изображены под углом 45°). Поэтому при решении практических задач удобно работать именно с этими осями.
Зачем нужен момент инерции сечения
Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.
В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.
Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.
Что такое момент инерции сечения
Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.
Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.
Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.
Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.
Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см4, м4, мм4). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см4». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм4». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, Ix, Iy). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, Wx, Wy).
Что такое главные оси
Главные оси инерции — оси, относительно которых центробежный момент инерции равен нулю.
Главные центральные оси — главные оси, проходящие через центр тяжести сечения.
Как найти момент инерции сечения
При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.
Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.
В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.
Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):
При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.
Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.
При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.
Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.
Размерность моментов сопротивления – единица длины в кубе (например, см3, м3, мм3).
Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.
Источники:
- Н.М. Беляев. Сопротивление материалов.
- Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
- А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
- reshusam.ucoz.ru — Примеры определения моментов инерции сечений.
Дополнительно на Геноне:
- Что такое сопромат